考虑挡墙厚度基坑稳态渗流场的解析解

余俊; 李东凯; 胡钟伟; 郑靖凡

doi:10.11779/CJGE20220357

考虑挡墙厚度基坑稳态渗流场的解析解 English Version

中南大学土木工程学院, 湖南长沙 410075

基金项目:

国家自然科学基金项目 52078496

详细信息

作者简介:
余俊(1978—)，男，博士，副教授，主要从事隧道与地下工程方面的教学和研究工作。E-mail: yujun@csu.edu.cn

中图分类号: TU463
计量
- 文章访问数: 345
- HTML全文浏览量: 56
- PDF下载量: 116
出版历程
- 收稿日期: 2022-03-24
- 网络出版日期: 2023-02-19
- 刊出日期: 2023-06-30

Analytical solution of steady seepage field of foundation pit considering thickness of retaining wall

School of Civil Engineering, Central South University, Changsha 410075, China

摘要

摘要: 对悬挂式考虑厚度挡墙支护下的各向同性土层中基坑的二维稳态渗流场进行了解析研究。根据对称性取基坑半截面，将周围土层划分为5个规则的区域，利用叠加法和分离变量法将5个区域内的水头分布表示为级数解的形式，结合区域间的连续条件得出基坑周围渗流场的显式解析解。将本文解析解得到的水头计算结果和挡墙上水压力计算结果与有限元软件进行对比，结果吻合较好，验证了本文解析解的正确性。将一维渗流、二维渗流中流网法以及不考虑挡墙厚度情况下和考虑挡墙厚度情况下本文解析解计算得到的挡墙上的水压力与有限元解进行对比分析，发现考虑挡墙厚度情况下本文解析解的计算结果最为精确，指出了其他几种解法的误差。最后对基坑渗流场影响因素进行了参数分析，基坑内侧宽度、不透水层顶面至挡墙底部距离、坑内水位、挡墙厚度等因素对基坑水头分布有较大影响，随着挡墙厚度增大，最大水力梯度降到挡墙底部，基坑外侧渗流场远场水头增大，挡墙底部水头明显减小。
- 二维稳态渗流 /
- 渗透各向同性 /
- 水压力 /
- 显式解析解 /
- 挡墙 /
- 总水头分布
Abstract: The two-dimensional steady-state seepage field of a foundation pit in an isotropic soil layer supported by a suspended retaining wall considering thickness is analytically studied. The distribution of water head in the five regions is expressed in the form of a graded solution by using the superposition method and the method of separation of variables, and the explicit analytical solution of the seepage field around the pit is derived by combining the continuity conditions between the regions. Compared with the angle-preserving transform solution, this analytical solution can directly solve the values of water head at any point inside and outside the pit without generating singularities. The correctness of the analytical solution is verified by comparing with the calculated results of the water head obtained from the finite element software. The distribution of total water head obtained from the analytical solution of this paper is curved. The factors such as the inner width of the pit, the distance from the top of the impermeable layer to the bottom of the retaining wall, the water level in the pit and the thickness of the retaining wall have a great influence on the distribution of water head of the pit. As the thickness of the retaining wall increases, the water heads in the far field of the seepage field of the pit and the bottom of the retaining wall change more, and the maximum hydraulic gradient drops to the bottom of the retaining wall. Compared with the flow network methods in one-dimensional seepage and two-dimensional seepage and the proposed analytical solution without considering the thickness of the retaining wall, it is more accurate to calculate the water pressure in the design by using the analytical solution of two-dimensional seepage considering the thickness of the retaining wall.
- two-dimensional steady seepage /
- permeability isotropy /
- water pressure /
- explicit analytic solution /
- retaining wall /
- distribution of total water head

HTML全文

0. 引言

近年来基坑工程难度越来越大，工程事故发生率也越来越高，地下水是致使基坑发生事故的重要因素之一，地下水不仅会引起土体应力状态的变化和围护结构水土压力的变化^[1-2]，当地下水渗流无法控制时还会引起基坑中管涌、流土等事故。据统计地下水导致的基坑工程事故占22%^[3]。悬挂式止水帷幕在基坑的止水、降水施工中广泛应用，并且在一些工程中取得良好效果^[4]，因此对有悬挂式挡墙的基坑中渗流场的研究非常重要。

目前基坑渗流场的研究中，主要包括数值法和解析法。采用数值法对基坑渗流场的研究已经较为成熟，大多采用有限元、有限差分法对基坑中的渗流进行分析，得到比较精确的水头解^[5-8]。相比于数值法，解析法能够直观地通过一个函数表达式将各影响因素表达出来，方便进一步研究地下水渗流规律。Li等^[9]根据一维固结理论得到基坑负超孔隙水压力和有效应力的一维解析公式。相对于一维模型，二维渗流模型更贴近实际工程。Bereslavski^[10]采用保角变换的方法，将复杂边界简化得到单板桩且一侧水位是自由水位时的渗流场隐式解。Harr^[11]为求解二维基坑在稳态情况下的渗流问题，利用保角变换求解的方法给出了一类解答。Xie等^[12]利用Hankel变换，得到承压含水层上表面圆形水源引起水流不连续边界条件问题的解析解。Fox等^[13]采用Schwarz Chracffell变换对Malhorta解进行改写得出基坑内外恒定水头差情况下二维渗流解析解，但在φ=1， ${\psi _1}$ =0情况下，这个基坑外侧挡墙角点并不是连续有限的。于佳卉^[14]通过多次应用保角映射建立位置与势函数流函数之间的关系式，并通过逆推解析解的方法解决模型边界各点的势函数、流函数确定问题，进而得出承压含水层基坑的渗流场分布隐式解。黄大中等^[15]采用Fourier变换推导出渗透各向异性土层中基坑二维稳定渗流的半解析隐式解。以上研究都假定基坑中挡墙厚度为零，未考虑挡墙厚度对基坑渗流的影响。应宏伟等^[16]通过Laplace变换、Fourier变换与逆变换给出考虑重力式挡墙厚度的二维基坑在地下水位波动情况下基坑周围孔压响应的半解析隐式解。但这些解析研究大多通过保角变换、积分变换、离散近似等方法求得隐式解或半解析解。

本文将带厚度挡墙基坑周围渗流场分解为5个矩形区域，利用叠加法和分离变量法将5个区域的水头分布表示成级数解的形式，再通过各区域间的边界条件和连续条件求解出带厚度挡墙基坑稳态渗流场的显式解。相对于保角变换求解方法，此解析解可以求解出基坑内外任意一点的水头值，不会产生奇异点。将解析解的水头计算结果和水压力计算结果与有限元软件PLAXIS的计算结果进行比较，对解析解的正确性进行验证。将一维渗流情况下、不考虑挡墙厚度时和考虑挡墙厚度时本文解、流网法、不考虑挡墙厚度时和考虑挡墙厚度时有限元软件PLAXIS的水压力计算结果进行对比分析。最后根据解析解，分析基坑宽度、悬挂式挡墙厚度、挡墙底至不透水层的距离等因素对基坑周围渗流场水头分布的影响。

1. 考虑挡墙厚度基坑二维渗流模型

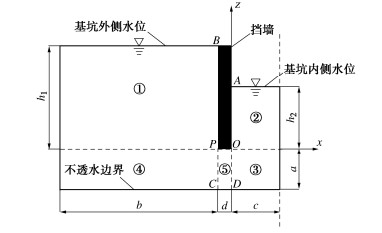
当基坑的长度远大于宽度时，与宽度平行的截面的渗流场可以近似为平面渗流。根据基坑渗流的对称性，取一半截面分析，如图 1所示。

图 1 基坑二维渗流模型

Figure 1. Model for two-dimensional seepage around foundation pit

下载: 全尺寸图片幻灯片

假定不透水层顶部上方的土层土质均匀，土体渗流各向同性，悬挂式带厚度挡墙不透水，基坑外侧为潜水条件且无穷大，可近似视为不透水；基坑内侧由于对称性，可视为不透水。基坑外侧挡墙顶部水位为h₁, 基坑内侧坑底水位为h₂，基坑外侧宽度为b，基坑内侧半宽度为c，悬挂式挡墙厚度为d，悬挂式带厚度挡墙底部到不透水层顶部的距离为a。

由于基坑外侧区域BPC、内侧区域AOD等边界条件是不连续的，不能直接应用分离变量法来进行求解，故根据叠加原理将渗流场分为几个区域进行分析求解。如图 1所示，BP为不透水边界，PC为透水边界，基坑外侧区域边界BPC是不连续的，故将基坑外侧分为区域①和区域④两个边界条件连续的区域，同理基坑内侧分为区域②和区域③两个区域，将剩下区域计为区域⑤。

假定土体中渗流符合达西定律，则5个区域中的渗流满足方程：

$\frac{{{\partial ^2}{H_i}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{H_i}}}{{\partial {z^2}}} = 0{\text{ }}(i = 1, 2, 3, 4, 5)。$

(1)

式中，H₁，H₂，H₃，H₄和H₅分别为区域①、区域②、区域③、区域④和区域⑤的总水头。

根据基坑边界条件和区域间连续条件得到各区域边界条件如下。

区域①边界条件：上边界(z=h₁)，H₁=h₁；外边界(x=-b-d)， $\partial {H_1}/\partial x = 0$ ; 内边界(x=-d)， $\partial {H_1}/\partial x = 0$ 。

区域②边界条件：上边界(z=h₂)，H₂=h₂；内边界(x=c)， $\partial {H_2}/\partial x = 0$ ；外边界(x=0)， $\partial {H_2}/\partial x = 0$ 。

区域③边界条件：下边界(z=-a)， $\partial {H_3}/\partial z = 0$ ；内边界(x=c)， $\partial {H_3}/\partial x = 0$ 。

区域④边界条件：下边界(z=-a)， $\partial {H_4}/\partial z = 0$ ；外边界(x=-b-d)， $\partial {H_4}/\partial x = 0$ 。

区域⑤边界条件：上边界(z=0)， $\partial {H_5}/\partial z = 0$ ；下边界(z=-a)， $\partial {H_5}/\partial z = 0$ 。

区域①和区域④的连续条件为

$\left\{ \begin{array}{l} {H_1}\left| {_{z = 0}} \right. = {H_4}\left| {_{z = 0}} \right.{\text{ (}} - b - d \leqslant x < - d) \hfill \\ \frac{{\partial {H_1}}}{{\partial z}}\left| {_{z = 0}} \right. = \frac{{\partial {H_4}}}{{\partial z}}\left| {_{z = 0}} \right.{\text{ (}} - b - d \leqslant x < - d) \hfill \\ \end{array} \right. 。$

(2)

区域②和区域③的连续条件为

$\left\{ \begin{array}{l} {H_2}\left| {_{z = 0}} \right. = {H_3}\left| {_{z = 0}} \right.{\text{ (}}0 \leqslant x < c) \hfill \\ \frac{{\partial {H_2}}}{{\partial z}}\left| {_{z = 0}} \right. = \frac{{\partial {H_3}}}{{\partial z}}\left| {_{z = 0}} \right.{\text{ }}(0 \leqslant x < c) \hfill \\ \end{array} \right. 。$

(3)

区域③和区域⑤的连续条件为

$\{\begin{array}{l}{H}_{3}|{}_{x=0}={H}_{5}|{}_{x=0}\text{ (}-a\le z < 0)\\ \frac{\partial {H}_{3}}{\partial x}|{}_{x=0}=\frac{\partial {H}_{5}}{\partial x}|{}_{x=0}\text{ (}-a\le z < 0)\end{array} 。$

(4)

区域④和区域⑤的连续条件为

$\left\{ \begin{array}{l} {H_4}\left| {_{x = - d}} \right. = {H_5}\left| {_{x = - d}} \right.{\text{ (}} - a \leqslant z < 0) \hfill \\ \frac{{\partial {H_4}}}{{\partial x}}\left| {_{x = - d}} \right. = \frac{{\partial {H_5}}}{{\partial x}}\left| {_{x = - d}} \right.{\text{ (}} - a \leqslant z < 0) \hfill \\ \end{array} \right. 。$

(5)

2. 模型求解

根据各区域边界条件，区域①、区域②、区域③、区域④和区域⑤利用叠加法和分离变量法将总水头写成级数和的形式。

区域①的左右边界都为不透水边界即 $\partial {H_1}/$ $\partial x = 0$ 。根据叠加法可以将区域①的边界条件写为

${\varPhi _1} = \varPhi _1^1 + \varPhi _1^2。$

(6)

式中： $\varPhi _1^1$ 对应于区域①左右边界为不透水边界，上边界水头为h₁，下边界水头为0的条件； $\varPhi _1^2$ 对应于区域①左右边界为不透水边界，上边界水头为0的条件。

基于分离变量法^[17]，当矩形区域左右边界为不透水边界时，拉普拉斯方程的通解可以写为

$H(x, z) = {a_0}z + {b_0} + \\ \sum\limits_{n = 1}^\infty {({A_{0n}}\cosh {k_n}z + {B_{0n}}\sinh {k_n}z)\cos {k_n}(x + d)} \text{，}$

(7)

式中，a₀，b₀，A_0n，B_0n为待定常数。

对于边界条件 $\varPhi _1^1$ ，将上边界水头为h₁，下边界水头为0的边界条件代入由分离变量法求解的通式(7)，可以解出水头表达式为

$H_1^1(x, z) = z。$

(8)

对于边界条件 $\varPhi _1^2$ ，将上边界水头为0的边界条件代入由分离变量法求解的通式(7)，可以解出水头表达式为

$H_1^2(x, z) = {A_{10}}{\text{(}}z - {h_1}{\text{)}} +\\ \sum\limits_{n = 1}^\infty {{A_n}\sinh {k_n}(z - {h_1})} \cos {k_n}(x + d) 。$

(9)

则区域①的总水头解由叠加法可以表示为式(8)，(9)相加：

${H_1}(x, z) = z + {A_{10}}(z - {h_1}) + \\ \sum\limits_{n = 1}^\infty {{A_n}\sinh {k_n}(z - {h_1})} \cos {k_n}(x + d)\text{，}$

(10)

式中，A₁₀，A_n为水头解中待求参数， ${k_n}$ =nπ/b，n=1，2，3，…。

区域②边界条件与区域①边界条件类似，采用与区域①相同的做法可将区域②的总水头解表示为

$\begin{array}{l} {H_2}(x, z) = z + {B_{10}}(z - {h_2}) + \hfill \\ \sum\limits_{m = 1}^\infty {{B_m}\sinh {k_m}(z - {h_2})\cos {k_m}x} \hfill \\ \end{array} 。$

(11)

式中，B₁₀，B_m为水头解中待求参数，k_m=mπ/c，m=1，2，3，…。

区域③右边界为不透水边界，即 $\partial {H_3}/\partial x = 0$ ，下边界为不透水边界，即 $\partial {H_3}/\partial z = 0$ 。根据叠加法可以将区域③的边界条件写为

${\varPhi _3} = \varPhi _3^1 + \varPhi _3^2。$

(12)

式中： $\varPhi _3^1$ 表示区域③左右边界为不透水边界，下边界为不透水边界； $\varPhi _3^2$ 表示区域③右边界为不透水边界，上边界水头为0，下边界为不透水边界。

相同于区域①的解法，对于边界条件 $\varPhi _3^1$ 由分离变量法可以写出水头表达式为

$H_3^1(x, z) = C_{10}^1 + \sum\limits_{m = 1}^\infty {{E_m}\cosh {k_m}(z + a)\cos {k_m}x} 。$

(13)

对于边界条件 $\varPhi _3^2$ 由分离变量法可以写出水头表达式为

$H_3^2(x, z) = C_{10}^2 + \sum\limits_{i = 1}^\infty {{C_i}\cosh {k_i}(x - c)\sin {k_i}z} 。$

(14)

则区域③的总水头解由叠加法可以表示为式(13)，(14)相加并整合常数项得到：

${H_3}(x, z) = {C_{10}} + \sum\limits_{i = 1}^\infty {{C_i}\cosh {k_i}(x - c)\sin {k_i}z} +\\ \sum\limits_{m = 1}^\infty {{E_m}\cosh {k_m}(z + a)\cos {k_m}x} 。$

(15)

式中，C₁₀，C_i，E_m为水头解中待求参数，k_m=mπ/c，k_i=(2i-1)π/2a，m，i=1，2，3，…。

区域④边界条件与区域③边界条件类似，采用与区域③相同的做法可将区域④的总水头解表示为

${H_4}(x, z) = {D_{10}} + \sum\limits_{i = 1}^\infty {{D_i}\cosh {k_i}(x + b + d)\sin {k_i}z} + \\ \sum\limits_{n = 1}^\infty {{F_n}\cosh {k_n}(z + a)\cos {k_n}(x + d)} 。$

(16)

式中，D₁₀，D_i，F_n为水头解中待求参数，k_n=nπ/b，k_i=(2i-1)π/2a，n，i=1，2，3，…。

区域⑤上下边界为不透水边界即 $\partial {H_5}/\partial z = 0$ ，根据叠加法可以将区域⑤的边界条件写为

${\varPhi _5} = \varPhi _5^1 + \varPhi _5^2。$

(17)

式中： $\varPhi _5^1$ 表示区域⑤上下边界为不透水边界，左边界导数为常数； $\varPhi _5^2$ 表示区域⑤上下边界为不透水边界，右边界导数为常数。

相同于区域①的解法，对于边界条件 $\varPhi _5^1$ 由分离变量法可以写出水头表达式为

$H_5^1{\text{(}}x, z{\text{)}} = H_{10}^1x + G_{10}^1 + \sum\limits_{j = 1}^\infty {{H_j}\cosh {k_j}(x + d)\cos {k_j}z} 。$

(18)

对于边界条件 $\varPhi _5^2$ 由分离变量法可以写出水头表达式为

$H_5^2(x, z) = H_{10}^2x + G_{10}^2 + \sum\limits_{j = 1}^\infty {{G_j}\cosh {k_j}x\cos {k_j}z} 。$

(19)

则区域⑤的总水头解由叠加法可以通过式(18)和式(19)相加并整合常数项得到

${H_5}(x, z) = {H_{10}}x + {G_{10}} +\\ \sum\limits_{j = 1}^\infty {({G_j}\cosh {k_j}x} + {H_j}\sinh {k_j}x)\cos {k_j}z。$

(20)

式中，H₁₀，G₁₀，G_j，H_j为水头解中待求参数，k_j=jπ/a，j=1，2，3，…。

根据区域①和区域④的连续条件式(2)可得

$- {A_{10}}{h_1} - \sum\limits_{n = 1}^\infty {{A_n}\sinh {k_n}{h_1}\cos {k_n}(x + d)}\\ = {D_{10}} + \sum\limits_{n = 1}^\infty {{F_n}\cosh {k_n}a\cos {k_n}(x + d)} \text{，}$

(21)

$\begin{array}{l} 1 + {A_{10}} + \sum\limits_{n = 1}^\infty {{A_n}{k_n}\cosh {k_n}{h_1}\cos {k_n}(x + d)} \\ = \sum\limits_{i = 1}^\infty {{D_i}{k_i}\cosh {k_i}(x + b + d)} + \\ \end{array} \\ \sum\limits_{n = 1}^\infty {{F_n}{k_n}\sinh {k_n}a\cos {k_n}(x + d)} 。$

(22)

根据区域②和区域③的连续条件式(3)可得

$- {B_{10}}{h_2} - \sum\limits_{m = 1}^\infty {{B_m}\sinh {k_m}{h_2}\cos {k_m}x} \\ = {C_{10}} + \sum\limits_{m = 1}^\infty {{E_m}\cosh {k_m}a\cos {k_m}x} \text{，}$

(23)

$1 + {B_{10}} + \sum\limits_{m = 1}^\infty {{B_m}{k_m}\cosh {k_m}{h_2}\cos {k_m}x} \\ = \sum\limits_{i = 1}^\infty {{C_i}{k_i}\cosh {k_i}(x - c)} + \sum\limits_{m = 1}^\infty {{E_m}{k_m}\sinh {k_m}a\cos {k_m}x} 。$

(24)

根据区域③和区域⑤的连续条件式(4)可得

${C_{10}} + \sum\limits_{i = 1}^\infty {{C_i}\cosh {k_i}c\sin {k_i}z} + \sum\limits_{m = 1}^\infty {{E_m}\cosh {k_m}(z + a)}\\ = {G_{10}} + \sum\limits_{j = 1}^\infty {{G_j}\cos {k_j}z} \text{，}$

(25)

$- \sum\limits_{i = 1}^\infty {{C_i}{k_i}\sinh {k_i}c\sin {k_i}z} = {H_{10}} + \sum\limits_{j = 1}^\infty {{H_j}{k_j}\cos {k_j}z} 。$

(26)

根据区域④和区域⑤的连续条件式(5)可得

${D_{10}} + \sum\limits_{i = 1}^\infty {{D_i}\cosh {k_i}b\sin {k_i}z} + \sum\limits_{n = 1}^\infty {{F_n}\cosh {k_n}(z + a)}\\ =-{H}_{10}d+{G}_{10}+{\displaystyle \sum _{j=1}^{\infty }({G}_{j}\mathrm{cosh}{k}_{j}d-{H}_{j}\mathrm{sinh}{k}_{j}d)\mathrm{cos}{k}_{j}z\text{ }}\text{，}$

(27)

$\sum\limits_{i = 1}^\infty {{D_i}{k_i}\sinh {k_i}b\sin {k_i}z}\\ ={H}_{10}+{\displaystyle \sum _{j=1}^{\infty }(-{G}_{j}{k}_{j}\mathrm{sinh}{k}_{j}d+{H}_{j}{k}_{j}\mathrm{cosh}{k}_{j}d)\mathrm{cos}{k}_{j}z\text{ }}。$

(28)

整理式(21)，(23)可得

$- {A_{10}}{h_1} - {D_{10}} \\ = \sum\limits_{n = 1}^\infty {({A_n}\sinh {k_n}{h_1} + {F_n}\cosh {k_n}a)\cos {k_n}(x + d)} \text{，}$

(29)

$- {B_{10}}{h_2} - {C_{10}} = \sum\limits_{m = 1}^\infty {({B_m}\sinh {k_m}{h_2} + {E_m}\cosh {k_m}a)\cos {k_m}x} 。$

(30)

根据式(29)，(30)，应用傅里叶级数的性质可得

${D_{10}} = - {A_{10}}{h_1}\text{，}$

(31)

${C_{10}} = - {B_{10}}{h_2}\text{，}$

(32)

${F_n} = - \frac{{\sinh {k_n}{h_1}}}{{\cosh {k_n}a}}{A_n}\text{，}$

(33)

${E_m} = - \frac{{\sinh {k_m}{h_2}}}{{\cosh {k_m}a}}{B_m}。$

(34)

将C₁₀，D₁₀，E_m，F_n代入式(22)，(24)~(28)得

$1 + {A_{10}} + \sum\limits_{n = 1}^\infty {{A_n}{k_n}\frac{{\cosh {k_n}({h_1} + a)}}{{\cosh {k_n}a}}\cos {k_n}(x + d)} - \\ \sum\limits_{i = 1}^\infty {{D_i}{k_i}\cosh {k_i}(x + b + d)} = 0 。$

(35)

$1 + {B_{10}} + \sum\limits_{m = 1}^\infty {{B_m}{k_m}\frac{{\cosh {k_m}({h_2} + a)}}{{\cosh {k_m}a}}\cos {k_m}x} - \\ \sum\limits_{i = 1}^\infty {{C_i}{k_i}\cosh {k_i}(x - c)} = 0 。$

(36)

$- {B_{10}}{h_2} + \sum\limits_{i = 1}^\infty {{C_i}\cosh {k_i}c\sin {k_i}z} - \\ \sum\limits_{m = 1}^\infty {{B_m}\frac{{\sinh {k_m}{h_2}}}{{\cosh {k_m}a}}\cosh {k_m}(z + a)} - {G_{10}} - \sum\limits_{j = 1}^\infty {{G_j}\cos {k_j}z} = 0 。$

(37)

$\sum\limits_{i = 1}^\infty {{C_i}{k_i}\sinh {k_i}c\sin {k_i}z} + {H_{10}} + \sum\limits_{j = 1}^\infty {{H_j}{k_j}\cos {k_j}z} = 0 。$

(38)

$\begin{array}{l} - {A_{10}}{h_1} + \sum\limits_{i = 1}^\infty {{D_i}\cosh {k_i}b\sin {k_i}z} - \hfill \\ \sum\limits_{n = 1}^\infty {{A_n}\frac{{\sinh {k_n}{h_1}}}{{\cosh {k_n}a}}\cosh {k_n}(z + a)} + {H_{10}}d - {G_{10}} - \hfill \\ \end{array}\\ \sum\limits_{j = 1}^\infty {({G_j}\cosh {k_j}d - {H_j}\sinh {k_j}d)\cos {k_j}z} = 0 。$

(39)

$\sum\limits_{i = 1}^\infty {{D_i}{k_i}\sinh {k_i}b\sin {k_i}z} - {H_{10}} -\\ \sum\limits_{j = 1}^\infty {( - {G_j}{k_j}\sinh {k_j}d + {H_j}{k_j}\cosh {k_j}d)\cos {k_j}z} = 0 。$

(40)

根据式(35)~(37)，(40)由傅里叶级数的性质确定常数项A₁₀，B₁₀，G₁₀，H₁₀：

${A_{10}} - \frac{1}{b}\sum\limits_{i = 1}^\infty {{D_i}\sinh {k_i}b} = - 1 \text{，}$

(41)

${B_{10}} - \frac{1}{c}\sum\limits_{i = 1}^\infty {{C_i}\sinh {k_i}c} = - 1 \text{，}$

(42)

${B_{10}}{h_2} + \sum\limits_{i = 1}^\infty {\frac{1}{{a{k_i}}}{C_i}\cosh {k_i}c} +\\ \sum\limits_{n = 1}^\infty {\frac{1}{{a{k_m}}}{B_m}} \frac{{\sinh {k_m}{h_2}\sinh {k_m}a}}{{\cosh {k_m}a}} + {G_{10}} = 0 \text{，}$

(43)

${H_{10}} = - \frac{1}{a}\sum\limits_{i = 1}^\infty {{D_i}\sinh {k_i}b} 。$

(44)

将式(35)~(40)两边分别乘以cosk_n(x+d)，cosk_mx，cosk_jz，sink_iz，sink_iz，cosk_jz，并分别在区间[-b-d，-d]，[0，c]，[-a，0]，[-a，0]，[-a，0]，[-a，0]上积分，则可得到

$\frac{b}{2}{A_n}{k_n}\frac{{\cosh {k_n}({h_1} + a)}}{{\cosh {k_n}a}} - \sum\limits_{i = 1}^\infty {{D_i}\sinh {k_i}b\frac{{k_i^2}}{{k_i^2 + k_n^2}}} = 0 \text{，}$

(45)

$\frac{c}{2}{B_m}{k_m}\frac{{\cosh {k_m}({h_2} + a)}}{{\cosh {k_m}a}} - \sum\limits_{i = 1}^\infty {{C_i}\sinh {k_i}c\frac{{k_i^2}}{{k_i^2 + k_m^2}}} = 0 \text{，}$

(46)

$\left\{ \begin{array}{l}-{\displaystyle \sum _{i=1}^{\infty }{C}_{i}\mathrm{cosh}{k}_{i}c\frac{{k}_{i}}{{k}_{i}^{2}-{k}_{j}^{2}}-{\displaystyle \sum _{m=1}^{\infty }{B}_{m}\frac{\mathrm{sinh}{k}_{m}{h}_{2}\mathrm{sinh}{k}_{m}a}{\mathrm{cosh}{k}_{m}a}}}\cdot \\ \frac{{k}_{m}}{{k}_{m}^{2}+{k}_{j}^{2}}-\frac{a}{2}{G}_{j}=0~~~~({k}_{i}\ne {k}_{j})\\ -{\displaystyle \sum _{m=1}^{\infty }{B}_{m}\frac{\mathrm{sinh}{k}_{m}{h}_{2}\mathrm{sinh}{k}_{m}a}{\mathrm{cosh}{k}_{m}a}\frac{{k}_{m}}{{k}_{m}^{2}+{k}_{j}^{2}}-\frac{a}{2}{G}_{j}=0~~~~({k}_{i}={k}_{j})}\end{array} \right.\text{，}$

(47)

$\left\{ \begin{array}{l}\frac{a}{2}{C}_{i}{k}_{i}\mathrm{sinh}{k}_{i}c-\frac{{H}_{10}}{{k}_{i}}-{\displaystyle \sum _{j=1}^{\infty }{H}_{j}{k}_{j}\frac{{k}_{i}}{{k}_{i}^{2}-{k}_{j}^{2}}}=0&&({k}_{i}\ne {k}_{j})\\ \frac{a}{2}{C}_{i}{k}_{i}\mathrm{sinh}{k}_{i}c-\frac{{H}_{10}}{{k}_{i}}=0&& ({k}_{i}={k}_{j})\end{array} \right.\text{，}$

(48)

$\left\{ \begin{array}{l}{A}_{10}\frac{{h}_{1}}{{k}_{i}}+\frac{a}{2}{D}_{i}\mathrm{cosh}{k}_{i}b+{\displaystyle \sum _{n=1}^{\infty }{A}_{n}\mathrm{sinh}{k}_{n}{h}_{1}\frac{{k}_{i}}{{k}_{n}^{2}+{k}_{i}^{2}}}+{G}_{10}\frac{1}{{k}_{i}}-\\ {H}_{10}d\frac{1}{{k}_{i}}+{\displaystyle \sum _{j=1}^{\infty }({G}_{j}\mathrm{cosh}{k}_{j}d-{H}_{j}\mathrm{sinh}{k}_{j}d)\frac{{k}_{i}}{{k}_{i}^{2}-{k}_{j}^{2}}}=0\\ ({k}_{i}\ne {k}_{j})\\ {A}_{10}\frac{{h}_{1}}{{k}_{i}}+\frac{a}{2}{D}_{i}\mathrm{cosh}{k}_{i}b+{\displaystyle \sum _{n=1}^{\infty }{A}_{n}\mathrm{sinh}{k}_{n}{h}_{1}\frac{{k}_{i}}{{k}_{n}^{2}+{k}_{i}^{2}}}+{G}_{10}\frac{1}{{k}_{i}}-\\ {H}_{10}d\frac{1}{{k}_{i}}=0&& ({k}_{i}={k}_{j})\end{array} \right.\text{，}$

(49)

$\left\{ \begin{array}{l}-{\displaystyle \sum _{i=1}^{\infty }{D}_{i}\mathrm{sinh}{k}_{i}b\frac{{k}_{i}^{2}}{{k}_{i}^{2}-{k}_{j}^{2}}}+\frac{a}{2}{G}_{j}{k}_{j}\mathrm{sinh}{k}_{j}d\\ -\frac{a}{2}{H}_{j}{k}_{j}\mathrm{cosh}{k}_{j}d=0&&({k}_{i}\ne {k}_{j})\\ \frac{a}{2}{G}_{j}{k}_{j}\mathrm{sinh}{k}_{j}d-\frac{a}{2}{H}_{j}{k}_{j}\mathrm{cosh}{k}_{j}d=0&& ({k}_{i}={k}_{j})\end{array} \right.。$

(50)

在求解上述参数时，式中的级数都是无穷级数，为了求解未知系数，必须将级数在第N项处截断。假定每个级数取前N项，联立式(41)~(50)，采用MATLAB求解矩阵，可求得A₁₀，B₁₀，C₁₀，D₁₀，G₁₀，H₁₀，A_n，B_m，C_i，E_m，F_n，G_j，H_j，从而得到基坑内外总水头分布情况。

3. 解析解的验证

3.1 水头计算结果对比验证

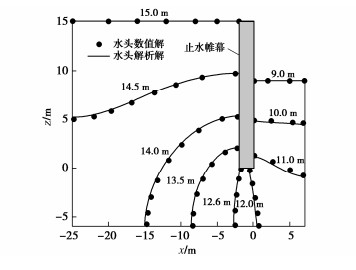
为了验证解析解的正确性，选取基坑工程参数如表 1所示，将解析解计算结果与有限元软件PLAXIS计算结果对比。经试算级数项数N≥30时，解析解计算结果收敛，故本文中的解析解对比分析均取级数项数N=30。PLAXIS模型采用二维平面模型，基坑内外侧边界以及底部边界为不透水边界，基坑内外水位分别与坑底和墙顶齐平，采用15节点的三角形单元对模型进行网格划分，对挡墙周围的网格局部加密。如图 2所示，本文解的水头计算结果和有限元软件吻合较好，验证了本文解的准确性。

表 1 基坑渗流模型的工程参数

Table 1. Parameters of seepage model for foundation pit (单位: m)

b	c	h₁	h₂	a	d
23	7	15	9	6	2

下载: 导出CSV

| 显示表格

图 2 本文解与有限元软件水头计算结果对比

Figure 2. Comparison between solution in this paper and calculated results of water head by finite element software

下载: 全尺寸图片幻灯片

相对于保角变换求解过程中会产生奇点和目前解析方法所求解析解大多为半解析解或隐式解的情况。Fox等^[13]利用保角变换得到的不考虑挡墙厚度基坑内外恒定水头差情况下二维渗流解析解，在φ=1，ψ₁=0这个基坑外侧挡墙角点处为奇点，并不是连续有限的，无法直接给出该点的解析解。黄大中等^[15]采用Fourier变换推导出渗透各向异性土层中基坑二维稳定渗流的隐式半解析解。本文解析解在潜水条件下的基坑范围内是有限且连续的显式解，可以直接求解出基坑内外任意一点的水头值，不会产生奇异点。

3.2 水压力计算结果对比验证

通当基坑出现雨水渗入、人工降水、基坑开挖时，渗流所产生的水头变化会引起支护结构上的水压力改变。为了简化问题和应用本文中的解析解，仅考虑二维稳定渗流下的水压力计算。

在流体力学中，根据伯努利方程，总水头由位置水头、压强水头、动能水头组成。二维渗流情况下，动能水头为0。则总水头表达式为

$H = z + p/\rho g \text{，}$

(51)

水压力p用水头H表示的表达式为

$p = (H - z)\rho g 。$

(52)

根据式(10)基坑外侧(x=-d)的水头为

${H_1}( - d, z) = z + {A_{10}}(z - {h_1}) + \sum\limits_{n = 1}^\infty {{A_n}\sinh {k_n}(z - {h_1})} 。$

(53)

将式(53)代入式(52)得到基坑外侧(x=-d)的水压力分布为

${p_{x = - d}} = [{A_{10}}(z - {h_1}) + \sum\limits_{n = 1}^\infty {{A_n}\sinh {k_n}(z - {h_1})} ]\rho g 。$

(54)

同理可得，基坑内侧(x=0)的水压力分布为

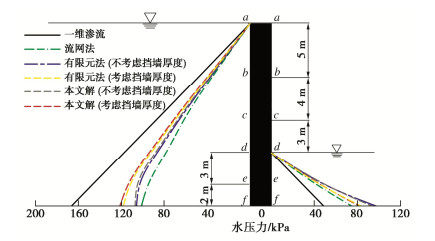
${p_{x = 0}} = [{B_{10}}(z - {h_2}) + \sum\limits_{m = 1}^\infty {{B_m}\sinh {k_m}(z - {h_2})} ]\rho g 。$

(55)

为验证本文解析解计算水压力的正确性，将本文解不考虑挡墙厚度时(d=0 m)和考虑挡墙厚度时的水压力计算结果、流网法的水压力计算结果^[18]、不考虑挡墙厚度时(d=0 m)和考虑挡墙厚度时有限元软件PLAXIS的水压力计算结果以及一维渗流情况下水压力计算结果进行对比。验证算例具体参数为：b=50 m，a=8 m，h₁=17 m，c=10 m，h₂=5 m，d=3 m。取 ${\gamma _{\text{w}}}$ =9.8 kN/m³，对比如图 3所示。图 3中a~f的水压力结果比较列于表 2~5中。

图 3 不同计算方法下水压力计算结果比较

Figure 3. Comparison of calculation results of water pressure among different calculation methods

下载: 全尺寸图片幻灯片

表 2 基坑外侧挡墙上各点的水压力分布

Table 2. Distribution of water pressure at each point on retaining wall outside foundation pit

计算点号	深度z_i /m	水压力/kPa
计算点号	深度z_i /m	一维渗流	本文解(考虑挡墙厚度)	有限元法(考虑挡墙厚度)	流网法	有限元法(不考虑挡墙厚度)	本文解(不考虑挡墙厚度)
a	0	0	0	0	0	0	0
b	5	49.00	40.49	39.76	36.00	37.71	38.45
c	9	88.20	71.97	70.62	62.10	66.73	68.04
d	12	117.60	94.23	92.54	78.50	86.76	88.46
e	15	147.00	113.67	111.63	94.90	102.85	104.91
f	17	166.60	121.41	118.16	101.30	105.85	107.12

下载: 导出CSV

| 显示表格

表 3 基坑外侧挡墙上各点水压力不同计算方法误差对比

Table 3. Comparison of errors among different methods for water pressure at each point on retaining wall outside foundation pit

计算点号	深度z_i /m	本文解(不考虑挡墙厚度)较有限元法(不考虑挡墙厚度)误差/%	流网法较有限元法(不考虑挡墙厚度)误差/%	一维渗流较本文解(不考虑挡墙厚度)误差/%	本文解(考虑挡墙厚度)较有限元法(考虑挡墙厚度)误差/%	本文解(不考虑挡墙厚度)较本文解(考虑挡墙厚度)误差/%
a	0	0	0	0	0	0
b	5	1.96	-4.53	27.44	1.84	-5.04
c	9	1.96	-6.94	29.63	1.91	-5.46
d	12	1.96	-9.52	32.94	1.83	-6.12
e	15	2.00	-7.73	40.12	1.83	-7.71
f	17	1.20	-4.30	55.53	2.75	-11.77

下载: 导出CSV

| 显示表格

表 4 基坑内侧挡墙上各点的水压力分布

Table 4. Distribution of water pressure at each point on retaining wall inside foundation pit

计算点号	深度z_i /m	水压力/kPa
计算点号	深度z_i /m	一维渗流	本文解(考虑挡墙厚度)	有限元法(考虑挡墙厚度)	流网法	有限元法(不考虑挡墙厚度)	本文解(不考虑挡墙厚度)
d	0	0	0	0	0	0	0
e	3	29.40	46.23	45.90	42.50	50.22	50.68
f	5	49.00	82.34	83.90	75.13	95.36	94.13

下载: 导出CSV

| 显示表格

表 5 基坑内侧挡墙上各点水压力不同计算方法误差对比

Table 5. Comparison of errors among different calculation methods of water pressure at each point on retaining wall inside foundation pit

计算点号	深度z_i /m	本文解(不考虑挡墙厚度)较有限元法(不考虑挡墙厚度)误差/%	流网法较有限元法(不考虑挡墙厚度)误差/%	一维渗流较本文解(不考虑挡墙厚度)误差/%	本文解(考虑挡墙厚度)较有限元法(考虑挡墙厚度)误差/%	本文解(不考虑挡墙厚度)较本文解(考虑挡墙厚度)误差/%
d	0	0	0	0	0	0
e	3	0.92	-15.37	-41.99	0.72	9.63
f	5	-1.29	-23.38	-47.94	-1.86	14.32

下载: 导出CSV

| 显示表格

由图 3和表 2~5得到以下结论：

(1) 本文解析解在不考虑挡墙厚度情况下和考虑挡墙厚度情况下的水压力计算结果与不考虑挡墙厚度情况下和考虑挡墙厚度情况下有限元法的水压力计算结果的最大误差绝对值分别为2.00%和2.75%，水压力计算结果与有限元吻合较好，验证了本文解析解的准确性。

(2) 相对于一维渗流时，二维渗流情况下本文解析解计算的基坑外侧水压力均明显减小，基坑内侧水压力均明显增大，且一二维计算结果的差距随着深度逐渐增大。故设计中考虑二维渗流情况很有必要。

(3) 在二维渗流情况下，流网法与不考虑挡墙厚度情况下有限元法的水压力计算结果误差绝对值最大达到23.38%。相较于流网法，在同样不考虑挡墙厚度的条件下本文解析解计算水压力更加精确。

(4) 不考虑挡墙厚度时本文解析解的水压力计算结果较考虑挡墙厚度时本文解析解的水压力计算结果的误差绝对值随着深度逐渐增大，最大为14.32%，挡墙厚度对挡墙上水压力的影响不可忽视。

4. 基坑水头分布情况分析

根据解析解计算不同工程参数变化时基坑挡墙周围的总水头分布情况。若无特殊说明，基坑工程参数如表 1所示。

(1) c(基坑内侧半宽度)变化对基坑挡墙周围总水头分布的影响。分别计算c为7，11，15 m时基坑挡墙周围总水头分布情况，如图 4所示。在挡墙底部附近，挡墙内外水头迅速变化。当基坑半宽度c增大时，挡墙外侧总水头分布线向上移动，挡墙底部总水头分布线向左移动，内侧总水头分布线大幅度向下移动。即当基坑半宽度c增大时，挡墙外侧和底部总水头减小，挡墙内侧总水头明显减小。

图 4 c对基坑周围总水头分布的影响

Figure 4. Effects of c on distribution of total water head around foundation pit

下载: 全尺寸图片幻灯片

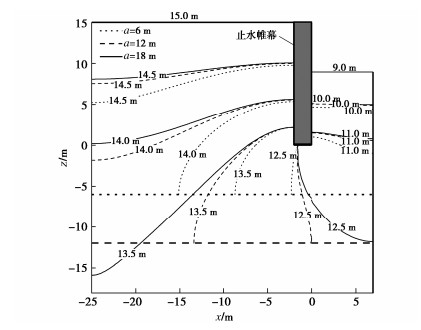
(2) a(挡墙底部至不透水层顶面的距离)变化对基坑挡墙周围总水头分布的影响。分别计算a为6，12，18 m时基坑挡墙周围总水头分布情况，如图 5所示。在挡墙底部附近，挡墙内外水头迅速变化。当挡墙底部至不透水层顶部的距离a增大时，挡墙内外侧总水头分布线向上移动，挡墙底部总水头分布线向右移动，基坑渗流场远场总水头变化较大，基坑挡墙边界附近的总水头分布几乎没有变化。即当a增大时，挡墙外侧的总水头减小，挡墙底部和挡墙内侧总水头增大，基坑挡墙附近水头影响较小，基坑渗流场远场水头分布影响较大。

图 5 a对基坑周围总水头分布的影响

Figure 5. Effects of a on distribution of total water head around foundation pit

下载: 全尺寸图片幻灯片

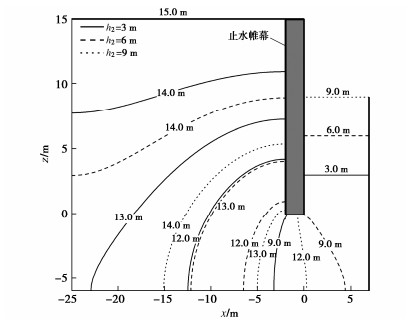
(3) h₂(基坑内侧水位)对基坑挡墙周围总水头分布的影响。分别计算h₂为3，6，9 m时基坑挡墙周围的总水头分布情况，如图 6所示。在挡墙底部附近，挡墙内外水头迅速变化。当基坑内侧水位h₂增大时，挡墙外侧总水头分布线向下移动，挡墙内侧总水头分布线向上移动，挡墙底部总水头分布线向右移动。即当h₂增大时，挡墙内外侧以及挡墙底部总水头值明显增大。

图 6 h₂对基坑周围总水头分布的影响

Figure 6. Effects of h₂ on distribution of total water head around foundation pit

下载: 全尺寸图片幻灯片

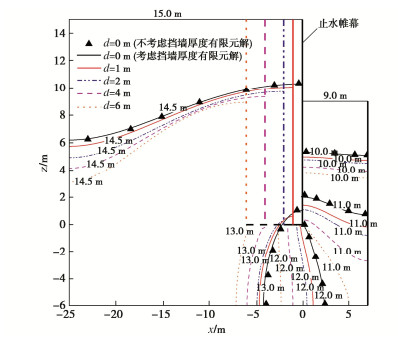
(4) d(悬挂式挡墙厚度)对基坑挡墙周围总水头分布的影响。分别计算d为0，1，2，4，6 m时基坑挡墙周围的总水头分布情况，如图 7所示。不考虑挡墙厚度时解析解的计算结果与有限元计算结果吻合较好，但相对于考虑挡墙厚度时水头计算结果的误差不可忽略。当挡墙厚度d增大时，挡墙内侧的总水头值减小，挡墙底部总水头值明显减小，挡墙外侧靠近基坑挡墙附近水头变化较小，基坑外侧远处水头明显增大。挡墙厚度的增大改变了地下水的渗流路径，使得地下水在挡墙底部附近水头变化较大，最大水力梯度降到挡墙底部，有利于防止基坑的渗流破坏。

图 7 d对基坑周围总水头分布的影响

Figure 7. Effects of d on distribution of total water head around foundation pit

下载: 全尺寸图片幻灯片

5. 结论

(1) 本文通过将二维各向同性土层中带厚度挡墙的基坑稳态渗流场的半截面分为5个规则的区域，利用叠加法和分离变量法将5区域水头表示为级数解的形式，并根据区域间连续条件解得渗透各向同性土层中带厚度挡墙的基坑二维稳态渗流的显式解。相对于保角变换求解方法，本文解析解可以求解出基坑内外任意一点的水头值，不会产生奇异点。

(2) 本文解析解的水头结果和水压力计算结果均与有限元软件吻合较好，验证了本文解析解的正确性。流网法、一维渗流情况下以及不考虑挡墙厚度时本文解析解的水压力计算结果相较于考虑挡墙厚度时本文解析解的水压力计算结果误差不可忽略，且误差随着深度逐渐增大，在设计中采用本文考虑挡墙厚度情况下的基坑二维渗流解析解更为精确。

(3) 二维渗流情况下基坑总水头分布为曲线分布，基坑内侧宽度、不透水层顶部距挡墙底部距离、坑内水位、挡墙厚度等因素对基坑水头分布有很大影响。随着挡墙厚度增大，挡墙内侧的总水头值减小，基坑外侧远处水头明显增大，地下水渗流路径改变，挡墙底部水头明显减小，最大水力梯度降到挡墙底部，有利于防止基坑渗流破坏。

图 1 基坑二维渗流模型

Figure 1. Model for two-dimensional seepage around foundation pit

下载: 全尺寸图片幻灯片

图 2 本文解与有限元软件水头计算结果对比

Figure 2. Comparison between solution in this paper and calculated results of water head by finite element software

下载: 全尺寸图片幻灯片

图 3 不同计算方法下水压力计算结果比较

Figure 3. Comparison of calculation results of water pressure among different calculation methods

下载: 全尺寸图片幻灯片

图 4 c对基坑周围总水头分布的影响

Figure 4. Effects of c on distribution of total water head around foundation pit

下载: 全尺寸图片幻灯片

图 5 a对基坑周围总水头分布的影响

Figure 5. Effects of a on distribution of total water head around foundation pit

下载: 全尺寸图片幻灯片

图 6 h₂对基坑周围总水头分布的影响

Figure 6. Effects of h₂ on distribution of total water head around foundation pit

下载: 全尺寸图片幻灯片

图 7 d对基坑周围总水头分布的影响

Figure 7. Effects of d on distribution of total water head around foundation pit

下载: 全尺寸图片幻灯片

表 1 基坑渗流模型的工程参数

Table 1 Parameters of seepage model for foundation pit (单位: m)

b	c	h₁	h₂	a	d
23	7	15	9	6	2

下载: 导出CSV

表 2 基坑外侧挡墙上各点的水压力分布

Table 2 Distribution of water pressure at each point on retaining wall outside foundation pit

计算点号	深度z_i /m	水压力/kPa
计算点号	深度z_i /m	一维渗流	本文解(考虑挡墙厚度)	有限元法(考虑挡墙厚度)	流网法	有限元法(不考虑挡墙厚度)	本文解(不考虑挡墙厚度)
a	0	0	0	0	0	0	0
b	5	49.00	40.49	39.76	36.00	37.71	38.45
c	9	88.20	71.97	70.62	62.10	66.73	68.04
d	12	117.60	94.23	92.54	78.50	86.76	88.46
e	15	147.00	113.67	111.63	94.90	102.85	104.91
f	17	166.60	121.41	118.16	101.30	105.85	107.12

下载: 导出CSV

表 3 基坑外侧挡墙上各点水压力不同计算方法误差对比

Table 3 Comparison of errors among different methods for water pressure at each point on retaining wall outside foundation pit

计算点号	深度z_i /m	本文解(不考虑挡墙厚度)较有限元法(不考虑挡墙厚度)误差/%	流网法较有限元法(不考虑挡墙厚度)误差/%	一维渗流较本文解(不考虑挡墙厚度)误差/%	本文解(考虑挡墙厚度)较有限元法(考虑挡墙厚度)误差/%	本文解(不考虑挡墙厚度)较本文解(考虑挡墙厚度)误差/%
a	0	0	0	0	0	0
b	5	1.96	-4.53	27.44	1.84	-5.04
c	9	1.96	-6.94	29.63	1.91	-5.46
d	12	1.96	-9.52	32.94	1.83	-6.12
e	15	2.00	-7.73	40.12	1.83	-7.71
f	17	1.20	-4.30	55.53	2.75	-11.77

下载: 导出CSV

表 4 基坑内侧挡墙上各点的水压力分布

Table 4 Distribution of water pressure at each point on retaining wall inside foundation pit

计算点号	深度z_i /m	水压力/kPa
计算点号	深度z_i /m	一维渗流	本文解(考虑挡墙厚度)	有限元法(考虑挡墙厚度)	流网法	有限元法(不考虑挡墙厚度)	本文解(不考虑挡墙厚度)
d	0	0	0	0	0	0	0
e	3	29.40	46.23	45.90	42.50	50.22	50.68
f	5	49.00	82.34	83.90	75.13	95.36	94.13

下载: 导出CSV

表 5 基坑内侧挡墙上各点水压力不同计算方法误差对比

Table 5 Comparison of errors among different calculation methods of water pressure at each point on retaining wall inside foundation pit

计算点号	深度z_i /m	本文解(不考虑挡墙厚度)较有限元法(不考虑挡墙厚度)误差/%	流网法较有限元法(不考虑挡墙厚度)误差/%	一维渗流较本文解(不考虑挡墙厚度)误差/%	本文解(考虑挡墙厚度)较有限元法(考虑挡墙厚度)误差/%	本文解(不考虑挡墙厚度)较本文解(考虑挡墙厚度)误差/%
d	0	0	0	0	0	0
e	3	0.92	-15.37	-41.99	0.72	9.63
f	5	-1.29	-23.38	-47.94	-1.86	14.32

下载: 导出CSV

参考文献(18)

[1]	李广信, 刘早云, 温庆博. 渗透对基坑水土压力的影响[J]. 水利学报, 2002, 33(5): 75-80. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200205015.htm LI Guangxin, LIU Zaoyun, WEN Qingbo. Influence of seepage on water and earth pressure in foundation pit[J]. Journal of Hydraulic Engineering, 2002, 33(5): 75-80. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200205015.htm
[2]	李玉岐, 周健, 谢康和. 基坑开挖卸载诱发的渗流分析[J]. 岩土工程学报, 2006, 28(10): 1259-1262. doi: 10.3321/j.issn:1000-4548.2006.10.015 LI Yuqi, ZHOU Jian, XIE Kanghe. Analysis of seepage induced by excavation[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(10): 1259-1262. (in Chinese) doi: 10.3321/j.issn:1000-4548.2006.10.015
[3]	裴桂红, 吴军, 刘建军, 等. 深基坑开挖过程中渗流-应力耦合数值模拟[J]. 岩石力学与工程学报, 2004, 23(增刊2): 4975-4978. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2004S2055.htm PEI Guihong, WU Jun, LIU Jianjun, et al. Numerical modeling of seepage-stress coupling of deep foundation pit excavation[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(S2): 4975-4978. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2004S2055.htm
[4]	李瑛, 陈东, 刘兴旺, 等. 悬挂式止水帷幕深基坑减压降水的简化计算方法[J]. 岩土力学, 2021, 42(3): 826-832, 862. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202103025.htm LI Ying, CHEN Dong, LIU Xingwang, et al. Simplified calculation method of decompression dewatering for deep excavation with suspended waterproof curtain[J]. Rock and Soil Mechanics, 2021, 42(3): 826-832, 862. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202103025.htm
[5]	姜忻良, 宗金辉. 基坑开挖工程中渗流场的三维有限元分析[J]. 岩土工程学报, 2006, 28(5): 564-568. doi: 10.3321/j.issn:1000-4548.2006.05.004 JIANG Xinliang, ZONG Jinhui. Three-dimensional finite element analysis of seepage fields in foundation pit[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(5): 564-568. (in Chinese) doi: 10.3321/j.issn:1000-4548.2006.05.004
[6]	马昌慧, 毛云, 黄魏, 等. 帷幕在降水条件下对基坑周边渗流及变形影响的研究[J]. 岩土工程学报, 2014, 36(增刊2): 294-298. doi: 10.11779/CJGE2014S2052 MA Changhui, MAO Yun, HUANG Wei, et al. Effects of dewatering methods on seepage and deformation of foundation pits[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(S2): 294-298. (in Chinese) doi: 10.11779/CJGE2014S2052
[7]	JIE Y X, JIE G Z, MAO Z Y, et al. Seepage analysis based on boundary-fitted coordinate transformation method[J]. Computers and Geotechnics, 2004, 31(4): 279-283. doi: 10.1016/j.compgeo.2004.01.010
[8]	GRIFFITHS D V. Seepage beneath unsymmetric cofferdams[J]. Géotechnique, 1994, 44(2): 297-305. doi: 10.1680/geot.1994.44.2.297
[9]	LI Y Q, YING H W, XIE K H. On the dissipation of negative excess porewater pressure induced by excavation in soft soil[J]. Journal of Zhejiang University (Science A), 2005, 6(3): 188-193.
[10]	BERESLAVSKII E N. The flow of ground waters around a Zhukovskii sheet pile[J]. Journal of Applied Mathematics and Mechanics, 2011, 75(2): 210-217. doi: 10.1016/j.jappmathmech.2011.05.010
[11]	HARR M E. Groundwater and seepage[M]. New York: McGraw-Hill, 1962.
[12]	XIE K H, WANG Y L, WANG K, et al. Application of Hankel transforms to boundary value problems of water flow due to a circular source[J]. Applied Mathematics and Computation, 2010, 216(5): 1469-1477.
[13]	FOX E N, MCNAMEE J. XXV. The two-dimensional potential problem of seepage into a cofferdam[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1948, 39(290): 165-203.
[14]	于佳卉. 悬挂式止水帷幕基坑降水承压含水层稳定流渗流场解析解[D]. 天津: 天津大学, 2018. YU Jiahui. Analytical Solution of Steady Seepage into Partially Penetrating Cutoff Wall during Excavation Dewatering[D]. Tianjin: Tianjin University, 2018. (in Chinese)
[15]	黄大中, 谢康和, 应宏伟. 渗透各向异性土层中基坑二维稳定渗流半解析解[J]. 浙江大学学报(工学版), 2014, 48(10): 1802-1808. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC201410013.htm HUANG Dazhong, XIE Kanghe, YING Hongwei. Semi-analytical solution for two-dimensional steady seepage around foundation pit in soil layer with anisotropic permeability[J]. Journal of Zhejiang University (Engineering Science), 2014, 48(10): 1802-1808. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC201410013.htm
[16]	应宏伟, 聂文峰, 黄大中. 地下水位波动引起重力式挡墙基坑周围地基土孔压变化及对挡墙稳定性的影响[J]. 岩石力学与工程学报, 2014, 33(11): 2370-2376. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201411021.htm YING Hongwei, NIE Wenfeng, HUANG Dazhong. Influences of groundwater level fluctuation on the stability of gravity retaining wall of pits[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(11): 2370-2376. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201411021.htm
[17]	丁君. 工程电磁场与电磁波[M]. 北京: 高等教育出版社, 2005. DING Jun. Engineering Electromagnetic Field and Electromagnetic Wave[M]. Beijing: Higher Education Press, 2005. (in Chinese)
[18]	王钊, 邹维列, 李广信. 挡土结构上的土压力和水压力[J]. 岩土力学, 2003, 24(2): 146-150. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200302001.htm WANG Zhao, ZOU Weilie, LI Guangxin. Earth pressure and water pressure on retaining structure[J]. Rock and Soil Mechanics, 2003, 24(2): 146-150. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200302001.htm

施引文献(5)

期刊类型引用(2)

1.	周志伟，田羽，张周爱. 横采内排追踪压帮技术下边坡稳定控制开采参数确定. 露天采矿技术. 2025(02): 41-45 . 百度学术
2.	余俊，郑靖凡，张志中，李东凯. 基坑二维稳态渗流场的解析解及简化解. 华南理工大学学报(自然科学版). 2024(05): 84-91 . 百度学术

其他类型引用(3)

资源附件(1)

其他相关附件
- PDF格式
  10-202307-G22-0357一文审稿意见与作者答复点击下载(451KB)

图(7) / 表(5)

计量

文章访问数: 345
HTML全文浏览量: 56
PDF下载量: 116
被引次数: 5

0. 引言
1. 考虑挡墙厚度基坑二维渗流模型
2. 模型求解
3. 解析解的验证
3.1 水头计算结果对比验证
3.2 水压力计算结果对比验证
4. 基坑水头分布情况分析
5. 结论

考虑挡墙厚度基坑稳态渗流场的解析解 English Version

作者简介: 余俊(1978—)，男，博士，副教授，主要从事隧道与地下工程方面的教学和研究工作。E-mail: yujun@csu.edu.cn

计量

出版历程

Analytical solution of steady seepage field of foundation pit considering thickness of retaining wall

0. 引言

1. 考虑挡墙厚度基坑二维渗流模型

2. 模型求解

3. 解析解的验证

3.1 水头计算结果对比验证

3.2 水压力计算结果对比验证

4. 基坑水头分布情况分析

5. 结论

期刊类型引用(2)

其他类型引用(3)

其他相关附件

PDF格式

计量

出版历程

目录

0. 引言

1. 考虑挡墙厚度基坑二维渗流模型

2. 模型求解

3. 解析解的验证

3.1 水头计算结果对比验证

3.2 水压力计算结果对比验证

4. 基坑水头分布情况分析

5. 结论

作者简介:
余俊(1978—)，男，博士，副教授，主要从事隧道与地下工程方面的教学和研究工作。E-mail: yujun@csu.edu.cn