THM coupled model for simulating frost heave based on a new water film pressure criterion
-
摘要: 冻胀融沉是多年冻土区的主要病害,其受水分场、温度场、应力场的复杂耦合作用影响。基于水膜理论提出了冻土未冻水膜压力作为冰透镜体生成的判据,并重新对水分迁移驱动作用进行描述,建立了以温度、土体孔隙比为变量的全耦合模型。通过考虑已冻区冰基质的影响,推导了涵盖原位冻胀与冰分凝两部分的冻胀量计算公式。基于Matlab和COMSOL Multiphysics的联立平台,提出了模型冰透镜体实时分布的数值求解方法,实现了冻土温度、水分、应力、冰透镜体分布的全耦合数值求解。通过与室内土柱冻结试验及现有水热力模型(Thermal-Hydraulic-Mechanical,又称THM模型)冻胀量结果进行对比分析,证明了温度、含水率与冻胀计算上的可靠稳定。最后通过探讨温度梯度、上覆压力、渗透系数与压缩模量对土柱冻结的影响发现,温度梯度能显著增加土体冻胀量,上覆压力会导致更多水分向冻结锋面迁移,但对冻胀量起着抑制作用,渗透系数与压缩模量均对冻胀量产生正影响。为冻胀理论研究与数值实现提供了新思路。Abstract: The frost heave and thaw settlement are the main frost damage in cold areas, which are the complex coupling process of water, temperature and stress fields. In this study, a coupled thermal-hydraulic-mechanical model is developed based on the water film theory, in which the temperature and void ratio of soils are the input variables. The novelty of this model is that the frozen water film pressure is used as the criterion for the generation of ice lens. The driving force of water migration is newly defined, and the frost heave includes the pristine frost heave and the amount of ice segregation. The fully coupled model is numerically solved based on the Matlab and COMSOL Multiphysics, generating the results of soil temperature, moisture, stress and the layered ice lens. The simulated results are then compared with those of the laboratory freezing tests, which shows that they match quite well and verify the validity of the proposed model. The simulation indicates that temperature gradient can promote the frost heave, and the overburden pressure can attract more water to the freezing front but decrease the amount of the frost heave. In addition, both the hydraulic conductivity and the compressive modulus have positive effects on the frost heave. The proposed model provides a new approach to understand the frost heave.
-
0. 引言
冻土地区表层土体极易受环境条件(特别是温度变化)影响产生冻胀融沉等病害,严重威胁着冻土区各类建筑设施、交通和能源工程的安全运营。冻胀融沉病害的发生主要受土体内的水分迁移与相变过程控制,是一个复杂的水分场、温度场和应力场耦合作用过程。
从冻胀的物理机制而言,当土体温度低于冻结温度时,部分孔隙水相变成冰,土颗粒与孔隙冰附近的未冻水,则以未冻水膜的形式包裹在颗粒表面,其自由能随着温度降低不断减小。温度较高区的未冻水不断被吸入产生新的孔隙冰颗粒,并逐渐相互连接形成冰透镜体。外部水分的迁移补给和冰透镜体的不断生长是土体冻胀的本质。
土体冻胀问题的研究已有近百年的历史,早在20世纪20年代,Taber[1]认为毛细水向上迁移的过程是诱发冻胀的原因,该观点在随后40余年冻胀问题的研究中一直沿用,但毛细理论并不能解释多层冰透镜体生成过程,由此诞生了刚性冰模型。Miller[2]认为冻结区与未冻区间存在部分冻结区域,称为冻结缘,未冻区的水在温度梯度影响下进入冻结缘形成孔隙冰,与冰透镜体形成刚性连接。当孔隙有效应力与上覆压力相等时,旧的冰透镜体停止生长,新的冰透镜体生成。Gilpin[3]认为冰压达到临界分离压力时冰透镜体形成;Fowler[4]则假设冻结缘厚度很小对Miller模型进行了简化。此外,在冻结缘理论基础上,Remple等[5]基于预融膜理论提出了物理意义更明确但更复杂的微观模型;Konrad等[6]则引入了外部荷载的作用,基于分凝势建立了外载下的冻胀模型。
刚性冰模型在成冰力学机制上比较明确,但在数值实现上较为繁琐复杂,以Harlan[7]、Talyor等[8]为代表的水热模型在工程上具有更广泛的应用。水热模型不考虑冰透镜体的形成,只考虑温度场与水分场的作用。因此结合刚性冰模型与水热模型,建立兼顾理论与工程实际的水热力耦合模型是冻胀模型研究的趋势。
国内外学者已提出了不少水热力耦合模型,近年模型差别主要体现在水热迁移方程、冰透镜体生长判据、土体冻胀计算3个层面。原国红[9]、李智明[10]、白青波等[11]在水热迁移方程中均采用扩散系数考虑了孔隙冰的阻滞作用,不过这些模型未能计算冻胀量与冰透镜体分布情况;Thomas等[12]采用有效应力判据判断冰透镜体生成;Zhou等[13]、Huang等[14]采用孔隙压力判据,提出了分离孔隙比的概念并给出了数值尝试;Lai等[15]、Feng等[16]推导了分离孔隙比的计算公式,并用其判断冰透镜体的厚度与位置。在冻胀量计算中,耦合模型[12-16]均将土体视为弹性,利用孔隙比计算原位冻胀。可以看出现有水热力模型主要存在以下不足:①以加权孔隙压力判断冰透镜体生成,忽略冰透镜体暖端未冻水膜的作用,冻胀判断误差大[17];②以分离孔隙比/率来判断冰透镜体的厚度缺乏依据与物理意义;③冻胀量多用孔隙比/率积分计算原位冻胀,与冻胀量在冰透镜体位置上发生量级改变的实际不符[18];④因冻结区渗透系数的选择问题,不少水热力耦合模型与试验结果吻合较差。
为解决以上问题,本研究以冻土未冻水膜为切入点,通过受力分析得到冰透镜体生长判据,建立以温度、孔隙比为变量的水热力耦合模型,考虑冻结区孔隙冰对渗流的阻滞作用,引入平均水压力作为水分迁移驱动力,计算包含多层冰透镜体厚度的冻胀量。通过与冻结试验的结果对比验证了模型的有效性,进而研究不同参数对模型含水率分布与冻胀量的影响。
1. 冻胀过程水热力耦合模型
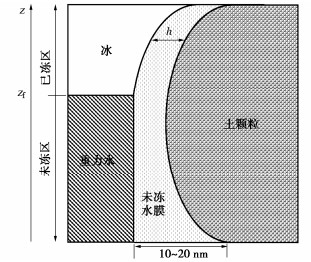
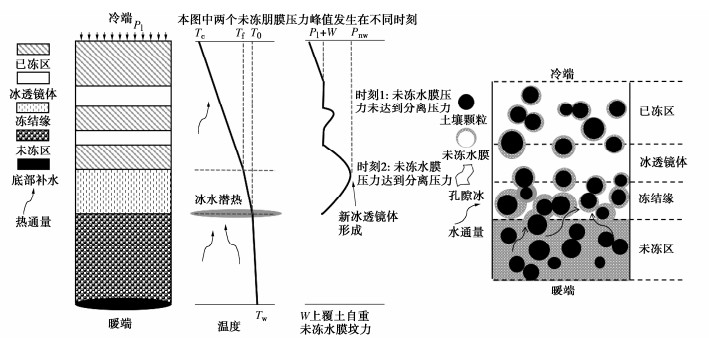
图 1为宏观和孔隙尺度下土体冻结及冰透镜体生长示意图。当土体温度低于冻结温度时,孔隙水在冻结锋面附近发生相变并释放出潜热,靠近孔隙冰与土颗粒的未冻水则包裹在颗粒外形成未冻水膜。未冻区的水分不断被吸引到冻结锋面,冻结锋面在土柱内不断前进。过程中同一高度冻结缘处未冻水膜厚度不断减小,未冻水膜压力逐渐增大。当未冻水膜压力增大到一定程度时,土颗粒周围和未冻水膜中的液体向冰透镜体移动,从而沿相反方向挤压土体颗粒。土颗粒被挤压分离,孔隙冰连接成整体,冰透镜体开始形成。未冻水膜作为水分迁移的通道,可以使液体流向冰透镜体造成冰透镜体的生长。
模型基本假设如下:①冻土为弹性且各向同性的饱和土体;②在一定的温度和压力条件下,土骨架、未冻水、孔隙冰均不能被压缩;③土体冻结温度恒定,且存在局部热平衡;④水分以液体形式运动并遵循达西定律,不考虑冰透镜体的移动。
1.1 冻土含水率与含冰率
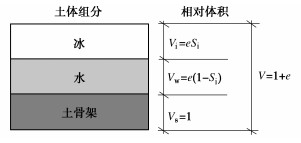
图 2为饱和冻土三相图,由图 2可知冻土中未冻水含量θw与孔隙冰含量θi可以表示为
θw=e(1−Si)1+e, (1a) θi=eSi1+e。 (1b) 式中:e为土体孔隙比;Si为孔隙冰饱和度,可以由与温度有关的函数表示[19]
Si={1−[1−(T−T0)]α(T⩽T0)0(T>T0) 。 (2) 式中:T0为冻结温度;α为经验参数。
由于试验中初始含水率配制与冻结完成后含水率测量中均采用质量含水率,定义质量含水率为
w=e(1−Si)ρw+eSiρiρs 。 (3) 式中,ρw,ρi,ρs分别为水的密度、冰的密度、土体密度。
1.2 冰透镜体生长模型
Gilpin等[3]考虑冰水界面的未冻水膜,并认为吸附水膜受固体基质吸引力(范德华力、双电层力)的作用,通过试验证实这种吸附水膜厚度约为10~20 nm,在土体中示意图如图 3所示,其中未冻区重力水与未冻水膜融为一体,以液态水形式表现。
固体颗粒表面对水膜的影响为
g(h)=−ΔvPLh−vsσSLˉK−Lln(TT0)。 (4) 式中:PLh为未冻水膜的相对压力;σSL为冰水界面张力,取值为0.04 J/m2[20];K为界面平均曲率,由于未冻水膜包裹在土颗粒四周并与冰接触,可认为界面平均曲率等于颗粒平均曲率,取值为100 mm-1;vs为冰的比容,表示单位质量物质所占有的容积,即1/ρi;Δv为冰与水的比容差,即vs-vL。
由此定义驱动水分迁移的平均水压力为[21]
P=Por+PLh−g(h)ρw−Patm。 (5) 式中:Por为参考压力,在未冻区为局部孔隙水压力,在冻土区其值为标准大气压;Patm为标准大气压。
在未冻区和冻结区,式(5)可以写成不同形式:
P={Por−Patm(z>zf)PLh−g(h)ρw(z⩽zf)。 (6) 式中:zf为冻结锋面位置。
冰透镜体的生长发生在土体冻结区,由式(6)可以求得未冻水膜相对压力。冰透镜体形成之前,外部荷载在无冰的情况下通过土颗粒间的接触点传递,当未冻水膜逐渐变薄,未冻水膜的相对压力也逐渐增大。当未冻水膜变薄到冰水界面可以侵入土颗粒内部时,土颗粒分离,此时冰透镜体承受外部荷载。
需要注意的是,未冻水膜压力值为正值,对冰透镜体起排斥作用,将冰推离土颗粒。而平均水压力为负值,可以将未冻水吸入冰透镜体暖端以促进冰透镜体生长。
在现有的成层冰透镜体模拟中,Zhou等[13]用分离孔隙比来判断冰透镜体的成层情况;Feng等[16]、Huang等[14]延用了这个概念和数值;Sheng等[22]、Teng等[23]以中性压力作为判据并引入成冰速度;Lai等[15]认为当孔隙应力大于分离压力时冰透镜体形成,并定义了分离孔隙率的表达式,以此为界限直接判断冰透镜体的位置与厚度。然而,分离孔隙比的参数选择没有理论与试验依据,且直接用其判断厚度是否合理值得进一步检验。同时孔隙应力和中性压力的判断标准同实际情况存在差异。
与代表有效应力的土骨架直接接触的是未冻水膜,本文选取未冻水膜相对压力来判断冰透镜体生成具有较明确的物理意义。
当未冻水膜压力在承受上覆总压下超出土颗粒极限抗拉强度时,未冻水膜厚度缩小到楔入土颗粒之间,土颗粒被挤开且孔隙冰连成整体,此时冰透镜体形成,即
PLh⩾W+σ∗tensile +∫lzγdz。 (7) 式中:W为土体上覆压力;σ∗tensile 为极限抗拉强度,积分项为土体自重。不等式右侧定义为分离压力Psep。
当式(7)的条件满足时,冰透镜体开始形成,未冻水膜压力下降。在顶部负温的情况下,第一层冰透镜体形成后,其下部未冻水膜压力再次满足式(7),此时第二层冰透镜体形成,并对下部未冻区水分迁移起到阻碍作用,认为第一层冰透镜体停止生长。
当冰透镜体生长时,其生长速度等于该冰透镜体暖端附近未冻水的迁移速度
VH=−k∇ψ|z=zb。 (8) 式中:VH为冻胀速度;zb为冰透镜体暖边的位置;Ψ为土水势,表示未冻水迁移的驱动作用,由重力、温度与平均水压力共同决定:
ψ=z+Pρwg。 (9) 土骨架本身的变形对冻胀的影响很小,冻胀绝大部分因冰透镜体的存在而产生。本文将冻胀量分为两部分,一部分表示未冻水变为孔隙冰时的体积膨胀,另一部分则表示为多层冰透镜体生成时的厚度累积:
ΔH1i=∫ti+1tiVHidt。 (10) 式中:ΔH1i为第i条冰透镜体的厚度;ti为第i条冰透镜体的产生时刻;ti+1为第i+1条冰透镜体的产生时刻。故冰透镜体的累计厚度可以表示为
ΔH1=n∑i=1ΔH1i。 (11) 式中,n为冻结时间结束时冰透镜体的数量。
由于未冻水冻结产生的体积膨胀可表示为
ΔH2=∫l00e−e01+e0dz。 (12) 因此,土体冻胀量可以表示为[24]
ΔH=n∑i=1(∫ti+1tiVHidt)+∫l00e−e01+e0dz。 (13) 1.3 渗流场控制方程
依据土体冻结过程中的质量守恒,基于Richards方程,冻土中未冻水的水分迁移方程为
∂(ρwθwdV)∂t+∂(ρiθi dV)∂t+ρw∇vwdV=0 。 (14) 式中:Ψ为土水势;vw为水分迁移速度,由达西定律确定为
vw=−k∇ψ=−k(z+Pρwg)。 (15) 式中:k为渗透系数。Taylor等[8]在确定水分扩散参数时,引入阻抗因子表示孔隙冰存在对未冻水迁移的阻碍作用。本文将该影响考虑在孔隙冰区域的渗透系数中,引入Teng等[25]从冰的赋存状态出发提出的负温区渗透系数模型:
k={ζw(1−Si)2b+3(k0T⩽T0,PLh⩽Psep)k0(T>T0,PLh⩽Psep)0(PLh>Psep)。 (16) 式中:k0为未冻水渗透系数;ζw为考虑温度变化对水性质影响的修正系数;b根据土性取值为3。式(16)比传统用温度来表示渗透系数得到的含水率更准确。
联立式(1),(14),(15),得到孔隙比、温度为变量的渗流场控制方程:
ρw(1−Si)+ρiSiρw(1+e)∂e∂t+(ρi−ρw)eρw(1+e)∂Si∂T∂T∂t=∇(k∇ψ)。 (17) 1.4 温度场控制方程
基于傅里叶定律,以相变潜热作为微元体内热源生成热,考虑热传导、水分迁移带走的热量,根据质量守恒定律可得微分方程:
C∂T∂t+Cwvw∇T=∇⋅(λ∇T)+ρiL∂θi∂t。 (18) 式中:L为相变潜热,取值334.56kJ/kg;Cw为水体积热容;Cwvw∇T表示水分迁移带走的热量。
土体体积热容C与导热系数λ为[26]
C=Csθs+Cwθw+Ciθi, (19) λ=λθss⋅λθww⋅λθii。 (20) 联立式(1),(15),(18),得以孔隙比和温度为变量的温度场控制方程:
(C−Lρie1+e∂Si∂T)∂T∂t−LρiSi1+e∂e∂t=∇λ∇T+Cwk∇ψ∇T 。 (21) 1.5 应力场控制方程
土体单位自重(图 2)可以表示为
γ=g1+e[ρs+eSiρi+e(1−Si)ρw]。 (22) 依据有效应力原理,引入O’Neil等[27]提出的应力分配因子概念,认为土骨架应力即有效应力:
σt=σ+χP+(1−χ)Pi。 (23) 式中:χ为应力分配因子,表示为(1-Si)1.5;σ为有效应力;Pi为冰压;σt为总应力,
σt=W+∫lzγdz。 (24) 基于Navier方程,在应变为0时,有效应力等于初始总应力,定义有效应力为
σ=−Esε+W+∫lzγ0dz。 (25) 式中:Es为土体弹性模量;ε为土体应变。
基于Clapeyron方程计算,得孔隙冰压与平均水压力的平衡方程为
Pρw−Piρi=Lln(TT0)。 (26) 联立式(5),(23)~(26),得平均水压力表达式:
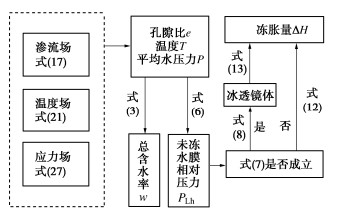
P=Es+∫lz(γ−γ0)dz+(1−χ)Lρiln(TT0)χ+ρiρw(1−χ)。 (27) 主要变量的变量说明汇总于表 1,模型的方程构成与计算流程见图 4。
表 1 冻胀模型主要变量说明Table 1. Description of main variables in THM model变量 物理意义 公式 来源 孔隙冰饱和度Si 孔隙冰与孔隙的体积之比 T+T0:1−[1−(T−T0)]α Tice等[19] 平均水压力P 驱动水分迁移的作用力 [σt−σ+(1−χ)Lln(T/T0)ρi]/[χ+(1−χ)ρi/ρw] Zhou等[13] 未冻水膜压力PLh 未冻水膜上的相对压力 P+g(h)ρw+Patm−Por Gilpin[3] 已冻区渗透系数k 单位水力梯度下的水流量 T+T0:ζw(1−Si)2b+3 Teng等[25] 土体体积热容C 单位体积土体温度改变1 ℃需要的热量 Csθs+Cwθw+Ciθi 徐学祖等[26] 导热系数λ 单位时间通过单位面积传递的热量 λθss+λθww+λθii 徐学祖等[26] 2. 模型的数值计算
为验证以上数值模型的准确性,选取COMSOL中的系数型偏微分方程模块(PDE模块)建立以温度、孔隙比、总应力为变量的耦合方程,依图 4计算流程确定未冻水膜压力,在COMSOL with Matlab中直接调用API,判断式(7)成立时的时间与对应土柱高度,定位水流速度,以分析土柱的温度、含水率、冻胀量、冰透镜体的分布情况。
2.1 试验概况
选取文献中4个试验进行模拟分析。试验均为土柱单侧冻结试验,顶部负温,底部正温。数值模拟采用的模型参数见表 2,试验材料属性与试验条件见表 3。
表 2 冻胀模型输入参数Table 2. Input parameters in THM model参数 取值 参数 取值 参数 取值 试验1:k0 /(m·s-1) 3.0×10-10 试验3:T0/℃ -0.3 λw/(W·(m·K)-1) 0.58 试验2:k0 /(m·s-1) 2.5×10-10 试验4:T0/℃ -0.3 Cs/(kJ·(m3·K) -1) 2160 试验3:k0 /(m·s-1) 2.5×10-10 试验1:ρs/(kg·m-3) 2720 Ci/(kJ·(m3·K) -1) 1874 试验4:k0 /(m·s-1) 2.5×10-10 试验2:ρs/(kg·m-3) 2700 Cw/(kJ·(m3·K) -1) 4180 试验1:Es/MPa 2.5 试验3:ρs/(kg·m-3) 2700 L/(kJ·kg-1) 334.56 试验2:Es/MPa 1.2 试验4:ρs/(kg·m-3) 2768 ξw 1 试验3:Es/MPa 0.8 ρi/(kg·m-3) 917 b 3 试验4:Es/MPa 12 ρw/(kg·m-3) 1000 α -5 试验1:T0/℃ 0 λs/(W·(m·K)-1) 1.2 β -8 试验2:T0/℃ -0.5 λi/(W·(m·K) -1) 2.22 σ∗tensile/kPa 12 表 3 不同试验的土性与边界条件参数Table 3. Soil properties and boundary conditions of different tests试验编号 顶部温度/℃ 底部温度/℃ 初始温度/℃ 底部状态 初始含水率/% 土的种类 干密度/(g·cm-3) 上覆压力/ kPa 土体高度/cm 冻结时间/h 来源 #1 -3℃ 3℃ 3℃ 补水 17 青海-西藏黏土 1.70 100 10 72 文献[16] #2 -1.7℃ 1℃ 1℃ 封闭 25.71 内蒙古粉质黏土 1.63 0 15 120 文献[26] #3 -2.3℃ 0.7℃ 0.7℃ 补水 18.9 黏土 1.70 0 10 72 文献[28] #4 1→-1 20 ℃/h
-1→-8 0.1 ℃/h1℃ 1℃ 补水 21.7 内蒙古粉质黏土 1.70 500 5 72 文献[24] 2.2 温度与含水率分布
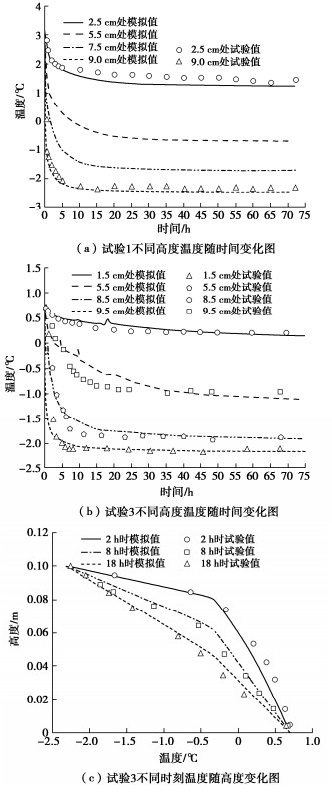
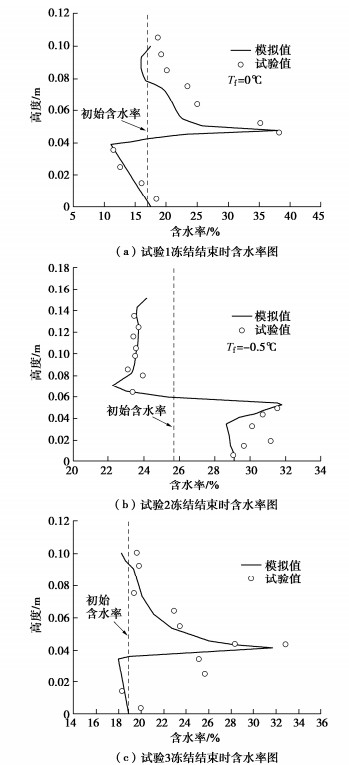
根据试验1,2,3的试验状况,计算不同时刻土柱温度随高度的变化以及不同高度处温度随时间的变化如图 5(a)~(c)所示,数值模拟结果与试验数据拟合较好。
图 5(a),5(b)显示在初始冻结的前10 h内,土柱冷端高处温度变化剧烈,此后温度变化趋于平缓,30 h后,温度几乎没有变化。不同高度虽然温度变化趋势相同,但降温幅度与降温速率不同,靠近冷端的位置温度变化更快,达到稳定状态所需要的时间更短。同时,稳定状态并不是保持不变,而是存在一些波动。图 5(c)显示在初始时刻,土柱的冻结速率比较快,温度变化快,随着时间的增加,冻结速率逐渐减慢,最终土柱温度沿着土柱高度呈线性变化,曲线转折点即相变点。在相变点附近,水转化为冰,相变产生大量的热抑制了冷能的传递,因此冻结区域的温度变化曲线的斜率更缓,温度变化缓慢。
土体含水率分布的数值计算与模拟值对比如图 6所示,图 6中显示含水率主要集中冻结锋面附近,随着未冻水减少,吸力增大,顶部未冻水与底部补水向冻结锋面处迁移,部分因冰的阻滞作用滞留,含水率增大形成峰值。顶部温度较低,含冰率较高,对水分的迁移有一定的阻碍作用,未冻区的水分很难进入冻结区。底部而言,试验1、试验3饱和土底部补水维持饱和状态不变。试验2虽封闭,但由于质量守恒总含水率不变,主要是顶部水分向冻结锋面移动。模拟与试验趋势与数值范围拟合较好,但个别点偏离曲线,这是因为实际土体中颗粒分布并不均匀,初始含水率在不同高度不一致。同时,由于现有试验条件的局限性,冻结试验结束时含水率由土柱分区烘干测得,所得含水率并不是某一高度的真实含水率。此外,模拟中一些输入参数的确定由土性决定,同试样的真实参数值有所出入。
2.3 冰透镜体分布
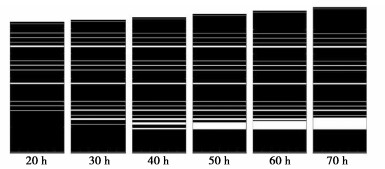
根据试验4的试验情况,图 7为不同时刻冰透镜体分布图,结果表明冰透镜体呈层状分布的,自冷端向暖端数量不断增加。随着时间的增长,冰透镜体厚度也不断增长,直到其下方新的冰透镜体形成。40 h前主要是冰透镜体数量的增加,从40 h开始,冻结锋面附近最靠近暖端的冰透镜体开始生长,土柱内稳定的温度梯度引起底部连续补充的水分向冻结锋面移动,冰透镜体不断发育形成较厚的冰透镜体。试验结束时冰透镜体实际分布图如图 8所示。
图 8为72 h时冰透镜体分布图,其中A区为整体状构造,此时细小的孔隙冰填充在土颗粒之间将土颗粒紧密的胶结在一起,部分冰推开土颗粒形成断续的冰透镜体;B区冰透镜体厚度较小,且连续性较差,层数比A区明显增多;C区冰透镜体较B区更厚一点,且连续性强,可以看出明显的层状结构;D区出现较厚的冰透镜体,下部为未冻区。
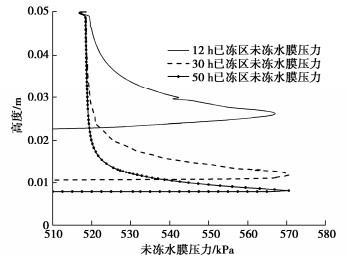
为直观探究冰透镜体生长机理,图 9为不同时刻未冻水膜压力随高度变化图。结果表明未冻水膜压力随时间在不同高度处存在峰值,当峰值大于分离压力时,冰透镜体形成。这是因为随着温度的降低,冰水界面与土颗粒之间的距离逐渐缩小,未冻水膜压力增大,颗粒间接触应力随之减小。当该处温度低于接触应力所对应的相变温度时,颗粒间的未冻水膜开始冻结,冰水界面楔入土颗粒之间,土颗粒发生分离,冰透镜体开始生长。所以最暖冰透镜体生长的位置,会出现当前位置未冻水膜压力的最大值。
2.4 冻胀量计算
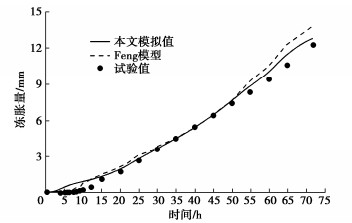
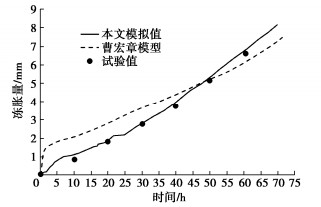
计算试验1、试验4的冻胀量分别与Feng模型[16]和曹鸿章模型[24]对比。
图 10为试验1模拟结果对比图,本文模型与Feng模型整体趋势一致,最终冻胀量更接近试验值。试验1的水平成层冰透镜体现象不明显,更多是冰体积膨胀产生的微裂缝,冰透镜体对冻胀量贡献较小。Feng模型在计算冻胀量时,渗透系数没有考虑成冰阻滞作用,进水量较大,计算冻胀量较大。本文模型在考虑成冰阻滞作用的同时,渗透系数依据冰透镜体生成与否进行了判断,原位冻胀计算准确性高,最终冻胀量与试验值误差更小。
图 11为试验4模拟结果对比图。试验4顶部温度低,两端温差大,具有非常明显的成层冰透镜体现象,分凝冻胀占主导。在试验开始时,由于冻结锋面穿透率较高,水在给定的地方没有足够的时间迁移和聚集,因此冻胀量较小,曲线平缓。此后降温速度加快,冻胀量趋势变陡。比起曹鸿章固定时间步长与空间步长,本文通过缩短初始时间步长,更适应试验开始时的快速降温阶段,模型计算结果相较曹鸿章模型同试验更为接近。
3. 参数分析
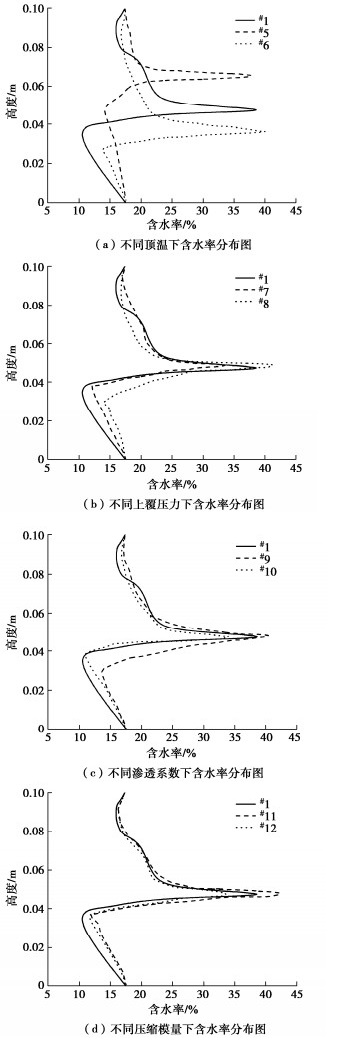
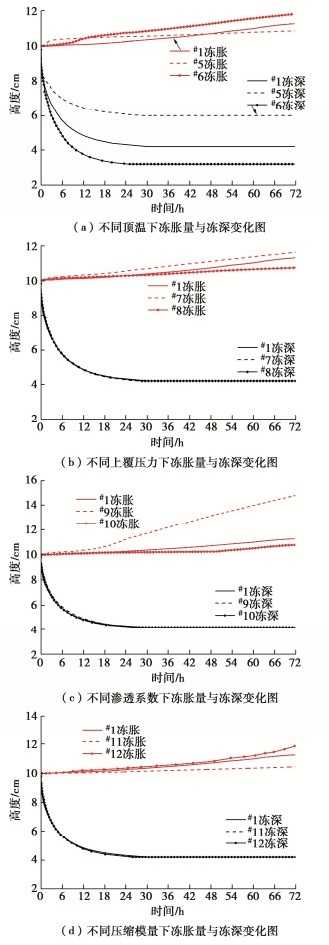
为探究顶部负温、上覆压力、渗透系数和压缩模量对模拟结果的影响,表 4以试验1为基础进行参数分析,不同工况改变参数用下划线表示。
表 4 不同模拟工况参数表Table 4. Parameters of different simulation conditions工况 顶温/℃ 上覆压力/ kPa 渗透系数/ (10-10 m·s-1) 压缩模量/ MPa #1 -3 100 3 2.5 #5 -1.5 100 3 2.5 #6 -4.5 100 3 2.5 #7 -3 50 3 2.5 #8 -3 200 3 2.5 #9 -3 100 30 2.5 #10 -3 100 1 2.5 #11 -3 100 3 0.5 #12 -3 100 3 5.0 图 12(a)中顶部温度改变会显著影响含水率峰值的位置,即冻结锋面的位置,但对含水率峰值大小的影响却很小。这是因为负温变化会影响冻结温度在土柱的位置,虽对冻结速度产生影响,冰透镜体厚度有所改变,但水分在冻结锋面处的聚集峰值是一定的。图 12(b)表明上覆压力越大,冻结锋面附近的含水率越大。上覆压力对驱动水分迁移的平均水压力没有影响,因此未冻水膜相对压力随上覆压力变化很小,但分离压力同上覆压力正相关。当上覆压力增大时,冰透镜体形成数量减少,成冰阻滞的影响减小,冻结锋面处渗流通道增加,冻结锋面附近渗透系数增大,含水率增加。图 12(c)中未冻区渗透系数影响水分迁移速度,渗透系数越大含水率峰值越大。图 12(d)中压缩模量显著影响含水率峰值大小,压缩模量越小,负平均水压力绝对值越大,水分聚集现象更明显。
图 13表明除顶温外,其他因素对冻深影响不大。图 13(a)显示负温对冻胀量与冻深产生较大的影响,顶部温度越低土柱内温度梯度越大,冻深越深,渗流速度增加促进冰透镜体生长导致冻胀量的增加。图 13(b)中上覆压力越大,冻胀量越小。当上覆压力较小时,随温度降低孔隙与颗粒接触间的水相变成冰产生膨胀,颗粒间距离增大,土体密实度减小,冻胀量较大;而当压力逐渐增大时,土体体积膨胀无法抵抗压力增大带来的压缩变形,后者占主导地位,使冻胀量减小。同时上覆压力的存在使土颗粒间受到挤压作用,冰透镜体难以形成,本身土体体积膨量减小。图 13(c)中渗透系数的改变会显著影响冻胀量,渗透系数增大时,水分迁移速度增大,成冰速度加快,冻胀量显著增加。但渗透系数过大时,土性发生改变,此时将不再产生成层冰透镜体现象,冻胀量反而减小。图 13(d)中压缩模量越大,负的平均水压力绝对值越小,未冻水膜压力越大,成层冰现象更明显,冻胀量增大。
4. 结论
冻土中的水分迁移和相变是一个复杂的过程。本文基于水膜理论提出了一个THM耦合模型,模拟了四类边界条件不同的冻结试验,并与文献模型进行了对比分析,验证了模型的准确性。同时,研究了上覆压力与温度边界条件对含水率与冻胀量的影响。得到4点结论。
(1)该模型采用平均水压力作为水分迁移驱动力,在未冻区能与现有模型实现兼容,在已冻区则考虑了冰表面的影响。选用未冻水膜相对压力代替以往模型孔隙压力对冰透镜体形成进行判断,概念清晰且更具物理意义。冻胀量计算包含冰透镜体厚度,结果更全面准确。此外,加入了成冰阻滞作用对渗透系数的影响,优化了含水率峰值计算。
(2)模型计算结果与实际试验结果对比表明,在冻胀量、温度、含水率、冰透镜体分布方面,模型与试验结果吻合较好,验证了模型的准确性。
(3)冻胀量计算结果与Feng模型对比表明,考虑成冰阻滞作用对渗透系数的影响优化了原位冻胀量计算,同时冻胀量包含冰透镜体厚度的累积,总冻胀量在数值与随时间变化趋势上与试验更接近;冻胀量计算结果与曹宏章模型对比表明,采取未冻水膜压力作为成冰判据,同时对时间与空间步长在初始高速降温阶段进行调整,在结果方面与试验拟合更好。
(4)顶温显著影响含水率峰值的位置,但对峰值大小几乎没有影响。顶温越低,冻胀量越大,冻深越深;上覆压力越大冻结锋面处聚集的水分含量越大,但冻胀量减小;未冻区渗透系数越大,含水率峰值与冻胀量均增加;压缩模量越大,含水率峰值越小,冻胀量增加。
-
表 1 冻胀模型主要变量说明
Table 1 Description of main variables in THM model
变量 物理意义 公式 来源 孔隙冰饱和度Si 孔隙冰与孔隙的体积之比 T+T0:1−[1−(T−T0)]α Tice等[19] 平均水压力P 驱动水分迁移的作用力 [σt−σ+(1−χ)Lln(T/T0)ρi]/[χ+(1−χ)ρi/ρw] Zhou等[13] 未冻水膜压力PLh 未冻水膜上的相对压力 P+g(h)ρw+Patm−Por Gilpin[3] 已冻区渗透系数k 单位水力梯度下的水流量 T+T0:ζw(1−Si)2b+3 Teng等[25] 土体体积热容C 单位体积土体温度改变1 ℃需要的热量 Csθs+Cwθw+Ciθi 徐学祖等[26] 导热系数λ 单位时间通过单位面积传递的热量 λθss+λθww+λθii 徐学祖等[26] 表 2 冻胀模型输入参数
Table 2 Input parameters in THM model
参数 取值 参数 取值 参数 取值 试验1:k0 /(m·s-1) 3.0×10-10 试验3:T0/℃ -0.3 λw/(W·(m·K)-1) 0.58 试验2:k0 /(m·s-1) 2.5×10-10 试验4:T0/℃ -0.3 Cs/(kJ·(m3·K) -1) 2160 试验3:k0 /(m·s-1) 2.5×10-10 试验1:ρs/(kg·m-3) 2720 Ci/(kJ·(m3·K) -1) 1874 试验4:k0 /(m·s-1) 2.5×10-10 试验2:ρs/(kg·m-3) 2700 Cw/(kJ·(m3·K) -1) 4180 试验1:Es/MPa 2.5 试验3:ρs/(kg·m-3) 2700 L/(kJ·kg-1) 334.56 试验2:Es/MPa 1.2 试验4:ρs/(kg·m-3) 2768 ξw 1 试验3:Es/MPa 0.8 ρi/(kg·m-3) 917 b 3 试验4:Es/MPa 12 ρw/(kg·m-3) 1000 α -5 试验1:T0/℃ 0 λs/(W·(m·K)-1) 1.2 β -8 试验2:T0/℃ -0.5 λi/(W·(m·K) -1) 2.22 σ∗tensile/kPa 12 表 3 不同试验的土性与边界条件参数
Table 3 Soil properties and boundary conditions of different tests
试验编号 顶部温度/℃ 底部温度/℃ 初始温度/℃ 底部状态 初始含水率/% 土的种类 干密度/(g·cm-3) 上覆压力/ kPa 土体高度/cm 冻结时间/h 来源 #1 -3℃ 3℃ 3℃ 补水 17 青海-西藏黏土 1.70 100 10 72 文献[16] #2 -1.7℃ 1℃ 1℃ 封闭 25.71 内蒙古粉质黏土 1.63 0 15 120 文献[26] #3 -2.3℃ 0.7℃ 0.7℃ 补水 18.9 黏土 1.70 0 10 72 文献[28] #4 1→-1 20 ℃/h
-1→-8 0.1 ℃/h1℃ 1℃ 补水 21.7 内蒙古粉质黏土 1.70 500 5 72 文献[24] 表 4 不同模拟工况参数表
Table 4 Parameters of different simulation conditions
工况 顶温/℃ 上覆压力/ kPa 渗透系数/ (10-10 m·s-1) 压缩模量/ MPa #1 -3 100 3 2.5 #5 -1.5 100 3 2.5 #6 -4.5 100 3 2.5 #7 -3 50 3 2.5 #8 -3 200 3 2.5 #9 -3 100 30 2.5 #10 -3 100 1 2.5 #11 -3 100 3 0.5 #12 -3 100 3 5.0 -
[1] TABER S. Frost heaving[J]. The Journal of Geology, 1929, 37(5): 428-461. doi: 10.1086/623637
[2] MILLER R D. Freezing and heaving of saturated and unsaturated soils[J]. Highway Research Record, 1972, 393: 1-11
[3] GILPIN R R. A model for the prediction of ice lensing and frost heave in soils[J]. Water Resources Research, 1980, 16(5): 918-930. doi: 10.1029/WR016i005p00918
[4] FOWLER A C. Secondary frost heave in freezing soils[J]. SIAM Journal on Applied Mathematics, 1989, 49(4): 991-1008. doi: 10.1137/0149060
[5] REMPEL A W, WETTLAUFER J S, WORSTER M G. Premelting dynamics in a continuum model of frost heave[J]. Journal of Fluid Mechanics, 2004, 498: 227-244. doi: 10.1017/S0022112003006761
[6] KONRAD J M, MORGENSTERN N R. A mechanistic theory of ice lens formation in fine-grained soils[J]. Canadian Geotechnical Journal, 1980, 17(4): 473-486. doi: 10.1139/t80-056
[7] HARLAN R L. Analysis of coupled heat-fluid transport in partially frozen soil[J]. Water Resources Research, 1973, 9(5): 1314-1323. doi: 10.1029/WR009i005p01314
[8] TAYLOR G S, LUTHIN J N. A model for coupled heat and moisture transfer during soil freezing[J]. Canadian Geotechnical Journal, 1978, 15(4): 548-555. doi: 10.1139/t78-058
[9] 原国红. 季节冻土水分迁移的机理及数值模拟[D]. 长春: 吉林大学, 2006. YUAN Guohong. The Mechanism and Numerical Simulation of Water Transfer in Seasonal Freezing Soil[D]. Changchun: Jilin University, 2006. (in Chinese)
[10] 李智明. 冻土水热力场耦合机理研究与工程应用[D]. 哈尔滨: 哈尔滨工业大学, 2017. LI Zhiming. Study on Mechanisum of Moisture-Heat-Stress Coupling for Frozen Soil and Engineering Application[D]. Harbin: Harbin Institute of Technology, 2017. (in Chinese)
[11] 白青波, 李旭, 田亚护, 等. 冻土水热耦合方程及数值模拟研究[J]. 岩土工程学报, 2015, 37(增刊2): 131-136. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16270.shtml BAI Qingbo, LI Xu, TIAN Yahu, et al. Equations and numerical simulation for coupled water and heat transfer in frozen soil[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(S2): 131-136. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16270.shtml
[12] THOMAS H R, CLEALL P, LI Y C, et al. Modelling of cryogenic processes in permafrost and seasonally frozen soils[J]. Géotechnique, 2009, 59(3): 173-184. doi: 10.1680/geot.2009.59.3.173
[13] ZHOU J Z, LI D. Numerical analysis of coupled water, heat and stress in saturated freezing soil[J]. Cold Regions Science & Technology, 2012, 72: 43-49.
[14] HUANG X, RUDOLPH D L. Coupled model for water, vapour, heat, stress and strain fields in variably saturated freezing soils[J]. Advances in Water Resources, 2021, 154: 103945. doi: 10.1016/j.advwatres.2021.103945
[15] LAI Y M, PEI W S, ZHANG M Y, et al. Study on theory model of hydro-thermal–mechanical interaction process in saturated freezing silty soil[J]. International Journal of Heat & Mass Transfer, 2014, 78: 805-819.
[16] MING F, LI D Q. Experimental and theoretical investigations on frost heave in porous media[J]. Mathematical Problems in Engineering, 2015: 1-9.
[17] 曾桂军, 张明义, 李振萍, 等. 正冻土中冰透镜体形成力学判据的分析讨论[J]. 冰川冻土, 2015, 37(1): 192-201. ZENG Guijun, ZHANG Mingyi, LI Zhenping, et al. Review of mechanical criterion for formation office lens in freezing soil[J]. Journal of Glaciology and Geocryology, 2015, 37(1): 192-201. (in Chinese)
[18] NIXON, DERICK J. Discrete ice lens theory for frost heave in soils[J]. Canadian Geotechnical Journal, 1991, 28(6): 843-859. doi: 10.1139/t91-102
[19] TICE A R, ANDERSON D M, BANIN A. The prediction of unfrozen water contents in frozen soils from liquid limit determinations[C]// Symposium on Frost Action on Roads. Oslo, 1973.
[20] 季雨坤. 冰透镜体生长机制及水热力耦合冻胀特性研究[D]. 徐州: 中国矿业大学, 2019. JI Yu-kun. Ice Lens Growth Mechanism and Hydro-Thermal-Mechanical Coupling Research on Frost Heave[D]. Xuzhou: China University of Mining and Technology, 2019. (in Chinese)
[21] ZHOU Y, ZHOU G Q. Intermittent freezing mode to reduce frost heave in freezing soils-experiments and mechanism analysis[J]. Canadian Geotechnical Journal, 2012, 49(6): 686-693. doi: 10.1139/t2012-028
[22] SHENG D C, ZHANG S, YU Z, et al. Assessing frost susceptibility of soils using PCHeave[J]. Cold regions science and technology, 2013, 95(11): 27-38.
[23] TENG J D, LIU J L, ZHANG S, et al. Frost heave in coarse-grained soils: experimental evidence and numerical modelling[J]. Géotechnique, 2022: 1-12
[24] 曹宏章. 饱和颗粒土冻结过程中的多场耦合研究[D]. 北京: 中国科学院研究生院, 2006. CAO Hongzhang. Research on Fields Coupling in Saturated Granular Soil Freezing Process[D]. Beijing: University of Chinese Academy of Sciences, 2006. (in Chinese)
[25] TENG J D, YAN H, LIANG S, et al. Generalising the kozeny-carman equation to frozen soils[J]. Journal of Hydrology, 2020, 594: 125885.
[26] 徐学祖, 王家澄, 张立新. 冻土物理学[M]. 北京: 科学出版社, 2001. XU Xuezu, WANG Jiacheng, ZHANG Lixin. Permafrost Physics[M]. Beijing: Science Press, 2001. (in Chinese)
[27] O'NEILL K, MILLER R D. Exploration of a rigid ice model of frost heave[J]. Water Resources Research, 1985, 21(3): 281-296.
[28] 周家作. 土在冻融过程中水、热、力的相互作用研究[D]. 北京: 中国科学院研究生院, 2012. ZHOU Jiazuo. Study on the Interaction of Water, Heat and Force in Soil during Freezing and Thawing[D]. Beijing: Graduate University of Chinese Academy of Sciences, 2012. (in Chinese)
-
期刊类型引用(6)
1. 张寿红. 气候变暖对青海湖水位变化成因的影响分析及未来水位预测. 科技和产业. 2025(05): 49-53 .  百度学术
百度学术
2. 崔新壮,张小宁,王艺霖,曾浩,高上,曹天才,吕伟,韩柏林. 路基湿度测量方法、演化规律及调控技术研究进展. 中国公路学报. 2024(06): 1-33 .  百度学术
百度学术
3. 李卓,姜鑫,张继勋,赵昱,王虞清,方艺翔. 土石坝护坡冻胀破坏水-热-力耦合数值模拟研究. 水利水运工程学报. 2024(03): 136-145 .  百度学术
百度学术
4. 李松,殷哲,焉莉,王鹏鹰,刘春慧,姜玲,郭洪宇,付辰琦. 农业冻土冰含量测量方法试验研究. 科技创新与应用. 2024(25): 80-83 .  百度学术
百度学术
5. 王长虹,魏永青,张海东,李飞. 地铁车站下水平冻结过程中冻胀的热-水-力耦合模型研究. 岩土力学. 2024(09): 2775-2785+2796 .  百度学术
百度学术
6. 唐先习,栾恩铭,董添春,李文龙,夏迪. 环青海湖铁路路基水热迁移与稳定性研究. 水利与建筑工程学报. 2024(06): 15-22 .  百度学术
百度学术
其他类型引用(11)
-
其他相关附件



 下载:
下载: