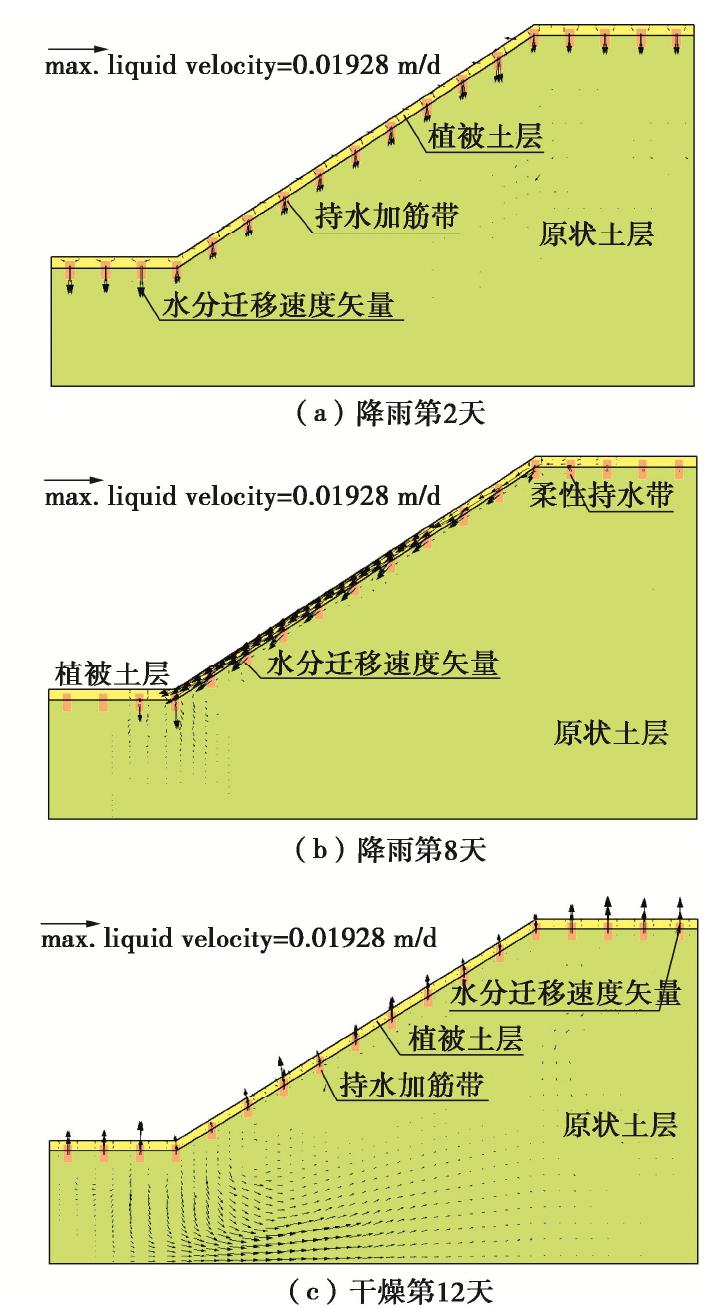
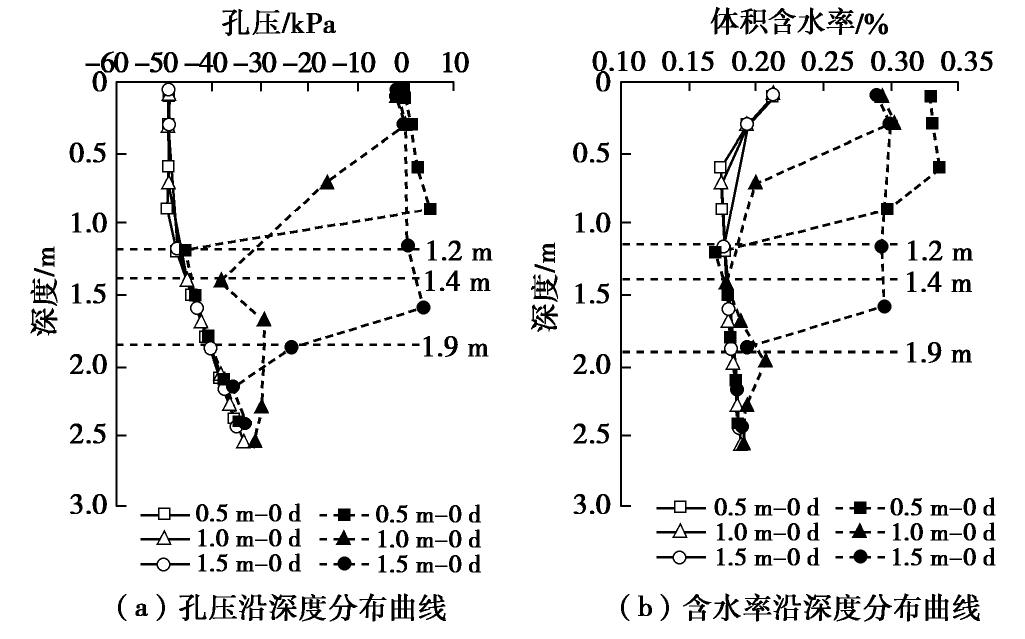
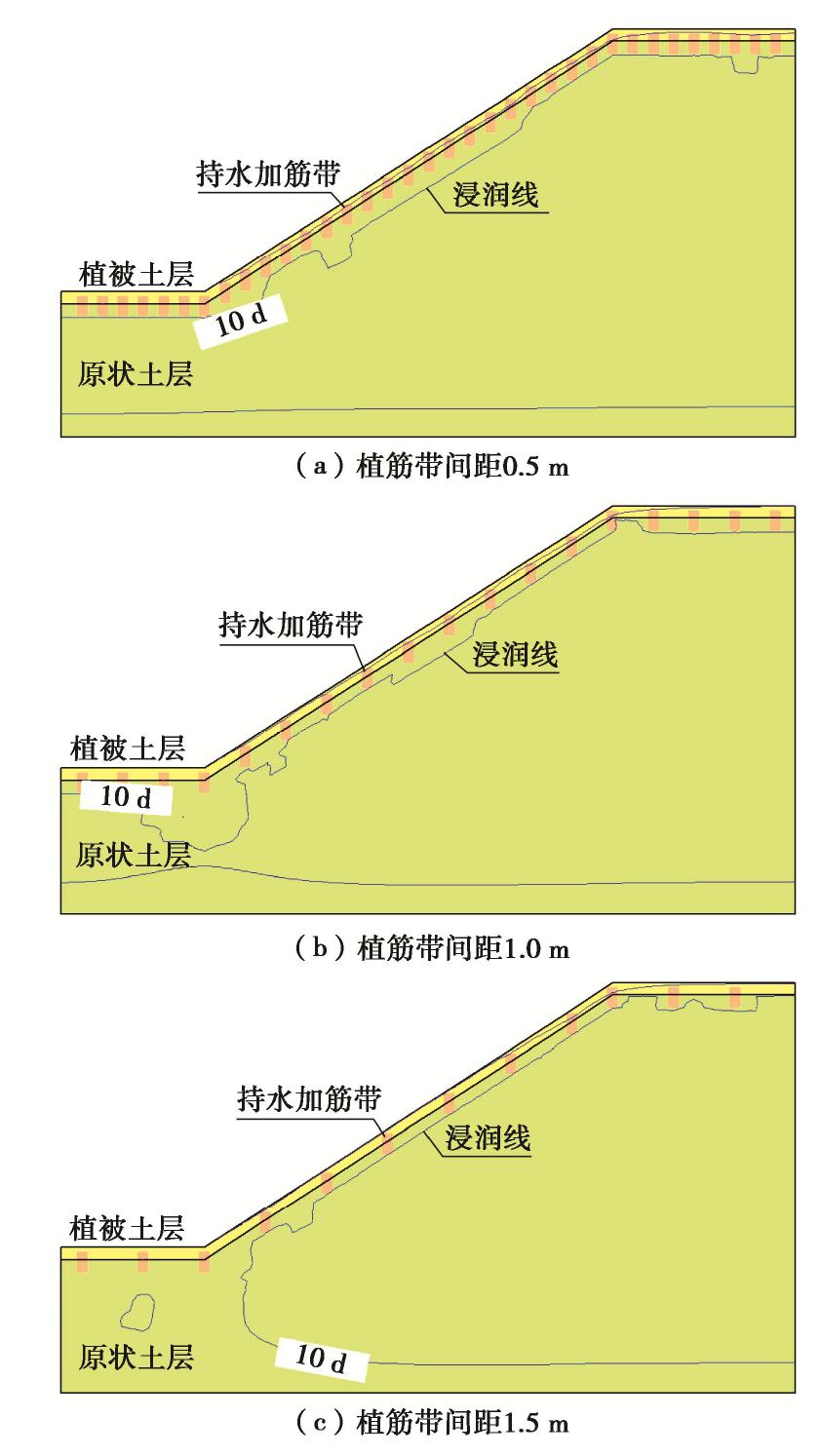
Numerical analysis of hydraulic characteristics of slopes reinforced by vertical geotextile belts and vegetation
-
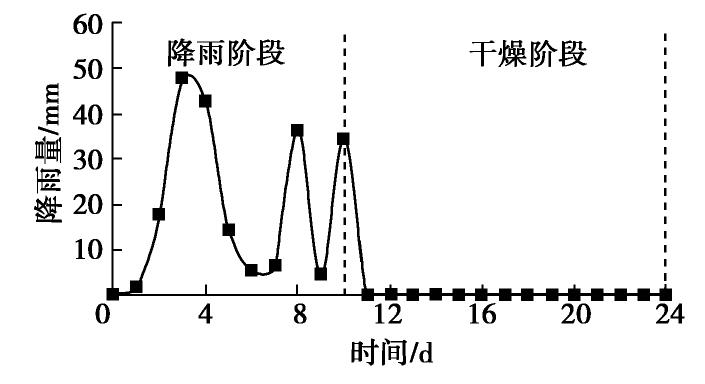
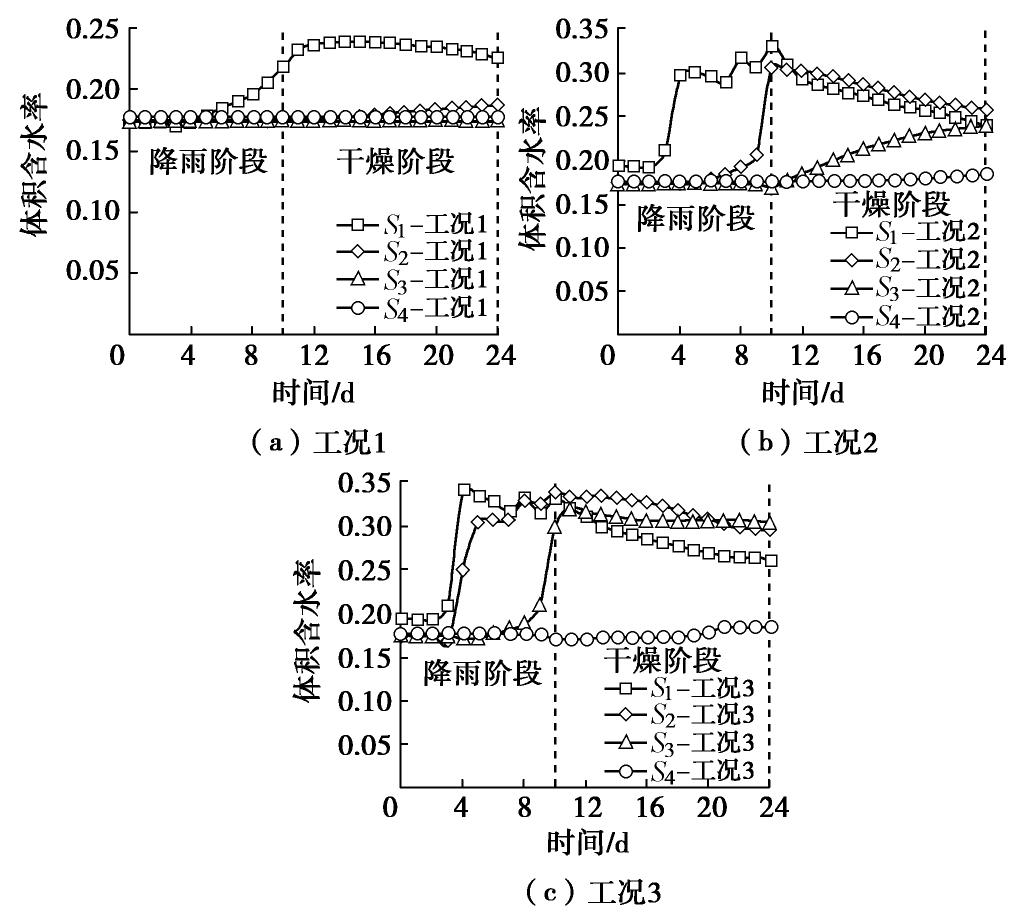
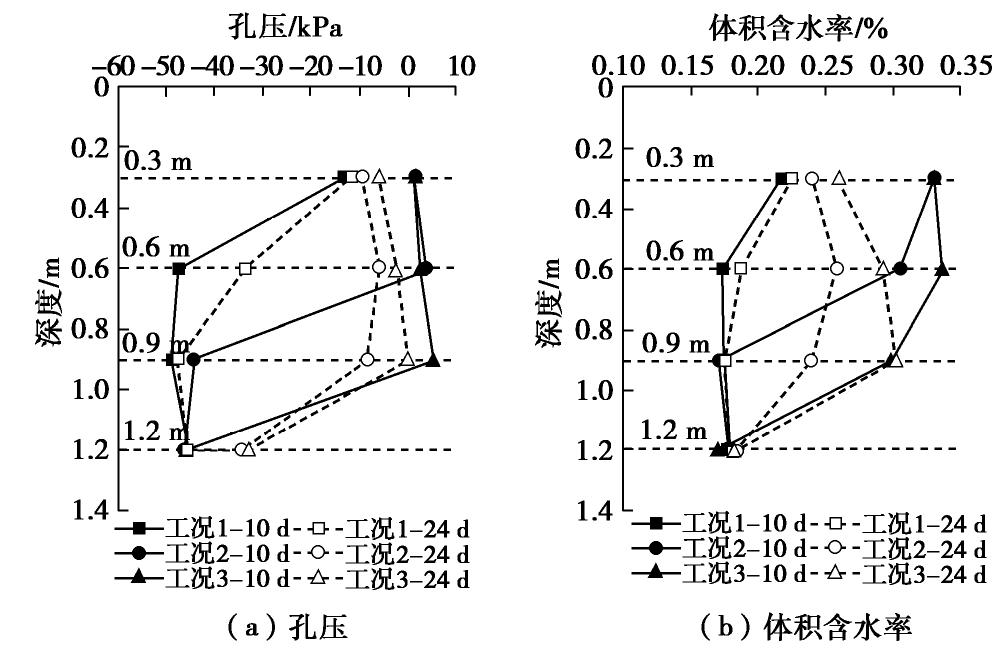
摘要: 植筋带(延长根)的抗拉强度能发挥比根系更长的力学加筋作用,但又会对降雨影响深度等产生影响,进一步改变边坡内部水力响应情况。因此本文对植被联合植筋带加固黏土边坡的水力特性开展数值计算,并结合裸土边坡和植被边坡进行对比分析。结果表明:降雨时植筋带很好地发挥了将雨水传送至深层坡土、干燥时将深处的水分运送至浅层坡土的作用。经历10 d降雨后,裸土边坡、植被边坡、植被联合植筋带加固的边坡(植被加固层20 cm厚、植筋带50 cm长)的降雨影响深度分别为0.6,0.9,1.2 m;再经历14 d的干燥过程后,坡体表层土含水率的大小顺序为:植被联合植筋带加固的边坡>植被边坡>裸土边坡。另外,竖向植筋带的设计参数例如长度和间距会影响坡土的降雨影响深度和坡面的雨量分配,植筋带长度越大,降雨影响深度越大;植筋带间距越小,坡面径流越小。布置细而密的植筋带可以改善坡脚积水状况,并抑制坡土表层裂隙开展,减小降雨滑坡风险。Abstract: The tensile strength of the vertical geotextile belts (the extended roots) can play a longer mechanical reinforcement than the plant roots, but it will also have an impact on the depth of rainfall, further change the hydrological response of slopes. The hydraulic characteristics of clay slopes reinforced by vegetation and vertical geotextile belts are calculated, and the comparison between bare clay slope and vegetated slope is made. The results show that the vertical geotextile belts play a good role in transferring rainwater to deep slope soils during rainfall and moisture from deep to shallow slope soils during drying. After 10 days of rainfall, the rainfall infiltration depths of the bare clay slope, the vegetated slope and the slope reinforced by vegetation and vertical geotextile belts (the vegetation reinforcement layer is 20 cm thick and the vertical geotextile belt is 50 cm long) are 0.6 m, 0.9 m and 1.2 m, respectively. After drying process for 14 days, the moisture contents of soils in the surface layer of slopes are as follows: the slope reinforced by vegetation and vertical geotextile belts > the vegetated slope > the bare clay slope. In addition, the design parameters such as length and spacing of the vertical geotextile belts will affect the rainfall infiltration depth of slope soils and rainfall distribution on slope surface. The longer the vertical geotextile belts, the deeper the rainfall influence depth; the smaller the spacing of vertical geotextile belts, the smaller the slope runoff, and the less the water accumulation at the toe of slopes. Planting thin and dense vertical geotextile belts can improve the water accumulation at the toe of slopes, restrain the development of surface cracks, and reduce the risk of landslides under rainfall.
-
0. 引言
土体冻结后并非土中所有的液态水都转变为固态冰,由于颗粒表面能的作用,土体中始终保持一定数量的液态水,称作未冻水[1],是影响冻土导热性、渗透性、强度、变形等特性的重要参数。冻结特征曲线描述了土中未冻水含量随温度变化的规律,给出适用不同土质的冻结特征曲线计算模型具有重要的工程价值。利用核磁共振技术测量土壤水分中氢原子核的横向弛豫时间,根据氢质子的含量及分布特性可以快速、准确、无损测试土壤水分含量及水分运动特性[2-4],已广泛应用于冻土未冻水含量的测试研究[5-9]。
Tsytovich[10]指出土中未冻水含量随温度的降低而减小,并根据温度变化1℃时未冻水含量变化大于1%、在0.1%~1%之间和小于0.1%,将土中未冻水变化过程分为剧烈相变阶段、过渡阶段和冻实阶段,如图 1所示。Michalowski等[11-12]认为剧烈变化阶段并不是一个温度区间,而是对应于土体的冻结温度Tf,并给出了过渡阶段未冻水含量的计算表达式,通常称为Michalowski模型:
wu=wb+(wa−wb)ea(T−Tf)。 (1) 式中:wu为温度T条件下的未冻水含量;Tf为土体冻结温度;wb为在温度极低情况下土体中存在的未冻水含量;wa为Tf温度下土体中最小未冻水含量;a是与土质有关的参数。
Tsytovich[10]描述的冻结曲线在温度点Tf处发生突变,具有不连续变化的特点,Michalowski模型描述的冻结特征曲线描述了过渡阶段的水分变化,不包括剧烈相变阶段和冻实阶段(图 1中曲线b所示),这样解决了冻结特征曲线在冻结温度点(剧烈相变阶段)处不连续的问题,在应用于数值模拟计算时十分方便,而且能很好地描述未冻水含量的变化规律。Michalowski模型中的有4个参数,其中Tf可由冻结温度曲线试验得到,wa和wb可由未冻水含量试验得到,a可利用未冻水含量的实测数据拟合得到,可见Michalowski模型参数的确定十分依赖实测数据,且试验测试的工作量较大,这限制了该模型的应用。
本文利用核磁共振技术对6种土体的冻结特征曲线进行了试验研究,分析了初始含水率和土体性质对Michalowski模型冻结特征曲线的影响,给出了土中最大结合水含量的测定方法,利用Michalowski模型参数的特征对其模型进行了改进,提升了该模型的实用价值。
1. 试验方法
1.1 试验材料
为了分析不同黏性土体的冻结曲线变化规律,试验使用的土体为黄土和蒙脱石混合而成,通过控制黄土和蒙脱石混合比例来控制土体黏性大小。6种土体的蒙脱石掺入量分别为0%,20%,40%,60%,80%,100%。其中0%代表土体为纯黄土,100%代表样品为纯蒙脱石。黄土采自甘肃兰州狗娃山,土颗粒相对质量密度为2.71;蒙脱石为钙基蒙脱石,蒙脱石含量 > 95%,土颗粒相对质量密度为2.45。采用Bettersize2600E激光粒度分布仪测量样品的粒径分布,得到黄土和蒙脱石样品的颗粒级配曲线,如图 2所示。采用X’Pert PRO多晶粉末X射线衍射仪,衍射角度范围为3°~40°,扫描速度为12°/min,得到的XRD衍射谱图,如图 3所示,蒙脱石主要矿物成分为蒙脱石、方石英,石英和钠长石,黄土主要矿物成分为石英,方解石、钠长石、高岭石和白云母。各试样的基本物理性质指标如表 1所示。
表 1 土的物理性质指标Table 1. Physical properties of soils土样编号 蒙脱石掺量S/% 土颗粒相对密度 塑限wP/% 液限wL/% 塑性指数IP #1 0 2.71 19.2 28.3 9 #2 20 — 26.1 39.6 14 #3 40 — 34.6 53.3 19 #4 60 — 41.3 73.4 32 #5 80 — 51.8 89.8 38 #6 100 2.45 62.2 104.5 42 1.2 试验仪器
(1)温度控制及测量设备
试验所采用的控温装置为低温冷浴,量程为-30℃~+100℃,精度为±0.1℃,测温装置采用中科院西北生态环境资源研究院生产的温度探头,精度为±0.01℃。
(2)核磁共振设备
采用纽迈分析仪器股份有限公司生产的PQ-001核磁共振分析仪进行未冻水含量测试。核磁共振分析仪主要由永磁体、试样管、射频系统和数据采集分析系统组成。永久磁体磁场强度为0.5±0.08T,共振频率为18~24 MHz,探头内径为28.6 mm,接收机死时间为11 μs,磁体均匀区范围为直径25 mm、高25 mm的圆柱体,为了保证主磁场的均匀性与稳定性,磁体温度维持在32±0.01℃。
1.3 试验方法
将配制好的土样装入直径为25 mm的玻璃试管中(土样高度20 mm),用隔水膜包裹后放入冷浴,由冷浴控制土样温度,样品达到目标温度并稳定1 h后,将试管从冷浴中取出,放入核磁共振分析仪中,测试该温度条件下未冻水的核磁信号。为避免采样过程中样品温度产生过大变化,采样时间控制在10 s左右。测试完成后放入冷浴,进行下一级目标温度控制。利用文献[4]给出的方法,对核磁信号进行温度校正后得到未冻水含量。由于降温过程中会存在过冷现象,过冷现象的触发会受试验过程中温度、振动、土体性质等方面的影响,并不稳定,所以会导致未冻水含量测试结果产生较大波动,采用升温过程测定未冻水含量可以避免过冷现象导致的数据波动。试验过程中利用冷浴将土样温度从室温降至-30℃,然后升温至30℃,在升温区间内对样品进行核磁共振测试,以此消除过冷现象的影响。
核磁共振测试序列采用CPMG序列,参数设置为:采样点数TD=12796,采样频率SW=200 kHz,采样间隔时间TW=600 ms,回波个数NECH=800个,回波时间TE=0.08 ms,累加次数NS=16次。
2. 试验结果与分析
2.1 初始含水率对冻结特征曲线的影响
关于土体冻结后的未冻水含量,是否受初始含水率的影响这一问题的认识存在争议。有学者认为土体初始含水率会显著影响未冻水含量,未冻水含量随着初始含水率的增大而增大[13-19];部分学者认为当土体总含水率大于液限时,初始含水率对未冻水含量没有影响或影响很小[10, 20],Watanabe等[21]、Kurylyk等[22]指出除了盐渍土或非常高孔隙率的土壤之外,土体未冻结水含量与初始总水分含量无关。本文对6种土体配制不同初始含水率的样品,利用核磁共振仪测定其降温条件下的未冻水含量,得到不同温度下土样的未冻结含水率曲线,如图 4所示。
图 4给出不同土质的样品的冻结曲线试验结果,可以看出,当土样温度高于冻结温度Tf时,土体含水率不随温度变化,当土样温度达到冻结温度Tf,土样含水率变化进入剧烈变化阶段,不同初始含水率土样中水分快速变化后,达到相同含水率wa,该过程对应于图 1中的曲线a。当土样温度小于冻结温度Tf时,土样含水率变化进入过渡阶段,土体含水率随着温度的降低,从含水率wa降低至含水率wb,且不同初始含水率土样的未冻水含量变化路径相同,该过程对应于图 1中的曲线b和曲线c(图 1中初始含水率w1和w2对应的未冻水变化路径所示)。上述情况在土样初始含水率大于wa时适用,当初始含水率小于wa时,土样的冻结曲线不存在快速变化阶段,随着温度降低,土体含水率保持不变,直到土样的温度-含水率曲线与冻结特征曲线相交时,土样含水率变化进入过渡阶段,其含水率开始随温度的降低而减小,且变化过程与冻结特征曲线保持一致(图 1中初始含水率w3对应的未冻水变化路径所示)。
上述规律表明冻结特征曲线与初始含水率无关,当土体的初始含水率大于wa,冻结过程中不同初始含水率土体的冻结特征曲线相同。从试验结果来看,这一规律对于本试验配制的6种土体均适用。冻结水的性质与未冻水有明显差异,所以Michalowski模型不考虑剧烈变化阶段的水分相变是合理的,且消除了初始含水率对冻结特征曲线的影响。
2.2 Michalowski模型参数分析
模型参数wa为土体冻结温度Tf条件下的土中未冻水含量,如何快速准确的确定模型参数wa和Tf,是在使用Michalowski模型前首先要解决的问题。在Michalowski模型冻结特征曲线上,以wa为分界点可以将Tf温度下的土中水分为两部分,这里将在剧烈变化阶段发生相变的水为冻结水,在剧烈变化阶段未发生相变的水为未冻水。很明显冻结水与未冻水的成分不同,由于二者土水相互作用存在差异,所以冻结水与未冻水的冰点不同。未冻水是吸附于土颗粒表面的薄膜水,土水相互作用较强,其冰点低于冻结水冰点,且其冰点随着薄膜水水膜厚度的减小逐渐降低。Michalowski模型Tf即为冻结水冰点,由于冻结水的土水相互作用较弱,Tf与纯水冰点十分接近受土质影响较小。基于上述规律,取纯水的冻结冻结温度0℃作为土体的冻结温度,则模型可以简化为三参数模型:
wu=wb+(wa−wb)eaT。 (2) 未冻水主要为吸附于土粒表面的薄膜水,未冻水含量wu和温度之间存在幂律关系[24]:
lgwu∝13lg(Tm−T)。 (3) 式中,Tm=0℃,T为试样温度。
图 5给出了6种土样在负温下未冻水含量wu与温度(Tm-T)幂律关系的拟合曲线。拟合结果见表 2,可以看出拟合方程可以很好地描述未冻水含量和温度的关系,但土体的拟合参数k值与理论值-1/3存在一定偏差,且不同土体的k值并不相同,变化范围为-0.38~-0.24。
表 2 拟合曲线参数Table 2. Parameters of fitting curve土体编号 斜率k 截距m 相关系数R2 #1 -0.38 0.56 0.99 #2 -0.28 1.01 0.97 #3 -0.25 1.22 0.98 #4 -0.26 1.38 0.95 #5 -0.23 1.47 0.95 #6 -0.24 1.58 0.98 影响水膜厚度的因素有很多,且影响机制也很复杂。范德华分子间力、静电力、固体颗粒表面水分子结构变化产生的作用都会影响水膜厚度,实测数据拟合得到的k值往往偏离理论值[24]。所以在没有实测数据时,式(3)难以直接应用于未冻水含量的预测。通过对实测数据进行拟合,可以得到wa(这里取温度为-1℃时的未冻水含量为wa),取实测数据最低温度对应的未冻水含量为wb,由wa,wb和实测数据的拟合,可以得到参数a,表 3给出6种土样的冻结特征曲线的参数。
表 3 Michalowski模型参数表Table 3. Parameters of Michalowski model土体编号 wa/% wb/% a #1 3.58 0.99 0.18 #2 10.09 3.99 0.15 #3 16.32 7.19 0.15 #4 23.75 9.53 0.13 #5 29.58 13.48 0.13 #6 37.38 15.94 0.12 将表 3中的模型参数代入式(2)可以得到6种土体冻结特征曲线的拟合方程,如图 6所示,可以看出,由Michalowski模型计算得到的未冻水含量理论值与试验值吻合很好,说明Michalowski模型可以很好地描述土体冻结过程中未冻水的变化规律,本文给出的Michalowski模型的参数wa,wb和a的取值方法是可行的。
2.3 土体性质对冻结特征曲线的影响
Michalowski[11]认为每种土体都有固定的冻结特征曲线,冻结特征曲线可以反映土体性质。利用表 1,3的数据可以得到土样的Michalowski模型参数wa,wb与蒙脱石掺量S的关系曲线,如图 7所示,可以看到Michalowski模型参数与蒙脱石掺量之间有明显相关性,这说明Michalowski模型参数带有土体的特征信息。
许多黏土表现出较高的膨胀和收缩特征、高压缩性、高保水性,这些特征主要取决于土颗粒的粒度分布和矿物组成,常用液塑限指标来反映。利用表 1,3的数据可以得到土样的Michalowski模型参数wa与液塑限指标wL,wP的关系曲线,如图 8所示,wa和界限含水率指标之间具有非常好的正相关性,wa越大,土体黏性越强,这表明wa可以很好地反映黏性土特征。wa和土体液塑限指标的拟合公式如下:
wL=2.35wa+17.58, (4) wP=1.272wa+13.619, (5) IP=1.073wa+3.965。 (6) 未冻水是存在于土颗粒表面薄膜吸附水,水膜厚度主要是由分子间作用力所控制。这种分子间作用力和土体颗粒表面矿物组成密切相关,主要包括固体表面所带电荷与极性水分子之间的静电力、vander Waals力、水分子电极与固体颗粒表面的相互作用力、氢键作用等。未冻水含量可用土颗粒比表面积和颗粒表面未冻水最大水膜厚度的乘积来计算。土体比表面积反映了土体颗粒的粒度分布,未冻水最大水膜厚度可以反映土体颗粒的矿物组成。wa带有土体颗粒粒度分布和矿物组成两方面信息,相较于土体的液塑限指标具有更加明确的物理含义,可以作为表征和分析黏性土特性的重要指标参数。从上文的分析可以看出,由wa作为分界点划分出的冻结水和未冻水在性质上存在明显的差异,可以近似认为冻结水主要成分为毛细水和自由水,未冻水主要成分为结合水。当不考虑温度对结合水含量的影响时,wa可以作为土中毛细水和结合水的含水率分界点[25]。当土体含水率大于wa时,wa即为该状态下土中结合水含量,当土体含水率小于于wa时,土体含水率为该状态下土中结合水含量,所以模型参数wa为土中最大结合水含量。
2.4 Michalowski未冻水模型改进
Michalowski模型方程是由未冻水含量的实测数据拟合得到,所以Michalowski模型的参数确定十分依赖实测数据,需要测定从0℃降温至一个极低温度(本文取-30℃附近)过程中的含水率变化。较准确未冻水含量测试需要使用核磁共振分析仪和控温设备,对试验设备的要求高,工作量大,极大限制了Michalowski模型的实用性。
图 9给出了三参数之间的关系曲线,wa和wb之间的相关度很高,二者线性方程的相关系数达到0.992,wa和a关系曲线的相关系数为0.85,这说明Michalowski模型3个参数之间存在联系,并非完全独立。利用3个参数之间的关系,可以简化模型参数,降低模型的使用难度。式(7),(8)分别给出了wa和wb、wa和a之间的相关关系,将式(7),(8)代入式(2),得到只有一个参数wa的Michalowski模型,见式(9),这里称为单参数Michalowski模型。
wb=0.448wa−0.5, (7) a=−0.00144wa+0.17224, (8) wu=0.448wa−0.5+(0.552wa+0.5)e(−0.00144wa+0.17224)T。 (9) 只需知道模型参数wa,就可以利用单参数模型得到描述土体未冻水含量冻结特征曲线,图 10给出了6种土体的单参数Michalowski模型计算值。可以看出,单参数模型的计算结果和改进前的三参数模型的计算结果差异不大,单参数模型计算值和实测值的吻合很好,说明简化后的单参数Michalowski模型可以实现对未冻水含量的良好预测。由于三参数模型简化为单参数模型,是基于Michalowski三参数之间存在一定的相关性,无疑相关性越强,简化后的误差越小,所以模型简化后的误差的大小,取决于Michalowski三参数之间相关关系的准确性,而本文给出的Michalowski三参数之间相关关系是否适用于所有土体,还需要更多土体的试验结果进行探索。
土体界限含水率指标和wa之间存在很强的相关性,利用单参数模型,在无未冻水含量测试相关设备时,使用土体液塑限指标,即可对未冻水含量进行预测。以土体液限为例,将土体液限代入式(4)可得wa,再将wa代入式(9),可以得到土体冻结特征曲线,结果如图 11所示。可以看到该方法可以实现对未冻水含量的良好预测,但是该方法中wa是利用液限指标由经验公式计算得到,和实测wa的方法相比,预测效果要差一些。
综上,单参数Michalowski模型能实现对未冻水含量的良好预测,同时可极大的降低Michalowski模型的使用难度,提升Michalowski模型的实用价值。本模型中未考虑盐分,外荷载、密度和冻融历史的影响,模型的适用范围,有待更多数据验证,在使用时应对其局限性予以考虑。
3. 结论
本文利用核磁共振技术对6种土体的冻结特征曲线进行了试验研究,从初始含水率和土质两方面对Michalowski模型参数进行了分析,利用Michalowski模型参数的特征对模型进行了改进,得到以下4点结论。
(1)冻结特征曲线与初始含水率无关,当土体的初始含水率大于wb,冻结过程中不同初始含水率土体的冻结特征曲线相同。
(2)在Michalowski模型冻结特征曲线上,以wa为分界点可以将Tf温度下的土中水划分为冻结水和未冻水两部分。冻结水主要成分是毛细水和自由水,与土颗粒表面作用较弱,其冰点接近纯水冰点。
(3)不考虑温度影响时,模型参数wa近似等于土中最大结合水含量,wa带有土体颗粒粒度分布和矿物组成两方面信息,相较于土体的液塑限指标具有更加明确的物理含义,可以作为表征和分析黏性土特性的重要指标参数。
(4)单参数Michalowski模型在实现对未冻水含量的良好预测的同时,可极大的降低模型的使用难度,提升模型的实用价值。模型中未考虑盐分,外荷载、密度和冻融历史的影响,应用时具有一定局限性,模型的适用范围,有待更多数据验证。
-
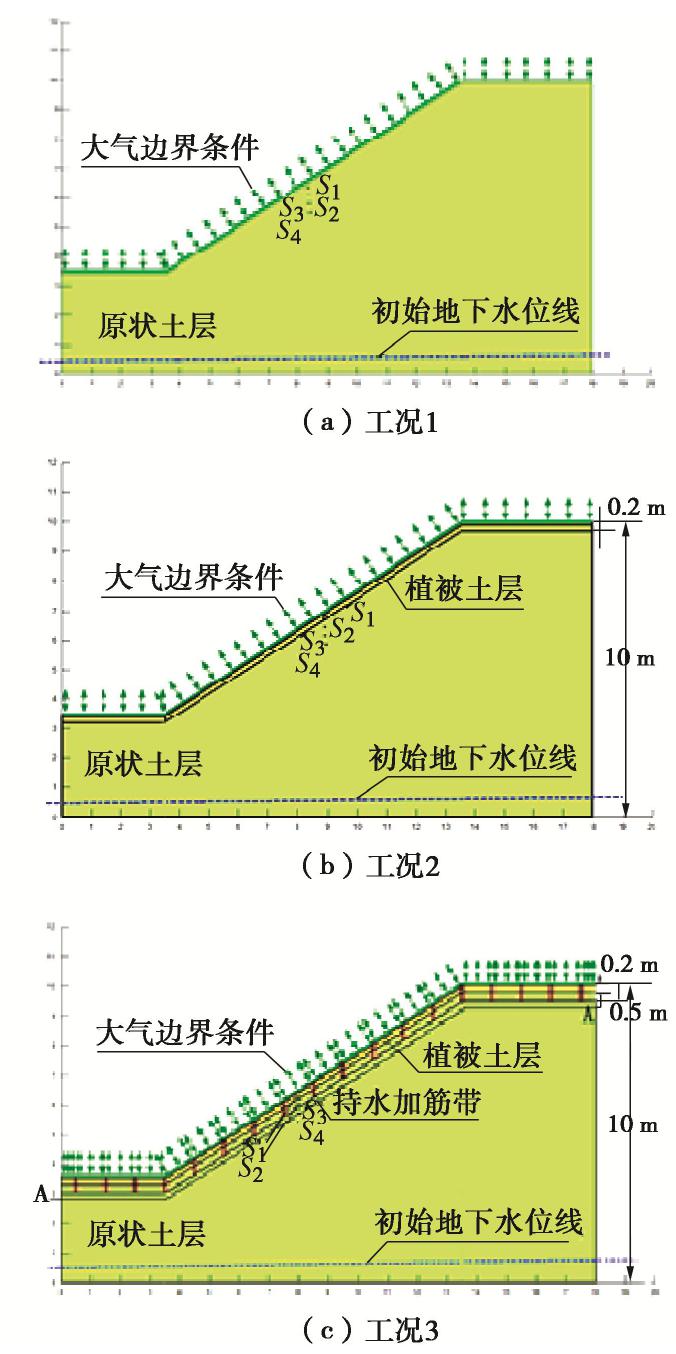
表 1 不同加固工况的方案设计
Table 1 Scheme design of different reinforcement conditions
工况设置 加固方式 说明 工况1 裸土边坡 无植被覆盖,作为对照组 工况2 植被固坡 考虑一般灌草植物根系的深度,植被加固土层厚度取为20 cm 工况3 植被+植筋带固坡 植被加固土层厚度取为20 cm,竖向植筋带间距为1 m,竖向植筋于坡面以下50 cm厚的土层内。 表 2 材料土水特征拟合参数
Table 2 Soil-water characteristic fitting parameters of materials
参数 材料 黏土 植被土层1 植被土层2 植筋带 θs 0.33 0.33 0.33 0.43 θr 0.002 0.001 0.001 0.004 /cm-1 0.04 0.10 0.15 0.30 n 1.215 1.114 1.052 1.305 Ks/(cm·d-1) 7 20 20 90 注: 植被土层1为仅受植被根系影响的土层,植被土层2为同时受到植被根系和植筋带影响的土层。 -
[1] MORGAN R P C, RICKSON R J. Slope stabilization and erosion control: a bioengineering approach[J]. Soil Technology, 1995, 8(1): 75-76. doi: 10.1016/0933-3630(95)90007-1
[2] POLLEN-BANKHEAD N, SIMON A. Hydrologic and hydraulic effects of riparian root networks on streambank stability: is mechanical root-reinforcement the whole story?[J]. Geomorphology, 2010, 116(3): 353-362.
[3] DEVITT D A, SMITH S D. Root channel macropores enhance downward movement of water in a mojave desert ecosystem[J]. Journal of Arid Environments, 2002, 50(1): 99-108. doi: 10.1006/jare.2001.0853
[4] NG C W W, ZHAN L T. Comparative study of rainfall infiltration into a bare and a grassed unsaturated expansive soil slope[J]. Canadian Geotechnical Journal, 2011, 47(2): 207-217.
[5] LEUNG A K, GARG A, NG C W W. Effects of plant roots on soil-water retention and induced suction in vegetated soil[J]. Engineering Geology, 2015, 193: 183-197. doi: 10.1016/j.enggeo.2015.04.017
[6] NG C W W, NI J J, LEUNG A K, et al. Effects of planting density on tree growth and induced soil suction[J]. Géotechnique, 2016, 66(9): 711-724. doi: 10.1680/jgeot.15.P.196
[7] INDRARATNA B, FATAHI B, KHABBAZ H. Numerical analysis of matric suction effects of tree roots[J]. Geotechnical Engineering, 2006, 159(2): 77-90. doi: 10.3969/j.issn.1007-2993.2006.02.007
[8] ZHU H, ZHANG L M. Evaluating suction profile in a vegetated slope considering uncertainty in transpiration[J]. Computers & Geotechnics, 2015, 63(26): 112-120.
[9] WU T H, KOKESH C M, TRENNER B R, et al. Use of live poles for stabilization of a shallow slope failure[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2014, 140(10): 05014001.
[10] 周成, 吴美苏, 党晓强, 等. 根系联合框架拉筋带生态防护黄土边坡的方法, CN106958251B[P]. 2019-02-12. [11] 杨文琦. 植被生态柔性防护土坡的水力特性研究[D]. 成都: 四川大学, 2019. YANG Wen-qi. Study on Hydraulic Characteristics of Clay Slope Stabilized by the Ecological Flexible Protection Structure[D]. Chengdu: Sichuan University, 2019. (in Chinese)
[12] GEO-SLOPE International Ltd. Vadose Zone Modeling with VADOSE/W 2007[S]. 2008.
-
期刊类型引用(6)
1. 佟彬,张斌,朱汉标,王树英. 双模盾构土压模式下下穿珠江断裂带开挖面稳定性研究. 中外公路. 2024(05): 232-240 .  百度学术
百度学术
2. 支斌,李树忱,朱颖,田垚,万泽恩. 土压平衡盾构螺旋输送机渣土运移及参数影响. 应用力学学报. 2023(01): 107-115 .  百度学术
百度学术
3. 刘晓明,王艺钢,赵明华. 岩溶发育区公路路基强夯处治方法研究与应用. 中外公路. 2023(02): 16-21 .  百度学术
百度学术
4. 王树英,汪来,杨鹏,龚振宇. 渣土改良下盾构掘进富水砾砂地层响应研究. 隧道建设(中英文). 2023(S1): 87-97 .  百度学术
百度学术
5. 尹志清,翟维骏,韩爱民,陈冬,郝保安,李彤,陈冲. 基于符号回归算法的地铁盾构刀盘扭矩预测研究. 城市轨道交通研究. 2021(01): 127-131 .  百度学术
百度学术
6. 展超. 基于BP神经网络的富水砂层渣土改良试验效果预测. 隧道建设(中英文). 2020(07): 988-996 .  百度学术
百度学术
其他类型引用(12)




 下载:
下载: