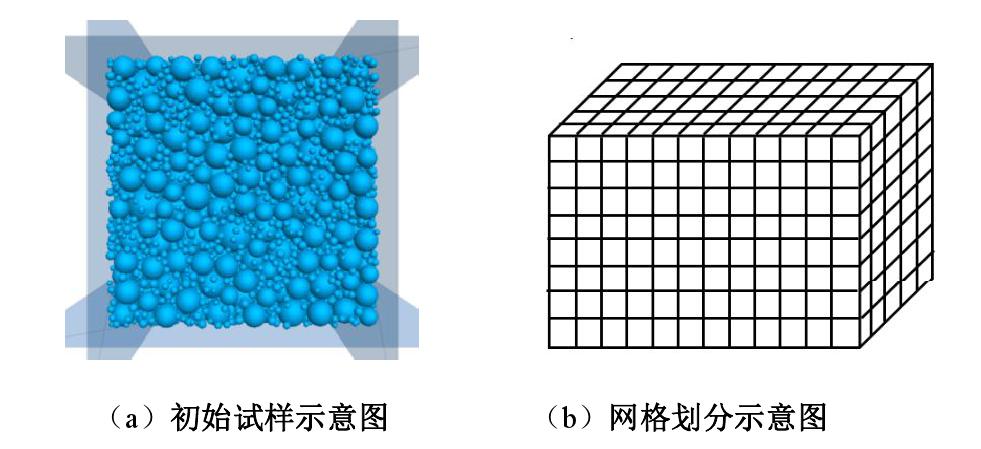
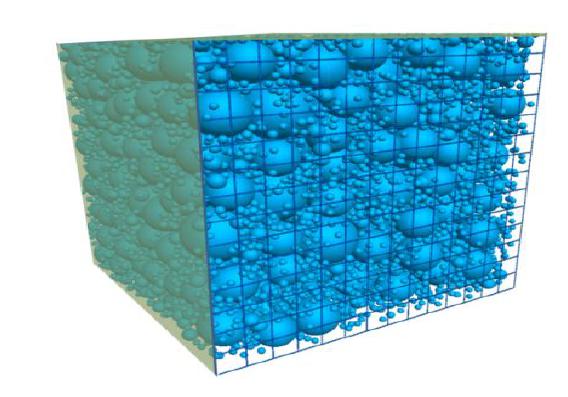
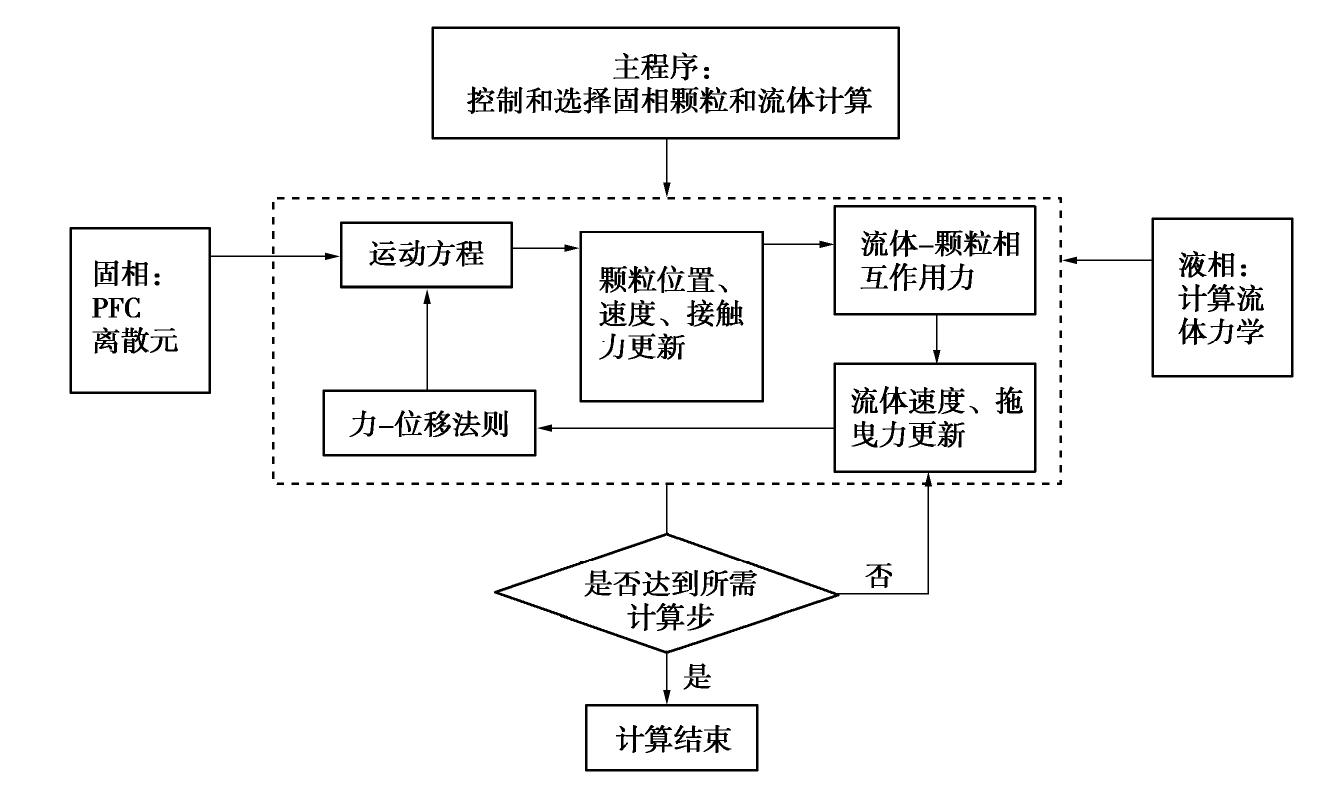
Permeability characteristics of silty sand under vertical and horizontal seepages
-
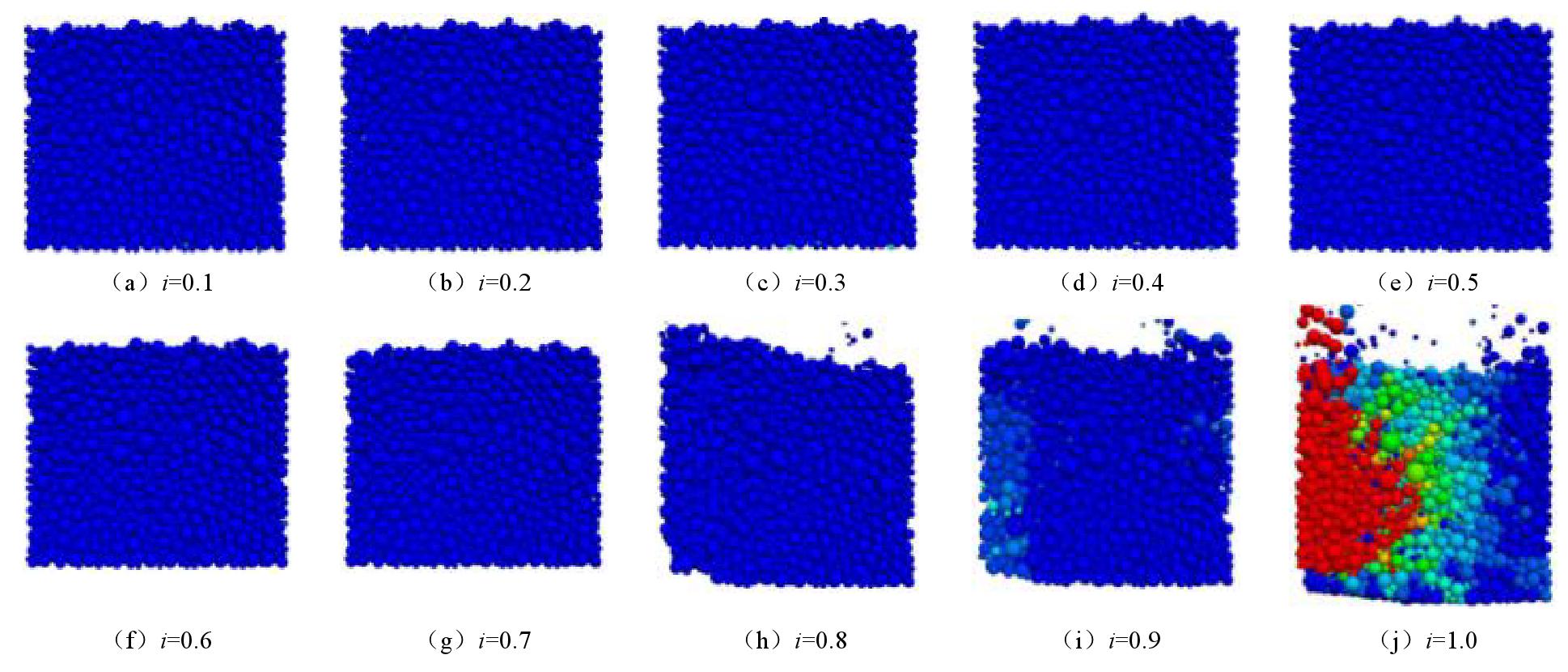
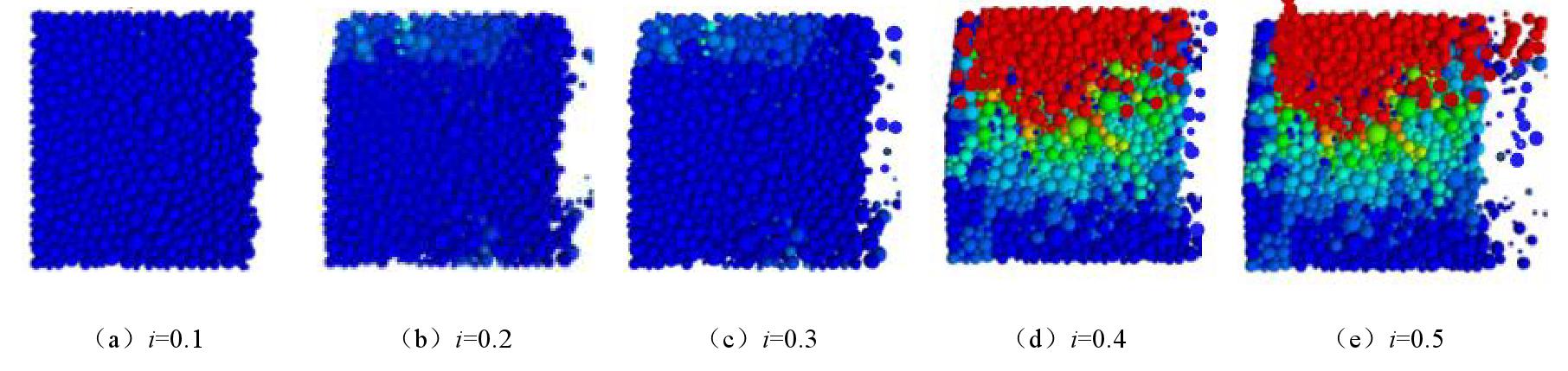
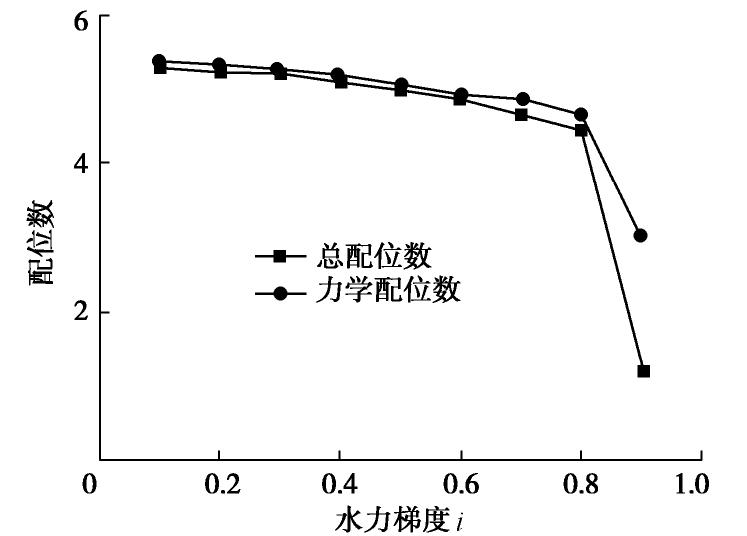
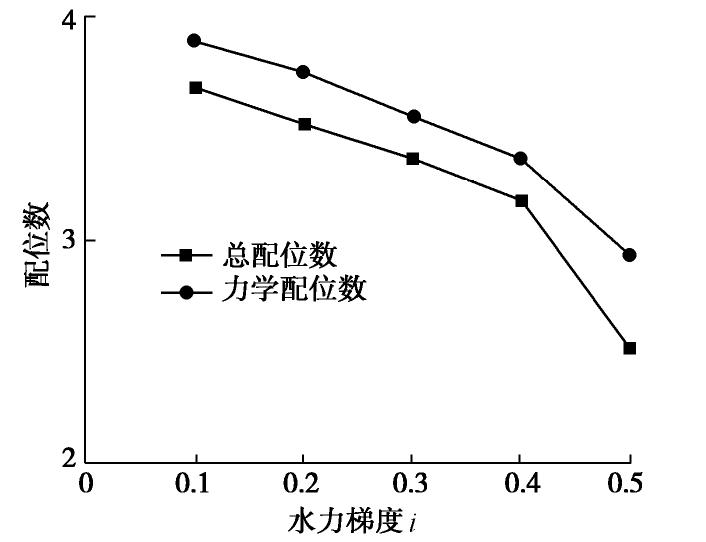
摘要: 采用自主研制的圆柱形渗流仪及水平渗流装置,开展了粉砂竖向和水平向的渗流试验,获取了两种渗流方向下粉砂的临界水力梯度及其渗透变形特性。在级配、密度、孔隙大小等影响因素相同的前提下,粉砂竖向渗流的临界水力梯度比水平向高出近44%,水平向渗流作用一般高于竖向。基于室内试验成果,采用离散元与计算流体力学耦合的细观力学模型,对粉砂在竖向和水平向的渗流情况进行分析和模拟。结果表明,粉砂的渗透变形拐点与模型试验结果吻合,水平渗流和竖向渗流分别在水力梯度i=0.8,0.4时出现颗粒簇的流失,在水力梯度分别为1.0和0.5时发生整体渗透破坏。Abstract: The influence of seepage direction on the silt permeability are studied. The vertical and horizontal seepage tests of silty sand are carried out by using the self-designed devices. The critical gradient and deformation characteristics of silt under two different seepage directions are obtained in the tests. When the other influencing factors such as gradation, density and pore size are the same, the vertical hydraulic gradient of horizontal seepage of silt is generally 44% higher than the critical one, and the horizontal seepage is generally higher than the vertical one. The data can be used for design of seepage control of the silt. Based on the indoor model tests, the micro-mechanical model is used to analyze and simulate the seepage behavior of the silt under vertical and horizontal directions. The hydraulic gradients of the two seepage directions calculated by numerical model are consistent with the test ones. The loss of particle clusters occurs in horizontal and vertical seepages at hydraulic gradients of 0.8 and 0.4, respectively. The research results may provide a theoretical basis for the design of seepage control in water conservancy and hydropower projects with silt layer.
-
Keywords:
- seepage direction /
- silty sand soil /
- permeability test /
- fluid-solid coupling
-
0. 引言
国家“十四五”规划《纲要》和《交通强国建设纲要》对建设现代化高质量综合交通网进行了统筹部署,提出推动交通发展要由追求速度向注重质量效益转变。提升公路基础设施建设与养护能力,是建成交通强国的重要举措。截至2022年底,中国公路通车总里程535×104 km,其中高速公路通车里程17.7×104 km[1]。伴随交通基础设施的大规模建设发展,路基结构老龄化问题日益突出,大量工程进入“带病害服役”阶段,可以预见未来中国交通基础设施养护工程量将大幅度增长[2]。
翻浆冒泥是路基主要病害类型,具有隐蔽性、渐进性和发生周期不规律特点。中国青藏公路[3]、朔黄铁路[4]和沪宁城际铁路[5]等翻浆路段,均不同程度出现路基结构裂损、填料侵蚀、路面/轨道平顺性变差,给车辆长期行车安全带来潜在威胁。对此,国内外专家先后提出增强防排水[6]、注浆[7]、铺设土工布或土工膜[8]等处治修复措施,但这些措施的中、长期处治效果并不理想,不少路段经处治后仍呈现翻浆反复发作趋势[9]。根本原因在于,目前缺乏对翻浆冒泥孕育与致灾机制的准确认识,造成制定病害处治措施时带有一定的盲目性。
翻浆冒泥是交通荷载下路基填料内水与细颗粒相互作用的结果,孕育过程涉及土动力学、渗流力学、颗粒介质力学等学科理论与方法。一般而言,行车引起的动水力作用下,土中细颗粒逐渐脱离、悬浮并迁移至上层路床,因此翻浆可以视为一个水-质迁移过程[10]。在理论和数值计算方面,Bedrikovetsky等[11]建立了描述渗流下细颗粒脱离、附着和拉伸运动的数学模型,探究了细颗粒在渗流场内的运动时变规律。Wank等[12]、Mawatari等[13]和周健等[14]研究了振动场下颗粒的流态化机理,表明增大加载频率和振幅,能够显著降低颗粒的最小流化速度。Zhou等[15]、Zhou等[16]研究了粒径、颗粒体积分数、以及流速和流量等对颗粒迁移和团聚效应的影响规律。由于不同学者采用的颗粒生成方法、粒径及接触模型不一致,导致研究结果的离散性较大,可靠性也很难得到验证。基于室内模型试验方法探究路基水-质迁移翻浆特征及驱动机制也得到了普遍应用,包括Alobaidi等[17]、Kermani等[18]、蔡袁强等[19]、韩博文等[20]试验发现超孔隙水压消散过程中路基土侵蚀发育明显,且细颗粒迁移规模很大程度上取决于超孔隙水压发展特性。白冰等[21]研究了粒径、颗粒浓度、渗流速度等对多孔介质中颗粒迁移的水动力学过程、以及弥散和沉积效应的物理机制。张升等[22]、Zhang等[23]、Gao等[24-25]发现动荷载下道床积水的晃动会形成振荡超孔压梯度,进一步描述了超孔隙水压变化与翻浆发展间的内在联系。上述研究先后剖析了土性、水及动力荷载等内外因素对翻浆发展的影响机制,为科学选择填料类型和管控交通流提供了理论和试验指导,但先前学者普遍关注单调循环加载下翻浆过程的颗粒运动规律,而考虑动静组合加载下颗粒迁移与沉积特征研究尚未见诸于报道。
应用自主研发的路基动力试验系统,开展了动-静组合荷载下分层砾石-砂粉土试样的翻浆试验。调查了泥浆浊度时空演变特征;分析了翻浆状态下动荷载强度和加载频率、静荷载间歇时长,以及动静组合加载重复次数对颗粒迁移和沉积运动的影响规律;探究了动水力响应分布和演化特征与颗粒运移间的内在关联。相关研究为推动建立路基翻浆病害等级评价标准,也为开展翻浆致灾机理的模型和数值计算提供了试验验证。
1. 室内试验
1.1 试验材料
试验材料为取自长沙地区的砾石和砂粉土。根据ASTM D6913规定的土体物理参数测定方法[26],砾石的相对质量密度Gs为2.64,最大孔隙比emax和最小孔隙比emin分别为0.78,0.56。砾石是由高强度的玄武岩材料组成,在本次加载试验中未出现破碎现象。砂粉土的相对质量密度Gs为2.68,有效粒径d10和平均粒径d50分别为0.01,0.40 mm,最大孔隙比emax和最小孔隙比emin分别为0.72,0.46,不均匀系数Cu和曲率系数Cc分别为53.0,8.3,细粒含量Fc(粒径小于0.075 mm)为15.8%,渗透系数ks为6.0×10-6 m/s。试验前砾石和砂粉土需进行烘干、筛分和清除杂质等系列预处理,经处理后的砾石和砂粉土颗粒级配曲线,如图 1所示。结合Tasalloti等[27]和Sheng等[28]对现场翻浆冒泥土颗粒组成的调查结果可知,本次研究使用的砂粉土级配介于常见翻浆冒泥土的级配组成范围内。
1.2 试验装置
自主研发的路基动力试验系统如图 2所示。试验系统主要包括竖向加载装置、水位调节装置和数据采集装置等。竖向加载装置可提供单调连续、动-静组合等加载条件;圆柱型模型箱内径为180 mm,高度为510 mm,其材质是透明有机玻璃。模型箱侧壁竖向布置5个测量层,每一层包括孔隙水压力计、湿度计(TDR)和泥浆收集器,且安装前需严格标定和校准。例如,孔隙水压力计需浸没在纯净水中超过24 h,并间断振动以彻底清除内部空气。基于颗粒沉积分析法[22],每隔30 min收集并测量泥浆浊度。使用佳能EOS 6D Mark Ⅱ高清相机放置在模型箱正前方,调整相机位置和焦距获得适合视场,以录像、拍照方式记录颗粒空间分布和运动情况。水位调节装置实现调控试样内饱和度、水力梯度和水位高度等。数据采集装置包括Datataker DT 85采集仪、电子计算机等,记录并存储孔隙水压和体积含水量指标,以及称重传感器和加速度计采集的动应力大小和加载频率。试验时室内温度维持在20±2 ℃。
1.3 试验步骤
(1)试样制作
采用分层装填压实方法制作试样,并按照《铁路路基设计规范》(TB 10001—2016)基床填料压实标准,设计150 mm厚的砂粉土层,初始密实度为90%;250 mm厚的上部砾石层,初始压实度为95%,试样总高度为400 mm。砾石层自上而下包括3个测量层,分别为砾石顶、中和底层(深度分别为60,140,220 mm);砂粉土层自上而下包括2个测量层,分别为砂粉土顶和底层(距土表面深度分别为50,130 mm)。需要注意的是,装填材料接近传感器时,应先固定传感器而后用少量材料包裹住传感器再仔细压实。
(2)水位上升
试样制作完成后,打开模型箱底部的进水阀,在静水压力下水位逐渐上升并浸没试样,且保持低渗流状态防止细粒流动。以试样底边界为零势能面,水位恒定时各层处的孔隙水压和体积含水量达到稳定,在整个加载过程中水位高度恒定为400 mm。
(3)加载测试
动-静组合荷载施加在试样表面,荷载参数考虑了列车轴重、运行速度和间歇时长影响。相关现场监测表明,轴重介于150~250 kN的列车运行速度从200 km/h增大到350 km/h时,路基表面动应力大致为10~40 kPa,加载频率介于13~30 Hz[29]。列车运营频次取决于地区的市场需求和运输成本,如京沪高速铁路在高峰时段的服务间隔时长不超过10 min,而夜间维护期则普遍超过数十小时[30]。基于此,设定了5种动静组合加载条件(表 1)。试样累积承受连续9次动静组合加载,且每一个重复周期内动、静荷载的加载时长均为30 min。以上加载方案能够造成较为显著的翻浆现象,为研究泥浆内颗粒迁移和沉积运动创造条件。
表 1 动静组合加载试验方案Table 1. Test schemes of combined dynamic and static loads试验序号 加载频率f/Hz 平均动应力σm/kPa 动应力幅值σd/kPa 动静组合加载重复次数M 动荷载单次循环次数N /103 静荷载单次间歇时长t/min 1 15 30 5.0 9 27 30 2 20 30 36 30 3 25 30 45 30 4 20 18 36 30 5 20 36 36 30 2. 试验结果与分析
2.1 泥浆浊度时变特性
通过高清相机捕捉颗粒运动全过程变化,图 3给出了动-静组合荷载下砾石-砂粉土接触面处的观测图像,砾石层内棕色越深代表泥浆越浑浊。加载前可以看到一条清晰的接触面,此时颗粒和孔隙流体均保持静止状态。施加动荷载后,砂粉土颗粒逐渐向上迁移进入砾石层,且迁移颗粒悬浮在泥浆中。进入静载间歇期,孔隙流体很快恢复平静,悬浮颗粒在重力下发生沉降并填充到砾石底层,该阶段内没有新的颗粒进入到砾石层。当再次施加动载,这些沉降颗粒会在动水力作用下快速悬浮,同时又有新的颗粒从砂粉土层进入砾石层内。
不同加载条件下砾石层内泥浆浊度随时间的变化,如图 4所示。受颗粒反复悬浮和沉降影响,不同深度处泥浆浊度随时间呈现波动增长。由于每个重复周期内存在一些颗粒进入砾石层内,因此泥浆最大浊度随重复次数增加而增大。但在砾石顶和中层,泥浆浊度增长趋势不如底层显著,分析原因是颗粒反复悬浮和沉积过程中,砾石层增大了颗粒的迁移阻力,并导致更多的悬浮颗粒倾向于聚集在砾石底层。值得注意的是,改变动静组合加载条件可以缩小砾石层不同深度层内的浊度差。例如,在加载频率f为20 Hz时,平均动应力σm为36 kPa的砾石顶和中层泥浆浊度远超过平均动应力σm为18 kPa的测量结果;而在同一动荷载应力水平下,改变加载频率也得到了相似的浊度分布情况。上述结果表明增大加载频率和平均动应力,有利于扩大颗粒迁移翻浆规模,特别是显著增加了悬浮颗粒向上的迁移距离,造成泥浆从砾石层表面“翻”出。
2.2 颗粒悬浮与沉积运动
忽略加载引起的砾石层体积压缩,根据泥浆浊度时空演变结果,分析颗粒在砾石层内悬浮和沉降运动特性。定义单位底面积泥浆中的颗粒迁移质量Ms为
Ms=n∑i=1(Tu)i⋅hij(n=3)。 (1) 式中:Ms为单位底面积泥浆中悬浮颗粒的质量(kg/m2);i为砾石层内测量层数, i=3;(Tu)i为各测量层的实时泥浆浊度(g/L)。hi表示砾石层的划分厚度,自上而下分别为h1=0.1 m,h2=0.08 m,h3=0.07m,泥浆浊度在砾石底层变化较为显著,因此深度划分上进行加密。
图 5(a)给出了泥浆中颗粒悬浮量随重复次数的变化。试验结果表明随重复次数的增加,动荷载下颗粒悬浮量先快速增大后趋于稳定。当重复次数小于5时,大量颗粒快速进入砾石层内并悬浮在泥浆中;而超过5次动静重复加载,泥浆中悬浮颗粒开始保持稳定,表明在砂粉土表层以难以移动的较粗颗粒为主。采用相同计算方法,也可以得到在间歇静荷载下泥浆中颗粒沉积情况,如图 5(b)所示。泥浆中的悬浮颗粒受重力作用逐渐发生沉降,并聚集到砾石底层,堵塞底层砾石间的孔隙。因此,随着重复次数的增加,每次静荷载间歇期内沉积的细颗粒逐渐在砾石底层处形成一个致密的低渗透夹层(图 6)。泥化夹层不仅降低了分层砾石-砂粉土试样的整体竖向渗透性,而且导致砾石层对悬浮颗粒产生更强的过滤效应,从而在一定程度上可能抑制翻浆发展[24]。
图 7给出了颗粒再悬浮增量随重复次数的变化。颗粒再悬浮增量可用于判断当前加载周期内进入砾石层内的迁移颗粒量。结果表明随重复次数增加,颗粒再悬浮增量总体上趋于降低。原因一方面是砂粉土表层中细粒含量逐渐降低,特别是当动静组合加载重复次数超过5次后,颗粒再悬浮增量总体上为0~10 kg/m2,表明砂粉土表层的绝大多数细颗粒已迁移殆尽。另一方面,颗粒再悬浮增量降低与动水力驱动作用减弱有关,下文将结合动水力响应分析诱发水-质迁移的驱动机制。
2.3 动水力响应与砂粉土稳定性关系分析
动-静组合荷载下分层砾石-砂粉土柱中不同深度处超孔压变化,如图 8所示。施加动荷载前砾石层内孔隙流体保持静止,各层的超孔压均为零。动荷载下泥浆产生晃动,对应超孔压发生振荡;而在间歇静荷载下泥浆晃动消失,超孔压迅速归零。试验发现随重复次数增加,泥浆中超孔压振荡幅值总体上呈减小趋势。对砂粉土层而言,粒间孔隙无论尺度还是连通性都不如砾石层,因此内部孔隙流体无法做到晃动,对应超孔压累积或消散程度不如砾石层明显。特别是随着砂粉土厚度增加,其底层超孔压始终接近零。砾石层内泥浆晃动引起的动水力作用有效降低了砂粉土表层的内部稳定性,从而驱动细颗粒迁移流动。随着砂粉土厚度的增加,这种动水力作用的影响也相应减弱。
根据太沙基有效应力原理可知[31],总应力σ是有效应力σ′与孔压u之和(σ=σ′+u),超孔压增长和有效应力降低将导致土的抗剪强度降低。特别是当超孔压接近或等于有效应力时,土骨架结构可能遭到破坏。翻浆冒泥不完全等同于土液化过程,但分析砂粉土层的液化特性对揭示水-质迁移翻浆机理具有启示作用。为评价砂粉土层液化程度,本次研究引入土液化度[32]。液化度越高,则土中存在更高比例的细颗粒产生悬浮迁移,其表达式为
χ=3Δuγ′pz(1+2K0)×100%。 (2) 式中:χ为土体液化度指标;Δu为超孔隙水压(Pa);γ′p为砂粉土的浮重度,γ′p=10.2 kN/m3;z为砂粉土层厚度(m);K0为静止土压力系数,K0=σ′h/σ′z,σ′h,σ′z分别为水平和竖向有效应力,试验前测定的砂粉土天然休止角接近42°,并将其作为有效内摩擦角φ′的近似值,获得静力土压力系数K0为0.33(K0=1− sinφ′)。
图 9给出了砂粉土顶和底层液化度时变曲线。动荷载下土体液化度呈现振荡特点,在间歇静荷载下则相对稳定。在整个加载过程中,加载条件为σm=30 kPa和f=25 Hz时,砂粉土顶层的最大液化度接近200%,其他加载条件下液化度则大多为0~100%,而底层液化度均不超过30%。这是因为随土层厚度增加,液体晃动引起的动水力作用趋于降低,且有效自重应力的增加也不利于底层液化度的增长。对砂土而言,通常认为液化度达到100%时已发生了完全液化。由于粉粒普遍黏结在砂粒表面或填充在砂骨架的周围孔隙内,增大砂粒之间的黏结作用,因此液化度一般需超过100%时砂粉土才可能完全液化[33]。完全液化意味着砂粉土呈现流动状态而不具备承载能力。根据本次试验中记录的试样最大沉降量为7.8 mm(对应竖向应变为2.0%),表明砂粉土层仍具有很好的承载能力,并没有发生完全液化,即土骨架颗粒及结构仍保持着稳定,仅是那些非骨架颗粒发生了脱离、悬浮和迁移运动。由于非骨架颗粒流失往往造成更多应力由土骨架承担,这在一定程度上增大试样的沉积量[34]。本次试验中,形成翻浆的非骨架颗粒主要来自砂粉土顶层,而更深处土仍是保持着较好的内部稳定性。
图 10给出了不同加载条件下砾石底层超孔压振荡幅值的变化情况。随动静重复次数增加,超孔压的振荡幅值发生了明显降低。考虑原因是同一加载强度下,颗粒迁移造成泥浆相对质量密度和动力黏度增加,从而增大泥浆的晃动阻尼[35],而阻尼提高将增大晃动能量损耗。提高动荷载的平均应力和加载频率,砾石层内的泥浆晃动趋于增强,随之造成超孔压振荡幅值有所增大。振荡超孔隙水压引起砂粉土表层内产生孔隙渗流,并促使土中细粒悬浮并与水相互作用形成泥浆。结合图 10测算的振荡超孔压变化可知,提高平均动应力和加载频率有助于形成更高的超孔隙水压振荡幅值,由此进一步降低砂粉土层的内部稳定性。
2.4 累积颗粒迁移质量
砾石层内颗粒迁移质量随超孔压振荡幅值的变化,如图 11所示。计算结果表明,在所有的重复周期中,颗粒迁移质量均随底层超孔压振荡幅值的增大而增加,证实了动荷载下泥浆晃动引起的振荡超孔压是驱动土颗粒发生迁移运动的关键因素。结合前文砂粉土层液化度的分析可知,泥浆中的悬浮颗粒主要来自土表层中非骨架颗粒,更强的动水力作用必然加剧非骨架颗粒的流失。图 12进一步给出了不同加载条件下砂粉土表层平均液化度与颗粒迁移质量间的关系。可以看到,提高动荷载加载条件(包括频率和平均动应力)普遍导致土层的平均液化度趋于增大。同时,相比于提高平均动应力,增大加载频率会造成更多的非骨架颗粒迁移进入上部砾石层,即加剧了土表层的内部侵蚀。
结合先前的翻浆试验结果可知[23],单调连续动载大小和频率影响泥浆浊度分布状态。在此基础上,进一步探究不同动静组合加载条件下悬浮颗粒在砾石层内的分布规律(图 13)。考虑到砾石层对迁移颗粒存在过滤效应,部分颗粒会不可避免地滞留在砾石孔隙内,这造成砾石顶和中层的泥浆浊度小于底层。随平均动应力增加,砾石底层处的颗粒悬浮量趋于减小,而砾石中和顶层则显著增大。因此,增大动荷载加载条件能够促使更多悬浮颗粒实现长距离迁移并来到砾石表层。其结果是砾石层内不同深度处的泥浆浊度将变得均匀,形成显著的翻浆现象。相似的变化也出现在增大加载频率试验中。
结合振荡超孔隙水压分布和演变特性分析可知,当加载引起的动水力作用不足以驱使悬浮颗粒产生长距离迁移时,它们会普遍聚集在砾石底层,堵塞砾石孔隙抑制更多的颗粒发生长距离移动,甚至进一步形成低渗透的泥化夹层;反之,悬浮颗粒会在周围渗流拖拽下持续向上迁移并最终充满整个砾石层。上述分析表明可能存在一个阈值动水压力,由其控制和改变颗粒迁移的运动特征,并最终影响泥浆浊度的时空分布规律,这为进一步研究和建立翻浆冒泥病害等级评价标准提供了必要的理论支撑。
3. 结论
通过开展一系列动-静组合荷载下分层砾石-砂粉土柱翻浆试验,得到4点结论。
(1)动静组合加载下翻浆过程中土颗粒受动水力和自身重力的共同作用,反复发生着悬浮和沉积运动,并由此造成砾石层不同深度处泥浆浊度随时间呈现波动型增长特点。
(2)随动静组合加载重复次数的增加,颗粒悬浮量先快速增大后趋于稳定,即对应每个重复周期内颗粒的再悬浮增量随重复次数增加而趋于降低。同时,随重复次数的增加,沉积在砾石底层的细颗粒也逐渐增多,堵塞砾石孔隙形成泥化夹层在一定程度上抑制翻浆发展。
(3)泥浆晃动导致砾石层内超孔隙水压呈现出明显的振荡特征,其振荡幅值受泥浆浊度增长影响总体上趋于减小。在砾石-砂粉土接触面处,振荡超孔压显著降低土表层的内部稳定性,导致非骨架颗粒在周围渗流裹挟下发生悬浮和迁移运动。
(4)增大动荷载的加载频率和平均动应力,能够显著增加颗粒迁移量和竖向迁移距离,从而形成更严重的翻浆现象。相比于提高平均动应力,增大动载频率对诱发水-质迁移翻浆效果更加明显,这对于从调控行车速度来缓解翻浆发展具有启发作用。
-
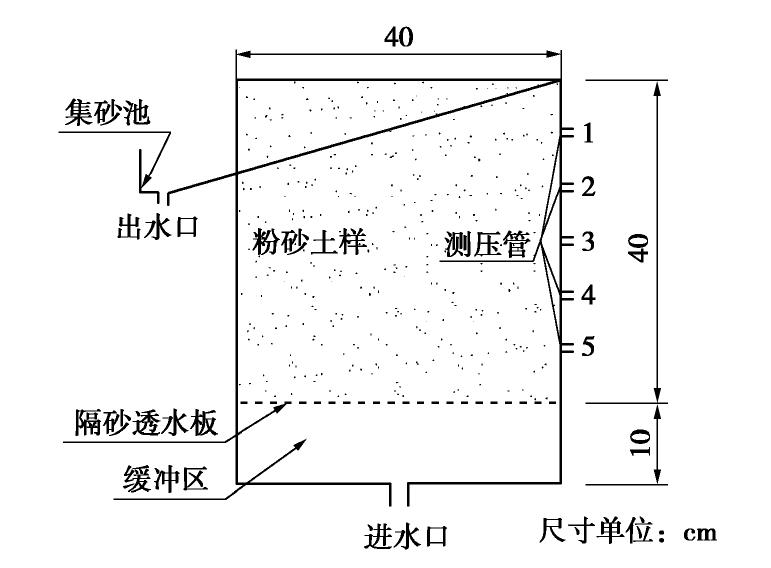
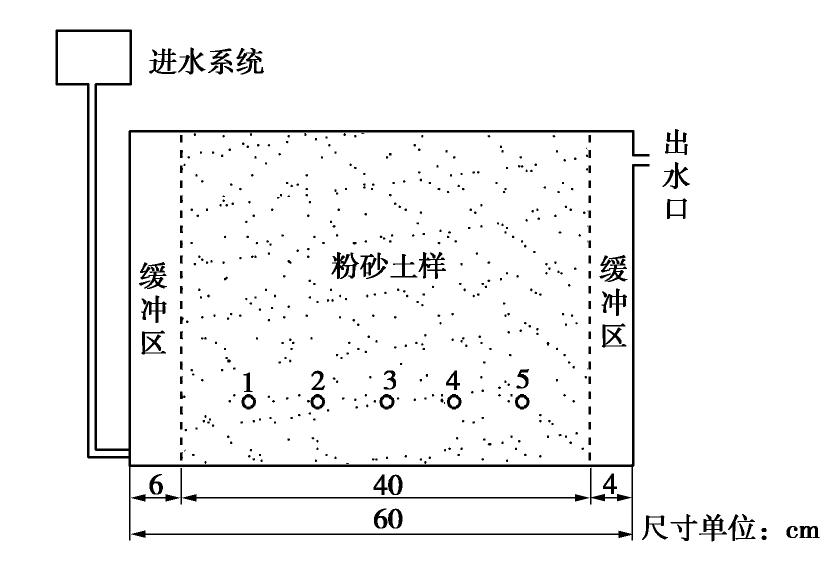
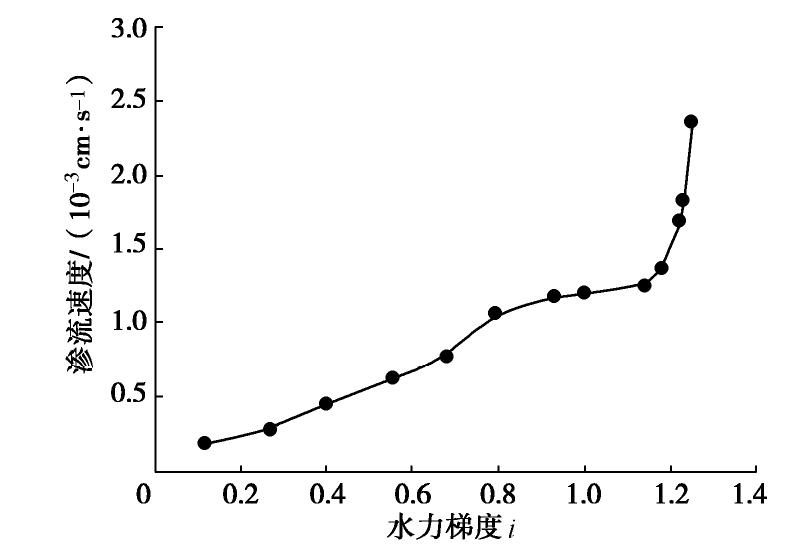
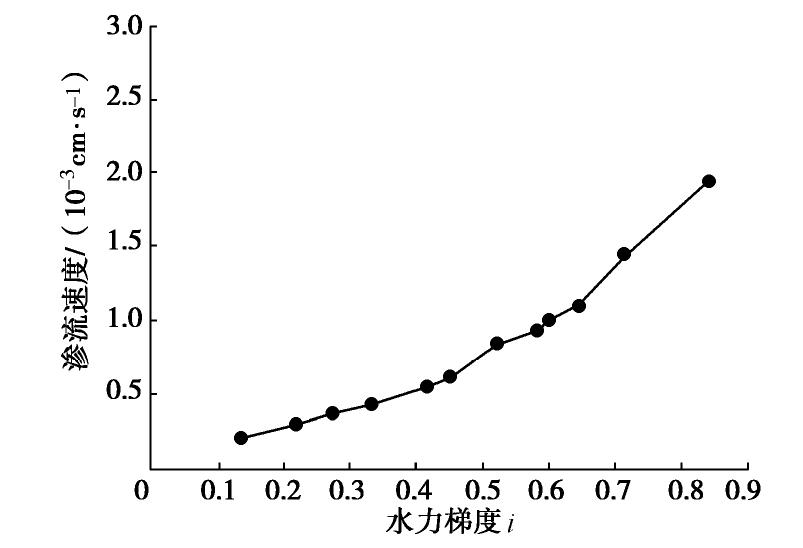
表 1 不同渗流方向下粉砂渗透系数、临界坡降和破坏坡降
Table 1 Datat of permeability coeffieient of silt, critical slope and failure slope under different seepage directions
渗流方向 渗透系数/(10-4 cm·s-1) 临界水力梯度 破坏水力梯度 竖向 6.13 0.787 1.10 水平 6.25 0.450 0.52 -
[1] 王新志, 王星, 胡明鉴, 等. 吹填人工岛地基钙质粉土夹层的渗透特性研究[J]. 岩土力学, 2017, 38(11): 3127-3135. doi: 10.16285/j.rsm.2017.11.007 WANG Xin-zhi, WANG Xing, HU Ming-jian, et al. Study of permeability of calcareous silty layer of foundation at an artificial reclamation island[J]. Rock and Soil Mechanics, 2017, 38(11): 3127-3135. (in Chinese) doi: 10.16285/j.rsm.2017.11.007
[2] 陈群, 谷宏海, 邹玉华, 等. 水平和竖向渗流情况下砾石土渗透性的对比分析[J]. 三峡大学学报(自然科学版), 2014, 36(5): 1-5. CHEN Qun, GU Hong-hai, ZOU Yu-hua, et al. Comparative analysis of horizontal and vertical permeability of clayey gravelly soil[J]. Journal of China Three Gorges University, 2014, 36(5): 1-5. (in Chinese)
[3] RICHARDS K S, REDDY K R. Experimental Investigation of Initiation of Backward Erosion Piping in Soils[J]. Geotechique, 2012, 62(10): 933-942. doi: 10.1680/geot.11.P.058
[4] 亓立成, 陈群, 朱亚军. 不同竖向应力和剪切位移下砂砾石与砂双层土渗透试验[J]. 岩土工程学报, 2018, 40(增刊2): 63-67. QI Li-cheng, CHEN Qun, ZHU Ya-jun. Seepage tests on double-layer soils composed of sandy gravel and sand under different stresses and shear displacements[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(S2): 63-67. (in Chinese)
[5] NI Xiao-dong, WANG Yuan, CHEN Ke, et al. Improved similarity criterion for seepage erosion using mesoscopic coupled PFC-CFD model[J]. Journal of Central South University, 2015, 22(8): 3069-3078. doi: 10.1007/s11771-015-2843-9
[6] JIANG Ming-jing, SHEN Zhi-fu, WANG Jian-feng. A novel three- dimensional contact model for granulates incorporating rolling and twisting resistances[J]. Computers and Geotechnics, 2015, 65: 147-163. doi: 10.1016/j.compgeo.2014.12.011
[7] 蒋中明, 袁涛, 刘德谦, 等. 粗粒土渗透变形特性的细观数值试验研究[J]. 岩土工程学报, 2018, 40(4): 752-758. JIANG Zhong-ming, YUAN Tao, LIU Xiao-fan, et al. Mesoscopic numerical tests on seepage failure characteristics of coarse grained soils[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(4): 752-758. (in Chinese)
-
期刊类型引用(3)
1. 韩博文,蔡国庆,苏彦林,单冶鹏,李舰. 间歇荷载–湿化耦合作用下有砟轨道路基翻浆冒泥机制及动力特性试验研究. 岩石力学与工程学报. 2025(01): 69-80 .  百度学术
百度学术
2. 蒋红光,王新宇,马川义,张宁,刘舜,王川. 高速铁路基床细颗粒动力迁移机制与临界水力梯度研究. 振动与冲击. 2025(06): 263-271 .  百度学术
百度学术
3. 高峰,曾宪璋,钟闻华,黄生勇,张军辉. 多年冻土区道路工程病害处治技术研究进展与展望. 中外公路. 2024(05): 1-16 .  百度学术
百度学术
其他类型引用(1)




 下载:
下载: