Elastic and plastic wetting mechanical parameters of rockfill based on deformation law
-
摘要: 湿化变形是土石坝的主要后期变形之一,对坝体的应力变形性状及初次蓄水坝体安全具有重要影响。基于前期湿化变形特性研究成果和提出的湿化变形模型,在进一步全面分析大量湿化试验成果的基础上,总结并完善了湿化应变间的相互关系及变化规律,推导了代表此特性的弹性和塑性力学参数。在非线性弹性理论框架下,提出了新的湿化泊松比计算公式,确立了湿化泊松比、平均有效应力和广义剪应力三者之间的密切关系;在塑性理论框架下,提出了精确的湿化剪胀方程。通过多组试验数据论证,发现提出的湿化泊松比与剪胀比的计算结果与试验数据的相关系数均在0.95以上。因此,提出的湿化泊松比和湿化剪胀比的计算方法是普遍适用且精确可靠的,研究成果可为堆石料湿化变形特性和堆石坝湿化变形弹塑性模拟等方面的研究提供重要的参考和支撑。Abstract: Wetting deformation is part of the main post-completion deformation of earth-rock dams, which has important influences on the stress deformation behavior of dam body and the safety of dam body for the initial impoundment. Based on the previous research results of wetting deformation characteristics, the proposed wetting deformation model and further comprehensive analysis of a large number of wetting test results, the relationship between wetting strains and their variation rules are summarized and improved, and the elastic and plastic mechanical parameters representing this characteristic are deduced. Under the framework of the nonlinear elasticity theory, a new formula for calculating the Poisson's ratio of wetting is proposed, and the close relationship among the wetting Poisson's ratio, the average effective stress and the generalized shear stress is established. In the framework of the plasticity theory, an accurate wetting dilatancy equation is proposed. It is found that the correlation coefficient between the calculated results of the Poisson's ratio and the dilatancy ratio proposed in this study and the test data is above 0.95. Therefore, the proposed methods for the wetting Poisson's ratio and the wetting dilatancy ratio are generally applicable, accurate and reliable, and the research results can provide important reference and support for the study of the wetting deformation characteristics of rockfill and the elastic or plastic simulation of the wetting deformation of rockfill dams.
-
0. 引言
堆石料的湿化变形是指堆石料由干态遇水变成湿态所导致的变形[1]。对于堆石坝工程,水库蓄水、水位上下波动、雨水入渗和下游尾水抬高等,都可使堆石料发生浸水从而产生湿化变形。湿化变形是堆石坝后期变形的主要组成部分之一。大量工程案例表明,堆石坝湿化变形量相当可观,如心墙堆石坝初次蓄水过程中由上游堆石产生的湿陷变形往往对大坝的安全运行产生影响,轻者会在坝顶产生湿陷裂缝,重者会造成坝肩等重要部位产生深度裂缝,甚至形成渗漏通道,威胁坝体安全[2]。因此,开展堆石料的浸水湿化变形研究具有非常重要的意义。
目前,堆石料浸水湿化变形多通过单线法三轴湿化试验测量湿化轴向应变与体积应变,拟合二者与应力状态的表达式,进而提出湿化模型。在计算土石坝湿化变形时,利用上述表达式计算湿化体积应变和剪切应变,并利用Prandtl-Reuss流动法则得到各方向的湿化应变分量,据此利用初应变法计算等效结点力,作用到坝体得到湿化变形[3]。大量学者研究发现这种方法存在较多问题,如在湿化试验过程中关于流变与湿化变形的界定目前尚存在较多争论,而此条件对湿化试验结果具有较大影响;在湿化体积应变和湿化剪切应变的形成上,不同岩性和不同级配堆石料在相同加载条件下会出现剪缩和剪胀两种截然相反的变化情况,单一的湿化模型表达式并不能很好表述这些不同情况,而且利用Prandtl-Reuss流动法则计算得到的湿化应变分量偏小[4];同时,监测资料和数值模拟结果也表明初次蓄水心墙堆石坝坝顶水平位移和沉降处于同一数量级,只注重湿化沉降研究是片面的,研究湿化应变之间的相互关系及发展规律也是极为重要的。为解决上述问题,学者们进行了大量的研究,部分近期研究如下。
丁艳辉等[5]认为堆石料湿化变形包括湿化瞬时变形和湿态流变变形两个部分,并基于此开展了响应试验和理论研究。张延亿等[6]基于湿化变形试验时程规律,建立了四参数双曲线型的固结湿化变形模型,模拟结果较为准确,能较好地反映宽级配粗粒料固结湿化变形特征。殷殷等[7-8]认为堆石料湿化变形发生在小湿化含水量条件下,堆石料非饱和湿化变形特性与饱和湿化变形特性相似,可采用广义荷载作用模型表征,认为堆石料湿化过程不仅发生湿化瞬时变形,也会发生一定大小的湿化湿态流变。左永振等[9]认为砾石土心墙料的湿化变形是明显的,且与应力水平、围压密切相关并提出砾石土料湿化变形模型及模型参数。
显然,对湿化变形发生过程特性的试验研究已有相当好的成果,但理论计算与工程应用方面的研究还较少。笔者前期基于非线性弹性理论提出了湿化变形的Ew-νw湿化模型[4],并利用此模型结合模量软化法进行了心墙堆石坝湿化变形的模拟[10]。但模型中计算湿化泊松比νw时,对于一些试验数据尚存在拟合度不高的情况。因此本文结合另一项研究成果中湿化应变关系普遍适用的公式[11-12]对湿化泊松比进行修正。同时,基于塑性理论的湿化变形研究较少。应力剪胀方程是建立土体本构模型的核心之一,是建立反映复杂变形特性的堆石料本构模型的重要基础,通常可以运用应力剪胀方程以及所谓正交条件,通过积分得到应力空间的塑性势函数[13]。王占军等[14]以三轴试验成果为基础,考虑颗粒破碎引起堆石料剪胀比与应力比之间的非线性关系,提出了能够反映堆石料低围压剪胀、高围压剪缩特性的剪胀方程。傅中志等[15]通过试验发现采用相同的塑性势函数同时确定加载塑性应变方向和流变黏塑性应变方向是不恰当的,建立了考虑堆石料流变的弹塑性模型时应该选用不同的应力剪胀方程或塑性势函数。石北啸等[16]根据试验结果,提出了堆石料初始孔隙比与其剪胀性和颗粒破碎的关系式,用于不同围压下堆石料剪胀特性的预测。因此,本文基于塑性理论和前期研究成果,推导了湿化剪胀比的计算方法, 为土石坝湿化变形规律的研究和模拟提供不同力学理论框架下普遍适用的参考成果。
首先,介绍提出的Ew-νw湿化模型和湿化应变关系普遍适用的公式,并分析湿化泊松比对Ew-νw湿化模型的影响;然后,结合大量三轴湿化试验成果修正湿化泊松比,从而提高Ew-νw湿化模型计算精度;最后,基于剑桥模型和湿化应变关系普遍适用的公式,推导新的湿化剪胀方程,并利用前人的试验数据验证新提出的剪胀方程的合理性。研究表明本文提出的湿化泊松比与剪胀比计算结果与试验数据的相关系数均在0.95以上,因此,本文提出的湿化泊松比和湿化剪胀比计算方法是精确可靠的。
1. 湿化变形特性及模型
1.1 湿化变形特性
周雄雄[3]在前人湿化试验基础上,对前人提出的湿化轴向应变与湿化应力水平的双曲函数形式和指数函数形式进行了对比,并均引入围压的影响,发现双曲线函数参数意义更加明确,拟合效果更加准确。其湿化轴向应变Δεwa与湿化应力水平SL关系式为
Δεwa=[K1(σ3pa)+A]SL1−SL+1K0(σ3pa)m。 (1) 式中:σ3为围压;pa为一个标准大气压强;K0,K1,m;A为试验参数。
此外,周雄雄等[11]经过对湿化单线法湿化试验数据的大量分析,发现湿化过程中湿化体变与湿化轴变呈线性关系,即湿化过程湿化体变与湿化轴变的比值k为常数,且它与平均主应力p和广义剪应力q满足扭面关系,进一步推导得到了三者的关系式为
k=logb(qap+b3)。 (2) 式中:a,b为试验参数。
1.2 湿化变形模型
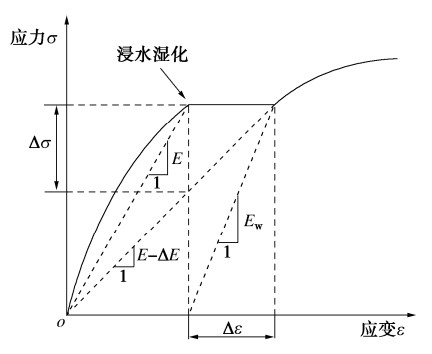
周雄雄[3]基于非线性弹性理论,认为堆石料湿化变形由其割线模量降低引起,割线模量降低即材料变软,会引起材料内部受力变形关系的调整,导致湿化变形。如图 1所示,浸水湿化前割线模量为E,浸水导致割线模量降低ΔE,变为E-ΔE。笔者通过逐步降低割线模量,推导模量降低微量dE时应变的变化,发现在湿化过程中湿化体变与湿化轴变呈线性关系变化的条件下,湿化过程中泊松比为常数。这一条件可以使得各个微小模量降低过程的轴向应变的累计,即总的湿化轴向应变Δεwa,可以很好的用湿化割线模量和湿化过程中的泊松比表示为
Δεwa=σ1Ew−2νwσ3Ew。 (3) 式中:Ew为湿化割线模量,见图 1;νw为湿化泊松比,左永振等[9]通过研究发现湿化泊松比与围压并无明显的关系,但与湿化应力水平大致呈线性关系,
νw=c+dSL。 (4) 式中:c,d为试验参数。
结合式(1),(3),推导得到了湿化割线模量的表达式为
Ew=(σ1−2νwσ3)[K1(σ3pa)+A]SL1−SL+1K0(σ3pa)m。 (5) 式(4),(5)即为笔者等提出的Ew-νw湿化模型。
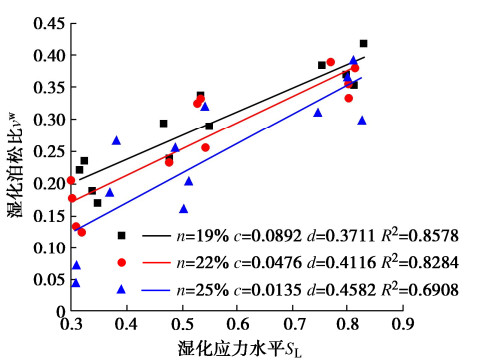
Ew-νw湿化模型基于非线性弹性理论,采用了湿化轴向应变和湿化应力水平之间满足很好的双曲线关系,而且在计算湿化应变张量时可以直接利用广义胡克定律计算,从而避免使用流动法则。同时,可以在非线性弹性理论框架下利用模量软化法很好的实现三轴湿化试验过程和堆石坝结构湿化变形的模拟。但是,利用式(4)确定湿化泊松比的过程中发现,对于一些试验数据存在拟合度不高的情况,如图 2为观音岩堆石料[17]的试验数据利用式(4)计算其湿化泊松比νw与湿化应力水平的拟合情况,可见其相关系数均在0.9以下,最低值尚未达到0.7。同时,从式(5)中可以看出湿化泊松比对湿化割线模量的计算亦有影响,因此有必要对其进行修正。
2. 湿化泊松比的修正
由前面的研究成果可知单线法三轴湿化试验中,湿化体变与湿化轴变的比值k与平均主应力p和广义剪应力q很好地满足式(2)中的关系,
k=εwvεwa=εwa+2εwrεwa=1−2νw=logb(qap+b3)。 (6) 式中:εwr为径向湿化应变。
因此,湿化泊松比可以表示为
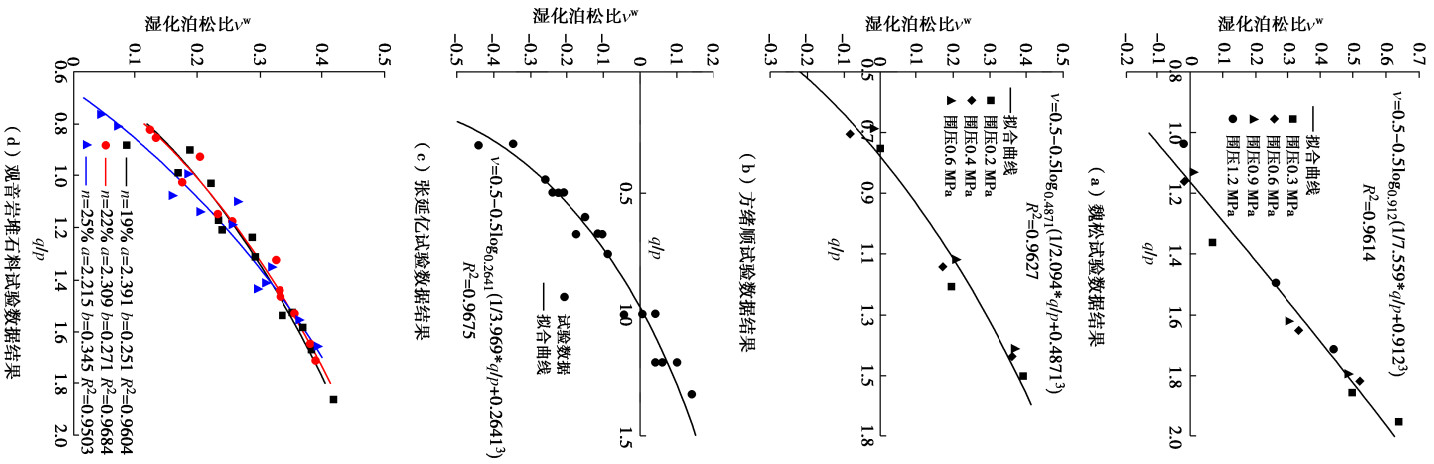
νw=0.5−0.5logb(qap+b3)。 (7) 根据魏松[18]、方绪顺[19]、张延亿[20]、观音岩堆石料[17]的试验数据,利用式(7)拟合并计算其湿化泊松比νw,将其与应力比q/p绘制于图 3中。可见利用修正后的湿化泊松比计算方法得到的湿化泊松比与试验数据具有非常高的相关性。将湿化泊松比修正前后的拟合的相关系数汇总于表 1。可见湿化泊松比的修正极大地提高了其与试验数据地拟合度,本文所收集地所有试验数据与修正后湿化泊松比地计算公式相关性系数均高于0.95。因此,利用式(7)进行湿化泊松比地修正是非常可靠的,结合式(5)组成的Ew-νw湿化模型可以更加准确地计算堆石料和堆石坝的湿化变形。
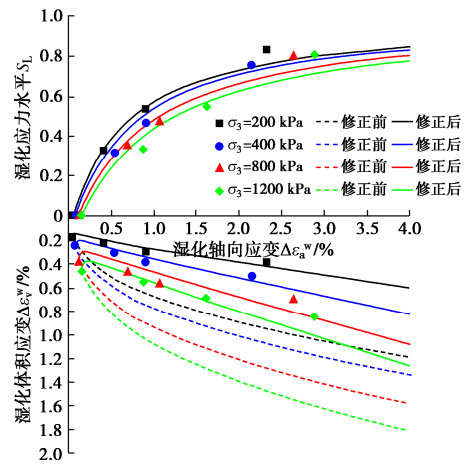
表 1 修正前后计算湿化泊松比与试验数据相关性对比Table 1. Correlation between calculated Poisson's ratio and experimental data before and after correction试验数据 修正前的R2 修正后的R2 魏松 0.8475 0.9614 方绪顺 0.9205 0.9627 张延亿 0.9509 0.9675 观音岩 n=19% 0.8578 0.9604 n=22% 0.8284 0.9684 n=25% 0.6908 0.9503 为体现修正前后湿化泊松比对Ew-vW模型计算湿化体积应变的影响,本文选取观音岩堆石料[17]进行的湿化变形试验数据进行三轴湿化变形模拟。表 2为孔隙比19%的湿化试验值,表 3为其拟合参数[4]。图 4为观音岩堆石料湿化试验模拟结果。可见采用修正湿化泊松比的Ew-νw模型计算湿化体积应变的结果与试验数据的拟合度较高。所以,对泊松比的修正是合理有效的。
表 2 观音岩堆石料湿化试验数据Table 2. Wetting test data of Guanyinyan rockfill materials围压/kPa 湿化应力水平 湿化轴变/% 湿化体变/% 200 0 0.057 0.17 0.324 0.417 0.221 0.534 0.906 0.293 0.830 2.322 0.378 400 0 0.081 0.244 0.316 0.541 0.301 0.468 0.908 0.376 0.755 2.147 0.497 800 0 0.126 0.378 0.347 0.695 0.459 0.477 1.073 0.561 0.798 2.643 0.69 1200 0 0.151 0.454 0.337 0.876 0.544 0.550 1.618 0.684 0.811 2.887 0.845 表 3 观音岩堆石料湿化参数Table 3. Wetting parameters of Guanyinyan rockfill materials参数 K0 m K1 A a b c d 数值 0.039 0.556 0.039 0.663 2.350 0.260 0.089 0.371 3. 湿化剪胀方程
剑桥模型[21]是影响最广泛的弹塑性模型,修正剑桥模型的剪胀方程为
dg=M2−η22η。 (8) 式中:dg为剪胀比,dg=dεpv/dεps;M为土体达到临界状态的应力比可根据临界状态时的应力分量确定[13];η为应力比,η=q/p。
本文根据剑桥模型中剪胀比的定义,考虑湿化对堆石料的力学特性的影响,将湿化剪胀比与应力比联系起来进而建立湿化剪胀方程。三轴湿化试验应力条件下湿化剪胀比dwg为
dwg=dεwvdεws=dεwvdεwa−dεwv/dεwv33=dεwv/dεwvdεwadεwa1−dεwv/dεwv3dεwa3dεwa。 (9) 式中:dεwv为湿化体积应变增量;dεws为湿化剪切应变增量;dεwa为湿化轴向应变增量。由前期研究可知湿化过程中湿化体变与湿化轴变呈线性关系,因此,
dwg=dεwv/dεwvdεwadεwa1−dεwv/dεwv3dεwa3dεwa=Δεwv/ΔεwvΔεwaΔεwa1−Δεwv/Δεwv3Δεwa3Δεwa=k1−k/k33。 (10) 将式(2)代入式(10)可得:
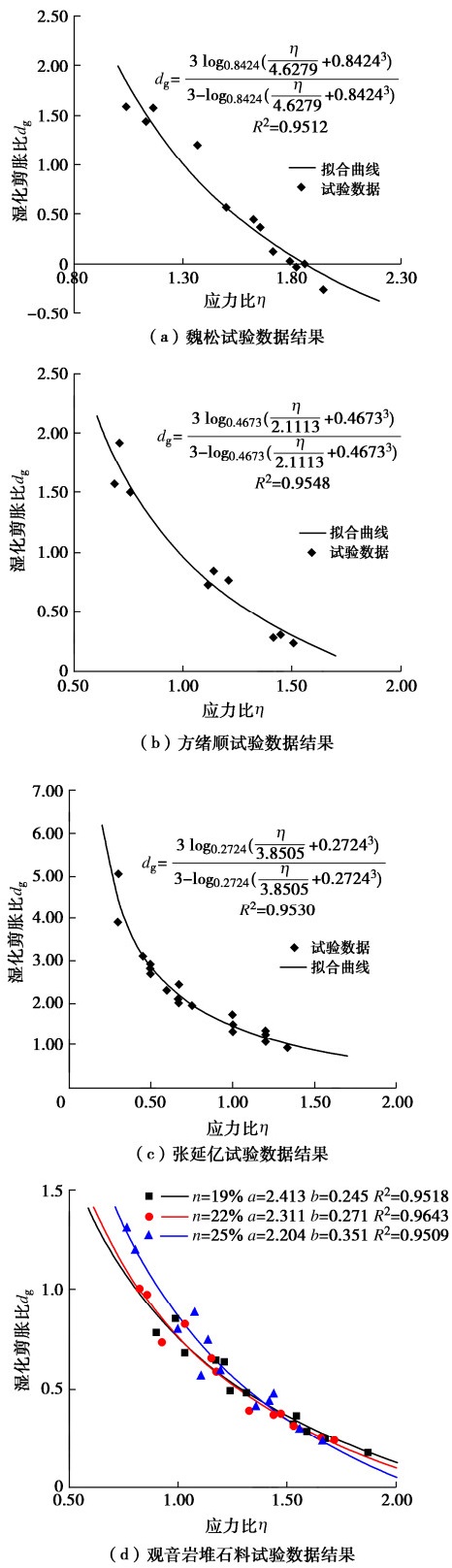
dwg=3logb(η/a+b3)3−logb(η/a+b3)。 (11) 根据魏松[18]、方绪顺[19]、张延亿[20]、观音岩堆石料[17]的试验数据,利用式(11)拟合并计算其湿化剪胀比dwg,将其与应力比η绘制于图 5中。
由图 5可见,利用新提出的湿化剪胀方程式(11)可计算不同湿化应力比条件下的湿化剪胀比,计算结果与试验数据高度拟合,可同时描述剪缩(剪胀比为正)和剪胀(剪胀比为负)不同情况,本文所收集的所有试验数据与计算公式相关性系数均高于0.95。因此,利用式(11)进行湿化剪胀比的计算是精确可靠的,可为湿化变形模型及湿化变形的塑性势函数的推导提供适用性强、精确度高的有效支持。
4. 结论
通过进一步总结和探索堆石料湿化变形的规律及其力学机理,给出了适用性更强的湿化泊松比计算公式,并结合湿化变形的通用规律提出了精确的湿化剪胀方程,为堆石料湿化变形和堆石坝蓄水变形在弹性和塑性不同力学理论框架下的研究提供了参考和支撑。
(1)本文修正后的湿化泊松比计算公式,参数数量未变,但与试验数据的拟合度更高,计算得到的湿化割线模量也更加精确。
(2)本文在剑桥模型的基础上提出了新的湿化剪胀方程,可计算不同湿化应力比条件下的湿化剪胀比,可同时描述剪缩和剪胀不同情况,计算得到的剪胀比与试验数据的拟合相关系数均高于0.95,可为湿化变形模型及湿化变形的塑性势函数的推导提供精确且高效的支持。
(3)本文对湿化泊松比的修正、湿化剪胀方程的提出都分析了众多前人的湿化试验,同时也符合众多前人试验资料。为堆石料湿化变形特性研究和堆石坝湿化变形弹塑性模拟等方面的研究提供了适用性广且精度高的参考和支撑。
-
表 1 修正前后计算湿化泊松比与试验数据相关性对比
Table 1 Correlation between calculated Poisson's ratio and experimental data before and after correction
试验数据 修正前的R2 修正后的R2 魏松 0.8475 0.9614 方绪顺 0.9205 0.9627 张延亿 0.9509 0.9675 观音岩 n=19% 0.8578 0.9604 n=22% 0.8284 0.9684 n=25% 0.6908 0.9503 表 2 观音岩堆石料湿化试验数据
Table 2 Wetting test data of Guanyinyan rockfill materials
围压/kPa 湿化应力水平 湿化轴变/% 湿化体变/% 200 0 0.057 0.17 0.324 0.417 0.221 0.534 0.906 0.293 0.830 2.322 0.378 400 0 0.081 0.244 0.316 0.541 0.301 0.468 0.908 0.376 0.755 2.147 0.497 800 0 0.126 0.378 0.347 0.695 0.459 0.477 1.073 0.561 0.798 2.643 0.69 1200 0 0.151 0.454 0.337 0.876 0.544 0.550 1.618 0.684 0.811 2.887 0.845 表 3 观音岩堆石料湿化参数
Table 3 Wetting parameters of Guanyinyan rockfill materials
参数 K0 m K1 A a b c d 数值 0.039 0.556 0.039 0.663 2.350 0.260 0.089 0.371 -
[1] NOBARI E S, DUNCAN J M. Movements in dams due to reservoir filling[C]// ASCE Spec Conf on Per of Earth and Earth Supported Structures. ASCE, New York, 1972.
[2] 刘祖德. 土石坝变形计算的若干问题[J]. 岩土工程学报, 1983, 5(1): 1-13. doi: 10.3321/j.issn:1000-4548.1983.01.001 LIU Zude. Some deformation calculation problem of earth and rockfill dam[J]. Chinese Journal of Geotechnical Engineering, 1983, 5(1): 1-13. (in Chinese) doi: 10.3321/j.issn:1000-4548.1983.01.001
[3] 周雄雄. 高心墙堆石坝湿化变形与数值模拟方法研究[D]. 大连: 大连理工大学, 2020. ZHOU Xiongxiong. Study on Wetting Deformation and Numerical Simulation Method of High Core Rockfill Dam[D]. Dalian: Dalian University of Technology, 2020. (in Chinese)
[4] 迟世春, 周雄雄. 堆石料的湿化变形模型[J]. 岩土工程学报, 2017, 39(1): 48-55. doi: 10.11779/CJGE201701002 CHI Shichun, ZHOU Xiongxiong. Slaking deformation model for rockfill materials[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(1): 48-55. (in Chinese) doi: 10.11779/CJGE201701002
[5] 丁艳辉, 张丙印, 钱晓翔, 等. 堆石料湿化变形特性试验研究[J]. 岩土力学, 2019, 40(8): 2975-2981. DING Yanhui, ZHANG Bingyin, QIAN Xiaoxiang, et al. Experimental study of the characteristics of wetting deformation of rockfill materials[J]. Rock and Soil Mechanics, 2019, 40(8): 2975-2981. (in Chinese)
[6] 张延亿, 邓刚, 张茵琪, 等. 土石混合料固结湿化变形试验研究[J]. 水利学报, 2020, 51(11): 1393-1400. ZHANG Yanyi, DENG Gang, ZHANG Yinqi, et al. Experimental study on the characteristics of consolidate-wetting deformation of soil-aggregate mixture materials[J]. Journal of Hydraulic Engineering, 2020, 51(11): 1393-1400. (in Chinese)
[7] 殷殷, 吴永康, 丁艳辉, 等. 堆石料非饱和湿化变形特性研究[J]. 岩石力学与工程学报, 2021, 40(增刊2): 3455-3463. YIN Yin, WU Yongkang, DING Yanhui, et al. Experimental study on the unsaturated wetting deformation behaviors of rockfill materials[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(S2): 3455-3463. (in Chinese)
[8] 殷殷, 刘盈斐, 吴永康, 等. 堆石料湿化试验变形过程分析[J]. 水利学报, 2022, 53(11): 1361-1368, 1382. YIN Yin, LIU Yingfei, WU Yongkang, et al. Process analysis of wetting deformation test of rockfill materials[J]. Journal of Hydraulic Engineering, 2022, 53(11): 1361-1368, 1382. (in Chinese)
[9] 左永振, 程展林, 潘家军, 等. 砾石土心墙料的湿化变形特性试验研究[J]. 岩土工程学报, 2023, 45(10): 2188-2193. doi: 10.11779/CJGE20220971 ZUO Yongzhen, CHENG Zhanlin, PAN Jiajun, et al. Experimental study on wetting deformation characteristics of gravelly soil core materials[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(10): 2188-2193. (in Chinese) doi: 10.11779/CJGE20220971
[10] ZHOU X X, CHI S C, JIA Y F. Wetting deformation of core-wall rockfill dams[J]. International Journal of Geomechanics, 2019, 19(8): 4019084. doi: 10.1061/(ASCE)GM.1943-5622.0001444
[11] 周雄雄, 迟世春, 贾宇峰. 粗粒料湿化变形特性研究[J]. 岩土工程学报, 2019, 41(10): 1943-1948. doi: 10.11779/CJGE201910020 ZHOU Xiongxiong, CHI Shichun, JIA Yufeng. Wetting deformation characteristics of coarse granular materials[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(10): 1943-1948. (in Chinese) doi: 10.11779/CJGE201910020
[12] ZHOU X X, CHI S C, WANG M H, et al. Study on wetting deformation characteristics of coarse granular materials and its simulation in core-wall rockfill dams[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2020, 44(6): 851-873. doi: 10.1002/nag.3042
[13] SCHOFIELD A N, WROTH P. Critical State Soil Mechanics[M]. New York: McGraw-Hill, 1968.
[14] 王占军, 陈生水, 傅中志. 堆石料的剪胀特性与广义塑性本构模型[J]. 岩土力学, 2015, 36(7): 1931-1938. WANG Zhanjun, CHEN Shengshui, FU Zhongzhi. Dilatancy behaviors and generalized plasticity constitutive model of rockfill materials[J]. Rock and Soil Mechanics, 2015, 36(7): 1931-1938. (in Chinese)
[15] 傅中志, 陈生水, 张意江, 等. 堆石料加载与流变过程中塑性应变方向研究[J]. 岩土工程学报, 2018, 40(8): 1405-1414. doi: 10.11779/CJGE201808005 FU Zhongzhi, CHEN Shengshui, ZHANG Yijiang, et al. Plastic strain directions of rockfill materials during loading and creeping[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(8): 1405-1414. (in Chinese) doi: 10.11779/CJGE201808005
[16] 石北啸, 刘赛朝, 吴鑫磊, 等. 考虑颗粒破碎的堆石料剪胀特性研究[J]. 岩土工程学报, 2021, 43(7): 1360-1366. doi: 10.11779/CJGE202107023 SHI Beixiao, LIU Saizhao, WU Xinlei, et al. Dilatancy behaviors of rockfill materials considering particle breakage[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(7): 1360-1366. (in Chinese) doi: 10.11779/CJGE202107023
[17] 米占宽, 李国英. 观音岩水电站心墙堆石坝坝料后期变形试验研究[R]. 南京: 南京水利科学研究院, 2016. MI Zhankuan, LI Guoyin. Experimental Study on Material Late Deformation of Core Wall Cockfill Dam in Guanyinyan Hydropower Station[R]. Nanjing: Nanjing Hydraulic Research Institute, 2016. (in Chinese)
[18] 魏松. 粗粒料浸水湿化变形特性试验及其数值模型研究[D]. 南京: 河海大学, 2006. WEI Song. Experimental Study on Wetting Deformation Characteristics of Coarse Grained Materials and its Numerical Model[D]. Nanjing: Hohai University, 2006. (in Chinese)
[19] 方绪顺. 砂砾石料浸水变形特性研究及砂砾石坝蓄水变形的数值模拟[D]. 南京: 河海大学, 2005. FANG Xushun. Study on Deformation Characteristics of Gravel in Water and Numerical Simulation of Water Storage Deformation of Gravel Dam[D]. Nanjing: Hohai University, 2005. (in Chinese)
[20] 张延亿. 浸水湿化和水位升降条件下堆石材料变形特性研究[D]. 北京: 中国水利水电科学研究院, 2018. ZHANG Yanyi. Study on Deformation Characteristics of Rockfill Materials Under Wetting and Water Level Rise and Fall[D]. Beijing: China Research Institute of Water Resources and Hydropower, 2018. (in Chinese)
[21] 殷宗泽. 土工原理[M]. 北京: 中国水利水电出版社, 2007. YIN Zongze. Geotechnical Principle[M]. Beijing: China Water & Power Press, 2007. (in Chinese)



 下载:
下载: