基于多切线技术的盾构隧道开挖面稳定性分析

钟军豪; CHIANSiau Chen; 李永鑫; 刘明芳; 陈明辉; 吴振元; 龙桂华; 杨小礼; 周德

doi:10.11779/CJGE20231160

基于多切线技术的盾构隧道开挖面稳定性分析 English Version

1.
中南大学土木工程学院, 湖南长沙 410075
2.
新加坡国立大学土木与环境工程系, 新加坡 117576
3.
合肥工业大学汽车与交通工程学院, 安徽合肥 230009
4.
深圳市市政工程总公司, 广东深圳 518000

基金项目:

国家自然科学基金项目 5210081105

安徽省自然科学基金项目 2108085QE250

湖南省研究生科研创新项目 CX20220239

国家留学基金项目（国家建设高水平大学公派研究生项目）

详细信息

作者简介:
钟军豪(1996—)，男，博士研究生，主要从事隧道开挖面稳定性和地层建模方面的研究工作。E-mail: zhongjunhao@csu.edu.cn

通讯作者:
周德, E-mail: 210026@csu.edu.cn

中图分类号: TU432
计量
- 文章访问数: 400
- HTML全文浏览量: 50
- PDF下载量: 85
出版历程
- 收稿日期: 2023-11-26
- 网络出版日期: 2024-04-18
- 刊出日期: 2024-12-31

Face stability of shield-driven tunnels using multi-tangent technique

1.
School of Civil Engineering, Central South University, Changsha 410075, China
2.
Department of Civil and Environmental Engineering, National University of Singapore, Singapore 117576
3.
School of Automotive and Transportation Engineering, Hefei University of Technology, Hefei 230009, China
4.
Shenzhen Municipal Engineering Corporation, Shenzhen 518000, China

摘要

摘要: 针对非线性条件下深埋隧道开挖面稳定性问题，采用多切线技术分段线性近似Power-Law（P-L）准则，基于极限分析上限定理，构建1种新的开挖面多曲线圆锥破坏机构，提出1种考虑拉应力截断Tension cut-off（T-C）效应的开挖面稳定性理论计算方法。通过与既有文献结果对比，验证所提方法的可靠性。根据反算的应力分布和破坏机构几何特点，探究不同参数条件下T-C对开挖面稳定性的影响。结果表明：①在线性条件下，黏聚力较大且内摩擦角较小时，T-C对开挖面临界支护力的影响较大；在非线性条件下，m的增加并不会放大T-C对开挖面稳定性的影响。②在抗拉强度较大时，T-C对开挖面稳定性影响较为显著，随着抗拉强度的折减，T-C控制的破坏机构尺寸逐渐减小，且顶部区域明显钝化。
- 开挖面稳定性 /
- 多切线技术 /
- Power-Law准则 /
- 拉应力截断 /
- 极限分析
Abstract: To address the face stability problem of deep-buried tunnels under nonlinear conditions, using Power-Law (P-L) criterion the approximate piecewise and by multi-tangent technique, a novel multi-cone failure mechanism is developed for tunnel faces based on the kinematic limit analysis theorem. A theoretical framework considering the tension cut-off (T-C) is proposed to evaluate the stability of tunnel faces. The reliability of the proposed method is validated through comparison with that in the existing literatures. Based on the back-calculated stress distribution and geometric feature of the failure mechanism, the influences of T-C under different parameters on the stability of tunnel faces are investigated. The results indicate that: (1) under the linear condition, the effects of T-C on the critical support pressure are more significant with high cohesion and small internal friction angle. Under the nonlinear condition, an increase in the nonlinear coefficient will not exacerbate the impact of T-C on the face stability. (2) For higher tensile strength, the effects of T-C on the stability of tunnel faces are significant. As the tensile strength decreases, the failure mechanism governed by T-C gradually shrinks, and the top of the failure mechanism exhibits noticeable blunting and looks like a dome.
- stability of tunnel face /
- multi-tangent technique /
- Power-Law criterion /
- tension cut-off /
- limit analysis

HTML全文

0. 引言

近年来，随着交通基建的大力发展，城市轨道交通作为沟通南北，贯穿东西的主要枢纽，在现代化建设过程中发挥着重要的作用。为了保证地铁隧道施工的安全，开挖面临界支护力预测一直是工程设计人员普遍关心的问题。

现阶段，计算开挖面临界支护力的方法有很多，主要包括：理论分析^[1-5]、数值模拟^[6-7]、模型试验等^[8-10]。在理论分析方面，主要以极限分析法和极限平衡法为研究手段。极限分析法和极限平衡法需要事先对开挖面的几何破坏机构做出假定，依据假定的破坏机构分别建立能量平衡方程和力平衡方程，进而求解临界支护力。Perazzelli等^[1]基于棱柱-楔形体破坏机构，采用极限平衡法推导了渗透力作用下的开挖面临界支护力解析解。该破坏机构假设棱柱体延伸至地表，对于深埋隧道而言这显然与实际不符。黄阜等^[6-7]从极限分析上限理论的角度出发，建立开挖面二维离散破坏机构，将上限机构与FLAC^3D数值模拟的渗流场相结合，推导了开挖面安全系数上限解，并将其拓展到岩质隧道，分析强度非线性对开挖面稳定性的影响。然而，该破坏机构局限于二维平面应变假设，忽略了开挖面失稳的三维空间效应，在考虑强度非线性时，用单切线法近似非线性强度准则，虽然依旧是严格的上限解，但未能妥善考虑强度非线性。

在实际工程中，线性Mohr-Coulomb（M-C）准则被广泛用于描述岩土体强度特性，而大量试验表明，由于地质成因、沉积、应力历史等原因，岩土材料具有不同程度的强度非线性特征，尤其是在低应力范围内，非线性特性更加明显。常见的非线性强度准则有Hoek-Brown（H-B）准则和Power-Law（P-L）准则，分别适用于岩体和土体。为了将非线性准则线性化并获得等效的M-C强度参数，众多线性化方法被提出，包括等效M-C参数法、单切线法和多切线法等。这些方法大多基于H-B准则，很少涉及P-L准则，此外，近年来，地下隧道逐渐朝着大断面的方向发展，拉伸破坏越来越常见，抗拉强度逐渐受关注。由强度包络线外推得到的理论抗拉强度与拉伸试验的结果相比，明显较高。Drucker等^[11]率先意识到这种差异，随后，Paul^[12]将拉应力截断引入M-C准则，使得抗拉强度在主应力平面上降低。Hoek等^[13]根据岩石类型将拉应力截断引入到H-B准则中，然后结合三轴和直接拉伸试验数据不断更新。对于土体而言，Charles等^[14]指出，大多数三轴试验是在高围压条件下进行的，低应力条件下的剪切试验和拉伸试验很少涉及，导致低应力区域和拉应力区域的强度包络线无法准确拟合，相应的抗拉强度可能会被过高估计，因此，为了进一步完善P-L准则，有必要引入折减系数对抗拉强度进行折减。

本文采用多切线技术分段近似非线性强度准则，研究强度非线性条件下的开挖面稳定性，妥善地将强度非线性耦合到理论分析中，同时，将拉应力截断的概念首次引入非线性P-L准则，并基于相关联流动法则建立开挖面新型多曲线圆锥破坏机制，推导非线性条件下开挖面临界支护力的解析表达式，利用智能优化算法对上限解进行快速寻优，通过参数分析，揭示强度非线性和不同拉应力截断程度对开挖面稳定性的影响，为实际工程开挖支护设计提供理论依据。

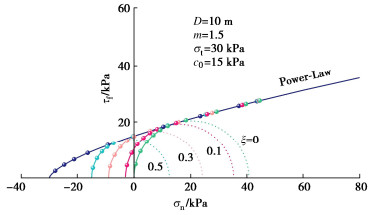
1. 考虑拉应力截断的Power-Law准则

根据大量试验的拟合结果，土体材料的强度非线性特性一般可由P-L强度准则表征：

${\tau _{\text{f}}} = {c_0}{\left( {1 + \frac{{{\sigma _{\text{n}}}}}{{{\sigma _{\text{t}}}}}} \right)^{\frac{1}{m}}} 。$

(1)

式中： ${\tau _{\text{f}}}$ 为切应力； ${\sigma _{\text{n}}}$ 为正应力； ${c_0}$ 为初始黏聚力； ${\sigma _{\text{t}}}$ 为单轴抗拉强度；m为非线性系数。

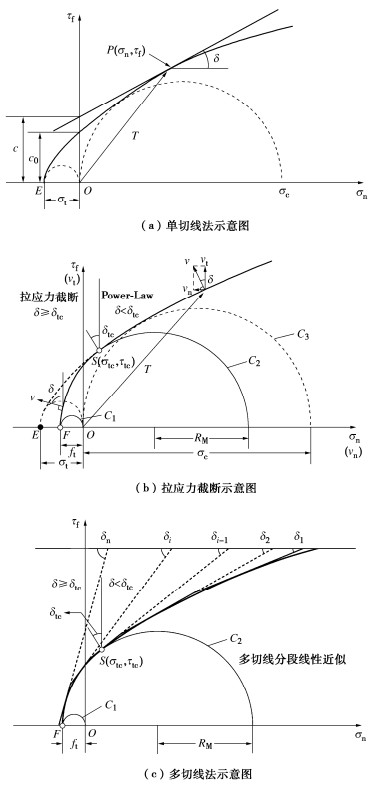
为单切线法示意图。在包络线上任意一点P（ ${\sigma _{\text{n}}}$ ， ${\tau _{\text{f}}}$ ）处做一条切线，切线方程为

${\tau _{\text{f}}} = c + {\sigma _{\text{n}}}\tan \delta 。$

(2)

图 1 考虑拉应力截断的非线性Power-Law强度准则

Figure 1. Nonlinear Power-Law criterion considering tension cut-off

下载: 全尺寸图片幻灯片

式中： $c$ 为切向黏聚力；δ为切向内摩擦角，联立方程（2），（3），可以将包络线上任意一点位置处的应力分量写成如下参数方程形式：

$\tau _{\text{f}}^{{\text{PL}}} = {c_0}{\left( {\frac{{m{\sigma _{\text{t}}}\tan \delta }}{{{c_0}}}} \right)^{\frac{1}{{1 - m}}}} \text{，}$

(3)

$\sigma _{\text{n}}^{{\text{PL}}} = {\sigma _{\text{t}}}{\left( {\frac{{m{\sigma _{\text{t}}}\tan \delta }}{{{c_0}}}} \right)^{\frac{m}{{1 - m}}}} - {\sigma _{\text{t}}} 。$

(4)

通过引入折减系数 $\xi$ ，真实的抗拉强度 ${f_{\text{t}}}$ 可以表示为

${f_{\text{t}}} = \xi {\sigma _{\text{t}}} 。$

(5)

图 1（b）为拉应力截断示意图。横轴上的F点代表折减后的抗拉强度，经过该点做一个莫尔圆（C₂）与包络线相切于点S，以圆弧SF替代包络线SE，从而实现对抗拉强度的折减。莫尔圆C₂表达式为

${({\sigma _{\text{n}}} + {f_{\text{t}}} - {R_{\text{M}}})^2} + \tau _{\text{f}}^2 = R_{\text{M}}^2 。$

(6)

式中：R_M为莫尔圆C₂半径，计算公式如下：

${R_{\text{M}}} = \frac{{{{({\sigma _{{\text{tc}}}} + {f_{\text{t}}})}^2} + \tau _{{\text{tc}}}^2}}{{2({\sigma _{{\text{tc}}}} + {f_{\text{t}}})}} 。$

(7)

式中： ${\sigma _{{\text{tc}}}}$ 和 ${\tau _{{\text{tc}}}}$ 为切点S处的应力坐标，可通过将S点处的瞬时内摩擦角δ_tc代入式（6），（7）计算得到。根据几何关系， ${\delta _{{\text{tc}}}}$ 可以通过以下隐式方程求解：

$- \frac{{{\sigma _{{\text{tc}}}} + {f_{\text{t}}} - {R_{\text{M}}}}}{{\sqrt {({\sigma _{{\text{tc}}}} + {f_{\text{t}}})(2{R_{\text{M}}} - {\sigma _{{\text{tc}}}} - {f_{\text{t}}})} }} = \tan {\delta _{{\text{tc}}}} 。$

(8)

进而可以获得圆弧段SF的参数方程：

$\tau _{\text{f}}^{{\text{TC}}}(\delta ) = {R_{\text{M}}}\cos \delta \text{，}$

(9)

$\sigma _{\text{n}}^{{\text{TC}}}(\delta ) = {R_{\text{M}}}(1 - \sin \delta ) - {f_{\text{t}}} \text{，}$

(10)

综上，对P-L强度准则的抗拉强度进行合理折减，并用圆弧替代部分包络线，建立了考虑T-C的强度准则。图 1（c）所示为多切线法示意图。在单切线法的基础上，将切线数量增加至n，同时引入n个切向内摩擦角作为自变量，从上到下依次分段线性替代强度包络线，相应的切向内摩擦角分别为δ₁~δ_n。

2. 开挖面上限分析

2.1 多曲线圆锥破坏机构

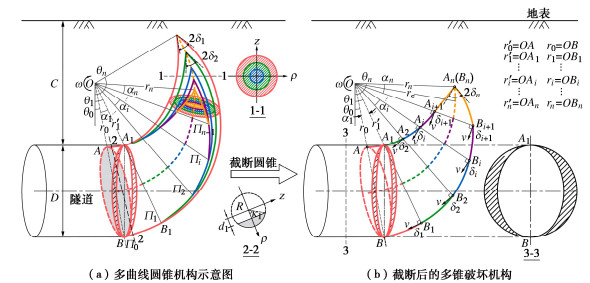
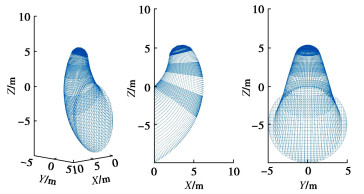
图 2所示为隧道开挖面多曲线圆锥破坏机构。隧道埋深为C，直径为D。该破坏机构以传统的单曲线圆锥破坏机构为基础，通过在适当位置截断多个不同的曲线圆锥，再将其组合形成新的多锥机构。在破坏瞬间，整个破坏机构作为刚性块体围绕着经过O点的轴以角速度 $\omega$ 在平面内转动，关于经过隧道轴线的竖直平面对称。第1个曲线圆锥（红色部分）从开挖面出发，经过拱顶A₁和拱底B，在拱顶处分别被开挖面和辐射面 $\mathit{\Pi }_1$ 截断，余下部分A₁B₁B即第1个截断圆锥体。第二个曲线圆锥（绿色部分）从辐射面 $\mathit{\Pi }_1$ 处开始，截面大小保持相同，在辐射面 $\mathit{\Pi }_2$ 处截断，依次类推，直至第n个曲线圆锥体。

图 2 隧道开挖面多曲线圆锥破坏模式

Figure 2. Multi-cone failure mechanism of tunnel face

下载: 全尺寸图片幻灯片

为了便于后续能量耗散分析，以O点为坐标原点建立极坐标系，先对破坏机构的几何表达式进行定义说明。根据相关联流动法则的要求，对称面与破坏机构的交线为对数螺旋线，对于第i个截断圆锥体而言，对数螺旋线表达式为

$r'(\theta ) = {r'_{i - 1}}{{\text{e}}^{\left( {\theta - {\theta _{i - 1}}} \right)\tan {\delta _i}}} \text{，}$

(11)

$r(\theta ) = {r_{i - 1}}{{\text{e}}^{\left( {{\theta _{i - 1}} - \theta } \right)\tan {\delta _i}}} 。$

(12)

式中： $\theta$ 为对数螺旋线上任意点处极角； ${\theta _{i - 1}}$ 为辐射面 ${\Pi _{i - 1}}$ 的极角； ${\delta _i}$ 为破裂角，即瞬时内摩擦角； ${r'_{i - 1}}$ 和 ${r'_{i - 1}}$ 计算公式如下：

${r'_i} = {r'_1}\prod\limits_{k = 2}^i {{{\text{e}}^{{\alpha _k}\tan {\delta _k}}}} = {r'_1}{{\text{e}}^{\sum\limits_{k = 2}^i {{\alpha _k}\tan {\delta _k}} }} \text{，}$

(13)

${r_i} = {r_0}\prod\limits_{k = 1}^i {{{\text{e}}^{{\alpha _k}\tan {\delta _k}}}} = {r_0}{{\text{e}}^{\sum\limits_{k = 1}^i {{\alpha _k}\tan {\delta _k}} }} 。$

(14)

式中： ${r'_1}$ 和 ${r_0}$ 分别为OA₁和OB的长度； ${\alpha _k}$ 为相邻辐射面的夹角， ${\alpha _k} = {\theta _i} - {\theta _{i - 1}}$ 。每个曲线圆锥轴线到原点的距离r_c以及半径R的计算公式为

${r_{\text{c}}} = \frac{{r(\theta ) + r'(\theta )}}{2} \text{，}$

(15)

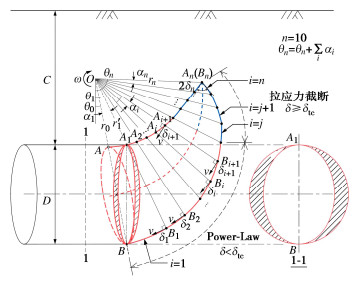
$R = \frac{{r(\theta ) - r'(\theta )}}{2} \text{，}$

(16)

图 3为修正后的多曲线圆锥破坏机构。红色部分为P-L控制区，蓝色部分为T-C控制区，第j个圆锥体是T-C部分的第1个圆锥体，即，δ_i=j是大于δ_tc的最小角度。

图 3 考虑拉应力截断修正的多锥破坏机构

Figure 3. Modified multi-cone failure mechanism considering tension cut-off

下载: 全尺寸图片幻灯片

2.2 功率平衡方程

根据极限分析上限定理^[15]，作用在破坏块体上的外力包括塌落块体自重和保持开挖面稳定的支护力 ${\sigma _{\text{s}}}$ ，块体自重功率根据以下体积分公式计算：

${W_\gamma } = 2\omega \gamma \sum\limits_{i = 1}^n {\int\limits_{{\theta _{i - 1}}}^{{\theta _i}} {\int\limits_{{r_{si}}}^r {{\rho ^2}\sqrt {{R^2} - (\rho - r_{\text{c}}^2)} {\text{sin}}\theta {\text{d}}\rho {\text{d}}\theta } } } 。$

(17)

式中： $\gamma$ 为土体重度；ρ为块体内任意位置到O点的距离；积分下限r_si为

$r_{\mathrm{s} i}=\left\{\begin{array}{ll} r_{i-1}^{\prime} \mathrm{e}^{\left(\theta-\theta_{i-1}\right) \tan \delta_i} & \left(\theta_{i-1} \leqslant \theta \leqslant \theta_i\right) \\ r_0 \frac{\sin \theta_0}{\sin \theta} & \left(\theta_0 \leqslant \theta \leqslant \theta_1\right) \end{array} {。}\right.$

(18)

开挖面与第1个曲线圆锥的相交区域为椭圆，假设支护力均匀分布于开挖面，通过在椭圆区域积分可得支护力功率为

${W_{{\sigma _{\text{s}}}}} = 2\omega {\sigma _{\text{s}}}\int\limits_{{\theta _0}}^{{\theta _1}} {\int\limits_0^{\sqrt {{R^2} - {d_1}} } {\frac{{{{({r_{\text{c}}} + {d_1})}^2}}}{{\tan \theta }}{\text{d}}z{\text{d}}\theta } } \text{，}$

(19)

${d_1} = {r'_1}\frac{{\sin {\theta _1}}}{{\sin \theta }} - {r_{\text{c}}} 。$

(20)

式中：d₁为开挖面到曲线圆锥中心线的距离，如图 2（a）中2-2剖面所示。

破坏机构的内能耗散为负功率，主要发生在塑性剪切区域（破坏面），为开挖面稳定提供抗力。单位面积上的耗散功率计算公式为

$d = \left[ v \right]({\tau _{\text{f}}}\cos \delta - {\sigma _n}\sin \delta ) 。$

(21)

将式（21）沿着所有破坏面进行积分，可以得到总的内能耗散功率计算公式为

$\begin{aligned} D_{\mathrm{s}}= & 2 \omega \sum\limits_{i=1}^{j-1} \int\limits_{\theta_{i-1}}^{\theta_i} \int\limits_{r_i}^r \frac{R \rho^2\left(\tau_{\mathrm{fi}}^{\mathrm{PL}}-\sigma_{n i}^{\mathrm{PL}} \tan \delta_i\right)}{\sqrt{R^2-\left(\rho-r_{\mathrm{c}}\right)^2}} \mathrm{d} \rho \mathrm{d} \theta+ \\ & 2 \omega \sum\limits_{i=1}^n \int\limits_{\theta_{i-1}}^{\theta_i} \int\limits_{r_i}^r \frac{R \rho^2\left(\tau_{\mathrm{fi}}^{\mathrm{TC}}-\sigma_{n i}^{\mathrm{TC}} \tan \delta_i\right)}{\sqrt{R^2-\left(\rho-r_{\mathrm{c}}\right)^2}} \mathrm{d} \rho \mathrm{d} \theta{。} \end{aligned}$

(22)

联立式（17），（19）和（22），得到临界支护力：

$\begin{aligned} \sigma_{\mathrm{s}}= & \frac{1}{\int\limits_{\theta_1}^{\sqrt{R^2-d_1}} \int\limits_0 \frac{\left(r_{\mathrm{c}}+d_1\right)^2}{\tan \theta} \mathrm{~d} z \mathrm{~d} \theta} \\ & {\left[\sum\limits_{i=1}^{j-1} \int\limits_{\theta_{i-1}}^{\theta_i} \int\limits_{r_{s i}}^r \frac{R \rho^2\left(\tau_{\mathrm{f} i}^{\mathrm{PL}}-\sigma_{n i}^{\mathrm{PL}} \tan \delta_i\right)}{\sqrt{R^2-\left(\rho-r_{\mathrm{c}}\right)^2}} \mathrm{~d} \rho \mathrm{~d} \theta+\right.} \\ & \sum\limits_{i=j}^n \int\limits_{\theta_{i-1}}^{\theta_i} \int\limits_{r_{s i}}^r \frac{R \rho^2\left(\tau_{\mathrm{fi}}^{\mathrm{TC}}-\sigma_{n i}^{\mathrm{TC}} \tan \delta_i\right)}{\sqrt{R^2-\left(\rho-r_{\mathrm{c}}\right)^2}} \mathrm{~d} \rho \mathrm{~d} \theta- \\ & \left.\gamma \sum\limits_{i=1}^n \int\limits_{\theta_{i-1}}^{\theta_i} \int\limits_{r_{s i}}^r \rho^2 \sqrt{R^2-\left(\rho-r_{\mathrm{c}}^2\right)} \sin \theta \mathrm{d} \rho \mathrm{~d} \theta\right] \end{aligned}$

(23)

对于在强度较高的地层中开挖的隧道而言，开挖面围岩一般可以通过应力重分布实现自稳，不需要额外施加支护力，此时需要引入其他指标来评价开挖面的稳定性，例如，稳定性系数和安全系数等。本文基于Saada等^[2]的定义，将开挖面安全系数定义为机动速度场中内能耗散功率与外力功率的比值，即

${F_{\text{S}}} = {{{D_{\text{s}}}} \mathord{\left/ {\vphantom {{{D_{\text{s}}}} {{W_\gamma }}}} \right. } {{W_\gamma }}} 。$

(24)

将式（17），（22）代入式（24），整理后得到安全系数计算公式如下：

$\begin{gathered} {F_{\text{S}}} = \left[ {\sum\limits_{i = 1}^{j - 1} {\int\limits_{{\theta _{i - 1}}}^{{\theta _i}} {\int\limits_{{r_{{\text{s}}i}}}^r {\frac{{R{\rho ^2}(\tau _{{\text{f}}i}^{{\text{PL}}} - \sigma _{ni}^{{\text{PL}}}\tan {\delta _i})}}{{\sqrt {{R^2} - {{(\rho - {r_{\text{c}}})}^2}} }}{\text{d}}\rho {\text{d}}\theta } } } + } \right. \hfill \\ \left. {{\text{ }}\sum\limits_{i = j}^n {\int\limits_{{\theta _{i - 1}}}^{{\theta _i}} {\int\limits_{{r_{{\text{s}}i}}}^r {\frac{{R{\rho ^2}(\tau _{{\text{f}}i}^{{\text{TC}}} - \sigma _{ni}^{{\text{TC}}}\tan {\delta _i})}}{{\sqrt {{R^2} - {{(\rho - {r_{\text{c}}})}^2}} }}{\text{d}}\rho {\text{d}}\theta } } } } \right] \cdot \hfill \\ \end{gathered}$

${\left\{ {\gamma \sum\limits_{i = 1}^n {\int\limits_{{\theta _{i - 1}}}^{{\theta _i}} {\int\limits_{{r_{{\text{s}}i}}}^r {{\rho ^2}\sqrt {{R^2} - (\rho - r_{\text{c}}^2)} {\text{sin}}\theta {\text{d}}\rho {\text{d}}\theta } } } } \right\}^{ - 1}} 。$

(25)

式（23）和（25）的值由2n个几何变量（θ₀，α_i，δ_i）决定。为了快速搜索最优上限解，本文采用组合优化的策略，首先利用遗传算法在全局快速搜索，并记录返回的自变量值，然后采用序列二次优化算法进行精细化搜索，充分利用两种算法各自的优势，提高效计算率。优化过程需满足以下约束条件：

$\text { s.t. }\left\{\begin{array}{l} \pi>\alpha_i>0 \\ \pi / 2>\theta_0, \theta_1 \\ \delta_{i+1}>\delta_i, i \in N_{+} \end{array}\right.{。}$

(26)

3. 对比与分析

3.1 对比验证

为本文计算结果与既有文献结果的对比。基于3组不同强度参数： ${c_0}$ =7 kPa， $\varphi$ =17°； ${c_0}$ =10 kPa， $\varphi$ =25°；c₀=15 kPa， $\varphi$ =15°，分别计算了线性M-C条件下考虑T-C和不考虑T-C时的开挖面临界支护力，并与既有文献进行对比。结果表明：多切线法计算的结果与Li等^[16]计算的结果保持高度吻合，这是因为两种方法所采用的上限机构均为曲线圆锥破坏机构，唯一不同的是处理强度非线性所采用的方法。本文采用的是多切线法分段线性近似非线性包络线，而Li等^[16]则采用Michalowski^[17]所提的建议，假设破裂角δ随旋转角θ线性变化，建立破裂角与实际破坏机构之间的几何关系，客观而言，两种方法计算结果几乎相同，但多切线法更侧重于处理非线性强度准则，在线性情况下由于引入了过多的独立变量，导致计算效率没有Li等^[16]的方法高，与Mollon等^[3]的计算结果相比，总体变化规律一致，但误差较大，并且土体强度越高，临界支护力越小，则计算结果的相对误差越大。这种差异主要是由破坏机构不同引起的，Mollon等^[3]采用的是基于离散法的旋转机构，辐射面OA₁和OB之间的破坏机构是从开挖面点到点逐步生成的，破坏范围可以覆盖整个开挖面，而本文采用1个截断的曲线圆锥替代，破坏范围无法覆盖整个圆形开挖面，导致计算结果存在较大差异，尤其是土体条件越好时，破坏机构越小，OA₁和OB之间的破坏体将占据主导因素，支护力的差异会被进一步放大。

表 1 临界支护力与理论解对比

Table 1. Comparison between critical support pressures with theoretical solutions 单位: kPa

工况	${c_0}$ /kPa	$\varphi$ /(°)	${\sigma _{\text{t}}}$ /kPa	破坏准则	Li等^[16]	Mollon等^[3]	本文结果	差异/%
情况1	7	17	22.9	T-C（ξ=0）	33.92	37.44	33.84	9.6
情况1	7	17	22.9	M-C	33.61	37.07	33.53	9.5
情况2	10	25	21.4	T-C（ξ=0）	11.34	14.23	11.32	20.4
情况2	10	25	21.4	M-C	10.63	13.71	10.74	21.7
情况3	15	15	55.0	T-C（ξ=0）	14.01	18.22	13.97	23.3
情况3	15	15	55.0	M-C	10.77	15.20	10.72	29.5

下载: 导出CSV

| 显示表格

表 2计算了考虑T-C和不考虑T-C情况下的临界支护力值。由表 2可知，在土体强度较低情况下，开挖面临界支护力较大，考虑T-C与否对结果影响不大，但对于强度较高的土体，临界支护力绝对误差不大，但相对误差显著增大，当开挖面接近极限状态时，若不考虑T-C，则开挖面为安全的，考虑T-C则不安全，这会对开挖面的极限状态做出错误判断，需要引起重视。

表 2 开挖面临界支护力对比

Table 2. Comparison of critical support pressures of tunnel faces for σ_t=20 kPa 单位: kPa

c₀	m = 1		m = 1.2		m = 1.4		m = 1.6
c₀	T-C	M-C	T-C	P-L	T-C	P-L	T-C	P-L
4	75.29	74.88	123.81	123.23	192.81	191.97	291.53	291.01
6	38.03	37.81	62.30	61.86	95.35	94.57	138.84	137.99
8	19.96	19.64	33.10	32.67	51.46	50.73	75.22	74.11
10	9.80	9.23	17.01	16.42	27.33	26.57	41.25	40.13
12	3.65	2.57	7.56	6.56	13.05	12.09	20.91	19.75
14	—	—	1.92	0.10	4.70	3.01	8.52	7.01
16	—	—	—	—	0.03	—	1.69	—
注：—表示不需要支护。

下载: 导出CSV

| 显示表格

表 3为线性M-C条件下不同文献计算的开挖面安全系数。由表 3可知，本文计算的安全系数与Vermeer等^[18]以及Pan等^[19]计算的结果保持一致，在土体强度较高时，本文计算的安全系数稍微偏大，这与之前所述临界支护力在土体强度较高时偏小的原因相同，是由破坏机构的差异引起。在完全忽略土体抗拉强度后，开挖面安全系数进一步减小，与不考虑拉应力截断的情况相比，最大差异高达11.6%，这充分说明考虑拉应力截断的必要性。

表 3 线性条件下开挖面安全系数对比

Table 3. Comparison of safety factors of tunnel faces under linear condition

c/kPa	φ/(°)	M-C	ξ = 0	Vermeer等^[18]	Pan等^[19]
15	15	0.84	0.75	0.87	0.81
15	20	0.92	0.82	0.91	0.87
20	25	1.33	1.20	1.21	1.15
20	15	1.12	0.99	1.12	1.02
25	20	1.53	1.36	1.41	1.30
25	25	1.67	1.52	1.46	1.36

下载: 导出CSV

| 显示表格

3.2 参数分析

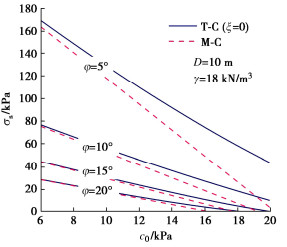
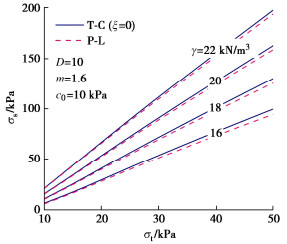
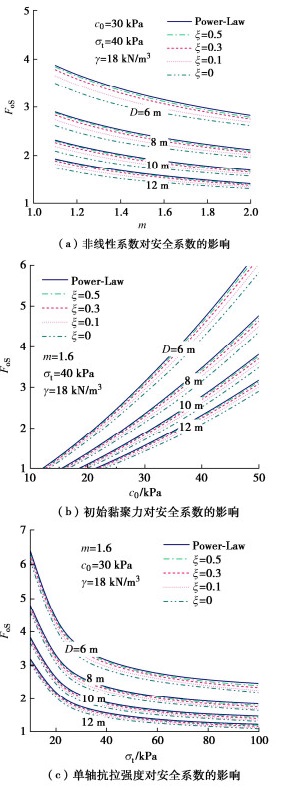
本节基于参数：D=6~12 m，γ = 16~22 kN/m³，c₀=6~20 kPa，φ=5°~20°，m=1~2，σ_t=10~50 kPa，分析不同非线性参数和拉应力截断效应对开挖面稳定性的影响。令m=1，P-L强度准则转变为线性M-C准则，相应的黏聚力为c₀，内摩擦角为φ=arctan(c₀/σ_t)。图 4为不同黏聚力时临界支护力的变化曲线。实线为T-C的结果，虚线为线性M-C准则的结果。在线性M-C条件下，临界支护力与黏聚力近似呈负相关，并且随着φ的增大，临界支护力显著下降，并且黏聚力和内摩擦角越大，两者之间的差异显著增加。

图 4

${c_0}$ 对临界支护力的影响

Figure 4. Effects of

${c_0}$ on critical support pressure

下载: 全尺寸图片幻灯片

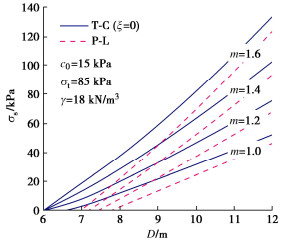
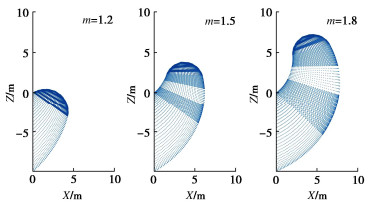
图 5为P-L准则条件下，不同隧道直径对应的临界支护力曲线。其中，实线为考虑T-C的结果，虚线为不考虑T-C的结果。由图 5可知，非线性程度越高，开挖面所需的支护力越高，并且隧道直径越小，T-C效应越明显。

图 5 隧道直径对临界支护力的影响

Figure 5. Effects of tunnel diameter on critical support pressure

下载: 全尺寸图片幻灯片

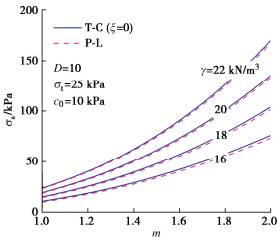
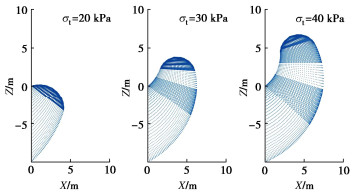
图 6，7分别为单轴抗拉强度和非线性系数对临界支护力的影响图。由图 6，7可知，支护力与单轴抗拉强度呈近似线性变化，与非线性系数呈非线性变化。值得注意的是，T-C效应随着单轴抗拉强度的增大逐渐显著，而非线性系数的增加并不会放大T-C效应。

图 6 σ_t对临界支护力的影响

Figure 6. Effects of σ_t on critical support pressure

下载: 全尺寸图片幻灯片

图 7 m对临界支护力的影响

Figure 7. Effects of m on critical support pressure

下载: 全尺寸图片幻灯片

3.3 破坏机构与应力分布

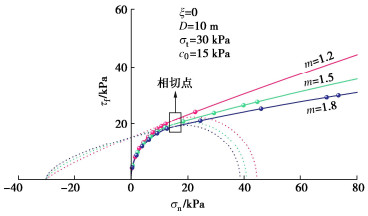
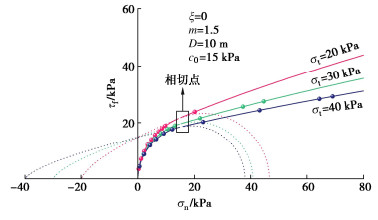
将临界支护力所对应的优化变量δ_i代入式（3），（4），（9），（10），可以反算出每个破裂面上的应力分量。虽然上限极限分析并不涉及应力分析，这些应力状态也不能代表真实极限状态的应力分布，但是通过分析这些应力分量的变化趋势，可以为开挖面稳定性的变化原因提供相应的解释。图 8~10分别为不同非线性系数和单轴抗拉强度条件下的应力分布图。

图 8 不同非线性系数反算的应力分量

Figure 8. Back-calculated stress components for different nonlinear coefficients

下载: 全尺寸图片幻灯片

图 9 不同单轴抗拉强度反算的应力分量

Figure 9. Back-calculated stress components for different uniaxial tensile strengths

下载: 全尺寸图片幻灯片

图 10 不同拉应力截断系数反算的应力分量

Figure 10. Back-calculated stress components for different ξ

下载: 全尺寸图片幻灯片

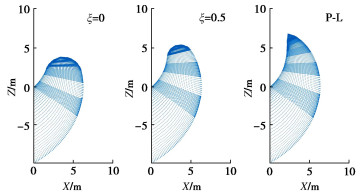
图 11~13为相应的临界破坏机构图。图 14为T-C条件下的三维破坏机构的立体图。其中，明暗相间的部分代表每一个单独的截断曲线圆锥。由图 8，9可知，非线性系数和抗拉强度的增大均会导致压应力区域的抗剪强度降低，拉应力区域的抗剪强度增加，并且落在P-L包络线部分的应力点数量也逐渐增加，这使得破裂角逐渐减小，相应的破坏机构逐渐变大，如图 11，12所示。随着拉应力截断程度的增加，T-C部分应力点所对应的破裂角逐渐增加，破坏机构顶点部分逐渐由尖锐变钝，如图 13所示，而其他由P-L控制的破坏区域在几何上没有明显差异。

图 11 非线性系数对多锥破坏机构的影响

Figure 11. Effects of nonlinear coefficient on geometry of multi-cone failure mechanism

下载: 全尺寸图片幻灯片

图 12 单轴抗拉强度对多锥破坏机构的影响

Figure 12. Effects of uniaxial tensile strength on geometry of multi-cone failure mechanism

下载: 全尺寸图片幻灯片

图 13 拉应力截断程度对多锥破坏机构的影响

Figure 13. Effects of T-C on geometry of multi-cone failure.mechanism

下载: 全尺寸图片幻灯片

图 14 考虑拉应力截断情况下隧道开挖面多曲线圆锥破坏机构

Figure 14. Multi-cone failure mechanism of tunnel faces considering T-C

下载: 全尺寸图片幻灯片

基于参数：D=6~12 m，m=1.1~2.0，c₀=10~50 kPa，σ_t=10~100 kPa，图 15给出了不同拉应力截断程度条件下的开挖面安全系数图表，为实际工程提供理论参考。由图 15可知，拉应力截断效应对安全系数的影响较大，因为在开挖面保持稳定状态时，其临界破坏机构的尺寸通常较小，T-C影响的破坏区域逐渐变大，因此，拉应力截断效应显著。

图 15 不同非线性参数对开挖面安全系数的影响

Figure 15. Effects of different nonlinear parameters on safety factors of the tunnel faces

下载: 全尺寸图片幻灯片

4. 结论

本文引入拉应力截断概念修正了非线性Power-Law强度准则，采用多切线技术处理强度非线性，提出了开挖面临界支护力和安全系数的理论计算方法，研究了不同参数影响下的深埋隧道开挖面稳定性问题，有以下3点结论。

（1）基于上限分析理论和多切线技术提出的开挖面稳定性评估的理论方法，考虑了强度非线性和抗拉强度过高的影响，能够快速准确地计算开挖面临界支护力和安全系数。

（2）在线性情况下，内摩擦角越小且黏聚力越大，拉应力截断对开挖面稳定性的影响越大。对于接近极限状态的隧道开挖面，考虑拉应力截断与否，可能会对开挖面稳定性状态造成截然不同的判断。

（3）在非线性情况下，当单轴抗拉强度较大时，拉应力截断对开挖面稳定性的影响显著增大；而非线性系数的变化并不会显著放大拉应力截断的影响。拉应力截断效应对开挖面临界支护力的影响较小，不足10%，但对安全系数的影响较大，差异超过10%。

图 1 考虑拉应力截断的非线性Power-Law强度准则

Figure 1. Nonlinear Power-Law criterion considering tension cut-off

下载: 全尺寸图片幻灯片

图 2 隧道开挖面多曲线圆锥破坏模式

Figure 2. Multi-cone failure mechanism of tunnel face

下载: 全尺寸图片幻灯片

图 3 考虑拉应力截断修正的多锥破坏机构

Figure 3. Modified multi-cone failure mechanism considering tension cut-off

下载: 全尺寸图片幻灯片

${c_0}$ 对临界支护力的影响

Effects of ${c_0}$ on critical support pressure

下载: 全尺寸图片幻灯片

图 5 隧道直径对临界支护力的影响

Figure 5. Effects of tunnel diameter on critical support pressure

下载: 全尺寸图片幻灯片

图 6 σ_t对临界支护力的影响

Figure 6. Effects of σ_t on critical support pressure

下载: 全尺寸图片幻灯片

图 7 m对临界支护力的影响

Figure 7. Effects of m on critical support pressure

下载: 全尺寸图片幻灯片

图 8 不同非线性系数反算的应力分量

Figure 8. Back-calculated stress components for different nonlinear coefficients

下载: 全尺寸图片幻灯片

图 9 不同单轴抗拉强度反算的应力分量

Figure 9. Back-calculated stress components for different uniaxial tensile strengths

下载: 全尺寸图片幻灯片

图 10 不同拉应力截断系数反算的应力分量

Figure 10. Back-calculated stress components for different ξ

下载: 全尺寸图片幻灯片

图 11 非线性系数对多锥破坏机构的影响

Figure 11. Effects of nonlinear coefficient on geometry of multi-cone failure mechanism

下载: 全尺寸图片幻灯片

图 12 单轴抗拉强度对多锥破坏机构的影响

Figure 12. Effects of uniaxial tensile strength on geometry of multi-cone failure mechanism

下载: 全尺寸图片幻灯片

图 13 拉应力截断程度对多锥破坏机构的影响

Figure 13. Effects of T-C on geometry of multi-cone failure.mechanism

下载: 全尺寸图片幻灯片

图 14 考虑拉应力截断情况下隧道开挖面多曲线圆锥破坏机构

Figure 14. Multi-cone failure mechanism of tunnel faces considering T-C

下载: 全尺寸图片幻灯片

图 15 不同非线性参数对开挖面安全系数的影响

Figure 15. Effects of different nonlinear parameters on safety factors of the tunnel faces

下载: 全尺寸图片幻灯片

表 1 临界支护力与理论解对比

Table 1 Comparison between critical support pressures with theoretical solutions 单位: kPa

工况	${c_0}$ /kPa	$\varphi$ /(°)	${\sigma _{\text{t}}}$ /kPa	破坏准则	Li等^[16]	Mollon等^[3]	本文结果	差异/%
情况1	7	17	22.9	T-C（ξ=0）	33.92	37.44	33.84	9.6
情况1	7	17	22.9	M-C	33.61	37.07	33.53	9.5
情况2	10	25	21.4	T-C（ξ=0）	11.34	14.23	11.32	20.4
情况2	10	25	21.4	M-C	10.63	13.71	10.74	21.7
情况3	15	15	55.0	T-C（ξ=0）	14.01	18.22	13.97	23.3
情况3	15	15	55.0	M-C	10.77	15.20	10.72	29.5

下载: 导出CSV

表 2 开挖面临界支护力对比

Table 2 Comparison of critical support pressures of tunnel faces for σ_t=20 kPa 单位: kPa

c₀	m = 1		m = 1.2		m = 1.4		m = 1.6
c₀	T-C	M-C	T-C	P-L	T-C	P-L	T-C	P-L
4	75.29	74.88	123.81	123.23	192.81	191.97	291.53	291.01
6	38.03	37.81	62.30	61.86	95.35	94.57	138.84	137.99
8	19.96	19.64	33.10	32.67	51.46	50.73	75.22	74.11
10	9.80	9.23	17.01	16.42	27.33	26.57	41.25	40.13
12	3.65	2.57	7.56	6.56	13.05	12.09	20.91	19.75
14	—	—	1.92	0.10	4.70	3.01	8.52	7.01
16	—	—	—	—	0.03	—	1.69	—
注：—表示不需要支护。

下载: 导出CSV

表 3 线性条件下开挖面安全系数对比

Table 3 Comparison of safety factors of tunnel faces under linear condition

c/kPa	φ/(°)	M-C	ξ = 0	Vermeer等^[18]	Pan等^[19]
15	15	0.84	0.75	0.87	0.81
15	20	0.92	0.82	0.91	0.87
20	25	1.33	1.20	1.21	1.15
20	15	1.12	0.99	1.12	1.02
25	20	1.53	1.36	1.41	1.30
25	25	1.67	1.52	1.46	1.36

下载: 导出CSV

参考文献(19)

[1]	PERAZZELLI P, LEONE T, ANAGNOSTOU G. Tunnel face stability under seepage flow conditions[J]. Tunnelling and Underground Space Technology, 2014, 43: 459-469. doi: 10.1016/j.tust.2014.03.001
[2]	SAADA Z, MAGHOUS S, GARNIER D. Stability analysis of rock slopes subjected to seepage forces using the modified Hoek-Brown criterion[J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 55: 45-54. doi: 10.1016/j.ijrmms.2012.06.010
[3]	MOLLON G, DIAS D, SOUBRA A H. Rotational failure mechanisms for the face stability analysis of tunnels driven by a pressurized shield[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2011, 35(12): 1363-1388. doi: 10.1002/nag.962
[4]	吕玺琳, 王浩然, 黄茂松. 盾构隧道开挖面稳定极限理论研究[J]. 岩土工程学报, 2011, 33(1): 57-62. LÜ Xilin, WANG Haoran, HUANG Maosong. Limit theoretical study on face stability of shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 57-62. (in Chinese)
[5]	徐前卫, 唐卓华, 朱合华, 等. 盾构隧道开挖面极限支护压力研究[J]. 岩土工程学报, 2017, 39(7): 1234-1240. doi: 10.11779/CJGE201707009 XU Qianwei, TANG Zhuohua, ZHU Hehua, et al. Limit support pressure at excavation face of shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(7): 1234-1240. (in Chinese) doi: 10.11779/CJGE201707009
[6]	黄阜, 潘秋景, 凌同华. 地下水渗流作用下的盾构隧道开挖面安全系数上限分析[J]. 岩土工程学报, 2017, 39(8): 1461-1469. doi: 10.11779/CJGE201708013 HUANG Fu, PAN Qiujing, LING Tonghua. Upper bound analysis of factor of safety for shield tunnel face subjected to underground water seepage[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(8): 1461-1469. (in Chinese) doi: 10.11779/CJGE201708013
[7]	黄阜, 王芬, 张芝齐, 等. 基于Hoek-Brown破坏准则的盾构隧道开挖面支护力上限研究[J]. 铁道科学与工程学报, 2018, 15(11): 2892-2900. HUANG Fu, WANG Fen, ZHANG Zhiqi, et al. Upper bound solution of supporting pressure for shield tunnel face subjected to Hoek-Brown failure criterion[J]. Journal of Railway Science and Engineering, 2018, 15(11): 2892-2900. (in Chinese)
[8]	金大龙, 袁大军, 郑浩田, 等. 高水压条件下泥水盾构开挖面稳定离心模型试验研究[J]. 岩土工程学报, 2019, 41(9): 1653-1660. doi: 10.11779/CJGE201909009 JIN Dalong, YUAN Dajun, ZHENG Haotian, et al. Centrifugal model tests on face stability of slurry shield tunnels under high water pressures[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(9): 1653-1660. (in Chinese) doi: 10.11779/CJGE201909009
[9]	徐涛, 史庆锋, 章定文, 等. 泥水盾构开挖面泥膜渗透特性与压力传递机制[J]. 岩土工程学报, 2023, 45(9): 1878-1887. doi: 10.11779/CJGE20220866 XU Tao, SHI Qingfeng, ZHANG Dingwen, et al. Permeability characteristics of filter cake and pressure transfer on face during slurry shield tunnelling[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(9): 1878-1887. (in Chinese) doi: 10.11779/CJGE20220866
[10]	陈仁朋, 尹鑫晟, 李育超, 等. 泥水盾构泥膜渗透性及其对开挖面稳定性影响[J]. 岩土工程学报, 2017, 39(11): 2102-2108. doi: 10.11779/CJGE201711018 CHEN Renpeng, YIN Xinsheng, LI Yuchao, et al. Permeability of filter cake and its influence on face stability of slurry shield-driven tunnels[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(11): 2102-2108. (in Chinese) doi: 10.11779/CJGE201711018
[11]	DRUCKER D C, PRAGER W. Soil mechanics and plastic analysis or limit design[J]. Quarterly of Applied Mathematics, 1952, 10(2): 157-165. doi: 10.1090/qam/48291
[12]	PAUL B. A modification of the Coulomb-Mohr theory of fracture[J]. Journal of Applied Mechanics, 1961, 28(2): 259-268. doi: 10.1115/1.3641665
[13]	HOEK E, MARTIN C D. Fracture initiation and propagation in intact rock: a review[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2014, 6(4): 287-300. doi: 10.1016/j.jrmge.2014.06.001
[14]	CHARLES J A, SOARES M M. The stability of slopes in soils with nonlinear failure envelopes[J]. Canadian Geotechnical Journal, 1984, 21(3): 397-406. doi: 10.1139/t84-044
[15]	CHEN W F. Limit Analysis and Soil Plasticity[M]. Amsterdam: Elsevier Scientific Pub Co, 1975.
[16]	LI T Z, YANG X L. Three-dimensional face stability of shallow-buried tunnels with tensile strength cut-off[J]. Computers and Geotechnics, 2019, 110: 82-93. doi: 10.1016/j.compgeo.2019.02.014
[17]	MICHALOWSKI R L. Failure potential of infinite slopes in bonded soils with tensile strength cut-off[J]. Canadian Geotechnical Journal, 2018, 55(4): 477-485. doi: 10.1139/cgj-2017-0041
[18]	VERMEER P A, RUSE N, MARCHER T. Tunnel heading stability in drained ground[J]. Felsbau, 2002, 20(6): 8-18.
[19]	PAN Q J, DIAS D. Upper-bound analysis on the face stability of a non-circular tunnel[J]. Tunnelling and Underground Space Technology, 2017, 62: 96-102. doi: 10.1016/j.tust.2016.11.010

施引文献(1)

期刊类型引用(1)

黄阜，王勇涛，张敏，杨子汉. 考虑抗拉强度截断和孔隙水影响下纵向倾斜盾构隧道的开挖面稳定性分析（英文）. Journal of Central South University. 2025(03): 1080-1098 .

百度学术

其他类型引用(0)

资源附件(1)

其他相关附件
- PDF格式
  07-202501-G23-1160⼀⽂审稿意见与作者答复点击下载(13326KB)

图(15) / 表(3)

计量

文章访问数: 400
HTML全文浏览量: 50
PDF下载量: 85
被引次数: 1

0. 引言
1. 考虑拉应力截断的Power-Law准则
2. 开挖面上限分析
2.1 多曲线圆锥破坏机构
2.2 功率平衡方程
3. 对比与分析
3.1 对比验证
3.2 参数分析
3.3 破坏机构与应力分布
4. 结论

基于多切线技术的盾构隧道开挖面稳定性分析 English Version

作者简介: 钟军豪(1996—)，男，博士研究生，主要从事隧道开挖面稳定性和地层建模方面的研究工作。E-mail: zhongjunhao@csu.edu.cn

通讯作者: 周德, E-mail: 210026@csu.edu.cn

计量

出版历程

Face stability of shield-driven tunnels using multi-tangent technique

0. 引言

1. 考虑拉应力截断的Power-Law准则

2. 开挖面上限分析

2.1 多曲线圆锥破坏机构

2.2 功率平衡方程

3. 对比与分析

3.1 对比验证

3.2 参数分析

3.3 破坏机构与应力分布

4. 结论

期刊类型引用(1)

其他类型引用(0)

其他相关附件

PDF格式

计量

出版历程

目录

0. 引言

1. 考虑拉应力截断的Power-Law准则

2. 开挖面上限分析

2.1 多曲线圆锥破坏机构

2.2 功率平衡方程

3. 对比与分析

3.1 对比验证

3.2 参数分析

3.3 破坏机构与应力分布

4. 结论

作者简介:
钟军豪(1996—)，男，博士研究生，主要从事隧道开挖面稳定性和地层建模方面的研究工作。E-mail: zhongjunhao@csu.edu.cn

通讯作者:
周德, E-mail: 210026@csu.edu.cn