Seismic vulnerability assessment of buried corroded steel pipes under different site conditions
-
摘要: 为评估不同场地中埋地腐蚀管道的抗震性能，建立管-土非线性相互作用分析模型，基于增量动力时程分析方法，以埋地钢管结构应变为性能参数，对不同场地中埋地腐蚀管道的地震易损性进行了分析。结果表明：同一场地条件和服役龄期下，随地震动强度的增大，管道处于基本完好状态的概率逐渐降低，处于严重破坏状态的概率逐渐增加；同一场地条件下，随管道服役龄期的延长，中等损坏极限的曲线斜率增长明显大于基本完好极限的曲线斜率，但管道失效的速率在逐渐变小，软弱场地中服役龄期50 a管道在抗震设防烈度8度时已发生中等损坏；同一地震动强度和服役龄期下，随场地等效剪切波速的减小，管道达到基本完好极限、中等损坏极限的失效概率逐渐增大，软弱场地中失效概率最大；同一服役龄期下，随场地等效剪切波速的减小，管道达到中等损坏、严重破坏的地震动峰值加速度明显降低，较低地震烈度下的软弱场地管道震害甚至高于较高地震烈度下的坚硬场地。本研究可为不同场地中埋地腐蚀管道的震害预测及灾后损失评估提供参考。Abstract: A nonlinear interaction analysis model for pipelines and soils is established to evaluate the anti-seismic performance of corroded steel pipes buried in different sites. Based on the incremental dynamic time-history analysis method, the seismic vulnerability of corroded steel pipes in different sites is analyzed by taking the structural strain of buried steel pipes as the performance parameter. The results show that under the same site condition and service age, the probability of pipelines in a basically intact state decreases gradually, while that in a seriously damaged state increases gradually with the increase of earthquake intensity. Under the same site condition, the slope of the curve of moderately damaged limit becomes significantly larger than that of the curve of basic ally intact limit, but the failure rate of pipelines decreases gradually with the increase of their service age. In the weak site, the pipelines with 50 years of service age are moderately damaged when the seismic fortification intensity is 8 degrees. Under the same earthquake intensity and service age, the failure probability of the pipelines that reaches the basically intact limit and moderately damaged limit gradually increases with the decrease of the site equivalent shear wave velocity. The failure probability is the highest in the weak field. Under the same service age, the peak acceleration of ground motion that the pipelines reach the moderate damage or severe damage decreases obviously with the decrease of the site equivalent shear wave velocity. The damage of pipelines in soft field at lower seismic intensity is even higher than that in hard field at higher seismic intensity. This study may provide reference for the earthquake damage prediction and post-disaster loss assessment of buried corroded pipelines in different sites.
-
Keywords:
- soil site /
- buried corroded pipeline /
- seismic intensity /
- vulnerability
-
0. 引言
长距离输送管道作为国家重要的基础设施和民生工程，以其连续性和高效性被广泛应用于石油、天然气的运输。埋地钢管在长期服役过程中极易受到内外环境的影响发生腐蚀，对管道的完整性和安全性造成了极大的威胁。美国在2008—2017年因腐蚀原因造成的管道事故占事故总量的19.19%，欧洲2007—2016年因腐蚀原因造成的管道事故占事故总量的25%，加拿大在1990—2005年间因腐蚀造成管道失效的比例为16.5%，由于中国早年管道生产及施工技术有限，腐蚀造成管道失效的事故率比发达国家高得多，1969—2003年间腐蚀造成管道失效的比例为39.3%[1]。
近年来国内外学者对腐蚀管道的研究，集中在管道腐蚀机理[2-3]、管道腐蚀模式[4-5]、腐蚀管道失效压力[6-7]和腐蚀管道可靠性评价[1, 8]等方面，而目前地震作用下的研究主要是针对无腐蚀埋地管道[9-10]，考虑地震作用下腐蚀管道地震响应及动力特性的研究相对较少，但已有学者开始关注地震作用下腐蚀管道的易损性分析[11-12]。但上述研究基本上都是针对某一场地中腐蚀管道的地震易损性，考虑不同场地影响的分析尚不多见。而历次震害调查表明，场地条件是影响埋地管道破坏程度的一个重要因素，如1976年的唐山地震震害调查表明，在较低烈度下的软弱场地管道震害甚至有可能高于较高烈度下的坚硬场地[13]。类似受场地条件影响严重的管道在国外的一些大地震中也得到了证实，如日本的浦和地震[14]。
在前人研究的基础上，本研究考虑不同服役龄期钢管腐蚀程度的影响，进一步深入探讨不同场地中腐蚀管道的抗震性能。基于ABAQUS软件平台，考虑等效土弹簧刚度的非线性，采用增量动力时程分析方法，以管道应变为结构损伤性能参数，对不同场地、不同服役龄期埋地钢管的地震易损性分析和抗震性能评估，得到了不同场地中腐蚀管道的地震易损性曲线和地震损伤概率表，可为埋地钢管系统震害预测及灾后损失评估提供参考。
1. 有限元数值分析模型验证
1.1 模型与参数
依据场地的类型划分和剪切波速范围[15]，本研究考虑了4种不同类型的土体条件：坚硬土、中硬土、中软土和软弱土。场地条件的不同主要体现在了地震动延时和非线性离散土弹簧的差异上。
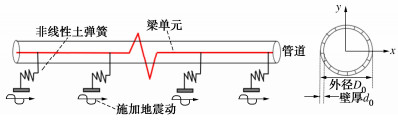
基于ABAQUS有限元平台建立2D梁单元模型，使用轴向非线性离散土弹簧来模拟管-土之间的相互作用，为避免端部约束对于梁模型的影响，设置管道总长为1200 m，足以消除模型两端边界效应的影响，采用B21梁单元对管道进行模拟，为便于土弹簧的施加，每6 m长度的管道上施加一轴向土弹簧模拟管土相互作用，管道左右两端为自由边界，在土弹簧远端各个土节点处分别输入考虑行波效应后的地震动加速度时程，管道模型如图 1所示。
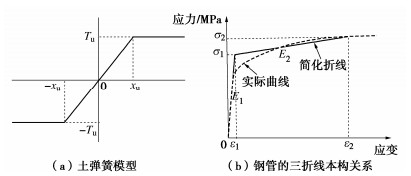
根据美国生命线联盟ALA《埋地钢管设计指南》[16]所建议的方法，土体在地震作用下的非线性动力特性采用弹塑性双折线曲线模型进行模拟，双折线模型是根据土体类型来确定管-土之间力与位移关系的一种简化模型，采用双折线模型可以评估土体的摩擦角、管道的直径和埋置深度等，如图 2（a）所示。管道轴向方向土弹簧刚度计算公式（式（1）~（3））参考规范[17]，对于4种不同的土体类型，轴向土弹簧单位长度的初始刚度和相应位移计算结果如表 1所示。
$$ {T_{\text{u}}} = {\text{π }}D\alpha c + {\text{π }}DH\bar \gamma \frac{{1 + {K_0}}}{2}\tan \delta , $$ (1) $$ \alpha = 0.608 - 0.123c - \frac{{0.274}}{{{c^2} + 1}} + \frac{{0.695}}{{{c^3} + 1}} , $$ (2) $$ {x}_{\text{u}}=\left\{\begin{array}{l}3\sim 5\text{ mm},对黏土\\ 8\sim 10\text{ mm},对砂土\end{array}\right. 。 $$ (3) 表 1 非线性土弹簧单位长度的初始刚度和相应的位移Table 1. Initial stiffnesses per unit length and corresponding displacements of nonlinear soil spring埋深/m 土体类型 参数 轴向 1.88 坚硬土 Tu 6.336×105 xu 0.003 中硬土 Tu 7.23×105 xu 0.005 中软土 Tu 2.01×106 xu 0.008 软弱土 Tu 2.442×106 xu 0.01 注：Tu表示初始刚度(N/m)；xu表示对应位移(m)。 式中：D为管道外径；c为回填土的土壤内聚力；H为管道的埋深；$ \overline \gamma $为土的有效重度；K0为静止土压力系数；α为附着系数；δ是指管土界面摩擦角，$ \delta = f\varphi $；$ \varphi $为内摩擦角；ƒ是将土壤的内摩擦角与管-土界面处的摩擦角相关联的涂层相关系数。
选用API 5L X65钢质管材，管道参数如表 2所示。钢管的应力应变本构关系采用油气管道规范[18]推荐的三折线模型如图 2（b）所示。其中，$ {\sigma _1} $和$ {\varepsilon _1} $分别是管材塑性变形的起点应力和应变，$ {\sigma _1} $取为管材的屈服强度，$ {\varepsilon _1} $取为管材屈服强度状态下的应变；$ {\sigma _2} $和$ {\varepsilon _2} $分别是管材弹塑性变形和塑性变形的临界应力和应变，$ {\sigma _2} $取为管材的极限强度，$ {\varepsilon _2} $取为管材极限强度状态下管道的应变；E1和E2分别是管材在弹性区域和弹塑性区域的切线模量，对于非理想的弹塑性分析E2可取为E1的1/10。
表 2 管道参数Table 2. Parameters of pipelines材质 外径/mm 单位重量/(kg·m-3) 弹性模量/GPa 壁厚/mm 屈服强度/MPa 极限强度/MPa API 5L-X65 762 7850 210 17.5 450 535 1.2 模型验证
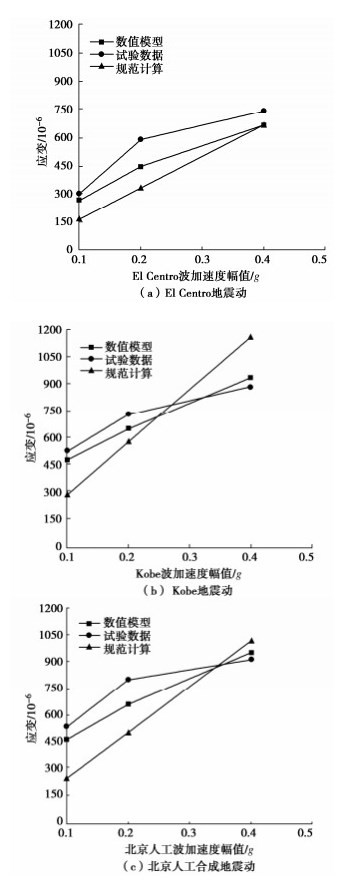
为验证本文有限元模型用于埋地腐蚀管道地震易损性分析的准确性，基于1.1节管道建模方法，选取El Centro地震动、Kobe地震动和北京人工合成地震动，对纵向非一致激励下管道轴向的峰值应变与文献[19]中的振动台试验数据进行对比，同时与《油气输送管道线路工程抗震技术规范：GB/T 50470—2017》中管道最大轴向应变进行对比（见图 3）。
数值模型的管道应变（黑色线）与振动台试验中管道应变（红色线）在趋势上基本一致。油气管道规范中计算的埋地直管道的应变呈现线性增加趋势，其原因在于根据规范进行计算时，埋地管道在地震动作用下确定场地的最大轴向应变与地震动峰值速度线性相关，而试验与数值模拟考虑了管-土相互作用的影响，管道应变随施加的地震动峰值速度是非线性的。因此，规范得到在加速度幅值较小与加速度幅值较大时管道应变差值更大，与试验和数值模拟相比，规范有一定的局限性。
数值模型在EL Centro地震动、Kobe地震动和北京人工合成地震动0.1g加速度幅值下的计算结果与试验的误差分别为8%，7%，22%；在0.2g加速度幅值下与试验的误差分别为0.2%，12%，4%；在0.4g加速度幅值下与试验的误差分别为1.3%，6%，29%。与试验相比，数值模型管道在加速度幅值0.4g及以下的管道应变相差不大，在0.62g地震动加速度幅值下误差相对较大。在加速度幅值较大的情况下，基本符合GB/T 50470—2017规范，说明该数值模型是合理的。
表 3 不同服役龄期下埋地管道的几何与力学性能参数Table 3. Geometrical and mechanical property parameters of buried pipelines under different service ages服役龄期/a 失重率/Dw E1/GPa $ {\varepsilon _1} $ $ {\sigma _1} $/MPa E2/GPa $ {\varepsilon _2} $ $ {\sigma _2} $/MPa 管半径/m 壁厚/m 0~20 0 210.0 0.00214 450 21.00 0.02548 535 0.3810 0.0175 30 0.244 162.0 0.00211 342 16.20 0.02590 420 0.3768 0.0133 40 0.486 115.0 0.00204 235 11.50 0.02665 306 0.3726 0.0091 50 0.725 68.3 0.00189 129 6.83 0.02843 194 0.3684 0.0049 2. 埋地腐蚀管道概率地震需求模型
2.1 腐蚀管道模型
随着非酸性土壤酸化的报道逐渐增多，本文主要研究由酸性环境造成的管道腐蚀，黄涛等[20]通过埋地钢管的加速腐蚀模拟试验指出，埋地钢管随着土体pH值的降低，由腐蚀速率较低的局部腐蚀转变为全面腐蚀，本文采用全面腐蚀模型来描述埋地钢管在酸性土壤条件下的腐蚀行为，并假定管道的腐蚀发展模型为线性腐蚀且简化为径向匀速发展过程，径向腐蚀速率考虑为确定性参数。
钢管的面积腐蚀率表示为
$$ \zeta = \frac{{{A_{\text{t}}}}}{{{A_0}}} = \frac{{{\text{π }}{d_0}({D_0} - {d_0}) - {\text{π }}({d_0} - {v_{\text{d}}}t)({D_0} - {d_0} - {v_{\text{d}}}t)}}{{{\text{π }}{d_0}({D_0} - {d_0})}} 。 $$ (4) 式中：$ \zeta $为钢管的面积腐蚀率；t=$ T - {t_0} $，T为钢管服役时间（年），$ {t_0} $为腐蚀发生的时刻（年），且当T < $ {t_0} $时，t=0；$ {A_0} $为埋地钢管的截面面积（mm2）；$ {A_{\text{t}}} $为钢管截面腐蚀面积（mm2）；D0为腐蚀前钢管的外径（mm）；d0为腐蚀前钢管的壁厚（mm）；$ {v_{\text{d}}} $表示管道径向平均腐蚀速率（mm/a），可参考文献[20]来取值。
根据相关研究[11]，为了定量描述钢材锈蚀程度，可使用失重率来描述管材的腐蚀程度，其表达式为
$$ {D_{\text{w}}} = ({W_0} - {W_1})/{W_0} 。 $$ (5) 式中：$ {D_{\text{w}}} $为钢材的失重率；$ {W_0} $和$ {W_1} $分别为钢材标准试件腐蚀前后的质量。
通过对锈蚀钢材拉伸性能试验获得钢材力学性能指标随失重率变化的退化模型[21]，其线性拟合结果为
$$ \left. \begin{array}{l} {{f'}_{\text{y}}}/{f_{\text{y}}} = 1 - 0.9833{D_{\text{w}}}{\text{ }} \\ {{f'}_{\text{u}}}/{f_{\text{u}}} = 1 - 0.8791{D_{\text{w}}} \\ \delta '/\delta = 1 - 7780{D_{\text{w}}} \\ E'/E = 1 - 0.9312{D_{\text{w}}} \\ \end{array} \right\} 。 $$ (6) 式中：$ {f_{\text{y}}} $，$ {f_{\text{u}}} $，$ \delta $和E分别为钢材腐蚀前的屈服强度、极限强度、伸长率和弹性模量；$ {f'_{\text{y}}} $，$ {f'_{\text{u}}} $，$ \delta ' $和$ E' $分别为钢材腐蚀后的屈服强度、极限强度、伸长率和弹性模量。
根据面积腐蚀率的定义，即可得到不同龄期的埋地钢管的外径和管道壁厚的表达式：
$$ {D_{\text{T}}} = {D_0} - 2{v_{\text{d}}}(T - {t_0}) \text{，} $$ (7) $$ {d_{\text{T}}} = {d_0} - {v_{\text{d}}}(T - {t_0}) 。 $$ (8) 式中：$ {D_{\text{T}}} $和$ {d_{\text{T}}} $分别表示服役龄期为T时钢管外径和壁厚（mm）。
根据文献[11]设定假设腐蚀前后的钢材密度保持不变，沿管道长度方向不同截面的腐蚀率相同，且忽略腐蚀对管道长度的影响。基于以上的假设可确定埋地钢管的失重率$ {D_{\text{w}}} $可近似等于其面积腐蚀率$ \xi $，由此，可得到埋地钢管的失重率与服役龄期的关系如下式：
$$ {D}_{\text{w}}=\frac{{\rho }_{\text{t}}{A}_{\text{t}}{L}_{\text{t}}}{{\rho }_{0}{A}_{0}{L}_{0}}=\frac{{A}_{\text{t}}}{{A}_{0}}=\frac{{d}_{0}({D}_{0}-{d}_{0})-({d}_{0}-{v}_{\text{d}}t)({D}_{0}-{d}_{0}-{v}_{\text{d}}t)}{{d}_{0}({D}_{0}-{d}_{0})}。 $$ (9) 式中：$ {\rho _0} $和$ {\rho _{\text{t}}} $分别为腐蚀前后的钢材密度；L0，Lt分别为腐蚀前后的管道长度；$ {A_0} $，$ {A_{\text{t}}} $为腐蚀前和腐蚀后的管道截面积。
管道参数根据表 2中的基本参数设定，钢管的本构关系采用图 2所示的三折线模型本构，经由式（9）即可求得不同服役龄期的管道的失重率，由此代入式（6）可得管道不同服役龄期下钢管性能退化后的模型本构参数变化，代入式（7），（8）可得不同服役龄期下几何参数（外径、壁厚）的变化，如表 3所示（钢管防腐涂层设计保护年限为20 a，即前20 a埋地钢管不发生腐蚀现象[11])。
2.2 地震动记录选取与处理
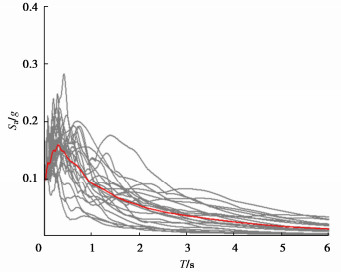
根据美国应用技术委员会ATC在FEMA-P695报告[22]中的建议，本文从（PEER，pacific earthquake engineering research center）地震动数据库中共选取了22条远场地震动记录进行管道模型的增量动力分析（incremental dynamic analysis，简称IDA），图 4为所选地震动记录的加速度反应谱曲线，图中红色曲线为加速度反应谱中位值。
基于地震峰值加速度（peak ground acceleration，简称PGA）对原始地震动记录进行调幅，缩放间隔为0.1g。地震动的非一致激励考虑了其传播过程中的行波效应，延时根据各场地土的剪切波速计算得到，进而得到每个土弹簧输入点处在传播方向上的地震动时程。据文献[23]土体试验相似比，并根据规范取值坚硬土、中硬土、中软土和软弱土的场地剪切波速分别取600，300，200，150 m/s。
3. 损伤性能参数及地震动强度指标
3.1 损伤性能参数
结构的地震响应与地震动强度参数之间服从双参数对数正态分布[24]，地震易损性旨在给出不同地震动强度作用下结构反应超过破坏阶段所定义的结构需求能力参数的条件概率，其公式可表示为
$$ {P_{\text{f}}}({d_{\text{s}}} \geqslant {d_{{\text{si}}}}/S) = \mathit{\Phi} \left[ {\frac{1}{{{\beta _{{\text{tot}}}}}}\ln \left( {\frac{S}{{{S_{{\text{mi}}}}}}} \right)} \right] 。 $$ (10) 式中：$ {P_{\text{f}}} $为在某地震动强度下结构失效的概率；ds为在某一地震动强度下，结构响应达到的某一性能水准限值；S为选定的地震动强度指标；$ \mathit{\Phi} $为标准正态累计概率函数；Smi为导致某一损伤状态下地震动强度指标的中间临界值；βtot为总的对数正态标准偏差。其中βtot的计算公式为
$$ {\beta _{{\text{tot}}}} = \sqrt {\beta _{{\text{DS}}}^{\text{2}} + \beta _{\text{C}}^{\text{2}} + \beta _{\text{D}}^{\text{2}}} 。 $$ (11) 式中：$ \beta _{{\text{DS}}}^{} $为结构损伤状态的不确定性，文献[25]中地震灾害损失风险评估软件对建筑物的要求取为0.4，而在本次管道的分析中其损伤状态已经确定，故不考虑该系数的影响；βC表示结构建设质量所引起的不确定性，参考FEMA-P695[22]报告，取经验值0.3；βD表示在输入不同地震动作用下得到的结构性能损伤的对数变量的平均标准偏差，其式为
$$ {\beta _{\text{D}}} = \sqrt {\frac{{\sum\nolimits_{i = 1}^n {[\ln ({\text{DM}}) - {{(a + b\ln ({\text{IM}})]}^2}} }}{{n - 2}}} 。 $$ (12) 3.2 管道损伤状态
管道抗震设计普遍采用的是应变设计[26]，应变设计是将结构的应变作为控制参数的一种设计方法。对于埋地钢管，轴向的地震响应被认为是更为关键的，轴向应变通常倾向于大于弯曲应变[27]。且连续管道常见失效模式是由于拉伸断裂引起的，因此，本文采用管道的峰值轴向拉伸应变(在此处表示为εmax)用作埋地钢管的损伤性能参数DM（damage measure）。
根据《生命线工程地震破坏等级划分：GB/T24336—2009》[28]以及中国工程力学研究所提出的管道地震破坏划分标准[21]，将钢管在地震作用下的破坏程度主要划分为三等级性能水准：基本完好、中等损坏和严重破坏，其不同损伤程度对应的功能性要求与应变限值的描述如表 4所示。通过计算，钢质管道的损伤指标阈值为：$ {\varepsilon _1} $=0.002，$ {\varepsilon _2} $=0.006。
表 4 埋地连续管道地震损伤指标Table 4. Seismic damage indices of buried continuous pipelines性能水准 性能要求 管道应变 基本完好 管道可能有轻微变形，无破损，无渗漏，无需修复即可正常运行 $ \varepsilon < {\varepsilon _1} $ 中等损坏 管道即将发生较大变形或者屈曲，或有轻度破损，有渗漏，需采取修理措施才能正常运行 $ {\varepsilon _1} < \varepsilon < {\varepsilon _2} $ 严重破坏 管道破裂，必须更换管道 $ \varepsilon > {\varepsilon _2} $ 3.3 地震动强度指标
目前分析中应用较为广泛且易于提取的能够用来描述地震动特性的参数有峰值加速度PGA、峰值速度PGV、峰值位移PGD，这些参数由于其简单明了、较易获得，从而经常用于关联结构破坏与地震强度。对于管道的性能分析，许多研究和经验公式均基于PGA进行描述[29]，PGA的优点是概念清晰，计算简单并且可以使用现有的地震动衰减关系来确定地震危险。因此本文采用PGA作为地震强度指标IM（intensity measure）的衡量标准。
4. 地震易损性分析
4.1 IDA分析
IDA分析基本步骤如下：
（1）进行埋地腐蚀管道模型的弹塑性动力分析计算，得到多条地震响应分析后的IDA曲线簇。
（2）将损伤指标的对数形式ln（DM）和地震动强度指标对数形式ln（IM）进行线性回归，通过线性拟合得到回归系数b，c。
（3）利用式（12）计算得到平均标准偏差βD和Smi，将其代入式（10）计算出结构在不同水平地震动作用下的失效概率，即可获得易损性曲线。
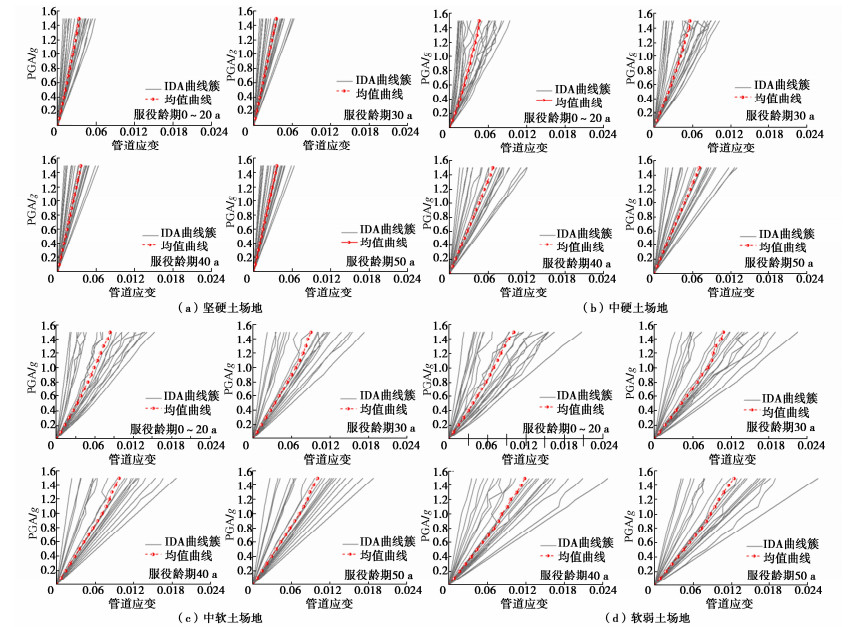
对服役龄期为0~20，30，40，50 a的不同场地中埋地钢管进行IDA分析，计算结果如图 5所示，图中给出了不同场地中管道最值应变的IDA曲线。从图 5中可以看出，各场地下腐蚀管道的曲线簇在一开始的阶段较为密集，随着地震动强度的增加，管道响应的离散型也逐渐在增大，并且出现一些波动现象，同时，采用不同的地震动输入，各条IDA曲线之间存在着差异，这说明埋地腐蚀管道地震响应与所输入的地震动特性密切相关。再者，随着场地等效剪切波速的减小，管道应变越来越大，管道响应的波动现象也越来越明显，说明场地土越软，埋地钢管在地震作用下越容易发生破坏。
![]()
图 5 不同场地下各服役龄期管道应变IDA曲线簇Figure 5. IDA curve clusters of pipeline strain at different service ages under each site condition4.2 地震易损性曲线
对埋地腐蚀管道在不同场地下的IDA数据分别进行线性回归分析，进而绘制出各场地中服役龄期为0~20，30，40，50 a的埋地钢管地震易损性曲线如图 6所示，用以表示在不同场地中各服役龄期管道在基本完好、中等损坏和严重破坏性能水准下的概率。
![]()
图 6 不同场地下各服役龄期管道地震易损性曲线Figure 6. Seismic vulnerability curves of pipelines at different service ages under each site condition（1）地震动强度的影响
由图 6可知，在场地条件和服役龄期不变的情况下，随地震动强度的增大，管道处于基本完好状态的概率逐渐降低，处于严重破坏状态的概率逐渐增加，但基本完好极限和中等损坏极限曲线的斜率在逐渐减小，说明随地震动强度的增大，管道失效的速率在减小。服役龄期50 a的软弱土场地中, PGA=1.0g时，对于失效阈值为0.002，0.006，管道处于基本完好极限和中等损坏极限的失效概率分别达到了97.6%，63.21%；当PGA=1.5g时，两极限状态下的失效概率最大，对于失效阈值为0.002，0.006，分别达到了99.52%，82.90%。由此可见，当地震动强度相对较大时，失效概率增长值已相对较小。
（2）服役龄期的影响
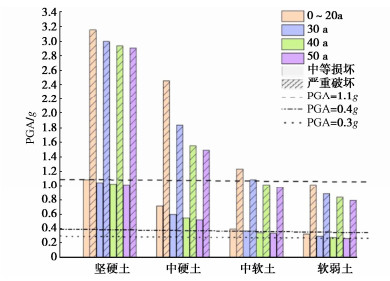
图 7是4种场地中不同服役龄期埋地钢管达到中等损坏、严重破坏的PGA值。可知各场地中埋地钢管随服役龄期的延长，相对较小的地震动强度就可以使管道达到中等损坏和严重破坏。软弱场地中无腐蚀管道在抗震设防9度（0.4g）时发生中等损坏，而服役了50 a的管道在抗震设防8度（0.3g）时就发生中等损坏。
![]()
图 7 管道中等损坏和严重破坏对应的PGA值Figure 7. PGA values corresponding to moderate damage and severe damage of pipelines且由图 6知各场地土中埋地钢管随服役龄期的增大，中等损坏极限的曲线斜率增长明显大于基本完好极限的曲线斜率，说明埋地钢管随服役龄期的增长越来越容易产生较严重的管道损坏，使生命线系统造成更为严重的破坏。
（3）场地条件的影响
由图 6，7可知，同一服役龄期下，随场地等效剪切波速的减小，在相对较小的地震动强度下管道已产生中等损坏和严重破坏。坚硬场地中无腐蚀管道在PGA为1.1g时达到中等损坏，而软弱场地中无腐蚀管道在PGA为0.4g即达到中等损坏。说明在较低地震烈度下的软弱场地管道震害甚至可能高于较高地震烈度下的坚硬场地，这与唐山地震震害调查结论相符[13]。腐蚀缺陷对处于坚硬场地中埋地钢管的影响最小，对软弱场地中埋地钢管的影响最大，这是由于当覆盖层厚度一定时，场地卓越周期随剪切波速的增大而减小[30]。场地土越软，剪切波速越小，软弱场地土对场地卓越周期值存在一定的放大作用，强震时将导致地下结构的自振周期与场地卓越周期相等或相近，不利于管道的抗震。以抗震设防烈度9度为例，表 5是埋地管道发生中等损坏和严重破坏的失效概率，同理可对其他抗震设防烈度等级下埋地钢管进行地震风险评估。
表 5 抗震设防烈度9度的埋地管道地震失效概率Table 5. Seismic damage probability of buried pipeline with seismic fortification intensity of 9 degrees场地条件 坚硬土 中硬土 服役龄期 0~20 a 30 a 40 a 50 a 0~20 a 30 a 40 a 50 a 失效概率P 中等损坏 7.18% 7.77% 7.90% 7.96% 21.45% 28.34% 32.56% 34.36% 严重破坏 0.13% 0.14% 0.15% 0.15% 0.71% 1.60% 2.48% 2.59% 场地条件 中软土 软弱土 服役龄期 0~20 a 30 a 40 a 50 a 0~20 a 30 a 40 a 50 a 失效概率P 中等损坏 49.53% 54.29% 57.44% 59.90% 60.66% 66.26% 69.44% 72.37% 严重破坏 5.58% 7.45% 8.26% 8.69% 9.05% 12.09% 13.61% 14.76% 4.3 失效概率增长值
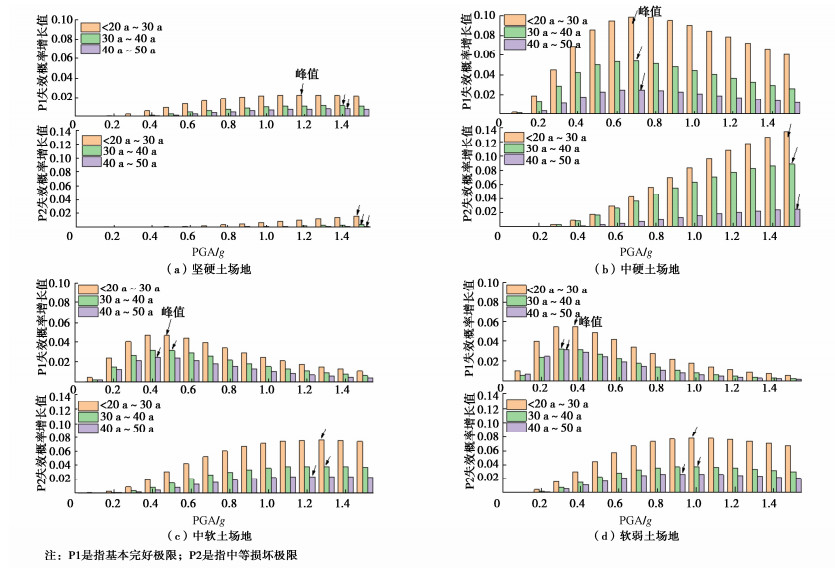
基于图 6进一步得到埋地钢管在不同服役龄期下随PGA增大的失效概率增长值，其式可表示为
$$ \Delta {P_{\rm{J}}} = {P_{Jn{\rm{a}}}} - {P_{J(n - 10){\rm{a}}}}{\rm{,}} $$ (13) $$\Delta {P_{\rm{Z}}} = {P_{Zn{\rm{a}}}} - {P_{Z(n - 10){\rm{a}}}} 。 $$ (14) 式中：ΔPJ为基本完好极限失效概率增长值；ΔPZ为中等损坏极限失效概率增长值；n取30，40，50。等式表示几种场地中各地震动强度下服役龄期30 a与服役龄期0~20 a管道的失效概率增长值、服役龄期40 a与服役龄期30 a管道的失效概率增长值；服役龄期50 a与服役龄期40 a管道的失效概率增长值。
由图 8可知，不同场地中埋地钢管处于基本完好极限和中等损坏极限的失效概率增长值，均表现为无腐蚀与服役30 a的失效概率增长值最大，其次为服役30 a与服役40 a的失效概率增长值，最小的失效概率增长值是服役40 a与服役50 a，由此说明，虽然埋地钢管的失效概率随服役龄期的增长越来越大，但失效的速率却逐渐变小，这与学者们对埋地钢管受土壤腐蚀影响机理研究的结论一致[6]。以钢管服役龄期为20 a到30 a的失效概率增长值为例，在坚硬场地下，管道处于基本完好极限和中等损坏极限的失效概率增长值的峰值PGA分别为1.2g和1.5g；在中硬场地下分别为0.7g和1.5g；在中软场地下分别为0.5g和1.3g；在软弱场地下分别为0.4g和1.0g。随着场地等效剪切波速的减小，失效概率增长值的峰值点对应的PGA值逐渐减小，表明场地土越软，管道失效概率增长最快时对应的地震动强度越小。各场地中均表现为服役龄期30 a的管道失效概率增长值最大，如软弱场地中，PGA=1.5g，服役龄期30 a的管道达到中等损坏和严重破坏的失效概率分别为99.07%, 77.77%，而服役龄期50 a时分别达到99.52%, 82.90%。由此可见，管道服役30 a后失效概率增长较为缓慢，对服役龄期已超过30 a的管道应及时检测其腐蚀程度，必要时采取措施进行修复或更换。
![]()
图 8 不同场地下各服役龄期管道失效概率增长值Figure 8. Growth values of failure probability of pipelines at different service ages under each site condition5. 结论
本文主要采用增量动力时程分析方法，对比分析了不同场地条件、不同服役龄期对埋地管道结构抗震性能的影响，主要得到以下3点结论。
（1）地震动强度：在场地条件和服役龄期不变的情况下，随地震动强度的增大，管道处于基本完好状态的概率逐渐降低，处于严重破坏状态的概率逐渐增加。
（2）服役龄期：随服役龄期的延长，各场地中管道在相对较小的地震动强度作用下将发生中等损坏和严重破坏；各场地中管道中等损坏极限的曲线斜率增长明显大于基本完好极限的曲线斜率，管道更容易发生更为严重的破坏；各场地中管道的失效速率随服役龄期的延长逐渐变小，在服役龄期30 a时失效概率增长值最大，应对服役龄期30 a的管道重点检测。
（3）场地条件：同一服役龄期下，随场地等效剪切波速的减小，管道达到中等损坏、严重破坏的地震动峰值加速度明显降低，较低地震烈度下的软弱场地管道震害甚至高于较高地震烈度下的坚硬场地中的管道。
-
![]()
图 5 不同场地下各服役龄期管道应变IDA曲线簇
Figure 5. IDA curve clusters of pipeline strain at different service ages under each site condition
![]()
图 6 不同场地下各服役龄期管道地震易损性曲线
Figure 6. Seismic vulnerability curves of pipelines at different service ages under each site condition
![]()
图 7 管道中等损坏和严重破坏对应的PGA值
Figure 7. PGA values corresponding to moderate damage and severe damage of pipelines
![]()
图 8 不同场地下各服役龄期管道失效概率增长值
Figure 8. Growth values of failure probability of pipelines at different service ages under each site condition
表 1 非线性土弹簧单位长度的初始刚度和相应的位移
Table 1 Initial stiffnesses per unit length and corresponding displacements of nonlinear soil spring
埋深/m 土体类型 参数 轴向 1.88 坚硬土 Tu 6.336×105 xu 0.003 中硬土 Tu 7.23×105 xu 0.005 中软土 Tu 2.01×106 xu 0.008 软弱土 Tu 2.442×106 xu 0.01 注：Tu表示初始刚度(N/m)；xu表示对应位移(m)。 
下载: 导出CSV
表 2 管道参数
Table 2 Parameters of pipelines
材质 外径/mm 单位重量/(kg·m-3) 弹性模量/GPa 壁厚/mm 屈服强度/MPa 极限强度/MPa API 5L-X65 762 7850 210 17.5 450 535
下载: 导出CSV
表 3 不同服役龄期下埋地管道的几何与力学性能参数
Table 3 Geometrical and mechanical property parameters of buried pipelines under different service ages
服役龄期/a 失重率/Dw E1/GPa /MPa E2/GPa /MPa 管半径/m 壁厚/m 0~20 0 210.0 0.00214 450 21.00 0.02548 535 0.3810 0.0175 30 0.244 162.0 0.00211 342 16.20 0.02590 420 0.3768 0.0133 40 0.486 115.0 0.00204 235 11.50 0.02665 306 0.3726 0.0091 50 0.725 68.3 0.00189 129 6.83 0.02843 194 0.3684 0.0049
下载: 导出CSV
表 4 埋地连续管道地震损伤指标
Table 4 Seismic damage indices of buried continuous pipelines
性能水准 性能要求 管道应变 基本完好 管道可能有轻微变形，无破损，无渗漏，无需修复即可正常运行 中等损坏 管道即将发生较大变形或者屈曲，或有轻度破损，有渗漏，需采取修理措施才能正常运行 严重破坏 管道破裂，必须更换管道
下载: 导出CSV
表 5 抗震设防烈度9度的埋地管道地震失效概率
Table 5 Seismic damage probability of buried pipeline with seismic fortification intensity of 9 degrees
场地条件 坚硬土 中硬土 服役龄期 0~20 a 30 a 40 a 50 a 0~20 a 30 a 40 a 50 a 失效概率P 中等损坏 7.18% 7.77% 7.90% 7.96% 21.45% 28.34% 32.56% 34.36% 严重破坏 0.13% 0.14% 0.15% 0.15% 0.71% 1.60% 2.48% 2.59% 场地条件 中软土 软弱土 服役龄期 0~20 a 30 a 40 a 50 a 0~20 a 30 a 40 a 50 a 失效概率P 中等损坏 49.53% 54.29% 57.44% 59.90% 60.66% 66.26% 69.44% 72.37% 严重破坏 5.58% 7.45% 8.26% 8.69% 9.05% 12.09% 13.61% 14.76%
下载: 导出CSV
-
[1] 张杰. 腐蚀管道结构可靠性评价与维修策略优化[D]. 北京: 中国石油大学, 2020. ZHANG Jie. Structural Reliability Evaluation and Maintenance Strategy Optimization of Corroded Pipelines[D]. Beijing: China University Of Petroleum, 2020. (in Chinese)
[2] BAI X L, HE B, HAN P J, et al. Corrosion behavior and mechanism of X80 steel in silty soil under the combined effect of salt and temperature[J]. RSC Advances, 2022, 12: 129-147. doi: 10.1039/D1RA08249C
[3] 马晓凤. 埋地保温管道腐蚀原因分析和腐蚀机理研究[D]. 西安: 西安石油大学, 2021. MA Xiaofeng. Corrosion Cause Analysis and Corrosion Mechanism Research of Buried Thermal Insulation Pipeline[D]. Xi'an: Xi'an Shiyou University, 2021. (in Chinese)
[4] WANG Y H, ZHANG P, QIN G J. Reliability assessment of pitting corrosion of pipeline under spatiotemporal earthquake including spatial-dependent corrosion growth[J]. Process Safety and Environmental Protection, 2021, 148: 166-178. doi: 10.1016/j.psep.2020.10.005
[5] 方卓钰, 董绍华, 段宇航. 含双点腐蚀缺陷海底管道剩余强度及失效分析[C]// 2021 IPPTC国际石油石化技术会议论文集, 北京, 2021: 546-558. FANG Zhuoyu, DONG Shaohua, DUAN Yuhang. Residual strength and failure analysis of submarine pipeline with double pitting corrosion defects[C]// Proceedings of 2021IPPTC International Petroleum and Petrochemical Technology Conference, Beijing, 2021: 546-558. (in Chinese)
[6] ARUMUGAM T, KARUPPANAN S, OVINIS M. Finite element analyses of corroded pipeline with single defect subjected to internal pressure and axial compressive stress[J]. Marine Structures, 2020, 72(C): 1-21.
[7] AMANDI K U, DIEMUODEKE E O, BRIGGS T A. Model for remaining strength estimation of a corroded pipeline with interacting defects for oil and gas operations[J]. Cogent Engineering, 2019, 6(1): 1-9.
[8] MOHSEN A, REZA B M. A new approach for finite element based reliability evaluation of offshore corroded pipelines[J]. International Journal of Pressure Vessels and Piping, 2021, 193: 1-13.
[9] ZHANG W, SHOKRABADI M, BOZORGNIA Y, et al. A methodology for fragility analysis of buried water pipes considering coupled horizontal and vertical ground motions[J]. Computers and Geotechnics, 2020, 126: 1-22.
[10] 王书锐. 垫衬法加固前后地下供水管道抗震易损性分析[D]. 北京: 北京工业大学, 2019. WANG Shurui. Seismic Vulnerability Analysis of Underground Water Supply Pipes Before and After Reinforcement by Cushion Lining Method[D]. Beijing: Beijing University of Technology, 2019. (in Chinese)
[11] 贺金川, 韩峰, 郑山锁, 等. 酸性土壤环境中多龄期埋地钢管地震易损性分析[J]. 天津大学学报, 2020, 53(9): 881-889. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDX202009001.htm HE Jinchuan, HAN Feng, ZHENG Shansuo, et al. Seismic vulnerability analysis of multi-age buried steel pipes in an acidic soil environment[J]. Journal of Tianjin University, 2020, 53(9): 881-889. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJDX202009001.htm
[12] 谢孝奎, 贺金川, 郑山锁, 等. 碱性及近中性土壤环境中埋地钢管时变地震易损性分析[J]. 天津大学学报, 2020, 53(12): 1254-1263. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDX202012006.htm XIE Xiaokui, HE Jinchuan, ZHENG Shansuo, et al. Time-varying seismic fragility analysis of buried steel pipes in alkaline and near-neutral soil environments[J]. Journal of Tianjin University, 2020, 53(12): 1254-1263. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJDX202012006.htm
[13] 姜华. 埋地钢管在地震波作用下的响应分析[D]. 武汉: 华中科技大学, 2011. JIANG Hua. Response Analysis of Buried Pipelines under Seismic Waves[D]. Wuhan: Huazhong University of Science and Technology, 2011. (in Chinese)
[14] 侯忠良. 地下管线抗震[M]. 北京: 学术书刊出版社, 1990. HOU Zhongliang. Earthquake Resistance of Underground Pipelines[M]. Beijing: Academic Book Publishing House, 1990. (in Chinese)
[15] 城市轨道交通结构抗震设计规范: GB 50909—2014[S]. 北京: 中国标准出版社, 2014. Code for Seismic Design of Urban Rail Transit Structures: GB 50909—2014[S]. Beijing: Standards Press of China, 2014. (in Chinese)
[16] American Lifelines Alliance(ALA). Guidelines for the Design of Buried Steel Pipe[M]. American Society of Civil Engineers, 2001.
[17] American Lifelines Alliance(ALA). Seismic Guidelines for Water Pipelines[M]. American Society of Civil Engineers, 2005.
[18] DADFAR B, M. NAGGAR M E, NASTEV M. Vulnerability of buried energy pipelines subject to earthquake-triggered transverse landslides in permafrost thawing slopes[J]. Journal of Pipeline Systems Engineering and Practice, 2018, 9(4): 1-12.
[19] 韩俊艳, 郭之科, 李满君, 等. 纵向非一致激励下非均匀场地中埋地管道的振动台试验研究[J]. 岩土工程学报, 2021, 43(6): 1147-1156. doi: 10.11779/CJGE202106019 HAN Junyan, GUO Zhike, LI Manjun, et al. Shaking table tests on buried pipelines in inhomogeneous soil under longitudinal non-uniform seismic excitation[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(6): 1147-1156. (in Chinese) doi: 10.11779/CJGE202106019
[20] 黄涛, 陈小平, 王向东, 等. pH值对Q235钢在模拟土壤中腐蚀行为的影响[J]. 中国腐蚀与防护学报, 2016, 36(1): 31-38. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGFF201601005.htm HUANG Tao, CHEN Xiaoping, WANG Xiangdong, et al. Effect of pH value on corrosion behavior of Q235 steel in an artificial soil[J]. Journal of Chinese Society for Corrosion and Protection, 2016, 36(1): 31-38. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGFF201601005.htm
[21] ZHENG S S, ZHANG X H, ZHAO X R. Experimental investigation on seismic performance of corroded steel columns in offshore atmospheric environment[J]. Structural Design of Tall and Special Buildings, 2019, 28(4): 1-17.
[22] Applied Technology Council, Federal Emergency Management Agency. Quantification of Building Seismic Performance Factors[R]. America: FEMA, 2008.
[23] 杜修力, 韩俊艳, 李立云. 长输埋地管道振动台试验设计中相似关系的选取[J]. 防灾减灾工程学报, 2013, 33(3): 246-252. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK201303003.htm DU Xiuli, HAN Junyan, LI Liyun. Selection of shaking table test similarity relations for long-distance buried pipeline[J]. Journal of Disaster Prevention and Mitigation Engineering, 2013, 33(3): 246-252. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK201303003.htm
[24] ARGYROUDIS S A, PITILAKIS K D. Seismic fragility curves of shallow tunnels in alluvial deposits[J]. Soil Dynamics and Earthquake Engineering, 2011, 35: 1-12.
[25] Hazus User & Technical Manuals[M]. Washington D C: Federal Emergency Management Agency and National Institute of Building Science, 2004.
[26] 刘爱文. 管道抗震设计规范有关地震作用的综述[J]. 国际地震动态, 2007(9): 29-35. https://www.cnki.com.cn/Article/CJFDTOTAL-GJZT200709004.htm LIU Aiwen. Discussion on the seismic input proposed by the different countries' seismic codes of pipeline[J]. Recent Developments in World Seismology, 2007(9): 29-35. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GJZT200709004.htm
[27] ZERVA A. Pipeline response to directionally and spatially correlated seismic ground motions[J]. Journal of Pressure Vessel Technology, 1993, 115: 53-58.
[28] 生命线工程地震破坏等级划分: GB/T 24336—2009[S]. 北京: 中国标准出版社, 2009. Classification of Earthquake Damage to Lifeline Engineering: GB/T 24336—2009[S]. Beijing: Standards Press of China, 2009. (in Chinese)
[29] 蒋家卫, 许成顺, 杜修力, 等. 浅埋地铁车站地下框架结构抗震设计的最优地震动强度指标[J]. 岩土工程学报, 2023, 45(2): 318-326. doi: 10.11779/CJGE20211498 JIANG Jiawei, XU Chengshun, DU Xiuli, et al. Optimal index of earthquake intensity measures for seismic design of underground frame structure of shallow-buried subway station[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(2): 318-326. (in Chinese) doi: 10.11779/CJGE20211498
[30] 许建聪, 简文彬, 岳尚全. 深厚软土地层地震破坏的作用机理研究[J]. 岩石力学与工程学报, 2005, 24(2): 313-320. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX20050200P.htm XU Jiancong, JIAN Wenbin, YUE Shangquan. Study on earthquake failure mechanism of deep soft soil layer[J]. Journal of Rock Mechanics and Engineering, 2005, 24(2): 313-320. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX20050200P.htm
-
期刊类型引用(0)
其他类型引用(1)
-
其他相关附件
计量
- 文章访问数: 382
- HTML全文浏览量: 49
- PDF下载量: 92
- 被引次数: 1
