0.   引言

土石坝变形的预测和控制是设计和运行的一个关键问题，其变形预测常采用数值计算手段，计算时的模型参数常采用三轴试验确定。随着高土石坝工程的不断涌现，筑坝堆石料直径逐渐加大，堆石坝最大粒径一般可达800~1200 mm，而常规三轴压缩试验试样直径为300 mm，其试验粒径更是被缩尺后限制到60 mm以内^[1]，这就带来了试验材料趋同性及由试验参数向原型筑坝材料参数回溯推求等问题^[2-4]。为解决尺寸效应问题，有学者采用超大型三轴仪或是现场硐室压缩试验以减小缩尺的影响^[5-7]，但试验可重复性差且推广性不足。

通过系列比例的缩尺试验，研究力学参数随缩尺比例的变化规律，提出从缩尺堆石料推求原型堆石料力学参数的外推方程，是解决尺寸效应问题的另一种研究途径^[8]，本研究推导建立了三维应力条件下球体材料变形特性参数尺寸效应理论模型，并开展了堆石料和砂砾石料在120~1000 mm试样尺度下的系列压缩实验，研究压缩模量的尺寸效应变化规律，通过破碎前后堆石料筛分试验，揭示破碎率的影响规律，并验证尺寸效应理论模型。

1.   土石料尺寸效应理论模型

1.1   尺寸效应统一模型

土石料的堆积结构单元为堆石(或砂卵石)颗粒，为从理论层面建立尺寸效应模型，将堆石颗粒简化为球体开展三维应力条件下推导，篇幅所限此处仅给出结过，推导过程见笔者发表的文献[9, 10]。

基于堆石料压缩模量随尺度参数的变化关系和压缩模量随颗粒破碎率的变化关系，建立考虑破碎修正的堆石料尺寸效应模型：

式中：$F({R_{\text{d}}}, {e_0}, E, \mu )$为尺寸效应方程，公式为

式中：${E_i}$为堆石料压缩模量；$E$和$\mu$分别为堆石料弹性模量与泊松比；${G_{\text{s}}}$为堆石料相对质量密度；a和b为模型参数；${k_0}$为侧压力系数$\left( {{k_0} = \frac{\mu }{{1 - \mu }}} \right)$。

$f({B_{\text{r}}})$为破碎修正方程，公式为

式中：$f({B_{\text{r}}})$为破碎修正函数；R_d为径径比；$\lambda$，β为方程参数。

1.2   破碎修正参量

土石料在压力所用下整体变形除了一部分为形变，还有一部分是由破碎引起的，由于颗粒破碎对压缩模量具有重要的影响，对颗粒破碎对尺寸效应影响进行专门分析，采用破碎修正方程式（3），分别讨论可破碎和不可破碎的土石料的尺寸效应变化规律。

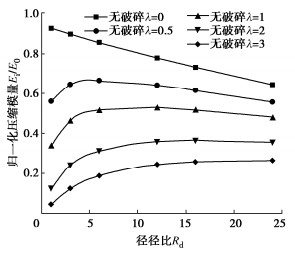
参数$\lambda$是描述颗粒破碎程度的参数，$\lambda = 0$表示破碎率为0，无颗粒破碎情况，而且，$\lambda$越大则颗粒破碎程度越大。将破碎系数$\lambda$=0，0.5，1.0，2.0，3.0代入尺寸效应统一模型式（1），得到考虑破碎修正的归一化压缩模量与径径比关系曲线，如图 1所示。

图  1  可破碎与不可破碎材料的尺寸效应曲线

Figure  1.  Size effect curves of crushable and non crushable materials

下载: 全尺寸图片 幻灯片

从图 1可以看出，当没有颗粒破碎（$\lambda$=0）时，压缩模量随径径比增加而减小；当破碎程度较低时（$\lambda$=0.5），小径径比区段（约为${R_{\text{d}}}$≤6）的压缩模量显著降低，出现了曲线反向、压缩模量随径径比增大而增大的现象，大径径比区段（约为${R_{\text{d}}}$ > 6）曲线变化趋势保持不变；随着破碎程度增加，尺寸效应曲线基本完全变为压缩模量随径径比增加而增加的变化曲线。

2.   压缩模量尺寸效应试验研究

2.1   试验设计

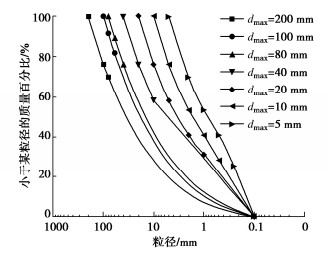
针对土石料尺寸效应问题，采用可反映破碎效应的堆石料和不发生破碎的砂砾石料进行侧限压缩试验，并在试验后进行筛分试验以研究压缩模量随颗粒破碎率的变化规律。试验设计时，为体现尺寸效应规律，突破常规300 mm直径试样筒的条件，对堆石料和砂砾石料同时开展试样直径为120~1000 mm、装样最大粒径5~200 mm、径径比从5~25的的系列试验，试验方案如表 1所示，设计级配如图 2所示。

表  1  尺寸效应试验方案

Table  1.  The size effect test plan

径径比Rd	装样最大粒径/mm	试件直径D/mm
5	200	1000
12.5	80
25	40
5	100	500
12.5	40
25	20
6	20	120
12	10
24	5

下载: 导出CSV 

| 显示表格

图  2  试样颗粒分析曲线

Figure  2.  Sample particle analysis curve

下载: 全尺寸图片 幻灯片

试验参照《土工试验方法标准：GB/T 50123—2019》进行，各组试验密度控制在1.88 g/cm³，加载速率为0.01 H/min，当轴向应变15%或轴向应力达到6 MPa时停止加载，以保证土石料处于弹性应变状态。

2.2   试验结果及分析

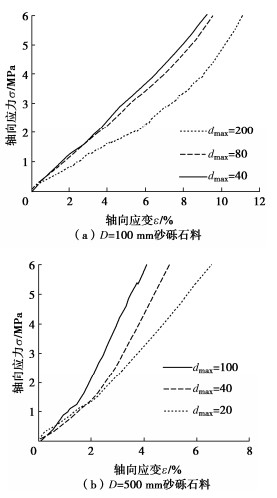
对各组试样进行侧限压缩试验，典型应力应变曲线如图 3所示，对其进行线性拟合，相关系数均达到0.95以上，斜率作为试验压缩模量。

图  3  典型试验应力应变曲线

Figure  3.  Typical experimental stress-strain curve

下载: 全尺寸图片 幻灯片

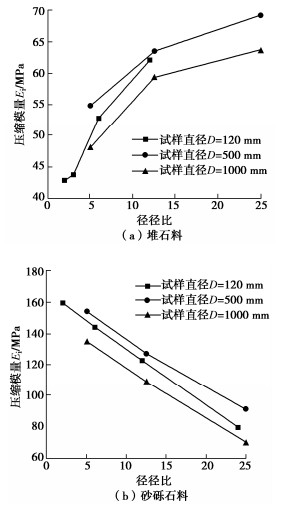
试验中既有不同的试件尺寸，也有不同的最大粒径，为将两者统一引入径径比的参量进行对比分析，各组试验所得压缩模量与径径比的关系如图 4所示。

图  4  压缩模量与径径比关系曲线

Figure  4.  Compression modulus and diameter to diameter ratio relationship curve

下载: 全尺寸图片 幻灯片

可以看出，有破碎效应的堆石料压缩模量随径径比增加而增加，但增加的幅值随径径比的增大逐渐减小；无破碎效应的砂砾石料压缩模量随径径比增加而减小。综合来看，尽管各组试验中的试样尺寸和最大粒径不同，但只要试样径径比相同，所测得的压缩模量非常接近，说明在其他条件相同情况下，径径比是影响压缩模量的主要因素。

2.3   颗粒破碎影响分析

土石料作为一个整体结构在外力作用发生压缩变形，在微观层面当某个或某些颗粒的边缘棱角发生破碎，这种现象在整个结构中累积将在宏观层面表现出形变，进行体现出压缩模量显著降低，为此，有必要研究压缩模量与颗粒破碎率的相关关系。

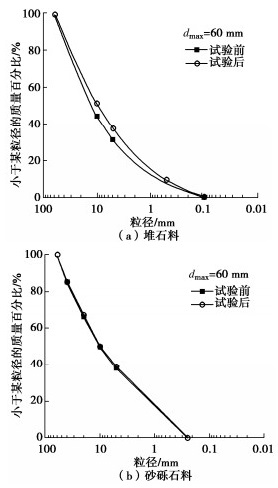
根据《土工试验方法标准：GB/T 50123—2019》对各组试验在压缩前后进行颗粒筛分试验，绘出堆石料和砂砾石料压缩前后典型颗粒分析曲线如图 5所示。

图  5  压缩前后颗分曲线变化

Figure  5.  Changes in particle size curve before and after compression

下载: 全尺寸图片 幻灯片

从图中可以看出，砂砾石料压缩前后基本无变化，而堆石料压缩后颗分曲线位于压缩前曲线上方，表明在试验中颗粒发生了破碎。

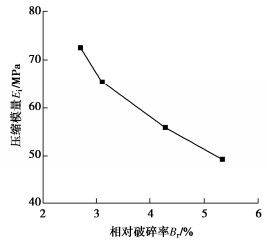
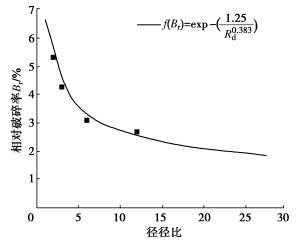
以Hardin提出的相对破碎率指标${B_{\text{r}}}$为评价破碎的程度，可得砂砾石试验后的破碎率为0.34%，可忽略其影响，按不可破碎材料分析；堆石料试验后的破碎率为2.7%~5.3%，建立压缩模量E_i与破碎率${B_{\text{r}}}$的关系曲线，如图 6所示。由图可得，破碎率越大则压缩模量越小，说明颗粒破碎将降低堆石结构变形模量，进一步建立径径比与相对破碎率关系如图 7所示，相对破碎率随径径比增加而减小，呈幂函数关系，将此关系采用式（3）表示，堆石料破碎修正因子为$f({B_{\text{r}}}) = {\text{exp}}\left( { - \frac{{1.25}}{{{R_{\text{d}}}^{{\text{0}}{\text{.383}}}}}} \right)$。

图  6  堆石料相对破碎率与压缩模量关系

Figure  6.  Relationship between relative crushing rate and compressive modulus of rockfill materials

下载: 全尺寸图片 幻灯片

图  7  堆石料相对破碎率与径径比关系

Figure  7.  Relationship between relative crushing rate and diameter to diameter ratio of rockfill materials

下载: 全尺寸图片 幻灯片

2.4   尺寸效应模型应用

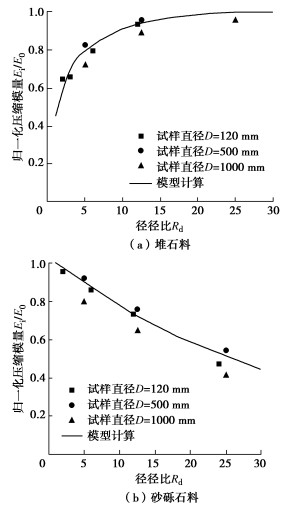
基于砂砾石料不破碎的特性，对于式（1）的尺寸效应模型应用中无破碎修正项，根据压缩试验结果和材料参数E=7751.3 MPa，μ=0.197，${\rho _{\text{d}}}$=1.88 g/cm³代入式（2）建立联立方程组，求解得到模型参数如表 1所示。将${R_{\text{d}}}$=1.0作为压缩模量归一化的基准${E_0}$，绘出归一化压缩模量${E_{\text{i}}}/{E_0}$与径径比${R_{\text{d}}}$关系曲线，如图 8（a）所示，可以看出，试验数据点落在模型计算曲线附近，相关系数R²为0.91。

图  8  尺寸效应模型应用

Figure  8.  Application of size effect model

下载: 全尺寸图片 幻灯片

堆石料在试验过程中发生了破碎，在尺寸效应模型应用时应考虑破碎修正项$f({B_{\text{r}}})$的因素，根据压缩试验结果、破碎修正因子方程和材料参数E=4320 MPa，μ=0.37，${\rho _{\text{d}}}$=1.88 g/cm³，求解得到模型参数如表 1所示。采用${R_{\text{d}}} = 30$的压缩模量计算值作为压缩模量归一化基准${E_0}$，绘出归一化压缩模量${E_{\text{i}}}/{E_0}$与径径比${R_{\text{d}}}$关系曲线，如图 8（b）所示，从图可以看出，试验数据点落在模型计算曲线附近，相关系数R²为0.93，综上可见模型具有良好的计算效果。

表  2  尺寸效应模型参数

Table  2.  Model parameters of size effects

名称	${a_{\text{2}}}$	b	ξ	${G_{\text{s}}}$	$\lambda$	$\beta$
砂砾石料	2.20	36	6	2.67	—	—
堆石料	1.35	64	3	2.67	1.15	0.38

下载: 导出CSV 

| 显示表格

3.   结论

针对堆石筑坝料的尺寸效应问题，将球体变形尺寸效应统一模型推广应用于筑坝料，通过砂砾石料和堆石料侧限压缩试验，研究了压缩模量的尺寸效应变化规律，揭示了破碎率的影响规律，并验证了尺寸效应理论模型，主要得到以下3点结论。

（1）压缩试验中砂砾石的破碎率为0.34%，可按不可破碎材料分析，堆石料的破碎率为2.7%~5.3%，颗粒破碎率越大，堆石料压缩模量越小。

（2）堆石料压缩模量随径径比增加而增加，砂砾石料压缩模量随径径比增加而减小，引起两者规律相反的原因是颗粒破碎的影响。

（3）采用破碎指标$\lambda$反映筑坝料的破碎程度，实现了不同类别土石料尺寸效应的统一描述，并能够准确的计算砂砾石料压缩模量随径径比增加而减小、堆石料压缩模量随径径比增加而增加的尺寸效应，且能够计算不同破碎率条件下的尺寸效应，实现了粗粒料尺寸效应模型化预测。