Bayesian estimation of probability distributions of undrained shear strength of soils with limited site data
-
摘要: 针对勘察数据有限或不完备条件下设计参数取值不可靠的问题,建立了包含141个场地共1679组数据的黏性土参数数据库,分别采用基于单个场地数据的特定场地贝叶斯方法(SBM)和可综合利用多场地数据的层次贝叶斯方法(HBM)对黏性土不排水抗剪强度的概率分布进行参数估计。结果表明,与SBM方法相比,在场地仅有少量实测数据的情况下HBM方法能有效降低参数估计的不确定性,且受数据量影响小。采用留一交叉验证法(LOO-CV),结合点预测密度的对数值(lppd)比较了上述两种方法的准确度,结果表明HBM方法的lppdloo-cv指标更大,整体预测准确度更高。因此,HBM方法比SBM方法更适用于场地有限数据情况下不排水抗剪强度概率分布的参数估计,且HBM方法得到的后验统计值还可用于新场地的参数估计。Abstract: To address the issue of poor reliability of the design parameters due to limited or incomplete geotechnical investigation data, a cohesive soil parameter database containing 1679 sets of data from 141 sites is established. The site-specific Bayesian method (SBM) and the hierarchical Bayesian method (HBM) are used to estimate the probability distribution of undrained shear strength of cohesive soils by utilizing the data from a specific site and multiple sites, respectively. The results show that compared with the SBM method, the HBM method can effectively reduce the uncertainty of parameter estimation when there is only limited measured data at the target site, and it is less affected by the number of measuring points at the target site. The leave-one-out cross-validation (LOO-CV) combined with the log pointwise predictive density (lppd) is used to compare the accuracy of the two methods. The results show that the lppdloo-cv index of the HBM method is larger, indicating that the overall prediction accuracy of the HBM method is higher. Therefore, the HBM method is more suitable for the estimation of undrained shear strength parameters in the case of limited site data, and the posterior means obtained by the HBM method can be used for parameter estimation of new sites.
-
0. 引言
参数确定是岩土工程设计的基础。土体性质不确定性显著,工程实践中受经济和技术等因素制约,单个场地的土工测试数量有限,基于有限数据确定设计参数存在可靠性低的问题[1-2]。以海上风电大直径单桩工程为例,砂土内摩擦角φ和黏土不排水抗剪强度su是水平承载力设计p-y曲线法的关键参数[3]。由于海洋工程勘察取样和测试成本高,数据量有限,一般根据有限的实测数据结合工程经验确定设计值,造成设计偏保守。利用有限数据对土体强度参数进行科学估计,降低大直径单桩设计参数的不确定性,实现设计优化,是当前海上风电工程提质增效的迫切需要。
目前,国内外在岩土体参数估计方面已开展了大量研究,提出了一些有效的方法,具体可分为3类。第一类方法将单个岩土体参数假定为随机变量,采用参数估计或非参数估计确定其概率分布[4-7]。然而,这类方法在单个场地、有限小样本数据条件下可靠度往往较低,且仅能利用待估计岩土体参数的测试数据,忽略了不同类型岩土体参数之间的相关性,因此不能利用不同类型的数据。第二类方法通过经验公式[8-12]将其它岩土体参数的实测值转换为待估参数。但经验公式一般通过全球或地区范围内实测数据拟合得到,具有显著的不确定性[9],不同经验公式的估计差异较大[13]。第三类方法将多种类型的岩土体参数视为多元随机变量,以多元随机变量概率分布表示参数之间的相互关系,利用实测数据对概率分布的模型参数进行估计,代表性的工作有,Ching等[14]针对9种岩体参数建立了岩体参数的多维联合分布;李典庆等[1]和Tang等[15]基于多维Gaussian Copula建立了多维土体参数的联合分布;汪海林等[16]针对黏土的9个土性参数,基于贝叶斯理论对土性参数的联合后验分布进行了研究。上述研究主要利用单个场地的数据,当数据量有限时,结果存在较大的不确定性,为此一些学者通过融合不同场地的数据来降低不确定性。张广文等[2]利用多场地数据建立黏聚力的先验分布,再利用某场地的实测数据得到后验分布;Bozorgzadeh等[17]和Xiao等[18]利用多场地数据分别对岩石力学特性参数和剪切波速参数进行了参数估计;Ching等[19-20]提出了多元土体参数的混合贝叶斯方法,可综合利用场地数据;Ching等[21]采用层次贝叶斯方法和混合贝叶斯方法对不排水抗剪强度比su/σ′v和归一化锥尖阻力(qt−σv)/σ′v进行了二元正态分布的参数估计。整体而言,当前针对黏土不排水抗剪强度的研究主要集中在前两种方法,采用第三类方法的还较为有限[21],也较少涉及多场地数据的融合,而且现有多场地的研究主要考虑场地间的相似性,忽略了场地间的差异性。
针对上述不足,本文将采用基于单个场地数据进行多维参数估计的特定场地贝叶斯方法(Site-specific Bayesian Method,SBM)和可利用多场地数据进行多维参数估计的层次贝叶斯方法(Hierarchical Bayesian Method,HBM)对不排水抗剪强度的概率分布进行估计,并对这两种方法的准确性和适用性进行定量评价,为海上风电桩基工程设计优化和参数确定提供理论依据。
1. 多维土体参数概率分布的贝叶斯估计方法
1.1 贝叶斯参数估计的基本原理
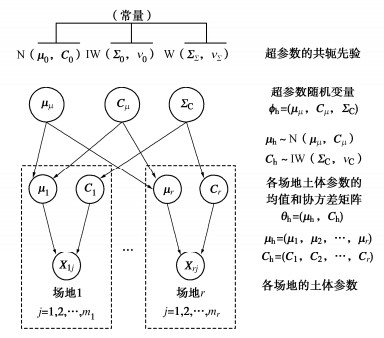
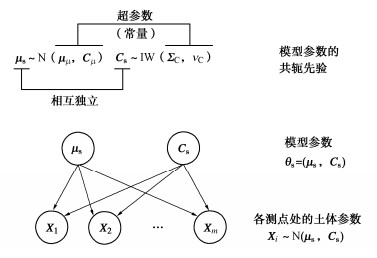
岩土工程勘察往往涉及多个土体参数[1],如重度、含水率、稠度指标、不排水抗剪强度等。假定土体参数X=(X1,X2,⋯,Xd)T为d维随机变量,其概率密度函数的模型参数设为θ。例如,当X服从多元正态分布时,记X∼N(μ,C),其中μ为均值列向量,C为协方差矩阵,则模型参数θ=(μ,C)。
由贝叶斯理论,可由X的观测数据得到θ的后验分布:
f(θ∣Data)=f(Data∣θ)f(θ)f(Data)∝f(Data∣θ)f(θ)。 (1) 式中:Data为X的观测数据;f(Data|θ)为似然函数,即给定θ条件下得到Data发生的概率;f(θ)为θ的先验分布;f(Data)是使后验概率总和为1的归一化常数。
需要指出的是,式(1)为通式。在不同数据条件下,需采用不同方法得到具体形式。特定场地贝叶斯方法利用本场地的数据对模型参数进行概率估计。层次贝叶斯方法通过构建多层级的贝叶斯模型,考虑不同场地的数据之间的相似性和差异性,利用多个场地的数据进行模型参数的概率估计。下面介绍特定场地贝叶斯方法和层次贝叶斯方法的基本原理。
1.2 特定场地贝叶斯方法
如图 1所示,假定土体参数X为d维随机变量,服从多元正态分布N(μs,Cs),模型参数θ=θs=(μs,Cs),下标s表示SBM。当在某一测点得到数据x=(x1,x2,⋯,xd)T时,式(1)中f(Data∣θ)可表示为
f(x∣θs)=N(x∣μs,Cs) =|Cs|−1/2(2π)−d/2exp[−12(x−μs)TC−1s(x−μs)]。 (2) 式中:N(x∣μs,Cs)为多元正态分布;(⋅)T表示转置。
如在m个测点获得观测数据xs=(x1,x2,⋯,xm)时,xs为d×m矩阵。假设各测点土体参数独立同分布,由式(2)可得f(Data|θ)为
f(xs|θs)=f(xs|μs,Cs)=m∏j=1N(xj|μs,Cs)。 (3) 假定μs和Cs相互独立,则由式(1)可得θs的后验分布为
f(θs|xs)=f(μs,Cs|xs)∝f(xs|μs,Cs)⋅[f(μs)f(Cs)]。 (4) 式中:f(μs,Cs|xs)为μs和Cs的联合后验分布;f(μs)和f(Cs)分别为μs和Cs的先验分布。这里分别取二者的共轭先验,使后验分布与先验分布属于同一分布族。其中μs的共轭先验为多元正态分布N(μμ,Cμ),Cs的共轭先验为逆威希特分布[22],记为IW(ΣC,νC),则μs和Cs的先验概率密度函数分别为
f(μs)=N(μs∣μμ,Cμ) =|Cμ|−1/2(2π)−d/2⋅exp[−12(μs−μμ)TC−1μ(μs−μμ)], (5) f(Cs)=IW(Cs∣ΣC,vC)=|ΣC|vc/22dvC/2⋅Γd(vC/2)|Cs|−vC+d+12⋅exp[−12tr(ΣC×C−1s)] 。 (6) 式中:μμ,Cμ分别为μs的均值列向量和协方差矩阵;ΣC,νC分别为逆威希特分布的尺度矩阵和自由度;Γd(⋅)表示自由度为d的多元伽马分布;tr(⋅)为矩阵的迹。一般称(μμ,Cμ)和(ΣC,νC)为超参数。
对式(4)中θs的联合后验分布积分可得μs和Cs的边缘后验分布分别为
f(μs|xs)=∫f(μs,Cs|xs)dCs, (7) f(Cs|xs)=∫f(μs,Cs|xs)dμs。 (8) 1.3 层次贝叶斯方法
如图 2所示,假设共有r个场地。其中第i个场地的土体参数为多维随机变量Xi,Xi服从多元正态分布,记为Xi∼N(μi,Ci),i=1,2,⋯,r。μi和Ci分别为Xi的均值列向量和协方差矩阵,记θh=(μh,Ch),其中μh=(μ1,μ2,⋯,μr),Ch=(C1,C2,⋯,Cr),下标h表示HBM。假设各场地的μi和Ci相互独立,但具有相同的统计特性,其中μi服从多元正态分布N(μμ,Cμ),Ci服从逆威希特分布IW(ΣC,νC)。假定超参数μμ,Cμ和ΣC为随机变量,超参数νC为常数,记超参数随机变量ϕh=(μμ,Cμ,ΣC)。
HBM方法中的模型参数θ既包含θh,也包含ϕh。由式(1),模型参数的联合后验分布可改写为
f(θh,ϕh∣Data)∝f(Data∣θh,ϕh)f(θh,ϕh)=f(Data∣θh)f(θh,ϕh)。 (9) 式中:f(Data|θh)为似然函数;f(θh,ϕh)为联合先验分布,
f(θh,ϕh)=f(θh|ϕh)f(ϕh)。 (10) 式中:f(θh|ϕh)为θh的先验分布;f(ϕh)为超参数的先验分布。式(9)中第二行等式成立是因为与Data直接相关的参数只有θh=(μh,Ch),而ϕh只能通过θh间接地影响Data[22]。由此体现了HBM方法的层级特性。
当第i个场地有mi个测点,且各测点都有完整的d维数据时,则Data可表示为xh=(x1,x2,⋯,xr),为d×(∑ri=1mi)矩阵,其中xi=(xi1,xi2,⋯,ximi),为d×mi维矩阵,i=1,2,⋯,r。此时,式(9)中f(Data|θh)对应为
f(xh∣μh,Ch)=r∏i=1f(xi∣μi,Ci)=r∏i=1[mi∏j=1 N(xij∣μi,Ci)]。 (11) 与式(4)的推导类似,假定μh,Ch相互独立,且超参数μμ,Cμ,ΣC相互独立,则可得θh,ϕh的联合后验分布为
f(θh,ϕh∣xh)∝f(xh∣θh)⋅f(θh∣ϕh)⋅f(ϕh)∝f(xh∣μh,Ch)⋅[f(μh∣μμ,Cμ)f(Ch∣ΣC,vC)]⋅[f(μμ)f(Cμ)f(ΣC)]。 (12) 式中:f(μh|μμ,Cμ)为μh的先验分布,μi∼ N(μμ,Cμ);f(Ch|ΣC,νC)为Ch的先验分布,Ci∼ IW(ΣC,νC);f(μμ),f(Cμ),f(ΣC)分别为超参数μμ,Cμ,ΣC的先验分布。这里取μμ和Cμ的共轭先验分别为N(μ0,C0),IW(Σ0,ν0),ΣC的共轭先验为威希特分布[22],记为W(ΣΣ,νΣ),则ΣC的先验分布为
f(ΣC)=W(ΣC∣ΣΣ,vΣ)=|ΣC|vΣ−d−122dvΣ2|ΣΣ|vΣ2Γd(vΣ2)exp[−12tr(ΣC×Σ−1Σ)]。 (13) 式中:W(ΣC|ΣΣ,νΣ)为威希特分布,其中ΣΣ,νΣ分别为尺度矩阵和自由度。
需要指出的是,式(12)所得为模型参数θh,ϕh的联合后验分布,各边缘后验分布可通过类似式(7),(8)的积分得到。
1.4 土体参数的估计
上述两种方法除了可以得到各模型参数的后验分布,还可对土体参数本身进行估计。
(1)测点缺失数据的估计
由于条件限制,在某一测点处不一定能获得土体参数X=(X1,X2,⋯,Xd)T的所有d维实测数据[9, 21]。例如,对某测点的土样只开展了含水率等基本物性试验,但并未开展不排水抗剪强度试验,则该测点缺失su的实测数据。此时可利用已知的数据,对缺失数据的土体参数进行估计。
假设在某测点d个土体参数中前k个有实测值,记为xok,对应式(1)中的Data;后d−k个参数无实测数据,记为xud−k,是待估计的参数。下文简化为实测值xo和缺失项xu。
基于观测数据得到模型参数θ的后验分布f(θ|Data)后,通过积分可得xu的后验分布为
f(xu∣Data)=∫f(xu∣Data,θ)f(θ∣Data)dθ=∫f(xu∣θ)f(θ∣Data)dθ。 (14) 式中:f(θ|Data)由式(4)或(12)得到f(xu|θ)为xu的似然函数:
f(xu∣μ,C)=N[xu∣μu+Cuo(Co)−1(xo−μo), Cu−Cuo(Co)−1Cou]。 (15) 式中:μ分块记为μ=(μo,μu)T,C分块记为
Cs=[CoCouCuoCu] 。 (16) 式中:μo为k维列向量,μu为d−k维列向量;Co为k×k矩阵,Cou为k×(d−k)矩阵,Cuo为(d−k)×k维矩阵,Cou=(Cuo)T,Cu为(d−k)×(d−k)矩阵。
(2)未知点处土体参数的估计
工程中有时还需要对未知点位(无任何实测数据的位置)的土体参数xnew进行估计。类似式(14),对模型参数进行积分可得xnew的后验分布为
f(xnew∣Data)=∫f(xnew∣θ)f(θ∣Data)dθ。 (17) 式中:f(xnew|θ)为似然函数,即多元正态分布。
式(7),(8),(14),(17)的积分可通过马尔科夫链-蒙特卡洛模拟方法(Markov Chain Monte Carlo,MCMC)进行求解。MCMC的核心思想是构造一条平稳分布为待估参数后验分布的马尔科夫链,再利用马尔科夫链达到平稳分布时的样本进行蒙特卡洛积分[22]。为提高计算效率,本文采用MCMC的吉布斯抽样算法,具体可见文献[22]。
2. 工程应用:不排水抗剪强度的参数估计
不排水抗剪强度su是风电大直径单桩设计的重要参数。由于含水率等物理性质试验较强度试验更易开展,实践中常利用液性指数IL来估计su[13]。本文以X1=LI和X2=ln(su/σ′v)为正态随机变量,假定X=(X1,X2)T服从二元正态分布,利用LI对ln(su/σ′v)进行估计。
2.1 数据集的建立
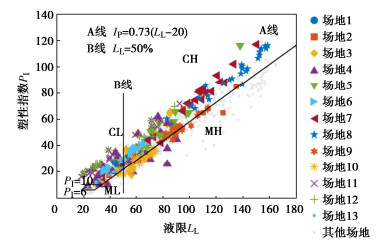
从CLAY/10/7490数据库[20, 23]中提取141个场地共1679组LI和ln(su/σ′v)数据建立数据集,各场地的数据量至少5组。液性指数IL和竖向有效应力σ′v分别由室内试验和现场孔压静力触探测定,su为不排水抗剪强度修正值,由各类不排水剪切试验的实测值转换得到,转换公式详见文献[23]。原数据库[20, 23]中部分场地仅有编号,无具体位置信息,故本文也仅用编号代表各场地。本文数据集中有13个场地含20组及以上数据,数据量较大,故将这13个场地作为目标场地进行参数估计,分别标记为场地1~场地13。如图 3所示为各场地土体的塑性图,其中高液限黏土CH和低液限黏土CL分别占49.1%,34.7%,高液限粉土MH和低液限粉土ML分别占13.1%,2.6%。
经Shapiro-Wilk检验[24],IL和ln(su/σ′v)的p值分别为1.33和4.85,均大于0.05,即在置信度为95%的条件下,IL和ln(su/σ′v)的边缘分布均满足正态性假设。采用表 1所示4种Copula函数对数据进行拟合,得到Copula参数θC,再利用AIC指标和BIC指标比较各Copula函数的拟合优度[15, 25],最终确定数据的最优拟合Copula函数为Gaussian Copula函数。因此,本文数据满足二元正态分布假设。
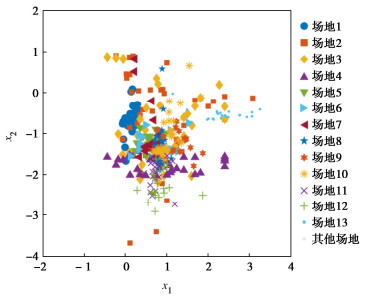
表 1 Copula函数拟合Table 1. Copula function fittingCopula C(u1,u2) θC AIC BIC Gaussian Φ2[Φ−1(u1),Φ−1(u2);θC] -0.05 -3.50 1.93 Clayton (u−θC1+u−θC2−1)−1/θC 1.45×10-6 2.00 7.43 Frank −1θCln[1+(e−θCu1−1)(e−θCu2−1)e−θC−1] -0.07 1.80 7.22 Gumbel exp{−[(−lnu1)θC+(−lnu2)θC]1/θC} 1.00 2.00 7.43 注:u1和u2分别为变量X1和X2的边缘累积分布;Φ2为标准二元正态分布的累积分布函数;Φ−1(⋅)为标准正态分布累积分布的逆函数;加粗值为AIC和BIC值的最小值,对应最优拟合Copula函数。 各目标场地的实测数据如图 4所示,X1=IL的分布区间为[−0.44,3.25],X2=ln(su/σ′v)的分布区间为[−3.68,0.91]。场地的均值¯x1、¯x2和协方差S11、S12(=S21)、S22汇总于表 2。
表 2 目标场地的样本统计量Table 2. Sample statistics of measured data编号 mi ˉx1 ˉx2 S11 S12 S22 1 22 0.131 -0.632 0.015 0.027 0.163 2 39 0.839 -0.666 0.603 -0.021 1.222 3 30 0.861 -0.761 0.637 -0.005 0.806 4 32 0.932 -1.752 0.648 -0.008 0.031 5 20 0.526 -1.176 0.036 0.011 0.028 6 21 0.728 -1.306 0.139 0.015 0.065 7 20 0.598 -1.067 0.032 -0.072 0.464 8 25 0.847 -1.256 0.007 0.006 0.265 9 21 1.236 -1.213 0.093 -0.017 0.066 10 34 1.019 -1.096 0.055 0.091 0.268 11 22 0.742 -1.969 0.037 0.002 0.105 12 20 0.827 -2.253 0.092 0.009 0.120 13 22 2.368 -0.526 0.246 -0.026 0.018 注:mi为第i个场地的数据量(测点数量)。 2.2 先验分布的参数确定
先验分布是贝叶斯估计的重要组成部分,前文已设定各先验均为共轭先验,本节确定先验分布中的参数。Cao等[26]基于文献总结了LI均值和标准差的先验范围分别为0.5~2.5,0.025~2.2,su/σ′v均值和标准差的先验范围分别为0.23~1.4,0.01~1.26。为降低先验分布对后验分布影响,本文参考Cao等[26]并采用更为平坦的先验分布:假定X1=IL和X2=ln(su/σ′v)的均值都为0,标准差都为5。
SBM方法中需要确定μs和Cs的先验分布N(μμ,Cμ),IW(ΣC,νC)中的参数取值。根据上述假定和相关研究[22, 27],确定如表 3所示的参数值。HBM方法中需要确定超参数μμ,Cμ,ΣC的先验分布N(μ0,C0),IW(Σ0,ν0),W(ΣΣ,νΣ)中的参数,以及超参数νC。这里假定μμ的标准差为μi标准差的一半,结合威希特分布期望的性质,确定先验分布参数的取值,汇总在表 3。
表 3 先验分布的参数取值Table 3. Parameter values of prior distributionsSBM HBM μμ Cμ ΣC νC μ0 C0 Σ0 ν0 ΣΣ νΣ νC (00) (250025) (250025) 4 (00) (6.25006.25) (250025) 4 (6.25006.25) 4 4 2.3 预测准确度的评价
采用留一交叉验证法(Leave-One-Out Cross- Validation,LOO-CV)对两种方法的预测准确度进行比较。该方法通过每次留出目标场地一个测点的X2实测值作为验证集,利用其他测点的实测数据和该测点的X1值对X2进行后验估计,循环直到场地内各测点都完成验证为止。
LOO-CV可结合点预测密度的对数值(log pointwise predictive density,lppd)[22, 28]作为评价指标。假设目标场地是第i个场地,mi为该场地的数据量,则目标场地lppdloo-cv指标的计算如下:
lppdloo-cv =mi∑j=1lgfpost(∖j)(xij,2∣xij,1)=mi∑j=1lg(1T−tbT∑t=tb+1f(xij,2∣xij,1,θt))。 (18) 式中:fpost(∖j)(⋅)为基于训练集x∖j得到的后验概率密度函数,相应的验证集为2×1维列向量xij=(xij,1,xij,2)T。SBM和HBM两种方法的训练集不同,SBM方法中x∖j=xs∖j=(xi1,…,xi,j−1,xi,j+1,…,ximi)为2×(mi−1)维矩;HBM方法中x∖j=xh∖j=(x1,⋯,xi∖j,⋯,xr)为2×(∑ri=1mi−1)维矩阵。其中r为场地总数;xk(k=1,⋯,i−1,i+1,⋯,r)为第k个场地所有测点数据的集合,为2×mk维矩阵;xi∖j=(xi1,⋯,xi,j−1,xi,j+1,⋯,ximi)为第i个场地除验证集xij以外测点数据的集合,为2×(mi−1)维矩阵。
3. 结果与讨论
3.1 数据缺失情况下的参数估计
为模拟实际工程中单个场地LI数据量大而ln(su/σ′v)数据量少的情形,只取本文数据集中的部分数据作为贝叶斯参数估计的Data,利用SBM方法和HBM方法分别对ln(su/σ′v)缺失数据xu2、未知点处的xnew2和场地ln(su/σ′v)均值μ2进行后验估计。
以场地1为例,场地1共22个测点,即数据集中有22组X=(X1,X2)T实测数据。采用SBM方法时,取该场地22个X1数据和n个X2数据构成Data,其中X2数据对应n个X1分别(近似)为该场地X1数据的n+1分位数。利用式(14),(17),(7)可分别得到xu2,xnew2和μ2的后验分布。采用HBM方法时,Data包括SBM方法中构造的本场地数据和数据集中其余140个场地的全部数据。
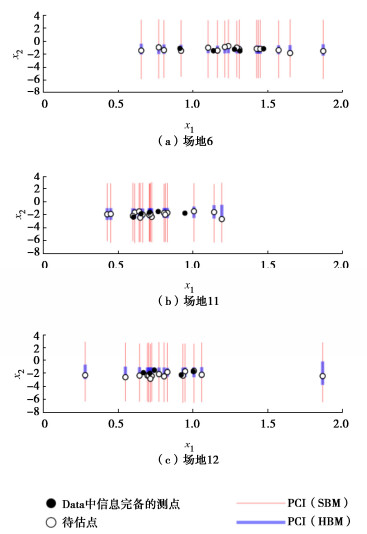
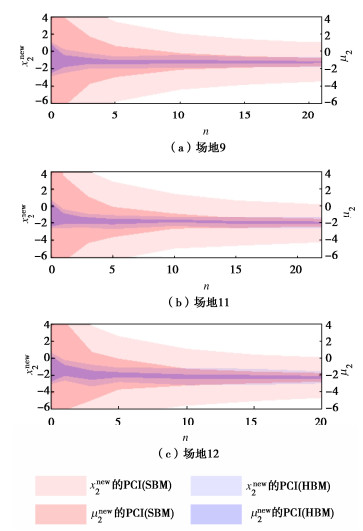
首先分析讨论给定数据量,即给定n值时,xu2的后验估计结果。这里以n=5为例。如图 5(a)所示,场地9共有21个测点,图中黑色圆点表示Data中5个信息完备的测点,白色圆点表示16个假设X2值缺失的测点(待估点),线段表示xu2的95%后验置信区间(posterior confidence interval,简称PCI)。由图 5(a)可见,测点真实值均位于PCI中。SBM方法所得PCI的范围(红线)大,甚至超过了图 4中X2的实际分布区间[−3.68,0.91],表明SBM方法无法提供有效估计。HBM方法的PCI范围(蓝线)相比SBM的显著缩小,恰好覆盖真实值的范围,表明HBM方法可有效降低土体参数估计的不确定性。
场地11和场地12的实测数据和PCI分别如图 5(b),5(c)所示,与上述结论基本一致,其余场地也得到了与图 5类似的结果,限于篇幅不再展示。各目标场地的估计中,MCMC抽样次数均为10000,由于抽样2000次后马尔科夫链即达到平稳,因此取后8000组样本作为后验分布的稳定样本,下文抽样过程与此一致。
下面讨论数据量n对场地未知点处xnew2和μ2后验估计的影响,并对两种方法进行比较。如图 6所示,x轴表示Data中有n组X2数据。以场地9(图 6(a))为例,当n=0时,SBM方法的PCI范围很大,xnew2的PCI范围为[−11.2,13.4],μ2的PCI范围为[−9.1,11.2]。这是因为SBM方法仅利用本场地的信息,当没有实测数据时,后验分布完全由先验分布决定。随着n的增大,PCI的范围大幅减小,表明SBM方法受数据量的影响显著。但即使Data使用了该场地的全部数据(n=21),PCI的范围仍较大,xnew2和μ2的不确定性也较大。
对于HBM方法,即使目标场地没有任何数据(n=0),xnew2和μ2的PCI([−2.8,1.1]和[−2.5,0.9])已经明显小于SBM方法的,说明HBM参数估计的不确定性更低,这是因为HBM方法可利用其余140个场地的数据降低估计的不确定性。当数据量n增大到5之后,HBM所得PCI的范围已基本稳定,表明HBM方法的结果受目标场地数据量的影响较小。场地11和场地12的结果分别如图 6(b),6(c)所示,与上述结论一致。
3.2 不同场地后验估计和预测准确度的比较
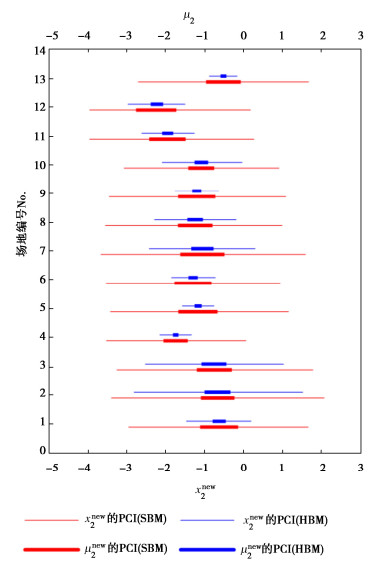
下面分别利用13个目标场地的全部数据进行后验估计,得到各场地xnew2和μ2的PCI如图 7所示。结果表明,SBM方法仅利用了单个场地的数据,因此PCI的范围较大;而HBM方法可结合多个场地的数据进行估计,因此PCI的范围显著缩小,xnew2和μ2的不确定性大幅降低。
13个目标场地的lppdloo-cv指标如表 4所示。lppdloo-cv越大,表示预测准确度越高。由表 4可知,各场地中HBM方法对应的lppdloo-cv基本都大于SBM方法的结果。其中场地2,3的数据离散、变异性较大(表 2),造成了两种方法的结果差异较小。将全部13个场地对应的评价指标求和,得到HBM方法的整体lppdloo-cv指标为-76.7,SBM方法的整体lppdloo-cv指标为-164.6,表明HBM方法的预测准确度更高,更适于有限数据下土体参数的概率估计。
表 4 两种方法的lppdloo-cv评价指标比较Table 4. Comparison of lppdloo-cv between SBM and HBM场地编号 lppdloo-cv(SBM) lppdloo-cv(HBM) 1 -10.6 -4.3 2 -26.9 -26.9 3 -18.7 -18.2 4 -11.6 3.4 5 -9.1 2.7 6 -9.6 -1.5 7 -11.5 -8.8 8 -12.4 -10.1 9 -9.6 -1.3 10 -15.4 -6.8 11 -10.2 -4.4 12 -9.7 -4.5 13 -9.5 4.2 整体求和 -164.6 -76.7 3.3 HBM方法统计量后验均值的工程应用
HBM方法所得13个目标场地统计量的后验均值汇总在表 5,与表 2对照可知,HBM方法所得统计量的后验均值与实测数据的统计量基本吻合。实际应用中,若需对这些目标场地中任一未知点的强度参数进行取值,则可直接根据μ2和测点处的σ′v求得不排水抗剪强度。本文重要研究成果之一是利用HBM方法得到了超参数μμ,Cμ,ΣC的后验均值,分别为μμ=(1.040,−0.931)T,Cμ=(0.539−0.018−0.0180.585),ΣC=(0.088−0.008−0.0080.313)。当需对一个新场地进行设计时,可直接利用上述结果确定新场地的不排水抗剪强度的设计值或者概率分布。
表 5 HBM所得场地统计量的后验均值Table 5. Posterior means of site statistics obtained by HBM编号 μ1 μ2 C11 C12 C22 1 0.132 -0.635 0.018 0.026 0.170 2 0.843 -0.678 0.589 -0.021 1.198 3 0.871 -0.771 0.619 -0.007 0.790 4 0.936 -1.751 0.631 -0.008 0.040 5 0.529 -1.174 0.038 0.010 0.042 6 0.733 -1.304 0.137 0.014 0.077 7 0.598 -1.064 0.034 -0.069 0.457 8 0.847 -1.251 0.010 0.006 0.266 9 1.234 -1.211 0.093 -0.017 0.077 10 1.020 -1.093 0.056 0.087 0.269 11 0.743 -1.959 0.039 0.001 0.115 12 0.829 -2.238 0.092 0.008 0.130 13 2.342 -0.524 0.240 -0.025 0.032 4. 结论
针对场地有限数据条件下黏土不排水抗剪强度不确定性大的问题,建立了一个LI和ln(su/σ′v)双变量参数数据集,应用特定场地贝叶斯SBM方法和层次贝叶斯HBM方法分别对13个目标场地进行参数估计,并对两种方法的估计结果进行了对比,得到2点结论。
(1)在测点缺失数据的情况下,SBM方法的PCI范围大,而HBM方法的PCI范围较小,刚好覆盖真实值的分布范围;随着数据量的增加,两种方法得到的PCI范围均有减小。SBM方法受测点数据量的影响更显著,且参数估计的不确定性较大。HBM方法受本场地数据量的影响较小,当数据量大于5时,PCI的范围就基本稳定,且参数估计的不确定性小。
(2)分别利用数据集中13个目标场地的全部实测数据对ln(su/σ′v)进行估计,结果表明HBM方法得到xnew2和μ2的PCI范围均小于SBM方法对应的结果。采用留一交叉验证法对两种方法的预测准确度进行比较,得到HBM方法的整体lppdloo-cv指标为-76.7,SBM方法的整体lppdloo-cv指标为-164.6,表明HBM方法的预测准确度更高。
综上,HBM方法更适用于场地有限数据下土体参数的概率估计。此外,HBM方法得到的超参数μμ,Cμ和ΣC的后验均值还可用于新场地的设计和可靠度计算。需要指出的是,上述结论依赖于本文数据集,在其他类型土体参数上的适用性有待后续研究。
-
表 1 Copula函数拟合
Table 1 Copula function fitting
Copula C(u1,u2) θC AIC BIC Gaussian Φ2[Φ−1(u1),Φ−1(u2);θC] -0.05 -3.50 1.93 Clayton (u−θC1+u−θC2−1)−1/θC 1.45×10-6 2.00 7.43 Frank −1θCln[1+(e−θCu1−1)(e−θCu2−1)e−θC−1] -0.07 1.80 7.22 Gumbel exp{−[(−lnu1)θC+(−lnu2)θC]1/θC} 1.00 2.00 7.43 注:u1和u2分别为变量X1和X2的边缘累积分布;Φ2为标准二元正态分布的累积分布函数;Φ−1(⋅)为标准正态分布累积分布的逆函数;加粗值为AIC和BIC值的最小值,对应最优拟合Copula函数。 表 2 目标场地的样本统计量
Table 2 Sample statistics of measured data
编号 mi ˉx1 ˉx2 S11 S12 S22 1 22 0.131 -0.632 0.015 0.027 0.163 2 39 0.839 -0.666 0.603 -0.021 1.222 3 30 0.861 -0.761 0.637 -0.005 0.806 4 32 0.932 -1.752 0.648 -0.008 0.031 5 20 0.526 -1.176 0.036 0.011 0.028 6 21 0.728 -1.306 0.139 0.015 0.065 7 20 0.598 -1.067 0.032 -0.072 0.464 8 25 0.847 -1.256 0.007 0.006 0.265 9 21 1.236 -1.213 0.093 -0.017 0.066 10 34 1.019 -1.096 0.055 0.091 0.268 11 22 0.742 -1.969 0.037 0.002 0.105 12 20 0.827 -2.253 0.092 0.009 0.120 13 22 2.368 -0.526 0.246 -0.026 0.018 注:mi为第i个场地的数据量(测点数量)。 表 3 先验分布的参数取值
Table 3 Parameter values of prior distributions
SBM HBM μμ Cμ ΣC νC μ0 C0 Σ0 ν0 ΣΣ νΣ νC (00) (250025) (250025) 4 (00) (6.25006.25) (250025) 4 (6.25006.25) 4 4 表 4 两种方法的lppdloo-cv评价指标比较
Table 4 Comparison of lppdloo-cv between SBM and HBM
场地编号 lppdloo-cv(SBM) lppdloo-cv(HBM) 1 -10.6 -4.3 2 -26.9 -26.9 3 -18.7 -18.2 4 -11.6 3.4 5 -9.1 2.7 6 -9.6 -1.5 7 -11.5 -8.8 8 -12.4 -10.1 9 -9.6 -1.3 10 -15.4 -6.8 11 -10.2 -4.4 12 -9.7 -4.5 13 -9.5 4.2 整体求和 -164.6 -76.7 表 5 HBM所得场地统计量的后验均值
Table 5 Posterior means of site statistics obtained by HBM
编号 μ1 μ2 C11 C12 C22 1 0.132 -0.635 0.018 0.026 0.170 2 0.843 -0.678 0.589 -0.021 1.198 3 0.871 -0.771 0.619 -0.007 0.790 4 0.936 -1.751 0.631 -0.008 0.040 5 0.529 -1.174 0.038 0.010 0.042 6 0.733 -1.304 0.137 0.014 0.077 7 0.598 -1.064 0.034 -0.069 0.457 8 0.847 -1.251 0.010 0.006 0.266 9 1.234 -1.211 0.093 -0.017 0.077 10 1.020 -1.093 0.056 0.087 0.269 11 0.743 -1.959 0.039 0.001 0.115 12 0.829 -2.238 0.092 0.008 0.130 13 2.342 -0.524 0.240 -0.025 0.032 -
[1] 李典庆, 吕天健, 唐小松. 基于多维Gaussian Copula的岩土体设计参数概率转换模型构建方法[J]. 岩土工程学报, 2021, 43(9): 1592-1601. doi: 10.11779/CJGE202109003 LI Dianqing, LÜ Tianjian, TANG Xiaosong. Establishing probabilistic transformation models for geotechnical design parameters using multivariate Gaussian Copula[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(9): 1592-1601. (in Chinese) doi: 10.11779/CJGE202109003
[2] 张广文, 刘令瑶. 确定随机变量概率分布参数的推广Bayes法[J]. 岩土工程学报, 1995, 17(3): 91-94. http://www.cgejournal.com/cn/article/id/9873 ZHANG Guangwen, LIU Lingyao. Extended Bayes method for determining probability distribution parameters of random variables[J]. Chinese Journal of Geotechnical Engineering, 1995, 17(3): 91-94. (in Chinese) http://www.cgejournal.com/cn/article/id/9873
[3] American Petroleum Institute. ANSI/API RECOMMENDED PRACTICE 2GEO Geotechnical and Foundation Design Considerations[M]. Washington: API Publishing Services, 2014.
[4] LUMB P. The variability of natural soils[J]. Canadian Geotechnical Journal, 1966, 3(2): 74-97. doi: 10.1139/t66-009
[5] LACASSE S, NADIM F. Uncertainties in characterising soil properties[C]//Uncertainty in the Geologic Environment: from Theory to Practice. New York, 1996.
[6] 宫凤强, 李夕兵, 邓建. 小样本岩土参数概率分布的正态信息扩散法推断[J]. 岩石力学与工程学报, 2006, 25(12): 2559-2564. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200612030.htm GONG Fengqiang, LI Xibing, DENG Jian. Probability distribution of small samples of geotechnical parameters using normal information spread method[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(12): 2559-2564. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200612030.htm
[7] 骆飞, 罗强, 蒋良潍, 等. 小样本岩土参数的Bootstrap估计及边坡稳定分析[J]. 岩石力学与工程学报, 2017, 36(2): 370-379. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201702009.htm LUO Fei, LUO Qiang, JIANG Liangwei, et al. Bootstrap estimation for geotechnical parameters of small samples and slope stability analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(2): 370-379. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201702009.htm
[8] KULHAWY F H, MAYNE P W. Manual on Estimating Soil Properties for Foundation Design: EL-6800[R]. Palo Alto: Electric Power Research Institute, 1990.
[9] PHOON K K, KULHAWY F H. Evaluation of geotechnical property variability[J]. Canadian Geotechnical Journal, 1999, 36(4): 625-639. doi: 10.1139/t99-039
[10] MESRI G. Discussion of "New design procedure for stability of soft clays"[J]. Journal of the Geotechnical Engineering Division, 1975, 101(4): 409-412. doi: 10.1061/AJGEB6.0005026
[11] MESRI G. A reevaluation of Su(mob) = 0.22σ′p using laboratory shear tests[J]. Canadian Geotechnical Journal, 1989, 26(1): 162-164. doi: 10.1139/t89-017
[12] CHANDLER R J. The in-situ measurement of undrained shear strength of clays using the field vane[C]//Vane Shear Strength Testing in Soils: Field and Laboratory Studies (ASTM STP 1014). Baltimore, 1988.
[13] CAO Z J, WANG Y. Bayesian model comparison and characterization of undrained shear strength[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140(6): 04014018. doi: 10.1061/(ASCE)GT.1943-5606.0001108
[14] CHING J, PHOON K K, LI K H, et al. Multivariate probability distribution for some intact rock properties[J]. Canadian Geotechnical Journal, 2019, 56(8): 1080-1097. doi: 10.1139/cgj-2018-0175
[15] TANG X S, LI D Q, RONG G, et al. Impact of copula selection on geotechnical reliability under incomplete probability information[J]. Computers and Geotechnics, 2013, 49: 264-278. doi: 10.1016/j.compgeo.2012.12.002
[16] 汪海林, 刘航宇, 顾晓强, 等. 基于多元概率分布模型的珠海黏土多参数预测[J]. 岩土工程学报, 2021, 43(增刊2): 193-196. doi: 10.11779/CJGE2021S2046 WANG Hailin, LIU Hangyu, GU Xiaoqiang, et al. Multi-parameter prediction of Zhuhai clay based on multivariate probability distribution model[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(S2): 193-196. (in Chinese) doi: 10.11779/CJGE2021S2046
[17] BOZORGZADEH N, HARRISON J P, ESCOBAR M D. Hierarchical Bayesian modelling of geotechnical data: application to rock strength[J]. Géotechnique, 2019, 69(12): 1056-1070. doi: 10.1680/jgeot.17.P.282
[18] XIAO S H, ZHANG J, YE J M, et al. Establishing region-specific N–Vs relationships through hierarchical Bayesian modeling[J]. Engineering Geology, 2021, 287: 106105. http://www.sciencedirect.com/science/article/pii/S0013795221001162
[19] CHING J, PHOON K K. Constructing site-specific multivariate probability distribution model using Bayesian machine learning[J]. Journal of Engineering Mechanics, 2019, 145(1): 04018126. http://www.onacademic.com/detail/journal_1000040914564910_437a.html
[20] CHING J, PHOON K K. Correlations among some clay parameters—the multivariate distribution[J]. Canadian Geotechnical Journal, 2014, 51(6): 686-704. http://www.researchgate.net/profile/Jianye_Ching/publication/262924656_Correlations_among_some_clay_parameters_-_The_multivariate_distribution/links/5476bda20cf29afed6142525.pdf
[21] CHING J, WU S, PHOON K K. Constructing quasi-site-specific multivariate probability distribution using hierarchical Bayesian model[J]. Journal of Engineering Mechanics, 2021, 147(10): 04021069. http://doc.paperpass.com/foreign/rgArti2021163572020.html
[22] GELMAN A, CARLIN J B, STERN H S, et al. Bayesian Data Analysis[M]. 3rd ed. New York: Chapman and Hall/CRC, 2013.
[23] CHING J, PHOON K K. Transformations and correlations among some clay parameters—the global database[J]. Canadian Geotechnical Journal, 2014, 51(6): 663-685. http://doc.paperpass.com/foreign/rgArti2014154070750.html
[24] WU X Z. Quantifying the non-normality of shear strength of geomaterials[J]. European Journal of Environmental and Civil Engineering, 2020, 24(6): 740-766. http://www.researchgate.net/profile/Xing_Wu12/publication/322198352_Quantifying_the_non-normality_of_shear_strength_of_geomaterials/links/5a5f6c700f7e9b964a1cbe84/Quantifying-the-non-normality-of-shear-strength-of-geomaterials.pdf
[25] TANG X S, WANG J P, YANG W, et al. Joint probability modeling for two debris-flow variables: copula approach[J]. Natural Hazards Review, 2018, 19(2) 05018004. http://smartsearch.nstl.gov.cn/paper_detail.html?id=28c2a8479af5c13c9ae131f6483b146c
[26] CAO Z J, WANG Y, LI D Q. Quantification of prior knowledge in geotechnical site characterization[J]. Engineering Geology, 2016, 203: 107-116.
[27] LUNN D, JACKSON C, BEST N, et al. The BUGS Book: A Practical Introduction to Bayesian Analysis[M]. 1st ed. Chapman and Hall/CRC, 2012.
[28] BOZORGZADEH N, BATHURST R J. Hierarchical Bayesian approaches to statistical modelling of geotechnical data[J]. Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 2022, 16(3): 452-469. doi: 10.1080/17499518.2020.1864411
-
其他相关附件



 下载:
下载: