A nonlinear cyclic constitutive model for soils considering pore-water-soil-skeleton coupling effects and its numerical realization in 3D stress space
-
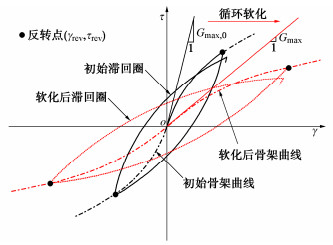
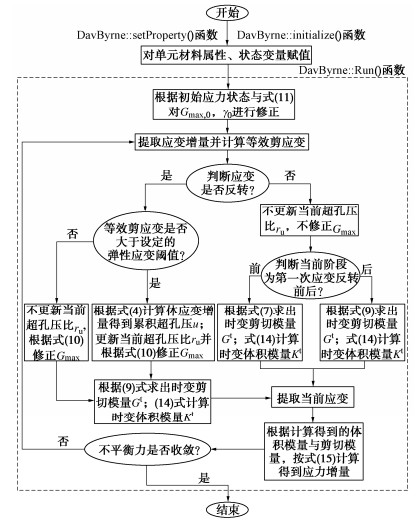
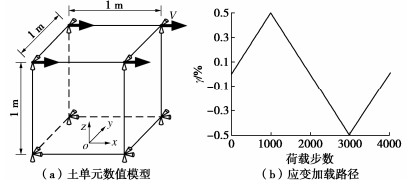
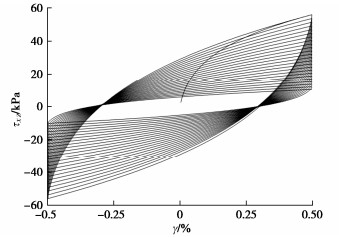
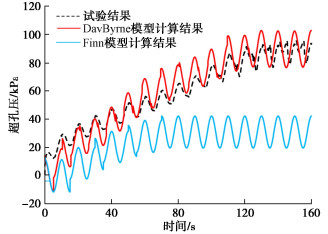
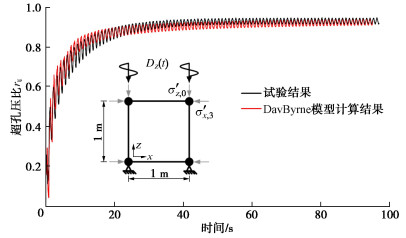
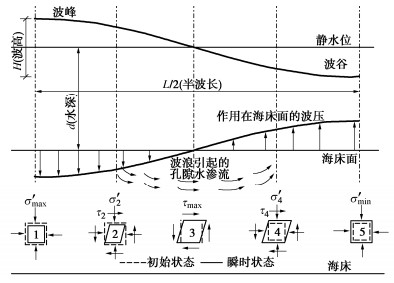
摘要: 波浪作用导致海床土体产生复杂的流固耦合效应，即土体受到正应力差和剪应力的三维耦合剪切作用，瞬态超孔隙水压力呈振荡与累积两种增长模式且引起土体循环软化。现有Masing型非线性动力本构模型未能完全考虑该流固耦合效应。现将Davidenkov骨架曲线拓展至三维应力空间，采用“扩展Masing”法则构造土体应力–应变滞回曲线，基于Biot动力固结理论，将Byrne提出的剪切-体积应变耦合模型引入体积相容方程作为累积超孔压增长的源项，建立了一个可描述流固耦合效应的土体非线性动力本构模型。基于FLAC3D计算平台实现了该本构模型的二次开发，通过与模型理论值对比保证了程序的计算精度，与土单元循环扭剪试验对比验证了该本构模拟土体动力流固耦合效应的可行性与合理性，为利用FLAC3D进行海洋岩土工程的研究提供了有效手段。Abstract: Wave action leads to complex pore-water-soil-skeleton coupling effects of seabed soils, that is, the soils are subjected to three-dimensional coupled shear action of normal stress difference and shear stress, and the transient excess pore water pressure increases in two modes of oscillation and accumulation, resulting in cyclic softening of soils. Most of the already-established Masing nonlinear dynamic constitutive models have failed to fully consider the growth mode of the excess pore water pressure and the cyclic softening effects of the soil skeleton. In this study, the Davidenkov skeleton curve is extended to the three-dimensional stress space, and the stress-strain hysteresis curve of soils is constructed by the "extended Masing" rule. Based on the Biot dynamic consolidation theory, the shear volume strain coupling model proposed by Byrne is introduced into the fluid continuity equation as the source term of the growth of the cumulative excess pore pressure, and a nonlinear dynamic constitutive model for soils is established to describe the pore-water-soil-skeleton coupling effects. Based on the FLAC3D platform, the secondary development of the constitutive model is realized. The calculation accuracy of the program is validated by comparing with the theoretical solution of the model. The feasibility and the rationality of the proposed nonlinear dynamic constitutive model to deal with such problems are verified by comparing with the soil element cyclic torsional shear tests. It provides an effective means for the study on marine geotechnical engineering using the FLAC3D.
-
-
![]()
图 2 DavByrne模型描述的应力-应变关系曲线示意图
Figure 2. Shear stress-strain curves described by DavByrne model
![]()
图 3 考虑流固耦合效应的非线性动力模型程序流程图
Figure 3. Program flowchart of nonlinear dynamic constitutive model considering pore-water-soil-skeleton coupling effects
![]()
图 7 计算与理论的应力-应变关系曲线对比
Figure 7. Comparison of stress-strain relationship curvess between calculation and theory
![]()
图 10 波浪荷载作用下试验与DavByrne模型和Finn模型的超孔压结果对比
Figure 10. Comparison of results among tests, DavByrne model and Finn model under wave loading
![]()
图 11 地震作用下试验与DavByrne模型的超孔压比结果对比
Figure 11. Comparison of excess pore pressure ratios between tests and DavByrne model under seismic loading
表 1 模拟循环剪切试验模型参数
Table 1 Model parameters of simulated cyclic shear tests
剪切模量G/MPa Davidenkov模型 Byrne模型 A B γ0/10-4 σ′ref/kPa C1 C2 γth/% 50 1.02 0.35 4 100 0.43 0.93 0.02 
下载: 导出CSV
表 2 模拟循环三轴试验模型参数
Table 2 Model parameters of simulated cyclic triaxial tests
剪切模量G/MPa Davidenkov模型 Byrne模型 A B γ0/10-4 σ′ref/kPa C1 C2 γth/% 53 1.02 0.43 4.1 100 0.55 1.38 0.02
下载: 导出CSV
-
[1] ZHAO K, WANG Q Z, CHEN W Y, et al. Uplift of immersed tunnel in liquefiable seabed under wave and current propagation[J]. Engineering Geology, 2020, 278: 105828. doi: 10.1016/j.enggeo.2020.105828
[2] 胡瑞庚, 刘红军, 时伟. 驻波作用下粉土海床累积液化机制分析[J]. 岩土工程学报, 2021, 43(7): 1228-1237. doi: 10.11779/CJGE202107007 HU Ruigeng, LIU Hongjun, SHI Wei. Mechanism of residual liquefaction of silty seabed under standing waves[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(7): 1228-1237. (in Chinese) doi: 10.11779/CJGE202107007
[3] SEED H B, RAHMAN M S. Wave-induced pore pressure in relation to ocean floor stability of cohesionless soils[J]. Marine Geotechnology, 1978, 3(2): 123-150. doi: 10.1080/10641197809379798
[4] SUMER B M, FREDSØE J. The Mechanics of Scour in the Marine Environment[M]. Singapore: World Scientific, 2002.
[5] JENG D S. Soil response in cross-anisotropic seabed due to standing waves[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1997, 123(1): 9-19. doi: 10.1061/(ASCE)1090-0241(1997)123:1(9)
[6] TOKUO Y, KONING H L, HANS S, et al. On the response of a poro-elastic bed to water waves[J]. Journal of Fluid Mechanics, 1978, 87(1): 193-206. doi: 10.1017/S0022112078003006
[7] ZHANG X L, XU C S, HAN Y. Three-dimensional poro-elasto-plastic model for wave-induced seabed response around submarine pipeline[J]. Soil Dynamics and Earthquake Engineering, 2015, 69: 163-171. doi: 10.1016/j.soildyn.2014.11.002
[8] 王小雯, 张建民. 随机波浪作用下饱和砂质海床弹塑性动力响应规律[J]. 工程力学, 2018, 35(6): 240-248, 256. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201806029.htm WANG Xiaowen, ZHANG Jianmin. Elasto-plastic dynamic behaviors of saturated sandy seabed under random waves[J]. Engineering Mechanics, 2018, 35(6): 240-248, 256. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201806029.htm
[9] LIAO C C, CHEN J J, ZHANG Y Z. Accumulation of pore water pressure in a homogeneous sandy seabed around a rocking mono-pile subjected to wave loads[J]. Ocean Engineering, 2019, 173: 810-822. doi: 10.1016/j.oceaneng.2018.12.072
[10] ARTHUR J R F, CHUA K S, DUNSTAN T, et al. Principal stress rotation: a missing parameter[J]. International Journal of Rock Mechanics and Mining Sciences, 1980, 17(6): A107.
[11] ISHIHARA K, TOWHATA I. Sand response to cyclic rotation of principal stress directions as induced by wave loads[J]. Soils and Foundations, 1983, 23(4): 11-26. doi: 10.3208/sandf1972.23.4_11
[12] CHEN G X, WANG Y Z, ZHAO D F, et al. A new effective stress method for nonlinear site response analyses[J]. Earthquake Engineering & Structural Dynamics, 2021, 50(6): 1595-1611.
[13] 周晓智, 陈育民, 刘汉龙. 驻波作用下有限厚度海床动应力路径特性研究[J]. 岩土工程学报, 2018, 40(5): 890-899. doi: 10.11779/CJGE201805014 ZHOU Xiaozhi, CHEN Yumin, LIU Hanlong. Study on characteristics of dynamic stress path of finite-thickness seabed under standing waves[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(5): 890-899. (in Chinese) doi: 10.11779/CJGE201805014
[14] CHEN G X, ZHAO D F, CHEN W Y, et al. Excess pore water pressure generation in cyclic undrained testing[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2019, 145(7): 04019022. doi: 10.1061/(ASCE)GT.1943-5606.0002057
[15] MARTIN P P, SEED H B. One-dimensional dynamic ground response analyses[J]. Journal of the Geotechnical Engineering Division, 1982, 108(7): 935-952. doi: 10.1061/AJGEB6.0001316
[16] 赵丁凤, 阮滨, 陈国兴, 等. 基于Davidenkov骨架曲线模型的修正不规则加卸载准则与等效剪应变算法及其验证[J]. 岩土工程学报, 2017, 39(5): 888-895. doi: 10.11779/CJGE201705013 ZHAO Dingfeng, RUAN Bin, CHEN Guoxing, et al. Validation of modified irregular loading-unloading rules based on Davidenkov skeleton curve and its equivalent shear strain algorithm implemented in ABAQUS[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(5): 888-895. (in Chinese) doi: 10.11779/CJGE201705013
[17] HASHASH Y M A, PARK D. Non-linear one-dimensional seismic ground motion propagation in the Mississippi embayment[J]. Engineering Geology, 2001, 62(1/2/3): 185-206.
[18] ZHANG Y, ZHAO K, YANJV P, et al. Dynamic shear modulus and damping ratio characteristics of undisturbed marine soils in the Bohai Sea, China[J]. Earthquake Engineering and Engineering Vibration, 2022, 21(2): 297-312.
[19] Itasca Consulting Group. Fast lagrangian analysis of continual in 3 dimensions[M]. MN: Itasca Consulting Group, Minneapolis, 2018.
[20] OLSON S M, MEI X, HASHASH Y M A. Nonlinear site response analysis with pore-water pressure generation for liquefaction triggering evaluation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146(2): 04019128.
-
期刊类型引用(2)
1. 占鑫杰，吕冲，桂书润，李振亚. 化学调质及固结作用下市政污泥水分转化规律. 科学技术与工程. 2025(05): 2057-2065 . 
百度学术
2. 张玉伟，宋战平，谢永利. 孔隙变化条件下黄土土水特征曲线预测模型. 岩土工程学报. 2022(11): 2017-2025 . 本站查看
其他类型引用(4)
-
其他相关附件
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
- 被引次数: 6
