珊瑚钙质砂导热系数与含水率关系的修正Côté-Konrad模型研究

刘志遐; 郭成超; 朱鸿鹄; 曹鼎峰; 黄锐; 王复明; 董璞

doi:10.11779/CJGE20220985

珊瑚钙质砂导热系数与含水率关系的修正Côté-Konrad模型研究 English Version

刘志遐^{1, 2, 3,},
郭成超^{1, 2, 3, ,},
朱鸿鹄⁴,
曹鼎峰^{1, 2, 3},
黄锐^{1, 2, 3},
王复明^{1, 2, 3},
董璞⁵

1.
中山大学土木工程学院和南方海洋科学与工程广东省实验室(珠海), 广东珠海 519082
2.
广东省海洋土木工程重点实验室, 广东广州 510275
3.
广东省地下空间开发工程技术研究中心, 广东广州 510275
4.
南京大学地球科学与工程学院, 江苏南京 210023
5.
惠州学院建筑与土木工程学院, 广东惠州 516007

基金项目:

国家自然科学基金项目 42377150

国家自然科学基金项目 42225702

详细信息

作者简介:
刘志遐(1998—)，女，博士研究生，主要从事珊瑚钙质砂力学性质方面的研究工作。E-mail: liuzhx57@mail2.sysu.edu.cn

通讯作者:
郭成超, E-mail: guochch25@mail.sysu.edu.cn

中图分类号: TU441
计量
- 文章访问数: 337
- HTML全文浏览量: 63
- PDF下载量: 79
出版历程
- 收稿日期: 2022-08-11
- 网络出版日期: 2023-03-09
- 刊出日期: 2023-10-31

Modified Côté-Konrad model for describing relationship between thermal conductivity and water content of coral calcareous sand

LIU Zhixia^{1, 2, 3,},
GUO Chengchao^{1, 2, 3, ,},
ZHU Honghu⁴,
CAO Dingfeng^{1, 2, 3},
HUANG Rui^{1, 2, 3},
WANG Fuming^{1, 2, 3},
DONG Pu⁵

1.
School of Civil Engineering, Sun Yat-sen University & Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai), Zhuhai 519082, China
2.
Guangdong Key Laboratory of Marine Civil Engineering, Guangzhou 510275, China
3.
Guangdong Engineering Technology Research Center for Underground Space Development, Guangzhou 510275, China
4.
School of Earth Science and Engineering, Nanjing University, Nanjing 210023, China
5.
School of Architecture and Civil Engineering, Huizhou University, Huizhou 516007, China

摘要

摘要: 掌握珊瑚钙质砂的热力学性质对于中国南海人工冻结法施工工艺的优化十分重要，但目前对其研究仍有不足。珊瑚钙质砂颗粒形状不规则、棱角度高，内部传热路径长且曲折，经典Côté-Konrad(CK)模型不能准确描述其含水率与导热系数之间的关系。提出相对颗粒评价参数 $\mu$ ，并结合CK模型得到了改进模型(modified Côté-Konrad模型，简称MCK模型)，用于定量描述非冻结状态下珊瑚钙质砂含水率与导热系数的关系。结果表明：非冻结状态下，MCK模型对珊瑚钙质砂导热系数的预测结果远远好于经典CK模型，改进后MAE，RMSE和MAPE分别从0.286，0.098 W/m℃和40%下降至0.098，0.011 W/m℃和10%。在冻结状态下，由于冰增强了砂土颗粒之间的联结，从而降低了颗粒形状不规则对导热系数的影响程度，因此经典CK模型仍然适用。
- 珊瑚钙质砂 /
- 导热系数 /
- 改进Côté-Konrad模型 /
- 含水率
Abstract: The artificial freezing construction process is determined through the thermal properties of coral calcareous sand in the South China Sea, however, the heat transfer among calcareous sand particles is still unclear. The classic Côté-Konrad (CK) model is difficult to be directly used in calcareous sand because of the irregular shape, high angularity and long heat transfer path among particles. To fill this gap, a relative particle evaluation parameter ( $\mu$ ) is defined, and a modified CK (MCK) model is established with consideration of $\mu$ . The MCK model is used to describe the relationship between water content and thermal conductivity in unfrozen calcareous sand. A serious of laboratory tests are conducted to verify the MCK model. The results indicate that the mean absolute error, root mean square error and mean absolute percentage error are 0.098 W/m℃, 0.011 W/m℃ and about 10%, respectively, which are much less than those of CK model (0.286 W/m℃, 0.098 W/m℃ and 40%). In the frozen calcareous sand, the CK model is still applicable because ice can fill the surface pores of solid particles and enhance connectivity, which reduces the influences of particle shape on thermal conductivity.
- coral calcareous sand /
- thermal conductivity /
- modified Côte-Konrad model /
- water content

HTML全文

0. 引言

珊瑚钙质砂在中国南海分布广泛，是近年来南海海域吹填造岛、工程建造的主要材料^[1]。珊瑚钙质砂中碳酸钙含量高达90%以上^[2]。相比石英砂，珊瑚钙质砂颗粒具有多孔隙、形状不规则、棱角度大等特点^[3-4]，导致其传热性能与石英砂有明显区别。在南海地区，地基基础工程施工通常采用人工冻结法，而珊瑚钙质砂的导热性直接决定着人工冻结法实施的设计参数和工艺手段。对于某一特定的土体，其结构和化学成分固定，导热性主要由含水率决定。因此，研究不同含水率下珊瑚钙质砂在冻结和非冻结状态下的导热系数变化规律并建立相应的预测模型，对南海陆地表层水热迁移、储热和地下设施施工建设等均具有重要意义。

关于土体含水率、冻结状态与导热系数的关系已有较多研究，其中最经典的是Jonhansen模型和Côté-Konrad模型^[5-6]。Jonhansen提出了归一化导热系数 ${K_{\text{e}}}$ ，并分别建立了未冻土和冻土的 ${K_{\text{e}}}$ 与含水率的关系^[7]。Côté等^[8]在Jonhansen模型的基础上，根据土颗粒大小将土体分成4类，并建立了每类土导热系数的预测模型。该模型在低含水率范围内误差相比Johansen模型小很多。Zhang等^[9]和Lu等^[10]针对Johansen模型对石英含量敏感的特点，进一步简化模型计算过程，提出了以石英含量为变量的非冻结土体导热系数模型。在土较干(含水率小于5%)时，水分主要以吸附水的形式存在，具有固体的传热特征，在此条件下，虽然Zhang等^[9]和Lu等^[10]提出的模型精度更高，但所需确定的参数也更多，在实际工程中难以推广利用。此外，接近干燥状态的土体在南海环境中很少存在，因此本研究着重讨论Côté-Konrad模型的应用效果。Côté-Konrad模型在建立导热系数与含水率关系的过程中，考虑了矿物成分、冻结状态、颗粒大小、有机质含量等影响因素。在矿物成分中，影响最大的是石英，为此Côté-Konrad模型确立了石英含量与导热系数的关系，并成功应用于大量石英砂案例。但是，现有基于石英砂建立的模型难以准确描述热量在珊瑚钙质砂中的传递，其原因是热量在土颗粒之间传递时，细观上颗粒形状、接触面积、接触点数量、传递路径等均影响宏观导热系数^[11]。珊瑚钙质砂和石英砂的矿物成分和颗粒形状均有明显区别。石英砂颗粒以椭球体为主，表面较光滑，不同颗粒接触良好，而珊瑚钙质砂颗粒形状不规则、表面粗糙，在热传导过程中其内部的传热路径更长、更曲折。

为了定量描述岩土材料颗粒形状对岩土体工程性质的影响，Wadell定义了颗粒球度Φ，即与实际颗粒具有等体积的球颗粒的表面积和实际颗粒表面积之比^[12]。在实践中，普遍认为Φ能够较好地描述不规则颗粒的形状，但是岩土材料颗粒比表面积很难通过试验准确测量。Dellino等^[13]研究发现Φ和圆度X的比值 $\psi$ 能够较好地从三维空间角度描述颗粒形状特性。任玉宾等^[14]将Wadell和Dellino模型相结合，并采用不等轴椭球体的表面积计算方法近似获得了非球形颗粒的表面积，定量研究了不同颗粒形状的珊瑚钙质砂、福建标准砂和玻璃珠的渗透特性，但尚未开展对其热力学性质的进一步研究。

已有学者研究了土颗粒形状对土体热力学性质的影响。Xiao等^[15]利用热探针试验测量了5种不同的圆形、角状玻璃颗粒-土混合料的导热系数，并采用包含了颗粒长宽比、球度、凸度的颗粒评价参数对土颗粒形状进行了定量描述，发现土样相对密度相同时土样热导率会随着圆形颗粒比例的增加而增加。Lee等^[16]测量了9种砂土的导热系数 $\lambda$ ，并采用球度、凸度、长宽比、长细比4种形状参数对颗粒形状进行了定量评价，研究发现土样中颗粒形状最近似圆形的砂土(Ottawa 20/30 sand) $\lambda$ 是颗粒最不规则的砂子(Hiroshima sand)的4倍，这说明砂颗粒形状与其导热系数具有很强的相关性，并且拥有更多圆形颗粒的砂土具有更高的 $\lambda$ 。以上研究都集中于土颗粒形状与土体导热系数之间关系，没有将土颗粒形状评价参数引入土体导热系数预测模型中。

为了研究具有不规则形状、粗糙表面和多棱角的珊瑚钙质砂的热力学性质，定量化确立含水率对其导热性的影响，本研究将 $\psi$ 引入Côté-Konrad模型对其进行修正。并设计了室内试验，分别在冻结和非冻结状态下测试修正Côté-Konrad模型的有效性。

1. 基本理论

1.1 Côté-Konrad模型

Côté和Konrad建立的土体导热系数预测模型(以下简称CK模型)为^[8]

$\lambda {\text{ = }}({\lambda _{{\text{sat}}}} - {\lambda _{{\text{dry}}}}){K_{\text{e}}} + {\lambda _{{\text{dry}}}} \text{，}$

(1)

${K_\text{e}} = \frac{{a{S_{\text{r}}}}}{{1 + (a - 1){S_{\text{r}}}}} 。$

(2)

式中： $\lambda$ 为土体导热系数(W/m℃)； ${K_{\text{e}}}$ 为归一化导热系数； ${\lambda _{{\text{sat}}}}$ ， ${\lambda _{{\text{dry}}}}$ 分别为土体饱和与干燥情况下导热系数(W/m℃)； $a$ 为与土的成分、结构和冻结状态有关的参数； ${S_{\text{r}}}$ 为土体饱和度(%)。

在非冻结情况下，饱和砂土导热系数 ${\lambda _{{\text{sat(u)}}}}$ 为

${\lambda _{{\text{sat}(}{{u}}{)}}} = \lambda _\text{s}^{{1 - }{n_{{\text{(u)}}}}}\lambda _\text{w}^{{{{n}}_{{\text{(u)}}}}} 。$

(3)

式中： ${\lambda _{\text{w}}}$ 为水的导热系数(W/m℃)； ${\lambda _{\text{s}}}$ 为砂土颗粒的导热系数(W/m℃)。

$\left. \begin{array}{l}{\lambda }_{\text{s}}\text{=}{\displaystyle \prod _{\text{j}}{\lambda }_{{\text{m}}_{\text{j}}}^{{\text{x}}_{\text{j}}}}, \\ {\displaystyle \sum _\text{j}{\text{x}}_\text{j}=1}\text{ }。\end{array} \right\}$

(4)

式中： ${\lambda _{{\text{mj}}}}$ 为各矿物成分导热系数(W/m℃)； ${x_{\text{j}}}$ 为各矿物成分的体积分数(%)； ${x_{\text{j}}}$ 之和等于1。

在非冻结状态下，土体孔隙率 ${n_{{\text{(u)}}}}$ 和饱和度 ${S_{{\text{r(u)}}}}$ 为

${n_{\text{(u)}}} = {1} - \frac{{{\rho _\text{d}}}}{{{\rho _\text{s}}}} \text{，}$

(5)

${S_{{\text{r(u)}}}} = \frac{{w}}{{100}}\frac{{{\rho _{\text{d}}}}}{{{{n}_{{\text{(u)}}}}{\rho _\text{w}}}}。$

(6)

式中： ${\rho _{\text{d}}}$ 为土体干密度(g/cm³)； ${\rho _{\text{s}}}$ 为土颗粒相对质量密度(g/cm³)； ${\rho _{\text{w}}}$ 为水的密度(g/cm³)； $w$ 为土体的质量含水率(%)。

干土的导热系数可为

${\lambda _{\text{dry}}} = {\chi } \times {1}{{0}^{{ - }{\eta n}}}。$

(7)

式中： $\chi$ ， $\eta$ 为材料参数； $n$ 为土体孔隙率(%)。

土体冻结后水分发生相变，从而产生体积膨胀。在0℃以下，未冻水仍存在于细粒土体之中，在计算时需综合考虑土体内部冰水共存的情况。在冻结状态下，饱和砂土的导热系数 ${\lambda _{{\text{sat(f)}}}}$ 为^[8]

${\lambda _{\text{sat(f)}}} = \lambda _\text{s}^{{1 - }{{n}_{{\text{(f)}}}}}\lambda _\text{i}^{{{n}_{{\text{(f)}}}}{ - }{{\theta }_{\text{(u)}}}}\lambda _\text{w}^{{{\theta }_{\text{(u)}}}} 。$

(8)

式中： ${\lambda _{\text{i}}}$ 为冰的导热系数(W/m℃)； ${n_{{\text{(f)}}}}$ 为冻土的孔隙率(%)。

${{n}_\text{(f)}} = \frac{{{{n}_\text{(u)}} + 0.09({{S}_{\text{r(u)}}}{{n}_\text{(u)}} - {{\theta }_{\text{(u)}}})}}{{1 + 0.09({{S}_{\text{r(u)}}}{{n}_\text{(u)}} - {{\theta }_{\text{(u)}}})}}。$

(9)

式中： ${\theta _{{\text{(u)}}}}$ 为未冻水的体积分数(%)。

冻结后土体的饱和度 ${S_{{r(f)}}}$ 为

${{S}_{\text{r(f)}}}{ = }\frac{{{1}{.09}{{S}_{\text{r(u)}}}{{n}_{\text{(u)}}} - {0}{.09}{{\theta }_{\text{(u)}}}}}{{{{n}_{\text{(u)}}}{ + 0}{.09(}{{S}_{\text{r(u)}}}{{n}_{\text{(u)}}} - {{\theta }_{\text{(u)}}}{)}}}。$

(10)

1.2 珊瑚钙质砂Côté-Konrad模型改进

相比石英砂，珊瑚钙质砂形状更加不规则、棱角度更高、具有内孔隙，导致二者的热量传递规律完全不同，需采用新的形状评价参数对CK模型进行改进。对于任玉宾等^[14]提出的土颗粒形状评价参数 $\psi$ ，其值越接近1，表示土颗粒形状越圆，颗粒表面起伏越平缓；其值越接近0，表示颗粒形状越不规则，颗粒表面起伏越大。图 1珊瑚钙质砂和标准石英砂颗粒形状示意图及照片^[14]。由经典传热学可知，砂颗粒形状越不规则，颗粒彼此间接触越不充分、接触面积越小，则传热路径越曲折，土体导热系数越小。由此，可将CK模型描述的珊瑚钙质砂导热系数与含水率的关系进一步改进为(以下简称MCK模型)

$\begin{array}{l}{\lambda }_{\text{(u)}}=\text{ }\mu \text{ }\cdot \text{ }\left[({\lambda }_{\text{sat}}-{\lambda }_{\text{dry}}){K}_{\text{e}}+{\lambda }_{\text{dry}}\right]\text{ }\text{，}\\ {\lambda }_{\text{(f)}}=\text{ }({\lambda }_{\text{sat}}-{\lambda }_{\text{dry}}){K}_{\text{e}}+{\lambda }_{\text{dry}}\text{ }\text{，}\end{array}\}$

(11)

$\mu =\frac{{\psi }_{珊瑚钙质砂}}{{\psi }_{标准砂}} 。$

(12)

图 1 珊瑚钙质砂、石英砂颗粒与球形玻璃珠形状对比图(来自任玉宾等^[14])

Figure 1. Comparison of shapes of coral calcareous sand, quartz sand particles and spherical glass beads(from Ren Yubin et al. ^[14])

下载: 全尺寸图片幻灯片

式中： $\mu$ 为相对颗粒形状参数，表示珊瑚钙质砂颗粒相对石英砂颗粒形状更加不规则的程度； $\psi$ 为任玉兵等提出的颗粒形状评价参数。

Wang等^[17]随机选取100粒珊瑚钙质砂和福建标准砂(石英砂)颗粒拍照，分别计算其颗粒形状评价参数 $\psi$ ，统计结果得到二者具有代表性的 $\psi$ 值分别为0.528，0.675，此时 $\mu$ =0.782。对于非冻结砂土，热量主要通过砂土颗粒以及砂颗粒接触间隙的水分传输。对于冻结珊瑚钙质砂，因为冻结后砂颗粒间的联结增强，所以颗粒形状对导热系数的影响减弱，可以忽略，依旧通过CK模型进行计算。

1.3 模型评估方法

为评估改进模型的预测效果，采用平均绝对误差MAE(W/m℃)、均方根误差RMSE(W/m℃)和平均绝对百分比误差MAPE(%)评估新模型性能，

$\text{MAE}=\frac{{\displaystyle \sum _{\text{num}}(\text{|}{\lambda }_{\text{p}}-{\lambda }_{\text{m}}\text{|})}}{\text{num}} \text{，}$

(13)

${\text{RMSE}} = \sqrt {\frac{{\sum\limits_{{\text{num}}} {{{{(}{\lambda _\text{p}} - {\lambda _\text{m}}{)}}^{2}}} }}{{{\text{num}}}}} \text{，}$

(14)

${\text{MAPE}} = \frac{{1}}{{{\text{num}}}}\sum\limits_{{\text{num}}} {\frac{{{|}{\lambda _\text{p}} - {\lambda _\text{m}}{|}}}{{{\lambda _\text{m}}}}} \times 100\% 。$

(15)

式中： ${\text{num}}$ 为土样数量； ${\lambda _{\text{p}}}$ 为预测导热系数(W/m℃)； ${\lambda _{\text{m}}}$ 为实测导热系数(W/m℃)。平均绝对误差MAE用于评价预测结果整体误差，MAE越大说明预测结果整体误差越大；均方根误差RMSE用于衡量预测值和实测值的偏差，对数据中特大或特小值敏感；平均绝对百分比误差MAPE表示误差占实测值百分比，用于描述预测误差相对实测值的大小。

2. 室内试验

2.1 试验土样

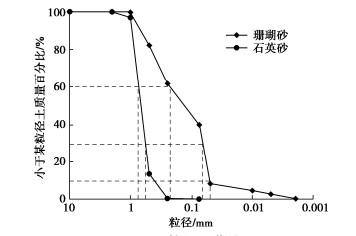
试验中使用的珊瑚钙质砂土样取样自中国南海西沙群岛海域，土样为白色。试验采用的石英砂呈现土黄色，主要矿物成分为石英、斜长石和钠长石。两种土样的粒径分布情况如图 2所示，矿物成分体积分数通过X射线光谱分析得到，各矿物成分导热系数取自Horai^[18]的研究结果(表 1)。珊瑚钙质砂和石英砂颗粒相对质量密度分别取2.73，2.65 g/cm³。由表 1可以看出，本文采用的珊瑚钙质砂中碳酸钙(文石和方解石)体积含量占比高达97.6%，明显区别于石英砂。

图 2 颗粒级配曲线

Figure 2. Grain-size distribution curves

下载: 全尺寸图片幻灯片

表 1 土样各矿物成分体积百分数与导热系数

Table 1. Volume percentages and thermal conductivities of each mineral component

土样	珊瑚砂	石英砂	导热系数 ${\lambda _{{\text{mj}}}}$ /(W/m℃)
文石	47.3%	0	2.24
方解石	50.3%	0	3.59
石英	2.4%	50.3%	7.69
斜长石	0	26.9%	2.49
钠长石	0	22.8%	1.96
注：少量含量小于1%的矿物不进行具体计算。

下载: 导出CSV

| 显示表格

土样的制备过程中，将土样烘干后过2 mm筛，去除贝壳等杂物。根据样品容器体积和土样干密度(1.4 g/cm³)，称取一定量土样，再按照目标含水率加入定量无气水，充分混合搅拌后，使用击实器将土分层击入样品容器内，制成圆柱形试样。非冻结砂土配置质量含水率为0%，5%，10%，15%，20%，25%，30%，饱和8种土样；冻结砂土配置质量含水率为7%，12%，17%，22%，25%，30%，饱和7种土样。根据规范《土工试验方法标准GB/T 50123—2019》，试验前测定试样含水率，确保配置土样的含水率误差小于1%。

2.2 试验设备与方法

试验使用的热常数分析仪是瑞典Hot Disk AB公司生产的Hot Disk TPS 2500S，如图 3所示。测试导热系数时，同一含水率土取5个平行样品进行测试。非冻结砂土导热系数测量试验在25±5℃的室温下进行，试验采用了单面法和双面法(图 4)两种测量方法。两种方法的区别：双面法需要将测量探头夹在两个样品之间，对样品表面平整度要求高；单面法只需要将探头夹在样品和泡沫块间，泡沫块上需放置重物块使探头和样品紧密接触，从而有效减少因样品表面不平整导致的测量误差。因泡沫块导热系数约为0.03 W/m℃，会对导热系数在0.3 W/m℃以下的样品造成较大干扰，所以导热系数小于0.3 W/m℃的样品只能选用双面法测试。冻结砂土导热系数测量试验全部采用单面法，在-30℃条件下测试。测量过程中，在样品中央插入频域反射传感器(FDR)^[19]，用于测量样品内部未冻水分和温度的变化。当液态水含量每小时变化小于1%时，可认为冻结过程结束，然后测量该温度与含水率条件下冻结土导热系数。为防止冻结过程中样品内部水分蒸发，实验过程中用单层保鲜膜(小于20 um以减小对试验的影响)将样品与探头包裹起来。

图 3 Hot Disk TPS 2500S仪器照片

Figure 3. Photos of Hot Disk TPS 2500S

下载: 全尺寸图片幻灯片

图 4 试验装置配置

Figure 4. Configuration of tests

下载: 全尺寸图片幻灯片

3. 结果和讨论

3.1 非冻结砂土导热系数与含水率的关系

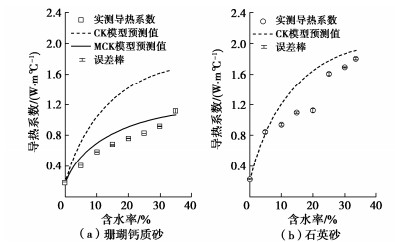
非冻结珊瑚钙质砂和石英砂导热系数模型参数如表 2所示，测量结果如图 5所示。图 5结果表明含水率对砂土导热系数影响显著，含水率为0%时，珊瑚钙质砂和石英砂导热系数均在0.19 W/m℃左右，石英砂略大于珊瑚砂。二者导热系数均随含水率增加而逐渐增大，其中含水率由0%增加至5%时导热系数变化幅度最大，其原因在于水很容易填充间隙并在亲水颗粒的接触周围形成弯液面^[20]，形成“水桥”。水桥的产生造成相邻固体颗粒之间形成更多的热量传输通道。当含水率大于5%时，水桥逐渐饱和，随着含水率的增加，水桥逐渐变粗，新增加的水桥产生量很少，并在样品底部形成重力水，此时，水分变化对导热系数影响减小。

表 2 各土样的CK及MCK模型参数^{[8, 14]}

Table 2. Parameters of CK and MCK models^{[8, 14]}

土样	${\lambda _{{\text{sat}}}}$ / (W·m^-1·℃^-1)	${\lambda _{{\text{dry}}}}$ / (W·m^-1·℃^-1)	a	${\lambda _{\text{w}}}$ (W·m^-1·℃^-1)	${\rho _{\text{w}}}$ / (g·cm^-3)	${\rho _{\text{s}}}$ / (g·cm^-3)	$\chi$ / (W·m^-1·℃^-1)	$\eta$	${\lambda _{\text{i}}}$ / (W·m^-1·℃^-1)	$\mu$	$\psi$
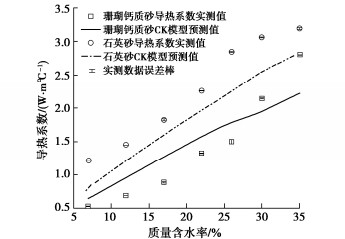
非冻结珊瑚砂	1.35	0.19	3.55	0.6	1	1.4	0.75	1.2	2.24	0.782	0.528
冻结珊瑚砂	1.35	0.19	0.95	0.6	1	1.4	0.75	1.2	2.24	0.782	0.528
非冻结石英砂	1.67	0.20	3.55	0.6	1	1.4	0.75	1.2	2.24	—	0.675
冻结石英砂	1.67	0.20	0.95	0.6	1	1.4	0.75	1.2	2.24	—	0.675
非冻结珊瑚砂^[21]	1.35	0.19	3.55	0.6	1	1.2	0.75	1.2	2.24	0.782	0.528
非冻结珊瑚砂^[28]	1.35	0.19	3.55	0.6	1	1.2	0.75	1.2	2.24	0.782	0.528

下载: 导出CSV

| 显示表格

图 5 非冻结砂土导热系数实测数据与模型预测结果对比

Figure 5. Comparison between measured and predicted thermal conductivities of unfrozen sand

下载: 全尺寸图片幻灯片

随着含水率的增加，相同含水率石英砂和珊瑚钙质砂导热系数差距迅速增大，石英砂导热系数明显大于珊瑚钙质砂，表明含水率对石英砂导热性能影响更大，与文献[21]结果一致。见，使用CK模型预测石英砂导热系数时，MAE为0.128 W/m℃，RMSE为0.024 W/m℃，MAPE为12%，和文献[]的预测误差基本一致，误差在可接受范围内。然而使用CK模型预测珊瑚钙质砂导热系数时，MAE为0.286 W/m℃，RMSE为0.098 W/m℃，MAPE为40%，误差超出工程中可接受范围。而采用MCK模型预测珊瑚钙质砂导热系数得到MAE，RMSE和MAPE分别降低至0.098，0.011 W/m℃和15%，与现有广泛应用于石英砂的模型误差接近。MCK模型精度更高的原因是其在CK模型中引入了相对颗粒形状评价参数 $\mu$ ，从而剔除了珊瑚钙质砂更加不规则的形状对导热性质的影响。

表 3 非冻结导热系数预测模型误差分析

Table 3. Error analysis of thermal conductivity for unfrozen soils

土样	模型	温度/ ℃	MAE/ (W·m^-1·℃^-1)	RMSE/ (W·m^-1·℃^-1)	MAPE/%
石英砂	CK	25 ± 5	0.128	0.024	12.0
珊瑚砂	CK	25 ± 5	0.286	0.098	40.0
珊瑚砂	MCK	25 ± 5	0.098	0.011	15.0
珊瑚砂^[21]	MCK	20	0.072	0.007	15.6
珊瑚砂^[28]	MCK	20	0.019	0.001	2.8

下载: 导出CSV

| 显示表格

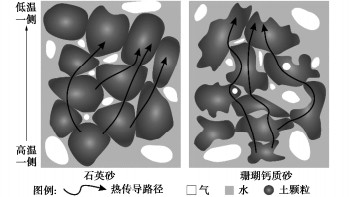
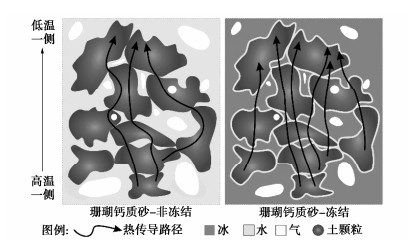
石英砂及珊瑚钙质砂固体颗粒间热量传递过程如图 6所示。固体导热由电子运动与粒子在平衡位置上的振动导致的晶格振动组成，二者均与固体颗粒接触面积及形式有关^[23]。因为珊瑚钙质砂颗粒形状更加不规则、棱角度更高，所以其颗粒间接触面积更小，传导路径更少、更曲折，造成CK模型失效^[24-27]。石英砂内热传导路径更多、更短，固体颗粒间热量传导效率更高。此外，珊瑚钙质砂颗粒内部还存在内孔隙，导致热量在颗粒内部的传导路径变长，宏观表现为珊瑚钙质砂颗粒导热性能更差，导热系数更小。而相对颗粒形状评价参数 $\mu$ 的提出能够减小不规则颗粒对导热系数产生的影响，进而对CK模型进行修正，使其能够有效描述热量在不规则形状珊瑚钙质砂中的传递。

图 6 非冻结砂土颗粒间热传导示意图

Figure 6. Schematic diagram of heat conduction between unfrozen sand particles

下载: 全尺寸图片幻灯片

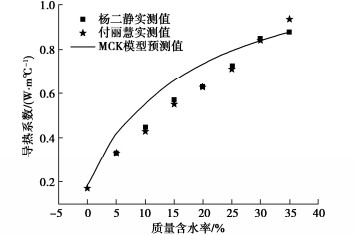
为了进一步验证MCK模型对非冻结珊瑚钙质砂导热系数的预测准确性，选取文献中付丽慧等^[21]和杨二静等^[28]在20℃下用热探针法测得的珊瑚钙质砂(干密度1.2 g/cm³)导热系数数据与MCK模型预测值进行对比，结果见图 7和表 3。关于付丽慧等^[21]的珊瑚钙质砂导热系数实测数据，MCK模型的MAE，RMSE和MAPE分别为0.072，0.007 W/m℃和15.6%，与本文中计算的结果基本相同。关于杨二静等^[28]的珊瑚钙质砂导热系数实测数据，MCK模型的MAE，RMSE和MAPE分别为0.019，0.001 W/m℃和2.8%，低于本文中计算结果。可得到MCK模型可以较为准确的预测用平面法和热探针法测量得到的珊瑚钙质砂导热系数数据。He HaiLong等收集了71种土壤和669个测量数据，对38种模型进行了测试，得到MAE和RMSE分别为0.01~1.04 W/m℃和0.13~1.28 W/m℃^[22]。与He Hailong收集的多个模型预测结果对比，MCK模型精度较高，MAE和RMSE结果均可接受^[22]。

图 7 改进模型验证

Figure 7. Validation of modified model

下载: 全尺寸图片幻灯片

3.2 冻结过程中砂土内部温度与水分的变化规律

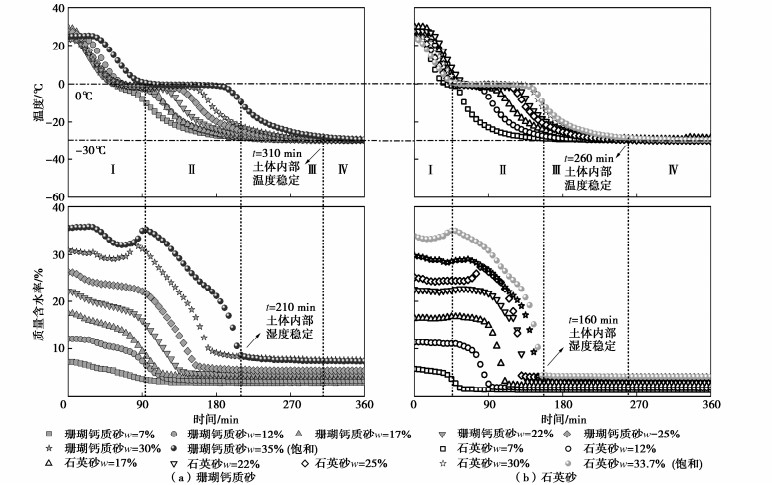
珊瑚钙质砂和石英砂在冻结过程中FDR测量得到的土体内部温度和质量含水率随时间的变化曲线见图 8。两种砂土含水率都是先于温度达到稳定条件，含水率和温度的稳定时间相差100 min左右。本文中对冻结砂土导热系数的测量在砂土含水率达到稳定后开始进行。随着含水率的增加，砂土冻结过程中温度和含水率稳定所需要的时间也逐渐增大。含水率低于30%时，随着砂土初始含水率增加，冻结砂土内未冻水含量也增加；含水率高于30%后，砂土初始含水率增大，冻结砂土内未冻水含量不变。相比石英砂，珊瑚钙质砂土体内温度和含水率达到稳定所需要的时间更久，相同含水率情况下珊瑚钙质砂内未冻水含量也更多，这是由于珊瑚钙质砂中热量传递更慢。由饱和砂土冻结过程中温度和含水率变化特征，可将其分为：①第I阶段，土体内部热量向外部环境传递，内部温度由箱温逐渐降低至0℃。土体内部温度高于冰点，水分未发生相变，故其含水率基本稳定。②第Ⅱ阶段，砂土内部温度维持在0℃，砂土内部大部分水分逐渐冻结成冰。砂土初始含水率越高，土体内部温度维持在0℃的时间越长。③第Ⅲ阶段，砂土内部水分相变已完成，含水率随着温度变化不明显。④到达第Ⅳ阶段后，砂土与环境热量达到平衡，含水率变化可忽略。

图 8 冻结过程中砂土内部温度、质量含水率变化情况

Figure 8. Change of internal temperature and mass moisture content of sand during freezing

下载: 全尺寸图片幻灯片

3.3 冻结土导热系数和含水率的关系

-30℃温度下冻结珊瑚钙质砂和石英砂导热系数测量结果见图 9。含水率30%石英砂导热系数由非冻结状态下1.69 W/m℃增大到3.17 W/m℃，增大了1.48 W/m℃；含水率30%珊瑚钙质砂则是从0.92 W/m℃增大到了2.15 W/m℃，增大了1.23 W/m℃，冻结以后两种砂土导热性能都明显提高。产生这种变化的原因是冰增强了土颗粒间的联结，并且冰具有固体传热的性质，其自身导热系数为2.24 W/m℃，是水的3.7倍。非冻结状态与冻结状态相比，含水率5%左右的珊瑚钙质砂导热系数提高了0.13 W/m℃，表明初始含水率越高，冻结后导热系数变化幅度越大。同时，CK模型的预测结果低估了冻结状态下石英砂的导热系数，高估了珊瑚砂导热系数。这是因为石英砂颗粒更圆、更光滑、颗粒间接触面积更大、未冻水含量更低，所以冰明显增强了土颗粒间的联结，使得实际导热系数高于模型预测结果。

图 9 冻结砂土导热系数实测数据与模型预测结果

Figure 9. Measured data and model prediction results of thermal conductivity of frozen sand

下载: 全尺寸图片幻灯片

表 4为冻结石英砂及珊瑚钙质砂CK模型误差分析结果。对于冻结状态下的石英砂和珊瑚钙质砂，CK模型预测结果的MAE分别为0.301，0.393 W(m℃，RMSE分别为0.11，0.183 W/m℃，MAPE分别为25%，18%。He Hailong等评估了39种冻土导热系数预测模型，各模型预测结果的RMSE为0.46~1.45 W/m℃，MAE为0.02~1.4 W/m℃^[5]，与表 4一致。

表 4 冻结砂土导热系数预测模型误差分析

Table 4. Error analysis of thermal conductivity evaluation models of frozen sand

土样	测试温度/℃	MAE/ (W·m·℃^-1)	RMSE/ (W·m·℃^-1)	MAPE/ %
石英砂	-30	0.301	0.110	25
珊瑚砂	-30	0.393	0.183	18

下载: 导出CSV

| 显示表格

当土中的水分冻结成冰以后，含水率30%珊瑚钙质砂导热系数从0.92 W/(m℃)增大到了2.15 W/(m℃)。这是因为，与非冻结状态下珊瑚钙质砂内部的导热过程相比，冻结后其内部的热传导路径增多，并且热传导路径变得更短、更平滑，导热效率明显增大，如图 10所示。水分由液态水变成冰后，砂颗粒之间热传导形式发生了改变，热量在冰内部的传递、以及在冰和砂颗粒之间的传导都明显增强，从而导致珊瑚钙质砂颗粒不规则形状产生的影响也减小。因此，对于冻结状态下的珊瑚钙质砂，依旧可以采用CK模型描述其导热系数与含水率之间的关系。

图 10 冻结与非冻结珊瑚钙质砂导热路径区别

Figure 10. Difference of heat conduction paths between frozen and nonfrozen coral calcareous sand

下载: 全尺寸图片幻灯片

4. 结论

(1) 珊瑚钙质砂具有形状不规则、表面粗糙、棱角度高的特点。土体内部发生热量传递时，珊瑚钙质砂颗粒间接触面积更小、传热路径更少更曲折，在非冻结状态下，经典CK模型不再适用。本研究中采用相对颗粒形状评价参数 $\mu$ 改进CK模型后，可以弥补颗粒不规则形状对土体导热系数产生的影响。

(2) 试验结果表明，MCK模型可以准确描述非冻结状态下珊瑚钙质砂含水率和导热系数之间的关系。MCK模型预测结果的MAE，RMSE和MAPE分别为0.098，0.011 W/m℃和10%左右，相比改进前CK模型，其精度大幅提高。

(3) 珊瑚钙质砂被人工冻结后，固体颗粒周围冰的存在增强了土颗粒之间的联结，增加了固体颗粒之间热量传输通道，提高了土体内部的热传导能力。同时，冰的存在减小了颗粒不规则对导热性能的影响，经典CK模型依然有效。

图 1 珊瑚钙质砂、石英砂颗粒与球形玻璃珠形状对比图(来自任玉宾等^[14])

Figure 1. Comparison of shapes of coral calcareous sand, quartz sand particles and spherical glass beads(from Ren Yubin et al. ^[14])

下载: 全尺寸图片幻灯片

图 2 颗粒级配曲线

Figure 2. Grain-size distribution curves

下载: 全尺寸图片幻灯片

图 3 Hot Disk TPS 2500S仪器照片

Figure 3. Photos of Hot Disk TPS 2500S

下载: 全尺寸图片幻灯片

图 4 试验装置配置

Figure 4. Configuration of tests

下载: 全尺寸图片幻灯片

图 5 非冻结砂土导热系数实测数据与模型预测结果对比

Figure 5. Comparison between measured and predicted thermal conductivities of unfrozen sand

下载: 全尺寸图片幻灯片

图 6 非冻结砂土颗粒间热传导示意图

Figure 6. Schematic diagram of heat conduction between unfrozen sand particles

下载: 全尺寸图片幻灯片

图 7 改进模型验证

Figure 7. Validation of modified model

下载: 全尺寸图片幻灯片

图 8 冻结过程中砂土内部温度、质量含水率变化情况

Figure 8. Change of internal temperature and mass moisture content of sand during freezing

下载: 全尺寸图片幻灯片

图 9 冻结砂土导热系数实测数据与模型预测结果

Figure 9. Measured data and model prediction results of thermal conductivity of frozen sand

下载: 全尺寸图片幻灯片

图 10 冻结与非冻结珊瑚钙质砂导热路径区别

Figure 10. Difference of heat conduction paths between frozen and nonfrozen coral calcareous sand

下载: 全尺寸图片幻灯片

表 1 土样各矿物成分体积百分数与导热系数

Table 1 Volume percentages and thermal conductivities of each mineral component

土样	珊瑚砂	石英砂	导热系数 ${\lambda _{{\text{mj}}}}$ /(W/m℃)
文石	47.3%	0	2.24
方解石	50.3%	0	3.59
石英	2.4%	50.3%	7.69
斜长石	0	26.9%	2.49
钠长石	0	22.8%	1.96
注：少量含量小于1%的矿物不进行具体计算。

下载: 导出CSV

表 2 各土样的CK及MCK模型参数^{[8, 14]}

Table 2 Parameters of CK and MCK models^{[8, 14]}

土样	${\lambda _{{\text{sat}}}}$ / (W·m^-1·℃^-1)	${\lambda _{{\text{dry}}}}$ / (W·m^-1·℃^-1)	a	${\lambda _{\text{w}}}$ (W·m^-1·℃^-1)	${\rho _{\text{w}}}$ / (g·cm^-3)	${\rho _{\text{s}}}$ / (g·cm^-3)	$\chi$ / (W·m^-1·℃^-1)	$\eta$	${\lambda _{\text{i}}}$ / (W·m^-1·℃^-1)	$\mu$	$\psi$
非冻结珊瑚砂	1.35	0.19	3.55	0.6	1	1.4	0.75	1.2	2.24	0.782	0.528
冻结珊瑚砂	1.35	0.19	0.95	0.6	1	1.4	0.75	1.2	2.24	0.782	0.528
非冻结石英砂	1.67	0.20	3.55	0.6	1	1.4	0.75	1.2	2.24	—	0.675
冻结石英砂	1.67	0.20	0.95	0.6	1	1.4	0.75	1.2	2.24	—	0.675
非冻结珊瑚砂^[21]	1.35	0.19	3.55	0.6	1	1.2	0.75	1.2	2.24	0.782	0.528
非冻结珊瑚砂^[28]	1.35	0.19	3.55	0.6	1	1.2	0.75	1.2	2.24	0.782	0.528

下载: 导出CSV

表 3 非冻结导热系数预测模型误差分析

Table 3 Error analysis of thermal conductivity for unfrozen soils

土样	模型	温度/ ℃	MAE/ (W·m^-1·℃^-1)	RMSE/ (W·m^-1·℃^-1)	MAPE/%
石英砂	CK	25 ± 5	0.128	0.024	12.0
珊瑚砂	CK	25 ± 5	0.286	0.098	40.0
珊瑚砂	MCK	25 ± 5	0.098	0.011	15.0
珊瑚砂^[21]	MCK	20	0.072	0.007	15.6
珊瑚砂^[28]	MCK	20	0.019	0.001	2.8

下载: 导出CSV

表 4 冻结砂土导热系数预测模型误差分析

Table 4 Error analysis of thermal conductivity evaluation models of frozen sand

土样	测试温度/℃	MAE/ (W·m·℃^-1)	RMSE/ (W·m·℃^-1)	MAPE/ %
石英砂	-30	0.301	0.110	25
珊瑚砂	-30	0.393	0.183	18

下载: 导出CSV

参考文献(28)

[1]	HE S H, DING Z, XIA T D, et al. Long-term behaviour and degradation of calcareous sand under cyclic loading[J]. Engineering Geology, 2020, 276: 105756. doi: 10.1016/j.enggeo.2020.105756
[2]	马维嘉, 陈国兴, 李磊, 等. 循环荷载下饱和南沙珊瑚砂的液化特性试验研究[J]. 岩土工程学报, 2019, 41(5): 981-988. doi: 10.11779/CJGE201905023 MA Weijia, CHEN Guoxing, LI Lei, et al. Experimental study on liquefaction characteristics of saturated coral sand in Nansha Islands under cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(5): 981-988. (in Chinese) doi: 10.11779/CJGE201905023
[3]	金宗川. 钙质砂的休止角研究与工程应用[J]. 岩土力学, 2018, 39(7): 2583-2590. doi: 10.16285/j.rsm.2017.2326 JIN Zongchuan. Study of natural repose angle of calcareous sand and engineering application[J]. Rock and Soil Mechanics, 2018, 39(7): 2583-2590. (in Chinese) doi: 10.16285/j.rsm.2017.2326
[4]	WANG X, WU Y, CUI J E, et al. Shape characteristics of coral sand from the South China Sea[J]. Journal of Marine Science and Engineering, 2020, 8(10): 803. doi: 10.3390/jmse8100803
[5]	HE H L, FLERCHINGER G N, KOJIMA Y, et al. A review and evaluation of 39 thermal conductivity models for frozen soils[J]. Geoderma, 2021, 382: 114694. doi: 10.1016/j.geoderma.2020.114694
[6]	WANG J M, HE H L, DYCK M, et al. A review and evaluation of predictive models for thermal conductivity of sands at full water content range[J]. Energies, 2020, 13(5): 1083. doi: 10.3390/en13051083
[7]	JOHANSEN O. Thermal Conductivity of Soils[R]. Hanover: Cold Regions Research and Engineering Lab. 1977.
[8]	CÔTÉ J, KONRAD J M. A generalized thermal conductivity model for soils and construction materials[J]. Canadian Geotechnical Journal, 2005, 42(2): 443-458. doi: 10.1139/t04-106
[9]	ZHANG N, YU X B, PRADHAN A, et al. A new generalized soil thermal conductivity model for sand-Kaolin clay mixtures using thermo-time domain reflectometry probe test[J]. Acta Geotechnica, 2017, 12(4): 739-752. doi: 10.1007/s11440-016-0506-0
[10]	LU S, REN T S, GONG Y S, et al. An improved model for predicting soil thermal conductivity from water content at room temperature[J]. Soil Science Society of America Journal, 2007, 71(1): 8-14. doi: 10.2136/sssaj2006.0041
[11]	YANG Y L, ZHANG T, LIU S Y. Influence factor analysis and calculation model for thermal/electrical resistivity of geomaterials[J]. Measurement, 2020, 152: 107373. doi: 10.1016/j.measurement.2019.107373
[12]	WADELL H. Volume, shape, and roundness of rock particles[J]. The Journal of Geology, 1932, 40(5): 443-451. doi: 10.1086/623964
[13]	DELLINO P, MELE D, BONASIA R, et al. The analysis of the influence of pumice shape on its terminal velocity[J]. Geophysical Research Letters, 2005, 32(21): L21306.
[14]	任玉宾, 王胤, 杨庆. 颗粒级配与形状对钙质砂渗透性的影响[J]. 岩土力学, 2018, 39(2): 491-497. doi: 10.16285/j.rsm.2016.0277 REN Yubin, WANG Yin, YANG Qing. Effects of particle size distribution and shape on permeability of calcareous sand[J]. Rock and Soil Mechanics, 2018, 39(2): 491-497. (in Chinese) doi: 10.16285/j.rsm.2016.0277
[15]	XIAO Y, MA G L, NAN B W, et al. Thermal conductivity of granular soil mixtures with contrasting particle shapes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146(5): 06020004-06020004. doi: 10.1061/(ASCE)GT.1943-5606.0002243
[16]	LEE C, SUH H S, YOON B, et al. Particle shape effect on thermal conductivity and shear wave velocity in sands[J]. Acta Geotechnica, 2017, 12(3): 615-625. doi: 10.1007/s11440-017-0524-6
[17]	WANG Y, REN Y B, YANG Q. Experimental study on the hydraulic conductivity of calcareous sand in South China Sea[J]. Marine Georesources & Geotechnology, 2017, 35(7): 1037-1047.
[18]	HORAI K I. Thermal conductivity of rock-forming minerals[J]. Journal of Geophysical Research, 1971, 76(5): 1278-1308. doi: 10.1029/JB076i005p01278
[19]	YU L M, GAO W L, SHAMSHIRI R R, et al. Review of research progress on soil moisture sensor technology[J]. International Journal of Agricultural and Biological Engineering, 2021, 14(3): 32-42. doi: 10.25165/j.ijabe.20211404.6404
[20]	ROSHANKHAH S, GARCIA A V, CARLOS SANTAMARINA J. Thermal conductivity of sand–silt mixtures[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2021, 147(2): 06020031. doi: 10.1061/(ASCE)GT.1943-5606.0002425
[21]	付慧丽, 莫红艳, 曾召田, 等. 钙质砂热传导性能试验[J]. 岩土工程学报, 2019, 41(增刊2): 61-64. doi: 10.11779/CJGE2019S2016 FU Huili, MO Hongyan, ZENG Zhaotian, et al. Experimental study on thermal conductivity of calcareous sand[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(S2): 61-64. (in Chinese) doi: 10.11779/CJGE2019S2016
[22]	HE H L, NOBORIO K, JOHANSEN O, et al. Normalized concept for modelling effective soil thermal conductivity from dryness to saturation[J]. European Journal of Soil Science, 2020, 71(1): 27-43. doi: 10.1111/ejss.12820
[23]	王晓东. 传热学[M]. 大连: 大连理工大学出版社, 2008. WANG X D. Transferts Thermiques[M]. Dalian: Dalian University of Technology Press, 2008. (in Chinese)
[24]	WANG Z Y, ZHANG N, DING J H, et al. Thermal conductivity of sands treated with microbially induced calcite precipitation (MICP) and model prediction[J]. International Journal of Heat and Mass Transfer, 2020, 147: 118899. doi: 10.1016/j.ijheatmasstransfer.2019.118899
[25]	CAO D F, ZHU H H, GUO C C, et al. Investigating the hydro-mechanical properties of calcareous sand foundations using distributed fiber optic sensing[J]. Engineering Geology, 2021, 295: 106440. doi: 10.1016/j.enggeo.2021.106440
[26]	CAO D F, ZHU H H, WU B, et al. Investigating temperature and moisture profiles of seasonally frozen soil under different land covers using actively heated fiber Bragg grating sensors[J]. Engineering Geology, 2021, 290: 106197. doi: 10.1016/j.enggeo.2021.106197
[27]	WU B, ZHU H H, CAO D F, et al. Feasibility study on ice content measurement of frozen soil using actively heated FBG sensors[J]. Cold Regions Science and Technology, 2021, 189: 103332.
[28]	杨二静, 曾召田, 车东泽, 等. 不同温度环境下珊瑚钙质砂导热系数试验[J]. 桂林理工大学学报, 2022, 42(3): 622-627. https://www.cnki.com.cn/Article/CJFDTOTAL-GLGX202203012.htm YANG Erjing, ZENG Zhaotian, CHE Dongze, et al. Thermal conductivity of coral calcareous sand under different temperatures[J]. Journal of Guilin University of Technology, 2022, 42(3): 622-627. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GLGX202203012.htm