Numerical modeling of influences of discontinuous centrifugation on contaminant migration in cutoff wall
-
摘要: 土-膨润土竖向阻隔墙广泛应用于场地管控和修复工程。正确评估阻隔墙的服役寿命,成为阻隔墙设计的关键。使用现场试验评估阻隔墙的长期服役性能往往需要数十年,而使用超重力模型试验能够将试验周期大大缩短。在高离心加速度下,土工离心机无法长时间工作,为解决该问题本文提出采用非连续转机的方法来模拟污染物长时间的运移。在非连续转机情况下,污染物的运移发生了变化,为正确评估阻隔墙的服役寿命,建立了一个数值模型来模拟污染物在离心加速度周期性变化下的运移行为。研究结果表明:①采用有效转机时长作为非连续转机情况下污染物运移的时间,则阻隔墙的服役寿命将低于连续转机。②离心机停机时,阻隔墙内污染物运移速度降低有限,污染物运移以扩散为主。③阻隔墙的服役寿命随离心机转机间隔的增大而减少。Abstract: The soil-bentonite vertical cutoff walls are widely used in the remediation and control of contaminated sites. The correct evaluation of the service life of the cutoff walls is the key to their design. It often takes decades to evaluate the long-term performance of the cutoff walls by field tests, and the centrifugal model tests can obviously shorten the test period. In the case of high centrifugal acceleration, the geotechnical centrifuge cannot work for a long time. To solve this problem, a method of discontinuous centrifugation is proposed to simulate the long-term migration of contaminants. In the case of discontinuous centrifugation, the migration behavior of contaminants is changed. To correctly evaluate the service life of the cutoff walls, a numerical model is established to simulate the migration of the contaminants under the periodic change of centrifugal acceleration. The results show that: (1) The service life of the cutoff walls in the case of discontinuous centrifugation will be lower than that of continuous centrifugation if the effective centrifugation time is used as the time of contaminant transport. (2) When the centrifuge shuts down, the decreased migration velocity of contaminants in the cutoff wall is limited, and diffusion has become the main migration mode of contaminants. (3) The service life of the cutoff walls decreases with the increase of the work interval of the centrifuge.
-
Keywords:
- cutoff wall /
- centrifugal model test /
- discontinuous centrifugation /
- numerical model /
- service life
-
0. 引言
土-膨润土竖向阻隔墙是阻滞污染物运移的屏障隔离措施,从20世纪80年代开始逐渐被应用于垃圾填埋场防渗和地下水污染控制工程,迄今在全美竖向隔离项目中使用率已超过80%[1]。阻隔墙体由回填基土、干膨润土、膨润土泥浆按一定比例配置而成,施工时在污染场地外围采用挖槽机开挖宽度0.6~1.5 m、深度20~40 m的槽,并使用泥浆护壁,然后用抓斗在槽内回填墙体材料形成连续的柔性墙体[2-4]。
由于阻隔墙渗透系数极低,污染物在阻隔墙中运移缓慢,原位场地试验难以实现长达数十年的污染物运移过程模拟。而超重力物理模拟技术通过缩小尺寸的模型再现原型应力场,能较为准确地模拟原型材料及水文地质条件,同时加速污染物的运移,使试验的周期大大缩短,已被广泛应用于污染物在均匀及不均匀介质中的运移问题[5-7]。
Zhan等[8]开展了污染物击穿土膨润土阻隔墙的离心模型试验。试验在100g下连续运行43.8 h,模拟了黄土改性和未改性土膨润土阻隔墙服役50 a的情况。若以源浓度的10%作为击穿标准,污染物在连续转机43.8 h后,只击穿了黄土改性土-膨润土阻隔墙0.448 cm,占墙体厚度(4 cm)的11.2%。若要研究污染物的击穿行为以及阻隔墙的长期服役性能,则需要更长的转机时间。而一般的土工离心机很难在高g值维持如此长时间的转机,因此本文提出采取非连续转机的方法来模拟污染物长时间的运移行为。
本文基于离心模型试验建立了离心机非连续转机情况下阻隔墙内污染物二维运移模型,同时考虑污染物对流、扩散、机械弥散和吸附过程,研究了非连续转机情况下阻隔墙污染物运移规律。
1. 计算模型
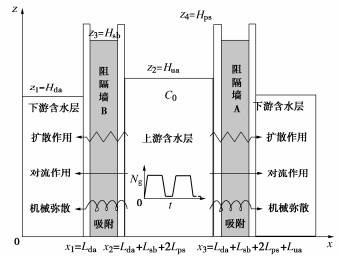
数值模型按照Zhan等[8]的离心模型试验建立,如图 1所示。模型中部为上游含水层,两侧为土-膨润土竖向阻隔墙,其中左侧为黄土改性阻隔墙,右侧为未改性阻隔墙,它们通过两层透水石固定。阻隔墙外侧为下游含水层。
1.1 模型假设
数值模型的主要假设:①含水层和透水石是均质、各向同性的多孔介质;②模型内液体的流动符合达西定律;③不考虑含水层和透水石对污染物的吸附;④不考虑土-膨润土阻隔墙的半透膜行为和电势梯度对污染物扩散系数的影响[9-11];⑤污染物浓度在墙体长度方向是一致的,则污染物在土体中的迁移方向是二维的(xz方向);⑥假定转机和停机条件下,土体的孔隙率、渗透系数不发生变化(停机后土体回弹量极小,且常重力下,水头较小,渗透系数的微小改变,对污染物运移影响不大)。
1.2 控制方程及边界条件
污染物由上游含水层依次进入透水石、阻隔墙,最后进入下游含水层,考虑污染物的二维对流、扩散、机械弥散以及阻隔墙对污染物的线性可逆吸附,建立离心模型中的污染物运移控制方程如下:
Rd,i∂Ci∂t=Dx,i∂Ci∂x2+Dz,i∂Ci∂z2−vx,i∂Ci∂x−vz,i∂Ci∂z。 (1) 式中Ci表示第i层中的污染物浓度(i=ua,sb,ps,da);Rd,i为阻滞因子;Dx,i和Dz,i为污染物水平和竖向水动力弥散系数,Dx,i=D∗x,i+Dmx,i,Dz,i=D∗z,i+Dmz,i (D∗x,i和D∗z,i为水平和竖向有效扩散系数,Dmx,i和Dmz,i为水平和竖向机械弥散系数);vx,i和vz,i为水平和竖向渗流速度,vx,i=vdx,i/ni,vz,i=vdz,i/ni (vdx,i和vdz,i为水平和竖向达西流速,ni为孔隙率)。下标ua、sb、ps和da分别代表上游含水层、阻隔墙、透水石和下游含水层。
污染物水平和竖向弥散系数为渗流速度的函数[12-13],可由下式计算:
Dmx,i=αL,ivx,i, (2a) Dmz,i=αL,ivz,i, (2b) 式中,αL,i为弥散度。
污染物的阻滞因子通过Henry定律公式确定:
Rd,i=1+ρd,iniKd,i, (3) 式中,Rd,i为土体干密度,Kd,i为分配系数。
模型中的渗流场符合达西定律,其控制方程如下所示[14]:
∂(niρf)∂t+∂(nivx,iρf)∂x+∂(nivz,iρf)∂z=0, (4a) nivx,i=−κiμ(∂pi∂x), (4b) nivz,i=−κiμ(∂pi∂z+ρfNg)。 (4c) 式中:ρf为流体的密度;κi为渗透率;κi=kiμ/γw (ki为渗透系数,μ为流体的水动力黏滞系数,μ=0.001 Pa⋅s,γw为流体的重度,γw=9800 N/m3);pi为孔隙水压力,N为离心机中加速度与重力加速度的比值;g为重力加速度,g=9.8 m/s2。使用渗透率可以避免离心加速度增大渗透系数还是水力梯度的问题,因为其只与土体本身的孔隙结构有关。
假定在初始时刻,上游含水层中污染物浓度为C0,其它位置污染物的浓度为0,即。
Ci(ua,t=0)=C0, (5a) Ci(sb,ps,da,t=0)=0, (5b) 式中,C0为上游含水层内的污染物浓度。
离心模型试验中上游含水层连接马氏瓶保持常水头,其污染物浓度在整个试验过程中保持不变:
Cua(x=x2,x3,0⩽z⩽z2,t)=C0。 (6) 离心模型试验中下游含水层外侧污染物浓度始终为0。
Cda(x=0,x2+x3,0⩽z⩽z1,t)=0。 (7) 离心模型的上边界为大气,下边界为模型箱,因此上下边界都无通量,采用Neumann边界条件(零梯度边界条件)表示[15]。
离心模型上游水箱和下游水箱水头的水位在整个试验过保持不变,因此入流边界和出流边界可以表示为:
pua(x=x2,x3,0⩽z⩽z2,t)=ρfNg(z2−z), (8a) pda(x=x1,x3+2Lps+Lsb,0≤z≤z1,t)=ρfNg(z1−z)。 (8b) 离心模型的上边界为大气,压力为0,下边界为模型箱无对流,压力梯度为0。不同土层界面处应满足孔压和流量连续条件以及污染物浓度和通量连续条件。
离心机在非连续转机时,模型所受到的重力加速度会在1g和Ng之间周期性变化,假定土工离心机每次转机时间为tc,两次转机之间的间隔为tn,转机与停机之间转换的时间为ts,g值的变换为线性变化,则离心加速度随时间的变化关系可以表示为
f(t)=f(t+T)={(N−1)gtst+g(0≤t≤ts)Ng(ts<t≤ts+tc)(N−1)gts(t−tc)+g(ts+tc<t≤2ts+tc)g(2ts+tc<t≤2ts+tc+tn) (9) 式中,T为变化周期,T=tc+tn+2ts。
1.3 模型验证
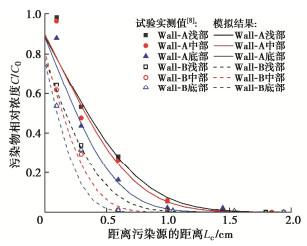
笔者采用大型有限元计算软件COMSOL multiphysics 5.5(国内外大量学者使用COMSOL成功模拟了污染物在多孔介质中的运移,证明了其作为评估土壤中污染物运移工具的可靠性[16-18])进行求解计算,得到离心模型中的污染物浓度分布,并与Zhan[8]的试验结果对比。模型各部位的物理参数及几何尺寸如表 1所示,其中阻隔墙沿深度分成了3部分,分别是浅部(180~280 mm),中部(100~180 mm)和底部(0~100 mm),每部分的干密度、孔隙率、渗透系数为实测值。由于其试验过程中透水石上部发生了弯折导致两种阻隔墙的浅部和中部厚度增加,对污染物的运移有较大影响,因此数值模型在几何方面参考试验实测结果做出了修改。离心加速度保持不变,始终为100g,阻隔墙两侧水头差为2 cm。试验采用的污染物为Pb2+离子,浓度为200 mg/L。
表 1 模型计算输入参数[8]Table 1. Input parameters for proposed model位置 层厚L/cm 层高H/cm 有效扩散系数D∗/
(m2·s-1)干密度ρd/(g·cm-3) 分配系数Kd/(mg·L-1) 孔隙率n 弥散度αL/m 渗透系数k/(m·s-1) 浅部 中部 底部 浅部 中部 底部 浅部 中部 底部 浅部 中部 底部 上游含水层 7 23.6 4.82×10-10 1.51 1.51 1.51 0 0 0 0.43 0.43 0.43 6 1×10-3 1×10-3 1×10-3 下游含水层 8.5 21.6 4.82×10-10 1.51 1.51 1.51 0 0 0 0.43 0.43 0.43 6 1×10-3 1×10-3 1×10-3 未改性阻隔墙 4 28 4.5×10-10 1.486 1.471 1.48 1.50 2.00 3.01 0.443 0.449 0.446 0.0028 9×10-8 9.74×10-8 9.67×10-8 改性阻隔墙 4 27 4.5×10-10 1.484 1.491 1.487 3.00 5.70 8.66 0.445 0.443 0.444 0.0028 6.2×10-8 8.03×10-8 6.89×10-8 透水石 2 30 4.16×10-10 1.66 1.66 1.66 0 0 0 0.38 0.38 0.38 0.5 1×10-3 1×10-3 1×10-3 图 2为本文COMSOL数值模型与离心模型试验测得的污染物浓度分布,发现本文模型的计算结果与试验结果较为吻合,验证了数值模型的正确性。
2. 连续与非连续转机污染物运移对比
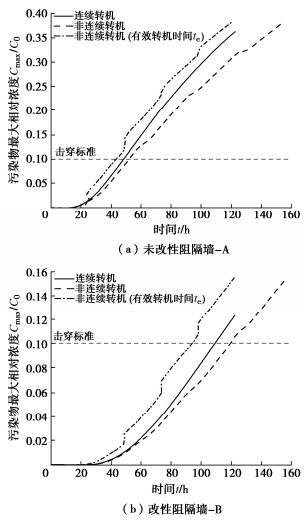
在Zhan[8]的离心模型试验中,按照源浓度的10%作为击穿标准,污染物击穿了未改性阻隔墙-A 0.804 cm,改性阻隔墙-B 0.448 cm,而实际工程中阻隔墙的厚度一般为1 m左右,换算成模型为1 cm。为了观察污染物击穿阻隔墙的行为,本节将开展连续和非连续转机情况下污染物运移的长时间模拟。
模型的几何尺寸和土层的物理参数仍然采用Zhan[8]试验的取值。土工离心机连续转机时间tc取24 h,转机间隔tn取8 h,转停机转换时间ts为0.5 h。有效转机时长te作为非连续转机中污染物运移的时间。
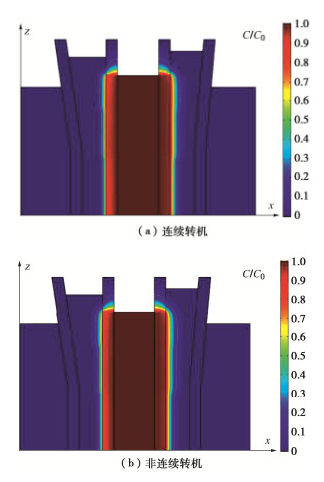
te=∑tc+12ts (10) 图 3对比了连续转机122.5 h和非连续转机157 h(有效转机时长te=122.5 h)后离心模型内的污染物分布。其中污染羽外侧的亮绿色外包线为C/C0=0.1的等值线,表示污染物刚击穿的位置。可以发现两种工况下污染物羽的形状十分接近,其中连续转机情况下,未改性阻隔墙-A的击穿厚度为1.720 cm,改性阻隔墙-B的击穿厚度为1.065 cm;而非连续转机情况下,未改性阻隔墙-A的击穿厚度为1.876 cm,改性阻隔墙-B的击穿厚度为1.165 cm。非连续转机情况下污染物击穿的厚度分别增大了9.07%和9.39%。
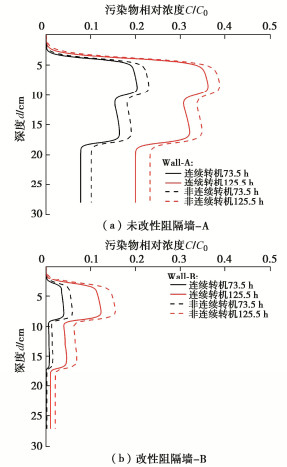
图 4选取了73.5,125.5 h两个时间点(后文若无特别说明,非连续转机的时间为有效转机时长te),分析了非连续转机对阻隔墙厚度1 cm处(Lc=1 cm)的污染物浓度的影响规律。未改性阻隔墙-A和改性阻隔墙-B,在不同时间段,连续转机和非连续转机情况下污染物延深度的分布趋势基本一致,接近于平行。在相同时间,两个阻隔墙非连续转机的浓度都要高于连续转机,且增大幅度都随时间的增加而增大,而改性阻隔墙-B的增大幅度要小于未改性阻隔墙-A。
3. 连续与非连续转机污染物通量及阻隔墙服役寿命分析
从第2节可知,非连续转机对阻隔墙内的污染物的运移产生了较大的影响,本节将通过阻隔墙内的通量变化来分析其产生的原因,同时评估非连续转机对阻隔墙服役寿命的影响。
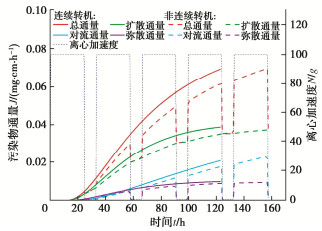
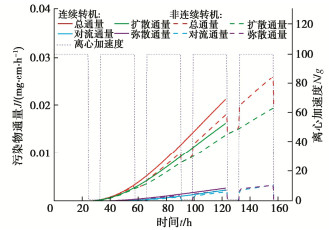
图 5对比了未改性阻隔墙-A厚度1 cm处,连续与非连续转机的污染物通量随时间的变化。连续转机的总通量随时间的增加而增加,总通量以扩散通量为主,其次为对流通量,最小为弥散通量。而非连续转机的总通量随着转停机而周期性变化。在转机时,总通量与连续转机一样也以扩散通量为主,但其各部分都要小于连续转机;在停机时,对流通量和弥散通量几乎为零,总通量等于扩散通量,这是因为停机时,流速减小为1%,与流速有关的对流作用和弥散作用因此大幅降低。由于整个试验过程中扩散作用占主导,而停机时扩散作用基本保持不变,导致非连续转机在相同的时间内击穿的厚度更大。
图 6对比了改性阻隔墙-B厚度1 cm处,连续与非连续转机的污染物通量。对比图 5,可以发现改性阻隔墙通量在试验结束时,仍处于上升阶段,而未改性阻隔墙已经趋于平稳,这是因为改性阻隔墙的阻滞因子更大,使得污染物运移的速度下降,稳定的时间延迟。其它现象则与未改性阻隔墙-A一致。
图 7对比了连续和非连续转机情况下,阻隔墙厚度1 cm处污染物最大相对浓度随时间的变化规律。在非连续转机情况下,污染物浓度随时间变化的曲线不再光滑,而是变成了台阶状上升。台阶段为离心机停机时浓度的变化情况,其浓度上升速度低于转机时的速度,这与对流和弥散作用降低有关。为了更好地分析非连续转机对污染物运移的影响,将非连续转机的实际试验时间变为有效转机时间。可以发现,浓度变化曲线变成了锯齿状,且同一时间的浓度高于连续转机。如果以有效转机时长作为阻隔墙的击穿时间将会低估阻隔墙的服役寿命,未改性阻隔墙-A的服役寿命会低估9.79%,改性阻隔墙-B的服役寿命会低估14.78%,可以发现阻滞因子越高,变化也会越大。
4. 非连续转机间隔对污染物运移的影响
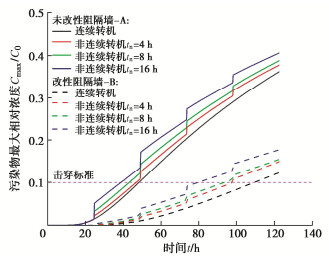
从第3节可知,离心机停机时,污染物的运移并没有停止,而是仍然以较快速度往下游运移,因此不同的转机方案可能对污染物运移产生较大影响。本节将分析转机间隔tn对阻隔墙服役寿命的影响。
图 8描述了不同转机间隔tn情况下,阻隔墙厚度1 cm处,污染物最大相对浓度随时间的变化规律。可以发现,阻隔墙的击穿时间随着转机间隔的增加而降低,对于未改性阻隔墙-A,tn=4816 h时分别降低了3.69%,9.79%和19.40%,对于改性阻隔墙-B,则分别降低了10.95%,14.78%,26.76%,改性阻隔墙的变化在不同转机间隔下均大于未改性阻隔墙。
5. 结论
本文建立了离心机非连续转机情况下阻隔墙内污染物二维运移模型。此模型采用真实的离心模型试验作为建模对象,同时考虑污染物对流、扩散、机械弥散和吸附过程,可用于评估离心机非连续转机对阻隔墙中污染物运移的影响,同时对土-膨润土阻隔墙离心模型试验的设计和计算具有一定的指导意义。分析算例首先对比了连续与非连续转机阻隔墙中的运移情况,然后探究了非连续转机情况下阻隔墙污染物通量和浓度变化规律,最后研究了转机间隔对阻隔墙寿命评估的影响。得到以下主要结论。
(1)离心机非连续转机时,若使用有效转机时长作为污染物的运移时间,在相同时间,非连续转机情况下污染物击穿的距离更远,阻隔墙的服役寿命更短,但在同一厚度处,浓度在深度方向的分布趋势一致。
(2)离心机转机和停机时,污染物在阻隔墙内的运移都以扩散为主。停机时,对流和机械弥散作用基本为零,但扩散作用基本不变,污染物运移的速度相较转机时降低的幅度有限。
(3)离心机非连续转机情况下,污染物的击穿曲线呈现台阶状上升,台阶的形成与停机时流速降低有关,阻隔墙的击穿时间在实际试验时间下大于连续转机,而在有效转机时长下则小于连续转机。
(4)当以有效转机时长作为污染物的运移时间时,阻隔墙的击穿时间随着转机间隔的增加而降低,阻滞因子较大的阻隔墙变化更为明显。
-
表 1 模型计算输入参数[8]
Table 1 Input parameters for proposed model
位置 层厚L/cm 层高H/cm 有效扩散系数D∗/
(m2·s-1)干密度ρd/(g·cm-3) 分配系数Kd/(mg·L-1) 孔隙率n 弥散度αL/m 渗透系数k/(m·s-1) 浅部 中部 底部 浅部 中部 底部 浅部 中部 底部 浅部 中部 底部 上游含水层 7 23.6 4.82×10-10 1.51 1.51 1.51 0 0 0 0.43 0.43 0.43 6 1×10-3 1×10-3 1×10-3 下游含水层 8.5 21.6 4.82×10-10 1.51 1.51 1.51 0 0 0 0.43 0.43 0.43 6 1×10-3 1×10-3 1×10-3 未改性阻隔墙 4 28 4.5×10-10 1.486 1.471 1.48 1.50 2.00 3.01 0.443 0.449 0.446 0.0028 9×10-8 9.74×10-8 9.67×10-8 改性阻隔墙 4 27 4.5×10-10 1.484 1.491 1.487 3.00 5.70 8.66 0.445 0.443 0.444 0.0028 6.2×10-8 8.03×10-8 6.89×10-8 透水石 2 30 4.16×10-10 1.66 1.66 1.66 0 0 0 0.38 0.38 0.38 0.5 1×10-3 1×10-3 1×10-3 -
[1] YEO S S, SHACKELFORD C D, EVANS J C. Consolidation and hydraulic conductivity of nine model soil-bentonite backfills[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(10): 1189–1198. doi: 10.1061/(ASCE)1090-0241(2005)131:10(1189)
[2] EVANS J C. Geotechnics of hazardous waste control systems[M]//Foundation Engineering Handbook. Boston, MA: Springer US, 1991: 750–777.
[3] D'APPOLONIA D J. Soil-bentonite slurry trench cutoffs[J]. Journal of the Geotechnical Engineering Division, 1980, 106(4): 399–417. doi: 10.1061/AJGEB6.0000945
[4] BAXTER D Y. Mechanical behavior of soil-bentonite cutoff walls[D]. Virginia Tech, 2000.
[5] TAYLOR R N. Geotechnical Centrifuge Technology[M]. London: Blackie Academic & Professional, 1995.
[6] ARULANANDAN K, THOMPSON P Y, KUTTER B L, et al. Centrifuge modeling of transport processes for pollutants in soils[J]. Journal of Geotechnical Engineering, 1988, 114(2): 185–205. doi: 10.1061/(ASCE)0733-9410(1988)114:2(185)
[7] LO I M C, HU J Z & L. Centrifuge modeling of cadmium migration in saturated and unsaturated soils[J]. Soil and Sediment Contamination: An International Journal, 2005.
[8] ZHAN L T, YOU Y Q, ZHAO R, et al. Centrifuge modelling of lead retardation in soil–bentonite cut-off walls. International Journal of Physical Modelling in Geotechnics, 2022: 1–14. doi: 10.1061/(ASCE)1090-0241(2005)131:4(418)
[9] YEO S S, SHACKELFORD C D, EVANS J C. Membrane behavior of model soil–bentonite backfills[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(4): 418–429. doi: 10.1061/(ASCE)1090-0241(2005)131:4(418)
[10] HENNING J T, EVANS J C, SHACKELFORD C D. Membrane behavior of two backfills from field-constructed soil-bentonite cutoff walls[J]. Journal of geotechnical and geoenvironmental engineering, 2006, 132(10): 1243–1249. doi: 10.1061/(ASCE)1090-0241(2006)132:10(1243)
[11] EVANS J C, SHACKELFORD C D, YEO S S, et al. Membrane behavior of soil-bentonite slurry-trench cutoff walls[J]. Soil & Sediment Contamination, 2008, 17(4): 316–322.
[12] ROTH K, JURY W A, FLÜHLER H, et al. Transport of chloride through an unsaturated field soil[J]. Water Resources Research, 1991, 27(10): 2533–2541. doi: 10.1029/91WR01771
[13] BEAR J, VERRUIJT A. Modeling Groundwater Flow and Pollution[M]. Springer: Science & Business Media, 1987.
[14] SMITH D W. One‐dimensional contaminant transport through a deforming porous medium: theory and a solution for a quasi‐steady‐state problem. International journal for numerical and analytical methods in geomechanics, 2000, 24(8): 693–722. doi: 10.1002/1096-9853(200007)24:8<693::AID-NAG91>3.0.CO;2-E
[15] DING X H, FENG S J, ZHENG Q T, et al. A two-dimensional analytical model for organic contaminants transport in a transition layer-cutoff wall-aquifer system[J]. Computers and Geotechnics, 2020, 128: 103816. doi: 10.1016/j.compgeo.2020.103816
[16] WHITMORE M K B, TROTT D W, PEERCY B E, et al. COMSOL modeling of groundwater flow and contaminant transport in two-dimensional geometries with heterogeneities[J]. UMBC Geography and Environmental Systems Department, 2011.
[17] FAISAL A A H, AL-WAKEL S F A, ASSI H A, et al. Waterworks sludge-filter sand permeable reactive barrier for removal of toxic lead ions from contaminated groundwater[J]. Journal of Water Process Engineering, 2020, 33: 101112. doi: 10.1016/j.jwpe.2019.101112
[18] 丁祥鸿, 冯世进. 固结作用下非均质隔离墙中污染物二维运移规律研究[J]. 岩土工程学报, 2022, 44(3): 584–590. doi: 10.11779/CJGE202203021 DING Xiang-hong, FENG Shi-jin. Two-dimensional migration of contaminants in non-homogeneous cutoff wall considering consolidation[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(3): 584–590. (in Chinese) doi: 10.11779/CJGE202203021



 下载:
下载: