震后地下结构在火灾下的力学性能初步分析

王国波; 刘强; 王鸿杰; 王建宁; 董正方

doi:10.11779/CJGE2022S2007

震后地下结构在火灾下的力学性能初步分析 English Version

1.
温州大学建筑工程学院, 浙江温州 325035
2.
中国机械工业集团有限公司, 北京 100080
3.
河南大学土木建筑学院, 河南开封 475004

基金项目:

国家自然科学基金项目 52078386

国家自然科学基金项目 51878529

详细信息

作者简介:
王国波(1979—)，男，湖北孝昌人，博士，教授，从事工程结构抗震研究。E-mail: wgb16790604@126.com

通讯作者:
董正方，E-mail: dzf@henu.edu.cn

中图分类号: TU435
计量
- 文章访问数: 141
- HTML全文浏览量: 23
- PDF下载量: 20
出版历程
- 收稿日期: 2022-11-30
- 网络出版日期: 2023-03-26
- 刊出日期: 2022-11-30

Preliminary analysis of mechanical properties of subway station under fire after earthquake

1.
College of Civil Engineering and Architecture, Wenzhou University, Wenzhou 325035, China
2.
China National Machinery Industry Co., Ltd., Beijing 100080, China
3.
School of Civil Engineering and Architecture, Henan University, Kaifeng, China

摘要

摘要: 地下结构等地下结构作为城市地下基础设施的重要组成部分，一旦遭受地震以及地震次生火灾会造成极大的经济损伤和人员伤亡，因此地下结构在地震以及地震火灾作用下的灾变行为亟待研究。基于某三跨两层车站建立其二维分析模型，首先对其进行了地震模拟，然后使用重启动分析，运用热-力耦合方法探讨了地下结构在地震次生火灾作用下响应。从地下结构中柱形变、层间位移等方面分析车站结构在地震及其次生火灾作用下灾变行为，讨论地震对地下结构抗火性能的影响，为地下结构受到地震以及次生火灾的性能评价提供参考。
- 地下结构 /
- 地震 /
- 地震次生火灾 /
- 性能评价
Abstract: As an important part of the urban underground infrastructure, the underground structures such as subway stations will cause great economic damage and casualties once they are subjected to earthquakes and earthquake-induced fires. Therefore, the catastrophic behaviors of the subway stations under the coupling of earthquakes and earthquake-induced fires needs to be studied. A two-dimensional analysis model is established based on a three-span two-story subway station. Firstly, the seismic simulation is carried out, and then the restart analysis is used to discuss the response of the subway station under the action of earthquake and the secondary fire by using the thermal-mechanical coupling method. The catastrophic behaviors of the subway station structure under earthquake and the secondary fire is analyzed from the aspects of column deformation and inter-layer displacement. The influences of earthquake on the fire resistance of the underground structures are discussed, which provides a reference for the performance evaluation of the underground structures under earthquakes and the secondary fire.
- subway station /
- earthquake /
- post-earthquake fire /
- performance evaluation

HTML全文

0. 引言

坝坡稳定对于土石坝工程的安全有着至关重要的影响。粗粒料作为主要的筑坝材料,其抗剪强度是影响坝坡稳定的关键因素。粗粒料为无黏性土,只有摩擦阻力,无黏聚力,其强度主要由剪胀性、颗粒破碎和颗粒的重新定向与排列所控制。大量试验表明^[1-7]：对于粗粒料,尤其是堆石料,在不高的围压时,颗粒会发生破碎现象,颗粒破碎引起颗粒间应力重新分布,颗粒间连结力变弱,颗粒易移动,从而引起内摩擦角降低,直接表现为强度包络线后段向下弯曲。同时,研究指出^[8-10]：对于土石坝尤其是高土石坝工程,传统土石坝稳定分析采用的莫尔–库伦理论（ $τ_{f} = c +$ $σ_{n} \tan φ$ ）将堆石料作为粗粒土,黏聚力为0,线性强度计算的滑弧很浅,属于表层滑动；而非线性强度参数 $φ$ 随应力变化,滑动破坏面向深度、应力较大的位置发展,属于深层滑动。土石坝在高应力下,抗剪强度呈显著地非线性变化,线性强度参数与实际工程不符,计算结果会存在误差；非线性强度参数更为合理,计算的结果比较符合实际情况。现有资料指出^[11-16]：筑坝堆石料受自身性质及荷载的影响,其强度参数为敏感的随机变量；同时,表征筑坝堆石料的非线性强度参数具有相关非正态分布特性。可靠度分析方法可以很好地解决非线性强度参数的不确定性与相关性对土石坝坝坡稳定的影响。在进行土石坝坝坡稳定可靠度分析时,需要构造非线性强度参数的联合分布函数,而相关非正态非线性强度参数联合分布函数的构造需要大量现场试验或室内试验数据,但受实际工程经济、技术等因素的限制,试验数据有限,样本数量无法达到统计要求,仅可通过上述试验数据获取非线性强度参数的边缘分布函数与相关系数,无法准确地表征非线性强度参数的统计特征和分布模型。为了便于计算,目前,大部分研究忽略了非线性强度参数的相关性,仅有的考虑相关性的研究也采用的是二维正态分布^[14]建立非线性强度参数二维分布模型,其不足之处在于二维正态分布要求非线性强度参数的边缘分布也为正态分布。因此,非常需要收集土石坝工程的相关资料,系统的整理土石坝筑坝材料非线性强度参数的试验数据,用以准确地表征非线性强度参数的统计特征和分布模型,建立合理地非线性强度参数的联合分布模型,对土石坝坝坡稳定可靠度分析具有重要意义。

由概率理论可知,通过已知变量的联合分布函数可以确定变量的边缘分布函数与相关系数,但已知变量的边缘分布函数与相关系数确定其变量的联合分布函数是非常困难的。Copula理论的发展为建立非线性强度参数联合分布模型提供了简单、有效的方法。Copula函数^[17]可以根据N个边缘分布函数和相关结构精确地建立N维联合分布函数模型,并在金融^[18-19]和水文^[20-21]等领域得到广泛应用。近年来,岩土工程领域逐步引入Copula函数分析参数的相关性,唐小松等^[22-23]建立了土体黏聚力与内摩擦角的二维Copula函数模型,并讨论了其对边坡可靠度的影响。唐小松等^[24]及Uzielli等^[25]建立了基桩荷载与位移的双曲线参数Copula函数模型。Li等^[26]详细分析了基桩正常使用极限状态下,不同Copula函数对其可靠度的影响。张蕾等^[27]收集了小浪底水利枢纽工程中土体抗剪强度参数试验数据,采用基于Copula函数建立了抗剪强度参数联合分布模型。邢婕等^[28]基于Copula函数结合1174组岩基抗剪强度试验数据,建立了抗剪强度参数联合分布模型。目前,并未见到关于筑坝堆石料非线性强度参数联合分布模型的研究,从而,无法准确地评估非线性强度参数对土石坝坝坡静、动力稳定可靠度的影响。因此,有必要对筑坝堆石料非线性强度参数联合分布模型进行研究,为土石坝坝坡静、动力可靠度分析提供可靠的模型、数据支持。

综上所述,本文系统地统计了多个土石坝工程堆石料非线性强度参数的试验数据,并基于最小二乘法得到相关系数；通过BIC准则对筑坝堆石料非线性强度参数的最优边缘分布及Copula函数进行识别；选择7种能够描述筑坝堆石料非线性强度参数正相关的Copula函数,建立筑坝堆石料非线性强度参数联合分布模型,并进行了分析对比。最后,与二维正态分布模型进行比较,讨论了基于Copula函数建立堆石料非线性强度参数联合分布模型的优越性。

1. 筑坝堆石料非线性强度参数的边缘分布函数模型

本文系统地汇总了国内外124座土石坝工程的1257组筑坝堆石料非线性强度参数数据,数据来源广、代表性强（图1）。根据材料类别将1257组数据分为堆石料、垫层料、过渡层料、排水体料、砂砾料、心墙料。由于试样及试验误差等因素的影响,统计的数据中可能存在异常点数据,所以本文选用工程上应用广泛的 $3 σ$ 法则对统计数据中的异常点进行剔除。对剔除异常点后的统计数据进行分析,得到非线性强度参数的统计特征和边缘分布模型。

图 1 124座土石坝工程及1257组非线性强度参数

Figure 1. 124 rockfill dams and 1257 groups of nonlinear strength parameters

下载: 全尺寸图片幻灯片

由非线性强度参数的定义可知, $φ_{0}$ , $Δ φ$ 的取值均为正值,工程中常用的正态分布、极值Ⅰ型分布函数描述的变量取值区间为[ $- \infty$ , $\infty$ ],在表征非线性强度参数概率分布函数时可能出现负值,而截尾分布能准确地表征变量的分布特性。因此,本文选择截尾正态分布、对数正态分布、截尾极值Ⅰ型分布、威布尔型分布、伽马分布5种边缘分布函数对非线性强度参数的最优边缘分布函数进行识别。表1列出了上述5种边缘分布类型的概率密度函数与累积分布函数, $μ$ 为均值, $σ$ 为标准差。

表 1 5种备选边缘分布函数

Table 1. Five marginal distribution functions

分布类型	概率密度函数	概率分布函数	备注
截尾正态分布	$φ (\frac{x - p}{q}) / [1 - Φ (\frac{0 - p}{q})]$	$[Φ (\frac{x - p}{q}) - Φ (\frac{0 - p}{q})] / [1 - Φ (\frac{0 - p}{q})]$	$\begin{array}{l} p = μ \\ q = σ \end{array}$
对数正态分布	$\frac{1}{\sqrt{2 π} q x} e x p [- \frac{1}{2} {(\frac{l n x - p}{q})}^{2}]$	$Φ (\frac{l n x - p}{q})$	$\begin{array}{l} p = l n \frac{μ}{\sqrt{1 + σ^{2} / μ^{2}}} \\ q = \sqrt{l n (1 + \frac{σ^{2}}{μ^{2}})} \end{array}$
截尾极值Ⅰ型分布	$\frac{q \exp {- q (x - p) - \exp [- q (x - p)]}}{1 - \exp [- \exp (p q)]}$	$\frac{\exp {- \exp [- q (x - p)]} - \exp [- \exp (p q)]}{1 - \exp [- \exp (p q)]}$	$\begin{array}{l} μ = p + \frac{0.5772}{q} \\ σ^{2} = \frac{π^{2}}{6 q^{2}} \end{array}$
威布尔型分布	$\frac{q}{p} {(\frac{x}{p})}^{q - 1} \exp [- {(\frac{x}{p})}^{q}]$	$1 - \exp [- {(\frac{x}{p})}^{q}]$	$\begin{array}{l} μ = p Γ (1 + \frac{1}{q}) \\ σ^{2} = p^{2} [Γ (1 + \frac{2}{q}) - Γ^{2} (1 + \frac{1}{q})] \end{array}$
伽马分布	$\frac{p^{q} x^{q - 1}}{Γ (q)} e^{- p x}$	$\frac{1}{Γ (q)} \int_{0}^{p x} t^{q - 1} e^{- t} d t$	$\begin{array}{l} μ = \frac{q}{p} \\ σ^{2} = \frac{q}{p^{2}} \end{array}$

下载: 导出CSV

| 显示表格

非线性强度参数最优边缘分布函数采用AIC准则或BIC准则进行识别确定。AIC准则^[29]和BIC准则^[30]工程应用广泛、计算简便,数据拟合效果准确、可靠。具体表达式为

$A I C = - 2 \sum_{i = 1}^{N} l n f (x_{i}; p, q) + 2 k_{1}$ ,

(1)

$B I C = - 2 \sum_{i = 1}^{N} l n f (x_{i}; p, q) + 2 k_{1} l n N$ 。

(2)

式中 $x_{i} (i = 1, 2, \dots, N)$ 为非线性强度参数的试验数据； $N$ 为样本数目； $f (x_{i}; p, q)$ 为备选边缘分布函数的概率密度函数,p,q为分布参数； $k_{1}$ 为备选边缘分布函数的分布参数数量。

当备选的边缘分布函数参数数量相同,基于AIC准则与BIC准则进行最优边缘分布函数的识别结果是相同的,本文采用BIC准则对非线性强度参数的最优边缘分布函数进行识别,计算结果中最小BIC值对应的边缘分布函数类型即为最优边缘分布类型。

表2列出了6种不同类别筑坝堆石料非线性强度参数的最优边缘分布类型识别结果。由表2可知,不同类别材料的非线性强度参数具有不同的最优边缘分布函数模型。5种备选的边缘分布函数类型比较全面的涵盖了筑坝堆石料非线性强度参数的最优边缘分布类型。

表 2 非线性强度参数最优边缘分布函数BIC识别结果

Table 2. BIC identification results of optimum marginal distributions of nonlinear strength parameters

筑坝材料	样本数	参数	均值/(°)	标准差/(°)	BIC值					最优边缘分布概型
筑坝材料	样本数	参数	均值/(°)	标准差/(°)	截尾正态	对数正态	截尾极值Ⅰ型	威布尔	伽马	最优边缘分布概型
堆石料	755	$φ_{0}$	49.61	4.73	4500.9	4561.70	5236.50	4486.9	4537.60	威布尔分布
堆石料	755	$Δ φ$	8.58	2.53	3554.2	3724.30	3787.20	3562.5	3959.50	截尾正态分布
垫层料	122	$φ_{0}$	51.27	4.63	728.94	749.54	1129.90	710.83	741.45	威布尔分布
垫层料	122	$Δ φ$	8.60	2.84	608.96	599.29	600.37	607.55	646.20	对数正态分布
过渡层料	175	$φ_{0}$	50.97	3.61	955.64	958.31	1020.40	971.19	956.32	截尾正态分布
过渡层料	175	$Δ φ$	8.28	2.53	831.13	839.50	848.41	829.64	861.91	威布尔分布
排水体	71	$φ_{0}$	46.76	5.18	442.47	452.86	534.27	430.42	448.83	威布尔分布
排水体	71	$Δ φ$	7.50	2.45	335.94	340.00	342.56	334.04	387.07	威布尔分布
砂砾料	116	$φ_{0}$	46.64	5.52	984.94	1003.90	1177.50	982.97	995.95	威布尔分布
砂砾料	116	$Δ φ$	7.00	2.61	750.44	756.81	752.39	747.53	860.11	威布尔分布
心墙料	18	$φ_{0}$	38.19	13.37	149.13	252.89	173.81	156.60	179.87	截尾正态分布
心墙料	18	$Δ φ$	10.30	6.12	119.37	112.40	114.77	116.30	134.88	对数正态分布

下载: 导出CSV

| 显示表格

为了更好的验证BIC法则识别最优边缘分布函数的准确性,图2～4展示了堆石料、砂砾料、过渡层料5种备选边缘分布的概率密度函数曲线与非线性强度参数直方图。由图可以看出,基于BIC法则识别的最优边缘分布类型能较准确地拟合非线性强度参数分布特征。

图 2 堆石料非线性强度参数直方图

Figure 2. Histograms of nonlinear strength parameters of main rockfill

下载: 全尺寸图片幻灯片

图 3 砂砾料非线性强度参数直方图

Figure 3. Histograms of nonlinear strength parameters of gravel

下载: 全尺寸图片幻灯片

图 4 过渡层料非线性强度参数直方图

Figure 4. Histograms of nonlinear strength parameters of transition layer

下载: 全尺寸图片幻灯片

2. 基于Copula函数的筑坝堆石料非线性强度参数二维分布模型

2.1 筑坝堆石料非线性强度参数的相关系数

由Duncan等^[31]建立双曲线应力–应变模型时,用对数关系描述强度参数的非线性,提出的非线性强度参数的指数模式为

$φ = φ_{0} - Δ φ l g (σ_{3} / p_{a})$ ,

(3)

式中, $φ$ 为土体滑动面摩擦角, $φ_{0}$ 为一个大气压下的摩擦角, $Δ φ$ 为 $σ_{3}$ 增加一个对数周期下 $φ$ 的减小值, $p_{a}$ 为大气压力。

采用线性回归方程对非线性强度参数试验结果进行整理：

$φ_{i} = φ_{0} - Δ φ l g (σ_{3}_{i} / p_{a}) + ε_{i} (i = 1, 2, \dots, n)$ ,

(4)

式中,n为来自样本的试样数目, $φ_{i}$ , $σ_{3}_{i}$ , $ε_{i}$ 分别为第i试样对应于某一强度特征摩擦角、正应力及随机扰动量。通过最小二乘法原理,采用下述公式可计算相关的统计量。

$φ$ 与 $l g (σ_{3} / p_{a})$ 的相关系数 $γ_{φ, l g (σ_{3 i} / p_{a})}$ ：

$\begin{array}{l} γ_{φ, l g (σ_{3} / p_{a})} = \\ \frac{n \sum φ_{i} (- l g (σ_{3 i} / p_{a})) - \sum φ_{i} \sum (l g (σ_{3 i} / p_{a}))}{\sqrt{[n \sum φ_{i}^{2} - {(\sum φ_{i})}^{2}] [n \sum {(- l g (σ_{3 i} / p_{a}))}^{2} - {(\sum - l g (σ_{3 i} / p_{a}))}^{2}]}} \end{array}$ 。

(5)

回归方程的标准差 $σ$ ：

$σ = \sqrt{\frac{\sum (φ_{i} + Δ φ l g (σ_{3 i} / p_{a}) - φ_{0})}{n - 2}}$ 。

(6)

令 $Δ = n {\sum (- l g (σ_{3 i} / p_{a}) - \bar{(- l g (σ_{3 i} / p_{a}))})}^{2}$ ,则 $φ_{0}$ 与 $Δ φ$ 的均值分别为

$\begin{matrix} φ_{0} = (\sum φ_{i} {\sum (- l g (σ_{3 i} / p_{a}))}^{2} - \\ \sum (- l g (σ_{3 i} / p_{a})) \sum φ_{i} (- l g (σ_{3 i} / p_{a})) / Δ, \\ Δ φ = (n \sum φ_{i} (- l g (σ_{3 i} / p_{a})) - \sum φ_{i} \sum (- l g (σ_{3 i} / p a)) / Δ \end{matrix}$

$φ_{0}$ , $Δ φ$ 的标准差分别为

$σ_{φ_{0}} = σ \sqrt{(\sum {(- l g (σ_{3 i} / p_{a}))}^{2}) / Δ}$ ,

(7)

$σ_{Δ φ} = σ \sqrt{(n / Δ)}$ 。

(8)

$φ_{0}$ 与 $Δ φ$ 的协方差为

$C ο v (φ_{0}, Δ φ) = \sum - l g (σ_{3 i} / p_{a}) (\frac{σ^{2}}{Δ})$ 。

(9)

$φ_{0}$ 与 $Δ φ$ 的相关系数为

$ρ_{φ_{0}, Δ φ} = \frac{C ο v (φ_{0}, Δ φ)}{σ_{φ_{0}} σ_{Δ φ}}$ 。

(10)

不同类别材料非线性强度参数的相关系数计算结果如表3所示。基于最小二乘法计算的相关系数 $ρ_{φ_{0}, Δ φ}$ 与Pearson线性相关系数相同。由表3可知,非线性强度参数具有显著的统计正相关性,相关系数的变化区间为[0.40,0.69]。

表 3 非线性强度参数的相关系数

Table 3. Correlation coefficients of nonlinear strength parameters

筑坝材料	样本数量	相关系数
堆石料	755	0.53
垫层料	122	0.40
过渡层料	175	0.69
排水体	71	0.58
砂砾料	116	0.44
心墙料	18	0.62

下载: 导出CSV

| 显示表格

2.2 基于Copula函数的筑坝堆石料非线性强度参数联合分布函数构造方法

基于二元分布Sklar定理^[17]：联合分布函数由变量的边缘分布函数及表征变量间的Copula函数两部分构成。对应的非线性强度参数 $φ_{0}$ , $Δ φ$ 的联合分布函数为 $F (φ_{0}, Δ φ)$ ：

$F (φ_{0}, Δ φ) = C [F_{1} (φ_{0}), F_{2} (Δ φ); θ] = C (u_{1}, u_{2}; θ)$ ,

(11)

式中, $u_{1} = F_{1} (φ_{0})$ , $u_{2} = F_{2} (Δ φ)$ 为非线性强度参数的边缘分布函数, $θ$ 为Copula函数的参数。

非线性强度参数的联合概率密度函数为

$f (φ_{0}, Δ φ) = f_{1} (φ_{0}) f_{2} (Δ φ) D [F_{1} (φ_{0}), F_{1} (Δ φ); θ]$ ,

(12)

式中, $f_{1} (φ_{0})$ , $f_{2} (Δ φ)$ 为非线性强度参数的边缘概率密度函数, $D [F_{1} (φ_{0}), F_{1} (Δ φ); θ]$ 为Copula函数的密度函数。

由式（11）,（12）可知,当已知Copula函数、非线性强度参数的边缘分布函数、概率密度函数及Copula函数的参数,便可求出非线性强度参数的联合分布函数和联合概率密度函数。

参数的相关性包含相关系数与相关结构类型两个方面。相关系数多采用Pearson线性相关系数和Kendall秩相关系数。Pearson线性相关系数是衡量参数间线性相关强弱程度的指标。Kendall秩相关系数是基于参数原始数据的秩,描述参数间的相关性。相关结构类型,则依据不同的Copula函数对参数间的相关结构类型进行描述。Copula理论^[32-33]中有多种Copula函数描述非线性强度参数的相关结构,由表3可知,筑坝堆石料非线性强度参数存在显著的统计正相关性,因此,本文选择可以描述堆石料非线性强度参数正相关性的Gaussian,t,Plackett,Frank,Clayton,Gumbel,CClayton 7种Copula函数对非线性强度参数的相关结构进行描述,7种Copula函数概率密度函数、分布函数、参数及生成元如表4所示。

表 4 7种二维Copula函数

Table 4. Seven types of bivariate Copula functions

Copula类型	Copula分布函数 $C (u_{1}, u_{2}; θ)$	Copula密度函数 $D (u_{1}, u_{2}; θ)$	生成元 $φ_{θ} (t, θ)$	$θ$ 取值范围
Gaussian	$Φ_{θ} (Φ^{- 1} (u_{1}), Φ^{- 1} (u_{2}); θ)$	$\frac{φ_{2} (Φ^{- 1} (u_{1}), Φ^{- 1} (u_{2}); θ)}{φ (Φ^{-}^{1} (u_{1})) φ (Φ^{- 1} (u_{2}))}$	—	[－1,1]
t	$T_{2} (T_{v}^{- 1} (u_{1}), T_{v}^{- 1} (u_{2}); θ, v)$	$\frac{t_{2} (T_{v}^{- 1} (u_{1}), T_{v}^{- 1} (u_{2}); θ, v)}{t_{v} (T_{v} {^{-}}^{1} (u_{1})) t_{v} (T_{v}^{- 1} (u_{2}))}$	—	[－1,1]
Plackett	$\frac{S - \sqrt{S^{2} - 4 u_{1} u_{2} θ (θ - 1)}}{2 (θ - 1)}; S = 1 + (θ - 1) (u_{1} + u_{2})$	$\frac{θ [1 + (θ - 1) (u_{1} + u_{2} - 2 u_{1} u_{2})]}{{{[1 + (θ - 1) (u_{1} + u_{2})]}^{2} - 4 u_{1} u_{2} θ (θ - 1)}^{3 / 2}}$	—	(0, 1)∪(1,∞)
Frank	$- \frac{1}{θ} \ln [1 + \frac{(e^{- θ u_{1}} - 1) (e^{- θ u_{2}} - 1)}{e^{- θ} - 1}]$	$\frac{- θ (e^{- θ} - 1) e^{- θ (u_{1} + u_{2})}}{{[(e^{- θ} - 1) + (e^{- θ u_{1}} - 1) (e^{- θ u_{2}} - 1)]}^{2}}$	$- \ln [\frac{e^{- θ t} - 1}{e^{- θ} - 1}]$	(－∞,∞)\ {0}
Clayton	${(u_{1}^{- θ} + u_{2}^{- θ} - 1)}^{- 1 / θ}$	$(1 + θ) {(u_{1} u_{2})}^{- θ - 1} {(u_{1}^{- θ} + u_{2}^{- θ} - 1)}^{- 2 - 1 / θ}$	$\frac{1}{θ} (t^{- θ} - 1)$	(0, ∞)
Gumbel	$\exp {- {[{(- \ln u_{1})}^{θ} + {(- \ln u_{2})}^{θ}]}^{1 / θ}}$		${(- \ln t)}^{θ}$	[1, ∞)
CClayton	$u_{1} + u_{2} - 1 + {(W_{1}^{- θ} + W_{2}^{- θ} - 1)}^{- 1 / θ}; W_{i}^{- θ} = 1 - u_{i}$	$(1 + θ) {(W_{1} W_{2})}^{- θ - 1} {(W_{1}^{- θ} + W_{2}^{- θ} - 1)}^{- 2 - 1 / θ}; W_{i} = 1 - u_{i}$	$\frac{1}{θ} (t^{- θ} - 1)$	(0, ∞)

下载: 导出CSV

| 显示表格

由表4可知,确定Copula函数的关键在于参数 $θ$ 。基于Pearson线性相关系数和Kendall秩相关系数可求得参数 $θ$ ^[32]。根据相关系数的定义,Copula函数的参数 $θ$ 与Pearson线性相关系数 $ρ$ 的关系^[32]：

$\begin{matrix} ρ = \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} (\frac{x_{1} - μ_{1}}{σ_{1}}) (\frac{x_{2} - μ_{2}}{σ_{2}}) \cdot \\ f_{1} (x_{1}) f_{2} (x_{2}) D (F_{1} (x_{1}), F_{2} (x_{2}); θ) d x_{1} d x_{2} \end{matrix}$ 。

由此,可求得Copula函数的参数 $θ$ 。但除Gaussian Copula函数外,大部分Copula函数进行积分求解比较困难。根据文献[28,33]的方法,先通过Pearson线性相关系数得到Gaussian Copula函数的参数 $θ$ ,

$\begin{matrix} ρ = \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} (\frac{φ_{0} - μ_{1}}{σ_{1}}) (\frac{Δ φ - μ_{2}}{σ_{2}}) \frac{f_{1} (φ_{0}) f_{2} (Δ φ)}{\sqrt{1 - θ^{2}}} \cdot \\ \exp {- \frac{ζ_{1}^{2} θ^{2} - 2 θ ζ_{1} ζ_{2} + ζ_{2}^{2} θ^{2}}{2 (1 - θ^{2})}} d φ_{0} d Δ φ \end{matrix}$

,式中, $ζ_{1} = Φ^{- 1} (u_{1})$ , $ζ_{2} = Φ^{- 1} (u_{2})$ 分别为标准正态分布的变量。

在求得Gaussian Copula函数的参数 $θ$ 后,由下式得到Kendall秩相关系数 $τ$ ：

$τ = \frac{2 \arcsin (θ)}{π}$ 。

(13)

最后利用下式得到不同Copula函数的相关参数 $θ$ 为

$τ = 4 \int_{0}^{1} \int_{0}^{1} C (u_{1}, u_{2}; θ) d C (u_{1}, u_{2}; θ) - 1$ 。

(14)

筑坝堆石料非线性强度参数的7种Copula函数相关参数 $θ$ 的计算结果如表5所示。

表 5 7种Copula函数相关参数的计算结果

Table 5. Calculated results of seven Copula functions-related parameters

筑坝材料	Pearson 相关系数	Kendall 秩相关系数	Copula函数的相关参数 $θ$ /(°)
筑坝材料	Pearson 相关系数	Kendall 秩相关系数	Gaussian	t	Plackett	Frank	Clayton	Gumbel	CClayton
堆石料	0.53	0.464	0.666	0.671	9.290	5.122	1.729	1.864	1.729
垫层料	0.40	0.483	0.688	0.674	10.327	5.429	1.865	1.933	1.865
过渡层料	0.69	0.535	0.745	0.694	14.016	6.412	2.301	2.151	2.301
排水体	0.58	0.553	0.763	0.759	15.601	6.785	2.470	2.235	2.470
砂砾料	0.44	0.361	0.539	0.526	4.563	3.643	1.129	1.564	1.129
心墙料	0.62	0.367	0.545	0.543	5.563	3.719	1.158	1.579	1.158

下载: 导出CSV

| 显示表格

与最优边缘分布函数的识别相同,采用BIC准则进行非线性强度参数最优Copula函数的识别,结果如表6所示。

表 6 最优Copula函数BIC识别结果

Table 6. BIC identification results of optimal Copula function

筑坝材料	样本数	BIC值							最优Copula分布类型
筑坝材料	样本数	Gaussian	t	Plackett	Frank	Clayton	Gumbel	CClayton	最优Copula分布类型
堆石料	755	-352.6264	-451.9866	-454.8823	-408.8209	-128.3470	-450.4442	-159.1417	Plackett Copula
垫层料	122	-27.8783	-83.2028	-73.5803	-60.6128	-33.6484	-53.7612	-23.3459	t Copula
过渡层料	175	-89.5941	-101.5961	-105.0397	-106.9065	16.0698	-109.5186	-53.641	Gumbel Copula
排水体	71	-28.3144	-53.3555	-54.5268	-52.9589	-9.6404	-47.8997	-23.4537	Plackett Copula
砂砾料	116	-40.7910	-45.6383	-45.0424	-40.8147	-13.5451	-49.4995	-0.9096	Gumbel Copula
心墙料	18	-2.8971	-6.4936	-2.7262	-1.7570	-1.5556	-4.3240	2.1961	t Copula

下载: 导出CSV

| 显示表格

结果表明：堆石料、排水体的最优Copula函数是Plackett Copula函数,垫层料及心墙料的最优Copula函数是t Copula函数,过渡层料、砂砾料的最优Copula函数是Gumbel Copula函数。因此,在实际工程中不同分区材料应选择能够表征非线性强度参数的最优Copula函数建立联合分布函数模型。

3. 基于不同Copula函数构造的堆石料非线性强度参数联合分布函数的比较

由条件概率分布的定义和式（12）可知,已知非线性强度参数 $Δ φ$ 条件下 $φ_{0}$ 的条件累积分布函数 $F (φ_{0} | Δ φ_{2} \leq Δ φ \leq Δ φ_{1})$ 为

$\begin{matrix} F (φ_{0} | Δ φ_{2} \leq Δ φ \leq Δ φ_{1}) \\ = \frac{C (F_{1} (φ_{0}), F_{2} (Δ φ_{1}); θ) - C (F_{1} (φ_{0}), F_{2} (Δ φ_{2}); θ)}{F_{2} (Δ φ_{1}) - F_{2} (Δ φ_{2})} \end{matrix}$ ,

(15)

式中, $Δ φ_{1}$ , $Δ φ_{2}$ 为 $Δ φ$ 的上、下限。同理,已知非线性强度参数 $φ_{0}$ 条件下 $Δ φ$ 的条件累积分布函 $F (Δ φ |$ $φ_{0}_{2} \leq$ $φ_{0} \leq φ_{0}_{1})$ 为

$\begin{array}{l} F (Δ φ | φ_{0}_{2} \leq φ_{0} \leq φ_{0}_{1}) \\ = \frac{C (F_{1} (φ_{0}_{1}), F_{2} (Δ φ); θ) - C (F_{1} (φ_{0}_{2}), F_{2} (Δ φ); θ)}{F_{1} (φ_{0}_{1}) - F_{1} (φ_{0}_{2})} \end{array}$ ,

(16)

式中, $φ_{01}$ , $φ_{02}$ 为 $φ_{0}$ 的上、下限。

水利水电工程中强度标准值采用小值平均值（即 $μ - 1.0 σ$ ）。因此,以堆石料为例,将 $Δ φ$ 分为 $μ - 0.25 σ$ $\leq Δ φ \leq μ + 0.25 σ$ 、 $μ - 1.0 σ \leq Δ φ \leq μ - 0.5 σ$ 及 $μ -$ $2 σ \leq Δ φ \leq μ - 1.5 σ$ 3个区间,对不同Copula函数构造的联合概率分布函数进行比较。其中, $μ$ 为均值, $σ$ 为标准差。由式（15）可得 $φ_{0}$ 的条件累积分布函数曲线（如图5所示）与分位数值（表7）。

图 5 不同Copula函数计算的

$φ_{0}$ 的条件累积分布函数曲线

Figure 5. Comparison of conditional cumulative distribution functions of frictional angle associated with various Copula functions

下载: 全尺寸图片幻灯片

表 7 不同Copula函数计算的非线性强度参数指标

$φ_{0}$ 的条件累积分布函数分位数值

Table 7. Comparison of fractiles of conditional cumulative distribution functions of

$φ_{0}$ associated with various Copula functions

Copula函数类型	$μ - 2 σ \leq Δ φ \leq μ - 1.5 σ$			$μ - 1.0 σ \leq Δ φ \leq μ - 0.5 σ$			$μ - 0.25 σ \leq Δ φ \leq μ + 0.25 σ$
Copula函数类型	25%	50%	75%	25%	50%	75%	25%	50%	75%
Gaussian	37.777	41.471	44.768	41.609	45.015	47.957	43.889	47.136	49.884
t	35.844	39.195	43.347	41.234	44.518	47.779	43.969	47.110	49.853
Plackett	40.183	43.534	46.944	42.029	45.097	48.013	44.037	47.034	49.608
Frank	41.481	44.552	47.284	42.449	45.470	48.100	43.993	47.008	49.552
Clayton	34.671	37.075	39.326	40.395	43.239	45.951	43.523	46.652	49.575
Gumbel	39.917	43.694	47.069	42.449	45.813	48.713	44.197	47.367	49.998
CClayton	43.358	46.439	49.016	43.749	46.810	49.341	44.515	47.558	50.147

下载: 导出CSV

| 显示表格

由图5可以看到,不同的Copula函数计算的 $φ_{0}$ 的条件累积分布函数存在显著的差异性,在均值附近差异性较小,随着 $Δ φ$ 的减小,差异性显著增大。表7从定量的角度很好地验证了上述结论。

为进一步分析不同Copula函数构造的非线性强度参数联合分布函数的差异性,图6,7给出了7种Copula函数构造的堆石料非线性强度参数联合概率密度函数等概率密度曲线。边缘分布函数采用表2计算的最优边缘分布函数。

图 6 不同Copula函数构造的非线性强度参数联合概率密度函数等概率密度值曲线

Figure 6. Comparison among probability density function isolines of nonlinear intensity parameters associated with different Copula functions

下载: 全尺寸图片幻灯片

图 7 概率密度值为0.001时不同Copula函数构造的非线性强度参数联合概率密度函数等概率密度值曲线

Figure 7. Curves of equal probability density value of joint probability density function of nonlinear intensity parameters constructed by different Copula functions (probability density value equals 0.001)

下载: 全尺寸图片幻灯片

如图6,7所示,相同的边缘分布函数和相关系数条件下,不同Copula函数构造的非线性强度参数联合概率密度函数差异显著。由于不同Copula函数表征不同的相关结构,所以,即便是相同的边缘分布函数和相关系数,不同Copula函数构造的非线性强度参数联合概率密度函数仍差异显著。因此,在采用Copula函数建立非线性强度参数联合分布函数模型时,避免从经验或简单的角度选择Gaussian Copula函数模型,应结合更多的试验数据确定最优Copula函数,继而建立非线性强度参数联合分布函数模型。

4. 二维正态分布函数与Copula函数构造的非线性强度参数联合分布函数的比较

二维正态分布函数与 Copula函数构造的联合分布函数的不同点：二维正态分布函数采用Gaussian Copula函数描述变量间的相关结构类型,其边缘分布必须为正态分布,而Copula函数构造的联合分布函数的边缘分布可取任意一种边缘分布类型。二维正态分布函数的概率密度函数为

$\begin{array}{l} f (φ_{0}, Δ φ) = \frac{1}{2 π σ_{φ_{0}} σ_{Δ φ} \sqrt{1 - ρ^{2}}} \exp {\frac{- 1}{2 (1 - ρ^{2})} \cdot \\ [\frac{{(φ_{0} - \bar{φ_{0}})}^{2}}{σ_{φ_{0}}^{2}} - 2 ρ \frac{(φ_{0} - \bar{φ_{0}}) (Δ φ - \bar{Δ φ})}{σ_{φ_{0}} σ_{Δ φ}} + \frac{{(Δ φ - \bar{Δ φ})}^{2}}{σ_{Δ φ}^{2}}]} \end{array}$ 。

(17)

图8展示了垫层料非线性强度参数的原始数据点与两种模型（二维正态分布函数和最优Copula函数）构造的非线性强度参数联合概率密度函数的等概率密度曲线（概率密度值0.0005）。图9描述了垫层料非线性强度参数原始数据点与两种模型的仿真数据分布情况。由图可见,与二维正态分布函数相比,Copula联合分布函数是基于最优边缘分布函数与最优Copula函数构建的,仿真数据与原始数据的变化趋势接近,能够较完整地匹配原始数据,可以较准确地表征原始数据相关结构。

图 8 非线性强度参数联合概率密度函数等概率密度线比较

Figure 8. Comparison of equal probability density lines of joint probability density functions of nonlinear strength parameters

下载: 全尺寸图片幻灯片

图 9 非线性强度参数联合分布模型仿真数据与原始数据的分布

Figure 9. Distribution of simulation data and original data of nonlinear intensity parameter joint distribution model

下载: 全尺寸图片幻灯片

5. 结论

合理地非线性强度参数的联合分布模型,对土石坝坝坡稳定可靠度分析具有重要意义。本文汇总了国内外124座土石坝工程的1257组筑坝材料非线性强度参数,开展了非线性强度参数相关性和分布模型研究,数据覆盖面广,具有较好的代表性。

（1）Copula函数能够很好地考虑筑坝材料非线性强度参数的不确定性与正相关性,构造任意边缘分布函数和不同相关结构的联合分布函数,为建立筑坝材料非线性强度参数的联合分布函数模型提供了简单、有效的方法。与传统二维正态分布函数相比,由Copula函数构造的非线性强度参数联合分布函数灵活性强、适用范围广、能更准确地表征原始数据的分布情况。

（2）相同的边缘分布函数与相关系数,基于不同Copula函数构造的非线性强度参数联合分布函数差异显著。同时,由条件累积分布函数可知,当非线性强度参数取值减小时,基于不同Copula函数构造的非线性强度参数的条件累计分布函数差异越显著。

（3）不同分区坝料的最优Copula函数不同,在实际工程中不同分区材料应选择能够表征非线性强度参数的最优Copula函数建立联合分布函数模型。

图 1 地铁地下车站结构横截面主要尺寸和配筋图

Figure 1. Main dimensions and distributed steels of cross section

下载: 全尺寸图片幻灯片

图 2 C30混凝土本构曲线

Figure 2. Constitutive curves of concrete No. 30

下载: 全尺寸图片幻灯片

图 3 土−地铁车站相互作用体系有限单元划分

Figure 3. Finite elements of soil-underground structure

下载: 全尺寸图片幻灯片

图 4 输入荷载曲线

Figure 4. Curves of input loads

下载: 全尺寸图片幻灯片

图 5 地震作用下地下结构侧墙层间变形响应时程

Figure 5. Time histories of inter-story drift of station wall under earthquake

下载: 全尺寸图片幻灯片

图 6 火灾中地下结构变形情况及温度变化云图（15, 30, 60min）

Figure 6. Structural deformations and heat distribution of station in fire (15, 30, 60 min)

下载: 全尺寸图片幻灯片

图 7 火灾中地下结构温度变化各部位最高温度变化曲线

Figure 7. Temperature curves of components in fire

下载: 全尺寸图片幻灯片

图 8 火灾中结构层间位移时程

Figure 8. Time histories of structural inter-story drift in fire

下载: 全尺寸图片幻灯片

表 1 场地土层参数

Table 1 Site parameters

土层编号	土性	重度/(kN·cm^-3)	弹模/MPa	厚度/m	剪切波速/(m·s^-1)	动泊松比
1	素填土	19.4	15.3	3.0	200	0.49
2	黏土	19.4	15.3	4.0	200	0.49

下载: 导出CSV

表 2 C30混凝土材料参数

Table 2 Material parameters for concrete No. C30

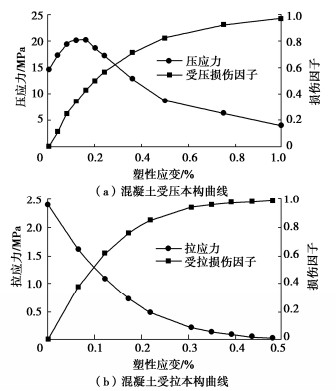
材料参数	参数值	材料参数	参数值
弹性模量	E₀ =3.0×10⁴ MPa	极限受压屈服应力	σ_cu =20.1 MPa
泊松比	ν = 0.2	初始受拉屈服应力	σ_t0 =2.4 MPa
密度	ρ =2450 kg/m³	受压刚度恢复系数	ω_c =1.0
膨胀角	Ψ=36.31°	受拉刚度恢复系数	ω_c =0.0
初始受压屈服应力	σ_c0 =13 MPa	损伤因子	d_c，d_t（图 2）

下载: 导出CSV

表 3 混凝土及钢筋的热工参数

Table 3 Thermal parameters of concrete and steel bars

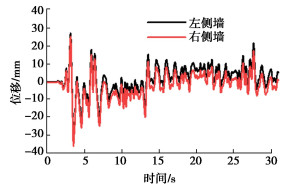
温度/℃	混凝土热工参数			钢筋热工参数
温度/℃	导热系数	比热容	热膨胀系数	导热系数	比热容	热膨胀系数
20	1.96	913	6.16×10^-6	53.3	440	1.2×10^-5
100	1.81	964	6.8×10^-6	50.7	489	1.22×10^-5
200	1.63	1022	7.6×10^-6	47.3	530	1.25×10^-5
300	1.47	1075	8.4×10^-6	44.0	565	1.27×10^-5
400	1.33	1122	9.2×10^-6	40.6	606	1.30×10^-5
500	1.21	1164	1.0×10^-5	37.3	667	1.32×10^-5
600	1.10	1200	1.08×10^-5	34.0	760	1.35×10^-5
700	1.01	1231	1.16×10^-5	30.7	991	1.37×10^-5
800	0.93	1256	1.24×10^-5	27.4	795	1.40×10^-5
900	0.87	1275	1.32×10^-5	27.3	650	1.42×10^-5
1000	0.83	1289	1.40×10^-5	27.3	650	1.45×10^-5

下载: 导出CSV

表 4 构件变形

Table 4 Deformations of components

构件	峰值变形/mm	残余变形/mm
左侧墙	33.77	5.44
右侧墙	35.85	1.14
楼板	39.92	3.75
左柱	37.93	4.03
右柱	37.30	5.35

下载: 导出CSV

参考文献(18)

[1]	赵凯, 王秋哲, 王彦臻, 等. 可液化地基地下结构地震反应特征简化有效应力分析[J]. 振动与冲击, 2021, 40(21): 39–46. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202121006.htm ZHAO Kai, WANG Qiu-zhe, WANG Yan-zhen, et al. Effects of soil-underground structure interaction on seismic response of liquefiable sit around underground structure[J]. Journal of Vibration and Shock, 2021, 40(21): 39–46. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202121006.htm
[2]	唐柏赞, 李小军, 陈苏, 等. 可液化地基-非规则截面地下结构地震变形研究[J]. 振动与冲击, 2020, 39(11): 217–225. TANG Bai-zan, LI Xiao-jun, CHEN Su, et al. Seismic deformation characteristics of liquefaction soil-irregular section underground structure[J]. Journal of Vibration and Shock, 2020, 39(11): 217–225. (in Chinese)
[3]	李延涛, 田野, 宗金辉, 等. 受相邻上部结构影响的隧道-土体系振动台试验研究[J]. 振动与冲击, 2020, 39(3): 233–241, 259. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202003033.htm LI Yan-tao, TIAN Ye, ZONG Jin-hui, et al. Shaking-table tests for seismic response of tunnel-soil system affected by adjacent upper structure[J]. Journal of Vibration and Shock, 2020, 39(3): 233–241, 259. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202003033.htm
[4]	王建宁, 马国伟, 窦远明, 等. 异跨框架式地铁地下车站结构抗震性能水平与评价方法研究[J]. 振动与冲击, 2020, 39(10): 92–100. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202010013.htm WANG Jian-ning, MA Guo-wei, DOU Yuan-ming, et al. Performance levels and evaluation method for seismic behaviors of a large-scale underground subway station with unequal-span frame[J]. Journal of Vibration and Shock, 2020, 39(10): 92–100. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202010013.htm
[5]	陈素文, 李国强. 地震次生火灾的研究进展[J]. 自然灾害学报, 2008, 17(5): 120–126. https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZH200805021.htm CHEN Su-wen, LI Guo-qiang. Advance in research on secondary fire of earthquake[J]. Journal of Natural Disasters, 2008, 17(5): 120–126. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZH200805021.htm
[6]	DANIELL J E, SCHAEFER A M, WENZEL F. Losses associated with secondary effects in earthquakes[J]. Frontiers in Built Environment, 2017, 3: 30.
[7]	陈适才, 田小明, 闫维明, 等. 建筑结构地震火灾效应分析方法[J]. 土木建筑与环境工程, 2011, 33(6): 90–95, 119. https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN201106016.htm CHEN Shi-cai, TIAN Xiao-ming, YAN Wei-ming, et al. A preliminary survey on analysis method of building structures under post-earthquake fire[J]. Journal of Civil, Architectural & Environmental Engineering, 2011, 33(6): 90–95, 119. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN201106016.htm
[8]	BURSI O S, FERRARIO F, PUCINOTTI R, et al. Seismic-induced fire analysis of steel-concrete composite beam-to-column joints: bolted solutions[C]// International Conference on Composite Construction in Steel and Concrete 2008. Reston, VA, 2008.
[9]	WEN B, WU B, NIU D T. Post-earthquake fire performance of reinforced concrete columns[J]. Structure and Infrastructure Engineering, 2016, 12(9): 1106–1126.
[10]	ARABLOUEI A, et al. Effect of fire insulation delamination on structural performance of steel structures during fire following an earthquake or an explosion[J]. Fire Safety Journal, 2016, 84: 40–49.
[11]	苗吉军, 王俊富, 刘才玮, 等. 损伤后混凝土框架结构火灾试验研究[J]. 建筑结构学报, 2012, 33(2): 1–9. https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201202002.htm MIAO Ji-jun, WANG Jun-fu, LIU Cai-wei, et al. Experimental research on RC frame structure with damages due to elevated temperature[J]. Journal of Building Structures, 2012, 33(2): 1–9. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201202002.htm
[12]	李文婷, 陈清军. 地震次生火灾中城市地铁地下结构的灾变性能研究[J]. 振动与冲击, 2021, 40(14): 153–161, 179. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202114021.htm LI Wen-ting, CHEN Qing-jun. Damage performance of underground structures in earthquake-induced fire[J]. Journal of Vibration and Shock, 2021, 40(14): 153–161, 179. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202114021.htm
[13]	陈阳, 陈清军. 火灾后CFRP加固下地下结构结构的地震反应[C]//第28届全国结构工程学术会议论文集(第Ⅰ册). 南昌, 2019: 401–405. CHEN Yang, CHEN Qing-jun. Seismic response of subway station structures reinforced by CFRP after fire[C]//The 28th National Conference on Structural Engineering (VolumeⅠ). Nanchang, 2019: 401–405. (in Chinese)
[14]	赵丁凤, 阮滨, 陈国兴, 等. 基于Davidenkov骨架曲线模型的修正不规则加卸载准则与等效剪应变算法及其验证[J]. 岩土工程学报, 2017, 39(5): 888–895. doi: 10.11779/CJGE201705013 ZHAO Ding-feng, RUAN Bin, CHEN Guo-xing, et al. Validation of modified irregular loading-unloading rules based on Davidenkov skeleton curve and its equivalent shear strain algorithm implemented in ABAQUS[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(5): 888–895. (in Chinese) doi: 10.11779/CJGE201705013
[15]	LEE J, FENVES G L. Plastic-damage model for cyclic loading of concrete structures[J]. Journal of Engineering Mechanics, 1998, 124(8): 892–900.
[16]	WANG J N, et al. Influence of diaphragm wall on seismic responses of large unequal-span subway station in liquefiable soils[J]. Tunnelling and Underground Space Technology, 2019, 91: 102988.
[17]	李国强, 韩林海, 楼国彪. 钢结构及钢-混凝土组合结构抗火设计[M]. 北京: 中国建筑工业出版社, 2006. LI Guo-qiang, HAN Lin-hai, LOU Guo-biao. And Fire Resistance Design of Steel Structure and Steel-Concrete Composite Structure[M]. Beijing: China Architecture & Building Press, 2006. (in Chinese)
[18]	庄海洋, 任佳伟, 王瑞, 等. 两层三跨框架式地铁地下车站结构弹塑性工作状态与抗震性能水平研究[J]. 岩土工程学报, 2019, 41(1): 131–138. doi: 10.11779/CJGE201901014 ZHUANG Hai-yang, REN Jia-wei, WANG Rui, et al. Elasto-plastic working states and seismic performance levels of frame-type subway underground station having two layers and three spans[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(1): 131–138. (in Chinese) doi: 10.11779/CJGE201901014