0.   引言

天然气水合物（简称水合物）是由天然气和水在一定的温度和压力下形成的笼形结晶化合物^[1]，广泛赋存于深海沉积物和陆地永冻区。全球已探明天然气水合物中碳储量相当于石油等常规化石能源总碳量的2倍^[2]。水合物资源量丰富、能量密度高、燃烧无污染，被公认为是具有广阔前景的新型清洁能源^[3]。水合物通常以孔隙填充、孔隙承载或胶结的形式赋存在沉积物中，改变温压条件或相边界可使其分解为水和气体^[4]。水合物分解产水产气导致沉积物孔压和有效应力改变，同时GHBS固相组分分解改变其强度和刚度，显著影响沉积层的变形特性。该过程导致沉积层变形，可能诱发海床不均匀沉陷、开采井失稳等工程灾害。因此，深入认识水合物分解过程中沉积物的力学和变形特性，对水合物能源安全、高效开采意义重大。

国内外学者针对GHBS变形和强度等力学特性进行了室内三轴试验。Hyodo等^[5]、Kajiyama等^[6]和吴杨等^[7]探究了水合物饱和度、围压、温度等因素对GHBS应力应变关系的影响，指出沉积物矿物成分、颗粒级配和磨圆度等均影响GHBS的三轴剪切行为。Wu等^[8]和颜荣涛等^[9]研究了含不同水合物饱和度砂土的强度特性。鉴于四氢呋喃水合物（THF）与甲烷水合物具有相似的力学特性^[10]，Yun等^[10]、张旭辉等^[11]和刘芳等^[12]探究了不同水合物饱和度、有效围压、反压和温度等条件下，沉积物颗粒级配对含THF水合物沉积物应力变形特性的影响，研究了其强度准则和破坏形式。上述文献主要研究水合物饱和度、围压、制样方法等因素对GHBS力学性质的影响，对含特定水合物饱和度沉积物的特性有了较深入的认识。

为进一步认识水合物分解过程中GHBS的力学特性，考虑分解过程的GHBS三轴试验随之开展。Hyodo等^[13]通过含水合物丰浦砂三轴试验，分析了水合物饱和度、降压速率等对应变的影响。Li等^[14]探究了南海以石英砂为骨料的GHBS降压分解变形特性。Choi等^[15]探究了不同初始应力下GHBS试样降压分解和水压回复过程中的体积应变、强度和破坏差异。现阶段室内三轴试验能够模拟水合物分解过程中GHBS特性响应，但存在一些不足，如人工制样困难、试样可重复性差等；此外不同地区的沉积物类型、应力状态、水合物赋存形态等存在较大差异，仅采用三轴试验难以全面探究其内在规律。建立能反应水合物固相分解效应的应力–时间–应变理论分析模型是研究水合物分解过程中GHBS变形特性的关键。

一些学者结合传统土力学中的非线弹性模型或弹塑性模型，将其应用于GHBS单元体或工程开采数值模拟。基于Duncan-Chang模型，Miyazaki等^[16]根据含水合物丰浦砂三轴试验，建立了刚度与饱和度关系以反映GHBS变形特性^[17]。Uchida等^[18]和Sultan等^[19]在Cam-clay模型基础上，通过修正屈服函数和剪胀函数以考虑水合物饱和度对刚度、剪胀性和强度的影响及体积屈服特性。蒋明镜等^[20]考虑GHBS结构性并以饱和度作为状态变量，将结构性砂土本构应用于GHBS应力应变分析，并进一步发展了水合物沉积物多场耦合离散元方法^[21]。上述模型在传统土力学领域有明确的物理意义和较好的研究基础，对特定水合物饱和度GHBS的应力应变特性具有较好的描述效果，但在描述水合物随时间分解并诱发GHBS力学特性改变的过程时遇到挑战。

综上所述，已有研究在GHBS物理力学特性及降压分解特性试验和特定水合物饱和度GHBS本构模型研究方面均取得了一定进展。但GHBS具有显著的相变性和动态结构性，在构建应力应变关系时需充分考虑固相组分分解演化的影响^[22]，探索能够模拟水合物分解过程中GHBS体积应变随时间变化的理论模型。本文根据水合物分解特性和GHBS力学特征，结合城市固废降解理论^[23-25]思想，将固相分为不可分解的惰性土骨架和可分解的水合物固相，引入随水合物饱和度变化的GHBS压缩参数，建立了能够描述GHBS应力和水合物分解耦合作用、体积应变随时间变化的分析模型。利用该模型模拟了GHBS单元体降压分解试验，对模型进行了初步验证；并针对不同降压速率、降压幅值和水合物分解速率等工况，探讨了GHBS体积应变随分解进程的发展规律。研究成果为水合物降压开采过程中GHBS变形的实时预测提供了新思路。

1.   GHBS体积应变分析模型

1.1   物理过程描述及基本假设

人工开采或地质环境变化时，GHBS孔压或温度条件改变打破水合物的相平衡状态，分解成气体和水，GHBS固相组分减少。目前主流的降压法保持温度不变，将GHBS局部孔压降至相平衡压力以下使水合物分解^[5]。该物理过程与考虑应力和降解作用的城市固废变形过程^[23-25]类似，均可将固相分为不可分解和可分解两部分。与城市固废降解固结理论^[23-25]相比，本文模型特点在于：水合物达到相平衡条件时开始分解，体积应变在孔压降至相平衡点时具有明显的突变性，固废降解过程从填埋场开始堆积就已产生；水合物分解产气过程剧烈，在分解进程上与固废降解不同；水合物分解受外界温度和压力影响敏感，相平衡线附近较小的温压变化幅值便影响分解和重生成进程。

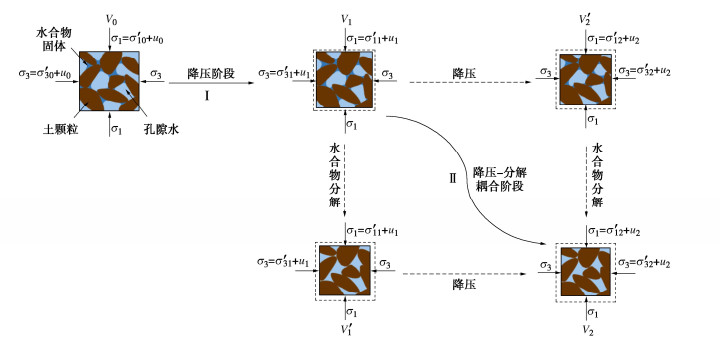
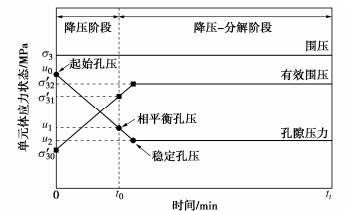
降压分解过程中GHBS的应力和变形特性可利用室内温控三轴试验进行研究。如图 1，假定GHBS初始条件下处于饱和状态，其围压和轴压分别为${\sigma _3}$，${\sigma _1}$，且在试验过程中保持不变；初始孔压为u₀。通过排出孔隙流体的方式降低孔隙压力，在t₀时刻达到相平衡状态，以t₀为分界点，单元体应力状态随时间变化可分为降压和降压-分解两个阶段：①降压阶段，以恒定速率降低孔隙压力，经时间t₀，孔压由初始孔压u₀降至相平衡孔压u₁，此阶段水合物不分解，孔隙流体排出使有效围压由${\sigma '_{30}}$增至${\sigma '_{31}}$，单元体体积由${V_0}$收缩至${V_1}$，如图 2中的路径Ⅰ。②降压-分解阶段，水合物处于分解过程，单元体有效应力不断改变，变形过程复杂，单元体应力及分解路径存在多种可能。假定水合物分解速率与应力水平不相关，该阶段任意时刻应变取决于分解时间和最终有效应力状态，即变形量与应力路径无关。如图 2中路径Ⅱ，虽然t₀至t_t（降压-分解阶段结束时间）间存在多条路径，但最终变形一致。以路径${V_1} \to {V'_1} \to {V_2}$为例，首先考虑水合物分解，然后考虑降压过程。由相平衡孔压u₁降至稳定孔压u₂，有效围压由${\sigma '_{31}}$增至${\sigma '_{32}}$，水合物分解产生水和气体并随着降压过程排出；该阶段体积应变由两部分组成：①一定有效应力下水合物分解导致的体积应变${V_1} \to {V'_1}$；②降压引起的体积应变，即孔隙流体排出引起的体积应变${V'_1} \to {V_2}$。

图  1  单元体应力状态随时间发展

Figure  1.  Change of stress states with time in GHBS

下载: 全尺寸图片 幻灯片

图  2  单元体降压分解过程体积应变路径

Figure  2.  Volumetric strain paths of depressurization process in GHBS

下载: 全尺寸图片 幻灯片

模型的基本假设：①孔隙气不溶于孔隙水，土颗粒、水合物和孔隙水均不可压缩；②不考虑水合物分解吸热导致冰的生成；③水合物分解速率与应力水平不相关；④GHBS在t时刻的总体积应变与应力路径无关，仅与t时刻的应力水平和分解时间（分解程度）相关；⑤不考虑机械作用下物质的相间变化。

本文模型基于有效应力进行计算，采用全量理论，考虑GHBS中水合物的分解特性，根据GHBS降压应力路径得到体积应变与应力和时间的关系。

1.2   公式表达

根据图 2，GHBS降压分解过程中体积应变路径为${V_0} \to {V_1} \to {V_2}$，依次为降压阶段和降压–分解阶段。

（1）降压阶段的体积应变

该过程体积变化路径如图 2中${V_0} \to {V_1}$，降压过程中孔隙流体排出单元体引起体积收缩，此阶段水合物不分解。侧限条件下降压引起的体积应变为^[26]

式中$\varepsilon _{{\text{vol}}}^{{\text{ps}}}$为孔压降低引起的体积应变；C_c为$e - \lg {\sigma '_{\text{v}}}$平面上压缩曲线的斜率；e为试样初始孔隙比；${\sigma '_{\text{v}}}$为侧限条件下的轴向有效应力；$\Delta u$为降压幅值。

单元体降压试验通常在三轴应力状态下进行，考虑体积应变与平均有效主应力$p'$相关。降压速率恒定时，平均有效应力${p'_1}$是时间t的线性函数，不考虑GHBS的蠕变效应，该阶段（$0\le t < {t}_{0}，{t}_{0}=\Delta u/D$）任意时刻t的体积应变为

式中${\varepsilon _{V\left( {0{\text{ - }}1} \right)}}{\text{(}}t{\text{)}}$为t时刻降压引起的体积应变；降压幅值$\Delta u = {u_0} - {u_1}$，D为降压速率，t为降压时间，t₀为单元体由初始孔压降至相平衡孔压所需时间；${p'_0}$为初始平均有效主应力，${p'_0} = ({\sigma '_{10}}{\text{ + 2}}{\sigma '_{30}})/3$，${p'_1}$为相平衡状态时的平均有效主应力，${p'_1} =$${\text{(}}{\sigma '_{11}}{\text{ + 2}}{\sigma '_{31}}{\text{)}}/3$；${e_0}$，${e_1}$为${p'_0}$，${p'_1}$作用下的单元体孔隙比；${\chi _0}{\text{(}}{S_{\text{h}}}{\text{)}}$为考虑初始孔隙比的修正斜率，${\chi _0}{\text{(}}{S_{\text{h}}}{\text{)}} =$${\lambda _0}{\text{/(1 + }}{e_{\text{0}}}{\text{)}}$，${\lambda _0}$为$e - \ln p'$压缩线斜率，与水合物初始饱和度${S_{\text{h}}}$相关；A为体积应变系数，与水合物分布形式相关。

（2）降压–分解阶段的体积应变

a）降压–分解阶段中水合物分解引起的体积应变

GHBS降压分解试验通过不断排出单元体内产生的水和气以维持孔压稳定，考虑分解气全部排出，而分解水体积小于水合物初始体积，单元体体积收缩；此外，水合物分解引起单元体内固相组分减少、土颗粒间胶结作用减弱，造成沉积物骨架弱化和体积收缩。李振赫^[27]通过含水合物石英砂降压分解试验发现甲烷水合物分解产气量与应变呈线性关系；人工制备的GHBS降压分解试验^[28-29]表明产气速率随降压时间逐渐降低直至趋于0，产气量逐渐趋于稳定，基于上述研究，${V_1} \to {V'_1}$过程中水合物分解体积应变可写为

式中${\varepsilon _{V\left( {1{\text{ - }}1}' \right)}}{\text{(}}t{\text{)}}$为$t$时刻水合物分解引起的体积应变；ε_∞为GHBS中水合物完全分解引起的体积应变，该值与水合物初始饱和度${S_h}$和有效围压${\sigma '_{31}}$，${\sigma '_{32}}$相关；C为分解过程中的体积应变速率，与水合物分解速率相关。

b）降压–分解阶段中降压引起的体积应变

孔压降至相平衡压力后，保持降压速率不变继续降至预定孔压u₂，此阶段孔隙流体从单元体内排出，有效球应力作用在软化后的土骨架上导致体积应变：

式中${\varepsilon _{V\left( {1'{\text{ - }}2} \right)}}{\text{(}}t{\text{)}}$为GHBS经历降压时间t-t₀（t₀≤t≤t_t）引起的体积应变；${p'_2}$为降至稳定孔压时试样的平均有效主应力，${p'_2} = ({\sigma '_{12}}{\text{ + 2}}{\sigma '_{32}})/3$；${\chi _t}(t)$为考虑初始孔隙比的修正斜率，反映GHBS的压缩特性，与t时刻单元体内的水合物饱和度相关，是关于时间t的函数，

式中${\chi _\infty }$为水合物完全分解后的沉积物压缩特性参数。

（3）GHBS总体积应变

GHBS降压分解过程的总体积应变分两阶段，图 2中降压阶段Ⅰ的体积应变为式（2）；降压–分解阶段Ⅱ的体积应变${V_1} \to {V_2}$可分为水合物分解体积应变${V_1} \to {V'_1}$和降压体积应变${V'_1} \to {V_2}$两部分，基于全量理论，降压-分解阶段（t₀≤t≤t_t）的体积应变可表示为

式中，${\varepsilon _{V{\text{(0 - 2)}}}}(t)$为${V_1} \to {V_2}$过程中t时刻单元体体积应变。

通过上述计算，降压分解过程中GHBS在任意时刻t的体积应变可基于式（2），（6）计算得到。

1.3   参数定义及确定方法

针对不同水合物饱和度、温度、沉积物类型的GHBS，国内外学者开展了系列三轴试验^[5-16]。本文模型参数可通过GHBS三轴试验和降压分解试验确定。

（1）GHBS完全分解引起的体积应变ε_∞

根据ε_∞的定义，ε_∞可通过一定水合物饱和度和无水合物的沉积物三轴试验确定。含甲烷水合物丰浦砂三轴试验表明^{[5, 16]}，GHBS强度随水合物饱和度和有效围压的增加而增加，温度、孔压等因素对GHBS模量、强度和变形的影响较小。蒋明镜等^[30]离散元模拟表明水合物饱和度较高的试样在低围压下易发生剪胀。根据对南海珠江口盆地水合物储层的钻井探测^[31]，珠江口水合物多以10%~14%和30%~50%的饱和度状态赋存于海床以下约10~200 m厚度范围内的沉积物层，为低饱和度GHBS在高围压条件下赋存，因此用于确定参数ε_∞的两组三轴试验均只考虑体积收缩情况。

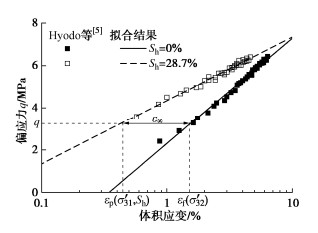
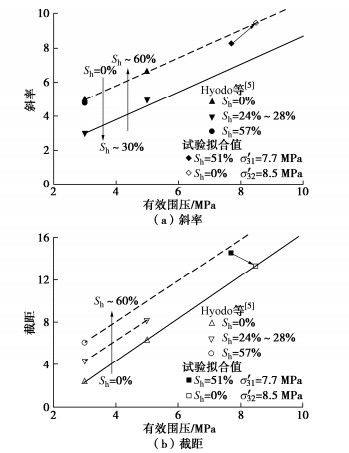
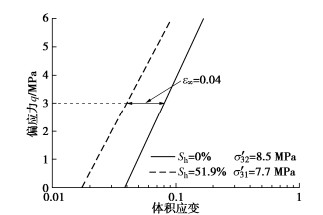
GHBS三轴压缩试验的体积应变与偏应力在半对数坐标系中线性相关，随着水合物饱和度增大、有效围压升高，直线向上平移并偏转。如图 3，水合物降压分解过程中单元体偏应力q不变，ε_∞为

图  3  参数ε_∞确定

Figure  3.  Determination method for parameter ε_∞

下载: 全尺寸图片 幻灯片

式中${\varepsilon _{\text{p}}}({\sigma '_{31}}, {S_{\text{h}}})$为水合物初始饱和度为${S_{\text{h}}}$的GHBS在有效围压${\sigma '_{31}}$下，$\lg {\varepsilon _{\text{v}}} - q$曲线上偏应力q引起的体积应变；${\varepsilon _{\text{f}}}{\text{(}}{\sigma '_{32}}{\text{)}}$为无水合物沉积物在有效围压${\sigma '_{32}}$下，偏应力q引起的体积应变。参数选取时，含水合物试样在水合物生成前初始孔隙比与无水合物试样相同。

（2）GHBS三轴压缩试验$e - \ln p'$曲线修正斜率${\chi _0}$

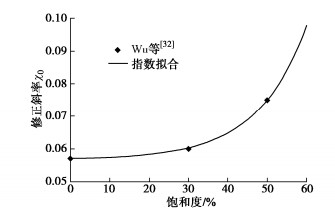
含水合物丰浦砂三轴试验^[32]表明，水合物的存在使临界状态线在$e - \ln p'$平面内平移并旋转，给出了不同饱和度下的临界状态线斜率（图 4）。根据${\chi _0}({S_{\text{h}}}) = {\lambda _0}({S_{\text{h}}})/(1 + {e_0})$得到的修正系数${\chi _0}$随饱和度呈指数形式增长，其拟合公式为

图  4  水合物饱和度对GHBS临界状态线修正斜率${\chi _0}$的影响

Figure  4.  Influences of hydrate saturation on slopes of critical state lines of GHBS

下载: 全尺寸图片 幻灯片

式中，a，b为拟合参数，与沉积物类型及单元体初始孔隙比相关。当饱和度${S_{\text{h}}}$=0时，${\chi _0}({S_{\text{h}}})$退化为水合物完全分解后的沉积物压缩特性参数${\chi _\infty }$。

（3）水合物分解体积应变速率C

式（3）中，水合物分解体积应变速率C可通过GHBS三轴降压分解试验确定，或参考已有试验数据。

2.   模型验证

为验证模型的适用性，将本文模型与Hyodo等^[13]和Choi等^[15]的GHBS降压分解试验进行对比验证。

2.1   Hyodo等^[13]降压分解试验

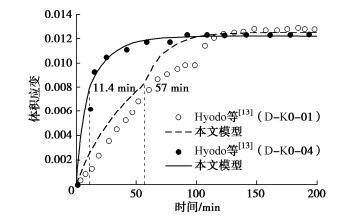
Hyodo等^[13]和李洋辉^[33]选取丰浦砂作为沉积物，人工制备GHBS试样开展了降压分解试验。保持温度恒定，通过降低孔隙压力实现水合物分解。本文选取K₀固结试样降压分解的两组体积应变–时间曲线进行对比，试验条件和试样参数见表 1。

表  1  Hyodo等^[13]试验条件和试样参数

Table  1.  Test conditions of Hyodo et al^[13]

试验名称	孔隙度/%	水合物饱和度/%	降压速率/(MPa·min-1)	偏应力/MPa	孔隙压力/MPa	有效围压/MPa	平均有效主应力/MPa
D-K0-01	39.9	51.9	0.1	3	10→4.3→3.5	2→7.7→8.5	3→8.7→9.5
D-K0-04	39.9	50.1	0.5	3	10→4.3→3.5	2→7.7→8.5	3→8.7→9.5

下载: 导出CSV 

| 显示表格

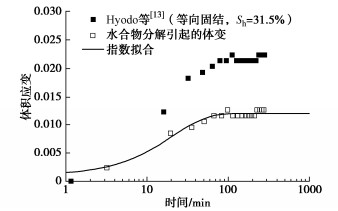
参数选取如下：χ₀和χ_∞参考Wu等^[32]的试验取值；结合等向固结条件下GHBS降压分解试验结果（图 5），对消除降压体积应变影响后的数据拟合，指数系数作为水合物分解体积应变速率C的取值；ε_∞通过有效围压${\sigma '_{31}}$=7.7 MPa和${\sigma '_{32}}$=8.5 MPa的三轴试验拟合得到，见图 6，7。A为体积应变系数，在水合物分布形态相同时取0.1，根据试验数据拟合得到。

图  5  参数C确定

Figure  5.  Determination method for parameter C

下载: 全尺寸图片 幻灯片

图  6  GHBS偏应力–体积应变曲线形态参数

Figure  6.  Morphological parameters of q-ε_v curves of GHBS

下载: 全尺寸图片 幻灯片

图  7  参数ε_∞确定

Figure  7.  Determination method for parameter ε_∞

下载: 全尺寸图片 幻灯片

D-K0-01和D-K0-04两组试验除降压速率和水合物饱和度外，其他条件均相同。模型参数取值如表 2，与沉积物性质和水合物分解特性相关的参数A，χ_∞，ε_∞和C保持不变。两组试验的降压速率为0.1，0.5 MPa/min，对应的t₀值为57，11.4 min；两组试验中GHBS试样初始饱和度为51.9%，50.1%，对应的χ_∞值为0.078，0.075。

表  2  模型参数

Table  2.  Model parameters of Hyodo et al

A	χ∞	ε∞	C/min-1
0.1	0.057	0.04	0.056

下载: 导出CSV 

| 显示表格

本文模型结果与试验结果^[13]对比如图 8，体积应变随降压和水合物分解逐渐增大并趋于稳定。模型能反映水合物降压分解的两个特性：①孔压降至相平衡压力前，试样体积随孔隙压力的降低而减小，这是由于水合物分解前试样体积变化源于孔隙水的排出^[33]，当降压速率较大时，体积应变呈近线性减小；②当孔压降至相平衡压力以下时，水合物胶结作用随分解的进行逐渐减小，直至消失。分解产生的水和气被排出试样，土颗粒在有效围压作用下排列更紧密，体积变形随水合物分解逐渐增大^[33]。模型可有效表征水合物开始分解后体积应变速率突变，能反映水合物分解对体积应变的贡献，与试验结果吻合较好。

图  8  本文模型模拟结果与Hyodo等^[13]试验对比

Figure  8.  Comparison of results by proposed model and tests^[13]

下载: 全尺寸图片 幻灯片

2.2   Choi等^[15]降压分解试验

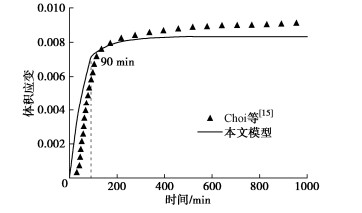
Choi等^[15]开展了含水合物硅砂降压分解三轴试验，试验条件和试样参数见表 3。

表  3  Choi等^[15]试验条件和试样参数

Table  3.  Test conditions of Choi et al^[15]

试验名称	孔隙度/%	水合物饱和度/%	降压速率/(MPa·min-1)	偏应力/MPa	孔隙压力/MPa	有效围压/MPa	平均有效主应力/MPa
#2	37	40.4	0.024	1.5	5.52→3.36→3	0.69→2.85→3.21	1.19→3.35→3.71

下载: 导出CSV 

| 显示表格

参数选取如下：t₀为试验中降压幅值与降压速率的比值；χ₀和χ_∞根据单元体初始孔隙比获得；水合物分解系数C参考已有试验数据；ε_∞通过GHBS在有效围压${\sigma '_{31}}$=2.85 MPa和${\sigma '_{32}}$=3.21 MPa时的三轴压缩试验得到。模型参数取值如表 4。如图 9所示，降压阶段体积应变迅速上升，t₀时刻后随着降压完成和水合物分解体积应变趋于平缓。由于缺乏相应的物理力学特性试验数据，在确定参数ε_∞时选用了含水合物丰浦砂的三轴试验数据^[5]，与含水合物硅砂的应力应变特性存在一定差异，导致模型预测的体积应变稳定值与试验结果存在偏差，但总体上与试验结果^[15]较一致。

表  4  模型参数

Table  4.  Model parameters of Choi et al^[15]

A	t0/min	χ0	χ∞	ε∞	C/min-1
0.1	90	0.069	0.059	0.006	0.011

下载: 导出CSV 

| 显示表格

图  9  本文模型模拟结果与Choi等^[15]试验对比

Figure  9.  Comparison of results by proposed model and tests^[15]

下载: 全尺寸图片 幻灯片

3.   水合物分解时GHBS体积应变特性

水合物降压开采时，降压速率、降压幅值和水合物分解速率等参数是重要控制指标，对开采效率和储层变形及稳定性影响显著。本节通过算例分析了降压速率、降压幅值和水合物分解速率对GHBS体积应变的影响，为工程中的水合物安全稳定开采提供参考。

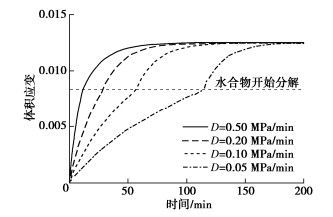
图 10展示了水合物降压分解过程中降压速率D对GHBS体积应变的影响。孔压达到相平衡压力前，降压速率越低孔隙流体排出速度越慢，降压阶段体积应变上升速度越慢，说明较低的降压速率有利于开采前期GHBS稳定，但由初始孔压降至水合物相平衡孔压所需时间随之增加。反之较大的降压速率加快了孔隙流体排出，GHBS体积应变增长较快导致变形发展迅速；同时水合物经历较短降压时间后开始分解，缩短了水合物分解所需的总时长。工程中选择合适的降压开采速率可以平衡储层稳定性和开采效率之间的矛盾。对于较低的降压开采速率，水合物开始分解时体积应变速率突然增大并在降压-分解阶段初期保持着高应变速率，需要在实际开采过程中监测该阶段储层变形响应，防止储层变形过大或变形发展过快对上覆开采平台等生产设施稳定性产生影响。

图  10  降压速率D对体积应变的影响

Figure  10.  Influence of depressurization rate D on volumetric strain of GHBS

下载: 全尺寸图片 幻灯片

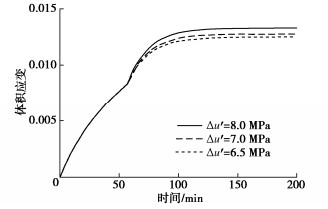
图 11比较了降压幅值$\Delta u^{\prime}=u_0-u_2$对水合物分解过程中GHBS体积应变的影响。随着稳定孔压u₂降低，降压幅值增大，有效应力增加使更多孔隙流体被排出，试样被压缩的更加紧密，体积应变稳定值随之增加，该现象与李洋辉^[33]的三轴试验结论一致。产气量随稳定孔压的降低而增大，水合物开采效率提高^[28]。现场开采时，开采结束后储层内较低的孔压与周围环境形成压力差，海水渗入引起孔压升高、有效球应力降低，可能造成储层回弹变形^{[13, 33]}。稳定孔压越低，水回复过程中有效应力增长幅值越大，储层可能的回弹变形越显著。本文模型能够预测不同降压幅值时的最终变形量，为水合物开采稳定孔压设计提供依据，满足生产经济性的同时确保地层变形在合理范围。

图  11  降压幅值$\Delta u'$对体积应变的影响

Figure  11.  Influences of pore pressure reduction $\Delta u'$ on volumetric strain of GHBS

下载: 全尺寸图片 幻灯片

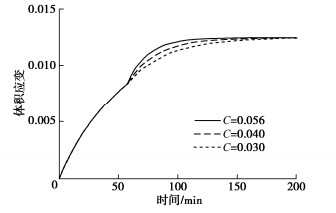
由图 12知，水合物分解体积应变速率C增加，降压–分解阶段的体积应变曲线变陡，但最终值不变。降压开采条件不变时，不同粒径组成的沉积物影响分解产气量和产气速率^[29]，即水合物分解体积应变速率C改变，实际生产中水合物分解区域沉积物类型存在差异，将导致降压分解过程中储层的体积应变发展不一致，本文模型可用于预测同一时刻不同水合物分解体积应变速率C引起的储层不均匀沉降。

图  12  水合物分解速率C对体积应变的影响

Figure  12.  Influences of hydrate dissociation rate C on volumetric strain of GHBS

下载: 全尺寸图片 幻灯片

4.   结论

本文基于水合物分解特性和GHBS基本力学特征，将固相骨架分为不可分解的惰性土骨架和可分解的水合物固相，引入随水合物饱和度变化的压缩参数，建立了一个能够描述GHBS应力和水合物分解耦合过程的体积应变分析模型。并针对不同降压速率、降压幅值和水合物分解速率等工况，探讨了GHBS体积应变随分解进程的发展规律。

（1）本文模型表达简洁，参数物理意义明确，所有参数均可通过三轴压缩试验或分解试验获得；通过与已有GHBS室内降压分解试验^{[13, 15]}对比，验证了模型的适用性。模型能够反映水合物降压分解试验过程中的GHBS体积应变特性，为水合物降压开采过程中储层变形的实时预测提供了新思路。

（2）本文模型将水合物降压开采过程分为降压和降压–分解两个阶段：①降压阶段，体积应变随降压速率变化；②降压–分解阶段，体积应变趋势可用指数形式表征。分阶段模型能够反映开采压力降至相平衡压力后水合物分解导致的体积应变速率突变，能较好地描述降压和水合物分解引起的体积应变特性。

（3）降压开采过程中降压速率、降压幅值和水合物分解速率对储层变形特性影响显著：降压速率增大，降压阶段体积应变速率增大，达相平衡时间缩短，最优降压速率应综合考虑开采过程中储层变形速率和开采效率间的关系；降压开采稳定孔压影响储层最终沉降量，降低稳定孔压可以提高开采效率，但最终变形量增大；不同类型的沉积物水合物分解速率存在差异，水合物分解速率对储层变形速率影响明显。

（4）GHBS试验难度较大、不确定性强，基础试验数据相对缺乏，本文假定还有待进一步验证和完善；部分地区的GHBS在试验中表现出剪胀和应变软化行为，本文模型目前尚未考虑该特性，后续将基于更全面的典型试验对模型进一步完善以提高其普适性。