Application of improved Picard method in unsaturated seepage
-
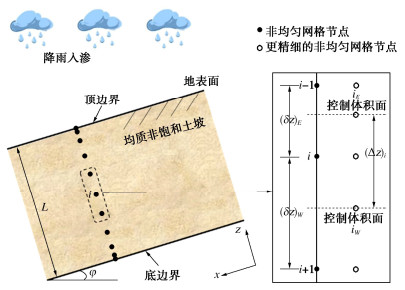
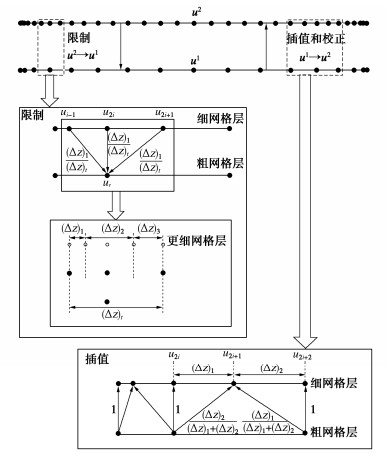
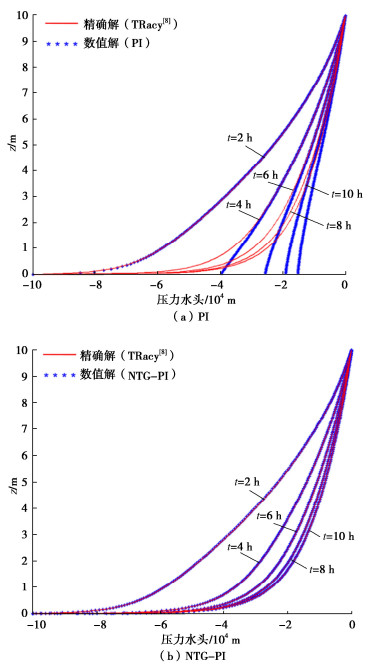
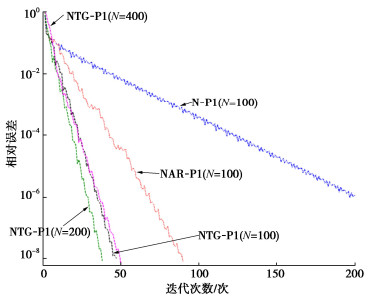
摘要: Richards方程广泛应用于非饱和渗流的数值模拟以及其他相关领域。在数值求解中，可以采用有限体积法进行数值离散，进而采用Picard方法进行迭代求解。然而，为了获得可靠准确的数值解，通常均匀网格的空间步长是很小的，特别是在一些不利的数值条件下，比如降雨入渗于干燥土壤中，这往往使得迭代过程耗时，甚至不收敛。因此，结合Chebyshev形式的非均匀网格，提出了一种基于非均匀网格的两层网格校正法的改进Picard迭代方法（NTG-PI）。通过3个非饱和渗流算例，并与传统方法和解析解对比，对改进方法的数值精度、收敛率和加速效果进行了验证。结果表明，相对于传统的Picard方法和自适应松弛Picard方法，提出的方法NTG-PI可以在较少的离散节点数下获得较高的数值精度，以及较高的计算效率。该方法可以对非饱和渗流的数值模拟提供一定参考。Abstract: Richards' equation is widely used in the simulation of unsaturated seepage and related fields. In the numerical solution, the finite volume method can be used for numerical discretization, and then the Picard method can be used for iterative solution. However, in order to obtain reliable and accurate numerical solutions, the spatial step size of a uniform grid is usually very small, especially under some unfavorable numerical conditions, such as rainfall infiltration into dry soil, which often makes the iterative process time-consuming or even unable to converge. Therefore, combined with the non-uniform grid in the form of Chebyshev, an improved Picard iteration method (NTG-PI) is proposed based on the non-uniform two-grid correction scheme. Through three examples of unsaturated seepage, the numerical accuracy, convergence rate and acceleration effect of the improved algorithm are validated by comparing the traditional methods and analytical solutions. The results show that compared with the traditional Picard and the adaptive relaxation Picard methods, the proposed method NTG-PI can obtain higher numerical accuracy with a smaller number of discrete nodes, and also has higher computational efficiency. The proposed method can provide a reference for the numerical simulation of unsaturated seepage.
-
0. 引言
深部裂隙岩体不仅力学性质展现出完全不同于浅部岩体的力学特征，而且所处应力环境也发生改变[1]，例如常受到由矿震、爆破、顶板断裂或断层滑移等形式产生的冲击载荷作用[2]。生产实践表明，冲击载荷作用下深部裂隙岩体的失稳灾变与内部裂隙的扩展、贯通息息相关，而锚杆在裂隙岩体中表现为明显的锚固效果[3]。但目前对冲击载荷作用下锚杆对岩体裂隙锚固作用机制尚未完全了解。因此，有必要研究冲击载荷作用下预应力锚杆对裂隙岩体的控制作用，以期为揭示冲击载荷作用下裂隙岩体锚固机制奠定基础。
国内外学者在锚杆对裂隙岩体锚固机理方面开展了大量研究。张波等[4]认为锚杆具有增强含交叉裂隙节理岩体抵抗裂隙扩展的能力；周辉等[5]通过对预制裂隙试件进行单轴压缩试验，提出锚杆对裂隙扩展的“轴压”作用机制；王平等[6]通过对预制锚固单排裂隙试件进行单轴破断试验，提出了主控裂纹的概念，认为在有效锚固范围内锚杆能延迟主控裂纹产生和提高裂隙试件强度；武东阳等[7]通过试验发现锚杆有利于降低裂隙岩体中拉伸裂纹萌生和扩展时的应力强度因子，能够限制拉伸/剪切裂纹的萌生和扩展；蒋宇静[8]通过开展系列锚固类岩石材料剪切试验，认为不同CNS（constant normal stiffness）边界条件下锚杆剪切破断后都呈现“Z”字型的变形特征，且锚杆的变形范围随着法向刚度的增加而逐渐减小。工程实践表明，锚杆支护在裂隙岩体中表现出明显的“销钉”加固作用，冲击动载作用下裂隙岩体与锚杆间相互作用关系有必要深入探讨。
除受静载作用外，地下岩体还常受到冲击载荷（由爆破、断层滑移或顶板断裂等产生）的作用，特别是深部地下工程岩体，在冲击动载作用下锚固系统破坏特征与静载条件有着显著差异[9-10]。吴拥政等[11]认为冲击载荷作用下，巷道锚固围岩受反复拉压作用，导致锚固系统锚固性能降低与失效；邱鹏奇等[12]通过开展加锚岩体冲击动载试验，提出了锚杆“抗冲时效”概念，认为抗冲时效与岩石/锚固剂和锚固剂/锚杆之间不协同变形直接相关；Wu等[13]通过对红砂岩进行冲击动载试验，认为锚杆通过分担试件的动态拉伸应力提高了锚固体的动态抗拉强度；在此基础上，李壮等[14]、宁建国等[15]提出高预应力、全长锚固有利于抑制动载作用下岩体裂纹激活，延缓主裂纹形成时间，提高了锚固体的动态抗拉强度与弹性模量，初步从裂隙扩展角度分析了动载作用下锚杆对围岩的加固作用。
本文利用分离式霍普金森压杆装置对锚固CCNBD试件进行冲击试验，试验测试不同预紧力、锚固方式等因素对锚固试件动态断裂韧性、裂纹扩展速度以及锚杆轴力的影响规律，获得不同预应力、锚固方式等条件下锚杆对CCNBD试件裂纹起裂、扩展阻碍作用特征，探讨预应力锚杆对裂隙岩体的抑损阻裂效应。
1. 加锚圆盘动态巴西劈裂试验
1.1 试件制备及试验方案
室内试验所用试样取自山东新河煤矿-980水平运输大巷同一层位的粉砂岩，试样密封后运送至山东科技大学实验室。
依据ISRM标准测试委员会1995年颁布的岩石类材料CCNBD（cracked Chevron notched Brazilians disc）断裂韧性测试标准制备试件[16]；在试件中部预制厚度为1 mm的人字形直切槽（代表原生裂隙），钻取直径r为4.2 mm的锚杆孔，如图 1所示，试件尺寸见表 1。
表 1 试件制备尺寸Table 1. Sizes of specimen直径D/mm 厚度B/mm 直切槽初始尺寸a0/mm 直切槽最终尺寸a1/mm 刀具半径as/mm 50 25 7 19 20 锚杆材料为直径3 mm的高强度螺纹钢，螺母、垫片均采用相同材质的钢材，具体力学参数见表 2。选用弹簧模拟让压结构，锚固剂材料选用环氧树脂胶。
表 2 锚固系统力学参数Table 2. Mechanical parameters of anchoring system锚杆类型 直径/mm 延伸率/% 弹性模量/GPa 抗拉强度/MPa 屈服强度/MPa 现场锚杆 18 ≥20 200 ≥490 ≥335 模拟锚杆 3 ≥40 193 ≥515 ≥205 1.2 试验方案与设备
（1）试验方案
依据试验目的设计试验方案，共设计两类试验，具体如下：
a）不同预紧力矩加锚岩体。利用机械式扭矩扳手为端头锚固试件分别施加0，2，4，6，8，10 N·m预紧力矩，与现场实际预紧力矩对照见表 3，每组制备3个试件。
表 3 预紧力矩对照Table 3. Comparison of preloading torques(单位: N·m) 实验室预紧力矩 0 2 4 6 8 10 现场预紧力矩 0 40 80 120 160 200 b）不同锚固方式加锚岩体。共设置无锚、端头锚固、全长锚固、让压+端头锚固4种锚固方式。其中，无锚试件作为空白对照组；其余试件均施加6 N·m预紧力矩，全长锚固与端头锚固的锚固长度分别为50，20 mm，选用弹簧模拟让压结构。每种锚固方式均制备3个试件，具体试验方案见表 4。
表 4 试验方案Table 4. Test programs试件编号 厚度D/mm 直径B/mm 预紧力矩/(N·m) 锚固方式 W-0-1 25.0 50.0 0 无锚 W-0-2 25.0 50.0 W-0-3 25.1 50.0 D-0-1 24.9 50.0 0 端头锚固 D-0-2 25.0 50.1 D-0-3 25.0 50.0 D-2-1 25.0 50.0 2 端头锚固 D-2-2 25.0 50.0 D-2-3 25.0 49.9 D-4-1 25.1 50.0 4 端头锚固 D-4-2 25.0 50.0 D-4-3 25.0 50.0 D-6-1 24.8 50.1 6 端头锚固 D-6-2 25.0 50.0 D-6-3 25.0 50.0 D-8-1 25.1 50.0 8 端头锚固 D-8-2 25.0 50.0 D-8-3 25.0 50.0 D-10-1 25.0 49.8 10 端头锚固 D-10-2 25.1 50.0 D-10-3 25.0 50.1 Q-6-1 25.0 50.0 6 全长锚固 Q-6-2 24.9 49.9 Q-6-3 25.0 50.0 R-6-1 25.0 50.0 6 让压+端头锚固 R-6-2 25.0 50.0 R-6-3 24.9 50.0 在预制裂缝尖端处粘贴10栅裂纹扩展应变片（CPG1）监测裂纹扩展速度；锚杆中部粘贴应变片（SG3）监测锚杆轴力变化，试验所需加锚岩体及应变片布置如图 2所示。
（2）试验设备
采用分离式霍普金森压杆（SHPB）试验系统开展加锚岩体冲击动载试验，如图 3所示，入射杆、透射杆、吸收杆直径均为50 mm，由高强度钢制备，入射杆与透射杆长3 m，吸收杆长1.5 m。为减少波形弥散，采用梭形子弹进行半正弦应力脉冲加载，其尺寸与ISRM所建议值保持一致。数据采集系统包括光电测速仪、高速动态采集仪、超高速数字摄像机。入射杆与透射杆均粘贴应变片（SG1、SG2），应变片与入射杆、透射杆端部相距1500 mm。
SHPB试验系统动力源为压缩氮气，通过控制气压调节子弹撞击速度。本次试验为保证试件的破坏程度，经测试，选定0.1 MPa气压。试验结果显示，此气压下冲击速度为6.358~6.6 m/s，速度浮动在3.8%以内。
（3）数据处理方法
SHPB试验系统简图及应力波波形如图 4所示，应用高速动态采集仪得到的入射波、反射波、透射波脉冲信号，依据三波法计算冲击载荷下的动态应变ε(t)、应变率˙ε(t)、应力σ(t)：
ε(t)=c0D∫t0[εi(t)−εr(t)−εt(t)]dt， (1) ˙ε(t)=c0D[εi(t)−εr(t)−εt(t)]， (2) σ(t)=AE2πDB[εi(t)+εr(t)+εt(t)]。 (3) 式中：c0为压杆的弹性波速（m/s）；D为试样的直径（m）；B为试件厚度（m）；εi(t)，εr(t)，εt(t)分别为入射波、反射波及透射波在独立传播时的时程应变；E为杆体弹性模量（GPa）；A为杆体横截面积（m2）。
2. 加锚岩体动态断裂韧性
2.1 动态断裂韧性的确定
断裂韧性可表征材料阻止裂纹扩展的能力[17]，确定在冲击动载条件下加锚岩体的动态断裂韧性，可判定预应力锚杆对岩石基体的增韧效应。根据断裂力学基本原理，加锚岩体动态断裂韧性的失稳点在最大载荷Pmax处，即
dσdt=0。 (4) 将试验获得的试件最大载荷代入ISRM推荐的测试公式[16, 18-21]，可得到动态断裂韧性：
Kid=PmaxB√RY∗min。 (5) 式中：Kid为动态断裂韧性；Pmax为动载冲击下试件所受的最大外载；B为试件厚度；R为试件半径；Y∗min为无量纲应力强度因子，Y∗min=u⋅ev⋅α1，其中待定系数u、v可利用试件几何参数计算获得，具体求解过程参考ISRM建议[16]。依据ISRM建议的方法，计算获得u=0.265404，v=1.730564。
2.2 不同加锚岩体动态断裂韧性的差异
利用SHPB试验设备开展加锚岩体动态冲击试验。图 5为监测获得的应力脉冲信号，入射波、反射波应力脉冲信号之和与透射波相等，表明试件两端达到了应力平衡。
通过三波法计算加锚岩体典型动态应力-时程曲线如图 6所示，图 7为加锚岩体平均峰值应力，结合式（5），计算获得加锚岩体的动态断裂韧性。相应计算结果如图 8所示。
由图 8（a）可知，对于端头锚固试件，随着预紧力矩增加，加锚岩体的动态断韧性呈近线性关系增加，可知高预紧力矩可提高加锚岩体动态断裂韧性，如预紧力为10 N·m，动态断裂韧性均值提高至11.99 MPa·m1/2，比0 N·m预紧力试件提高了86.7%，其主要原因为提高预紧力矩使加锚岩体产生沿锚杆轴向的约束力，加锚岩体裂纹扩展时，需克服其自身阻抗与锚杆轴向约束力。
由图 8（b）可知，全长锚固试件动态断裂韧性均值为10.28 MPa·m1/2，比端头锚固试件提高了7.34%。锚杆发挥主动约束的核心是通过锚固界面剪应力约束基岩产生相对形变，其大小正比于锚固长度。相比于端头锚固方式，全长锚固方式轴向约束得到强化，试件动态断裂韧性更高，预应力锚杆的作用更加显著。相比而言，让压+端头锚固试件动态断裂韧性均值为8.78 MPa·m1/2，比端头锚固试件下降8.26%。冲击动载作用下，让压结构的强变形能力为裂纹的张开提供了一定的补充空间，加锚岩体动态断裂韧性相对降低。
3. 不同加锚岩体裂纹扩展时程特征
裂纹扩展应变片作为裂纹监测的重要方法，其原理如图 9所示。加锚岩体裂纹扩展导致应变片电阻丝断裂，引起电压信号升高，相邻两次波动信号时间差Δti为裂纹扩展所需时间。裂纹扩展应变片第一栅置于预制裂纹尖端处，裂纹尖端至试件边缘为6 mm，取前6组监测数据为有效数据进行分析。
以加锚岩体初次受载时间作为零点，分析裂纹扩展应变片监测数据，获得不同加锚岩体的裂纹扩展时程曲线，如图 10，11所示。因加锚岩体为煤系粉砂岩制备而成，是典型不均匀脆性材料，该材料内部含有不规则的裂隙与多种粒径不一的颗粒，裂纹扩展过程中易于向材料局部强度较低的区域偏折[22]，导致电压信号在原有变化趋势上存在一定范围的波动，属于正常现象。
![]()
图 10 不同预紧力矩下加锚岩体典型裂纹扩展时程曲线Figure 10. Typical time-history curves of crack expansion of anchored rock mass under different preloading torques通过超高速摄像机及数字散斑获得冲击载荷作用下加锚岩体表面主应变云图，监测结果如图 10，11所示。加载初期，动态载荷产生的动态拉伸应力作用于试件中部，在预制裂隙上下两侧形成中部高两端低的应力区，冲击载荷继续增加，裂纹尖端开始出现应变积聚，此时微裂纹开始发育，当裂隙尖端处岩石基体与预应力锚杆形成的应力场无法抵抗冲击载荷形成的动态拉伸应力时，加锚岩体宏观裂纹开始发育扩展。由图 10可知，随着加锚岩体预紧力的增大，加锚岩体表面主应变的最大值逐渐减小，说明在裂纹发育扩展过程中，预应力锚杆通过自身的作用约束岩石基体，使其在受到同等冲击载荷时，产生较小的应变，维持自身稳定性，这种作用程度与预应力锚杆所施加的预紧力矩呈正相关。由图 11可知：在相同预紧力矩下，加锚岩体采用全长锚固时的主应变最大值小于端头锚固，分析认为预应力锚杆与岩石基体充分锚固时，岩石基体的应变可以由锚杆大幅度承担，相比端头锚固存在相应长度的自由端，可以更大程度地约束岩石基体变形；让压结构的强变形能力大幅度弱化了锚杆的约束作用，使得加锚岩体采用让压+端头锚固时的最大主应变高于端头锚固。
![]()
图 11 不同锚固方式加锚岩体典型裂纹扩展时程曲线Figure 11. Typical time-history curves of crack expansion of anchored rock mass by different anchoring methods由图 12（a）可知，当预紧力矩由0 N·m增加至10 N·m，端锚试件裂纹平均起裂时间由2 μs变为18.4 μs，延缓了89.1%，说明高预紧力矩有利于锚杆抑制裂纹起裂。由图 12（b）可知，全长锚固试件的裂纹起裂时间比端头锚固试件延缓60.54%，让压+端头锚固比端头锚固试件提前2.74%，可知全长锚固有利于抑制裂纹起裂，强变形能力的让压结构会削弱预应力锚杆对裂纹起裂的抑制作用。分析认为，在初期加载时，预应力锚杆通过施加的预紧力及锚固界面提供的剪应力对预制裂隙尖端形成锚杆轴向压应力，形成“轴压紧固”效应，抑制裂纹起裂，高预紧力矩及全长锚固方式会强化此效应。
4. 不同加锚岩体裂纹动态扩展速度
裂纹扩展速度是衡量裂纹扩展、延伸快慢的重要指标。将第3节得到的裂纹扩展单位时间Δti代入下式获得裂纹扩展速度：
vi=ΔlΔti。 (6) 式中：vi为单位长度内裂纹扩展速度（m/s）；Δl为裂纹扩展应变片相邻电阻丝间距取1 mm；Δti为单位长度裂纹扩展所需时间（s）。
图 13为距裂纹尖端不同位置处裂纹扩展速度，图 14为不同预紧力矩及锚固方式下加锚岩体的裂纹平均扩展速度。
![]()
图 13 加锚岩体典型裂纹扩展速度与裂纹尖端位置关系曲线Figure 13. Typical crack expansion rate of anchored rock mass versus position of crack tip![]()
图 14 不同预紧力矩与锚固方式下裂纹平均扩展速度Figure 14. Average crack expansion speeds under different preloading torque and anchoring method由图 13可知，不同加锚岩体均具有相似的裂纹扩展速度变化趋势。在冲击载荷初步加载时，岩体裂隙尖端会发生应变能积聚，随着冲击载荷加载，裂隙尖端裂纹开始扩展，此时积聚应变能释放，裂纹扩展速度急剧增长，随着应变能释放，裂纹扩展速度逐渐下降并趋于平缓。
由图 14（a）可知，预紧力矩与裂纹平均扩展速度之间呈现近线性负相关。端头锚固试件（10 N·m）裂纹扩展的平均速度为89.1 m/s，比端头锚固试件（0 N·m）减缓33.7%。由此可见高预紧力可显著降低裂纹扩展速度，强化锚杆阻裂的能力。
由图 13（b）可知，在同等预紧力矩下，全长锚固试件裂纹平均扩展速度为89.7 m/s，比端头锚固试件减缓13.7%；让压+端头锚固裂纹扩展平均速度为123.6 m/s，比端头锚固试件（6 N·m）增幅37.8%。表明在施加同等预应力的条件下，全长锚固试件的阻裂效应优于端头锚固试件，而让压结构的存在会削弱预应力锚杆的阻裂效应。
5. 加锚岩体裂纹扩展过程中锚杆轴力变化规律
冲击载荷作用时，加锚岩体因动载应力波在轴向产生动态拉应力（垂直于加载方向），锚杆因拉伸变形而微应变增加。故通过粘贴于锚杆中部的应变片监测锚杆的轴向拉伸应变，考察动载冲击时锚杆受载状态。图 15，16为不同加锚岩体锚杆微应变（SG3）的时程曲线。图 15，16中锚杆微应变时程曲线斜率越大，锚杆轴力增长越明显。因锚杆-围岩协同变形受载，故利用锚杆微应时程曲线的斜率表征预应力锚杆阻裂效应的发挥程度。
![]()
图 15 不同预紧力矩典型加锚岩体轴力时程曲线Figure 15. Time-history curves of axial force of anchored rock mass under different preloading moments![]()
图 16 不同锚固方式典型加锚岩体轴力时程曲线Figure 16. Time-history curves of axial force of a typical anchored rock mass by different anchoring methods由上述分析可知，锚杆的阻裂效应主要为“轴压紧固”效应，“轴压紧固”效应主要由施加的预紧力及加锚岩体受载时锚杆与岩石基体之间的剪应力提供。由图 15，16可知，不同加锚岩体锚杆微应变时程曲线趋势近似相同，可依次划分为裂纹孕育阶段、裂纹扩展阶段、锚杆承载阶段。每个阶段对应的预应力锚杆阻裂效应存在差异性，现分析如下：
（1）第Ⅰ阶段为裂纹孕育阶段。冲击载荷作用初期，锚杆轴力（以轴向应变表征）缓慢增加，说明岩石基体黏聚力足以抵御裂纹扩展，“轴压紧固”效应主体为预紧力，锚固界面无明显变形，剪应力随冲击载荷加载逐渐发挥作用但是在此阶段作用并不显著，如图 17（a）所示。
![]()
图 17 加锚岩体冲击动载加载过程示意图Figure 17. Time-history curves of axial force of a typical anchored rock mass by different anchoring methods（2）冲击载荷继续加载，裂纹起裂，进入裂纹扩展阶段。此阶段加锚岩体基体承载能力降低，裂纹尖端区域凝聚力逐渐减弱，锚杆因受拉变形而载荷持续增加。在此阶段，锚杆与岩石基体间的变形量增大，锚固界面剪应力逐渐成为“轴压紧固”效应的主体，如图 17（b）所示。
（3）随着裂纹持续扩展，加锚岩体裂纹扩展贯通，进入锚杆承载阶段。此阶段，破裂面贯穿整个锚固试件，岩石基体凝聚力消失，锚杆将劈裂岩石锚固在一起继续抵抗外部冲击荷载，加锚岩体仍具有承载能力，锚杆成为外部载荷承载主体，随着外载的持续增加，锚杆继续被拉伸，其轴力也继续增加。在此阶段，岩石基体已经贯穿失效，初始施加的预紧力失去效果，此时的“轴压紧固”效应仅为锚固界面提供的剪应力，且随着冲击载荷的继续增加，逐渐达到锚固界面抗剪强度，锚固界面逐渐滑移失效，所提供的“轴压紧固”效应减弱，如图 17（c）所示。
以上分析可知，锚杆峰值应变可表征锚杆阻碍裂纹扩展的程度。由图 15，16可知，端头锚固试件的锚杆峰值应变集中在（2800~3000）×10-6，全长锚固试件的锚杆峰值应变为6251.7×10-6，让压+端头锚固试件的锚杆峰值应变为1235.8×10-6。分析认为，增加锚固段长度，可以强化锚固界面的承载能力，延长锚杆与岩石基体协同变形的时间，增强预应力锚杆的阻裂效应；端头锚固增加让压结构，增加了锚杆的变形能力，使其适应瞬时变形而并不脱锚，但锚杆自身轴向延伸量的减少也就意味着锚杆阻碍裂纹扩展能力的弱化。因此，全长锚固阻裂效应优于端头锚固优于让压+端头锚固。
6. 结论
本文利用SHPB动载冲击试验系统，开展不同预紧力矩、锚固方式的加锚CCNBD试件冲击动载试验，从动态断裂韧性、裂纹起裂时间及裂纹扩展速度等方面，分析预应力锚杆对裂纹扩展的阻裂效应，得到以下3点结论。
（1）全长锚固、端头锚固、让压+端头锚固等锚固方式均强化锚固岩体的韧性，其中全长锚固强化作用最明显。此外，提高锚杆预紧力矩也助于提升锚固岩体的韧性，试验发现端头锚固（预紧力矩10 N·m）动态断裂韧性比端头锚固（0 N·m）提高86.7%。
（2）预应力锚杆的阻裂作用不仅体现在延缓锚固岩体裂纹起裂，同时表现为阻碍裂纹的扩展。试验发现全长锚固的阻裂效应优于端头锚固，而让压结构的存在削弱了预应力锚杆的阻裂效应。
（3）冲击载荷作用下加锚岩体变形破坏过程具有裂纹孕育阶段、裂纹扩展阶段、锚杆承载阶段等3个阶段，高预紧力与全长锚固有利于锚杆发挥“轴压紧固”作用，使其阻碍裂纹扩展，强化了锚固阻裂效应。
-
![]()
图 1 基于非均匀网格节点均质土坡的有限体积法和一维入渗模型的示意图
Figure 1. Schematic drawing of control volume method based on non-uniform grid nodes and 1D infiltration model for homogeneous soil slope
![]()
图 2 非均匀两层网格校正方法的示意图
Figure 2. Schematic drawing of non-uniform two-grid correction scheme
![]()
图 3 不同迭代方法下获得的数值解和精确解的比较
Figure 3. Comparison between numerical solutions obtained using different iteration methods and exact solutions
![]()
图 4 比较不同迭代方法的收敛率
Figure 4. Comparison of convergence rates for different iteration methods
![]()
图 7 两层土质边坡压力水头的计算剖面
Figure 7. Computed profiles of pressure head for two-layer soil slopes
表 1 t = 6 h时不同方法的数值精度对比
Table 1 Comparison of numerical accuracy of different methods at t = 6 h
数值离散条件 RSE RE/% MRE/% N Δt PI NTG-PI PI NTG-PI PI NTG-PI 100 0.10 0.135 1.6×10-2 5.87 1.330 55.03 2.98 0.05 0.138 9.1×10-3 6.70 0.570 55.44 3.25 0.01 0.141 5.9×10-3 7.35 0.032 55.76 3.46 200 0.10 0.121 1.5×10-2 4.67 1.460 56.32 1.87 0.05 0.123 7.7×10-3 5.52 0.710 56.75 0.94 0.01 0.126 2.0×10-3 6.19 0.100 57.09 0.83 400 0.10 0.090 1.5×10-2 2.57 1.490 53.15 1.86 0.05 0.093 7.7×10-3 3.44 0.740 53.67 0.93 0.01 0.095 1.6×10-3 4.14 0.130 54.09 0.18 
下载: 导出CSV
表 2 在N= 100时比较改进方法相对于N-PI的加速比
Table 2 Comparison of speed-up ratios of improved schemes relative to N-PI when N= 100
条件 加速比 Δt SN - PI/NAR - PI SN - PI/NTG - PI 0.1 h 3.33 46.69 0.05 h 1.72 25.99 0.01 h 1.07 14.12
下载: 导出CSV
表 3 参数拟合值
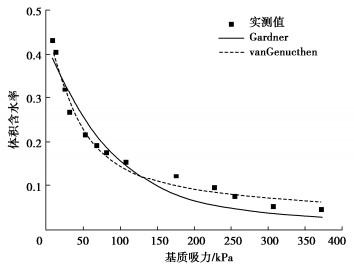
Table 3 Fitting values of parameters
模型 θr θs |α| β n R2 Gardner 0.02 0.43 0.011 — — 0.945 van Genuchten 0.02 0.43 — 0.014 1.74 0.953
下载: 导出CSV
表 4 比较不同SWCCs下改进方法相对于N-PI的加速比
Table 4 Comparison of speed-up ratios of improved schemes relative to N-PI under different SWCCs
条件 加速比SN - PI/NTG - PI N Gardner van Genuchten 120 1.66 1.38 240 2.39 2.30 480 3.35 4.23
下载: 导出CSV
表 5 两层土质边坡的模型参数
Table 5 Model parameters for two-layer soil slopes
土层参数 Ks/(m·h-1) θs θr β n 土层1 5.46×10-3 0.4686 0.106 1.04 1.3954 土层2 2.25×10-1 0.3658 0.0286 2.8 2.239
下载: 导出CSV
-
[1] 李梦姿, 蔡国庆, 李昊, 等. 考虑抗拉强度剪断的非饱和土无限边坡稳定性分析[J]. 岩土工程学报, 2020, 42(4): 705–713. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202004017.htm LI Meng-zi, CAI Guo-qing, LI Hao, et al. Stability of infinite unsaturated soil slopes with tensile strength cut-off[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(4): 705–713. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202004017.htm
[2] 覃小华, 刘东升, 宋强辉, 等. 强降雨条件下考虑饱和渗透系数变异性的基岩型层状边坡可靠度分析[J]. 岩土工程学报, 2017, 39(6): 1065–1073. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201706014.htm QIN Xiao-hua, LIU Dong-sheng, SONG Qiang-hui, et al. Reliability analysis of bedrock laminar slope stability considering variability of saturated hydraulic conductivity of soil under heavy rainfall[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(6): 1065–1073. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201706014.htm
[3] WU L Z, SELVADURAI A P S, ZHANG L M, et al. Poro-mechanical coupling influences on potential for rainfall-induced shallow landslides in unsaturated soils[J]. Advances in Water Resources, 2016, 98: 114–121. doi: 10.1016/j.advwatres.2016.10.020
[4] 陈永贵, 蔡叶青, 叶为民, 等. 处置库膨润土胶体吸附迁移性及核素共同迁移特性研究进展[J]. 岩土工程学报, 2021, 43(12): 2149–2158. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202112001.htm CHEN Yong-gui, CAI Ye-qing, YE Wei-min, et al. Progresses in researches on adsorption and migration properties of bentonite colloids and their co-migration with nuclide in repository[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(12): 2149–2158. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202112001.htm
[5] RICHARDS L A. Capillary conduction of liquids through porous mediums[J]. Physics, 1931, 1(5): 318–333. doi: 10.1063/1.1745010
[6] WU L Z, HUANG J S, FAN W, et al. Hydro-mechanical coupling in unsaturated soils covering a non-deformable structure[J]. Computers and Geotechnics, 2020, 117: 103287. doi: 10.1016/j.compgeo.2019.103287
[7] SRIVASTAVA R, YEH T C J. Analytical solutions for one-dimensional, transient infiltration toward the water table in homogeneous and layered soils[J]. Water Resources Research, 1991, 27(5): 753–762. doi: 10.1029/90WR02772
[8] TRACY F T. Clean two- and three-dimensional analytical solutions of Richards' equation for testing numerical solvers[J]. Water Resources Research, 2006, 42(8): 1–11.
[9] PANICONI C, PUTTI M. Physically based modeling in catchment hydrology at 50: survey and outlook[J]. Water Resources Research, 2015, 51(9): 7090–7129. doi: 10.1002/2015WR017780
[10] ZHA Y Y, YANG J Z, SHI L S, et al. Simulating one-dimensional unsaturated flow in heterogeneous soils with water content-based richards equation[J]. Vadose Zone Journal, 2013, 12(2): 1–13. doi: 10.2136/vzj2012.0142
[11] AN H, ICHIKAWA Y, TACHIKAWA Y, et al. Three-dimensional finite difference saturated-unsaturated flow modeling with nonorthogonal grids using a coordinate transformation method[J]. Water Resources Research, 2010, 46(11): 1–18.
[12] ZHANG Z Y, WANG W K, YEH T C J, et al. Finite analytic method based on mixed-form Richards' equation for simulating water flow in vadose zone[J]. Journal of Hydrology, 2016, 537: 146–156. doi: 10.1016/j.jhydrol.2016.03.035
[13] HERRERA P A, MASSABÓ M, BECKIE R D. A meshless method to simulate solute transport in heterogeneous porous media[J]. Advances in Water Resources, 2009, 32(3): 413–429. doi: 10.1016/j.advwatres.2008.12.005
[14] WU L Z, ZHU S R, PENG J B. Application of the Chebyshev spectral method to the simulation of groundwater flow and rainfall-induced landslides[J]. Applied Mathematical Modelling, 2020, 80: 408–425. doi: 10.1016/j.apm.2019.11.043
[15] LOTT P A, WALKER H F, WOODWARD C S, et al. An accelerated Picard method for nonlinear systems related to variably saturated flow[J]. Advances in Water Resources, 2012, 38: 92–101. doi: 10.1016/j.advwatres.2011.12.013
[16] BRENNER K, CANCÈS C. Improving Newton's method performance by parametrization: the case of the richards equation[J]. SIAM Journal on Numerical Analysis, 2017, 55(4): 1760–1785. doi: 10.1137/16M1083414
[17] ZENG J C, ZHA Y Y, YANG J Z. Switching the Richards' equation for modeling soil water movement under unfavorable conditions[J]. Journal of Hydrology, 2018, 563: 942–949. doi: 10.1016/j.jhydrol.2018.06.069
[18] ZHA Y Y, YANG J Z, YIN L H, et al. A modified Picard iteration scheme for overcoming numerical difficulties of simulating infiltration into dry soil[J]. Journal of Hydrology, 2017, 551: 56–69. doi: 10.1016/j.jhydrol.2017.05.053
[19] FARTHING M W, OGDEN F L. Numerical solution of richards' equation: a review of advances and challenges[J]. Soil Science Society of America Journal, 2017, 81(6): 1257–1269. doi: 10.2136/sssaj2017.02.0058
[20] CHÁVEZ-NEGRETE C, DOMÍNGUEZ-MOTA F J, SANTANA-QUINTEROS D. Numerical solution of Richards' equation of water flow by generalized finite differences[J]. Computers and Geotechnics, 2018, 101: 168–175. doi: 10.1016/j.compgeo.2018.05.003
[21] DOLEJŠÍ V, KURAZ M, SOLIN P. Adaptive higher-order space-time discontinuous Galerkin method for the computer simulation of variably-saturated porous media flows[J]. Applied Mathematical Modelling, 2019, 72: 276–305. doi: 10.1016/j.apm.2019.02.037
[22] CELIA M A, BOULOUTAS E T, ZARBA R L. A general mass-conservative numerical solution for the unsaturated flow equation[J]. Water Resources Research, 1990, 26(7): 1483–1496. doi: 10.1029/WR026i007p01483
[23] LIST F, RADU F A. A study on iterative methods for solving Richards' equation[J]. Computational Geosciences, 2016, 20(2): 341–353. doi: 10.1007/s10596-016-9566-3
[24] 陈曦, 于玉贞, 程勇刚. 非饱和渗流Richards方程数值求解的欠松弛方法[J]. 岩土力学, 2012, 33(增刊1): 237–243. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2012S1039.htm CHEN Xi, YU Yu-zhen, CHENG Yong-gang. Under-relaxation methods for numerical solution of Richards equation of variably saturated flow[J]. Rock and Soil Mechanics, 2012, 33(S1): 237–243. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2012S1039.htm
[25] 李文涛, 马田田, 韦昌富. 基于自适应松弛Picard法的高效非饱和渗流有限元分析[J]. 岩土力学, 2016, 37(1): 256–262 https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201601031.htm LI Wen-tao, MA Tian-tian, WEI Chang-fu. An efficient finite element procedure for unsaturated flow based on adaptive relaxed Picard method[J]. Rock and Soil Mechanics, 2016, 37(1): 256–262. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201601031.htm
[26] BENZI M. Preconditioning techniques for large linear systems: a survey[J]. Journal of Computational Physics, 2002, 182(2): 418–477. doi: 10.1006/jcph.2002.7176
[27] WANG K, ZHANG J. MSP: a class of parallel multistep successive sparse approximate inverse preconditioning strategies[J]. SIAM Journal on Scientific Computing, 2003, 24(4): 1141–1156. doi: 10.1137/S1064827502400832
[28] LIU C Y, KU C Y, HUANG C C, et al. Numerical solutions for groundwater flow in unsaturated layered soil with extreme physical property contrasts[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2015, 16(7/8): 325–335.
[29] BRIGGS W L, HENSON V E, MCCORMICK S F. A Multigrid Tutorial, Second Edition[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2000.
[30] IVERSON R M. Landslide triggering by rain infiltration[J]. Water Resources Research, 2000, 36(7): 1897–1910. doi: 10.1029/2000WR900090
[31] GARDNER W R. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table[J]. Soil Science, 1958, 85(4): 228–232. doi: 10.1097/00010694-195804000-00006
-
期刊类型引用(5)
1. 杨尚，宁建国，王俊，高明涛，史新帅，张朝辉. 动载作用下锚固体动态失稳试验研究. 岩石力学与工程学报. 2025(02): 409-426 . 
百度学术
2. 常聚才，郭钇君，吴博文，史文豹，齐潮，王宏达. 深部沿空掘巷含软弱夹层顶板离层破坏特征及控制研究. 煤炭科学技术. 2024(09): 88-102 . 百度学术
3. 刘玉宾，朱斯陶，张修峰，王绪友，李增强，周均忠，张斌，王高昂. 厚煤层掘进工作面强震动诱发底煤卸压失效机理研究. 采矿与岩层控制工程学报. 2024(05): 107-118 . 百度学术
4. 李青海，张浩然，纪永虎，马小勇，张存智. 深部巷道预应力锚固防冲作用机制研究. 采矿与岩层控制工程学报. 2024(06): 78-88 . 百度学术
5. 胡斌，曹建军，王泽祺，李京，张峻珲，徐心语. 冲击扰动下泥页岩剪切蠕变试验及蠕变损伤模型研究. 煤炭学报. 2024(S2): 900-910 . 百度学术
其他类型引用(7)
计量
- 文章访问数: 299
- HTML全文浏览量: 90
- PDF下载量: 187
- 被引次数: 12
