月壤临界尺度颗粒运移特性对钻采阻力影响研究

崔建国; 田野; 刘君巍; 侯绪研; 崔江磊; 杨飞; 王晶; 关祥毅

doi:10.11779/CJGE202109017

月壤临界尺度颗粒运移特性对钻采阻力影响研究 English Version

1.
哈尔滨商业大学轻工学院,黑龙江　哈尔滨　150028
2.
哈尔滨工业大学机电工程学院,黑龙江　哈尔滨　150006

基金项目:

国家自然科学基金项目 41772387

黑龙江省自然科学基金项目 LH2020E027

哈尔滨商业大学青年创新人才支持项目 2019CX04

哈尔滨商业大学校级科研项目 18XN070

详细信息

作者简介:
崔建国(1996— ),男,硕士研究生,主要从事深空探测地面模拟技术及取芯钻具钻进机理的研究。E-mail：cuijianguo_huc@163.com

通讯作者:
田野, E-mail：tian8154@126.com

中图分类号: TU192;TU193
计量
- 文章访问数: 342
- HTML全文浏览量: 27
- PDF下载量: 114
出版历程
- 收稿日期: 2020-10-11
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-08-31

Influences of critical fragment migration characteristics of lunar soil on drilling resistance

1.
Department of Light Industry, Harbin University of Commerce, Harbin 150028, China
2.
School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150006, China

摘要

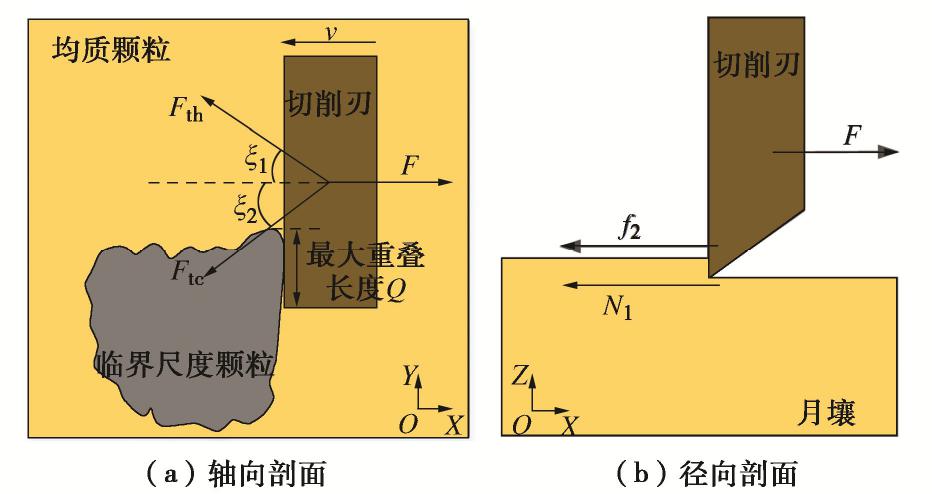
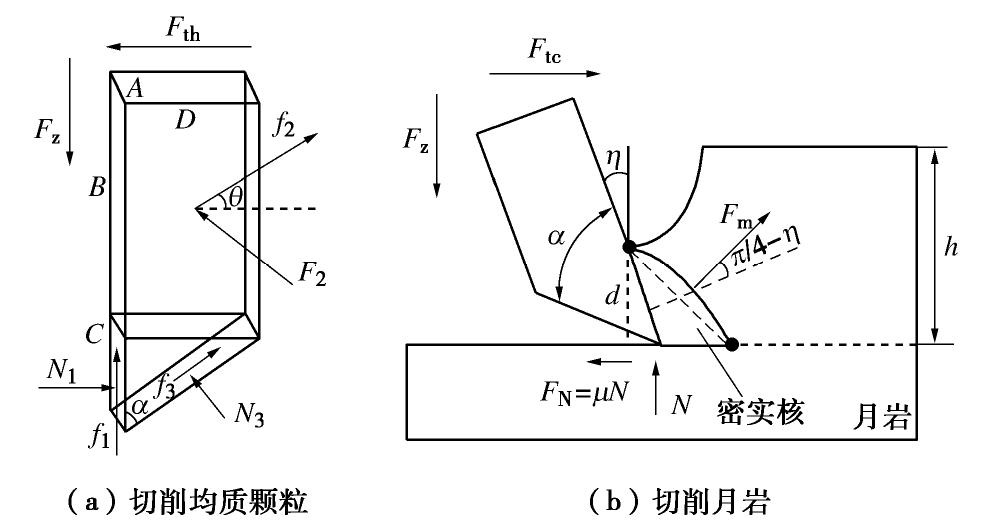
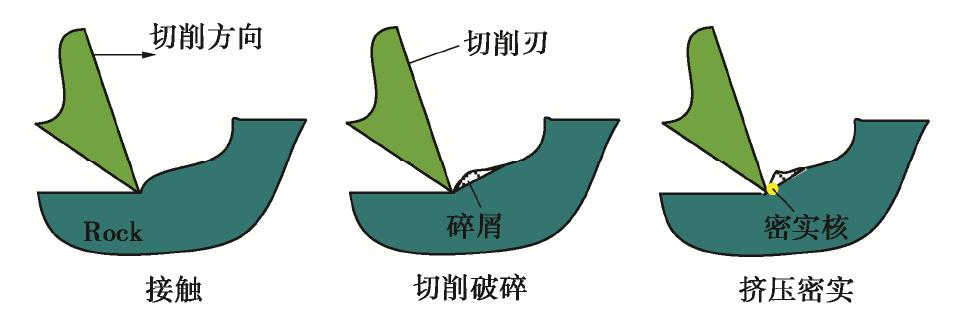
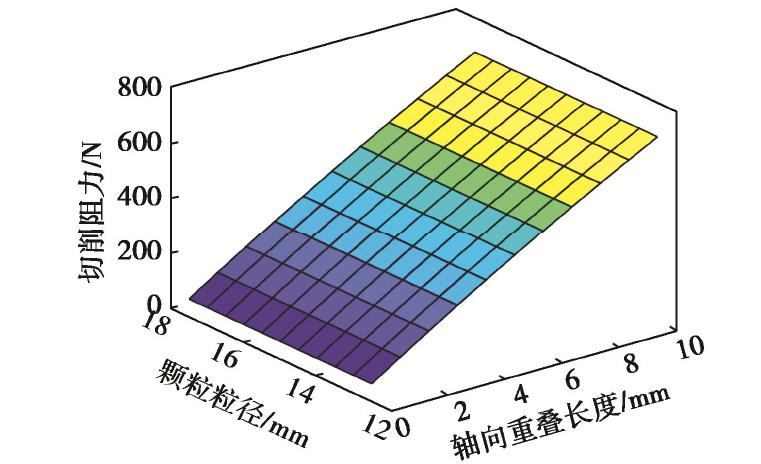
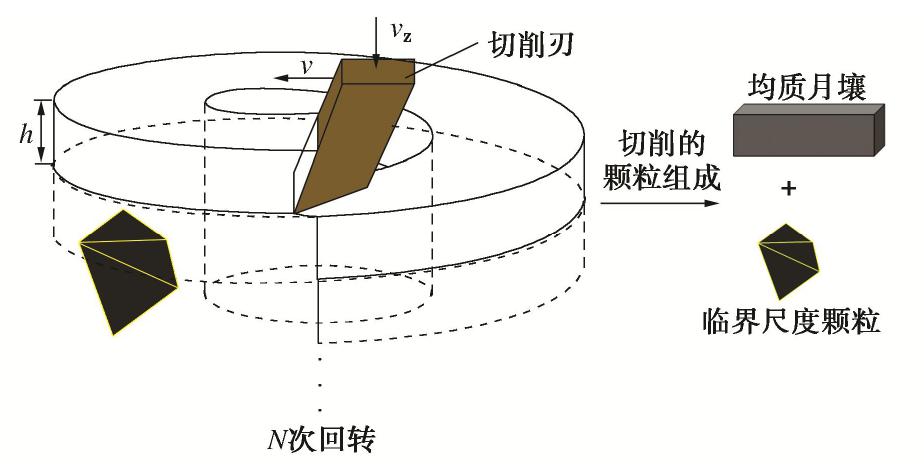
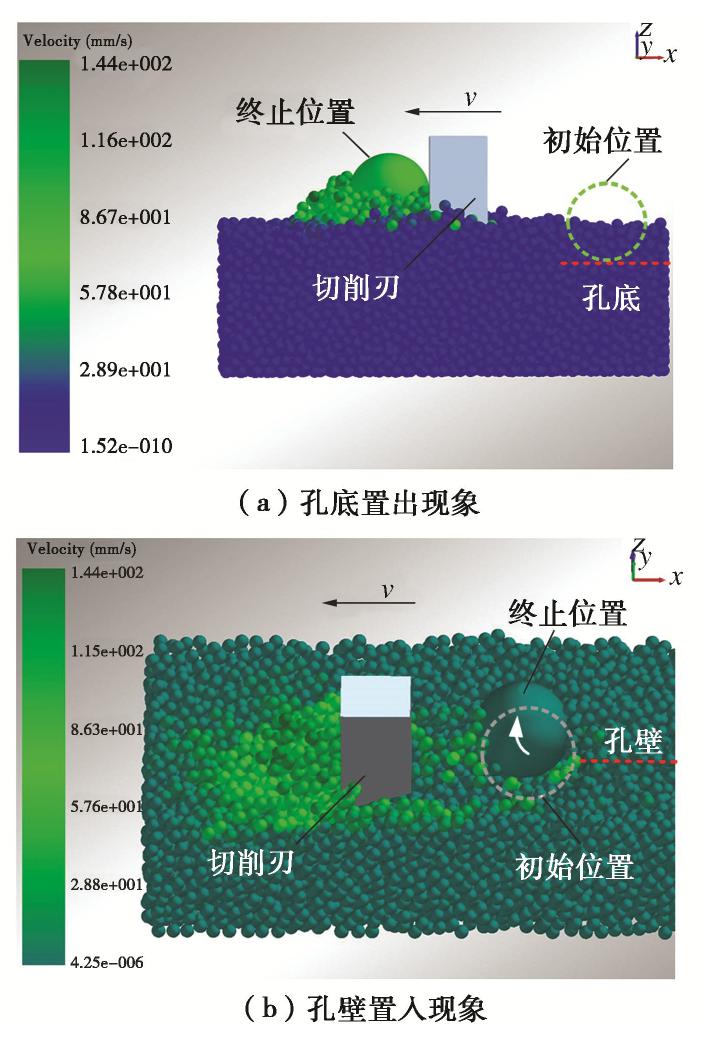
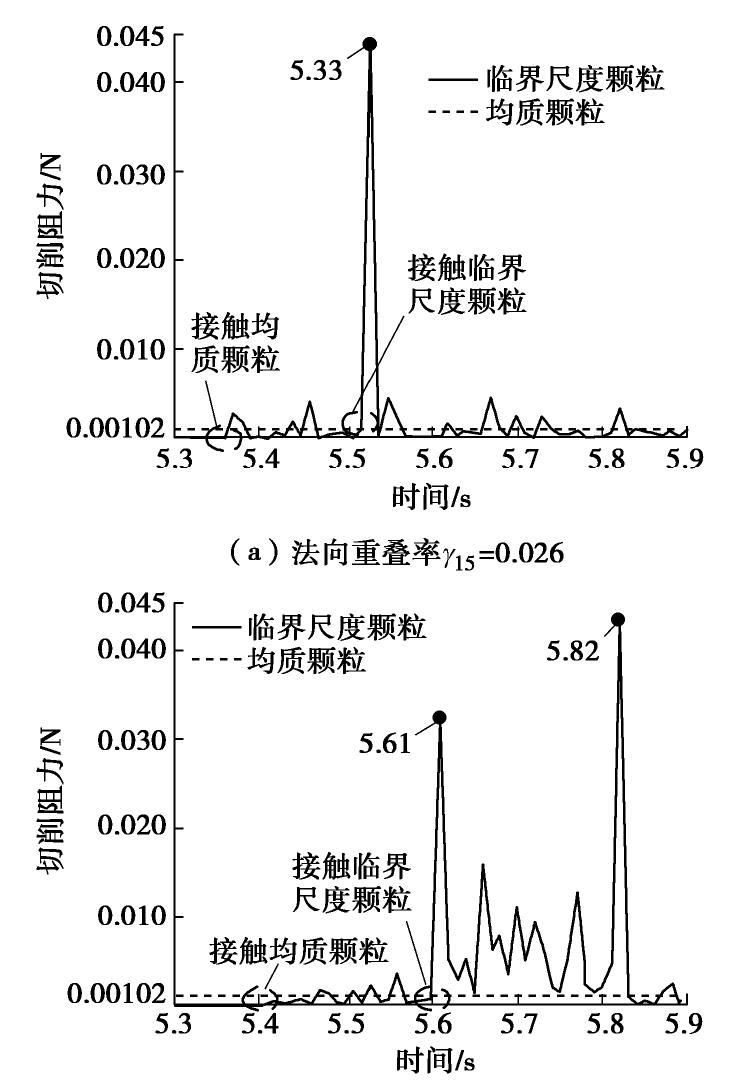
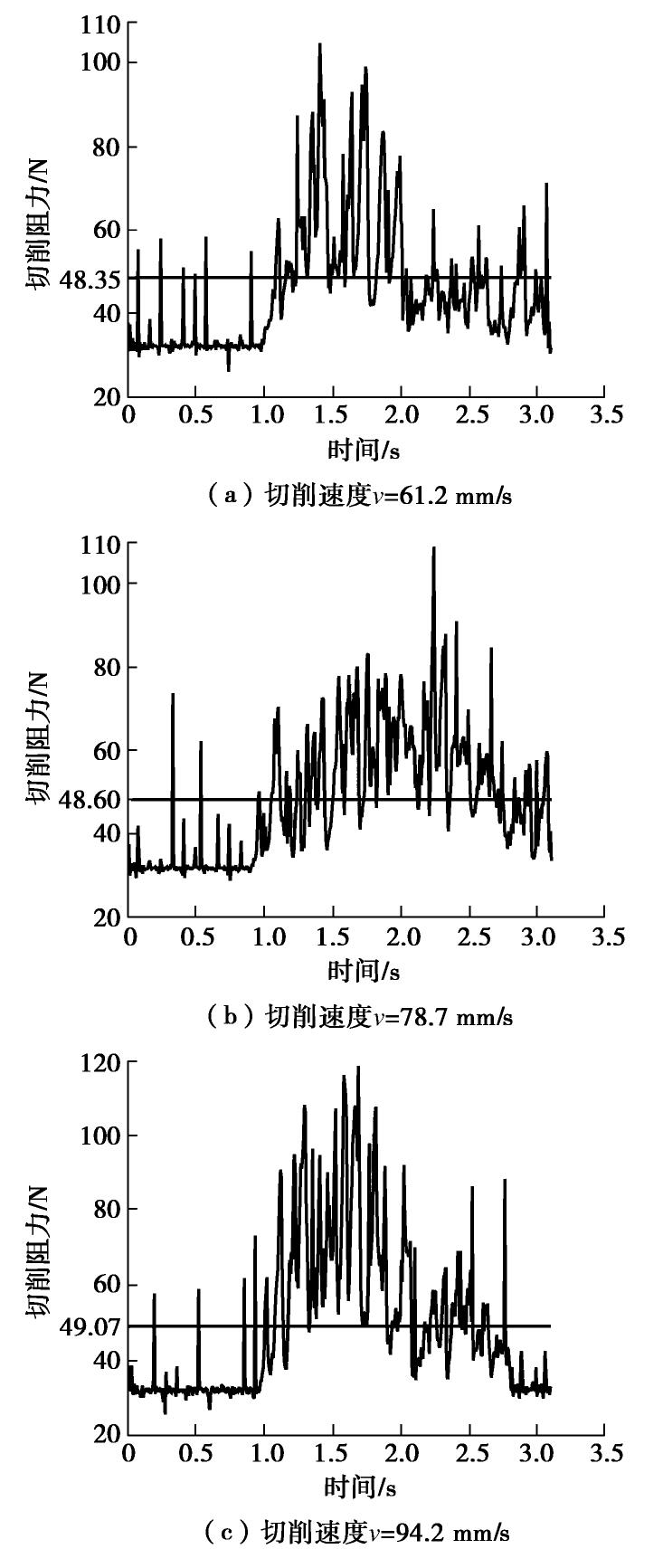
摘要: 临界尺度颗粒是指平均直径大于或等于钻头取芯孔直径的月球土壤颗粒,其广泛分布于月球次表层土壤中。在钻进过程中受到钻削作用,一部分临界尺度颗粒被从孔底置出,并被嵌入钻孔壁产生孔壁置入现象,从而增大了切削负载功耗；另一部分跟随钻具回转无法被取芯孔采集,从而增加了钻进失败的风险。通过建立月壤临界尺度颗粒切削模型,考虑临界尺度颗粒粒径及其与切削刃相互作用位置,对切削阻力的影响进行敏感度分析,得到位置的变化对切削阻力影响最明显。提出法向重叠率的概念,用以研究位置变化对临界尺度颗粒运移特性及切削阻力的影响关系。将切削刃的回转运动等效为直线运动,采用离散元方法验证法向重叠率对切削阻力的影响,得到法向重叠率与临界尺度颗粒孔底置出和孔壁置入现象之间的关系,以及对应的切削阻力时域变化曲线的特征。通过临界尺度颗粒运移特性模拟试验,得到法向重叠率与切削阻力呈同方向的线性关系,当临界尺度颗粒分别产生孔底置出和孔壁置入现象时,对应的切削阻力时域曲线特征分别为连续峰值和仅有一个峰值点。研究可为月球采样任务中的钻进工况参数识别提供理论依据。
- 月壤钻采 /
- 临界尺度颗粒 /
- 切削阻力 /
- 运移特性
Abstract: The critical fragment refers to the lunar soil particles with average diameter greater than or equal to the diameter of coring bit hole, which is widely distributed in lunar subsurface soil. On one hand, due to the drilling effect in the drilling process, some of the critical fragments are placed from the bottom of the hole and embedded into the borehole wall to produce the hole wall insertion phenomenon, thus increasing consumption of the cutting load power. On the other hand, the others cannot be collected by the coring hole following the rotation of the drilling tool, thus increasing the risk of drilling failure. Firstly, the critical fragment cutting model for lunar soil is established, the particle size of the critical fragment and its interaction position with cutting edge are considered, the sensitivity of cutting resistance is analyzed, and it is obtained that the change of position has the most obvious influences on cutting resistance. Then, the concept of normal overlap ratio is put forward to study the influences of position change on the migration characteristics and cutting resistance of the critical fragment. The rotary motion of cutting edge is equivalent to the linear one, and the influences of normal overlap ratio on the cutting resistance are verified by the discrete element method, so as to obtain the relationship between the normal overlap ratio and the phenomenon of being placed from the bottom of the hole and embedded into the borehole wall to produce the hole wall insertion, as well as the characteristics of the corresponding time-domain change curve of cutting resistance. Finally, through the simulation tests on the migration characteristics of the critical fragment, it is found that the normal overlap ratio and cutting resistance have a linear relationship in the same direction. When the critical fragment produces the process of being placed from the bottom of the hole and embedded into the wall, the time-domain curve features of the corresponding cutting resistances are continuous peak points and only one peak point respectively. The above results may provide the theoretical basis for the parameter identification of drilling conditions in lunar sampling mission.
- lunar soil drilling /
- critical fragment /
- cutting resistance /
- migration characteristic

HTML全文

0. 引言

桩基水平瞬态响应的研究开展于20世纪80年代。过去40 a中,国内外学者在桩基水平瞬态响应方面的研究已经取得了丰硕的成果。已有的方法主要包括以差分法^[1-2]、有限元^[3-4]和边界元^[5-7]为代表的数值方法和Laplace变换法^[8-9]。有限差分法等数值方法需要迭代运算,过程较为繁琐且计算耗时较长,且需合理设置人工边界,来满足能量在边界的透射作用。其中Mamoon等^[5]构造了两种不同的边界元分别对桩基在冲击荷载作用下的瞬态响应进行了分析,并与采用Laplace变换方法的计算结果进行了对比。Küçükarslan^[7]对有限和无限域分别采用隐式积分和边界元法,研究了群桩在冲击荷载下的瞬态响应。Chang等^[4]采用二阶Higdon吸收边界和交错网格有限差分法进行数值计算,得到了一类水平冲击荷载下的桩顶动力阻抗。Laplace变换法过程较为简便,在已有的文献中常作为对照组为数值方法可靠性提供验证。其中龙丽丽等^[8]和刘圆圆等^[9]分别基于动力Winkler地基梁法（BDWF）和饱和土的连续介质解考虑桩土相互作用,并采用Laplace变换法,研究了桩顶受水平冲击荷载作用下的瞬态响应问题。但是,以上文献均假定桩土接触面为连续介质,没有考虑到桩土局部分离的影响,计算得到的桩、土动力响应往往偏小,因而高估了桩、土动力阻抗。

实际单桩与群桩的现场试验记录表明,水平动力荷载作用下,桩前被动区的土体随桩身一起运动,桩后主动区的土体则会与桩身分离,并可能随运动产生间隙^[10]。桩土接触面的这一特性,不仅会削弱桩基的水平动力阻抗,对桩周土位移分布和群桩动力相互作用也有明显影响^[11]。已有的文献中指出,桩土接触面的局部分离特性往往受到桩身表面粗糙程度、桩周土体黏聚力和内摩擦角的影响^[12]。因此对于采用预制桩及桩周土为砂土、粉质黏土的情况,考虑桩土局部分离是相当重要的。此外,在桩身受到船舶、车辆撞击等具有较大能量的瞬时冲击荷载作用时,桩土接触面部分分离的特性往往更加显著。

针对这一问题,Mostafa等^[13]采用串联的非线性和线性弹簧指代近场和远场土体,其中非线性弹簧的参数考虑了桩土局部分离的影响。Allotey等^[14]和Heidari等^[15]采用两组不受拉弹簧指代桩前被动区和桩后主动区的土体,假定弹簧受拉时断开连接以允许桩土接触面间隙的生成。但是,已有的理论研究往往采用经验化的公式或者包含理想化的假设,且大多只考虑静力作用,因而不适用于瞬态响应问题的研究。因此在现阶段的桩基设计中,有效的理论依据仍不够完备,需要采取较大的安全系数来确保结果的可靠性。本文通过定义桩土接触面边界条件,考虑了桩前被动区和桩后主动区土体和桩身的接触关系,从而得到了能够在动力水平荷载作用下考虑桩土局部分离的辐射应力解。

1. 模型建立与假设

水平冲击荷载作用下,各向同性半空间中考虑桩土局部分离的桩土相互作用问题的计算模型如图1所示。冲击荷载P(t)作用于桩顶中心,在冲击荷载的作用下,桩身与桩前被动区土体紧密接触,与桩后主动区土体相互分离。运动过程中,土层处于对称受力状态。桩土竖向及水平剖面分别如图1（a）,（b）所示, $u, u_{r}, u_{θ}$ 分别为桩身水平振动位移和桩周土的径向、切向水平振动位移, $σ_{r}, τ_{r θ}$ 分别为桩周土的法向和切向有效应力,其中 $r, θ, z$ 分别为模型的径向、切向和竖向坐标。

图 1 桩-土相互作用计算模型

Figure 1. Computational model for pile-soil interaction

下载: 全尺寸图片幻灯片

在图1所示的桩土相互作用模型中,土体在水平方向无限远处有边界条件：

$\begin{matrix} \lim_{r \to \infty} u_{r} (r, θ, z, t) = 0 & , & \lim_{r \to \infty} u_{θ} (r, θ, z, t) = 0 \end{matrix}$ 。

(1)

在弧段 $θ \in (- π / 2, π / 2)$ 上,桩前被动区土体与桩身的接触面有位移边界条件：

${u_{r} (r, θ, z, t) |}_{r = \frac{d}{2}} = u (z, t) \cos θ$ ,

(2a)

${u_{θ} (r, θ, z, t) |}_{r = \frac{d}{2}} = - u (z, t) \sin θ$ 。

(2b)

在桩后主动区土体与桩身的接触面上,有应力边界条件：

$\begin{matrix} {σ_{r} (r, θ, z, t) |}_{r = \frac{d}{2}} = 0 & , & {τ_{r θ} (r, θ, z, t) |}_{r = \frac{d}{2}} = 0 \end{matrix}$ 。

(3)

2. 基本理论与方程

2.1 土体控制方程

采用Novak薄层单元方法^[16],在忽略竖向位移的条件下,任意深度土体运动基本控制方程为

$G \nabla^2 u_r+(\lambda+G) \frac{\partial e}{\partial r}-\frac{G}{r^2}\left(2 \frac{\partial u_\theta}{\partial \theta}+u_r\right)=\rho \ddot{u}_r，$

(4a)

$G \nabla^{2} u_{θ} + (λ + G) \frac{1}{r} \frac{\partial e}{\partial r} - \frac{G}{r^{2}} (u_{θ} - 2 \frac{\partial u_{r}}{\partial θ}) = ρ {\ddot{u}}_{θ}$ ,

(4b)

式中, $G$ , $ν$ , $ρ$ 分别为桩周土体的动剪切模量、动泊松比和密度,拉梅常数 $λ = 2 ν G / (1 - 2 ν)$ 。Laplace算子 $\nabla$ 形式 $\nabla^{2} = \frac{\partial^{2}}{\partial r^{2}} + \frac{1}{r} \frac{\partial}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2}}{\partial θ^{2}}$ , $e = \frac{\partial u_{r}}{\partial r} + \frac{u_{r}}{r} + \frac{1}{r} \frac{\partial u_{θ}}{\partial θ}$ 为桩周土体积应变。对式（4）中土体位移引入势函数分解：

$\begin{matrix} u_{r} = \frac{\partial φ}{\partial r} + \frac{1}{r} \frac{\partial ϕ}{\partial θ} & , & u_{θ} = \frac{1}{r} \frac{\partial φ}{\partial θ} - \frac{\partial ϕ}{\partial r} \end{matrix}$ 。

(5)

采用无量纲化 $\bar{λ} = λ / G$ , $\bar{r} = 2 r / d$ , $\bar{t} =$ $2 t \sqrt{G / ρ_{s}} / d$ , $\bar{u} = 2 u / d$ , ${\bar{u}}_{r} = 2 u_{r} / d$ , ${\bar{u}}_{θ} = 2 u_{θ} / d$ , ${\bar{σ}}_{r} = σ_{r} / G$ , ${\bar{τ}}_{r θ} = τ_{r θ} / G$ ,并对时间域进行Laplace变换,其变换形式为 $\overset{⌢}{f} (δ) = \int_{0}^{\infty} f (t) e^{- δ t} d t$ 。并将式（5）代入式（4）,有

$\begin{array}{l} (\nabla^{2} + β_{1}^{2}) φ = 0, \\ (\nabla^{2} + β_{2}^{2}) ϕ = 0, \end{array}}$

(6)

式中,

$\begin{array}{l} β_{1}^{2} = - \frac{δ^{2}}{\bar{λ} + 2}, \\ β_{2}^{2} = - δ^{2} 。 \end{array}}$

(7)

当土层处于对称受力状态时, ${\overset{⌢}{\bar{u}}}_{r}$ , ${\overset{⌢}{\bar{σ}}}_{r}$ 为 $θ$ 的偶函数, ${\overset{⌢}{\bar{u}}}_{θ}$ , ${\overset{⌢}{\bar{τ}}}_{r θ}$ 为 $θ$ 的奇函数,有

${\overset{⌢}{\bar{u}}}_{r} = \sum_{s = 0}^{\infty} [\partial A_{1 s} H_{s}^{(1)} (β_{1} \overset{⌢}{r}) / \partial \overset{⌢}{r} + s A_{2 s} H_{s}^{(1)} (β_{2} \overset{⌢}{r}) / \overset{⌢}{r}] \cos s θ$ ,

(8a)

${\overset{⌢}{\bar{u}}}_{θ} = - \sum_{s = 0}^{\infty} [s A_{1 s} H_{s}^{(1)} (β_{1} \overset{⌢}{r}) / \overset{⌢}{r} + \partial A_{2 s} H_{s}^{(1)} (β_{2} \overset{⌢}{r}) / \partial \overset{⌢}{r}] \sin s θ$ ,

(8b)

${\overset{⌢}{\bar{σ}}}_{r} = \frac{2}{{\overset{⌢}{r}}^{2}} \sum_{s = 0}^{\infty} (A_{1 s} f_{1 s} + A_{2 s} f_{2 s}) \cos s θ$ ,

(9a)

${\overset{⌢}{\bar{τ}}}_{r θ} = \frac{2}{{\overset{⌢}{r}}^{2}} \sum_{s = 0}^{\infty} (A_{1 s} f_{3 s} + A_{2 s} f_{4 s}) \sin s θ$ ,

(9b)

式中, $H_{s}^{(1)}, H_{s}^{(2)}$ 分别为第1,2种汉克尔函数,下标s指代汉克尔函数的阶数。 $f_{1 s}$ ～ $f_{4 s}$ 有如下形式：

$f_{1 s} = [s^{2} + s - β_{2}^{2} {\bar{r}}^{2} / 2] H_{s}^{(1)} (β_{1} \bar{r}) - β_{1} \bar{r} H_{s - 1}^{(1)} (β_{1} \bar{r})$ ,

(10a)

$f_{2 s} = - s (s + 1) H_{s}^{(1)} (β_{2} \bar{r}) + s β_{2} \bar{r} H_{s - 1}^{(1)} (β_{2} \bar{r})$ ,

(10b)

$f_{3 s} = s (s + 1) H_{s}^{(1)} (β_{1} \bar{r}) + s β_{1} \bar{r} H_{s - 1}^{(1)} (β_{1} \bar{r})$ ,

(10c)

$f_{4 s} = - [s^{2} + s - β_{2}^{2} {\bar{r}}^{2} / 2] H_{s}^{(1)} (β_{2} \bar{r}) + β_{2} \bar{r} H_{s - 1}^{(1)} (β_{2} \bar{r})$ 。

(10d)

当土层处于反对称受力状态时, ${\overset{⌢}{\bar{u}}}_{r}$ , ${\overset{⌢}{\bar{σ}}}_{r}$ 为 $θ$ 的奇函数, ${\overset{⌢}{\bar{u}}}_{θ}$ , ${\overset{⌢}{\bar{τ}}}_{r θ}$ 为 $θ$ 的偶函数,有

${\overset{⌢}{\bar{u}}}_{r} = \sum_{s = 0}^{\infty} [\partial B_{1 s} H_{s}^{(1)} (β_{1} \overset{⌢}{r}) / \partial \overset{⌢}{r} + s B_{2 s} H_{s}^{(1)} (β_{2} \overset{⌢}{r}) / \overset{⌢}{r}] \sin s θ$ ,

(11a)

${\overset{⌢}{\bar{u}}}_{θ} = \sum_{s = 0}^{\infty} [s B_{1 s} H_{s}^{(1)} (β_{1} \overset{⌢}{r}) / \overset{⌢}{r} + \partial B_{2 s} H_{s}^{(1)} (β_{2} \overset{⌢}{r}) / \partial \overset{⌢}{r}] \cos s θ$ ,

(11b)

${\overset{⌢}{\bar{σ}}}_{r} = \frac{2}{{\overset{⌢}{r}}^{2}} \sum_{s = 0}^{\infty} (B_{1 s} f_{1 s} + B_{2 s} f_{2 s}) \sin s θ$ ,

(12a)

${\overset{⌢}{\bar{τ}}}_{r θ} = - \frac{2}{{\overset{⌢}{r}}^{2}} \sum_{s = 0}^{\infty} (B_{1 s} f_{3 s} + B_{2 s} f_{4 s}) \cos s θ$ 。

(12b)

2.2 混合边界辐射应力解

分别假设桩土接触面上弧元 $θ \in (- θ_{0}, θ_{0})$ 内有均布拉力 ${\overset{⌢}{\bar{σ}}}_{r}$ , ${\overset{⌢}{\bar{τ}}}_{r θ}$ ,将 ${\overset{⌢}{\bar{σ}}}_{r}$ , ${\overset{⌢}{\bar{τ}}}_{r θ}$ 各自沿桩周进行Fourier余弦级数展开：

$\begin{matrix} {\overset{⌢}{\bar{σ}}}_{r} = \frac{{\overset{⌢}{\bar{σ}}}_{0}}{π} (θ_{0} + 2 \sum_{s = 1}^{\infty} \frac{1}{s} \sin s θ_{0} \cos s θ) & ({\overset{⌢}{\bar{τ}}}_{r θ} = 0) \end{matrix}$ ,

(13)

$\begin{matrix} {\overset{⌢}{\bar{τ}}}_{r θ} = \frac{{\overset{⌢}{\bar{τ}}}_{0}}{π} (θ_{0} + 2 \sum_{s = 1}^{\infty} \frac{1}{s} \sin s θ_{0} \cos s θ) & , & {\overset{⌢}{\bar{σ}}}_{r} = 0 \end{matrix}$ 。

(14)

将式（13）,（14）分别代入式（9a）,（9b）,（12a）,（12b）,解得

$\begin{matrix} A_{1 s} = a_{s} {\overset{⌢}{\bar{σ}}}_{0} L_{1 s} & , & A_{2 s} = a_{s} {\overset{⌢}{\bar{σ}}}_{0} L_{2 s} \end{matrix}$ ,

(15)

$\begin{matrix} B_{1 s} = a_{s} {\overset{⌢}{\bar{τ}}}_{0} L_{3 s} & , & B_{2 s} = a_{s} {\overset{⌢}{\bar{τ}}}_{0} L_{4 s} \end{matrix}$ ,

(16)

式中, $s = 0$ 时, $a_{s} =$ $\frac{θ_{0}}{2 π}$ , $s \neq 0$ 时, $a_{s} = \frac{1}{π} \frac{\sin s θ_{0}}{s}$ ； $L_{1 s}$ ～ $L_{4 s}$ 形式可以被写为

$\begin{matrix} L_{1 s} = \frac{F_{4 s}}{F_{1 s} F_{4 s} - F_{2 s} F_{3 s}} & , & L_{2 s} = \frac{- F_{3 s}}{F_{1 s} F_{4 s} - F_{2 s} F_{3 s}} \end{matrix}$ ,

(17)

$\begin{matrix} L_{3 s} = \frac{F_{2 s}}{F_{1 s} F_{4 s} - F_{2 s} F_{3 s}} & , & L_{4 s} = \frac{- F_{1 s}}{F_{1 s} F_{4 s} - F_{2 s} F_{3 s}} \end{matrix}$ ,

(18)

式中, $F_{1 s} = {f_{1 s} |}_{r = \frac{d}{2}}$ ,类似的,有 $F_{2 s}$ ～ $F_{4 s}$ 。

将式（15）,（16）分别代入式（8a）,（8b）,（11a）,（11b）,可以分别得到包含参数 $L_{1 s}$ ～ $L_{4 s}$ 的 ${{\overset{⌢}{\bar{u}}}_{r} |}_{\overset{⌢}{r} = 1}, {{\overset{⌢}{\bar{u}}}_{θ} |}_{\overset{⌢}{r} = 1}$ 形式,即弧元 $θ \in (- θ_{0}, θ_{0})$ 内均布拉力 ${\overset{⌢}{\bar{σ}}}_{r}$ $,$ ${\overset{⌢}{\bar{τ}}}_{r θ}$ 对桩土接触面上位移的影响函数。用 $(ξ - θ)$ 替换其中 $θ$ 值并除以弧元上均布拉力之和,令 $θ_{0} \to 0$ ,可得到任意一点所受应力对接触面位移分布的影响函数 $G_{1 s}$ ～ $G_{4 s}$ ,其形式可以写为

$\begin{matrix} G_{1 s} = b_{s} R_{1 s} \cos s (ξ - θ) & , & G_{2 s} = b_{s} R_{2 s} \sin s (ξ - θ) \end{matrix}$ ,

(19)

$\begin{matrix} G_{3 s} = b_{s} R_{3 s} \sin s (ξ - θ) & , & G_{4 s} = b_{s} R_{4 s} \cos s (ξ - θ) \end{matrix}$ ,

(20)

式中, $s = 0$ 时 $b_{s} = \frac{1}{4 π}$ , $s \neq 0$ 时 $b_{s} = \frac{1}{2 π}$ ； $R_{1 s}$ ～ $R_{4 s}$ 形式可以被写为

$R_{1 s} = L_{1 s} \partial H_{s}^{(1)} (β_{1} \bar{r}) / \partial \bar{r} + s L_{2 s} H_{s}^{(1)} (β_{2} \bar{r}) / \bar{r}$ ,

(21)

$R_{2 s} = s L_{1 s} H_{s}^{(1)} (β_{1} \bar{r}) / \bar{r} + L_{2 s} \partial H_{s}^{(1)} (β_{2} \bar{r}) / \partial \bar{r}$ ,

(22)

$R_{3 s} = L_{3 s} \partial H_{s}^{(1)} β_{1} \bar{r} / \partial \bar{r} + s L_{4 s} H_{s}^{(1)} (β_{2} \bar{r}) / \bar{r}$ ,

(23)

$R_{4 s} = s L_{3 s} H_{s}^{(1)} (β_{1} \bar{r}) / \bar{r} + L_{4 s} \partial H_{s}^{(1)} β_{2} \bar{r} / \partial \bar{r}$ 。

(24)

土体中辐射应力 ${\overset{⌢}{\bar{σ}}}_{r}$ 为偶函数, ${\overset{⌢}{\bar{τ}}}_{r θ}$ 为奇函数,因此对其进行Fourier正弦及余弦展开有

$\begin{matrix} {\overset{⌢}{\bar{σ}}}_{r} = \sum_{m = 0}^{\infty} c_{1 m} \cos m θ & , & {\bar{\overset{⌢}{τ}}}_{r θ} = \sum_{m = 0}^{\infty} c_{2 m} \sin m θ \end{matrix}$ 。

(25)

将式（19）,（20）代入式（25）,由于辐射应力的作用,孔壁上土层中任意一点产生的位移有如下形式：

${\overset{⌢}{\bar{u}}}_{r} = [\sum_{s = 0}^{\infty} b_{s} R_{1 s} \sum_{m = 0}^{\infty} c_{1 m} Φ_{m s} - \sum_{s = 0}^{\infty} b_{s} R_{3 s} \sum_{m = 0}^{\infty} c_{2 m} Ψ_{m s}] \cos s θ$ ,

(26)

${\overset{⌢}{\bar{u}}}_{θ} = - [\sum_{s = 0}^{\infty} b_{s} R_{2 s} \sum_{m = 0}^{\infty} c_{1 m} Φ_{m s} + \sum_{s = 0}^{\infty} b_{s} R_{4 s} \sum_{m = 0}^{\infty} c_{2 m} Ψ_{m s}] \sin s θ$ ,

(27)

式中, $Φ_{m s}$ , $Ψ_{m s}$ 有如下形式：

$Φ_{m s} = {\begin{matrix} \frac{\sin (\frac{m - s}{2}) π}{m - s} + \frac{\sin (\frac{m + s}{2}) π}{m + s} & (m \neq s), \\ \frac{π}{2} & (m = s), \end{matrix}$

(28a)

$Ψ_{m s} = {\begin{matrix} \frac{\sin (\frac{m - s}{2}) π}{m - s} - \frac{\sin (\frac{m + s}{2}) π}{m + s} & (m \neq s), \\ \frac{π}{2} & (m = s) 。 \end{matrix}$

(28b)

同时土体中位移 ${\overset{⌢}{\bar{u}}}_{r}$ 为偶函数, ${\overset{⌢}{\bar{u}}}_{θ}$ 为奇函数,分别对 ${\overset{⌢}{\bar{u}}}_{r}$ , ${\overset{⌢}{\bar{u}}}_{θ}$ 进行余弦和正弦级数展开,有

$\begin{matrix} {\overset{⌢}{\bar{u}}}_{r} = \frac{h_{0}}{2} + \sum_{p = 0}^{\infty} h_{p} \cos p θ & {\overset{⌢}{\bar{u}}}_{θ} = \sum_{p = 0}^{\infty} k_{p} \sin p θ \end{matrix}$ ,

(29)

式中, $h_{p} = \frac{2}{π} \int_{0}^{π} {\overset{⌢}{\bar{u}}}_{r} \cos p θ d θ$ , $k_{p} = \frac{2}{π} \int_{0}^{π} {\overset{⌢}{\bar{u}}}_{θ} \sin p θ d θ$ 。

将式（29）代入式（2）,（3）,（26）,（27）,在桩土接触面上对满足位移、应力边界条件的不同区域分别进行积分,可得

$\begin{matrix} γ_{p} \overset{⌢}{\bar{u}} - \sum_{s = 0}^{\infty} b_{s} {Φ^{'}}_{s p} [R_{1 s} \sum_{m = 0}^{\infty} c_{1 m} Φ_{m s} - R_{3 s} \sum_{m = 0}^{\infty} c_{2 m} Ψ_{m s}] \\ \begin{matrix} = \frac{1}{4 b_{p}} (c_{1 p} R_{1 p} - c_{2 p} R_{3 p}) & (p = 0, 1, 2, \dots,) \end{matrix} \end{matrix}$ ,

(30)

$\begin{matrix} δ_{p} \overset{⌢}{\bar{u}} - \sum_{s = 0}^{\infty} b_{s} {Ψ^{'}}_{s p} [R_{2 s} \sum_{m = 0}^{\infty} c_{1 m} Φ_{m s} + R_{4 s} \sum_{m = 0}^{\infty} c_{2 m} Ψ_{m s}] \\ \begin{matrix} = \frac{1}{4 b_{p}} (c_{1 p} R_{2 p} + c_{2 p} R_{4 p}) & (p = 1, 2, 3, \dots,) \end{matrix} \end{matrix}$ 。

(31)

式中, ${Φ^{'}}_{s p}$ , ${Ψ^{'}}_{m s}$ , $γ_{p}$ , $δ_{p}$ 有如下形式：

${Φ^{'}}_{s p} = {\begin{matrix} \frac{\sin (\frac{s - p}{2}) π}{s - p} + \frac{\sin (\frac{s + p}{2}) π}{s + p} & (s \neq p), \\ - \frac{π}{2} & (s = p), \end{matrix}$

(32a)

${Ψ^{'}}_{s p} = {\begin{matrix} \frac{\sin (\frac{s - p}{2}) π}{s - p} - \frac{\sin (\frac{s + p}{2}) π}{s + p} & (s \neq p), \\ - \frac{π}{2} & (s = p), \end{matrix}$

(32b)

$γ_{p} = {\begin{matrix} \frac{\sin (\frac{p + 1}{2}) π}{p + 1} + \frac{\sin (\frac{p - 1}{2}) π}{p - 1} & (p \neq 1), \\ \frac{π}{2} & (p = 1), \end{matrix}$

(32c)

$δ_{p} = {\begin{matrix} \frac{\sin (\frac{p + 1}{2}) π}{p + 1} - \frac{\sin (\frac{p - 1}{2}) π}{p - 1} & (p \neq 1), \\ - \frac{π}{2} & (p = 1), \end{matrix}$

(32d)

联立式（30）,（31）,令阶数m=p=s,并将 $c_{1 m}$ , $c_{2 m}$ 的系数展开为矩阵形式进行求解。在计算中,需要对阶数s取合适的值。为了确保结果的收敛性,在本文后续计算中均取 $s =20$ 。需要指出的是,这里得到的 $c_{1 m}$ , $c_{2 m}$ ,是包含Laplace域桩身位移 $\overset{⌢}{\bar{u}}$ 的函数。由此可以得到冲击荷载作用下Laplace域内土层动力阻抗：

$\overset{⌢}{\bar{q}} = \int_{- \frac{π}{2}}^{\frac{π}{2}} {\overset{⌢}{\bar{σ}}}_{r} \cos θ d θ - {\overset{⌢}{\bar{τ}}}_{r θ} \sin θ d θ$ 。

(33)

土层动刚度和动阻尼分别为

${\overset{⌢}{\bar{q}}}_{k} = - \frac{1}{\overset{⌢}{\bar{u}}} Re (\sum_{m = 0}^{\infty} c_{1 m} γ_{m} + c_{2 m} δ_{m})$ ,

(34a)

${\overset{⌢}{\bar{q}}}_{c} = \frac{1}{\overset{⌢}{\bar{u}}} Im (\sum_{m = 0}^{\infty} c_{1 m} γ_{m} + c_{2 m} δ_{m})$ 。

(34b)

2.3 桩顶瞬态响应的Adomian分解法

根据欧拉–伯努利梁简化理论求解桩身水平振动位移幅值,其偏微分方程为

$\begin{matrix} E_{p} I_{p} \frac{\partial^{4}}{\partial z^{4}} u (z, t) + ρ_{p} A_{p} \frac{\partial^{2}}{\partial t^{2}} u (z, t) + (q_{k} + i q_{c}) u (z, t) = 0 \\ z \in (0, l) \end{matrix}$ ,

(35)

式中,l为桩身长度, $I_{p}$ , $ρ_{p}$ , $E_{p}$ , $A_{p}$ 分别是桩的截面惯性矩、密度、弹性模量和截面积。对式（35）进行无量纲化和Laplace变换,有

$\frac{d^{4}}{d {\bar{z}}^{4}} \overset{⌢}{\bar{u}} = 4 \frac{δ^{2} {\bar{ρ}}_{p} + ({\overset{⌢}{\bar{q}}}_{k} + i {\overset{⌢}{\bar{q}}}_{c}) / π}{{\bar{E}}_{p}} \overset{⌢}{\bar{u}}$ ,

(36)

式中, ${\bar{E}}_{p} = E_{p} / G$ , $\bar{z} = 2 z / d$ , $\bar{l} = 2 l / d$ , ${\bar{ρ}}_{p} = ρ_{p} / ρ_{s}$ 。

根据Adomian分解方法,桩在Laplace域内瞬态响应可以分解表示为

$\overset{⌢}{\bar{u}} = \sum_{n = 0}^{\infty} {\overset{⌢}{\bar{u}}}^{[n]}$ 。

(37)

令 $α^{4} = 4 \frac{δ^{2} {\bar{ρ}}_{p} + ({\overset{⌢}{\bar{q}}}_{k} + i {\overset{⌢}{\bar{q}}}_{c}) / π}{{\bar{E}}_{p}}$ ,线性算子 $L = \frac{d^{4}}{d {\bar{z}}^{4}}$ ,同时代入式（36）,（37）,有

$L^{- 1} L \overset{⌢}{\bar{u}} = \overset{⌢}{\bar{u}} - {\overset{⌢}{\bar{u}} |}_{\bar{z} = 0} - {\frac{d \overset{⌢}{\bar{u}}}{d \bar{z}} |}_{\bar{z} = 0} \bar{z} - {\frac{d \overset{⌢}{\bar{u}}}{d {\bar{z}}^{2}} |}_{\bar{z} = 0} \frac{{\bar{z}}^{2}}{2} - {\frac{d \overset{⌢}{\bar{u}}}{d {\bar{z}}^{3}} |}_{\bar{z} = 0} \frac{{\bar{z}}^{3}}{6}$ ,

(38)

$L^{- 1} L \overset{⌢}{\bar{u}} = α^{4} L^{- 1} \overset{⌢}{\bar{u}} = α^{4} L^{- 1} \sum_{n = 0}^{\infty} {\overset{⌢}{\bar{u}}}^{[n]}$ 。

(39)

将式（39）代入式（38）,有

$\overset{⌢}{\bar{u}} = {\overset{⌢}{\bar{u}} |}_{\bar{z} = 0} + {\frac{d \overset{⌢}{\bar{u}}}{d \bar{z}} |}_{\bar{z} = 0} \bar{z} + {\frac{d \overset{⌢}{\bar{u}}}{d {\bar{z}}^{2}} |}_{\bar{z} = 0} \frac{{\bar{z}}^{2}}{2} + {\frac{d \overset{⌢}{\bar{u}}}{d {\bar{z}}^{3}} |}_{\bar{z} = 0} \frac{{\bar{z}}^{3}}{6} + α^{4} L^{- 1} \sum_{n = 0}^{\infty} {\overset{⌢}{\bar{u}}}^{[n]} 。$

(40)

式（40）可以用如下的递推关系表示：

${\overset{⌢}{\bar{u}}}^{[0]} = {\overset{⌢}{\bar{u}} |}_{\bar{z} = 0} + {\frac{d \overset{⌢}{\bar{u}}}{d \bar{z}} |}_{\bar{z} = 0} \bar{z} + {\frac{d \overset{⌢}{\bar{u}}}{d {\bar{z}}^{2}} |}_{\bar{z} = 0} \frac{{\bar{z}}^{2}}{2} + {\frac{d \overset{⌢}{\bar{u}}}{d {\bar{z}}^{3}} |}_{\bar{z} = 0} \frac{{\bar{z}}^{3}}{6}$ ,

(41)

${\overset{⌢}{\bar{u}}}^{[n]} = α^{4} L^{- 1} \sum_{n = 0}^{\infty} {\overset{⌢}{\bar{u}}}^{[n - 1]}$ 。

(42)

对于如图1所示的桩土相互作用模型,假设桩上下边界均为自由边界,桩顶受到水平冲击荷载 $P (t)$ 作用。由此在桩顶、桩底分别有边界条件：

$\begin{matrix} {\frac{d^{2}}{d z^{2}} u (z, t) |}_{z = 0} = 0 & {\frac{d^{3}}{d z^{3}} u (z, t) |}_{z = 0} = - \frac{P (t)}{E_{p} I_{p}} \end{matrix}$ ,

(43)

$\begin{matrix} {\frac{d^{2}}{d z^{2}} u (z, t) |}_{z = l} = 0 & {\frac{d^{3}}{d z^{3}} u (z, t) |}_{z = l} = 0 \end{matrix}$ 。

(44)

将式（43）,（44）代入式（41）,（42）,整理递推式得

$λ_{11} {^{\frac{⌢}{u}} |}_{\bar{z} = 0} + λ_{12} {{\frac{d}{d \bar{z}}}^{\frac{⌢}{u}} |}_{\bar{z} = 0} + λ_{13} \frac{⌢}{P} = 0$ ,

(45a)

$λ_{21} {^{\frac{⌢}{u}} |}_{\bar{z} = 0} + λ_{22} {{\frac{d}{d \bar{z}}}^{\frac{⌢}{u}} |}_{\bar{z} = 0} + λ_{23} \frac{⌢}{P} = 0$ ,

(45b)

式中, $\bar{P} (t) = 4 P (t) / π d^{2} G$ , $λ_{11}$ , $λ_{12}$ , $λ_{13}$ , $λ_{21}$ , $λ_{22}$ , $λ_{23}$ 是由桩、土参数和边界条件决定的常数,对于确定的桩、土参数和边界条件,其均为定值。因此,解得

${^{\frac{⌢}{u}} |}_{\bar{z} = 0} = - \frac{λ_{22} λ_{13} - λ_{12} λ_{23}}{λ_{11} λ_{22} - λ_{12} λ_{21}} \frac{⌢}{P}$

(46a)

${{\frac{d}{d \bar{z}}}^{\frac{⌢}{u}} |}_{\bar{z} = 0} = - \frac{λ_{11} λ_{23} - λ_{21} λ_{13}}{λ_{11} λ_{22} - λ_{12} λ_{21}} \frac{⌢}{P}$ 。

(46b)

3. 算例对比与参数分析

3.1 Laplace数值反演计算方法

对由式（46）得到的Laplace域内瞬态响应解进行Laplace逆变换,可以得到瞬态动力响应的时域解,Laplace逆变换公式为

$f (t) = \frac{1}{2 πi} \int_{c - i \infty}^{c + i \infty} \overset{⌢}{f} (δ) e^{δ t} d δ$ 。

(47)

对于较复杂的函数形式,其时域形式很难直接解出。Durbin^[17]基于Fourier级数展开,将Laplace逆变换的问题转化为一个广义积分问题,给出了两组计算公式：

$f_{(I)} (t) = \frac{2}{T} [\frac{1}{2} \overset{⌢}{f} (c) + \sum_{k = 1}^{N} Re \overset{⌢}{f} (c + \frac{k π}{T} i) \cos \frac{k π t}{T}]$ ,

(48)

$f_{(II)} (t) = - \frac{2 e^{c t}}{T} [\sum_{k = 1}^{N} Im \overset{⌢}{f} (c + \frac{k π}{T} i) \sin \frac{k π t}{T}]$ 。

(49)

通过令其中 $f (t) = [f_{(Ι)} (t) + f_{(ΙΙ)} (t)] / 2$ ,可以有效处理 $f (t)$ 具有间断点的情况。另外, $f_{(Ι)} (t)$ 与 $f_{(ΙΙ)} (t)$ 相对 $f (t)$ 的误差偏向相反,因此对于不同的参数c,T,利用优化模型 $\min_{c \in (0, \infty)} | f_{(Ι)} (t) - f_{(ΙΙ)} (t) |$ ,可以得到较为精确的解答。另外本文采用了ε-algorithm（EPAL）优化了计算的收敛过程,ε-algorithm（EPAL）是将Durbin逆运算算法分解为如下的级数形式,其收敛性和应用范围的论述参考于Crump^[18]与Honig^[19]。

$C_{k} = \frac{e^{c t}}{T} [Re \overset{⌢}{f} (c + \frac{k π}{T} i) \cos \frac{k π t}{T} - Im \overset{⌢}{f} (c + \frac{k π}{T} i) \sin \frac{k π t}{T}],$

(50)

$f_{N} (t) = \frac{1}{2} C_{0} + \sum_{k = 1}^{N} C_{k}$ 。

(51)

3.2 算例对比与分析Ⅰ

为验证本文解的有效性及探讨考虑桩土局部分离对桩、土位移瞬态响应的影响。参考文献[9]中参数,本文采用如图2所示的三角形冲击荷载,其中 $P_{\max} = 10^{6}$ kN,冲击荷载持续时间 $Δ \bar{t}$ =10,桩周土体泊松比 $ν_{s}$ =0.4,桩身弹性模量 ${\bar{E}}_{p}$ =280,密度 ${\bar{ρ}}_{p}$ =1.6,直径d=2 m,桩身长度 $\bar{l}$ =75。

图 2 三角形冲击荷载时程

Figure 2. Time histories of triangular impact force

下载: 全尺寸图片幻灯片

分别采用本文方法和有限元法计算桩–土的位移时程,并与边界元法^[5-6]和连续介质解^[9]的计算结果进行对比。其中边界元法和连续介质解均假定桩土接触面连续紧密接触,有限元法假定桩土相互作用为硬接触,摩擦系数取 $\tan (0.8 φ^{'})$ ^[12],其中 $φ^{'}$ 为桩周土体内摩擦角。如图3所示,与边界元法和连续介质解相比,采用本文方法得到的桩顶位移幅值增大57.3%～61.0%,证明了文献[5]中关于“实际工程中,桩土接触面会发生部分屈服和局部脱开、滑移,因而,实际位移可能与文中计算结果相距甚远”的推论。相对于有限元法,采用本文方法得到的桩顶位移幅值减小19.6%,这是由于有限元法计算中桩土接触面存在相对滑移。此外,由图3中桩顶运动时程可以看出,采用本文方法、有限元和边界元法计算得到的桩顶位移均有较为明显冲击—回弹—再冲击的现象,而连续介质解则没有这种现象。原因是基于平面应变模型计算得到的土层水平动阻尼较三维模型偏大^[20],忽略桩土局部分离特性和高频冲击荷载^[21]使其偏差更为显著。因而在桩土模量比较小时,采用连续介质解的桩土相互作用模型呈现出“过阻尼”的状态,此时计算结果与实际情况可能存在较大差异。

图 3 桩顶水平位移对比

Figure 3. Comparison of transverse displacements at pile top

下载: 全尺寸图片幻灯片

图4,5分别给出了采用本文方法、有限元法和连续介质解^[9]计算得到的地表x,y方向位移场分布,其中x,y方向分别平行和垂直于桩身运动方向（见图1）。时间因子 $\bar{t}$ 取6.2,如图3所示,此时上述几种方法得到的桩顶位移均接近于时程曲线最大值。如图4（b）,（c）所示,本文方法和有限元法计算得到的地面位移场较为接近。与图4（a）中连续介质解的结果相比,桩后主动区土体位移较小,与桩身出现较为明显的相对位移。

图 4

$\bar{t}$ =6.2时刻地表x方向位移场分布

Figure 4. Displacement fields in x direction when

$\bar{t} = 6.2$

下载: 全尺寸图片幻灯片

图 5

$\bar{t}$ =6.2时刻地表y方向位移场分布

Figure 5. Displacement fields in y direction when

$\bar{t} = 6.2$

下载: 全尺寸图片幻灯片

另外,如图5（a）,（b）所示,考虑桩土局部分离时,桩身运动对桩侧后土体的动力作用较不考虑桩土局部分离的结果有一定削弱。图5（c）中有限元法由于考虑了桩侧土体的滑移,桩身运动对桩侧土体影响进一步降低。可以看出,是否考虑桩土局部分离,对桩周土位移场分布有显著影响。值得指出的是,在Tuladhar等^[11]采用有限元法和现场试验对桩土局部分离特性的研究中,所得到的桩周土位移场与本文结果有相同的规律。此外,文献[11]中同时采用有限元法分析了不考虑桩土局部分离的对比组,所得到的桩周土位移场和采用连续介质解^[9]的结果相似,且均与试验结果存在较大差异。以上对比进一步地表明了在计算中考虑桩土局部分离的必要性和本文方法的可信度。

3.3 算例对比与分析Ⅱ

为研究桩土局部分离在不同模量比下对桩、土位移瞬态响应的影响,参考文献[6]中参数,采用如图6所示的阶跃荷载,其中 $Δ \bar{t}$ =0.1761,桩周土体剪切模量G=1.716 MPa,泊松比 $ν_{s}$ =0.4,桩身无量纲密度 ${\bar{ρ}}_{p}$ =1.5,桩长 $\bar{l}$ =55,直径d=0.8 m。

图 6 阶跃荷载时程

Figure 6. Time histories of Heaviside force

下载: 全尺寸图片幻灯片

图7给出了采用本文方法和边界元法^[6]在不同模量比下计算得到的桩顶水平位移时程曲线。如图7所示,考虑桩土分离时,模量比对桩顶位移的影响与不考虑桩土分离的情况较为一致。随着桩土模量比的增加,桩身刚度逐渐增加,桩顶位移逐渐减小。值得指出的是,在 $\bar{t} =25 Δ \bar{t}$ 时,桩土模量比E_p/E_s=50情况下的桩顶位移约为模量比E_p/E_s=1000的209.5%,而文献[6]中采用边界元法的结果约为161.4%。对比可见,计算中若不考虑桩土局部分离,得到的桩土模量比对桩身瞬态动力响应的影响,较考虑桩土局部分离的结果偏小。

图 7 不同模量比下桩顶水平位移对比

Figure 7. Comparison of transverse displacements at pile top under different modulus ratios

下载: 全尺寸图片幻灯片

3.4 参数分析

为分析考虑桩土局部分离时,桩土各参数对桩身瞬态响应的影响。本文采用如图2所示的三角形冲击荷载进行分析讨论。其中 $P_{\max} = 10^{3}$ kN,冲击荷载持续时间 $Δ \bar{t}$ =10,泊松比 $ν_{s}$ =0.3,桩身弹性模量 $E_{p}$ =25 GPa,无量纲密度 ${\bar{ρ}}_{p}$ =1.6,桩长l=12 m,直径d=0.6 m。

图8给出了不同模量比（E_p/E_s）情况下,桩身位移在时域上的变化过程。可见,桩顶位移与所施加荷载的变化规律较为一致。如图8所示,随着桩土模量比的增加,桩周土体刚度逐渐减小,桩身位移逐渐增加,位移中性点逐渐下移,表现出桩身运动对桩周土影响深度逐渐增加的趋势。需要说明的是,图7,8的计算中分别假定桩周土和桩身弹性模量保持一致,因此模量比对桩顶水平位移产生了不同的影响。此外,不同模量比情况下,桩顶位移到达峰值所需时长均较为接近,但位移沿深度向下传递时间逐渐缩短。另外,桩顶受冲击荷载时,在时域上能明显观察到冲击—回弹—再冲击的过程和波动前进的趋势,显示出了桩身位移在时域上的波动性。

图 8 冲击荷载作用下桩身位移时程

Figure 8. Time histories of displacement of pile under impact force

下载: 全尺寸图片幻灯片

图9给出了在不同时刻,桩土模量比（E_p/E_s）和桩身长径比（ $\bar{l}$ ）对桩顶位移的影响。可见,随着长径比的增加,各时刻桩顶位移呈现逐渐减小的趋势,且在长径比较小时减小的速率较大；当长径比较大时桩顶位移逐渐趋于稳定,此时长径比对桩顶位移影响可以忽略不计。图中★指代长径比限值l^*的位置,其对应的桩顶位移与40倍长径比作用下的桩顶位移相差5%。如图9所示,随着桩土模量比的逐渐增加,长径比l^*总体上有逐渐增大的趋势,指出桩身运动对桩周土体的影响深度逐渐增加。对于不同类型的桩土模量比,l^*的取值大致在区间[8.6～18]内。

图 9 冲击荷载作用下长径比对桩顶位移幅值的影响

Figure 9. Effects of slenderness ratio on displacement of pile top under impact force

下载: 全尺寸图片幻灯片

4. 结论

（1）采用本文方法计算出的桩顶位移瞬态响应和桩周土位移场与实验结果和有限元法结果更接近。而忽略桩土局部分离,一方面过高地估计了桩周土体的动力阻抗,导致冲击荷载作用下,桩身位移过小,且能量在土体中较快消散,使得桩顶位移呈现出类似“过阻尼”的状态；另一方面,计算得到的桩后主动区土体位移场分布与试验结果存在较大差异。上述现象和规律,可以为桩基设计提供初步参考。

（2）冲击荷载作用下,桩土模量比对桩身瞬态动力响应影响较为显著。忽略桩土局部分离,会导致低估模量比对桩顶位移响应的影响。

（3）冲击荷载作用下,桩身长径比较小时,桩顶位移响应受桩身长径比影响较大。桩土模量比较大时,桩身运动对桩周土体的影响范围较大。

图 1 取芯钻具在着陆器上的安装位置

Figure 1. Mounting position of coring drill on lander

下载: 全尺寸图片幻灯片

图 2 临界尺度颗粒的运移特性示意图

Figure 2. Migration characteristics of critical fragments

下载: 全尺寸图片幻灯片

图 3 临界尺度工况地面钻取试验

Figure 3. Surface drilling tests on critical fragments

下载: 全尺寸图片幻灯片

图 4 临界尺度颗粒与切削刃作用示意图

Figure 4. Schematic diagram of overlap of critical fragments and cutter

下载: 全尺寸图片幻灯片

图 5 切削刃与月壤作用受力示意图

Figure 5. Schematic diagram of axial section forces on cutter and lunar soil interaction

下载: 全尺寸图片幻灯片

图 6 切削月壤力学示意图

Figure 6. Diagram of mechanics of lunar soil cutting

下载: 全尺寸图片幻灯片

图 7 密实核成型描述

Figure 7. Description of dense nucleation

下载: 全尺寸图片幻灯片

图 8 固定钻进深度下的单刃切削阻力

Figure 8. Cutting resistances of fixed single edge at depth of drilling

下载: 全尺寸图片幻灯片

图 9 回转轨迹等效示意图

Figure 9. Schematic diagram of equivalent rotation trajectory

下载: 全尺寸图片幻灯片

图 10 仿真切削过程速度云图

Figure 10. Simulation of cutting process speed nephogram

下载: 全尺寸图片幻灯片

图 11 切削阻力时域变化曲线

Figure 11. Time-domain variation curves of cutting resistance

下载: 全尺寸图片幻灯片

图 12 SLC-1试验台结构图

Figure 12. Structure drawing of SLC-1 testing bench

下载: 全尺寸图片幻灯片

图 13 模拟月壤样品

Figure 13. Simulated lunar soil samples

下载: 全尺寸图片幻灯片

图 14 平均切削阻力变化曲线

Figure 14. Average cutting resistance curves

下载: 全尺寸图片幻灯片

图 15 切削阻力时域变化曲线

Figure 15. Time-domain variation curves of cutting resistance

下载: 全尺寸图片幻灯片

图 16 切削过程结束

Figure 16. Completion of cutting process

下载: 全尺寸图片幻灯片

图 17 切削阻力–法向重叠率试验曲线

Figure 17. Curves of cutting resistance-normal overlap rate tests

下载: 全尺寸图片幻灯片

表 1 钻具回转速度与线速度换算表

Table 1 Conversion of rotary speed and linear speed of drilling tool

回转速度/rpm	60	80	100	120
线速度/(mm·s^-1)	47.1	61.2	78.7	94.2

下载: 导出CSV

表 2 仿真环境参数标定

Table 2 Parameter calibration of simulation environment

参数	数值
颗粒泊松比	0.35
均质颗粒半径/mm	1.0
临界尺度颗粒粒径/mm	15
颗粒密度/(kg·m^-3)	2900
颗粒剪切模量/Pa	1×10⁸
切削刃泊松比	0.3
切削刃密度/(kg·m^-3)	7800
切削刃杨氏模量/Pa	7×10⁷
切削深度/mm重力加速度/(m·s^-2)	41.6
切削速度/(mm·s^-1)	94.2
颗粒-颗粒恢复系数	0.1
颗粒-颗粒静摩擦系数	0.514
颗粒-颗粒动摩擦系数	0.1
颗粒-几何体恢复系数	0.2
颗粒-几何体静摩擦系数	0.3
颗粒-几何体动摩擦系数	0.1

下载: 导出CSV

表 3 试验制备均质月壤物理力学参数

Table 3 Physical and mechanical parameters of prepared homogeneous lunar soil

参数	密度/(g·cm^-3)	泊松比	孔隙比	内摩擦角/(°)
数值	2.1	0.35	0.31	34.96

下载: 导出CSV

参考文献(23)

[1]	蒋明镜. 现代土力学研究的新视野——宏微观土力学[J]. 岩土工程学报, 2019, 41(2): 195-254. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902002.htm JIANG Ming-jing. New paradigm for modern soil mechanics: Geomechanics from micro to macro[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(2): 195-254. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902002.htm
[2]	尹振宇, 许强, 胡伟. 考虑颗粒破碎效应的粒状材料本构研究：进展及发展[J]. 岩土工程学报, 2012, 34(12): 2170-2180. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201212006.htm YIN Zhen-yu, XU Qiang, HU Wei. Research on the constitutive properties of granular materials considering the effect of particle breakage: Progress and development[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(12): 2170-2180. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201212006.htm
[3]	唐钧跃, 全齐全, 姜生元, 等. 模拟月壤钻进力载建模及试验验证[J]. 机械工程学报, 2017, 53(7): 85-93. https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201707013.htm TANG Jun-yue, QUAN Qi-quan, JIANG Sheng-yuan, et al. Mechanics modeling and experimental validation for lunar regolith simulant drilling[J]. Journal of Mechanical Engineering, 2017, 53(7): 85-93. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201707013.htm
[4]	郭汝坤, 冯春, 李战军, 等. 牙轮钻工作参数与岩体强度对应关系的理论分析与实验研究[J]. 岩土工程学报, 2016, 38(7): 1221-1229. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201607008.htm GUO Ru-kun, FENG Chun, LI Zhanjun, et al. Theoretical and experimental studies on relationship between working parameters of cone drill and rock strengths[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(7): 1221-1229. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201607008.htm
[5]	张宇, 陈善雄, 余飞, 等. 低应力水平下CAS-1模拟月壤力学特性试验研究[J]. 岩石力学与工程学报, 2015, 34(1): 174-181. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201501019.htm ZHANG Yu, CHEN Shan-xiong, YU Fei, et al. Esperimental study of mechanocal properties of lunar soil simulant CAS-1 under low stress[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(1): 174-181. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201501019.htm
[6]	李宁, 李骞, 宋玲. 基于回转切削的岩石力学参数获取新思路[J]. 岩石力学与工程学报, 2015, 34(2): 323-329. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201502013.htm LI Ning, LI Qian, SONG Ling. Acquiring mechanical parameters of rock basd on rotational cutting[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(2): 323-329. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201502013.htm
[7]	刘泉声, 刘建平, 时凯, 等. 评价岩石脆性指标对滚刀破岩效率的影响[J]. 岩石力学与工程学报, 2016, 35(3): 498-510. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201603007.htm LIU Quan-sheng, LIU Jian-ping, SHI Kai, et al. Evaluation of rock brittleness indexes on rock fragmentation efficiency by disc cutter[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(3): 498-510. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201603007.htm
[8]	DOSHVARPASSAND S, RICHARD T, MOSTOFI M. Effect of groove geometry and cutter in rock cutting[J]. Journal of Petroleum Science and Engineering, 2017, 151(10): 1-1.
[9]	LI P, JIANG S Y, TANG D W, et al. Design and testing of coring bits on drilling lunar rock simulant[J]. Advances in Space Research, 2017, 59(4): 1057-1076.
[10]	CHE D, ZHANG W Z, EHMANN K. Chip Formation and force responses in linear rock cutting: an experimental study[J]. Journal of Manufacturing Science and Engineering, 2017, 139(8): 1-12.
[11]	DAGRAIN F, QUICKELBERGHE F V, TSHIBANGU J P. A new procedure to analyse the wear of cutting elements[C]//Eurock 2006, 2006, Belgium.
[12]	刘天喜, 魏承, 马亮, 等. 大颗粒岩块对月壤钻取过程的影响分析[J]. 岩土工程学报, 2014, 36(11): 2118-2126. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201411024.htm LIU Tian-xi, WEI Cheng, MA Liang, et al. Effect of large granular rocks on drilling process of lunar soils[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(11): 2118-2126. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201411024.htm
[13]	庞勇, 冯亚杰, 孙启臣, 等. 月壤大颗粒对钻进力载影响的仿真及试验研究[J]. 北京大学学报(自然科学版), 2019, 55(3): 397-404. https://www.cnki.com.cn/Article/CJFDTOTAL-BJDZ201903001.htm PANG Yong, FENG Ya-jie, SUN Qi-chen, et al. Simulation and experimental study on the effect of large granular rocks in lunar soil on drilling load[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2019, 55(3): 397-404. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BJDZ201903001.htm
[14]	QIAN Y Q, XIAO L, YIN S, et al. The regolith properties of the Chang'e-5 landing region and the ground drilling experiments using lunar regolith simulants[J]. Elsevier Inc, 2020, 337(5): 113508-113521.
[15]	TIAN Y, TANG B, YANG F, et al. Lunar critical fragment layer simulant identification using an impact method[J]. Acta Astronautica, 2020, 173(6): 294-302.
[16]	林呈祥, 凌道盛, 钟世英, 等. TJ-1模拟月壤颗粒几何特性[J]. 东北大学学报(自然科学版), 2016, 37(3): 451-456. https://www.cnki.com.cn/Article/CJFDTOTAL-DBDX201603031.htm LIN Cheng-xiang, LING Dao-sheng, ZHONG Shi-ying, et al. Geometric characteristics of TJ-1 lunar soil simulant particles[J]. Journal of Northeastern University (Natural Science), 2016, 37(3): 451-456. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DBDX201603031.htm
[17]	郑永春, 欧阳自远, 王世杰, 等. 月壤的物理和机械性质[J]. 矿物岩石, 2004, 24(4): 14-19. https://www.cnki.com.cn/Article/CJFDTOTAL-KWYS200404003.htm ZHENG Yong-chun, OUYANG Zi-yuan, WANG Shi-jie, et al. Physical and mechanical properties of lunar regolith[J]. Journal of Mineralogy and Petrology, 2004, 24(4): 14-19. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KWYS200404003.htm
[18]	胡伟, 孟建伟, 刘顺凯, 等. 单螺旋锚桩水平承载机理试验与理论研究[J]. 岩土工程学报, 2020, 42(1): 158-167. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202001025.htm HU Wei, MENG Jian-wei, LIU Shun-kai, et al. Experimental and theoretical researches on horizontal bearing mechansim of single screw anchor pile[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(1): 158-167. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202001025.htm
[19]	WHEELER P, GODWIN R. Soil dynamics of single and multiple tines at speeds up to 20km/h[J]. Journal of Agricultural Engineering Research, 1996, 63(3): 243-249.
[20]	LI P, JIANG S Y, TANG D W, et al. A PFC3D-based numerical simulation of cutting load for lunar rock simulant and experimental validation[J]. Advances in Space Research, 2017, 59(10): 2583-2599.
[21]	戴北冰, 杨峻, 刘锋涛, 等. 散粒土自然堆积的宏细观特征与形成机制[J]. 岩土工程学报, 2019, 41(增刊2): 57-60. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2019S2016.htm DAI Bei-bing, YANG Jun, LIU Feng-tao, et al. Macro- and micro-properties and formation mechanisms of granular piles[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(S2): 57-60. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2019S2016.htm
[22]	CARRIER W. Geotechnical Properties of Lunar Soil[R]. Lake Land: Lunar Geotechnical Institute, 2005.
[23]	田野, 陈萌萌, 杨飞, 等. 用于砂土层连续采样的柔性软袋式钻取采样技术研究[J]. 农业机械学报, 2018, 49(12): 246-252. https://www.cnki.com.cn/Article/CJFDTOTAL-NYJX201812030.htm TIAN Ye, CHEN Meng-meng, YANG Fei, et al. Technology of coring drill with flexible tube for sand layers continuous sampling[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(12): 246-252. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-NYJX201812030.htm