一种实用型深海能源土多场耦合离散元数值方法

蒋明镜; 陈意茹; 卢国文

doi:10.11779/CJGE202108003

一种实用型深海能源土多场耦合离散元数值方法 English Version

蒋明镜^{1, 2, 3, 4,},
陈意茹¹,
卢国文¹

1.
天津大学建筑工程学院,天津　300350
2.
天津大学水利工程仿真与安全国家重点实验室,天津300350
3.
同济大学土木工程防灾重点实验室,上海　200092
4.
同济大学土木工程学院地下建筑与工程系,上海　200092

基金项目:

国家自然科学基金重大项目 51890911

国家重点研发计划项目 2019YFC0312304

土木工程防灾国家重点试验室自主研究课题项目 SLDRCE19-A-06

详细信息

作者简介:
蒋明镜(1965— ),男,教授,博士生导师,主要从事天然结构性黏土、砂土、非饱和土、太空土和深海能源土宏观微观试验、本构模型和数值分析研究。E-mail：mingjing.jiang@tju.edu.cn

中图分类号: TU411
计量
- 文章访问数: 350
- HTML全文浏览量: 21
- PDF下载量: 300
出版历程
- 收稿日期: 2020-12-15
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-07-31

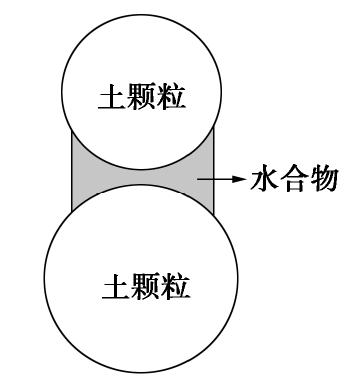
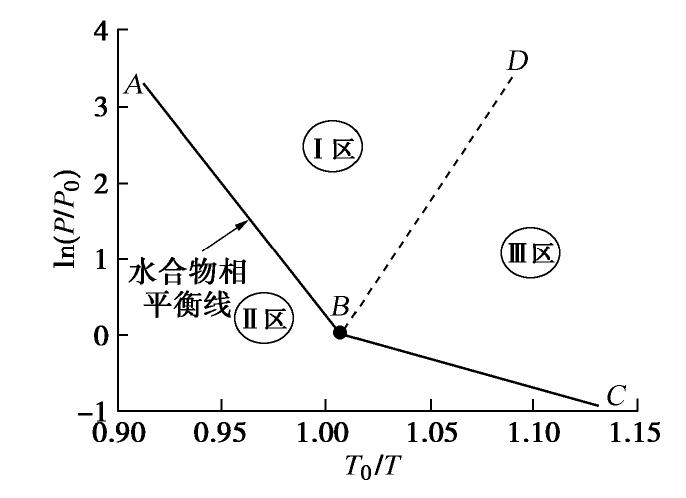
A practical multi-field coupling distinct element method for methane hydrate bearing sediments

JIANG Ming-jing^{1, 2, 3, 4,},
CHEN Yi-ru¹,
LU Guo-wen¹

1.
School of Civil Engineering, Tianjin University, Tianjin 300350, China
2.
State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300350, China
3.
State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China
4.
Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China

摘要

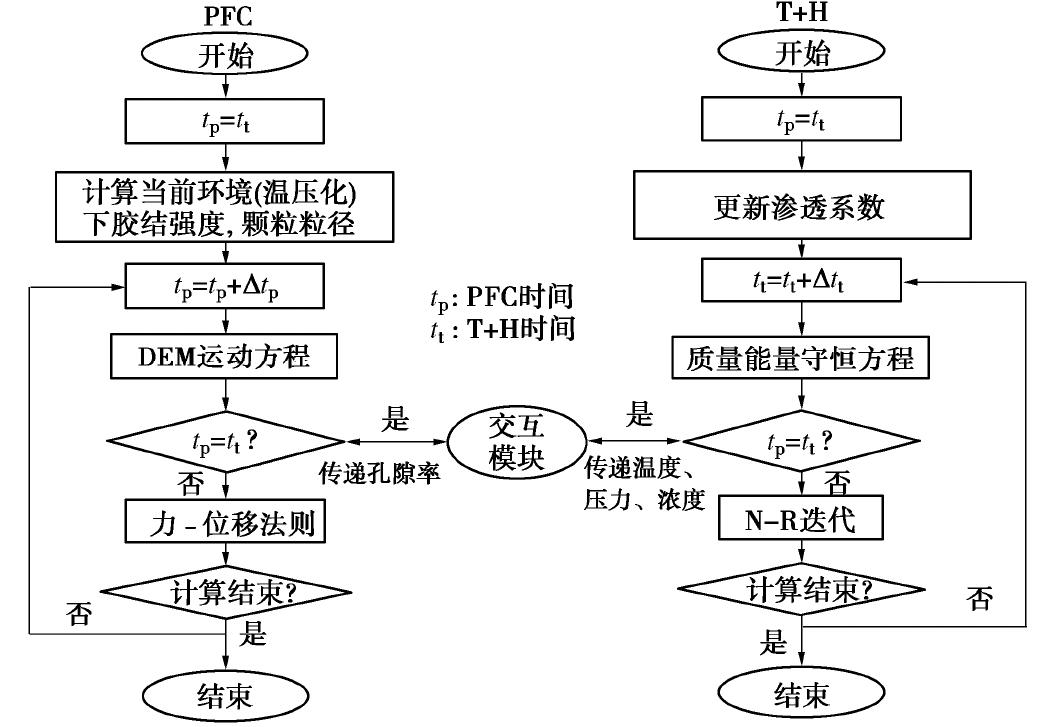
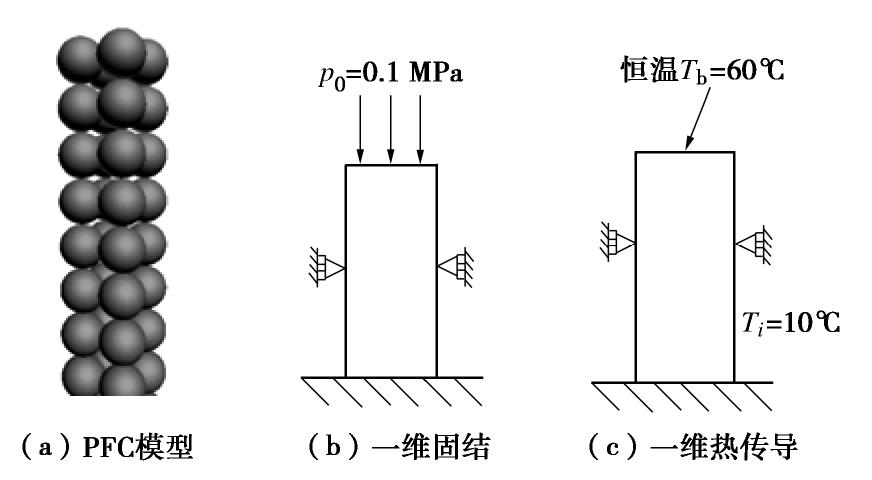
摘要: 水合物储量丰富且污染小,是全球关注的未来绿色能源。而水合物的大规模开采将致使水合物沉积物（即能源土）力学性质劣化,从而引发出砂、海底滑坡等工程和地质灾害,制约水合物的安全高效开采。针对目前大多数多场耦合分析框架无法准确描述颗粒运移等大变形问题,基于离散元商业计算软件Particle Flow Code (PFC)和含水合物多孔介质的多相流分析程序TOUGH+HYDRATE (T+H),构建了一种实用型水合物开采多场耦合分析框架T+H+PFC。通过将力学计算模块PFC所得孔隙率参数和T+H计算所得温度、压力、盐浓度信息交换、更新,实现了T+H与PFC的耦合计算。然后,通过一维固结和一维热传导试验验证了该耦合程序的有效性。最后,模拟分析了一维降压、升温开采下能源土动态响应的与水合物弱化过程。结果表明,耦合模拟与试验结果较为吻合,T+H+PFC在多场耦合下水合物开采引起的地层变形、出砂、海底滑坡等问题分析中具有良好的应用前景。
- 能源土 /
- 水合物开采 /
- 数值模拟 /
- 离散单元法
Abstract: The methane hydrate (MH) has been attracting extensive attention as a promising green energy source because of the abundant reserve and more environmental friendliness. However, large-scale exploitation induces the weakening of MH bearing sediments (MHBS) structure, which can result in engineering problems such as sand jamming, and environmental disasters such as landslide, and this will constrain efficient and safe exploitation of MH. Given that several multi-field coupling simulators fail to accurately describe large deformation of soils such as particle migration, a practical multi-field method T+H+PFC for MH exploitation analysis is established based on the commercial distinct element method (DEM), software particle flow code (PFC) and numerical code TOUGH+HYDRATE (T+H) for the multiphase flow analysis of hydrate-bearing geologic systems. The coupling computation can be achieved by exchanging the information between the porosity obtained by DEM and the temperature, pressure and salinity obtained by T+H. Then, the method is validated by conducting numerical modeling of one-dimensional (1D) consolidation and 1D heat conduction tests. Finally, focus is on the dynamic responses of MHBS and weakening of MH under the conditions of 1D dissociation tests with depressurization and heat stimulating methods. The numerical results are found to be in good agreement with the experimental data available, which demonstrates that the T+H+PFC method has a great promise in the MH decomposition-induced multi-field coupling analysis, such as deformation of seabed, sand production and submarine landslide.
- methane hydrate bearing sediment /
- hydrate dissociation /
- numerical simulation /
- distinct element method

HTML全文

0. 引言

当前，描述非饱和土变形本构模型通常也可分为非线性弹性模型和弹塑性模型。对于非饱和土非线性弹性模型，主要是基于常用的邓肯-张的E-μ模型，以及在该模型基础上发展建立的E-B模型、K-G模型上进行改进的，通常将非饱和土的净应力和基质吸力的影响考虑到非线性模型的参数上^[1-3]，或是通过考虑引入含水率或是初始饱和度来考虑吸力的变化的^[4-5]，进而扩展为非饱和土的非线性弹性模型。

对于非饱和土弹塑性模型，由于弹塑性理论是一个有力而灵活的框架，因而弹塑性本构模型仍然是非饱和土变形本构理论研究的一个特征^[6]。在弹塑性模型中，Alonso等^[7]提出的BBM模型是一个具有相当广泛代表性的非饱和土弹塑性模型，该模型是在修正剑桥(MCC)模型基础上拓展的，在p-q-s所建立的应力空间内探索非饱和土的变形问题。后继的很多非饱和土模型都是在Alonso等^[7]提出的BBM的基础上建立的。Josa等^[8]认为在某净围压下存在最大湿陷量，对加载-湿陷（LC）屈服曲线进行了修正。黄海等^[9]和苗强强等^[10]等根据大量非饱和黄土和非饱和含黏砂土三轴试验资料，分别利用得到的初始屈服线的形状、压缩指数的变化规律、广义土-水特征曲线和建立的p-s平面上屈服点连线的统一函数表达式对BBM模型进行了修正和验证。陈正汉^[11]以BBM模型为基础，结合原状湿陷黄土的大量CT-三轴试验得到的细观结构演化规律，构建了原状湿陷性黄土的结构性模型（弹塑性损伤模型），并用于大厚度湿陷性黄土的现场浸水试验分析。陈正汉^[11]通过对Gens等^[12]提出的BBM膨胀土模型进行了不区分宏观和微观结构层次变形、针对膨胀变形特点增加SD屈服面、补充水量变化数学描述3点改进，改进模型能够预测重塑膨胀土的主要变形特征。姚仰平等^[13]将BBM模型和UH模型，建立适用超固结土的非饱和土模型。张登飞^[14]考虑力水作用的影响，对BBM模型屈服面的方程进行改进，建立了能够描述原状黄土力水耦合相关特性的弹塑性本构模型。刘帅帅^[15]采用平均骨架应力对BBM模型中的LC屈服曲线进行改进，建立了吸力、变形与饱和度三者之间的关系，来描述非饱和土黄土的水力与力学的耦合。

可见，对于非饱和土变形特性的研究就是对非饱和土的各个应力状态变量与土粒、孔隙气和孔隙水各相间应变关系的研究。描述非饱和土体积变化行为的本构关系是将非饱和土的应力状态变量与应变状态变量联系起来，其中正确反映吸力在土变形中的贡献是非饱和土本构模型的关键。大多数的研究仍采用净应力 ${\text{(}}\sigma - {u_{\text{a}}}{\text{)}}$ 和基质吸力 ${\text{(}}{u_{\text{a}}} - {u_{\text{w}}}{\text{)}}$ 为两个独立的应力变量作为相关的应力状态变量，来建立本构模型模拟非饱和土的相关力学行为。本文对基于临界状态提出的非饱和土BBM模型进行分析、研究、验证，并做进一步的修正，使模型更符合非饱和黄土基质吸力的变化规律，为解决实际工程中的非饱和黄土工程问题提供理论基础，对指导黄土地区的工程建设及运行、地质灾害的评价及预测具有重要意义。

1. 非饱和土BBM模型

Alonso等^[7]提出的基于临界状态的非饱和土BBM模型是对Roscoe和Burland提出的修正剑桥模型（MCC）的扩展。非饱和土BBM模型由4个状态变量来定义，即净平均应力 $p = {\text{(}}{\sigma _1}{\text{ + }}{\sigma _2}{\text{ + }}{\sigma _3}{\text{)/3}} -$ ${u_{\text{a}}}$ ，剪应力 $q = {\sigma _1} - {\sigma _3}$ ，基质吸力 $s = {u_{\text{a}}} - {u_{\text{w}}}$ ，比体积 $v = 1 + e$ 。

BBM模型具有两个状态边界面：一个曲面和一个平面。当土体状态位于状态边界面内时，模型表现为弹性应变；当土体状态到达状态边界面时，模型开始表现为塑性应变；当土体状态越过状态边界面时，塑性行为对应于屈服面在 $p:q:s$ 空间上扩展。

1.1 各向等压应力状态

Alonso等^[7]认为，对于各向等压状态，在恒定基质吸力s下，净平均p对比体积v的影响可定义为

。

$v = N{\text{(}}s{\text{)}} - \lambda {\text{(}}s{\text{)ln}}\frac{p}{{{p^{\text{c}}}}} 。$

(1)

式中： $N{\text{(}}s{\text{)}}$ 为 $p = {p^{\text{c}}}$ 时的比体积； ${p^{\text{c}}}$ 为参考应力参数； $\lambda {\text{(}}s{\text{)}}$ 为吸力为 $s$ 时的刚度参数， $\lambda {\text{(}}s{\text{)}}$ 定义为

。

$\lambda {\text{(}}s{\text{)}} = \lambda {\text{(}}0{\text{)[(}}1 - r{\text{)exp(}} - \beta s{\text{)}} + r{\text{]}} 。$

(2)

式中： $r = \frac{{\lambda (s \to \infty )}}{{\lambda (0)}}$ ； $\beta$ 为土体刚度随吸力增加速率的参数。

Alonso等^[7]认为在一定基质吸力值 $s$ 下，非饱和土的加载再卸载变形是弹性的，体积的变化可表示为

。

${\text{d}}v = - \kappa \frac{{{\text{d}}p}}{p} 。$

(3)

式中：κ为 $p$ 变化时的刚度系数（），在非饱和土BBM模型中，假定 $\kappa$ 恒定的，不随基质吸力的变化而改变。

图 1 饱和土与非饱土的比体积的变化曲线

Figure 1. Change curves of specific volume of saturated and unsaturated soils

下载: 全尺寸图片幻灯片

为饱和土和非饱和土在各向等压应力状态下的比体积变化曲线。 $p_0^{\text{*}}$ 为饱和土屈服应力， ${p_0}{\text{(}}s{\text{)}}$ 为基质吸力s时的屈服净应力。不同吸力值下的屈服应力值 ${p_0}{\text{(}}s{\text{)}}$ 组合成了一条加载-湿陷屈服曲线（图 2），即LC屈服线。Alonso等^[7]定义了LC屈服线的表达式为

$\frac{{{p_0}{\text{(}}s{\text{)}}}}{{{p_{\text{c}}}}} = {\left[ {\frac{{p_0^{\text{*}}}}{{{p_{\text{c}}}}}} \right]^{\frac{{\lambda {\text{(0)}} - \kappa }}{{\lambda {\text{(}}s{\text{)}} - \kappa }}}} 。$

(4)

图 2 LC屈服线和SI屈服线

Figure 2. LC and yield loci

下载: 全尺寸图片幻灯片

如所示，LC屈服线和SI屈服线（吸力增加屈服线）在( $p,s$ )平面上包围的区域为弹性区域，SI屈服线的表达式为

$s = {s_0} \text{，}$

(5)

式中， ${s_0}$ 为土在历史上曾经受过的最大吸力^[12]。

1.2 剪切应力状态

BBM是基于临界状态框架的弹塑性本构模型，是对修正剑桥模型的扩展，将基质吸力 $s = {u_{\text{a}}} - {u_{\text{w}}}$ 作为第三种应力状态变量来考虑基质吸力的影响。屈服面仍采用修正剑桥模型的椭圆形。基质吸力变化时，椭圆也变化，椭圆的大小由不同基质吸力下的屈服应力 ${p_0}(s)$ 来确定。BBM模型中假定黏聚力的增大是与基质吸力的增大是呈线性变化的。从而给出了该模型在 $(p,q)$ 平面上的屈服面（图 3）的表达式为

${q^2} - {M^2}(p + {p_{\text{s}}})[{p_0}(s) - p] = 0 。$

(6)

图 3 (

$p,q$ )和(

$p,s$ )面上的屈服轨迹

Figure 3. Yield loci on (

$p,q$ ) and (

$p,s$ ) planes

下载: 全尺寸图片幻灯片

式中：M为临界状态线的斜率； ${p_{\text{s}}} = ks$ ， $k$ 为常数。

1.3 硬化规律和流动法则

（1）应变硬化规律

在非饱和土模型建立过程中，需要同时考虑净平均应力和基质吸力对弹塑性体应变产生的影响，分别定义如下。

弹性体应变：

${\text{d}}\varepsilon _{\text{v}}^{\text{e}} = {\text{d}}\varepsilon _{{\text{vp}}}^{\text{e}} + {\text{d}}\varepsilon _{{\text{vs}}}^{\text{e}} 。$

(7)

式中： ${\text{d}}\varepsilon _{\text{v}}^{\text{e}}$ 为弹性体应变； ${\text{d}}\varepsilon _{{\text{vp}}}^{\text{e}}$ 为由净平均应力引起的弹性体应变； ${\text{d}}\varepsilon _{{\text{vs}}}^{\text{e}}$ 为由基质吸力引起的弹性体应变。

塑性体应变：

${\text{d}}\varepsilon _{\text{v}}^{\text{p}} = {\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}} + {\text{d}}\varepsilon _{{\text{vs}}}^{\text{p}} 。$

(8)

式中： ${\text{d}}\varepsilon _{\text{v}}^{\text{p}}$ 为塑性体应变； ${\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}}$ 为由净平均应力引起的塑性体应变； ${\text{d}}\varepsilon _{{\text{vs}}}^{\text{p}}$ 为由基质吸力引起的塑性体应变。

总体应变：

${\text{d}}\varepsilon _{\text{v}}^{} = {\text{d}}\varepsilon _{\text{v}}^{\text{e}} + {\text{d}}\varepsilon _{\text{v}}^{\text{p}} 。$

(9)

根据式（3），弹性区域内由净平均应力导致的弹性体积应变 ${\text{d}}\varepsilon _{{\text{vp}}}^{\text{e}}$ 为

${\text{d}}\varepsilon _{{\text{vp}}}^{\text{e}} = - \frac{{{\text{d}}v}}{v} = \frac{\kappa }{v}\frac{{{\text{d}}p}}{p} 。$

(10)

同样，弹性区域内由吸力导致的弹性体应变 ${\text{d}}\varepsilon _{{\text{vs}}}^{\text{e}}$ 为

${\text{d}}\varepsilon _{{\text{vs}}}^{\text{e}} = \frac{{{\kappa _{\text{s}}}}}{v}\frac{{{\text{d}}s}}{{(s + {p_{\text{at}}})}} 。$

(11)

在一定的基质吸力下，当净平均应力p增大到屈服净应力 ${p_0}{\text{(}}s{\text{)}}$ 时，由 $p$ 导致的土体总体变 ${\text{d}}\varepsilon _{{\text{vp}}}^{}$ 为

${\text{d}}{\varepsilon _{{\text{vp}}}} = \frac{{\lambda (s)}}{v}\frac{{{\text{d}}{p_0}(s)}}{{{p_0}(s)}} 。$

(12)

则由 $p$ 引起的塑性体变 ${\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}}$ 为

${\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}} = {\text{d}}\varepsilon _{{\text{vp}}}^{} - {\text{d}}\varepsilon _{{\text{vp}}}^{\text{e}} = \frac{{\lambda (s) - \kappa }}{v}\frac{{{\text{d}}{p_0}(s)}}{{{p_0}(s)}} 。$

(13)

在一定净平均应力下，当基质吸力s增加到 ${s_{\text{0}}}$ 时，由s导致的土体总体变 ${\text{d}}\varepsilon _{{\text{vs}}}^{}$ 为

${\text{d}}\varepsilon _{{\text{vs}}}^{} = \frac{{{\lambda _{\text{s}}}}}{v}\frac{{{\text{d}}{s_0}}}{{({s_0} + {p_{{\text{at}}}})}} 。$

(14)

则由基质吸力 $s$ 引起的塑性体变 ${\text{d}}\varepsilon _{{\text{vs}}}^{\text{p}}$ 为

${\text{d}}\varepsilon _{{\text{vs}}}^{\text{p}} = {\text{d}}\varepsilon _{{\text{vs}}}^{} - {\text{d}}\varepsilon _{{\text{vs}}}^{\text{e}} = \frac{{{\lambda _{\text{s}}} - {\kappa _{\text{s}}}}}{v}\frac{{{\text{d}}{s_0}}}{{({s_0} + {p_{{\text{at}}}})}} 。$

(15)

BBM模型硬化规律使硬化参数与塑性体应变相联系，相应的硬化规律可为

$\frac{{{\text{d}}p_0^{\text{*}}}}{{p_0^{\text{*}}}} = \frac{v}{{\lambda (0) - \kappa }}{\text{d}}\varepsilon _{\text{v}}^{\text{p}} \text{，}$

(16)

$\frac{{{\text{d}}{s_0}}}{{{s_0} + {p_{{\text{at}}}}}} = \frac{v}{{{\lambda _{\text{s}}} - {\kappa _{\text{s}}}}}{\text{d}}\varepsilon _{\text{v}}^{\text{p}} 。$

(17)

（2）流动法则

BBM模型采用的是非关联的流动法则，考虑到通常的临界状态模型过高地估计了侧压力系数 ${K_0}$ 值，故引入一修正参数 $\alpha$ 对相关联的流动法则进行了修正，得流动法则为

$\frac{{{\text{d}}\varepsilon _{\text{d}}^{\text{p}}}}{{{\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}}}}{\text{ = }}\frac{{2q}}{{{M^2}[2p + {p_{\text{s}}} - p{}_0(s)]}}\alpha 。$

(18)

式中： ${\text{d}}\varepsilon _{\text{d}}^{\text{p}}$ 为塑性偏应变增量； ${\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}}$ 为塑性体应变增量；其中修正系数 $\alpha$ 为

$\alpha {\text{ = }}\frac{{M(M - 9)(M - 3)}}{{9(6 - M)}}\frac{1}{{1 - \frac{\kappa }{{\lambda (0)}}}} 。$

(19)

1.4 模型迭代计算方法

对文献[16]中控制吸力常规三轴压缩试验在固结排水条件下非饱和土BBM模型本构关系的迭代计算方法进行修正，得到真三轴条件下等b等p且 $b = 0$ 时BBM模型的迭代计算方法，其中常规三轴压缩试验即为真三轴试验中等b等 ${\sigma _3}$ 试验中 $b = 0$ 路径下的试验。下面给出本次真三轴条件下等b等p且 $b = 0$ 时模型的详细计算步骤，以下计算步骤将结合图 4进行阐述。

图 4 等b（b=0）等p下BBM模型计算示意图

Figure 4. Schematic diagram of BBM model calculation under constant b (b=0) and constant-p

下载: 全尺寸图片幻灯片

（1）首先需要根据试验结果得出到相关试验参数， $\lambda (0)$ ，r， $\beta$ ， ${p_{\text{c}}}$ ， $\kappa$ ， $p_0^{\text{*}}$ ，G，M，k。

（2）根据式（2）计算 $\lambda (s)$ 。

（3）计算B点的屈服应力 ${p_0}^B(s)$ （图 4（a）），根据式（4）得

${p_0}^B{\text{(}}s{\text{)}} = {p_{\text{c}}}{\left[ {\frac{{p_0^*}}{{{p_{\text{c}}}}}} \right]^{\frac{{\lambda {\text{(0)}} - \kappa }}{{\lambda {\text{(}}s{\text{)}} - \kappa }}}} 。$

(20)

（4）计算初始屈服点B的坐标，以B点作为塑性应变增量的起点，由式（5）得

$\left.\begin{array}{l}{p}_{B}={p}_{\text{net}}\text{ }\text{，}\\ {q}_{B}=M\sqrt{\text{(}{p}_{\text{net}}+{p}_{\text{s}}\text{)(}{p}_{0}{}^{B}\text{(}s\text{)}-{p}_{\text{net}}\text{)}}\text{ }。\end{array}\right\}$

(21)

（5）计算AB段弹性剪应变增量，

${\text{d}}\varepsilon _{\text{d}}^{\text{e}} = \frac{1}{{3G}}{q_B} 。$

(22)

（6）计算最终点E的坐标，

$\left\{\begin{array}{l}{p}_{E}={p}_{\text{net}}\hfill \\ {q}_{E}=M\text{(}{p}_{\text{net}}+{p}_{\text{s}}\text{)}\hfill \end{array}\text{ }。\right.$

(23)

（7）在BE段上将 ${q_B}$ 到 ${q_E}$ 之间划分成若干个相等的dq，以下以BE段中的BC段为例。

（8）计算C点的坐标，

$\left.\begin{array}{l}{p}_{C}={p}_{\text{net}}\text{ }\text{，}\\ {q}_{C}={q}_{B}+\text{d}q\text{ }。\end{array}\right\}$

(24)

（9）计算C点的屈服应力 $p_{\text{o}}^C{\text{(}}s{\text{)}}$ ，由式（5）得：

$p_{\text{o}}^C{\text{(}}s{\text{)}} = {p_C} + \frac{{{{{\text{(}}{q_C}{\text{)}}}^2}}}{{{M^2}{\text{(}}{p_C} + {p_{\text{s}}}{\text{)}}}} = {p_{{\text{net}}}} + \frac{{{{{\text{(}}{q_C}{\text{)}}}^2}}}{{{M^2}{\text{(}}{p_{{\text{net}}}} + {p_{\text{s}}}{\text{)}}}} 。$

(25)

（10）计算对应于B点在NCL线上的比体积 $v_N^B$ ：

$v_N^B = {v_A} - \kappa {\text{ln}}\frac{{p_0^B(s)}}{{{p_{{\text{net}}}}}} = {v_{{\text{ini}}}} - \kappa {\text{ln}}\frac{{p_0^B(s)}}{{{p_{{\text{net}}}}}} 。$

(26)

（11）计算对应于C点在NCL线上的比体积 $v_N^C$ ：

$v_N^C = v_N^B - \lambda (s){\text{ln}}\frac{{p_0^C{\text{(}}s{\text{)}}}}{{p_0^B{\text{(}}s{\text{)}}}} 。$

(27)

（12）计算对应于C点的比体积 ${v_C}$ ：

${v_C} = v_N^C + \kappa \ln \frac{{p_0^C}}{{{p_D}}} = v_N^C + \kappa \ln \frac{{p_0^C}}{{{p_{{\text{net}}}}}} 。$

(28)

（13）计算BC段弹性剪应变增量 ${\text{d}}\varepsilon _{\text{d}}^{\text{e}}$ 和弹性体应变增量 ${\text{d}}\varepsilon _{{\text{vp}}}^{\text{e}}$ ：

${\text{d}}\varepsilon _{\text{d}}^{\text{e}} = \frac{1}{{3G}}{\text{(}}{q_C} - {q_C}{\text{)}} = \frac{1}{{3G}}{\text{d}}q \text{，}$

(29)

${\text{d}}\varepsilon _{{\text{vp}}}^{\text{e}} = \frac{\kappa }{{{\nu _B}}}\left( {\frac{{{p_C} - {p_B}}}{{{p_B}}}} \right) = {\text{0}} 。$

(30)

（14）计算BC段总体应变增量 ${\text{d}}{\varepsilon _{{\text{vp}}}}$ 和塑性体应变增量 ${\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}}$ ：

${\text{d}}{\varepsilon _{{\text{vp}}}} = \frac{{{v_B} - {v_C}}}{{{v_B}}} \text{，}$

(31)

${\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}} = {\text{d}}{\varepsilon _{{\text{vp}}}} - {\text{d}}\varepsilon _{{\text{vp}}}^{\text{e}} = {\text{d}}{\varepsilon _{{\text{vp}}}} 。$

(32)

（15）计算BC段塑性剪应变增量 ${\text{d}}\varepsilon _{\text{d}}^{\text{p}}$ ：

${\text{d}}\varepsilon _{\text{d}}^{\text{p}} = {\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}}\frac{{2q}}{{{M^2}{\text{[}}2p + {p_{\text{s}}} - {p_0}{\text{(}}s{\text{)]}}}}\alpha 。$

(33)

（16）计算BC段塑性总应变增量 ${\text{d}}{\varepsilon _{\text{d}}}$ ：

${\text{d}}{\varepsilon _{\text{d}}} = {\text{d}}\varepsilon _{\text{d}}^{\text{e}} + {\text{d}}\varepsilon _{\text{d}}^{\text{p}} 。$

(34)

（17）BE其余点都按照以上BC段重复，即可绘制出相应的应力应变预测曲线。

如若初始屈服应力 ${p_0}{\text{(}}s{\text{)}}$ 未超过 ${p_{{\text{net}}}}$ ，如所示，此时以 ${p_{{\text{net}}}}$ 点作为塑性应变增量的起点开始计算。

（1）以 ${p_{{\text{net}}}}$ 点作为塑性应变增量的起点：

$p_0^{{A^{\prime}}}{\text{(}}s{\text{)}} = {p_{{\text{net}}}} 。$

(35)

（2）计算最终点E的坐标：

$\left.\begin{array}{l}{p}_{E}={p}_{\text{f}}={p}_{\text{net}}\text{ }\text{，}\\ {q}_{E}={q}_{\text{f}}=M\text{(}{p}_{\text{net}}+{p}_{\text{s}}\text{) }。\end{array}\right\}$

(36)

（3）在A´E段上将q_A'到q_E之间划分成若干个相等的dq，其余步骤重复以上（7）~（17）。

2. 模型预测

2.1 各向等压状态模型参数

真三轴重塑黄土试样的目标干密度为ρ_d=1.40 g/cm³，根据土-水特征曲线得到基质吸力s=100 kPa对应的含水率为w=19.5%，确定重塑试样含水率为w=19.5%。对重塑黄土试样进行了控制吸力s分别为50，100，200，300 kPa的真三轴条件下的等向压缩试验，根据试验测试结果绘制出等向压缩试验曲线，比体积ν与净平均应力p的关系曲线如图 5所示。根据等向压缩试验结果，确定相关土性参数，同一吸力的试验点近似的位于两条相交的直线上，两条直线的交点可看作屈服点^[17-18]，该点的净平均应力p即为屈服净应力 ${p_0}{\text{(}}s{\text{)}}$ 。

图 5 等向压缩曲线

Figure 5. Isotropic compression curves

下载: 全尺寸图片幻灯片

根据等向压缩试验结果得： $s{\text{ = 50 kPa}}$ 时， ${p_0} =$ ${\text{76 kPa}}$ ， $\lambda = {\text{0}}{\text{.2533}}$ ， $\kappa = 0.0243$ ； $s = {\text{100}}$ kPa时， ${p_0} = {\text{116 kPa}}$ ， $\lambda = {\text{0}}{\text{.2208}}$ ， $\kappa = 0.0201$ ； $s{\text{ = 200 kPa}}$ 时， ${p_0}{\text{ = 164 kPa}}$ ， $\lambda = {\text{0}}{\text{.1984}}$ ， $\kappa =$ $0.0208$ ； $s = {\text{300 kPa}}$ 时， ${p_0} = {\text{200 kPa}}$ ， $\lambda =$ ${\text{0}}{\text{.1870}}$ ， $\kappa = 0.0191$ 。根据所得试验结果，由式（2）可拟合得到不同基质吸力的刚度参数 $\lambda {\text{(}}s{\text{)}}$ 与基质吸力 $s$ 之间的关系，如所示，得到相应的拟合参数分别为： $\lambda {\text{(}}0{\text{)}} = 0.3140$ ， $\beta = {\text{12}}{\text{.6211 MP}}{{\text{a}}^{ - 1}}$ ， $r =$ $0.5865$ ，所得拟合曲线为

$\lambda {\text{(}}s{\text{)}} = 0.3140 \times {\text{[(}}1 - 0.5865{\text{)}}{{\text{e}}^{ - 12.6211s}} + 0.5865{\text{]}} 。$

(37)

图 6 刚度参数λ(s)随基质吸力s的变化关系

Figure 6. Relationship between stiffness parameters λ(s) and matric suction s

下载: 全尺寸图片幻灯片

根据试验结果和式（37），利用式（4）对屈服净应力 ${p_0}{\text{(}}s{\text{)}}$ 与刚度参数 $\lambda {\text{(}}s{\text{)}}$ 之间的关系进行拟合，得到相应的拟合参数： ${p_0}^*{\text{ = 46}}{\text{.5 kPa}}$ ， ${p_c}{\text{ = 7}}{\text{.0 kPa}}$ ；根据Alonso等^[7]提出的非饱和土BBM模型中的假定 $\kappa$ 为恒定值，在此 $\kappa$ 取不同基质吸力试验下的平均值为 $\kappa = 0.0211$ 。得到屈服净应力 ${p_0}{\text{(}}s{\text{)}}$ 与刚度参数 $\lambda {\text{(}}s{\text{)}}$ 之间的关系曲线为

${p_{\text{0}}}{\text{(}}s{\text{)}} = 7.0 \times {\left( {\frac{{46.5}}{{7.0}}} \right)^{\frac{{0.3140 - 0.0211}}{{\lambda {\text{(}}s{\text{)}} - 0.0211}}}} 。$

(38)

根据式（37）和（38）可以得到非饱和土BBM模型预测的基质吸力s和屈服净平均应力p之间的关系曲线，见图 7。

图 7 基质吸力和屈服净平均应力关系曲线

Figure 7. Relationship between matric suction and yield net mean stress

下载: 全尺寸图片幻灯片

2.2 轴对称剪切应力状态下模型参数

Alonso等^[7]给出不同基质吸力下轴对称剪切试验的试验结果在 $p - q$ 平面上可以统一表示为

$q = Mp + Mks 。$

(39)

式中： $p$ 为净平均应力； $q$ 为剪应力； $s$ 为基质吸力； $M$ 为临界状态线的斜率； $k$ 为黏聚力随基质吸力 $s$ 变化的速率。

对制备的真三轴重塑黄土试样进行了控制吸力s分别为50，100，200 kPa时真三轴条件下的等 $b$ 等 $p$ 剪切试验^[19-20]，利用式（39）对b=0的试验结果进行拟合（），得到最佳拟合参数，临界状态线的斜率 $M = 1.381$ ，黏聚力随基质吸力s变化的速率 $k = 0.980$ 。

图 8 p-q面上临界状态线（

$p(s)$ 随s线性变化）

Figure 8. Critical state lines on p-q plane (

$p(s)$ varies linearly with s)

下载: 全尺寸图片幻灯片

对于本文等b等p且b=0试验，弹性段剪切应变增量参见式（22），因此可通过应力应变曲线初始线性段来确定剪切模量G^[16]，对所有 $b{\text{ = }}0$ 时得到的G求平均值，得G=6.7 MPa。

2.3 BBM预测结果

BBM模型预测需要根据试验结果得到相关试验参数为 $\lambda (0)$ ，r， $\beta$ ， ${p_{\text{c}}}$ ， $\kappa$ ， $p_0^{\text{*}}$ ，G，M，k，其余初始状态参数为：p_i=5 kPa，q_i=0，s_i=100 kPa，v₀=1.93。由2.1和2.2节已经求得所使用的黄土试样的模型参数分别为 $\lambda (0) = 0.3140$ ， $r = 0.5865$ ， $\beta =$ ${\text{12}}{\text{.6211 MP}}{{\text{a}}^{ - 1}}$ ， ${p_{\text{c}}} = {\text{7}}{\text{.0 kPa}}$ ， $\kappa = 0.0211$ ， $p_0^{\text{*}} = {\text{46}}{\text{.5}}$ ${\text{kPa}}$ ， $G = {\text{6}}{\text{.7 MPa}}$ ， $M = 1.381$ ， $k = 0.890$ 。图 9~11分别为不同净平均应力下、不同基质吸力下BBM模型预测结果，可以看到BBM模型对于低净平均应力的预测结果偏差相对较大。

图 9 s=50 kPa下BBM模型的预测曲线

Figure 9. Predicted curves of BBM model at s=50 kPa

下载: 全尺寸图片幻灯片

图 10 s=100 kPa下BBM模型的预测曲线

Figure 10. Predicted curves of BBM model at s=100 kPa

下载: 全尺寸图片幻灯片

图 11 s=200 kPa下BBM模型的预测曲线

Figure 11. Predicted curves of BBM model at s=200 kPa

下载: 全尺寸图片幻灯片

3. BBM模型的修正

3.1 BBM模型的修正方法

在BBM模型中，模型在 $(p,q)$ 平面上的屈服面的表达式为

${q^2} - {M^2}(p + {p_{\text{s}}})[{p_0}(s) - p] = 0 。$

(40)

在该模型中假定黏聚力的增大是与基质吸力的增大是呈线性变化的，即在该模型中假定 ${p_{\text{s}}} = ks$ ， $k$ 为常数。但是，根据本次及已有文献中黄土试验结果^[21-24]，黄土的总黏聚力与基质吸力的关系并非是呈线性增大的。因此，在修正BBM模型中构建 ${p_{\text{s}}}$ 和s的非线性关系为双曲线形式：

${p_{\text{s}}} = \frac{s}{{M{\text{(}}a + ms)}} \text{，}$

(41)

式中，a，m为控制黏聚力随基质吸力变化的土性参数。

在p-q面上不同基质吸力s下的临界状态线可由以下表达式进行描述（图 12）：

$q = Mp + \mu (s) 。$

(42)

图 12 p-q面上临界状态线（p(s)随s非线性变化）

Figure 12. Critical state lines on p-q plane (p(s) varies non-linearly with s)

下载: 全尺寸图片幻灯片

在式（42）中依然假定临界状态线的斜率M不随基质吸力变化， $\mu (s)$ 为不同基质吸力s下临界状态线的纵截距。如图 12所示，得

${p_{\text{s}}} = \frac{{\mu (s)}}{M} 。$

(43)

利用式（42）对不同基质吸力s下的试验数据点进行拟合，得到M=1.219， $\mu (50) = {\text{106}}{\text{.569 kPa}}$ ， $\mu (100) = {\text{168}}{\text{.210 kPa}}$ ， $\mu (200) = 2{\text{68}}{\text{.363 kPa}}$ ，利用式（43）求得 ${p_{\text{s}}}$ ， ${p_{\text{s}}}(50) = {\text{87}}{\text{.423 kPa}}$ ， ${p_{\text{s}}}(100) = {\text{137}}{\text{.990}}$ ${\text{kPa}}$ ， ${p_{\text{s}}}(200) = {\text{220}}{\text{.150 kPa}}$ 。

利用式（41）对不同吸力的结果进行拟合，得到的双曲线的拟合参数为：a=0.4055，m=1.7183，R²=0.9980。 ${p_{\text{s}}}$ 和s的关系式为

${p_{\text{s}}} = \frac{s}{{1.291 \times (0.4055 + 1.7183s)}} 。$

(44)

将修正BBM模型的预测曲线和BBM模型的预测曲线都显示在p-s平面上，如图 13所示，可以看出在目前所测试的吸力范围内，BBM中的假定过于偏小与试验结果有差距。

图 13 修正BBM与BBM的对比

Figure 13. Comparison between improved BBM and BBM

下载: 全尺寸图片幻灯片

3.2 BBM模型的修正后模型预测结果

修正BBM模型需要根据试验结果得到相关试验参数为 $\lambda (0)$ ，r， $\beta$ ， ${p_{\text{c}}}$ ， $\kappa$ ， $p_0^{\text{*}}$ ，G，M，a，m，本次黄土试所使用的黄土试样的模型参数分别为 $\lambda (0) = 0.3140$ ， $r = 0.5865$ ， $\beta = {\text{12}}{\text{.6211 MP}}{{\text{a}}^{ - 1}}$ ， ${p_{\text{c}}} =$ ${\text{7}}{\text{.0 kPa}}$ ， $\kappa = 0.0211$ ， $p_0^{\text{*}} = {\text{46}}{\text{.5 kPa}}$ ， $G = {\text{6}}{\text{.7 MPa}}$ ， $M = 1.219$ ， $a = 0.4055$ ， $m = 1.7183$ 。图 14~16分别为不同基质吸力下的修正BBM模型预测结果，可以看到修正BBM模型整体预测结果都比较理想，尤其是对于低吸力低净平均应力下的预测结果相较于BBM模型的预测结果比较理想。

图 14 s=50 kPa下修正BBM模型的预测曲线

Figure 14. Predicted curves of modified BBM model at s=50 kPa

下载: 全尺寸图片幻灯片

图 15 s=100 kPa下修正BBM模型的预测曲线

Figure 15. Predicted curves of modified BBM model at s=100 kPa

下载: 全尺寸图片幻灯片

图 16 s=200 kPa下修正BBM模型的预测曲线

Figure 16. Predicted curves of modified BBM model at s=200 kPa

下载: 全尺寸图片幻灯片

4. 结论

（1）利用重塑黄土控制吸力等向压缩下的试验结果，拟合得到非饱和黄土不同基质吸力的刚度参数 $\lambda {\text{(}}s{\text{)}}$ 与基质吸力 $s$ 之间的关系及屈服净应力 ${p_0}{\text{(}}s{\text{)}}$ 与刚度参数 $\lambda {\text{(}}s{\text{)}}$ 之间的关系，并且可以较好地利用非饱和土BBM模型得到基质吸力s和屈服净应力 ${p_0}{\text{(}}s{\text{)}}$ 之间的预测曲线。

（2）对Alonso等^[7]提出的基于临界状态的非饱和土BBM模型进行了分析，对等 $b$ 等 ${\sigma _3}$ 且 $b{\text{ = }}0$ 时的BBM模型的迭代计算方法进行修正，给出等 $b$ 等 $p$ 且 $b{\text{ = }}0$ 时的BBM模型的迭代计算方法。

（3）修正BBM模型和BBM模型在p-s平面上预测曲线表明，在试验所测试的吸力范围内，BBM中的假定过于偏小，与试验测试结果差距较大。

（4）考虑p_s随基质吸力s变化的非线性关系，构建了p_s和s的双曲线形式的函数关系对BBM模型进行修正，且修正BBM模型对非饱和黄土剪切应力状态下试验结果的预测结果整体比较理想，尤其是对于低吸力低净平均应力下的预测结果更为理想。

图 1 能源土离散元简化

Figure 1. DEM sketch for MHBS

下载: 全尺寸图片幻灯片

图 2 水合物相平衡线

Figure 2. Phase equilibrium line for MH

下载: 全尺寸图片幻灯片

图 3 TOUGH+HYDRATE+PFC耦合流程图

Figure 3. Flow chart of TOUGH+HYDRATE+PFC

下载: 全尺寸图片幻灯片

图 4 模型和加载示意

Figure 4. Sketch map of model and loading schemes

下载: 全尺寸图片幻灯片

图 5 一维固结模拟结果与理论对比

Figure 5. Comparison between simulated results and theoretical solution of 1D consolidation tests

下载: 全尺寸图片幻灯片

图 6 一维热传导模拟与理论结果对比

Figure 6. Comparison between simulated results and analytical solutions of 1D heat conduction tests

下载: 全尺寸图片幻灯片

图 7 一维开采模型示意图

Figure 7. Schematic illustration of 1D dissociation

下载: 全尺寸图片幻灯片

图 8 一维降压开采试验和T+H模拟结果

Figure 8. Comparison of 1D dissociation test results obtained from experiments and T+H simulations

下载: 全尺寸图片幻灯片

图 9 深海能源土模拟颗粒级配曲线

Figure 9. Grain-size distribution curve of MHBS in DEM simulation

下载: 全尺寸图片幻灯片

图 10 一维降压下开采产气量、变形、胶结破坏、压力演化

Figure 10. Evolution of gas production, vertical strain, percentage of bond breakage and pressure for 1D depressurization tests

下载: 全尺寸图片幻灯片

图 11 胶结破坏与变形关系曲线

Figure 11. Relationship between strain and percentage of bond breakage during hydrate dissociation

下载: 全尺寸图片幻灯片

图 12 一维升温开采产气量、变形、胶结破坏演化

Figure 12. Evolution of gas production, vertical strain and percentage of bond breakage from 1D heat stimulation tests

下载: 全尺寸图片幻灯片

图 13 一维升温开采中分解前沿面与t^1/2关系

Figure 13. Evolution of dissociation front location against t^1/2 from 1D heat stimulation tests

下载: 全尺寸图片幻灯片

表 1 水合物分解模型参数

Table 1 Parameters for MH dissociation

模型网格	网格尺寸/mm			初始压力/MPa	温度/℃	盐度/%	开采压力/MPa	土体参数
模型网格	Δx	Δy	Δz	初始压力/MPa	温度/℃	盐度/%	开采压力/MPa	渗透系数/m²	土体密度/(kg·m^-3)	土体比热容/(J·kg^-1·K^-1)	土体湿导热系数/(W·m^-1·℃^-1)
1×1×10	45	45	15	10.5	12.5	0	4	1.5×10^-12	2650	1000	3.3

下载: 导出CSV

参考文献(36)

[1]	MILKOV A V. Global estimates of hydrate-bound gas in marine sediments: how much is really out there?[J]. Earth-Science Reviews, 2004, 66(3/4): 183-197.
[2]	WAITE W F, SANTAMARINA J C, CORTES D D, et al. Physical properties of hydrate-bearing sediments[J]. Reviews of Geophysics, 2009, 47(4): 465-484.
[3]	SOGA K, NG M Y A, LEE S L, et al. Characterisation and Engineering Properties of Methane Hydrate Soils[M]. London: Taylor and Francis, 2006: 2591-2642.
[4]	SONG Y C, YANG L, ZHAO J F, et al. The status of natural gas hydrate research in China: A review[J]. Renewable and Sustainable Energy Reviews, 2014, 31: 778-791. doi: 10.1016/j.rser.2013.12.025
[5]	YAN C, REN X, CHENG Y, et al. Geomechanical issues in the exploitation of natural gas hydrate[J]. Gondwana Research, 2020, 81: 403-422. doi: 10.1016/j.gr.2019.11.014
[6]	MORIDIS G J, COLLETT T S, DALLIMORE S R, et al. Numerical studies of gas production from several CH4 hydrate zones at the Mallik site, Mackenzie Delta, Canada[J]. Journal of Petroleum Science and Engineering, 2004, 43(3/4): 219-238.
[7]	TANG L G, LI X S, FENG Z P, et al. Control mechanisms for gas hydrate production by depressurization in different scale hydrate reservoirs[J]. Energy and Fuels, 2007, 21(1): 227-233. doi: 10.1021/ef0601869
[8]	MORIDIS G J, REAGAN M T. Estimating the upper limit of gas production from Class 2 hydrate accumulations in the permafrost: 2. Alternative well designs and sensitivity analysis[J]. Journal of Petroleum Science and Engineering, 2011, 76(3/4): 124-137.
[9]	OYAMA H, KONNO Y, MASUDA Y, et al. Dependence of depressurization-induced dissociation of methane hydrate bearing laboratory cores on heat transfer[J]. Energy & Fuels, 2009, 23(10): 4995-5002.
[10]	YIN Z Y, MORIDIS G, CHONG Z R, et al. Numerical analysis of experiments on thermally induced dissociation of methane hydrates in porous media[J]. Industrial & Engineering Chemistry Research, 2018, 57(17): 5776-5791.
[11]	MIYAZAKI K, MASUI A, SAKAMOTO Y, et al. Triaxial compressive properties of artificial methane-hydrate-bearing sediment[J]. Journal of Geophysical Research, 2011, 116(B6): B06102.
[12]	HYODO M, YONEDA J, YOSHIMOTO N, et al. Mechanical and dissociation properties of methane hydrate-bearing sand in deep seabed[J]. Soils and Foundations, 2013, 53(2): 299-314. doi: 10.1016/j.sandf.2013.02.010
[13]	HYODO M, LI Y H, YONEDA J, et al. Effects of dissociation on the shear strength and deformation behavior of methane hydrate-bearing sediments[J]. Marine and Petroleum Geology, 2014, 51(2): 52-62.
[14]	SONG Y C, ZHU Y M, LIU W G, et al. Experimental research on the mechanical properties of methane hydrate-bearing sediments during hydrate dissociation[J]. Marine and Petroleum Geology, 2014, 51(2): 70-78.
[15]	KIMOTO S, OKA F, FUSHITA T, et al. A chemo-thermo- mechanically coupled numerical simulation of the subsurface ground deformations due to methane hydrate dissociation[J]. Computers and Geotechnics, 2007, 34(4): 216-228. doi: 10.1016/j.compgeo.2007.02.006
[16]	RUTQVIST J, MORIDIS G J. Numerical studies on the geomechanical stability of hydrate-bearing sediments[J]. SPE Journal, 2009, 14(2): 267-282. doi: 10.2118/126129-PA
[17]	UCHIDA S. Numerical Investigation of Geomechanical Behaviour of Hydrate Bearing Sediments[D]. Cambridge: University of Cambridge, 2012.
[18]	GUPTA S, WOHLMUTH B, HELMIG R. Multi-rate time stepping schemes for hydro-geomechanical model for subsurface methane hydrate reservoirs[J]. Advances in Water Resources, 2016, 91: 78-87. doi: 10.1016/j.advwatres.2016.02.013
[19]	ZHOU M L, SOGA K, YAMAMOTO K, et al. Geomechanical responses during depressurization of hydrate- bearing sediment formation over a long methane gas production period[J]. Geomechanics for Energy and the Environment, 2020, 23: 100111. doi: 10.1016/j.gete.2018.12.002
[20]	蒋明镜, 付昌, 贺洁, 等. 不同开采方法下深海能源土的离散元模拟[J]. 岩土力学, 2015, 36(增刊2): 639-647. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2015S2093.htm JIANG Ming-jing, FU Chang, HE Jie, et al. Distinct element simulations of exploitation of methane hydrate bearing sediments with different methods[J]. Rock and Soil Mechanics, 2015, 36(S2): 639-647. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2015S2093.htm
[21]	CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 1979, 29(1): 47-65. doi: 10.1680/geot.1979.29.1.47
[22]	JIANG M J, SUN R H, ARROYO M, et al. Salinity effects on the mechanical behaviour of methane hydrate bearing sediments: a DEM investigation[J]. Computers and Geotechnics, 2021, 133: 104067. doi: 10.1016/j.compgeo.2021.104067
[23]	MORIDIS G. User's manual for the hydrate v1. 5 option of TOUGH+ v1. 5: A code for the simulation of system behavior in hydrate-bearing geologic media[M]. Oak, Ridge US Lawrence Berkeley National Laboratory, 2014.
[24]	蒋明镜. 现代土力学研究的新视野——宏微观土力学[J]. 岩土工程学报, 2019, 41(2): 195-254. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902002.htm JIANG Ming-jing. New paradigm for modern soil mechanics: Geomechanics from micro to macro[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(2): 195-254. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902002.htm
[25]	ITASCA PFC 6.0 (Particle Flow Code) Documentation[M]. Minmeapolics: ITASCA Inc, 2019.
[26]	KIM H C, BISHNOI P R, HEIDEMANN R A, et al. Kinetics of methane hydrate decomposition[J]. Chemical Engineering Science, 1987, 42(7): 1645-1653. doi: 10.1016/0009-2509(87)80169-0
[27]	LIU X, FLEMINGS P B P. Dynamic multiphase flow model of hydrate formation in marine sediments[J]. Journal of Geophysical Research: Solid Earth, 2007, 112(B3): B03101.
[28]	ZHANG A, JIANG M J, THORNTON C. A coupled CFD-DEM method with moving mesh for simulating undrained triaxial tests on granular soils[J]. Granular Matter, 2020, 22(1): 1-13. doi: 10.1007/s10035-019-0969-4
[29]	HU L T, WINTERFELD P H, FAKCHAROENPHOL P, et al. A novel fully-coupled flow and geomechanics model in enhanced geothermal reservoirs[J]. Journal of Petroleum Science and Engineering, 2013, 107: 1-11. doi: 10.1016/j.petrol.2013.04.005
[30]	JAEGER J C, COOK NGW, ZIMMERMAN R W, Fundamentals of Rock Mechanics[M]. 4th eds. Malden: Blackwell Publishing, 2007.
[31]	WANG Y, KOU X, FENG J C, et al. Sediment deformation and strain evaluation during methane hydrate dissociation in a novel experimental apparatus[J]. Applied Energy, 2020, 262: 114397. doi: 10.1016/j.apenergy.2019.114397
[32]	蒋明镜, 张望城. 一种考虑流体状态方程的土体CFD-DEM耦合数值方法[J]. 岩土工程学报, 2014, 36(5): 793-801. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201405002.htm JIANG Ming-jing, ZHANG Wang-cheng. Coupled CFD-DEM method for soils incorporating equation of state for liquid[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(5): 793-801. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201405002.htm
[33]	CHEN F, DRUMM E C, GUIOCHON G. Coupled discrete element and finite volume solution of two classical soil mechanics problems[J]. Computers and Geotechnics, 2011, 38(5): 638-647. doi: 10.1016/j.compgeo.2011.03.009
[34]	JIANG M J, KONRAD J M, LEROUEIL S. An efficient technique for generating homogeneous specimens for DEM studies[J]. Computers and Geotechnics, 2003, 30(7): 579-597. doi: 10.1016/S0266-352X(03)00064-8
[35]	JIANG M J, SHEN Z F, WANG J F. A novel three- dimensional contact model for granulates incorporating rolling and twisting resistances[J]. Computers and Geotechnics, 2015, 65: 147-163. doi: 10.1016/j.compgeo.2014.12.011
[36]	WEIBULL W. The phenomenon of rupture in solids[J]. Proceedings of Royal Swedish Institute of Engineering Research, 1939, 153: 1-55.

施引文献(3)

期刊类型引用(1)

任占雷，李泽杰，段梦强，翁效林. 考虑基质吸力影响的重塑黄土的临界状态模型. 公路交通科技. 2025(03): 104-114 .

百度学术

其他类型引用(2)

资源附件(0)

图(13) / 表(1)

计量

文章访问数: 350
HTML全文浏览量: 21
PDF下载量: 300
被引次数: 3

0. 引言
1. 非饱和土BBM模型
1.1 各向等压应力状态
1.2 剪切应力状态
1.3 硬化规律和流动法则
1.4 模型迭代计算方法
2. 模型预测
2.1 各向等压状态模型参数
2.2 轴对称剪切应力状态下模型参数
2.3 BBM预测结果
3. BBM模型的修正
3.1 BBM模型的修正方法
3.2 BBM模型的修正后模型预测结果
4. 结论

0. 引言
1. 非饱和土BBM模型
1.1 各向等压应力状态
1.2 剪切应力状态
1.3 硬化规律和流动法则
1.4 模型迭代计算方法
2. 模型预测
2.1 各向等压状态模型参数
2.2 轴对称剪切应力状态下模型参数
2.3 BBM预测结果
3. BBM模型的修正
3.1 BBM模型的修正方法
3.2 BBM模型的修正后模型预测结果
4. 结论

参考文献(36)

施引文献

资源附件(0)

一种实用型深海能源土多场耦合离散元数值方法 English Version

作者简介: 蒋明镜(1965— ),男,教授,博士生导师,主要从事天然结构性黏土、砂土、非饱和土、太空土和深海能源土宏观微观试验、本构模型和数值分析研究。E-mail：mingjing.jiang@tju.edu.cn

计量

出版历程

A practical multi-field coupling distinct element method for methane hydrate bearing sediments

0. 引言

1. 非饱和土BBM模型

1.1 各向等压应力状态

1.2 剪切应力状态

1.3 硬化规律和流动法则

1.4 模型迭代计算方法

2. 模型预测

2.1 各向等压状态模型参数

2.2 轴对称剪切应力状态下模型参数

2.3 BBM预测结果

3. BBM模型的修正

3.1 BBM模型的修正方法

3.2 BBM模型的修正后模型预测结果

4. 结论

期刊类型引用(1)

其他类型引用(2)

计量

出版历程

目录

0. 引言

1. 非饱和土BBM模型

1.1 各向等压应力状态

1.2 剪切应力状态

1.3 硬化规律和流动法则

1.4 模型迭代计算方法

2. 模型预测

2.1 各向等压状态模型参数

2.2 轴对称剪切应力状态下模型参数

2.3 BBM预测结果

3. BBM模型的修正

3.1 BBM模型的修正方法

3.2 BBM模型的修正后模型预测结果

4. 结论

作者简介:
蒋明镜(1965— ),男,教授,博士生导师,主要从事天然结构性黏土、砂土、非饱和土、太空土和深海能源土宏观微观试验、本构模型和数值分析研究。E-mail：mingjing.jiang@tju.edu.cn