0.   引言

大型振动台试验具有尺寸大、承载力高和可实现多台协同加载的优点,是开展地下结构抗震研究工作常用且重要的试验方法^[1-3]。

近年来,中国地震模拟振动台的建设逐渐加快,尤其是大型、高性能振动台逐渐增多,已规划建设的振动台台面尺寸和竖向承载力分别可达10 m×8 m和1600 kN,可为开展考虑土–结构相互作用的大型地下结构动力模型试验提供良好工作条件^[4]。然而,地下结构大型振动台试验成本极高,周期长,通常难以在短期内多次重复开展；此外,开展试验所涉及的专业知识较多,对试验人员的要求很高。因此,为保证试验顺利开展,提前发现试验方案中可能存在的问题,有必要在试验前对模型试验结果开展预测工作。

对于地上结构的大型振动台试验,已经有学者采用数值方法预测其试验结果,甚至已举办过一些“盲测”比赛,结果显示可采用数值模拟方法较好地预测结构在振动台中的地震响应^[5-6]。

但目前对于地下结构在振动台试验中的预测工作还很少,其主要难点在于如何获取可靠的场地地震响应信息。以采用反应位移法的数值预测为例,计算前须获取试验场地的地震分析结果,但采用常规测试手段难以直接获取模型箱内任意高度位置处土体的计算参数,这对开展试验场地的地震响应数值分析造成一定困难；其次,因试验在单位重力加速度下开展,土体较软,非线性极强,现有的一维场地分析方法本身还存在对强非线性场地计算精度欠佳的问题^[7-8]。因此,若直接采用传统的全数值方法开展地下模型结构在振动台试验中地震响应的预测工作,可能会产生较大的误差。

值得注意的是,在进行地下结构的振动台模型试验前,经常会开展相应的自由场振动台试验^[9-12]。其中,有学者将自由场土体视为大型土样,由动力试验结果估算其剪切波速、动剪切模量比和阻尼比^[13-15]。因此,若可直接通过自由场试验获取场地的地震响应与计算参数,并将其应用至地下模型结构的数值计算中,则可更加准确地预测其在振动台试验中的地震响应。

本文提出采用自由场试验和整体式反应位移法^[16-18]相结合的方法预测地下结构模型在振动台试验中地震响应,主要目的为开展考虑土–结构相互作用大型振动台模型试验的技术人员提供一种初步预测试验结果并掌握试验概况的方法,其计算结果可用以指导选择合适的地震动强度、传感器量程,并保障试验安全。首先介绍采用自由场试验结果估算整体式反应位移法所需计算参数的方法,在此基础上,分别采用本文所提出方法和传统全数值方法预测某地铁车站模型结构在振动台试验中的地震响应,并将预测结果与后续试验结果进行对比。所提出方法可同时用来预测地下模型结构在振动台试验和离心机振动台试验中的地震响应,具有较强的实用价值。

1.   自由场振动台试验方案

本节主要介绍自由场振动台试验的试验方案,包括砂土的级配和部分物理力学特性、试验设备、填土方案、传感器布置方案和地震动及其输入顺序等。

1.1   砂土的级配和部分物理力学特性

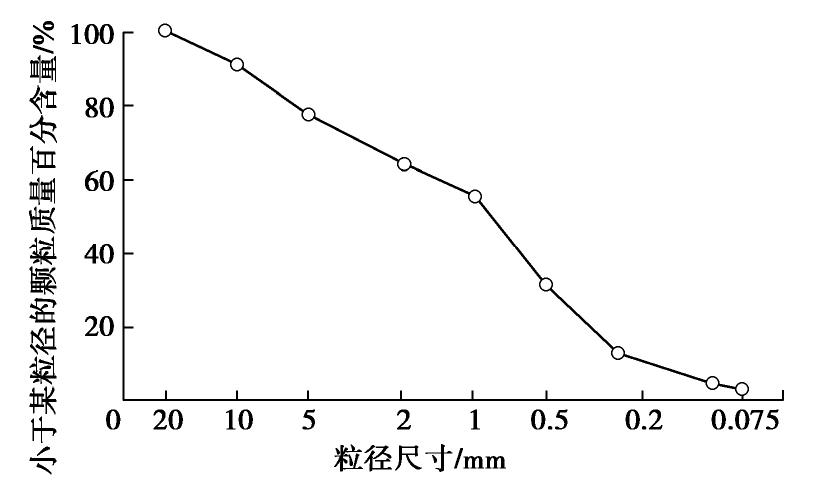
试验用土的最大粒径约为2 cm,级配详见图1。土的不均匀系数C_u为8.3,曲率系数C_c为0.75,粒度中值D₅₀为0.82 mm,属于级配不良的砂土。土的初始含水率w为6.3%,初始重度${\gamma }_{\text{t}}$为17.6 kN/m³,最大孔隙率e_max为0.92,最小孔隙率e_min为0.43,初始相对密度为68.6%。

图  1  砂土的级配曲线

Figure  1.  Grain-size distribution curve of sand

下载: 全尺寸图片 幻灯片

1.2   试验设备和填土方案

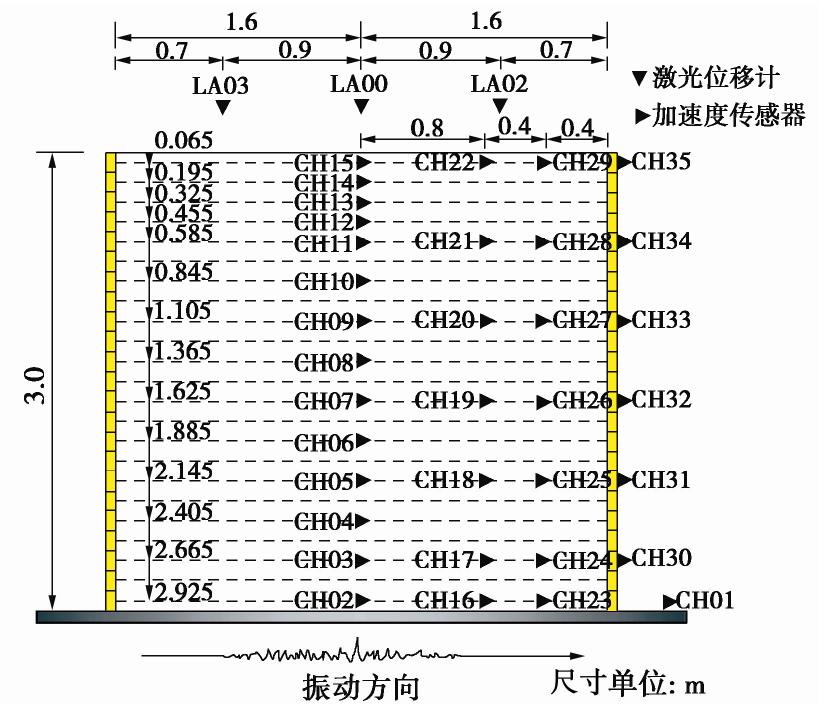
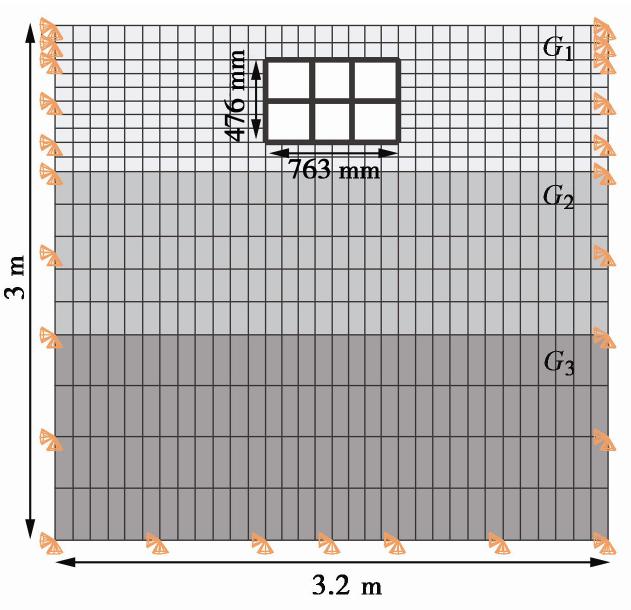
振动台试验在中国建筑科学院建筑安全与环境国家重点试验室中完成,振动台的台面尺寸为6 m×6 m,额定工作频率范围为0.1～50 Hz。模型箱为叠层剪切箱,可为土体提供等效一维场地边界条件^[19],其尺寸为3.2 m×2.4 m×3 m（长×宽×高）^[20],由23个叠环构成,每个叠环高度为13 cm。动力荷载沿模型箱的长度方向水平单向加载,模型箱在震动方向的2个侧边界未设置约束,内壁配有1 cm厚的橡胶膜,用来吸收震动过程中的散射能量。振动台和模型箱详见图2。

图  2  振动台和模型箱

Figure  2.  Shaking table and model box

下载: 全尺寸图片 幻灯片

砂土以人工扬土的方式填至模型箱内,在填土过程中,每隔10 cm人工夯实一次,同时在土内埋设传感器。

1.3   传感器布置方案

试验中使用的加速度传感器为圆柱体,尺寸为4 cm×3 cm（直径×高）,采样频率为256 Hz。共布设了35个加速度传感器,其布置方案如图3所示。传感器的编号为CHn（n=01, 02, …, 35）,其中CH01布置在振动台台面上,用来采集台面的加速度记录；CH02～CH29被埋置于土中,用来记录土体的运动；CH30～CH35则用来记录模型箱的运动。此外,还在土体表面上方布置3个激光位移计,用于测量土体的沉降。

图  3  传感器布置方案

Figure  3.  Schematic diagram of arrangement of sensors

下载: 全尺寸图片 幻灯片

1.4   地震动及其输入顺序

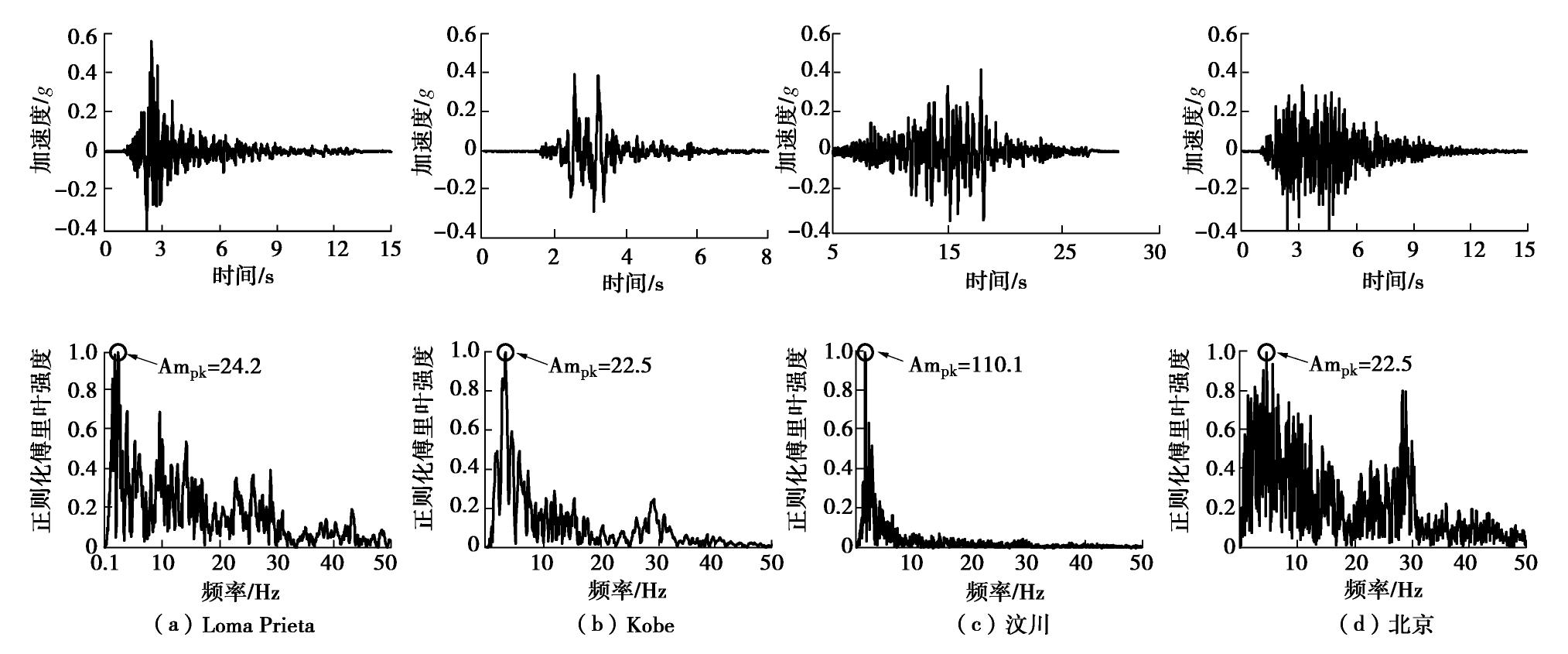
试验使用了1条白噪声记录、1条脉冲记录和4条地震动记录。其中地震动的台面记录及其正则化傅里叶频谱如图4所示,图中的A_mpk为傅里叶频谱的幅值。输入的地震动记录包括3条天然记录和一条人工记录,3条天然记录分别取自1989年美国Loma Prieta地震（台站：Gilroy Array ^#3,H20F）、1995年日本Kobe地震（台站：KJMA,H1）和2008年汶川卧龙地震（20～40 s,台站：51WCW,EW）。试验用土取自北京市石景山区,人工地震动的设计采用了石景山区的地震动参数,并以抗震规范中的设计谱为目标拟合而成。

图  4  0.4g阶段台面地震记录及其正则化傅里叶频谱(A_mpk为傅里叶幅值)

Figure  4.  Input seismic motions and normalized Fourier amplitudes with peak amplitude A_mpk

下载: 全尺寸图片 幻灯片

试验前采用场地分析软件预测了自由场土体的卓越频率,并通过对地震动频谱进行缩尺的方式使其卓越频率接近场地的卓越频率,目标为激发土体的最不利地震响应。但同时为确保工作人员和试验设备的安全,响应又不宜过大,综合考虑,最终确定Loma Prieta、Kobe、汶川和北京人工地震动的缩尺比分别为1/3,1/4,1/3,1/2。

动力荷载的输入顺序如表1所示。地震动按其峰值加速度不同分为两个阶段加载,分别为0.2g和0.4g阶段。白噪声和脉冲荷载在每个阶段的开始和结尾输入,其峰值加速度为0.05g,分别共输入3次。

表  1  动力荷载的输入顺序

Table  1.  Sequence of input motions

工况序号	动力荷载	峰值加速度/g	试验阶段/g
IM-1	第一次白噪声	0.05
IM-2	第一次脉冲	0.05
IM-3	Loma Prieta (LP)	0.20	0.20
IM-4	Kobe	0.20
IM-5	汶川	0.20
IM-6	北京人工记录	0.20
IM-7	第二次白噪声	0.05
IM-8	第二次脉冲	0.05
IM-9	Loma Prieta (LP)	0.40	0.40
IM-10	Kobe	0.40
IM-11	汶川	0.40
IM-12	北京人工记录	0.40
IM-13	第三次白噪声	0.05
IM-14	第三次脉冲	0.05

下载: 导出CSV 

| 显示表格

2.   由自由场试验获取整体式反应位移法计算参数的方法

开展整体式反应位移法计算的关键是获取结构周围土体的位移、加速度、材料属性和剪应力等计算参数,本节主要介绍采用自由场振动台试验结果获取这些计算参数的方法。

2.1   土体在结构区域的加速度与位移

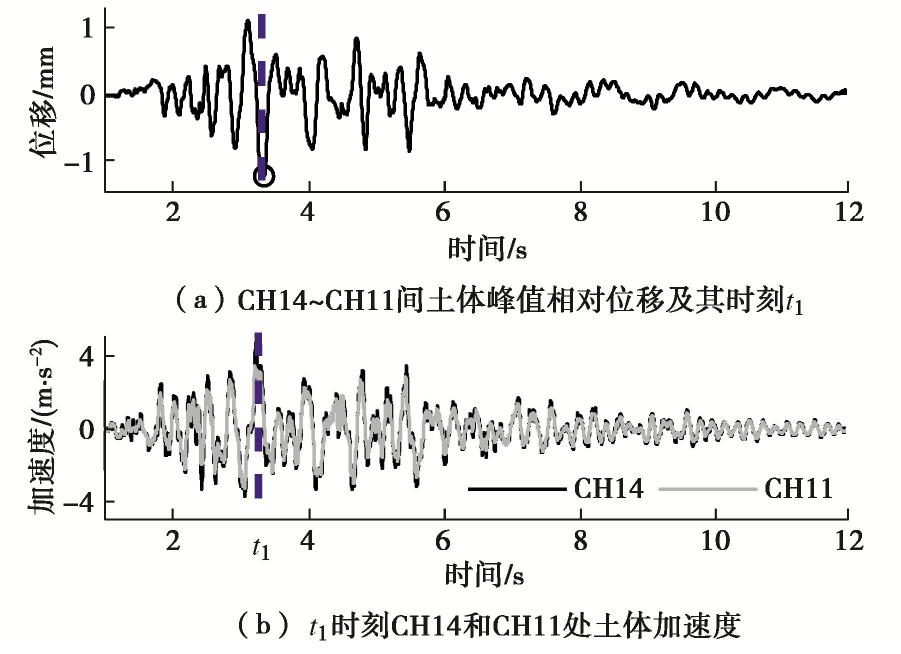
由自由场中心位置处的加速度传感器（CH01～CH15）可获取试验体系在不同高度处的加速度和积分位移响应。假设在后续试验中,模型车站结构顶板和底板大致位于自由场试验中的CH14和CH11位置处,则可获取此范围内土体的峰值相对位移,以及同时刻t₁土体在结构顶、底板对应位置处的加速度响应。以工况IM-12地震作用为例,结构位置处土体的峰值相对位移及同时刻加速度如图5所示。

图  5  土体的相对位移与加速度

Figure  5.  Relative displacements and accelerations of soil at structural region

下载: 全尺寸图片 幻灯片

2.2   土体的材料属性

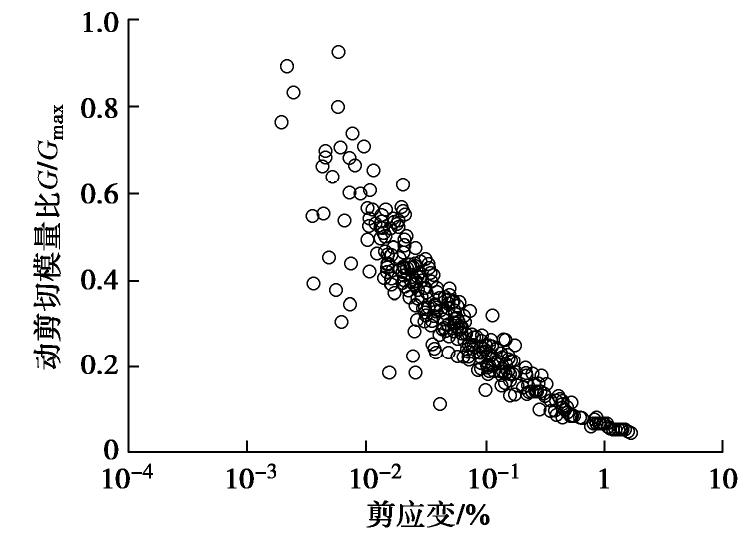
在开展整体式反应位移法计算前,还须获取结构周围土体的材料属性,也即土体在t₁时刻的动剪切模量G。在获取土层的动剪切模量G之前,需首先估算土体的最大剪切模量G_max和动剪应变–动剪切模量比的关系($\gamma$–G/G_max)。

受试验条件的限制,准确获取土体在任意位置处的最大剪切模量G_max是较为困难的。在已有的振动台试验中,通常使用经验法估算砂土的G_max。Tsai等^[15]通过振动台试验的动力数据获取了土体动剪应变–动剪切模量关系,通过拟合由Seed等^[21]得出的$\gamma$–G/G_max关系曲线来估算G_max；Dihoru等^[14]通过试验体系的一阶自振频率和剪切波长估算了G_max的大小；Sadrekarimi^[22]和Anjali等^[23]则通过经验公式来估算G_max。

本文采用脉冲荷载在3 m土体内的传播时间估算砂土的剪切波速v_s。当脉冲荷载在振动台台面激发时,由加速度传感器CH01～CH15可记录其在土体内的传播时间,并获取任意传感器之间的时间差t_s,相应土体的剪切波速即为v_s=h_s/t_s（h_s为传感器之间的距离）。可进一步结合砂土的密度$\rho$获取土体在CH15～CH10、CH10～CH06和CH06～CH01范围内的土体的平均最大剪切模量(G_max=$\rho v_{\text{s}}^{\text{2}}$)。因CH13、CH08和CH04分别处于3个范围的中心位置处,因此可采用CH13、CH08和CH04处的G_max近似代表这3个土层的平均最大剪切模量G_max,其在两次脉冲作用下的数值详见表2。

表  2  土层的最大剪切模量G_max估算结果

Table  2.  Maximum shear moduli of soil layers  (MPa)

工况	土层1	土层2	土层3
第一次脉冲	5.0	21.7	55.4
第二次脉冲	4.0	12.0	32.4

下载: 导出CSV 

| 显示表格

由自由场试验可获取土体的加速度和积分位移响应,在此基础上,可进一步可由式（1）和式（2）获取砂土的剪应力–剪应变($\tau$–$\gamma$)关系^[24-25]：

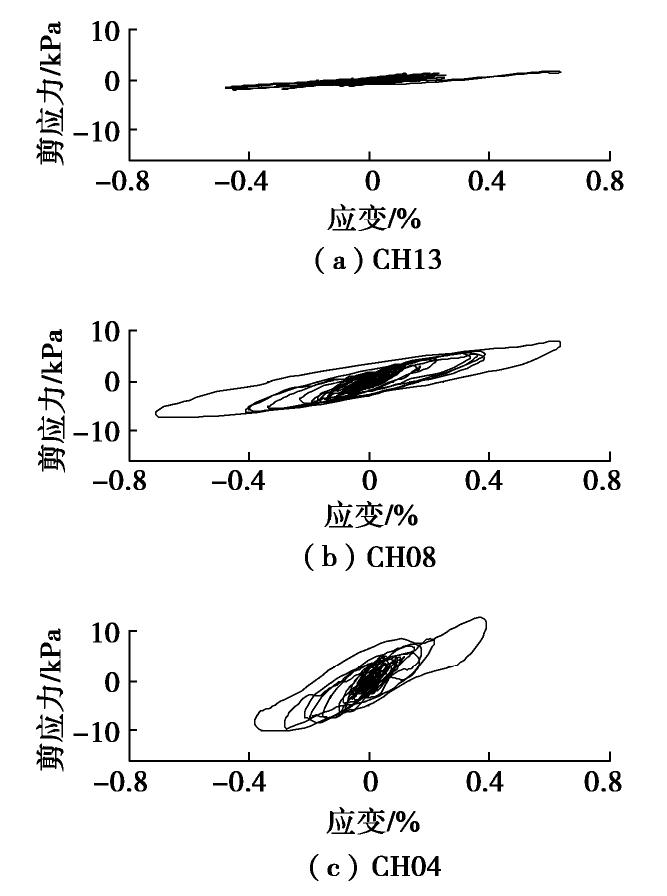
式中 ${\gamma }_i$为土体在CHi(i=2, 3, 4, …, 14)处的剪应变；$u_i$为土体在CHi处的水平位移；$h$为相邻两个加速度传感器之间的高度；${\tau }_i(z)$为深度为z处土体的剪应力,$z_i$为土体表面至CHi之间的距离；${\ddot{u}}_i$为土体在CHi处的水平加速度。

以工况IM-12为例,在CH04、CH08和CH13处的$\tau$–$\gamma$关系如图6所示。图6中第i个滞回圈所对应的动剪切模量表达式为^[24-25]

图  6  地震荷载作用下土体的剪应力–剪应变关系(IM-12)

Figure  6.  Shear stress vs. shear strain hysteresis of sand under seismic motion at IM-12

下载: 全尺寸图片 幻灯片

式中,$G_i$为第i个滞回圈所对应的动剪切模量,${\tau }_{i,\max }$和${\tau }_{i,\min }$分别为第i个滞回圈的最大和最小剪应力,${\gamma }_{i,\max }$和${\gamma }_{i,\min }$分别为第i个滞回圈的最大和最小剪应变。

将一次地震作用下的多个滞回圈所对应的G与其所对应的最大剪应变一一对应,即可得到G随$\gamma$的变化关系,进一步将其采用G_max正则化,即可获取土体的动剪应变–动剪切模量比（$\gamma$–G/G_max）。

采用上述方法,可获取土体在0.4g阶段4条地震动荷载作用下的$\gamma$–G/G_max,如图7所示。同时,由式（1）可获取土体在t₁时刻的剪应变$\gamma$大小,并由图7获取土体的动剪切模量比G/G_max,进而结合表2中的最大剪切模量G_max获取土体在t₁时刻的动剪切模量G。采用上述方法可获取任意传感器高度位置处土体的材料属性,并可将其应用至整体式反应位移法的数值计算中。

图  7  自由场试验中土体的动剪应变–动剪切模量比估算结果(CH08, 0.4g阶段)

Figure  7.  Estimated shear modulus degradation relationships obtained from shaking table tests (CH08, 0.4g stage)

下载: 全尺寸图片 幻灯片

2.3   结构周围土体的剪应力

假设模型车站结构顶、底板分别位于CH14和CH11位置处,则可由式（2）获取自由场试验中土体在顶、底板位置处的剪应力时程,进而获取土体在t₁时刻的剪应力大小。对于矩形地下车站结构,其侧壁剪应力则可在顶、底板剪应力大小的基础上,采用规范^[26]中的方法估算。

3.   预测地下结构在振动台试验中地震响应典型案例

本节以某装配整体式地铁车站结构模型为对象^[27],介绍采用本文所提出方法和传统全数值方法预测其在后续振动台试验中地震响应的典型案例。

3.1   试验与数值计算相结合预测方法及其计算参数

拟预测某矩形地铁车站结构模型在振动台试验中的地震响应,试验中使用的试验设备、土和模型箱与自由场试验中的一致,模型结构的顶、底板大致位于自由场试验中CH14和CH11位置处。采用适用于矩形断面的整体式反应位移法^[16]对其开展预测工作,计算参数均直接源于自由场振动台试验结果。

分别预测地铁车站模型结构在0.2g和0.4g两个阶段下的地震响应,作为典型案例,选取工况IM-6和IM-12开展预测工作。在开展预测前,采用第2节中介绍的参数估算方法,分别获取在结构顶—底板位置处土体的峰值相对位移,及同时刻土体的加速度、土层动剪切模量和剪应力等计算参数,详见表3,4。

表  3  整体式反应位移法计算中所使用的荷载参数

Table  3.  Loads for integral response displacement method

工况	土体相对位移/mm	加速度/(m·s-2)		结构周围剪应力/kPa
		顶板	底板	顶板	底板	左墙	右墙
IM-6	0.47	3.00	2.73	-0.70	-2.63	-0.97	0.97
IM-12	-1.23	-3.46	-3.14	0.81	3.08	1.14	-1.14

下载: 导出CSV 

| 显示表格

表  4  土层的材料属性G

Table  4.  Estimated dynamic shear moduli G of soil  (MPa)

工况	土层1(G1)	土层2(G2)	土层3(G3)
IM-6	1.8	7.9	25.9
IM-12	1.5	2.7	9.2

下载: 导出CSV 

| 显示表格

3.2   传统全数值预测方法及其计算参数

同时采用传统全数值方法开展对车站结构在相同试验工况下的地震响应预测,作为预测工作的对比。仍采用整体式反应位移法^[16]开展预测工作,但计算参数主要源于已有文献中常用的研究成果和场地等效线性化地震响应分析结果。

其中土体的$\gamma$–G/G_max关系取自文献[21],3层土体的最大剪切模量G_max则为^[25]

式中,${\sigma }_0^{}$为有效围压,C为常数,取0.47^[25]。

基于此,可开展场地的等效线性化地震响应分析,并采用规范中的方法^[26]获取土体在结构顶底板位置处的峰值相对位移,及同时刻土体的加速度、剪应力和动剪切模量等计算参数。

3.3   试验预测的数值模型

在有限元软件ABAQUS中开展预测计算,土体和地铁车站结构分别采用二维实体单元和梁单元建模,其中土体被划分为3层,计算厚度分别为0.84,1.04,1.10 m。

车站模型为两层三跨矩形断面装配整体式结构,由已有研究可知,装配整体式地铁车站结构在地震作用下的地震响应可近似等同为现浇地铁车站结构的地震响应^[28],因此将其简化为现浇车站结构。

车站横断面长和高分别为76.3,47.6 cm,埋深为15 cm。结构底板、中板、顶板和侧墙的厚度分别为2.7,1.3,2.3,2.3 cm。柱在试验中的纵向间距为26.67 cm,横截面尺寸为2.3 cm×3 cm。因计算在平面应变状态下开展,将柱横截面面积等效至纵向为1 m的长度上,可得其的计算截面宽度为0.259 cm。结构和土体间采用摩擦接触,计算模型如图8所示。

图  8  整体式反应位移法有限元计算模型

Figure  8.  Finite element model of integral response deformation method

下载: 全尺寸图片 幻灯片

模型结构采用钢丝和微粒混凝土材料制作,因计算在线弹性范围内开展计算,这里采用微粒混凝土材料的室内试验结果来近似代表其在计算中的材料属性,即结构的弹性模量为13.8 GPa^[27]。车站结构的材料与截面属性详见表5。

表  5  结构的材料与截面属性

Table  5.  Properties of material and section

密度/(kg·m-3)	弹性模量/GPa	截面厚度/cm
		底板	中板	顶板	墙	柱
2400	13.8	2.7	1.3	2.3	2.3	0.259

下载: 导出CSV 

| 显示表格

4.   预测与后续试验结果对比

结构的水平和竖向位移,以及典型位置处的应变响应可由后续车站结构振动台模型试验中的加速度传感器和应变片获取。在工况IM-6和IM-12地震作用下,结构顶—底板峰值相对位移,及其同时刻结构顶板右端竖向位移、地下一层和二层右侧柱底应变、地下一层和二层右侧墙底截面平均应变如表6所示。试验中使用的车站模型结构如图9所示。

图  9  后续试验中的模型车站结构

Figure  9.  Model structure in subsequent tests

下载: 全尺寸图片 幻灯片

表  6  预测与后续试验结果对比

Table  6.  Comparison between predicted and subsequent test results

工况		后续试验结果	本文方法预测结果	全数值方法预测结果
IM-6	顶一底板水平相对位移/mm	0.35	0.45	0.15
	顶板右端竖向位移/mm	0.05	0.09	0.02
	地下一层右侧柱底应变/με	2.15	5.54	7.32
	地下一层右侧柱顶应变/με	1.95	6.10	7.24
	地下一层左侧墙底应变/με	0.27	0.70	1.96
	地下一层左侧墙顶应变/με	0.86	0.46	1.35
	地下一层右侧墙底应变/με	0.44	0.75	1.96
	地下二层右侧柱底应变/με	3.02	3.43	6.41
	地下二层左侧柱底应变/με	1.48	3.45	6.39
	地下二层左侧墙顶应变/με	0.81	0.79	2.47
	地下二层右侧墙顶应变/με	0.76	0.80	2.47
	地下二层右侧墙底应变/με	1.21	1.22	3.08
IM-12	顶-底板水平相对位移/mm	0.88	0.75	0.35
	顶板右端竖向位移/mm	1.10	0.15	0.10
	地下一层右侧柱底应变/με	5.01	7.93	13.33
	地下一层右侧柱顶应变/με	7.80	7.94	14.32
	地下一层左侧墙底应变/με	1.06	0.93	2.61
	地下一层左侧墙顶应变/με	2.59	0.51	1.20
	地下一层右侧墙底应变/με	1.63	0.93	2.44
	地下二层右侧柱底应变/με	2.82	3.62	10.32
	地下二层左侧柱底应变/με	3.36	3.59	10.28
	地下二层左侧墙顶应变/με	2.79	0.93	3.28
	地下二层右侧墙顶应变/με	1.82	0.92	3.39
	地下二层右侧墙底应变/με	1.38	1.44	4.27
注：表中的位移和应变均为相应地震工况作用下的峰值大小。

下载: 导出CSV 

| 显示表格

同时,还可分别采用本文方法和传统全数值方法获取对后续试验预测结果,如表6所示。对比后续试验结果与传统全数值方法可知,在两个计算工况下,无论结构的顶—底板相对位移,还是地下一层和二层墙底、柱底处的截面平均应变大小,试验与预测结果均具有较大差异,预测结果不能还原地下结构在试验中的地震响应。

产生这种现象的主要原因为目前常用土体属性估算方法尚不能很好地获取任意类型土体在低围压下（围压不高于50 kPa）的场地计算参数；此外,等效线性化场地地震分析方法本身也存在一定计算精度的问题。

而在本文所提出预测方法中,所有计算参数均直接源于自由场试验结果,可获取更为合理的计算参数。因此,对比后续试验结果与采用本文方法得到的预测结果可知,无论是结构顶—底板相对位移,还是墙、柱截面应变结果,二者的差异均相对较小,采用本文方法得到的预测结果相对于全数值预测方法具有大幅提升。但需要注意的是,在试验中观察到了结构较为明显的横断面内摇摆现象,也即结构左右两端产生了一定的竖向位移,而本文方法未能很好地预测结构的竖向位移响应。

在实践中,影响振动台试验结果的因素较多,如振动台设备性能、模型箱性能、土和微粒混凝土材料的离散性以及传感器数据采集误差等,由此可知,定量地预测后续振动台试验结果是较为困难的。而由表6中的预测结果可知,尽管采用本文方法得到的预测结果与后续试验结果仍存在一定差异,但总体来说,所提出的预测方法已较好地预测后续试验中地下结构的剪切变形和应变结果,可在一定程度上指导并完善后续试验方案。

5.   结语

本文提出一种试验与数值计算相结合的方法,可用以预测地下结构模型在振动台试验中的地震响应,并结合典型案例和后续振动台试验结果验证了方法的有效性。相对于全数值预测方法,本文提出的自由场试验与整体式反应位移法相结合的振动台试验预测方法可大幅提升预测结果的准确性,方法可用以定性地预测地铁车站模型结构在振动台试验中的地震响应,并可在一定程度上指导和完善后续试验方案。