盐溶液饱和高庙子膨润土的强度特性

郑新江; 徐永福

doi:10.11779/CJGE202104022

盐溶液饱和高庙子膨润土的强度特性 English Version

上海交通大学船舶海洋与建筑工程学院,上海　200240

详细信息

作者简介:
郑新江(1994—),男,博士研究生,主要从事化学溶液对膨胀性黏土影响的研究。E-mail: zhengxinjiang1994@sjtu.edu.cn

中图分类号: TU443
计量
- 文章访问数: 0197
- HTML全文浏览量: 0
- PDF下载量: 0166
出版历程
- 收稿日期: 2020-06-22
- 网络出版日期: 2022-12-04
- 刊出日期: 2021-03-31

Strength characteristics of GMZ bentonite saturated with salt solutions

Department of Civil Engineering, Shanghai Jiao Tong University, Shanghai 200030, China

摘要

摘要: 膨润土因具有高膨胀性、低渗透性、优良的核素吸附性等性质,被选作深层地质处置库的缓冲和回填材料。为研究围岩孔隙溶液对膨润土强度的影响,将GMZ07膨润土试样在不同浓度的Na₂SO₄溶液中饱和、固结后进行直剪试验,分析溶液浓度对GMZ07膨润土抗剪强度的影响。试验结果表明,随着盐溶液浓度的增加,膨润土试样的黏聚力及内摩擦角均增大,强度显著提高。在膨润土表面分形模型的基础上,引入考虑渗透吸力的修正有效应力对试验结果进行了解释。将通过修正有效应力计算得到的GMZ07膨润土在Na₂SO₄溶液中的抗剪强度与实测抗剪强度进行比较,二者基本吻合,验证了考虑渗透吸力的修正有效应力的正确性。
- 膨润土 /
- 盐溶液 /
- 抗剪强度 /
- 修正有效应力
Abstract: Bentonite is selected as a buffer and backfill material for deep geological repositories due to its high expansibility, low permeability, and excellent nuclide adsorptive. In order to study the effect of the pore solution of the surrounding rock on the strength of bentonite, GMZ07 bentonite specimens are saturated and consolidated in Na₂SO₄ solution with different concentrations for direct shear tests. The test results show that as the concentration of the salt solution increases, the cohesive intercept and internal friction angle of the bentonite sample increase, and the strength increases significantly. Based on the fractal model for bentonite surface, the modified effective stress that considers the osmotic suction is introduced to explain the test results. The shear strength of GMZ07 bentonite in Na₂SO₄ solution calculated by the modified effective stress is compared with the measured value, and the two are basically in agreement, which verifies the correctness of the modified effective stress considering the osmotic suction.
- bentonite /
- salt solution /
- shear strength /
- modified effective stress

HTML全文

0. 引言

膨润土作为深层地下处置库的缓冲和回填材料,应当具有一定的强度以抵抗围岩地应力。为了更好地评估处置库的长期稳定性,必须确定压实膨润土的抗剪强度,确保其在极端条件下也不会因滑动而导致核素的泄露^[1]。同时,与膨润土垫层接触的围岩孔隙中的流体中溶解有各种化学元素,对膨润土缓冲层的力学行为影响很大^[2]。因此有必要研究盐溶液对膨润土性质的影响,由此更好的评估处置库的安全性^[3]。

孔隙液体的化学成分构成化学负荷,可能会影响膨润土垫层的力学性能。研究发现,孔隙流体中化学成分的变化引起的膨润土与孔隙流体之间的物理化学相互作用可能会影响膨润土的力学性能^[4-8]。膨润土的强度响应高度依赖于孔隙流体化学成分的类型和浓度^[9-12]。Hueckel等^[13]从微观和宏观的角度讨论了化学成分导致黏土的水力传导率和力学性能变化的可能机理。Di^[14]通过Bisaccia膨润土在去离子水、NaCl、KCl溶液以及乙醇中的直剪试验,发现液体成分对膨润土的峰值强度和残余强度影响很大。同时,Di^[15]还研究了NaCl溶液浓度对Ponza膨润土强度的影响,试验结果表明,随着盐溶液浓度的增加,膨润土残余强度增大。随后很多学者也通过试验验证了这种现象^[16-18]。Anson等^[19]分析了膨润土强度随盐溶液浓度的变化,发现膨润土峰值强度随盐溶液浓度增大而增大,残余强度与盐溶液浓度不存在单调变化关系,而与土的结构及自身性质有关。Zhang等^[20]通过GMZ07膨润土在不同浓度NaCl溶液中的直剪试验,发现GMZ07膨润土的峰值强度随NaCl溶液浓度增大而增大。徐永福^[21]和李晓月等^[22-23]在膨润土表面分形模型的基础上,通过考虑盐溶液渗透吸力的影响,研究了化学溶液对膨润土膨胀性能及强度的影响。

黏土的剪切强度可以通过莫尔–库仑准则计算,其大小取决于所受有效应力的大小,且与自身的内摩擦角和黏聚力有关。张龙^[24]通过对不同浓度盐溶液下的膨润土进行了扫描电镜测试,分析在不同盐溶液浓度下膨润土的微观结构,发现在NaCl溶液作用下,蒙脱石颗粒表面呈现细粒化,并随着NaCl溶液浓度增加,颗粒表面的细粒化程度更加明显,比表面积增大,导致蒙脱石颗粒之间的作用力及摩擦作用增强,导致试样内摩擦角变大。另一方面,由于黏土颗粒水平上的静电引力和静力斥力对其力学性质有很强的影响,Sridharan等^[25]考虑静电引力和斥力的影响,提出黏土的有效应力可表示为

$p^{'} = σ - u_{w} + F - F_{r}$ ,

(1)

式中, $p'$ 是有效应力, $σ$ 是总应力, $u_{w}$ 为孔隙水压,F和 $F_{r}$ 分别为颗粒间吸引力和排斥力。黏土颗粒间的吸引力可以定量计算,但是排斥力还未有准确的计算方法,只能通过双电层理论进行定性分析^[26]。此外,扩散双电层理论要求晶层间距达到一定距离,因此双电层理论不能用于高压实膨润土的分析^[27]。

Rao等^[28]考虑渗透吸力的影响,提出黏土的有效应力表达式为

$p^{'} = σ - u_{w} + α Δ π$ ,

(2)

式中, $Δ π$ 为渗透吸力梯度, $α$ 是表示渗透效率的参数,其值在0～1之间。然而,参数 $α$ 的确定十分困难。

为了研究高庙子膨润土在盐溶液中的强度特性,本文通过GMZ07膨润土试样在不同浓度的Na₂SO₄溶液中的直剪试验,分析盐溶液浓度对GMZ07膨润土抗剪强度的影响。引入考虑渗透吸力的修正有效应力对试验结果进行了解释。分析用修正有效应力定量计算膨润土在盐溶液中抗剪强度的准确性。为进一步研究化学因素对膨润土性质的影响提供支持。

1. 试验过程

本次试验所用膨润土为GMZ07膨润土,其主要矿物成分为蒙脱石,此外还含有石英、方石英、斜长石和微斜长石,GMZ07膨润土的矿物组成及基本物理指标见表1。

表 1 GMZ07膨润土矿物组成及基本物理指标

Table 1. Mineral compositions and basic physical index of GMZ07 bentonite

相对质量密度	含水率/%	液限/%	塑限/%	塑性指数	矿物组成/%
相对质量密度	含水率/%	液限/%	塑限/%	塑性指数	蒙脱石	石英	方石英	斜长石	微斜长石
2.76	9.3	125.0	30.0	95.0	61	23	3	7	6

下载: 导出CSV

| 显示表格

膨润土的初始含水率约为9.3%。试验用盐溶液为实验室专用纯Na₂SO₄化学试剂。本次试验为直接剪切试验,所用仪器为美国Geocomp公司生产的HUS-25sixtyShear型气动直剪仪。

将GMZ07膨润土在不同浓度的Na₂SO₄溶液饱和固结后再进行直剪试验,预设垂直压力为50,100,200,300,400 kPa,膨润土试样初始干密度为1.50 g/cm³,配制Na₂SO₄溶液浓度为0,0.2,0.5,1.0 mol/L。

将一定量膨润土粉末与蒸馏水或盐溶液均匀拌合后,装入保鲜袋中放置24 h以上。称取一定量混合料至自制的模具中,用千斤顶将其压成直径5 cm、高2 cm的试样。将压实好的膨润土试样装入直径5 cm、高3 cm的环刀中,安装到固结仪上,往固结盒内加入一定溶度的盐溶液,调节砝码重量,使试样高度保持不变。待试样高度稳定24 h后,视其饱和完成。将饱和完成后的试样通过逐级加载的方式加压至预设垂直压力进行固结,待试样高度在预定固结压力下保持不变,即固结完成。用千斤顶将固结完成后的试样顶出,放入剪切盒内,设定好剪切参数后开始剪切。为评估核废料处置库中高压实膨润土缓冲层在荷载作用下长期的强度,本次直剪试验宜采用慢剪的方式。根据中国人民共和国水利部颁布的《土工试验规程》（SL237—1999）中关于直剪试验慢剪的规定,剪切速率应小于0.02 mm/min,当剪应力与位移关系曲线出现峰值时,定义峰值应力为抗剪强度；当没有峰值强度时,定义当剪切位移达到4 mm时对应的剪切应力为抗剪强度。本次试验剪切速率为0.01 mm/min,剪切在位移达到6 mm时停止。表2为本次试验工况。

表 2 GMZ07膨润土试样试验工况

Table 2. Test states of GMZ07 bentonite for shear tests

浓度/(mol·L^-1)	$σ_{v}$ /kPa	初始干密度/(g·cm^-3)	固结干密度/(g·cm^-3)	饱和度/%
0	50	1.50	1.23	93.01
	100	1.49	1.26	96.95
	200	1.51	1.33	94.40
	300	1.51	1.39	93.24
	400	1.51	1.45	94.31
0.2	50	1.50	1.32	94.07
	100	1.51	1.34	94.58
	200	1.50	1.38	93.74
	300	1.50	1.42	93.10
	400	1.51	1.47	94.85
0.5	50	1.50	1.34	92.33
	100	1.50	1.40	92.67
	200	1.50	1.48	94.51
	300	1.51	1.52	95.26
	400	1.50	1.58	93.28
1	50	1.49	1.48	94.85
	100	1.49	1.50	93.61
	200	1.50	1.53	91.70
	300	1.50	1.56	92.27
	400	1.50	1.59	93.20

下载: 导出CSV

| 显示表格

2. 试验结果

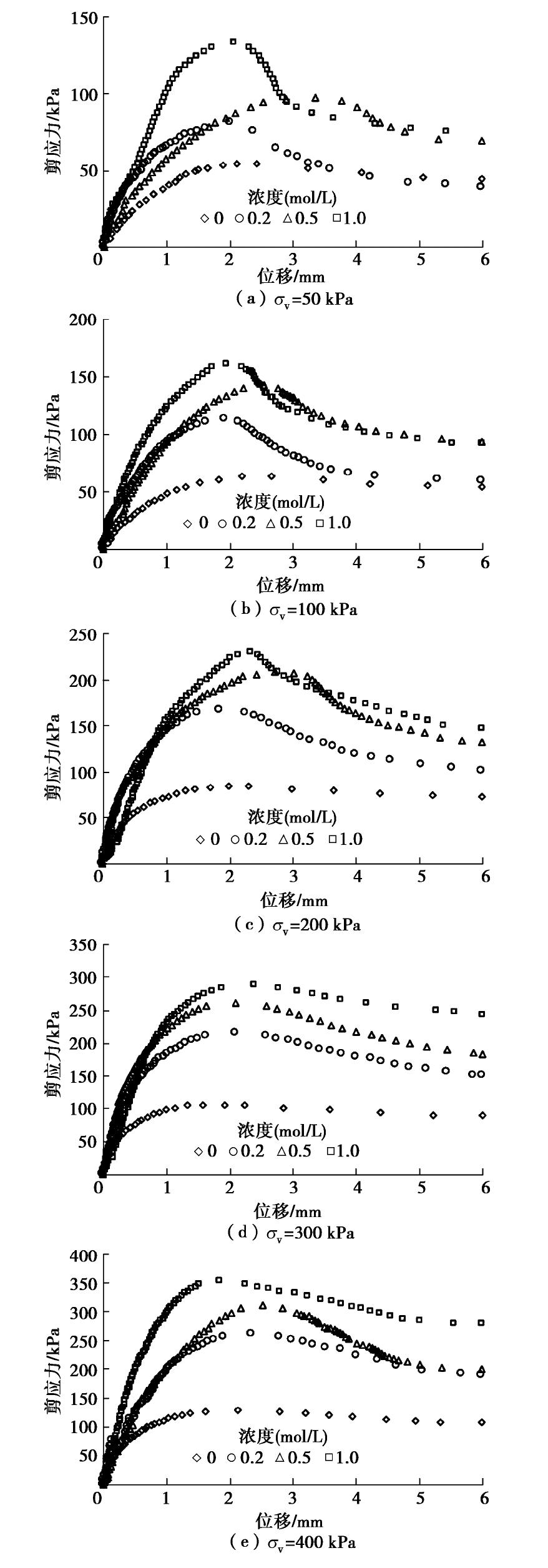
综合分析所有试样的应力–应变关系曲线,发现均出现应变软化现象,且全部试样均已破坏（见图1）,故定义应力–应变关系曲线的峰值为该试样的抗剪强度。

图 1 试样破坏断面

Figure 1. Failure section of specimens

下载: 全尺寸图片幻灯片

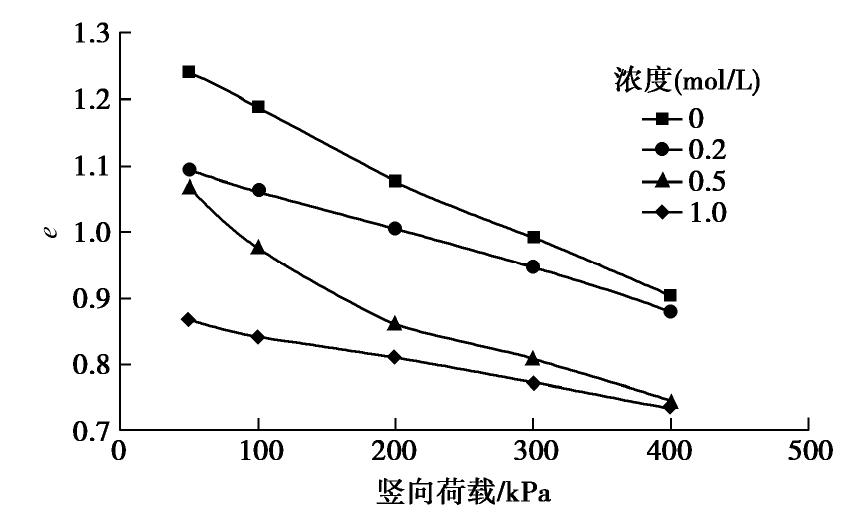
图2为膨润土试样在不同浓度Na₂SO₄溶液中固结后的高度。可以看出,随着盐浓度和垂直应力的增大,GMZ07膨润土试件的变形逐渐减小。

图 2 膨润土试样在不同浓度Na₂SO₄溶液中饱和固结后的孔隙比

Figure 2. Void ratios of bentonite specimens consolidated in Na₂SO₄ solution with different concentrations

下载: 全尺寸图片幻灯片

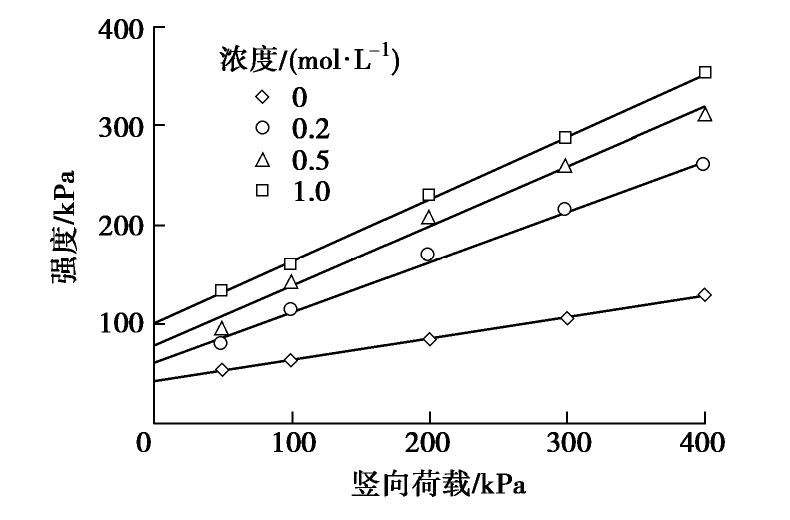
图3为不同浓度Na₂SO₄溶液中的膨润土试样在不同垂直压力下的应力–应变关系曲线。图4为不同浓度Na₂SO₄溶液的膨润土试样抗剪强度与竖向荷载的关系。由图3,4可知,膨润土试样的强度随Na₂SO₄溶液浓度的增大而显著增大,膨润土试样的强度随竖向荷载的增大而线性增大,符合莫尔–库仑准则。

图 3 GMZ07膨润土试样在Na₂SO₄溶液中的剪应力与剪切位移关系曲线

Figure 3. Curves of shear stress and shear displacement of GMZ07 bentonite in Na₂SO₄ solutions

下载: 全尺寸图片幻灯片

图 4 GMZ07膨润土试样在不同浓度Na₂SO₄溶液中的强度线

Figure 4. Shear strength curves of GMZ07 bentonite in Na₂SO₄ solution with different concentrations

下载: 全尺寸图片幻灯片

表3为GMZ07膨润土试样在Na₂SO₄溶液中的强度指标。可以看出,膨润土试样在Na₂SO₄溶液中的黏聚力及内摩擦角均随溶液浓度的增大而增大。

表 3 GMZ07膨润土试样在不同浓度Na₂SO₄溶液中的强度指标

Table 3. Strength indexes of GMZ07 bentonite specimens in Na₂SO₄ solution with different concentrations

浓度/(mol·L^-1)	黏聚力/kPa	内摩擦角/(°)
0	43.119	12.079
0.2	60.871	26.976
0.5	78.024	30.951
1.0	101.410	32.174

下载: 导出CSV

| 显示表格

3. 分析与讨论

如前文所述,膨润土的抗剪强度随着盐溶液浓度增加而增大。由于盐分升高,在相同垂直应力下的空隙率降低。其他类型的膨润土的测试结果也显示出相似的现象^{[8, 15, 29-31]}。膨润土的饱和渗透率非常低,约为10^-13～10^-14 m/s,可以将其视为半透膜^[32]。当外部盐溶液浓度高于膨润土层内部流体的浓度时,会产生渗透梯度,从而导致孔隙流体从膨润土内部流向外部液体。通过膨润土内部孔隙流体的减少和体积减小的趋势来平衡内外渗透压差。这种与渗透梯度的存在相关的体积变化称为渗透固结^[8]。显然,对于膨润土,化学渗透可能导致膨润土所受总应力增大。此外,膨润土由于其高表面电荷和比表面积而对孔隙流体化学变化高度敏感。从微观结构的角度来看,大多数黏土矿物具有带负电荷的净负表面电荷,该负电荷是由带负电荷的黏土表面和与黏土颗粒相邻的带正电荷的吸附水的叠加所产生的,称为弥散双电层^[33]。黏土颗粒之间的吸引力和排斥力是其扩散双层之间相互作用的结果。通常,黏土颗粒之间的主要作用力是静电排斥力。但是,当外部溶液中的溶质离子扩散进入黏土内部后,会导致孔隙流体离子的增加,从而使得扩散双电层的厚度和膨润土颗粒之间的静电排斥力均减小。这进而导致双层的抑制和孔隙率的降低^[7]。与孔隙流体中溶解的化学离子增加有关的体积减小称为化学固结^[34]。这两种机制都使膨润土所受总应力增大。因此随着外部溶液化学性质的变化,膨润土体积和剪切强度也会发生变化。

前文已经介绍了2种考虑化学作用的有效应力的计算方法及局限性。为了准确、便捷计算膨润土的有效应力,Xu^[35]基于膨润土表面的分形模型,提出了考虑渗透吸力的修正有效应力计算公式：

$p^{'} = p + π {(\frac{p}{π})}^{D_{s} - 2}$ ,

(3)

式中,p为竖向外荷载,π为盐溶液的渗透吸力,D_s为膨润土的表面分维。

盐溶液的渗透吸力π根据范德华公式计算：

$π = ζ R T m ϕ$ ,

(4)

式中, $ζ$ 为溶质的离子数（如Na₂SO₄为3）,R为理想气体常数（8.31 J/mol/K）,T为绝对温度,m为质量莫尔浓度（mol/kg）, $ϕ$ 为渗透吸力系数。

根据莫尔–库仑准则,盐溶液饱和膨润土的抗剪强度表示为

$τ_{f} = c^{'} + p^{'} \tan φ^{'}$ ,

(5)

式中,c'为有效黏聚力,φ'为有效内摩擦角。

根据李晓月等^[36]计算出不同浓度Na₂SO₄溶液的渗透吸力系数ϕ,可通过式（4）计算出不同浓度Na₂SO₄溶液的渗透吸力π。计算结果见表4。

表 4 不同浓度Na2SO4溶液的渗透吸力系数及渗透吸力

Table 4. Values of osmotic suction coefficient and osmotic suction of Na₂SO₄ solutions with different concentrations

浓度	$ϕ$	π
0	1	0
0.2	0.754	1120.7
0.5	0.691	2566.8
1.0	0.641	4764.4

下载: 导出CSV

| 显示表格

GMZ07膨润土的表面分维可根据氮吸附试验测得,项国圣^[37]通过测定不同浓度NaCl溶液中高庙子膨润土的分维,得出溶液浓度对膨润土表面分维的影响可忽略不计。Xu等^[38]通过氮吸附试验测得GMZ07膨润土的表面分维为2.78。根据式（3）可计算出膨润土试样在不同浓度Na₂SO₄溶液中,各竖向荷载下的有效应力。

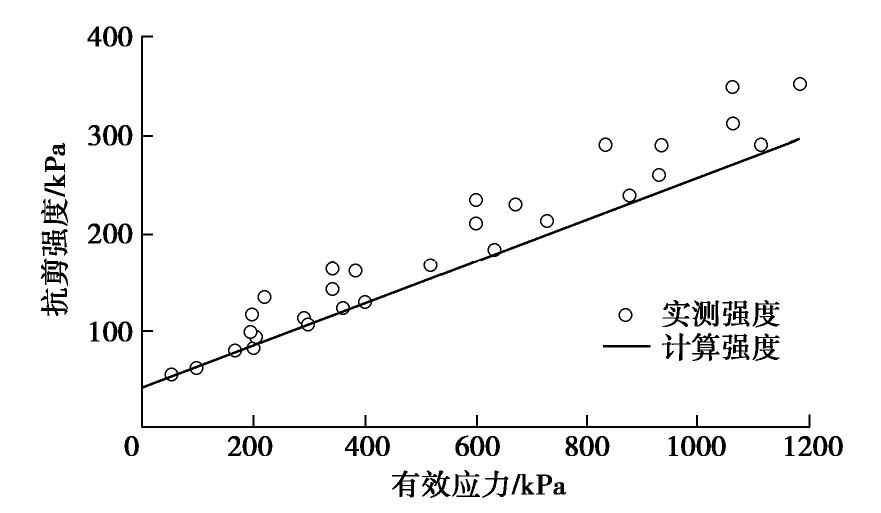
根据莫尔–库仑准则（式（5））及GMZ07膨润土试样在蒸馏水中的强度指标（c=43.1 kPa,φ=12.1°）,可以计算出GMZ07膨润土试样在不同浓度Na₂SO₄溶液中的强度。计算得到的强度与试验测得的强度对比如图5。

图 5 GMZ07膨润土在Na₂SO₄溶液中抗剪强度的计算值与实测值

Figure 5. Calculated and measured values of shear strength of GMZ07 bentonite in Na₂SO₄ solutions

下载: 全尺寸图片幻灯片

由图5可以看出,用考虑渗透吸力的修正有效应力计算得到的强度与实测的强度大致吻合。实测强度比计算得到的强度略微偏高,且偏差随着有效应力的增大而增大。这是由于盐溶液对膨润土强度特性的影响,不仅表现在有效应力的增大,同时,膨润土颗粒表面的细粒化程度随盐溶液浓度的增大而增大,这使得颗粒间的联结更为紧密,具体表现为内摩擦角的增大^[22]。而以修正有效应力计算膨润土的抗剪强度时没有考虑这一因素的影响,这也是今后要研究的方向。

4. 结论

为研究盐溶液饱和高庙子膨润土的强度特性,本文对在不同浓度Na₂SO₄溶液中的GMZ07膨润土饱和试样进行了直剪试验。并用考虑渗透吸力的修正有效应力对试验结果进行了分析。分析并总结试验结果可得到以下结论。

（1）饱和GMZ07膨润土试样的强度与盐溶液的浓度有关。在Na₂SO₄溶液中,随着溶液浓度的升高,GMZ07膨润土的黏聚力、内摩擦角及强度均增大。

（2）在膨润土表面分形模型的基础上,提出的考虑渗透吸力的修正有效应力可以定量计算盐溶液中膨润土的强度。

（3）用修正有效应力计算膨润土在盐溶液中的强度时,未考虑盐溶液对膨润土颗粒微观结构的影响,忽略了内摩擦角随盐溶液浓度的变化情况。

图 1 试样破坏断面

Figure 1. Failure section of specimens

下载: 全尺寸图片幻灯片

图 2 膨润土试样在不同浓度Na₂SO₄溶液中饱和固结后的孔隙比

Figure 2. Void ratios of bentonite specimens consolidated in Na₂SO₄ solution with different concentrations

下载: 全尺寸图片幻灯片

图 3 GMZ07膨润土试样在Na₂SO₄溶液中的剪应力与剪切位移关系曲线

Figure 3. Curves of shear stress and shear displacement of GMZ07 bentonite in Na₂SO₄ solutions

下载: 全尺寸图片幻灯片

图 4 GMZ07膨润土试样在不同浓度Na₂SO₄溶液中的强度线

Figure 4. Shear strength curves of GMZ07 bentonite in Na₂SO₄ solution with different concentrations

下载: 全尺寸图片幻灯片

图 5 GMZ07膨润土在Na₂SO₄溶液中抗剪强度的计算值与实测值

Figure 5. Calculated and measured values of shear strength of GMZ07 bentonite in Na₂SO₄ solutions

下载: 全尺寸图片幻灯片

表 1 GMZ07膨润土矿物组成及基本物理指标

Table 1 Mineral compositions and basic physical index of GMZ07 bentonite

相对质量密度	含水率/%	液限/%	塑限/%	塑性指数	矿物组成/%
相对质量密度	含水率/%	液限/%	塑限/%	塑性指数	蒙脱石	石英	方石英	斜长石	微斜长石
2.76	9.3	125.0	30.0	95.0	61	23	3	7	6

下载: 导出CSV

表 2 GMZ07膨润土试样试验工况

Table 2 Test states of GMZ07 bentonite for shear tests

浓度/(mol·L^-1)	$σ_{v}$ /kPa	初始干密度/(g·cm^-3)	固结干密度/(g·cm^-3)	饱和度/%
0	50	1.50	1.23	93.01
	100	1.49	1.26	96.95
	200	1.51	1.33	94.40
	300	1.51	1.39	93.24
	400	1.51	1.45	94.31
0.2	50	1.50	1.32	94.07
	100	1.51	1.34	94.58
	200	1.50	1.38	93.74
	300	1.50	1.42	93.10
	400	1.51	1.47	94.85
0.5	50	1.50	1.34	92.33
	100	1.50	1.40	92.67
	200	1.50	1.48	94.51
	300	1.51	1.52	95.26
	400	1.50	1.58	93.28
1	50	1.49	1.48	94.85
	100	1.49	1.50	93.61
	200	1.50	1.53	91.70
	300	1.50	1.56	92.27
	400	1.50	1.59	93.20

下载: 导出CSV

表 3 GMZ07膨润土试样在不同浓度Na₂SO₄溶液中的强度指标

Table 3 Strength indexes of GMZ07 bentonite specimens in Na₂SO₄ solution with different concentrations

浓度/(mol·L^-1)	黏聚力/kPa	内摩擦角/(°)
0	43.119	12.079
0.2	60.871	26.976
0.5	78.024	30.951
1.0	101.410	32.174

下载: 导出CSV

表 4 不同浓度Na2SO4溶液的渗透吸力系数及渗透吸力

Table 4 Values of osmotic suction coefficient and osmotic suction of Na₂SO₄ solutions with different concentrations

浓度	$ϕ$	π
0	1	0
0.2	0.754	1120.7
0.5	0.691	2566.8
1.0	0.641	4764.4

下载: 导出CSV

参考文献(38)

[1]	KIMURA S, NAKAMURA S, VITHANA S B, et al. Shearing rate effect on residual strength of landslide soils in the slow rate range[J]. Landslides, 2014, 11: 969-979. doi: 10.1007/s10346-013-0457-6
[2]	WANG J. High-level radioactive waste disposal in China: update 2010[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2010, 2(1): 1-11.
[3]	BOLT G H. Physico-chemical analysis of the compressibility of pure clays[J]. Géotechnique, 1956, 6(2): 86-93. doi: 10.1680/geot.1956.6.2.86
[4]	SRIDHARAN A, RAO V G. Mechanisms controlling volume change of saturated clays and the role of the effective stress concept[J]. Géotechnique, 1973, 23(3): 359-382. doi: 10.1680/geot.1973.23.3.359
[5]	BARBOUR S L, FREDLUND D G. Mechanisms of osmotic flow and volume change in clay soils[J]. Canadian Geotechnical Journal, 1989, 26(4): 551-562. doi: 10.1139/t89-068
[6]	GREENBERG J A, MITCHELL J K, WITHERSPOON P A. Coupled salt and water flows in a groundwater basin[J]. Journal of Geophysical Research, 1973, 78: 6341-6353. doi: 10.1029/JC078i027p06341
[7]	FERNANDEZ F, QUIGLEY R M. Controlling the destructive effects of clay-organic liquid interactions by application of effective stress[J]. Canadian Geotechnical Journal, 1991, 28: 388-398. doi: 10.1139/t91-049
[8]	MITCHELL J K, SOGA K. Fundamentals of Soil Behavior[M]. 3rd ed. New York: Wiley, 2005.
[9]	SUN D A, ZHANG J Y, ZHANG J, et al. Swelling characteristics of GMZ bentonite and its mixtures with sand[J]. Applied Clay Science, 2013, 83: 224-230.
[10]	SRIDHARAN A, PRAKASH K. Mechanisms controlling the undrained shear strength behaviour of clays[J]. Canadian Geotechnical Journal, 1999, 36: 1030-1038. doi: 10.1139/t99-071
[11]	DUECK A, BÖRGESSON L. Thermo-mechanically induced brittleness in compacted bentonite investigated by unconfined compression tests[J]. Engineering Geology, 2015, 193: 305-309. doi: 10.1016/j.enggeo.2015.05.005
[12]	DI MAIO C, SCARINGI G. Shear displacements induced by decrease in pore solution concentration on a pre-existing slip surface[J]. Engineering Geology, 2016, 200: 1-9. doi: 10.1016/j.enggeo.2015.11.007
[13]	HUECKEL T. Chemo-plasticity of clays subjected to flow of a single contaminant and stress[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1997, 21(1): 43-72. doi: 10.1002/(SICI)1096-9853(199701)21:1<43::AID-NAG858>3.0.CO;2-1
[14]	MAIO D C. Shear strength of clays and clayey soils: the influence of pore fluid composition[J]. CISM Courses and Lectures, 2004, 462: 45-55.
[15]	MAIO D C. Exposure of bentonite to salt solution: osmotic and mechanical effects[J]. Géotechnique, 1996, 46(4): 695-707. doi: 10.1680/geot.1996.46.4.695
[16]	于海浩, 韦昌富, 颜荣涛, 等. 孔隙溶液浓度的变化对黏土强度的影响[J]. 岩土工程学报, 2015, 37(3): 564-569. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201503027.htm YU Hai-hao, WEI Chang-fu, YAN Rong-tao, et al. Effects of pore solution concentrations on shear strength of clay[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(3): 564-569. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201503027.htm
[17]	SPAGNOLI G, FERNANDEZ-STEEGER T, FEINENDEGEN M, et al. The influence of the dielectric constant and electrolyte concentration of the pore fluids on the undrained shear of smecite[J]. Soils and Foundations, 2010, 50(5): 757-763. doi: 10.3208/sandf.50.757
[18]	姚传芹, 韦昌富, 马田田, 等. 孔隙溶液对膨胀土力学性质影响[J]. 岩土力学, 2017, 38(2): 116-122. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2017S2016.htm YAO Chuan-qin, WEI Chang-fu, MA Tian-tian, et al. Effects of pore solution on mechanical properties of expansive soil[J]. Rock and Soil Mechanics, 2017, 38(2): 116-122. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2017S2016.htm
[19]	ANSON R W, HAWKINS A B. The effect of calcium ions in pore water on residual shear strength of kaolinite and sodium montmorillonite[J]. Géotechnique, 1998, 48(6): 787-800. doi: 10.1680/geot.1998.48.6.787
[20]	ZHANG L, SUN D A, JIA D. Shear strength of GMZ07 bentonite and its mixture with sand saturated with saline solution[J]. Applied Clay Science, 2016, 132: 24-32.
[21]	徐永福. 考虑渗透吸力影响膨润土的修正有效应力及其验证[J]. 岩土工程学报, 2019, 41(4): 631-638. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201904006.htm XU Yong-fu. Modified effective stress induced by osmotic suction and its validation in volume change and shear strength of bentonite in saline solutions[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(4): 631-638. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201904006.htm
[22]	李晓月, 徐永福. 盐溶液中膨润土膨胀变形的计算方法[J]. 岩土工程学报, 2019, 41(12): 2353-2359. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201912030.htm LI Xiao-yue, XU Yong-fu. Method for calculating swelling deformation of bentonite in salt solution[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(12): 2353-2359. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201912030.htm
[23]	李晓月, 徐永福. 盐溶液中膨润土峰值剪切强度的计算方法[J]. 岩土工程学报, 2019, 41(5): 885-891. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201905014.htm LI Xiao-yue, XU Yong-fu. Calculation of peak shear strength of bentonite in salt solutions[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(5): 885-891. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201905014.htm
[24]	张龙. 高庙子膨润土力学和化学特性及预测[D]. 上海: 上海大学, 2018. ZHANG Long. Chemical and Mechanical Behaviour of GMZ Bentonite and Its Predictions[D]. Shanghai: University of Shanghai, 2018. (in Chinese)
[25]	SRIDHARAN A, RAO V G. Shear strength behaviour of saturated clays and the role of the effective stress concept[J]. Géotechnique, 1979, 29(2): 177-193.
[26]	LIU L, MORENO L, NERETNIEKS I. A dynamic force balance model for colloid expansion and its DLVO-Based application[J]. Langmuir, 2009, 25: 679-687.
[27]	贾景超. 膨胀土膨胀机理及细观膨胀模型研究[D]. 大连: 大连理工大学, 2010. JIA Jing-chao. Study on the Swelling Mechanism and Mesomechanical Swelling Model of Expansive Soil[D]. Dalian: Dalian University of Technology, 2010. (in Chinese)
[28]	RAO S M, THYAGARAJ T. Swell-compression behaviour of compacted clays under chemical gradients[J]. Canadian Geotechnical Journal, 2007, 44(5): 520-532.
[29]	NEUZIL C E. Osmotic generation of ‘anomalous’ fluid pressure in geological environments[J]. Nature, 2000, 403: 182-184.
[30]	KEIJZER T H J S, LOCH J P G. Chemical osmosis in compacted dredging sludge[J]. Soil Science Society of America Journal, 2000, 65, 1045-1055.
[31]	MANASSERO M, DOMINIJANNI A. Modelling the osmosis effect on solute migration through porous media[J]. Géotechnique, 2003, 53, 481-492.
[32]	CHEN G J, GALLIPOLI D, LEDESMA A. Chemo-hydro- mechanical coupled consolidation for a poroelastic clay buffer in a radioactive waste repository[J]. Transportation in Porous Media, 2007, 69: 189-213.
[33]	GOUY G. The constitution of the electric charge on the surface of an electrolyte[J]. Annales de Physique, 1910, 9: 457-68. (in French)
[34]	KARNLAND O, MUURINEN A, KARLSSON F. Advances in Understanding Engineered Clay Barriers[M]. Netherlands: Balkema, 2005.
[35]	XU Y F. Peak shear strength of compacted GMZ bentonites in saline solution[J]. Engineering Geology, 2019, 251: 93-99.
[36]	李晓月, 徐永福. 盐溶液的渗透吸力计算方法[J]. 地质力学学报, 2018, 24(5): 723-729. https://www.cnki.com.cn/Article/CJFDTOTAL-DZLX201805016.htm LI Xiao-yue, XU Yong-fu. The calculation method for osmotic suction of saline solution[J]. Journal of Geomechanics, 2018, 24(5): 723-729. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZLX201805016.htm
[37]	项国圣. 含盐环境中膨润土的膨胀理论及膨胀衰减机理研究[D]. 上海: 上海交通大学, 2015. XIANG Guo-sheng. Theory of Swelling Properties and Mechanism on Swell Attenuation of Bentonite in Salt Solution[D]. Shanghai: Shanghai Jiao Tong University, 2015. (in Chinese)
[38]	XU Y F, XIANG G S, JIANG H, et al. Role of osmotic suction in volume change of clays in salt solution[J]. Applied Clay Science, 2014, 101: 354-361.