不同应力路径下钙质砂力学特性的排水三轴试验研究

张季如; 罗明星; 彭伟珂; 张弼文

doi:10.11779/CJGE202104001

不同应力路径下钙质砂力学特性的排水三轴试验研究 English Version

武汉理工大学土木工程与建筑学院,湖北　武汉　430070

基金项目:

国家自然科学基金面上项目 41272334

详细信息

作者简介:
张季如(1964—),男,教授,博士生导师,主要从事岩土工程方面的教学和科研。E-mail: zhangjr@whut.edu.cn

中图分类号: TU431
计量
- 文章访问数: 564
- HTML全文浏览量: 43
- PDF下载量: 447
出版历程
- 收稿日期: 2020-06-27
- 网络出版日期: 2022-12-04
- 刊出日期: 2021-03-31

Drained triaxial tests on mechanical properties of calcareous sand under various stress paths

School of Civil Engineering and Architecture, Wuhan University of Technology, Wuhan 430070, China

摘要

摘要: 钙质砂的力学性质既有强度低、易破碎的特点,又有应力路径依附性的特性。为了研究不同应力路径对钙质砂的颗粒破碎和力学性质的影响,对不同固结压力的钙质砂进行了5种应力路径下的排水三轴压缩试验。结果表明：不同应力路径对钙质砂的应力–应变关系、抗剪强度和颗粒破碎特性有较大的影响。相同固结压力下,等轴向应力试验的剪胀现象最为明显,颗粒破碎率最小,峰值内摩擦角最大；等围压试验的剪胀现象最不明显,颗粒破碎率最大,峰值内摩擦角最小；等平均主应力试验的这些性质介于上述两种试验之间。等主应力比和等向固结试验在加载过程中主要表现为试样的体积压缩,因此与另外3种应力路径试验差别很大。不同应力路径对钙质砂应力–应变关系和强度的影响,除了砂土具有应力路径依附性的特性外,主要来自于应力路径和固结压力的不同产生的颗粒破碎程度不一致造成的影响,使得在不同的应力路径试验中钙质砂的力学性质表现出更大的差异。
- 钙质砂 /
- 力学特性 /
- 排水三轴试验 /
- 应力路径 /
- 颗粒破碎
Abstract: The mechanical properties of calcareous sand are low in strength and easy to crush and have the characteristics of stress path dependence. In order to study the effects of different stress paths on the particle crushing and mechanical properties of calcareous sand, a series of drained triaxial compression tests under five stress paths are carried out on calcareous sand with different consolidation pressures. The results show that the stress path has a great influence on the stress-strain relationship, shear strength and particle breakage of the calcareous sand. Under the same consolidation pressure, the dilation phenomenon is obvious in the constant axial stress tests where the particle breakage index is the smallest, and the peak internal friction angle is the largest. The dilation phenomenon is less noticeable in the constant confining pressure tests with the largest particle breakage index and the smallest peak internal friction angle. These properties of the constant average principal stress tests are in between the above tests. The isotropic principal stress ratio tests and the isotropic stress consolidation tests mainly show the volume compression of samples during loading, so they are very different from the other three stress path tests. The influence factors of different stress paths on the stress-strain relationship and strength of calcareous sands, in addition to the characteristics of sands with stress path dependence, mainly come from the effects of inconsistent particle breakage caused by different stress paths and consolidation pressures. This is why the mechanical properties of the calcareous sand show great differences in the tests with different stress paths.
- calcareous sand /
- mechanical property /
- drained triaxial test /
- stress path /
- particle breakage

HTML全文

0. 引言

钙质砂是一种以碳酸钙为主要成分的特殊砂土,具有粒内富含孔隙、形状不规则、颗粒易破碎的特点,在常应力状态下就能产生颗粒破碎,从而影响钙质砂的力学特性。另一方面,砂土的力学性质具有很强的应力路径依附性,不同应力路径对应力–应变关系和强度有很大的影响^[1-2]。因此,对这种既有砂土特性,同时又容易颗粒破碎的钙质砂,需要探索在不同应力路径和颗粒破碎双重因素作用下的力学特性。

自20世纪80年代开始,许多研究者将应力路径视为一条主线来分析各类岩土工程问题。一些学者研究了不同应力路径对砂土的应力–应变关系和抗剪强度的影响^[2-5]。砂土的本构方程研究也逐步考虑到了应力路径的依附性,目的是建立一种能适合于各种复杂应力路径条件的本构方程^[6-9]。这些研究的对象通常是标准的石英砂,颗粒质地坚硬、形状比较规则,在常应力范围的应力路径作用下,很少考虑颗粒破碎对其力学性质和本构关系的影响。

同为粒状材料的堆石料也具有应力路径依附性的特性。与颗粒坚硬的石英砂相比,堆石料的强度偏低,具有易破碎的特点。近年来随着土石坝的筑坝高度不断增加,堆石料的颗粒破碎特性受到广泛重视,一些学者利用大型三轴试验设备研究了应力路径对堆石料颗粒破碎和力学性质的影响^[10-13]。然而针对复杂应力路径下堆石料颗粒破碎的研究,目前的成果仍比较少。此外,堆石料与砂土的矿物成分、颗粒大小相差悬殊,二者的力学性质存在明显差异。

近年来随着海洋开发和岛礁建设的不断发展,钙质砂的工程性质受到重视。钙质砂的颗粒破碎与力学性质的关系,已经成为土力学研究的热点之一^[14]。许多学者利用三轴试验研究颗粒破碎对钙质砂力学性质的影响^[15-17],并将颗粒破碎指标纳入到钙质砂的临界状态和本构模型的研究^[18-20]。这些研究主要采取的是单一的、常规的三轴应力路径,而复杂应力路径条件下钙质砂的三轴试验研究,迄今为止尚不多见,目前对不同应力路径下的三轴压缩和剪切过程中钙质砂的颗粒破碎特性,以及颗粒破碎对应力–应变关系和抗剪强度影响规律的认识仍十分有限。鉴于此,本文采用高压三轴试验系统,对不同固结条件的钙质砂进行5种不同应力路径下的排水三轴压缩试验,研究不同应力路径对钙质砂的应力–应变关系、抗剪强度和颗粒破碎特性的影响规律,旨在深入认识不同应力路径下钙质砂的力学特性,为建立复杂应力路径下考虑颗粒破碎的钙质砂本构模型提供依据。

1. 土样与试验方法

1.1 土样

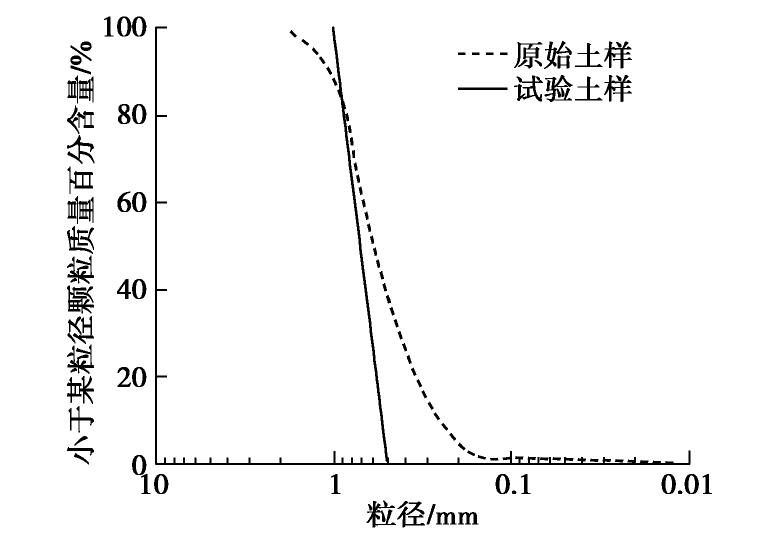
原始土样取自中国南海岛礁的钙质砂。经测试,钙质砂的CaCO₃含量为96.39%,土粒相对质量密度为2.76,粒径分布曲线见图1。考虑到在相同的应力水平下,均匀分布的钙质砂比非均匀分布时的颗粒破碎程度更高,为便于研究不同应力路径试验对颗粒破碎的影响,采用筛分法制备粒径范围为1～0.5 mm的单一粒组的试样,该粒组的颗粒占原始级配钙质砂的质量百分比超过50%。

图 1 钙质砂的粒径分布曲线

Figure 1. Grain-size distribution curves of calcareous sand

下载: 全尺寸图片幻灯片

1.2 试验方法

试验采用英国GDS公司生产的高压三轴试验系统（HTPAS）。试验过程采用伺服电机控制,围压和反压均由电机控制的压力体积控制器施加,围压可达16 MPa,反压可达4 MPa。位移传感器量程±25 mm,荷重传感器量程100 kN。试样为圆柱形,直径50 mm,高100 mm。在圆柱形底座上包裹一个1 mm厚橡皮膜,膜内采用砂雨法撒干砂制备试样。制成试样的干密度ρ_d=1.45 g/cm³,孔隙比e=0.9,相对密度D_r=0.72。为抑制试样的边缘效应,试样帽、底座与试样之间各采用一个6 mm厚的抛光金属透水板相连。试验中的压力室和进、排水管道均为钢制,围压采用液压油加载,避免了仪器的压力变形。试样在三轴试验系统中反压饱和后,即可进行不同应力路径下的三轴试验。

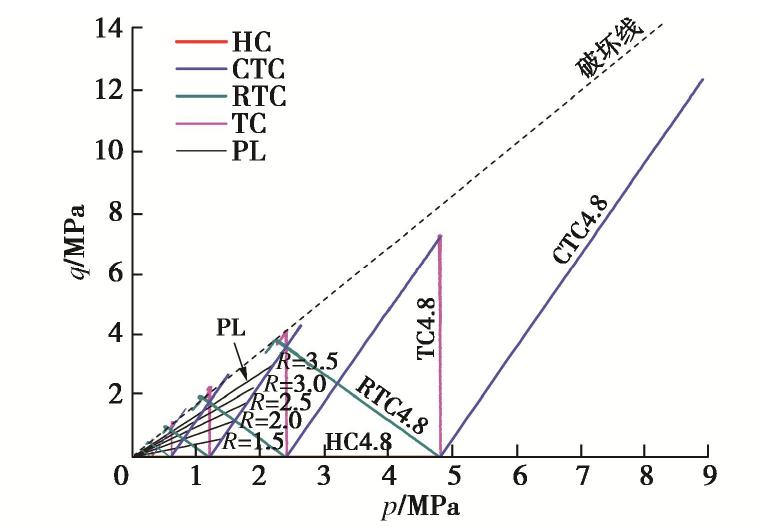
本文采用的三轴试验应力条件下应力和应变的符号意义如下：固结压力 $σ_{c}$ $σ_{c}$ ,轴向应力 $σ_{1}$ $σ_{1}$ ,围压 $σ_{3}$ $σ_{3}$ ,轴向应变 $ε_{1}$ $ε_{1}$ ,体应变 $ε_{v}$ $ε_{v}$ ,平均主应力p=（ $σ_{1} + 2 σ_{3}$ $σ_{1} + 2 σ_{3}$ ）/ 3,偏应力q= $σ_{1} - σ_{3}$ $σ_{1} - σ_{3}$ ,与q相适应的剪应变 $ε_{s}$ $ε_{s}$ = $ε_{1}$ $ε_{1}$ - $ε_{v}$ $ε_{v}$ / 3,主应力比R= $σ_{1} / σ_{3}$ $σ_{1} / σ_{3}$ ,应力比η=q/p=3（R-1）/（R+2）。各试验在p–q平面内的应力路径见图2,进行了固结压力 $σ_{c}$ $σ_{c}$ =0.3,0.6,1.2,2.4,4.8 MPa的等向压缩试验（HC）,以及在上述5种固结压力的等向固结条件下,进行了等 $σ_{3}$ $σ_{3}$ 而增大 $σ_{1}$ $σ_{1}$ （CTC）、等 $σ_{1}$ $σ_{1}$ 而减小 $σ_{3}$ $σ_{3}$ （RTC）和等p（TC）的排水三轴压缩试验。此外还进行了不固结条件下等主应力比的排水三轴压缩试验（PL）,选取了5个主应力增量比 $Δ σ_{1} / Δ σ_{3}$ $Δ σ_{1} / Δ σ_{3}$ =1.5,2.0,2.5,3.0,3.5,对应的应力增量比Δq/Δp=0.43,0.75,1,1.2,1.36。应力路径试验方案见表1,共进行了5种应力路径下的25组试验,其中,HC试验将试样的体积变化率小于5 mm³/min作为试验终止标准,PL试验将σ₃增至1.2 MPa设为试验终止条件,CTC,RTC和TC试验将控制轴向应变ε₁=20%作为试验终止标准,旨在尽量增大钙质砂的颗粒破碎量。

图 2 p–q平面内的应力路径

Figure 2. Stress paths in p–q plane

下载: 全尺寸图片幻灯片

表 1 应力路径试验方案

Table 1. Schemes of stress path tests

试验编号	应力增量比		固结压力 $σ_{c}$ $σ_{c}$ /MPa	应力路径	控制方式	剪切速率
试验编号	$\frac{Δ σ_{1}}{Δ σ_{3}}$ $\frac{Δ σ_{1}}{Δ σ_{3}}$	$\frac{Δ q}{Δ p}$ $\frac{Δ q}{Δ p}$	固结压力 $σ_{c}$ $σ_{c}$ /MPa	应力路径	控制方式	剪切速率
HC0.3	1	0	0.3	$σ_{1}$ $σ_{1}$ = $σ_{3}$ $σ_{3}$ = $σ_{c}$ $σ_{c}$ 不变	应力控制	无
HC0.6			0.6
HC1.2			1.2
HC2.4			2.4
HC4.8			4.8
CTC0.3	∞	3	0.3	$σ_{1}$ $σ_{1}$ 增大 $σ_{3}$ $σ_{3}$ = $σ_{c}$ $σ_{c}$ 不变	应变控制	Δε₁=0.05 mm/min
CTC0.6			0.6
CTC1.2			1.2
CTC2.4			2.4
CTC4.8			4.8
RTC0.3	0	-3/2	0.3	$σ_{1}$ $σ_{1}$ = $σ_{c}$ $σ_{c}$ 不变 $σ_{3}$ $σ_{3}$ 减小	应力控制	$Δ σ_{3} = 5$ $Δ σ_{3} = 5$ kPa/min
RTC0.6			0.6
RTC1.2			1.2
RTC2.4			2.4
RTC4.8			4.8
TC0.3	-2	∞	0.3	$σ_{1}$ $σ_{1}$ 增大 $σ_{3}$ $σ_{3}$ 减小 p= $σ_{c}$ $σ_{c}$ 不变	应力控制	$Δ σ_{1} = 5$ $Δ σ_{1} = 5$ kPa/min $Δ σ_{3} = 2.5$ $Δ σ_{3} = 2.5$ kPa/min
TC0.6			0.6
TC1.2			1.2
TC2.4			2.4
TC4.8			4.8
PL1.5	1.5	0.43	无	$σ_{1}$ $σ_{1}$ 增大 $σ_{3}$ $σ_{3}$ 增大	应力控制	$Δ σ_{3} = 5$ $Δ σ_{3} = 5$ kPa/min
PL2.0	2.0	0.75
PL2.5	2.5	1.00
PL3.0	3.0	1.20
PL3.5	3.5	1.36

下载: 导出CSV

| 显示表格

各组试验完毕后,小心取出试样,利用筛析法进行粒度分析,以获取试样的粒径分布曲线来量化颗粒破碎程度。本文采用Hardin^[21]提出的相对破碎率B_r来量化钙质砂的颗粒破碎,即分别将试验前和试验后的粒径分布曲线与0.075 mm粒径截断线所围成的面积,定义为试验前和试验后的破碎势。将试验前和试验后的破碎势之差定义为破碎量,则相对破碎率为破碎量与试验前破碎势的比值。

2. 结果与分析

2.1 应力–应变特性

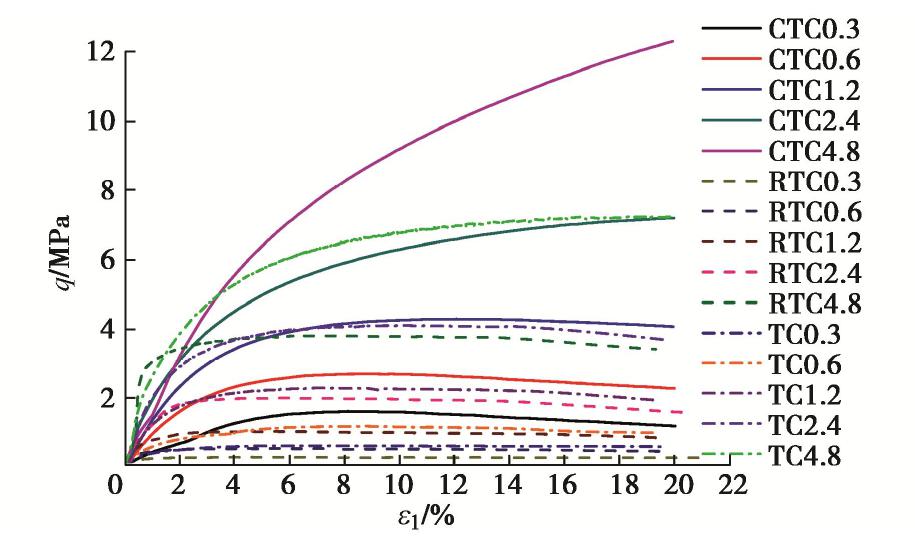
图3为CTC,RTC和TC试验中的偏应力与轴向应变的关系曲线。从图中可以看见,3种应力路径的应力–应变曲线形状基本相似,大致呈非线性的双曲线型。相同应力路径下,应力–应变曲线的起始坡度随固结压力增大而变陡。不同应力路径下,应力–应变曲线的起始坡度也不同,CTC试验的较缓,TC试验的变陡,RTC试验的最陡,偏应力到达峰值的轴向应变很小。除了高固结压力的CTC4.8试验外,其它试验的应力–应变曲线均表现为应变软化现象,固结压力越小,应变软化特征越明显,峰值偏应力随着固结压力增大而增大。

图 3 偏应力与轴向应变的关系曲线

Figure 3. Curves of deviator stress versus axial strain

下载: 全尺寸图片幻灯片

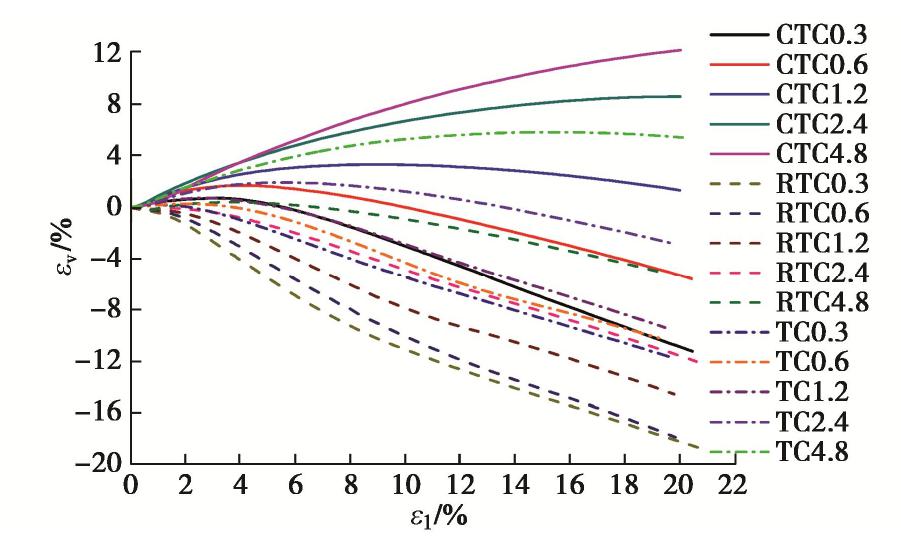
图4为CTC,RTC和TC试验中的体应变与轴向应变的关系曲线,其中体应变是从试验的总体应变中,扣除了等向固结条件下由固结压力σ_c产生的体应变,为试验在剪切阶段产生的体应变。从图4可以看见,除了高固结压力的CTC4.8试验外,其它试验随着轴向应变的增加,体应变先缩小,后膨胀。固结压力越小,剪胀现象越显著,随着固结压力的增大,剪胀倾向减少。不同应力路径对钙质砂剪胀的影响较为明显,剪胀的大小、体应变为零时对应的轴向应变、体应变终值的大小等都有很大区别。

图 4 体应变与轴向应变的关系曲线

Figure 4. Curves of volumetric strain versus axial strain

下载: 全尺寸图片幻灯片

从图4还可以看见,RTC试验开始就表现为剪胀现象,试验过程中体应变基本上为负值；TC试验总体表现为剪胀,在低固结压力时的剪胀现象更加明显,在较小的轴向应变时,体应变由正转负值；CTC试验只在低固结压力时的剪胀现象较为明显,轴向应变增加到一定量时,体应变转为负值,但随着固结压力的增大,剪胀倾向减少。高固结压力的CTC4.8试验的体应变始终为剪缩,需要相当大的轴向应变,才会趋于不胀不缩。

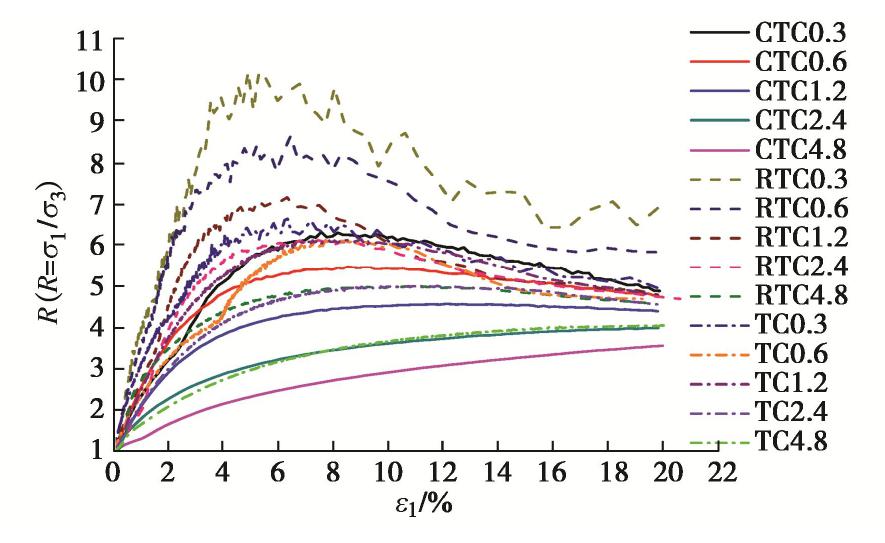
图5为CTC,RTC和TC试验中的主应力比与轴向应变的关系曲线。从图中可以看见,主应力比随轴向应变的增加而增加,达到峰值后又逐渐降低,降低幅度与剪胀变化趋势相一致。相同应力路径下,固结压力越低,剪胀效应越显著,曲线上主应力比出现峰值的现象越明显。不同应力路径下,由于RTC试验的剪胀效应显著,曲线上具有明显的峰值主应力比,应变软化现象十分明显；CTC试验只是在低围压时曲线具有较为明显的峰值主应力比,在高围压下,随着轴向应变的增加,主应力比不出现峰值；TC试验的曲线特点介于RTC和CTC试验之间,低围压时曲线具有明显的峰值主应力比,高围压时的曲线无明显峰值主应力比。

图 5 主应力比与轴向应变的关系曲线

Figure 5. Curves of principal stress ratio versus axial strain

下载: 全尺寸图片幻灯片

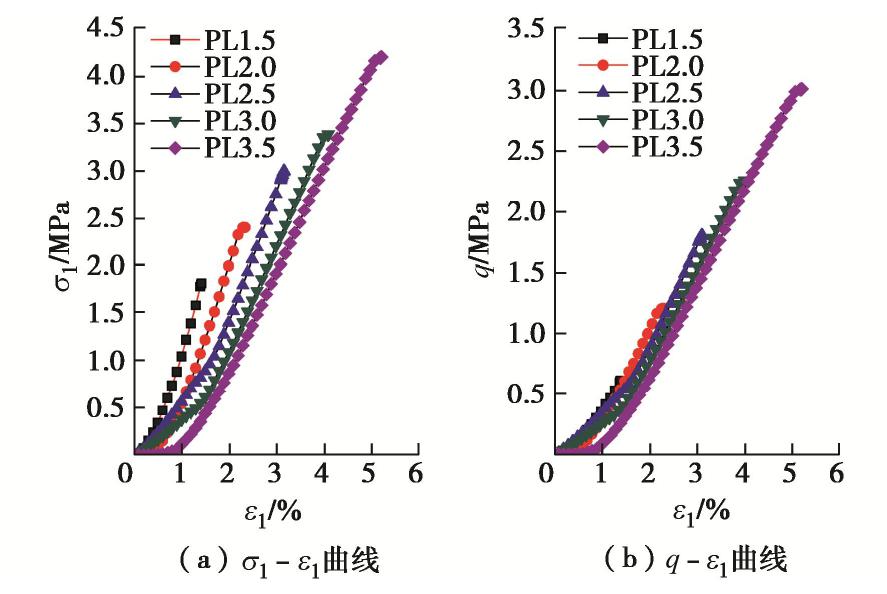
图6为PL试验中的轴向应力和偏应力分别与轴向应变的关系曲线,从图中可以看出,两种应力–应变曲线大致呈幂函数型。随着主应力比值的增大,轴向应力与轴向应变关系曲线的后段逐渐变缓,见图6（a）。这一特征在偏应力与轴向应变关系曲线上表现的不明显,随主应力比值的增大,曲线后段的差别很小,见图6（b）。

图 6 轴向应力和偏应力与轴向应变的关系曲线

Figure 6. Curves of axial stress and deviator stress versus axial strain

下载: 全尺寸图片幻灯片

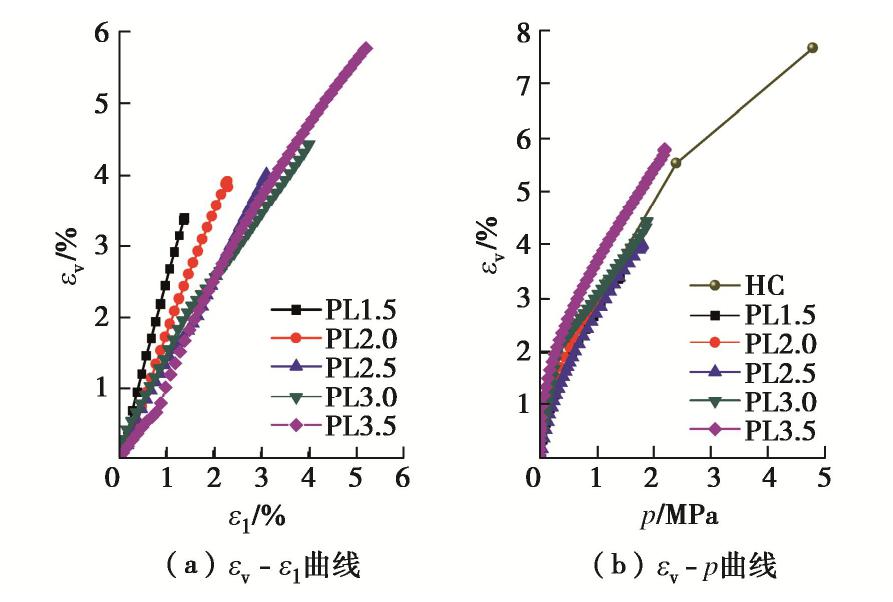
图7为PL试验中的体应变分别与轴向应变和平均主应力的关系曲线,HC试验作为R=1的PL试验,试验结果也绘在图7（b）中。图7（a）显示,体应变与轴向应变关系曲线近似呈直线关系,说明在PL试验的加载过程中,试样均表现为体积压缩。随着主应力比值的增大,直线的斜率变缓,并出现相互交叉的现象。这一特点在体应变与平均主应力的关系曲线上也有所体现,图7（b）显示,曲线近似呈双曲线型,各种不同主应力比值的曲线相互交织在一起。孙岳崧等^[3]对承德中密砂进行了类似的研究,在不同主应力比的PL试验中也观察到体应变曲线相互交叉的现象,这说明体应变同时受到平均主应力和偏应力的影响。

图 7 体应变与轴向应变和平均主应力的关系曲线

Figure 7. Curves of volumetric strain versus axial strain and average principal stress

下载: 全尺寸图片幻灯片

各种应力路径试验成果的比较见表2,从中可以发现,应力–应变曲线为双曲线型的CTC,RTC和TC试验,曲线的初始斜率随着固结压力的增加而增加,即应力–应变曲线的起始坡度随固结压力增大而变陡（图3）。峰值主应力差和峰值平均主应力随着固结压力的增加而增加,而峰值主应力比和峰值应力比则随着固结压力的增加而减小；相同固结压力下的峰值主应力差和峰值平均主应力,CTC试验的最大,TC试验的其次,RTC试验的最小。而峰值主应力比和峰值应力比却正好相反,CTC试验的最小,TC试验的居中,RTC试验的最大；TC,CTC试验中,体变为零时的轴向应变值随固结压力的增大而增大。

表 2 各种应力路径试验成果的比较

Table 2. Comparison of test results of various stress paths

试验编号	固结类型	固结压力 $σ_{c}$ $σ_{c}$ /MPa	应力增量比 $Δ q / Δ p$ $Δ q / Δ p$	应力应变曲线线型	曲线初始斜率/MPa	峰值主应力差q_max/MPa	峰值平均主应力p_max/MPa	峰值主应力比R_max	峰值应力比η_max	体变零时的轴向应变/%	最终体变ε_vmax/%	最终破碎率B_r/%	峰值内摩擦角φ_p/(°)	最终内摩擦角φ_f/(°)
HC0.3	等向固结	0.3	0	幂函数型	—	0	0.30	1.00	0	—	1.28	0.59	—	—
HC0.6		0.6			—	0	0.60	1.00	0	—	2.23	0.89	—	—
HC1.2		1.2			—	0	1.20	1.00	0	—	3.33	1.09	—	—
HC2.4		2.4			—	0	2.40	1.00	0	—	5.52	1.64	—	—
HC4.8		4.8			—	0	4.80	1.00	0	—	7.66	2.11	—	—
CTC0.3	等向固结	0.3	3	双曲线型	28.18	1.60	0.84	6.33	1.92	5.60	-11.20	2.38	46.65	41.36
CTC0.6		0.6			75.14	2.69	1.50	5.48	1.80	10.20	-5.68	4.69	43.75	40.76
CTC1.2		1.2			112.02	4.29	2.64	4.58	1.63	—	1.06	8.97	39.91	39.03
CTC2.4		2.4			123.34	7.20	4.81	4.00	1.47	—	8.56	14.93	36.86	36.86
CTC4.8		4.8			139.20	12.32	8.91	3.57	1.30	—	12.15	22.00	34.20	34.20
RTC0.3	等向固结	0.3	-3/2	双曲线型	90.15	0.27	0.29	10.20	2.21	0.16	-18.79	0.83	55.23	48.54
RTC0.6		0.6			150.52	0.52	0.61	8.64	2.12	—	-17.82	0.82	52.42	45.03
RTC1.2		1.2			170.26	1.02	1.20	7.17	1.94	—	-14.51	1.31	49.05	40.94
RTC2.4		2.4			192.46	1.99	2.40	6.13	1.88	—	-11.99	3.09	46.02	40.48
RTC4.8		4.8			253.23	3.82	4.80	5.00	1.70	—	-5.08	8.16	41.82	40.01
TC0.3	等向固结	0.3	∞	双曲线型	66.50	0.60	0.34	6.66	1.92	2.15	-11.73	1.78	47.63	41.68
TC0.6		0.6			89.05	1.17	0.64	6.14	1.89	3.83	-10.19	2.57	46.04	40.48
TC1.2		1.2			93.20	2.28	1.23	6.15	1.89	5.46	-9.36	4.70	46.07	40.99
TC2.4		2.4			217.46	4.12	2.42	5.02	1.71	13.94	-2.83	9.53	41.88	39.86
TC4.8		4.8			266.15	7.26	4.82	4.06	1.51	—	5.39	18.43	37.20	37.20
PL1.5	不固结	—	0.43	幂函数型	—	—	1.41	1.50	0.43	—	3.40	1.30	—	—
PL2.0		—	0.75		—	—	1.60	2.00	0.75	—	3.84	1.46	—	—
PL2.5		—	1.00		—	—	1.80	2.50	1.00	—	4.02	1.87	—	—
PL3.0		—	1.20		—	—	1.89	3.00	1.20	—	4.44	2.01	—	—
PL3.5		—	1.36		—	—	2.20	3.50	1.36	—	5.79	2.67	—	—

下载: 导出CSV

| 显示表格

2.2 应力路径的归一化分析

孙岳崧等^[3]对承德中密砂进行了6种不同应力路径的三轴试验研究,其中与本文相同的有HC,CTC,TC,PL等4种试验。本文借鉴其对应力路径归一化的处理方法,旨在能够将钙质砂的试验结果与承德砂进行比较。该方法是将各种应力路径的偏应力q除以相对应的平均主应力p,得到应力比η,即对各种应力路径都用平均主应力进行归一化处理,再将应力比η与剪应变ε_s整理成η–ε_s曲线和ε_s/η–ε_s曲线来分析应力路径的影响。

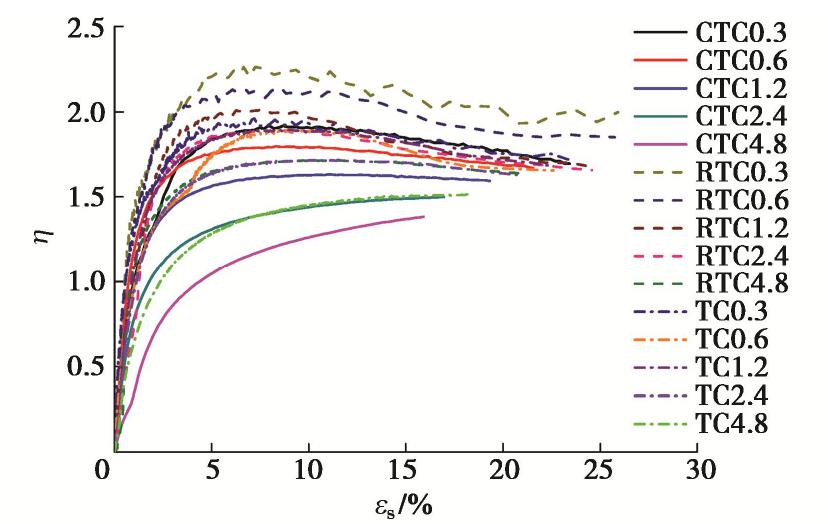
图8为CTC,RTC和TC试验的η–ε_s关系曲线,从中可以发现,钙质砂在3种应力路径下的应力–应变曲线,归一化结果相差较远。而承德砂在CTC和TC试验中的应力–应变曲线,归一化结果比较接近^[3],可见应力路径对钙质砂的影响较为明显。

图 8 应力比与剪应变的关系曲线

Figure 8. Curves of stress ratio versus shear strain

下载: 全尺寸图片幻灯片

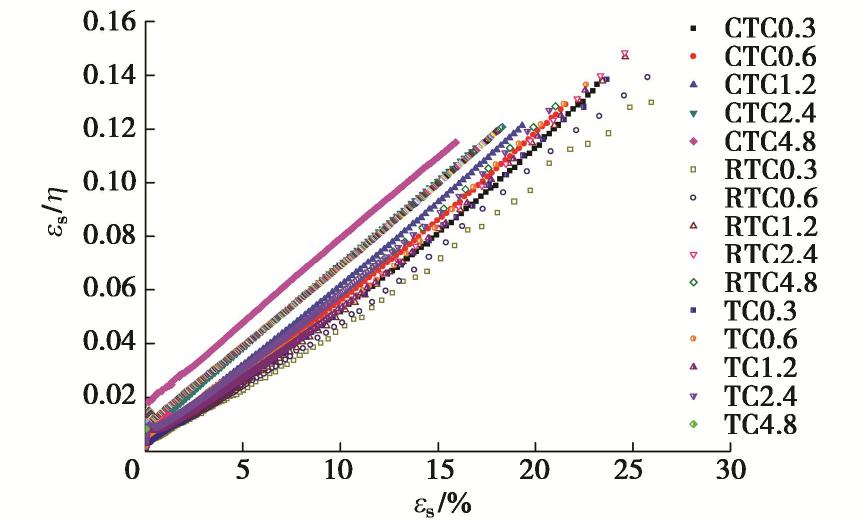
将CTC,RTC和TC试验数据整理成ε_s/η–ε_s关系,并绘于图9,从中可以发现,各应力路径下的ε_s/η–ε_s关系近似呈直线关系,其中CTC和TC试验的直线关系较好,RTC试验的稍差。故ε_s/η与ε_s的关系可写成

图 9 ε_s/η与剪应变的关系曲线

Figure 9. Curves of ε_s/η versus shear strain

下载: 全尺寸图片幻灯片

ε_{s} / η = a + b ε_{s}

$ε_{s} / η = a + b ε_{s}$ ,

(1)

式中,a,b分别为直线在纵坐标轴上的截距和斜率。

孙岳崧等^[3]在含CTC,TC在内的4种应力路径试验中,发现承德砂在不同固结压力下的ε_s/η–ε_s关系,可以用一条直线来描述,即无论应力路径是怎样的,也不管固结压力是多少,式（1）中的参数a是恒定不变的,显然该结论与钙质砂的试验结果有较大差别。从图9可以发现,各试验的ε_s/η–ε_s关系近似为一组相互平行的直线,表明直线斜率基本相等,但纵轴上的截距a各不相同。相同应力路径下,固结压力越大,a值越大；不同应力路径下,同一固结压力下的a值,CTC试验的最大,TC试验的其次,RTC试验的最小,说明a值大小与试验的固结条件和应力路径有关。

Muir等^[22]依据砂土应力–应变关系中利用峰值应力比表示的应变软化曲线特征,提出了一种采用应力比与剪应变表征的双曲线模型,即

η / η_{max} = ε_{s} / (B + ε_{s})

$η / η_{max} = ε_{s} / (B + ε_{s})$ ,

(2)

式中,B为试验常数。

比较式（1）,（2）可得a = B/η_max,表明参数a的大小与峰值应力比成反比。从图8和表2中的峰值应力比变化规律,也可看出a值并非恒定值,而且不同应力路径和固结条件下的各个a值之间的大小关系,与图9显示的结果完全一致,即相同应力路径下,参数a随固结压力增大而增大。同一固结压力对应的a值大小依次是,CTC试验的最大,TC试验的其次,RTC试验的最小。

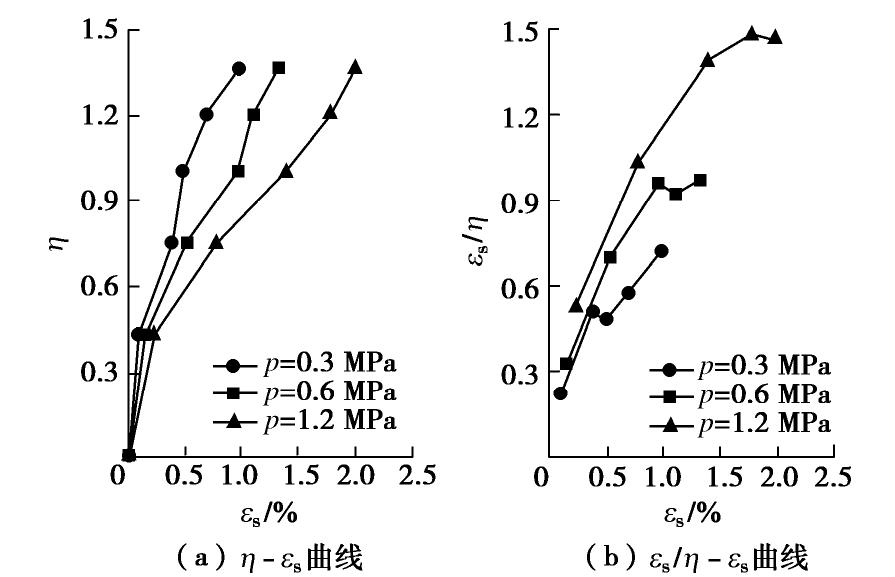
PL试验的归一化处理是从5个主应力比值的试验中,采集当平均主应力分别到达0.3,0.6,1.2 MPa时的有关数据进行归一化,为的是在相同的应力条件下进行比较。图10为PL试验的η–ε_s及ε_s/η–ε_s曲线,从中可发现,不同主应力比的PL试验的应力–应变曲线不能归一化到一起,见图10（a）,ε_s/η–ε_s曲线也不是一条直线,见图10（b）,其特点与承德砂的试验结果基本类似,说明钙质砂不能忽视应力路径的影响。

图 10 应力比和ε_s/η与剪应变的关系曲线

Figure 10. Curves of stress ratio and ε_s/η versus shear strain

下载: 全尺寸图片幻灯片

2.3 颗粒破碎特性

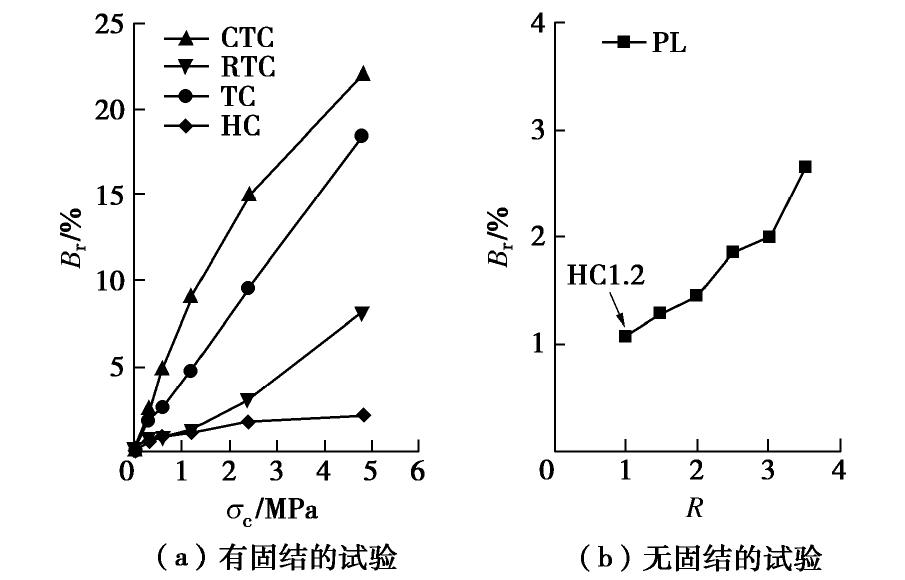
表2所示的CTC,RTC和TC试验中各试样的颗粒最终破碎率,是从试验完毕后获得的总破碎率中,扣除了等向固结条件下由相应固结压力σ_c产生的颗粒破碎率,整理出试验在剪切阶段产生的颗粒破碎率。图11为颗粒破碎率与固结压力和主应力比的关系曲线。对有等向固结的各试验,给出了颗粒破碎率与固结压力的关系,见图11（a）；对无固结阶段的PL试验,则给出了颗粒破碎率与主应力比的关系,见图11（b）,由于HC1.2也是R=1的PL试验,故将其结果也绘于其中。

图 11 颗粒破碎率与固结压力和主应力比的关系曲线

Figure 11. Curves of breakage index versus consolidation pressure and principal stress ratio

下载: 全尺寸图片幻灯片

图11（a）显示,各试验中钙质砂的颗粒破碎率随固结压力增大而增大。在HC试验中只有压缩而无剪切过程,因此即便在较高的固结压力下,钙质砂的颗粒破碎量也较小。其余3种试验中,相同固结压力下钙质砂的颗粒破碎率,CTC试验的最大,TC试验的其次,RTC试验的最小。PL试验中钙质砂的颗粒破碎率随主应力比值的增大而增大,因在加载过程中主要表现为体积压缩,故颗粒破碎量也较小,见图11（b）。

图11（a）还显示,应力路径和固结条件对钙质砂的颗粒破碎率和参数a的影响规律完全一致,即在相同应力路径下,固结压力越大,颗粒破碎率越大,a值也越大；固结压力相同而应力路径不同时,颗粒破碎率的大小依次为,CTC试验的最大,TC试验的其次,RTC试验的最小,而对应的a值的大小具有与之完全相同的次序。考虑到钙质砂与承德砂的主要差别在于其显著的颗粒破碎特性,这表明钙质砂与承德砂在a值上的差异,也即二者的应力–应变关系在归一化结果上出现的差别,主要是由试验过程中钙质砂的颗粒破碎引起的,说明固结压力和应力路径对钙质砂应力–应变关系的影响,除了源自于砂土具有应力路径依附性的特性外,还来自于因应力路径和固结条件的不同,造成的颗粒破碎程度不一致带来的影响。

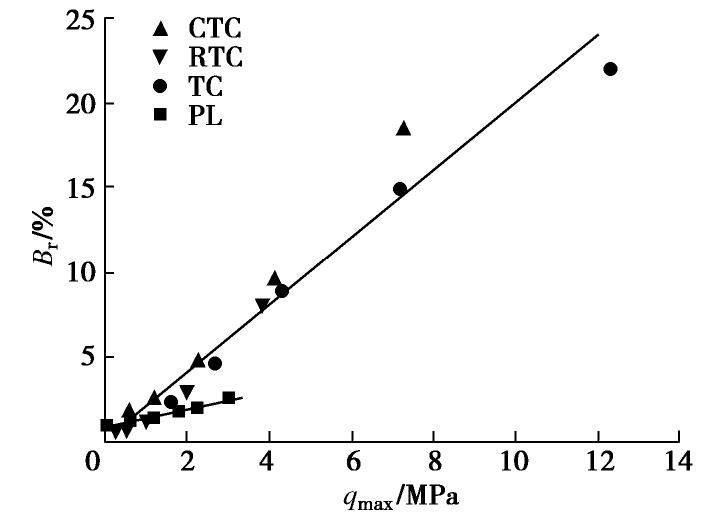
图12为4种应力路径试验中的偏应力峰值与颗粒破碎率的关系。从图中可看见,CTC,RTC和TC试验的偏应力峰值与颗粒破碎率的关系近似呈相同的直线关系。峰值偏应力越大,颗粒破碎率越高,直线关系基本上不受应力路径的影响。PL试验的峰值偏应力与颗粒破碎率也呈现类似的直线关系,但比CTC,RTC和TC 3种试验的直线平缓。

图 12 颗粒破碎率与最大偏应力的关系

Figure 12. Relationship between breakage index and maximum deviator stress

下载: 全尺寸图片幻灯片

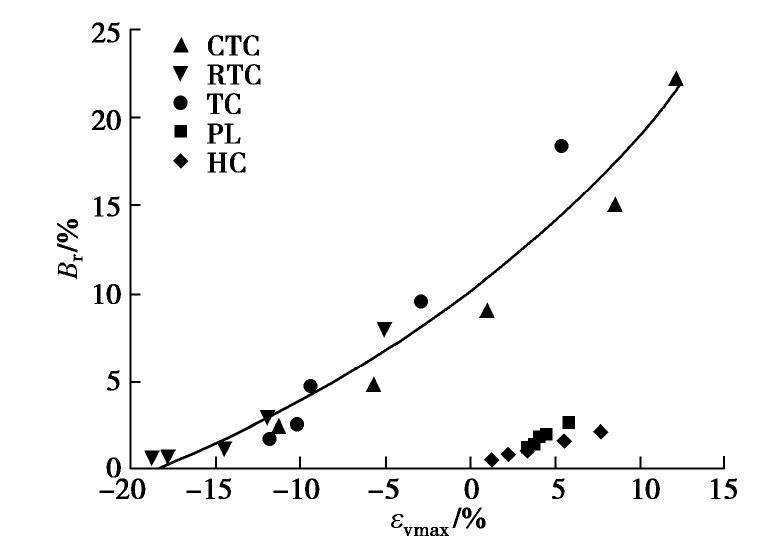
图13给出了5种应力路径试验中的最大体应变与颗粒破碎率的关系。从图中可发现,CTC,RTC和TC试验中的体应变,无论是剪胀、剪缩,还是先缩后胀,各试验中的最大体应变与颗粒破碎率的关系也具有相同的变化规律,同样不受应力路径的影响。HC和PL试验在加载过程主要表现为压缩,颗粒破碎率随体应变增长而增大,变化规律与CTC,RTC和TC 3种试验差别较大。

图 13 颗粒破碎率与最大体应变的关系

Figure 13. Relationship between breakage index and maximum volumetric strain

下载: 全尺寸图片幻灯片

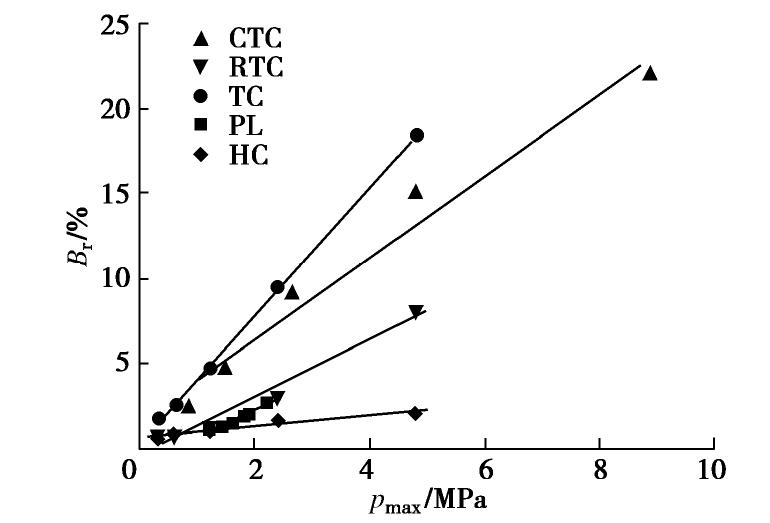
图14给出了5种应力路径试验中的最大平均主应力与颗粒破碎率的关系。图中显示,相同应力路径下,各试验中的最大平均主应力与颗粒破碎率近似呈直线关系,最大平均主应力越大,颗粒破碎率越大。不同应力路径下,最大平均主应力与颗粒破碎率的直线关系各不相同,其中,TC试验的直线最陡,其后依次为CTC,RTC和PL试验,HC试验的直线最为平缓,说明最大平均主应力随颗粒破碎率的变化规律受到了应力路径的影响。

图 14 颗粒破碎率与最大平均主应力的关系

Figure 14. Relationship between breakage index and maximum average principal stress

下载: 全尺寸图片幻灯片

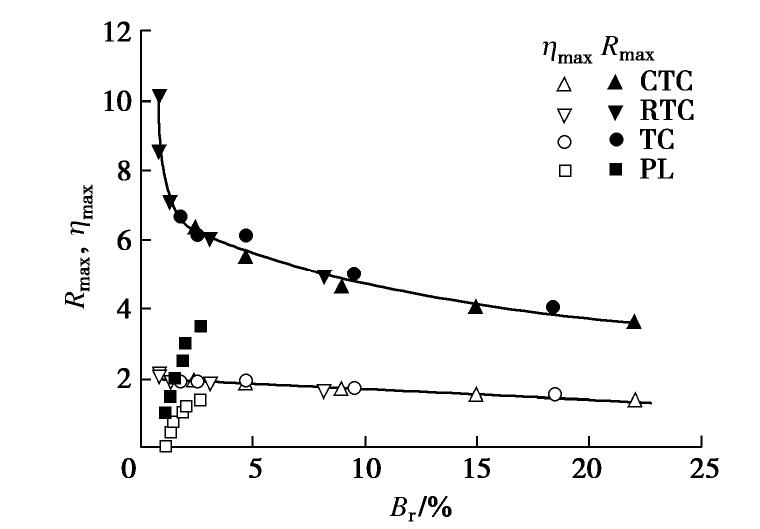
图15给出了4种应力路径试验中的峰值主应力比R_max和峰值应力比η_max与颗粒破碎率的关系。图中可见,CTC,RTC和TC试验中的峰值主应力比随着颗粒破碎率的增加而降低,各试验的R_max–B_r关系基本相同,不受应力路径的影响。RTC试验在低破碎率阶段对应的峰值主应力比偏高,与对应的低固结压力下钙质砂应变软化现象和剪胀效应十分显著的特性有关。图15还显示,峰值应力比与颗粒破碎率也有类似的关系,峰值应力比随颗粒破碎率增大而减低,变化趋势近似直线变化。PL试验中的峰值主应力比和峰值应力比均随颗粒破碎率增加而增加,但与CTC,RTC和TC试验存在很大差别。

图 15 峰值主应力比和峰值应力比与颗粒破碎率的关系

Figure 15. Relationship between maximum principal stress ratio or maximum stress ratio and breakage index

下载: 全尺寸图片幻灯片

2.4 抗剪强度特性

按照莫尔–库仑强度理论,无黏性土在三轴排水剪切中的内摩擦角φ与主应力比 $σ_{1} / σ_{3}$ $σ_{1} / σ_{3}$ 的关系为

φ = \sin^{- 1} \frac{σ_{1} / σ_{3} - 1}{σ_{1} / σ_{3} + 1}

$φ = \sin^{- 1} \frac{σ_{1} / σ_{3} - 1}{σ_{1} / σ_{3} + 1}$ 。

(3)

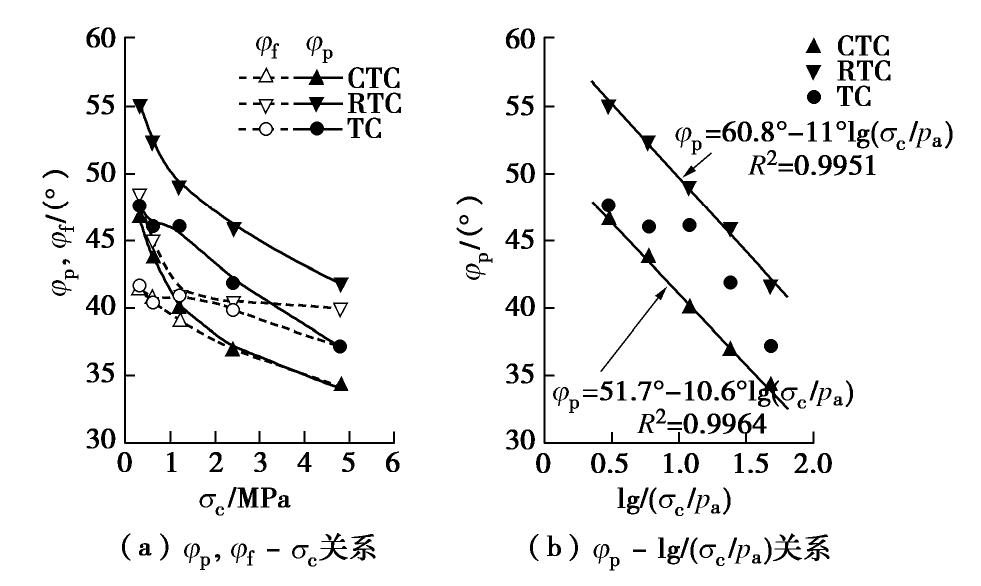
基于式（3）,分别利用峰值主应力比R_max= ${(σ_{1} / σ_{3})}_{max}$ ${(σ_{1} / σ_{3})}_{max}$ 和试验终止时（ε₁=20%）的主应力比R_f= ${(σ_{1} / σ_{3})}_{f}$ ${(σ_{1} / σ_{3})}_{f}$ ,计算出对应的峰值内摩擦角φ_p和最终内摩擦角φ_f,计算结果见表2。图16给出了CTC,RTC和TC试验中钙质砂的φ_p和φ_f与固结压力的关系,图16（a）显示,相同应力路径下,φ_p随固结压力的增大而减小；不同应力路径下,相同固结压力时φ_p差别较大,其中RTC试验的最大,TC试验的其次,CTC试验的最小,三者φ_p的差幅为1°～9°。钙质砂的φ_f也有类似的规律,但差幅减小,约为1°～7°。

图 16 φ_p, φ_f与固结压力的关系

Figure 16. Relationship among φ_p, φ_f and consolidation pressure

下载: 全尺寸图片幻灯片

本文采用Duncan等^[23]提出的非线性强度准则来分析不同应力路径下钙质砂的峰值内摩擦角与固结压力的关系,即

φ_{p} = φ_{0} - Δ φ \lg (σ_{c} / p_{a})

$φ_{p} = φ_{0} - Δ φ \lg (σ_{c} / p_{a})$ ,

(4)

式中, $φ_{0}$ $φ_{0}$ 为一个大气压下的内摩擦角, $Δ φ$ $Δ φ$ 为随 $σ_{c}$ $σ_{c}$ 增加内摩擦角的减小值,p_a为标准大气压。

按照式（4）对不同应力路径下的试验结果进行拟合分析,结果如图16（b）所示,CTC试验的 $φ_{0}$ $φ_{0}$ =51.7°, $Δ φ$ $Δ φ$ =10.6°,拟合度R²=0.9964；RTC试验的 $φ_{0}$ $φ_{0}$ = 60.8°, $Δ φ$ $Δ φ$ =11°,拟合度R²=0.9951,二者的直线斜率基本一致,但截距不同,说明应力路径对峰值内摩擦角有影响,式（4）对CTC和RTC试验具有良好的适用性。但TC试验数据的离散性较大,不能用式（4）的直线规律来描述,见图16（b）。秦尚林等^[11]对粗粒料也进行了类似的研究,得到了同样的结论。

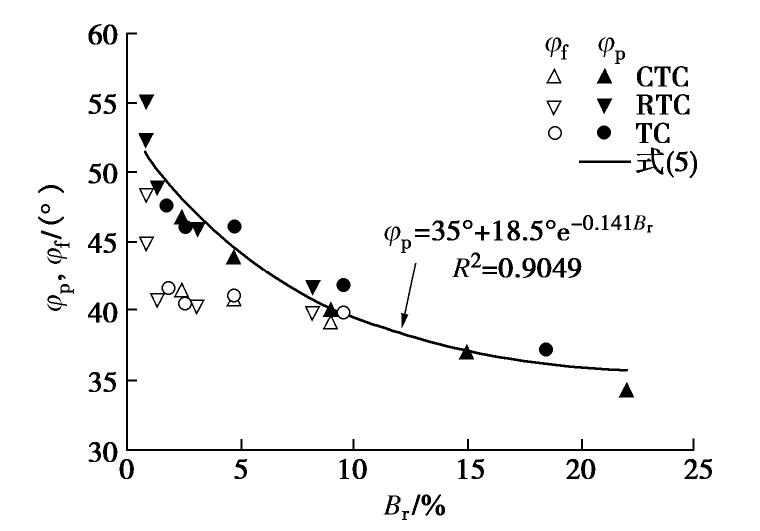
图17给出了CTC,RTC和TC试验中钙质砂的 $φ_{p}$ $φ_{p}$ 及φ_f与颗粒破碎率的关系,从中可以看见,钙质砂的峰值内摩擦角随颗粒破碎率的增大而降低,不同应力路径下的变化规律基本相同,没有受到应力路径的影响。孙岳崧等^[3]对不同固结条件的承德砂进行了5种应力路径的三轴试验结果显示,内摩擦角仅相差1°左右,因而得出了不同固结条件和应力路径对砂土抗剪强度指标影响不大的结论,显然这与钙质砂有很大区别。无论是图16中的试验结果,还是式（4）代表的变化规律,都表明钙质砂的峰值内摩擦角受到了固结条件和应力路径的影响。但是从图17给出的钙质砂峰值内摩擦角随颗粒破碎率的变化规律来看,这一差别还是由于试验过程中颗粒破碎引起的,说明不同应力路径及固结条件对钙质砂强度的影响,主要还是来自不同应力路径和固结压力产生的颗粒破碎程度不同而造成的影响。

图 17 φ_p, φ_f与颗粒破碎率的关系

Figure 17. Relationship among φ_p, φ_f and breakage index

下载: 全尺寸图片幻灯片

图17显示,RTC试验在破碎率很小时具有很高的峰值内摩擦角,该现象与颗粒的咬合作用有关。在低固结压力下的RTC试验,钙质砂的剪胀作用十分突出,极大地增大了颗粒的咬合摩擦,因此需要更多的能量来克服,因而就具有了较高的峰值内摩擦角。但随着颗粒破碎率的增大,颗粒破碎抵消了剪胀作用,剪胀性逐渐消失,咬合作用消除,峰值内摩擦角逐渐降低。

钙质砂在常规三轴固结排水剪试验中的峰值内摩擦角与颗粒破碎率关系的关系,可以采用指数函数来描述^[24],即

φ_{p} = φ_{1} + φ_{2} e^{- A B_{r}}

$φ_{p} = φ_{1} + φ_{2} e^{- A B_{r}}$ ,

(5)

式中, $φ_{1}$ $φ_{1}$ , $φ_{2}$ $φ_{2}$ ,A为试验常数。

本文利用式（5）对CTC,RTC和TC试验中的峰值内摩擦角与颗粒破碎率的试验数据进行拟合分析,结果显示拟合度R²=0.9049,其中的参数 $φ_{1}$ $φ_{1}$ =35°, $φ_{2}$ $φ_{2}$ =18.5°,A=0.141,见图17,说明式（5）也适用于描述不同应力路径下钙质砂的峰值内摩擦角随颗粒破碎率的非线性变化规律。

图17还显示,最终内摩擦角的试验数据较为离散,规律不明显,但可以大致看出最终内摩擦角随着颗粒破碎率的增加而呈现降低的趋势,但是与峰值内摩擦角相比,降幅较小,说明即便在试验终止时的大应变下,试样的胀缩已经很小,但仍存在一些咬合作用,不能完全消除咬合摩擦。与峰值内摩擦角相比,最终内摩擦角较为稳定,意味着颗粒破碎对消除咬合摩擦的作用已经不大了。

3. 结论

本文对钙质砂进行了不同固结压力下5种应力路径的排水三轴压缩试验,研究应力路径对钙质砂应力–应变关系、抗剪强度及颗粒破碎特性的影响,主要结论如下：

（1）应力路径对钙质砂的应力–应变关系有较大的影响。RTC试验的剪胀效应显著,TC试验的剪胀现象比较明显,CTC试验的剪胀性最弱。随着固结压力的增加,剪胀倾向减小。PL和HC试验在加载过程中主要表现为体积压缩,因此与CTC,RTC和TC试验的应力–应变关系差别很大。

（2）应力路径和固结条件对颗粒破碎的影响规律是,颗粒破碎率随固结压力的增大而增大。相同固结压力的钙质砂在不同应力路径下的颗粒破碎率不同,颗粒破碎率CTC试验的最大,TC试验的其次,RTC试验的最小。PL试验的颗粒破碎率随主应力比值的增大而增大。峰值应力与应变与颗粒破碎率的关系受应力路径的影响较小。

（3）应力路径和固结条件对强度的影响规律是,内摩擦角随固结压力的增大而减小。相同固结压力时钙质砂在不同应力路径下的峰值内摩擦角不同,峰值内摩擦角RTC试验的最大,TC试验的其次,CTC试验的最小。最终内摩擦角与峰值内摩擦角也有类似的变化规律。

（4）颗粒破碎对抗剪强度的影响规律是,内摩擦角随颗粒破碎率增大而减小,变化规律不受应力路径的影响。不同应力路径下钙质砂的峰值内摩擦角与颗粒破碎率的关系,可以用相同的指数函数来描述。

（5）固结条件和应力路径对钙质砂应力–应变关系的影响,除了源于砂土具有应力路径依附性的特性外,还来自应力路径和固结压力的不同,所造成的颗粒破碎不一致带来的影响。而不同应力路径及固结条件对钙质砂强度的影响,也是因不同应力路径和固结压力产生的颗粒破碎不同而造成的,使得钙质砂在不同的应力路径试验中的抗剪强度有所差异。

图 1 钙质砂的粒径分布曲线

Figure 1. Grain-size distribution curves of calcareous sand

下载: 全尺寸图片幻灯片

图 2 p–q平面内的应力路径

Figure 2. Stress paths in p–q plane

下载: 全尺寸图片幻灯片

图 3 偏应力与轴向应变的关系曲线

Figure 3. Curves of deviator stress versus axial strain

下载: 全尺寸图片幻灯片

图 4 体应变与轴向应变的关系曲线

Figure 4. Curves of volumetric strain versus axial strain

下载: 全尺寸图片幻灯片

图 5 主应力比与轴向应变的关系曲线

Figure 5. Curves of principal stress ratio versus axial strain

下载: 全尺寸图片幻灯片

图 6 轴向应力和偏应力与轴向应变的关系曲线

Figure 6. Curves of axial stress and deviator stress versus axial strain

下载: 全尺寸图片幻灯片

图 7 体应变与轴向应变和平均主应力的关系曲线

Figure 7. Curves of volumetric strain versus axial strain and average principal stress

下载: 全尺寸图片幻灯片

图 8 应力比与剪应变的关系曲线

Figure 8. Curves of stress ratio versus shear strain

下载: 全尺寸图片幻灯片

图 9 ε_s/η与剪应变的关系曲线

Figure 9. Curves of ε_s/η versus shear strain

下载: 全尺寸图片幻灯片

图 10 应力比和ε_s/η与剪应变的关系曲线

Figure 10. Curves of stress ratio and ε_s/η versus shear strain

下载: 全尺寸图片幻灯片

图 11 颗粒破碎率与固结压力和主应力比的关系曲线

Figure 11. Curves of breakage index versus consolidation pressure and principal stress ratio

下载: 全尺寸图片幻灯片

图 12 颗粒破碎率与最大偏应力的关系

Figure 12. Relationship between breakage index and maximum deviator stress

下载: 全尺寸图片幻灯片

图 13 颗粒破碎率与最大体应变的关系

Figure 13. Relationship between breakage index and maximum volumetric strain

下载: 全尺寸图片幻灯片

图 14 颗粒破碎率与最大平均主应力的关系

Figure 14. Relationship between breakage index and maximum average principal stress

下载: 全尺寸图片幻灯片

图 15 峰值主应力比和峰值应力比与颗粒破碎率的关系

Figure 15. Relationship between maximum principal stress ratio or maximum stress ratio and breakage index

下载: 全尺寸图片幻灯片

图 16 φ_p, φ_f与固结压力的关系

Figure 16. Relationship among φ_p, φ_f and consolidation pressure

下载: 全尺寸图片幻灯片

图 17 φ_p, φ_f与颗粒破碎率的关系

Figure 17. Relationship among φ_p, φ_f and breakage index

下载: 全尺寸图片幻灯片

表 1 应力路径试验方案

Table 1 Schemes of stress path tests

试验编号	应力增量比		固结压力 $σ_{c}$ $σ_{c}$ /MPa	应力路径	控制方式	剪切速率
试验编号	$\frac{Δ σ_{1}}{Δ σ_{3}}$ $\frac{Δ σ_{1}}{Δ σ_{3}}$	$\frac{Δ q}{Δ p}$ $\frac{Δ q}{Δ p}$	固结压力 $σ_{c}$ $σ_{c}$ /MPa	应力路径	控制方式	剪切速率
HC0.3	1	0	0.3	$σ_{1}$ $σ_{1}$ = $σ_{3}$ $σ_{3}$ = $σ_{c}$ $σ_{c}$ 不变	应力控制	无
HC0.6			0.6
HC1.2			1.2
HC2.4			2.4
HC4.8			4.8
CTC0.3	∞	3	0.3	$σ_{1}$ $σ_{1}$ 增大 $σ_{3}$ $σ_{3}$ = $σ_{c}$ $σ_{c}$ 不变	应变控制	Δε₁=0.05 mm/min
CTC0.6			0.6
CTC1.2			1.2
CTC2.4			2.4
CTC4.8			4.8
RTC0.3	0	-3/2	0.3	$σ_{1}$ $σ_{1}$ = $σ_{c}$ $σ_{c}$ 不变 $σ_{3}$ $σ_{3}$ 减小	应力控制	$Δ σ_{3} = 5$ $Δ σ_{3} = 5$ kPa/min
RTC0.6			0.6
RTC1.2			1.2
RTC2.4			2.4
RTC4.8			4.8
TC0.3	-2	∞	0.3	$σ_{1}$ $σ_{1}$ 增大 $σ_{3}$ $σ_{3}$ 减小 p= $σ_{c}$ $σ_{c}$ 不变	应力控制	$Δ σ_{1} = 5$ $Δ σ_{1} = 5$ kPa/min $Δ σ_{3} = 2.5$ $Δ σ_{3} = 2.5$ kPa/min
TC0.6			0.6
TC1.2			1.2
TC2.4			2.4
TC4.8			4.8
PL1.5	1.5	0.43	无	$σ_{1}$ $σ_{1}$ 增大 $σ_{3}$ $σ_{3}$ 增大	应力控制	$Δ σ_{3} = 5$ $Δ σ_{3} = 5$ kPa/min
PL2.0	2.0	0.75
PL2.5	2.5	1.00
PL3.0	3.0	1.20
PL3.5	3.5	1.36

下载: 导出CSV

表 2 各种应力路径试验成果的比较

Table 2 Comparison of test results of various stress paths

试验编号	固结类型	固结压力 $σ_{c}$ $σ_{c}$ /MPa	应力增量比 $Δ q / Δ p$ $Δ q / Δ p$	应力应变曲线线型	曲线初始斜率/MPa	峰值主应力差q_max/MPa	峰值平均主应力p_max/MPa	峰值主应力比R_max	峰值应力比η_max	体变零时的轴向应变/%	最终体变ε_vmax/%	最终破碎率B_r/%	峰值内摩擦角φ_p/(°)	最终内摩擦角φ_f/(°)
HC0.3	等向固结	0.3	0	幂函数型	—	0	0.30	1.00	0	—	1.28	0.59	—	—
HC0.6		0.6			—	0	0.60	1.00	0	—	2.23	0.89	—	—
HC1.2		1.2			—	0	1.20	1.00	0	—	3.33	1.09	—	—
HC2.4		2.4			—	0	2.40	1.00	0	—	5.52	1.64	—	—
HC4.8		4.8			—	0	4.80	1.00	0	—	7.66	2.11	—	—
CTC0.3	等向固结	0.3	3	双曲线型	28.18	1.60	0.84	6.33	1.92	5.60	-11.20	2.38	46.65	41.36
CTC0.6		0.6			75.14	2.69	1.50	5.48	1.80	10.20	-5.68	4.69	43.75	40.76
CTC1.2		1.2			112.02	4.29	2.64	4.58	1.63	—	1.06	8.97	39.91	39.03
CTC2.4		2.4			123.34	7.20	4.81	4.00	1.47	—	8.56	14.93	36.86	36.86
CTC4.8		4.8			139.20	12.32	8.91	3.57	1.30	—	12.15	22.00	34.20	34.20
RTC0.3	等向固结	0.3	-3/2	双曲线型	90.15	0.27	0.29	10.20	2.21	0.16	-18.79	0.83	55.23	48.54
RTC0.6		0.6			150.52	0.52	0.61	8.64	2.12	—	-17.82	0.82	52.42	45.03
RTC1.2		1.2			170.26	1.02	1.20	7.17	1.94	—	-14.51	1.31	49.05	40.94
RTC2.4		2.4			192.46	1.99	2.40	6.13	1.88	—	-11.99	3.09	46.02	40.48
RTC4.8		4.8			253.23	3.82	4.80	5.00	1.70	—	-5.08	8.16	41.82	40.01
TC0.3	等向固结	0.3	∞	双曲线型	66.50	0.60	0.34	6.66	1.92	2.15	-11.73	1.78	47.63	41.68
TC0.6		0.6			89.05	1.17	0.64	6.14	1.89	3.83	-10.19	2.57	46.04	40.48
TC1.2		1.2			93.20	2.28	1.23	6.15	1.89	5.46	-9.36	4.70	46.07	40.99
TC2.4		2.4			217.46	4.12	2.42	5.02	1.71	13.94	-2.83	9.53	41.88	39.86
TC4.8		4.8			266.15	7.26	4.82	4.06	1.51	—	5.39	18.43	37.20	37.20
PL1.5	不固结	—	0.43	幂函数型	—	—	1.41	1.50	0.43	—	3.40	1.30	—	—
PL2.0		—	0.75		—	—	1.60	2.00	0.75	—	3.84	1.46	—	—
PL2.5		—	1.00		—	—	1.80	2.50	1.00	—	4.02	1.87	—	—
PL3.0		—	1.20		—	—	1.89	3.00	1.20	—	4.44	2.01	—	—
PL3.5		—	1.36		—	—	2.20	3.50	1.36	—	5.79	2.67	—	—

下载: 导出CSV

参考文献(24)

[1]	LADE P V, DUNCAN J M. Stress-path dependent behavior of cohesionless soil[J]. Journal of Geotechnical Engineering Division, ASCE, 1976, 102(GT1): 42-48.
[2]	FEDA J. Stress-path dependent shear strength of sand[J]. Journal of Geotechnical Engineering Division, ASCE, 1994, 120(6): 958-974. doi: 10.1061/(ASCE)0733-9410(1994)120:6(958)
[3]	孙岳崧, 濮家骝, 李广信. 不同应力路径对砂土应力-应变关系影响[J]. 岩土工程学报, 1987, 9(6): 78-88. doi: 10.3321/j.issn:1000-4548.1987.06.009 SUN Yue-song, PU Jia-liu, LI Guang-xin. The effects of different stress paths on stress-strain behavior of sand[J]. Chinese Journal of Geotechnical Engineering, 1987, 9(6): 78-88. (in Chinese) doi: 10.3321/j.issn:1000-4548.1987.06.009
[4]	丘金营. 应力路径对砂土应力应变关系的影响[J]. 岩土工程学报, 1995, 17(2): 75-82. doi: 10.3321/j.issn:1000-4548.1995.02.011 QIU Jin-ying. Effects of stress path on stress-strain behavior of sand[J]. Chinese Journal of Geotechnical Engineering, 1995, 17(2): 75-82. (in Chinese) doi: 10.3321/j.issn:1000-4548.1995.02.011
[5]	许成顺, 文利明, 杜修力, 等. 不同应力路径条件下的砂土剪切特性试验研究[J]. 水利学报, 2010, 41(1): 108-112. doi: 10.13243/j.cnki.slxb.2010.01.017 XU Cheng-shun, WEN Li-ming, DU Xiu-li, et al. Experimental study on shear behaviors of sand under different stress path[J]. Journal of Hydraulic Engineering, 2010, 41(1): 108-112. (in Chinese) doi: 10.13243/j.cnki.slxb.2010.01.017
[6]	路德春, 罗汀, 姚仰平. 砂土应力路径本构模型的试验验证[J]. 岩土力学, 2005, 26(5): 717-722. doi: 10.3969/j.issn.1000-7598.2005.05.008 LU De-chun, LUO Ting, YAO Yang-ping. Test validating of constitutive model of sand considering complex stress path[J]. Rock and Soil Mechanics, 2005, 26(5): 717-722. (in Chinese) doi: 10.3969/j.issn.1000-7598.2005.05.008
[7]	赖勇, 施建勇, 雷国辉. 砂土在小应变下考虑应力路径影响的本构模型的试验研究[J]. 岩土工程学报, 2006, 28(6): 745-749. doi: 10.3321/j.issn:1000-4548.2006.06.013 LAI Yong, SHI Jian-yong, LEI Guo-hui. Experimental study on constitutive model of sandy soil with consideration of stress path at small strain[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(6): 745-749. (in Chinese) doi: 10.3321/j.issn:1000-4548.2006.06.013
[8]	曹培, 蔡正银. 砂土应力路径试验的数值模拟[J]. 岩土工程学报, 2008, 30(1): 133-137. doi: 10.3321/j.issn:1000-4548.2008.01.021 CAO Pei, CAI Zheng-yin. Numerical simulation of stress path tests on sand[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(1): 133-137. (in Chinese) doi: 10.3321/j.issn:1000-4548.2008.01.021
[9]	侯世伟, 路德春, 程星磊, 等. 基于数字图像测量技术的砂土应力路径试验研究[J]. 岩土工程学报, 2011, 33(增刊1): 403-408. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2011S1078.htm HOU Shi-wei, LU De-chun, CHENG Xing-lei, et al. Experimental study on stress path of sand based on digital image processing technique[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(S1): 403-408. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2011S1078.htm
[10]	杨光, 张丙印, 于玉贞, 等. 不同应力路径下粗粒料的颗粒破碎试验研究[J]. 水利学报, 2010, 41(3): 338-342. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201003013.htm YANG Guang, ZHANG Bing-yin, YU Yu-zhen, et al. An experimental study on particle breakage of coarse-grained materials under various stress paths[J]. Journal of Hydraulic Engineering, 2010, 41(3): 338-342. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201003013.htm
[11]	秦尚林, 杨兰强, 高惠, 等. 不同应力路径下绢云母片岩粗粒料力学特性试验研究[J]. 岩石力学与工程学报, 2014, 33(9): 1932-1938. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201409026.htm QIN Shang-lin, YANG Lan-qiang, GAO Hui, et al. Experimental study on mechanical properties of coarse aggregates of sericite schist under different stress paths[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(9): 1932-1938. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201409026.htm
[12]	王远, 张胜, 敖大华, 等. 复杂应力路径下堆石料的颗粒破碎特性研究[J]. 岩土工程学报, 2018, 40(4): 698-706. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201804020.htm WANG Yuan, ZHANG Sheng, AO Da-hua, et al. Particle breakage characteristics of rockfills under complex stress paths[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(4): 698-706. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201804020.htm
[13]	孔宪京, 宁凡伟, 刘京茂, 等. 应力路径和干湿状态对堆石料颗粒破碎的影响研究[J]. 岩土力学, 2019, 40(6): 2059-2065. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201906005.htm KONG Xian-jing, NING Fan-wei, LIU Jing-mao, et al. Influences of stress paths and saturation on particle breakage of rockfill materials[J]. Rock and Soil Mechanics, 2019, 40(6): 2059-2065. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201906005.htm
[14]	尹振宇, 许强, 胡伟. 考虑颗粒破碎效应的粒状材料本构研究：进展及发展[J]. 岩土工程学报, 2012, 34(12): 2170-2180. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201212006.htm YIN Zhen-yu, XU Qiang, HU Wei. Constitutive relations for granular materials considering particle crushing: review and development[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(12): 2170-2180. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201212006.htm
[15]	张家铭, 张凌, 蒋国盛, 等. 剪切作用下钙质砂颗粒破碎试验研究[J]. 岩土力学, 2008, 29(10): 2789-2793. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200810039.htm ZHANG Jia-ming, ZHANG Ling, JIANG Guo-sheng, et al. Research on particle crushing of calcareous sands under triaxial shear[J]. Rock and Soil Mechanics, 2008, 29(10): 2789-2793. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200810039.htm
[16]	王刚, 叶沁果, 查京京. 珊瑚礁砂砾料力学行为与颗粒破碎的试验研究[J]. 岩土工程学报, 2018, 40(5): 802-810. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201805006.htm WANG Gang, YE Qin-guo, ZHA Jing-jing. Experimental study on mechanical behavior and particle crushing of coral sand-gravel fill[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(5): 802-810. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201805006.htm
[17]	王刚, 查京京, 魏星. 循环三轴应力路径下钙质砂颗粒破碎演化规律[J]. 岩土工程学报, 2019, 41(4): 755-760. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201904025.htm WANG Gang, ZHA Jing-jing, WEI Xing. Evolution of particle crushing of carbonate sands under cyclic triaxial stress path[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(4): 755-760. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201904025.htm
[18]	蔡正银, 侯贺营, 张晋勋, 等. 考虑颗粒破碎影响的珊瑚砂临界状态与本构模型研究[J]. 岩土工程学报, 2019, 41(6): 989-995. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201906002.htm CAI Zheng-yin, HOU He-ying, ZHANG Jin-xun, et al. Critical state and constitutive model for coral sand considering particle breakage[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(6): 989-995. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201906002.htm
[19]	ZHANG J R, LUO M X. Dilatancy and critical state of calcareous sand incorporating particle breakage[J]. International Journal of Geomechanics, 2020, 20(4): 04020030.
[20]	LUO M X, ZHANG J R, LIU X X, et al. Critical state elastoplastic constitutive model of angular-shaped and fragile granular materials[J]. Marine Georesources & Geotechnology, 2020, 1785065.
[21]	HARDIN B O. Crushing of soil particles[J]. Journal of Geotechnical Engineering, 1985, 111(10): 1177-1192.
[22]	MUIR WOOD D, BELKHEIR K, LIU D F. Strain softening and state parameter for sand modelling[J]. Géotechnique, 1994, 44(2): 335-339.
[23]	DUNCAN J M, CHANG C Y. Nonlinear analysis of stress and strain in soils[J]. Journal of the Soil Mechanics and Foundation Division, ASCE, 1970, 96(SM5): 1629-1653.
[24]	张季如, 华晨, 罗明星, 等. 三轴排水剪切下钙质砂的颗粒破碎特性[J]. 岩土工程学报, 2020, 42(9): 1593-1602. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202009007.htm ZHANG Ji-ru, HUA Chen, LUO Ming-xing, et al. Behavior of particle breakage in calcareous sands during drained triaxial shearing[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(9): 1593-1602. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202009007.htm

施引文献(4)

期刊类型引用(2)

1.	戴玉明，贺佐跃. 粉煤灰对水泥土三轴剪切峰值强度的影响性分析. 广东土木与建筑. 2024(03): 18-22 . 百度学术
2.	戴玉明，贺佐跃. 基于三轴试验的水泥土抗剪强度参数分析. 交通科学与工程. 2024(03): 65-73 . 百度学术

其他类型引用(2)

资源附件(0)

图(17) / 表(2)

计量

文章访问数: 564
HTML全文浏览量: 43
PDF下载量: 447
被引次数: 4

0. 引言
1. 土样与试验方法
1.1 土样
1.2 试验方法
2. 结果与分析
2.1 应力–应变特性
2.2 应力路径的归一化分析
2.3 颗粒破碎特性
2.4 抗剪强度特性
3. 结论

试验编号	应力增量比		固结压力 $σ_{c}$ /MPa	应力路径	控制方式	剪切速率
试验编号	$\frac{Δ σ_{1}}{Δ σ_{3}}$	$\frac{Δ q}{Δ p}$	固结压力 $σ_{c}$ /MPa	应力路径	控制方式	剪切速率
HC0.3	1	0	0.3	$σ_{1}$ = $σ_{3}$ = $σ_{c}$ 不变	应力控制	无
HC0.6			0.6
HC1.2			1.2
HC2.4			2.4
HC4.8			4.8
CTC0.3	∞	3	0.3	$σ_{1}$ 增大 $σ_{3}$ = $σ_{c}$ 不变	应变控制	Δε₁=0.05 mm/min
CTC0.6			0.6
CTC1.2			1.2
CTC2.4			2.4
CTC4.8			4.8
RTC0.3	0	-3/2	0.3	$σ_{1}$ = $σ_{c}$ 不变 $σ_{3}$ 减小	应力控制	$Δ σ_{3} = 5$ kPa/min
RTC0.6			0.6
RTC1.2			1.2
RTC2.4			2.4
RTC4.8			4.8
TC0.3	-2	∞	0.3	$σ_{1}$ 增大 $σ_{3}$ 减小 p= $σ_{c}$ 不变	应力控制	$Δ σ_{1} = 5$ kPa/min $Δ σ_{3} = 2.5$ kPa/min
TC0.6			0.6
TC1.2			1.2
TC2.4			2.4
TC4.8			4.8
PL1.5	1.5	0.43	无	$σ_{1}$ 增大 $σ_{3}$ 增大	应力控制	$Δ σ_{3} = 5$ kPa/min
PL2.0	2.0	0.75
PL2.5	2.5	1.00
PL3.0	3.0	1.20
PL3.5	3.5	1.36

不同应力路径下钙质砂力学特性的排水三轴试验研究 English Version

作者简介: 张季如(1964—),男,教授,博士生导师,主要从事岩土工程方面的教学和科研。E-mail: zhangjr@whut.edu.cn

计量

出版历程

Drained triaxial tests on mechanical properties of calcareous sand under various stress paths

0. 引言

1. 土样与试验方法

1.1 土样

1.2 试验方法

2. 结果与分析

2.1 应力–应变特性

2.2 应力路径的归一化分析

2.3 颗粒破碎特性

2.4 抗剪强度特性

3. 结论

期刊类型引用(2)

其他类型引用(2)

计量

出版历程

目录

0. 引言

1. 土样与试验方法

1.1 土样

1.2 试验方法

2. 结果与分析

2.1 应力–应变特性

2.2 应力路径的归一化分析

2.3 颗粒破碎特性

2.4 抗剪强度特性

3. 结论

作者简介:
张季如(1964—),男,教授,博士生导师,主要从事岩土工程方面的教学和科研。E-mail: zhangjr@whut.edu.cn