水溶性植物胶改性水泥–水玻璃封堵材料试验研究

李召峰; 高益凡; 张健; 齐延海; 王衍升; 刘超

doi:10.11779/CJGE202007015

水溶性植物胶改性水泥–水玻璃封堵材料试验研究 English Version

山东大学岩土与结构工程研究中心,山东　济南　250061

基金项目:

国家自然科学基金项目 51709158

详细信息

作者简介:
李召峰(1986—),男,博士(后),副教授,主要从事地下工程灾害治理及注浆材料的研发工作。E-mail：lizf@sdu.edu.cn

中图分类号: TU472
计量
- 文章访问数: 345
- HTML全文浏览量: 18
- PDF下载量: 205
出版历程
- 收稿日期: 2019-09-25
- 网络出版日期: 2022-12-05
- 刊出日期: 2020-06-30

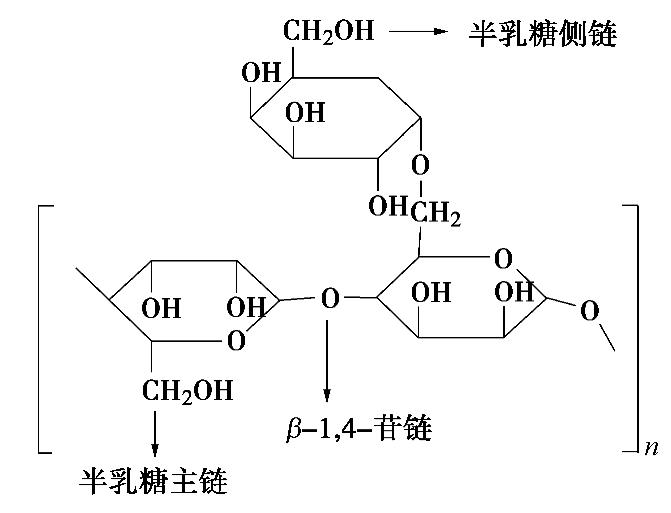
Experimental study of water-soluble vegetable gum-modified cement-sodium silicate plugging materials

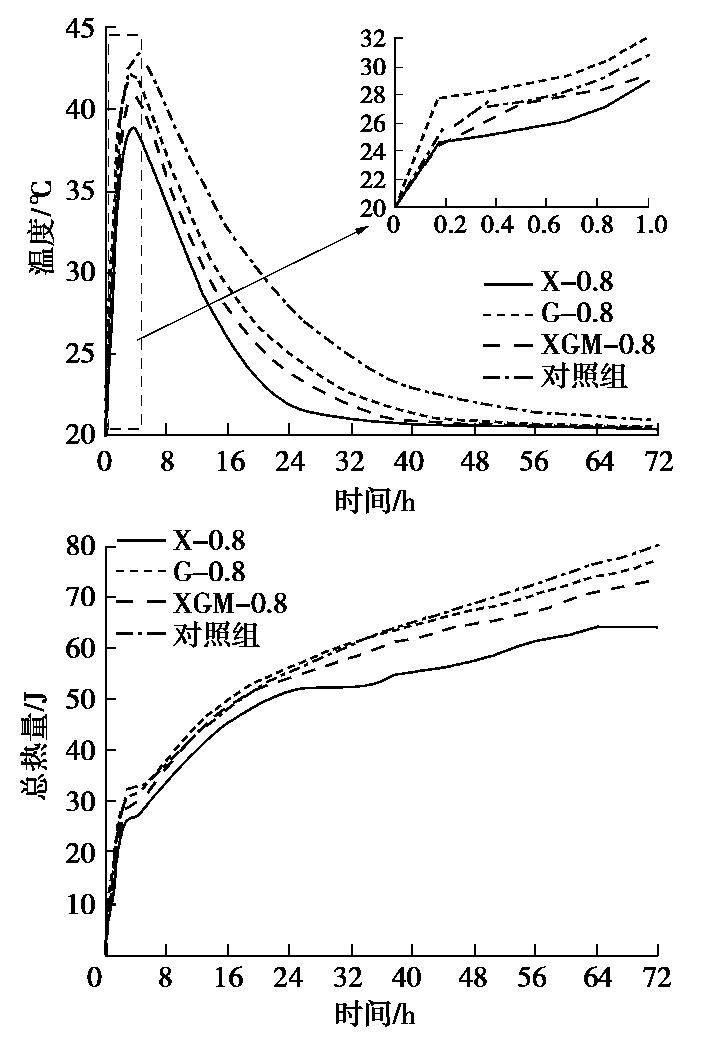
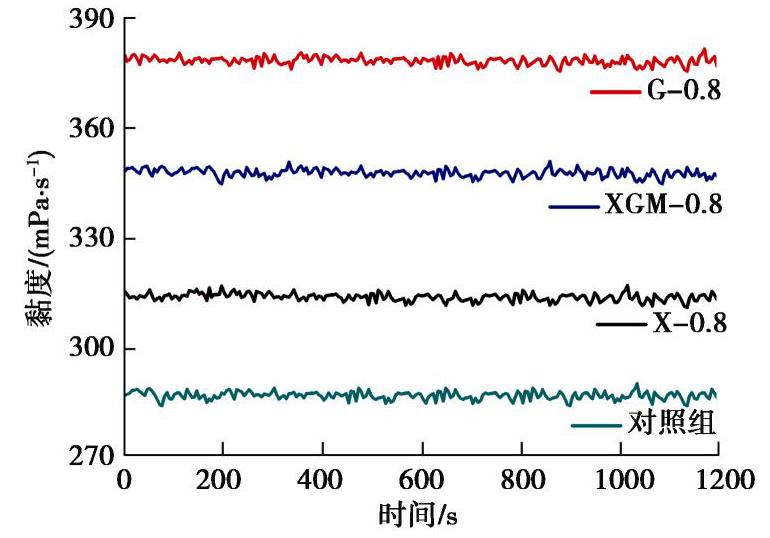
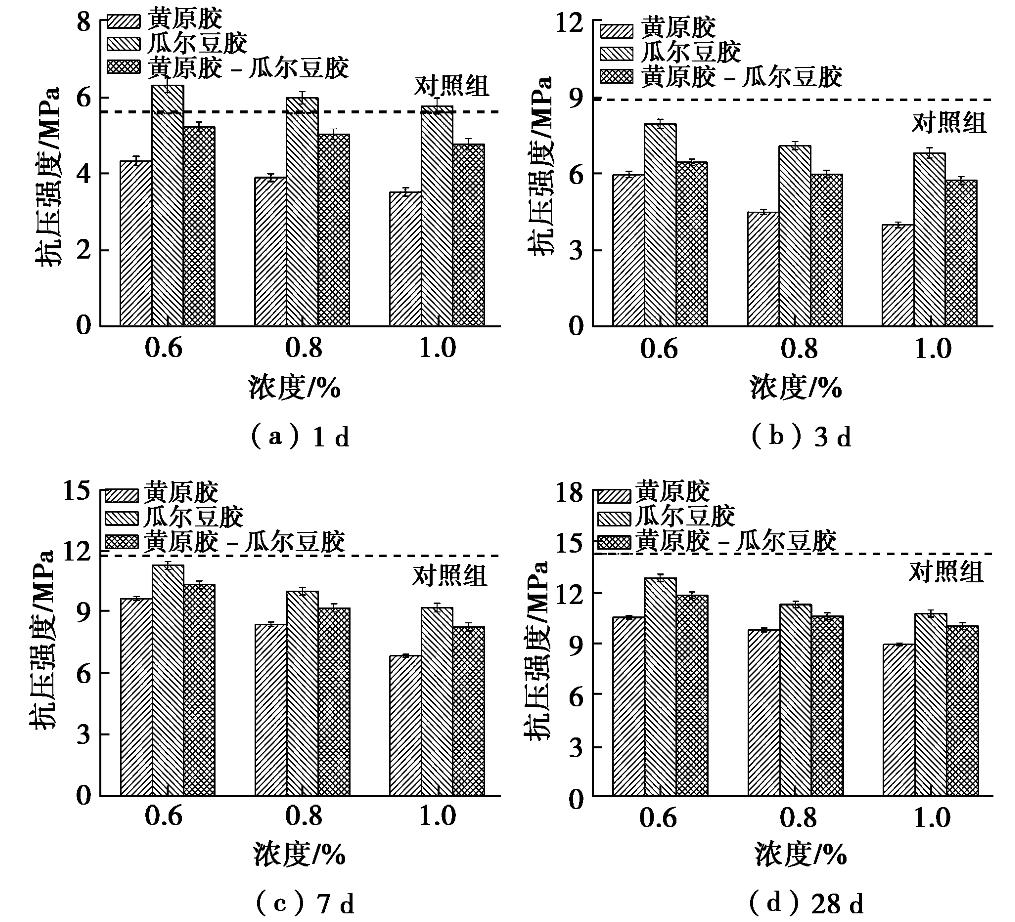
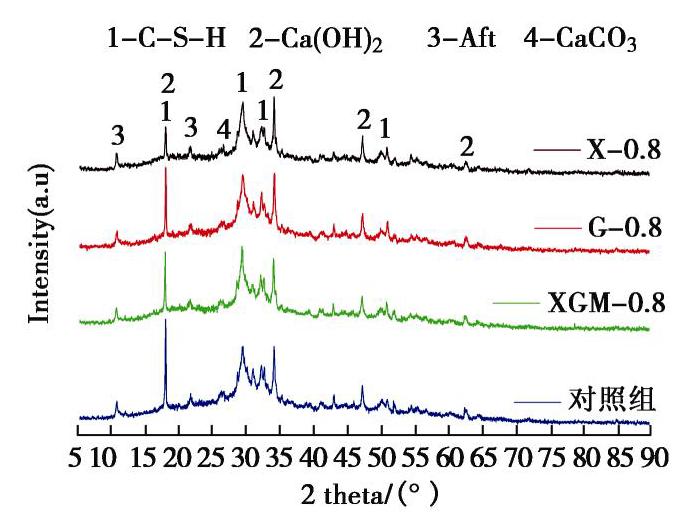
Geotechnical and Structural Engineering Research Center, Shandong University, Jinan 250061, China

摘要

摘要: 中国西南地区岩溶地区发育,岩溶动水灾害对地下工程建设造成极大影响,为了解决水泥–水玻璃封堵材料浆液留存率低等问题,通过水溶性植物胶对传统水泥–水玻璃浆液进行改性处理,并从凝结时间、抗压强度、浆液留存率、黏度时变性、水化过程及微观结构角度进行分析,系统研究了水溶性植物胶对水泥–水玻璃封堵材料性能的影响机理。试验结果表明：①水溶性植物胶可提高浆液动水抗分散性能,其中,瓜尔豆胶掺量为0.8%时水泥–水玻璃浆液留存率最高为96.4%；②通过不同水溶性植物胶的改性,水泥–水玻璃浆液的凝结时间可调,增加了浆液的使用范围；③瓜尔豆胶提高浆液结石体早期强度,但降低其后期强度,黄原胶和黄原胶–瓜尔豆胶均降低浆液结石体的抗压强度；④水溶性植物胶可抑制水泥–水玻璃浆液的水化过程,通过水溶性植物胶的高黏度特性及其活性基团与水泥中阳离子之间的络合作用来提高其动水抗分散性能；⑤水溶性植物胶改性水泥–水玻璃浆液成功应用于岩溶地区石灰石矿山涌水工程,有效地解决了岩溶管道高流速、高流量突涌水问题。
- 水泥–水玻璃浆液 /
- 水溶性植物胶 /
- 凝结时间 /
- 浆液留存率 /
- 力学性能
Abstract: Karst areas are well developed in Southwest China, and karst hydrodynamic disasters have a great impact on underground engineering construction. In order to solve the problems of low slurry retention rate of cement-sodium silicate plugging materials, the traditional cement-soidium silica slurry is modified by water-soluble vegetable gum. The mechanism of water-soluble vegetable gum affecting the properties of cement-sodium silicate plugging materials is studied. The influence mechanism of the water-soluble vegetable gum on performance of karst water inrush plugging materials is investigated from the perspectives of setting time, compressive strength, slurry retention rate, viscosity evolution characteristics, hydration process and microstructure. The experimental results show that: (1) The water-soluble vegetable gum can improve the dynamic water anti-dispersion performance of the slurry, and the retention rate of the slurry can reach 96.4%. (2) Through the modification of different water-soluble vegetable gums, the setting time of the cement-sodium silicate slurry can be adjusted, and its application range can be increased. (3) Guar gum improves the early strength of the slurry paste matrix, but decreases its later strength. Both xanthan gum and xanthan gum-guar gum decrease the compressive strength of the slurry paste matrix. (4) The water-soluble vegetable gum can inhibit the hydration process of cement-sodium silicate slurry and improve the dynamic water anti-dispersion performance through the high viscosity property of the water-soluble vegetable gum and the cooperation of the reactive group with the cation in the cement. (5) The cement-sodium silicate slurry modified by the water-soluble vegetable gum is used in the water inrush project of limestone mine in Karst area, which effectively solves the problem of high flow rate and high flow inrush of karst pipelines.
- Cement-sodium silicate slurry /
- water-soluble vegetable gum /
- setting time /
- slurry retention rate /
- mechanical property

HTML全文

0. 引言

小孔扩张理论在岩土工程的各个领域得到了广泛的应用，比如顶管安装、圆锥贯入试验、水平定向钻井过程中的最大泥浆压力分析、隧道稳定性分析等。在实际工程中，真实应力场主要是以水平地应力和竖向地应力存在差异的两向不等压应力场为主^[1]，并且在旋转钻孔/开挖、螺旋桩和旋转圆锥贯入试验等^[2-3]过程中，孔口周边会产生较大的剪切应力。因此开展对同时考虑两向不等压应力场和孔口剪切应力下的小孔扩张理论进行研究具有重要的实际意义。

为此众多研究人员开展了相关研究。Galin^[4]基于Tresca屈服准则和理想弹塑性模型，采用复变函数法对两向不等压应力场和孔口无剪切应力共同作用下的柱形孔口进行了弹塑性分析；Zhou等^{[3, 5-6]}基于Tresca屈服准则和理想弹塑性模型，分别对两向等压应力场和孔口剪切应力共同作用下的柱形孔口以及两向不等压应力场和孔口无剪切应力共同作用下的柱形孔口进行了弹塑性分析；Zhuang等^[7-8]基于Tresca屈服准则和理想弹塑性模型对两向不等压应力场和孔口剪切应力，以及基于Mohr-Coulomb强度准则和理想弹塑性模型对两向不等压应力场和孔口无剪切应力共同作用下，均采用复变函数法对柱形孔口进行了弹塑性分析；Wang等^[9]基于Mohr-Coulomb强度准则和理想弹塑性模型，采用一种半解析方法对两向不等压应力场和孔口无剪切应力共同作用下的柱形孔口进行了弹塑性分析；武孝天等^[10]基于三维统一硬化（UH）本构模型对两向等压应力场和孔口无剪切应力共同作用下的柱/球形孔口进行了弹塑性分析；于旭光等^[11]基于统一强度理论和弹脆塑性模型对两向不等压应力场和孔口无剪切应力共同作用下的柱形孔口进行了弹塑性分析。

大量真三轴试验^[12]、广义强度理论与试验对比^[13]均表明：岩土类材料与中间主应力 ${\sigma _2}$ 紧密相关，而从上述文献[3~]研究中可以看出两点不足之处：①只有文献[，]采用了考虑中间主应力 ${\sigma _2}$ 对柱形孔口进行了弹塑性分析，其他均未考虑中间主应力效应；②未见综合考虑两向不等压应力场和孔口剪切应力共同作用情况下，推导出采用统一强度理论得到的统一解。

综上所述，本文首先提出一种理论计算框架，将弹性区的应力函数采用三角级数表示，进而推导出弹性区应力和位移，塑性区采用统一强度理论和相关联流动法则推导出塑性区应力和位移，而弹塑性边界线采用一种新的保角映射函数来进行确定；接着与基于Tresca屈服准则、Mohr-Coulomb强度准则并采用复变函数法得到的已有解答、试验值进行了对比验证；最后探讨了理论计算框架、柱形孔口周边均匀切应力以及侧压力系数对弹塑性交界线、应力和位移的影响。

1. 基本假定与基本方程

1.1 基本假定

在两向不等压应力场下，为了提供一种柱形孔口周边存在均匀切应力作用下的柱形孔扩张问题解析解，作如下3条假设：

（1）柱形孔口周边的土体塑性区完全包围孔口。

（2）柱形孔扩张过程中柱形孔口的扩孔压力是均匀的，且孔口周边切应力为常量。

（3）土体为各向均匀、连续且满足统一强度理论的理想弹塑性材料，在柱形孔土体扩张过程中面外应力始终作为中间主应力，且中间主应力表达式 ${\sigma _2} = {\text{(}}{\sigma _1} + {\sigma _3}{\text{)}}/2$ 。

以拉应力为正，采用黏聚力c、内摩擦角 $\varphi$ 表达的统一强度理论为^[14]

当 ${\sigma _2} \leqslant \frac{1}{2}({\sigma _1} + {\sigma _3}) + \frac{{\sin \varphi }}{2}({\sigma _1} - {\sigma _3})$ 时，

${\sigma _1} - \frac{{1 - \sin \varphi }}{{(1 + b)(1 + \sin \varphi )}}(b{\sigma _2} + {\sigma _3}) = \frac{{2c\cos \varphi }}{{1 + \sin \varphi }}。$

(1)

当 ${\sigma _2} \geqslant \frac{1}{2}({\sigma _1} + {\sigma _3}) + \frac{{\sin \varphi }}{2}({\sigma _1} - {\sigma _3})$ 时，

$\frac{1}{{1 + b}}({\sigma _1} + b{\sigma _2}) - \frac{{1 - \sin \varphi }}{{1 + \sin \varphi }}{\sigma _3} = \frac{{2c\cos \varphi }}{{1 + \sin \varphi }}。$

(2)

在平面应变状态下，将 ${\sigma _2} = ({\sigma _1} + {\sigma _3})/2$ 代入式（1），可得塑性区应力满足的统一强度理论表达式为

${\sigma _1} = A{\sigma _3} + B。$

(3)

式中： $A=\frac{(2+b)(1-\mathrm{sin}\varphi )}{2+b+(2+3b)\mathrm{sin}\varphi }；B=\frac{4(1+b)c\mathrm{cos}\varphi }{2+b+(2+3b)\mathrm{sin}\varphi }。$ b为统一强度理论参数，用来代表中间主应力 ${\sigma _2}$ 对土体材料强度的影响程度，其取值范围为 $0 \leqslant b \leqslant 1$ 。不同的b值可对应不同的强度准则，比如：当 $b = 0$ 时可对应为Mohr-Coulomb强度准则（作为特例当 $\varphi = {0^ \circ }$ ，此时 $A = 1$ 、 $B = 2c$ ，此时式（3）可对应为Tresca屈服准则）；当 $b = 1$ 时可对应为双剪应力强度准则；当 $0 < b < 1$ 时可对应为一系列新的强度准则。参数 $b$ 的确定可参考文献[15]。

在平面应变状态下，最大主应力、最小主应力与极坐标应力之间的关系式为

${\sigma _1} = \frac{1}{2}({\sigma _r} + {\sigma _\theta }) + \frac{1}{2}\sqrt {{{{\text{(}}{\sigma _r} - {\sigma _\theta }{\text{)}}}^2} + 4\tau _{r\theta }^2} \text{，}$

(4)

${\sigma _3} = \frac{1}{2}({\sigma _r} + {\sigma _\theta }) - \frac{1}{2}\sqrt {{{({\sigma _r} - {\sigma _\theta })}^2} + 4\tau _{r\theta }^2} 。$

(5)

将式（4）、（5）代入式（3），可得

$Q=(1+A)\sqrt{{({\sigma }_{r}-{\sigma }_{\theta })}^{2}+4{\tau }_{r\theta }^{2}}-({\sigma }_{r}+{\sigma }_{\theta })(A-1)-2B=0。$

(6)

式中： ${\sigma _r}$ ， ${\sigma _\theta }$ ， ${\tau _{r\theta }}$ 分别为径向正应力、切向正应力和切应力，求解时规定正应力以受拉为正，切应力以顺时针为正。

在上述假设情况下，柱形孔扩张力学模型如图 1所示。

图 1 柱形孔扩张力学模型

Figure 1. Mechanical model for cylindrical cavity expansion

下载: 全尺寸图片幻灯片

中 ${p_0}$ 为竖向地应力， $\lambda$ 为侧压力系数， ${r_{\text{i}}}$ 为柱形孔口半径， ${p_{\text{i}}}$ 为扩孔压力， ${\tau _{\text{i}}}$ 为洞壁处切应力， ${r_{\text{p}}}$ 为柱形孔口塑性区半径， $\theta$ 为极角，以逆时针旋转方向为正。

1.2 基本方程

极坐标中的平衡微分方程为^[16]

$\frac{{\partial {\sigma _r}}}{{\partial r}} + \frac{1}{r}\frac{{\partial {\tau _{r\theta }}}}{{\partial \theta }} + \frac{{{\sigma _r} - {\sigma _\theta }}}{r} = 0\text{，}$

(7)

$\frac{1}{r}\frac{{\partial {\sigma _\theta }}}{{\partial \theta }} + \frac{{\partial {\tau _{r\theta }}}}{{\partial r}} + \frac{{2{\tau _{r\theta }}}}{r} = 0。$

(8)

极坐标中的几何方程为

${\varepsilon _r} = \frac{{\partial {u_r}}}{{\partial r}}\text{，}$

(9)

${\varepsilon _\theta } = \frac{{{u_r}}}{r} + \frac{1}{r}\frac{{\partial {u_\theta }}}{{\partial \theta }}\text{，}$

(10)

${\gamma _{r\theta }} = \frac{1}{r}\frac{{\partial {u_r}}}{{\partial \theta }} + \frac{{\partial {u_\theta }}}{{\partial r}} - \frac{{{u_\theta }}}{r}。$

(11)

将中无穷远处的初始竖向和水平地应力转换为无穷远处的初始径向正应力 ${\sigma _{r0}}$ 、初始切向正应力 ${\sigma _{\theta 0}}$ 和初始切应力 ${\tau _{r\theta 0}}$ ，

${\sigma _{r0}} = - \frac{{1 + \lambda }}{2}{p_0} + \frac{{1 - \lambda }}{2}{p_0}\cos 2\theta \text{，}$

(12)

${\sigma _{\theta 0}} = - \frac{{1 + \lambda }}{2}{p_0} - \frac{{1 - \lambda }}{2}{p_0}\cos 2\theta \text{，}$

(13)

${\tau _{r\theta 0}} = - \frac{{1 - \lambda }}{2}{p_0}\sin 2\theta 。$

(14)

因此在平面应变状态下，扣除初始地应力下的本构方程为

${\varepsilon _r} = \frac{{1 - {\nu ^2}}}{E}\left[ {({\sigma _r} - {\sigma _{r0}}) - \frac{\nu }{{1 - \nu }}({\sigma _\theta } - {\sigma _{\theta 0}})} \right]\text{，}$

(15)

${\varepsilon _\theta } = \frac{{1 - {\nu ^2}}}{E}\left[ {{\text{(}}{\sigma _\theta } - {\sigma _{\theta 0}}{\text{)}} - \frac{\nu }{{1 - \nu }}({\sigma _r} - {\sigma _{r0}})} \right]\text{，}$

(16)

${\gamma _{r\theta }} = \frac{{2(1 + \nu )}}{E}({\tau _{r\theta }} - {\tau _{r\theta 0}})。$

(17)

式中：E， $\nu$ 分别为围岩弹性模量和泊松比。

2. 弹塑性解答

2.1 弹性区应力和位移解答

（1）弹性区应力解答

在极坐标系中，弹性区采用应力函数 $\varPhi$ 表示的双调和方程为^[16]

${\left( {\frac{{{\partial ^2}}}{{\partial {r^2}}} + \frac{1}{r}\frac{\partial }{{\partial r}} + \frac{1}{{{r^2}}}\frac{{{\partial ^2}}}{{\partial {\theta ^2}}}} \right)^2}\varPhi = 0。$

(18)

文献[]将应力函数 $\varPhi$ 展开成三角级数的形式，并求解得到应力函数 $\varPhi$ 的表达式为

$\begin{array}{l} \varPhi = {C_0}\ln r + {D_0}{r^2}\ln r + {F_0}{r^2} + \sum\limits_{k = 1}^{ + \infty } {\left[ {({L_k}{r^k}} \right.} + \\ \;\;\;\;\;\;\;\;\left. {{M_k}{r^{ - k}} + {N_k}{r^{k + 2}} + {P_k}{r^{ - k + 2}})\cos k\theta } \right]。 \end{array}$

(19)

式中： ${C_0}$ ， ${D_0}$ ， ${F_0}$ ， ${L_k}$ ， ${M_k}$ ， ${N_k}$ ， ${P_k}$ 为待定系数，可根据应力边界条件进行确定， $k = 1,2, \cdot \cdot \cdot$ 。

径向正应力 ${\sigma _r}$ 、切向正应力 ${\sigma _\theta }$ 、切应力 ${\tau _{r\theta }}$ 和应力函数 $\varPhi$ 的关系表达式为

${\sigma _r} = \frac{1}{r}\frac{{\partial \varPhi }}{{\partial r}} + \frac{1}{{{r^2}}}\frac{{{\partial ^2}\varPhi }}{{\partial {\theta ^2}}}\text{，}$

(20)

${\sigma _\theta } = \frac{{{\partial ^2}\varPhi }}{{\partial {r^2}}}\text{，}$

(21)

${\tau _{r\theta }} = \frac{1}{{{r^2}}}\frac{{\partial \varPhi }}{{\partial \theta }} - \frac{1}{r}\frac{{{\partial ^2}\varPhi }}{{\partial r\partial \theta }}。$

(22)

将式（19）分别代入式（20）~（22）可得围岩弹性区的径向正应力、切向正应力和切应力为

$\begin{array}{l} \sigma _r^{\text{e}} = \frac{{{C_0}}}{{{r^2}}} + {D_0}(2\ln r + 1) + 2{F_0} - \sum\limits_{k = 1}^{ + \infty } {\left[ {{L_k}\frac{{{k^2} - k}}{{{r^2}}}{r^k}} \right.} + \\ \;\;\;\;{M}_{k}\frac{{k}^{2}+k}{{r}^{k+2}}+{N}_{k}({k}^{2}-k-2){r}^{k}+{P}_{k}\frac{{k}^{2}+k-2}{{r}^{k}}]\mathrm{cos}k\theta \text{，} \end{array}$

(23)

$\begin{array}{l} \sigma _\theta ^{\text{e}} = - \frac{{{C_0}}}{{{r^2}}} + {D_0}(2\ln r + 3) + 2{F_0} + \sum\limits_{k = 1}^{ + \infty } {\left[ {{L_k}\frac{{{k^2} - k}}{{{r^2}}}{r^k}} \right.} + \\ \;\;\;\;{M}_{k}\frac{{k}^{2}+k}{{r}^{k+2}}+{N}_{k}({k}^{2}+3k+2){r}^{k}+{P}_{k}\frac{{k}^{2}-3k+2}{{r}^{k}}]\mathrm{cos}k\theta \text{，} \end{array}$

(24)

$\begin{array}{c} \tau _{r\theta }^{\text{e}} = \sum\limits_{k = 1}^{ + \infty } {k\left[ {{L_k}\frac{{k - 1}}{{{r^2}}}{r^k}} \right.} - {M_k}\frac{{k + 1}}{{{r^{k + 2}}}} + {N_k}(k + 1){r^k} - \\ \left. {{P_k}\frac{{k - 1}}{{{r^k}}}} \right]\sin k\theta 。 \end{array}$

(25)

式中：上角标加 ${\text{e}}$ 代表围岩弹性区，下同。

一方面在无穷远处，应力不能是无限大，因此根据式（23）~（25）可得

${D_0} = 0\text{，}{N_k} = 0 （k = 1,2, \cdot \cdot \cdot ） \text{，}$

(26)

${L_k} = 0 （k = 3,4, \cdot \cdot \cdot ）。$

(27)

另一方面在无穷远处，径向正应力、切向正应力、切应力应分别和式（12）~（14）相等，即

$\sigma _r^{\text{e}}\left| {_{r \to + \infty }} \right. = 2{F_0} - 2{L_2}\cos 2\theta = {\sigma _{r0}}\text{，}$

(28)

$\sigma _\theta ^{\text{e}}\left| {_{r \to + \infty }} \right. = 2{F_0} + 2{L_2}\cos 2\theta = {\sigma _{\theta 0}}\text{，}$

(29)

$\tau _{r\theta }^{\text{e}}\left| {_{r \to + \infty }} \right. = 2{L_2}\sin 2\theta = {\tau _{r\theta 0}}。$

(30)

通过式（28）~（30）可得

${F_0} = - \frac{{1 + \lambda }}{4}{p_0}\text{，}{L_2} = - \frac{{1 - \lambda }}{4}{p_0}。$

(31)

由于在式（23）~（25）中包含 ${L_1}$ 和 ${P_1}$ 的项恒为0，因此 ${L_1}$ 和 ${P_1}$ 不用求解，其他的 $2k$ 个待定系数 ${C_0}$ ， ${M_k}$ ， ${P_k}$ （注意此处 ${P_k}$ 从 ${P_2}$ 开始）需要在弹塑性交界线 $r = {r_{\text{p}}}$ 处，根据式（23）~（25）通过最小二乘法进行求解，即

$\boldsymbol{\sigma} - {{\boldsymbol{U}}_1}{\boldsymbol{ = }}{{\boldsymbol{R}}_{\boldsymbol{\theta }}}{\boldsymbol{U}} 。$

(32)

式中： $\boldsymbol{\sigma} = ({\sigma _{r1}},{\sigma _{\theta 1}},{\tau _{r\theta 1}}, \cdot \cdot \cdot ,{\sigma _{r{k_1}}},{\sigma _{\theta {k_1}}},{\tau _{r\theta {k_1}}})_{3{k_1} \times 1}^{\text{T}}$ ，其值可根据弹塑性交界线处应力值连续，进而采用塑性区应力值来确定； $\boldsymbol{U}_{1}=({(2{F}_{0}-2{L}_{2}\mathrm{cos}2\theta )}_{1}，$ ${(2{F}_{0}+2{L}_{2}\mathrm{cos}2\theta )}_{1}，$ ${(2{L_2}\sin 2\theta )_1}, \cdot \cdot \cdot ,{(2{F_0} - 2{L_2}\cos 2\theta )_{{k_1}}},$ $(2{F_0} + 2{L_2}\cos \cdot$ $2\theta {)}_{{k}_{1}},{(2{L}_{2}\mathrm{sin}2\theta )}_{{k}_{1}}{)}_{3{k}_{1}\times 1}^{\text{T}}；\boldsymbol{U}={({C}_{0},{M}_{1},\cdot \cdot \cdot ,{M}_{k},{P}_{2},\cdot \cdot \cdot ,{P}_{k})}_{2k\times 1}^{\text{T}}；$ ${{\boldsymbol{R}}_{\boldsymbol{\theta }}}$ 为系数矩阵，可通过式（23）~（25）得出，在极角 $\theta$ 为0°∶360°，将弹塑性交界线等分成 ${k_1}$ 个点（ ${k_1} = 1,2, \cdot \cdot \cdot$ ，且需满足 $3{k_1} > 2k$ ，此时方程数大于待定系数个数），则 ${{\boldsymbol{R}}_{\boldsymbol{\theta }}}$ 为 $3{k_1} \times 2k$ 的系数矩阵，限于篇幅，不再列出。

根据式（32），可得

${\boldsymbol{U}} = {({\boldsymbol{R}}_{\boldsymbol{\theta }}^{\text{T}}{{\boldsymbol{R}}_{\boldsymbol{\theta }}})^{ - 1}}{\boldsymbol{R}}_{\boldsymbol{\theta }}^{\text{T}}(\boldsymbol{\sigma} - {{\boldsymbol{U}}_1}) 。$

(33)

（2）弹性区位移解答

联立式（9）~（11）、（15）~（17）、（23）~（25），可得围岩弹性区的径向位移和切向位移为

$u_r^{\text{e}} = \frac{{1 + \nu }}{E}\left[ {\sum\limits_{k = 1}^{ + \infty } {\frac{{{M_k}k}}{{{r^{k + 1}}}}\cos k\theta } + } \right.\left. {\sum\limits_{k = 2}^{ + \infty } {\frac{{{P_k}(k + 2 - 4\nu )}}{{{r^{k - 1}}}}\cos k\theta } } \right]\text{，}$

(34)

${u}_{\theta }^{\text{e}}=\frac{1+\nu }{E}\left[{\displaystyle \sum _{k=1}^{+\infty }\frac{{M}_{k}k}{{r}^{k+1}}\mathrm{sin}k\theta }+{\displaystyle \sum _{k=2}^{+\infty }\frac{{P}_{k}(k-4+4\nu )}{{r}^{k-1}}\mathrm{sin}k\theta }\right]\text{ }。$

(35)

2.2 塑性区应力和位移解答

（1）塑性区应力解答

当围岩塑性区完全包围孔口时，由于孔口处的应力边界和几何形状属于轴对称情况，因此可假定围岩塑性区应力与极角 $\theta$ 无关，即

$\frac{{\partial \sigma _r^{\text{p}}}}{{\partial \theta }} = 0 \text{，} \frac{{\partial \sigma _\theta ^{\text{p}}}}{{\partial \theta }} = 0 \text{，} \frac{{\partial \tau _{r\theta }^{\text{p}}}}{{\partial \theta }} = 0 。$

(36)

式中：上角标加 ${\text{p}}$ 代表围岩塑性区，下同。

根据式（8），可得围岩塑性区切应力为

$\tau _{r\theta }^{\text{p}} = {\tau _{\text{i}}}\frac{{r_{\text{i}}^2}}{{{r^2}}} 。$

(37)

由于 $({\sigma _\theta } - {\sigma _r})$ 与 $2{\tau _{r\theta }}$ 的大小不能确定，因此利用公式 $\sqrt {{m^2} + {n^2}} \approx 1.0m + 0.38n$ ^[18]（当 $5n \geqslant m > n$ ， $n > 0$ 时，相对误差 $< 7\%$ ；当 $m > 5n$ ， $n > 0$ 时，相对误差 $< 5\%$ ）来近似简化式（6）时，可分成3种情况。简化后的式（6）具体表达式为

$Q = {\sigma _\theta } + {J_1}{\sigma _r} + {J_2}{\tau _{r\theta }} + {J_3} = 0。$

(38)

式中：当 ${\tau _{r\theta }} > 0$ （当 ${\tau _{r\theta }} < 0$ 时，前面加“-”号即可）时， ${J_1}$ ， ${J_2}$ ， ${J_3}$ 表达式分别为

${J_1} = \left\{ \begin{array}{l} - A & ({\sigma _\theta } - {\sigma _r}) > 2{\tau _{r\theta }} \hfill \\ - \frac{{(\sqrt 2 + 1)A + \sqrt 2 - 1}}{{(\sqrt 2 - 1)A + \sqrt 2 + 1}} & ({\sigma _\theta } - {\sigma _r}) = 2{\tau _{r\theta }}{\text{ }} \hfill \\ \frac{{0.31 - 0.69A}}{{0.69 - 0.31A}} & ({\sigma _\theta } - {\sigma _r}) < 2{\tau _{r\theta }} \hfill \\ \end{array} \right. \text{，}$

${J_2} = \left\{ \begin{array}{l} 0.38(A + 1) & ({\sigma _\theta } - {\sigma _r}) > 2{\tau _{r\theta }} \hfill \\ 0 & ({\sigma _\theta } - {\sigma _r}) = 2{\tau _{r\theta }} \hfill \\ \frac{{A + 1}}{{0.69 - 0.31A}} & ({\sigma _\theta } - {\sigma _r}) < 2{\tau _{r\theta }}{\text{ }} \hfill \\ \end{array} \right. \text{，}$

${J_3} = \left\{ \begin{array}{l} - B & ({\sigma _\theta } - {\sigma _r}) > 2{\tau _{r\theta }} \hfill \\ - \frac{{2B}}{{(\sqrt 2 - 1)A + \sqrt 2 + 1}} & ({\sigma _\theta } - {\sigma _r}) = 2{\tau _{r\theta }} \hfill \\ - \frac{B}{{0.69 - 0.31A}} & ({\sigma _\theta } - {\sigma _r}) < 2{\tau _{r\theta }} \hfill \\ \end{array} \right. 。$

当 ${\tau _{r\theta }} = 0$ 时，式（38）将退化为 $Q = {\sigma _\theta } + {J_1}{\sigma _r} +$ ${J_3} = 0$ ，此时 ${J_1} = - A$ ， ${J_3} = - B$ 。

联立式（7），（37），（38），并以 ${\sigma _r}\left| {_{r = {r_{\text{i}}}}} \right. = - {p_{\text{i}}}$ 为边界条件，可得围岩塑性区径向正应力和切向正应力为

当 ${J_1} = - 1$ （此时对应 $A = 1$ ）时，

$\sigma _r^{\text{p}} = - {p_{\text{i}}} - {J_3}\ln \frac{r}{{{r_{\text{i}}}}} - \frac{{{J_2}{\tau _{\text{i}}}}}{2}\left( {1 - \frac{{r_{\text{i}}^2}}{{{r^2}}}} \right) \text{，}$

(39)

$\sigma _\theta ^{\text{p}} = - {p_{\text{i}}} - {J_3}\left( {\ln \frac{r}{{{r_{\text{i}}}}} + 1} \right) - \frac{{{J_2}{\tau _{\text{i}}}}}{2}\left( {1 + \frac{{r_{\text{i}}^2}}{{{r^2}}}} \right) 。$

(40)

当 ${J_1} \ne - 1$ （此时对应 $A \ne 1$ ）时，

$\begin{array}{l} \sigma _r^{\text{p}} = \left( { - {p_{\text{i}}} + \frac{{{J_3}}}{{{J_1} + 1}} + \frac{{{J_2}{\tau _{\text{i}}}}}{{{J_1} - 1}}} \right){\left( {\frac{r}{{{r_{\text{i}}}}}} \right)^{ - \left( {{J_1} + 1} \right)}} - \\ \;\;\;\;\;\;\;\;\frac{{{J_2}{\tau _{\text{i}}}}}{{{J_1} - 1}}\frac{{r_{\text{i}}^2}}{{{r^2}}} - \frac{{{J_3}}}{{{J_1} + 1}} \text{，} \end{array}$

(41)

$\begin{array}{l} \sigma _\theta ^{\text{p}} = - {J_1}\left( { - {p_{\text{i}}} + \frac{{{J_3}}}{{{J_1} + 1}} + \frac{{{J_2}{\tau _{\text{i}}}}}{{{J_1} - 1}}} \right){\left( {\frac{r}{{{r_{\text{i}}}}}} \right)^{ - \left( {{J_1} + 1} \right)}} + \\ \;\;\;\;\;\;\;\; \frac{{{J_2}{\tau _{\text{i}}}}}{{{J_1} - 1}}\frac{{r_{\text{i}}^2}}{{{r^2}}} - \frac{{{J_3}}}{{{J_1} + 1}} 。 \end{array}$

(42)

因此，式（39），（40），（37）或式（41），（42），（37）即为围岩塑性区的径向正应力、切向正应力和切应力。

（2）塑性区位移解答

在围岩塑性区，根据相关联流动法则可得

${\text{d}}\varepsilon _{ij}^{\text{p}}{\text{ = d}}\lambda \frac{{{\text{d}}Q}}{{{\text{d}}{\sigma _{ij}}}} 。$

(43)

式中： $\varepsilon _{ij}^{\text{p}}$ 为塑性应变。

将式（38）代入式（43）可得

$\left.\begin{array}{l}\text{d}{\varepsilon }_{\theta }^{\text{p}}\text{=d}\lambda \frac{\partial Q}{\partial {\sigma }_{\theta }}=\text{d}\lambda \text{，}\\ \text{d}{\varepsilon }_{r}^{\text{p}}\text{=d}\lambda \frac{\partial Q}{\partial {\sigma }_{r}}={J}_{1}\text{d}\lambda \text{，}\\ \text{d}{\varepsilon }_{r\theta }^{\text{p}}\text{=d}\lambda \frac{\partial Q}{\partial {\tau }_{r\theta }}={J}_{2}\text{d}\lambda 。\end{array}\right\}$

(44)

由式（44）可得

${\text{d}}\varepsilon _\theta ^{\text{p}} = \frac{1}{{{J_1}}}{\text{d}}\varepsilon _r^{\text{p}} \text{，} {\text{d}}\varepsilon _{r\theta }^{\text{p}}{\text{ = }}\frac{{{J_2}}}{{{J_1}}}{\text{d}}\varepsilon _r^{\text{p}} 。$

(45)

对式（45）两式的两端进行积分，并根据弹塑性交界线处的塑性应变为0，可得

$\varepsilon _\theta ^{\text{p}} = \frac{1}{{{J_1}}}\varepsilon _r^{\text{p}} \text{，} \varepsilon _{r\theta }^{\text{p}}{\text{ = }}\frac{{{J_2}}}{{{J_1}}}\varepsilon _r^{\text{p}} 。$

(46)

根据式（46），可得塑性区的应变表达式为

${\varepsilon _\theta } - \frac{1}{{{J_1}}}{\varepsilon _r} = \varepsilon _\theta ^{\text{e}} + \varepsilon _\theta ^{\text{p}} - \frac{1}{{{J_1}}}(\varepsilon _r^{\text{e}} + \varepsilon _r^{\text{p}}) = \varepsilon _\theta ^{\text{e}} - \frac{1}{{{J_1}}}\varepsilon _r^{\text{e}} \text{，}$

(47)

${\varepsilon _{r\theta }} - \frac{{{J_2}}}{{{J_1}}}{\varepsilon _r} = \varepsilon _{r\theta }^{\text{e}} + \varepsilon _{r\theta }^{\text{p}} - \frac{{{J_2}}}{{{J_1}}}(\varepsilon _r^{\text{e}} + \varepsilon _r^{\text{p}}) = \varepsilon _{r\theta }^{\text{e}} - \frac{{{J_2}}}{{{J_1}}}\varepsilon _r^{\text{e}} 。$

(48)

将式（9）~（11）分别代入式（47），（48），同时考虑 ${\varepsilon _{r\theta }} = \frac{1}{2}{\gamma _{r\theta }}$ ，可得

$\frac{{{u_r}}}{r} + \frac{1}{r}\frac{{\partial {u_\theta }}}{{\partial \theta }} - \frac{1}{{{J_1}}}\frac{{\partial {u_r}}}{{\partial r}} = \varepsilon _\theta ^{\text{e}} - \frac{1}{{{J_1}}}\varepsilon _r^{\text{e}}\text{，}$

(49)

$\frac{1}{2}\left( {\frac{1}{r}\frac{{\partial {u_r}}}{{\partial \theta }} + \frac{{\partial {u_\theta }}}{{\partial r}} - \frac{{{u_\theta }}}{r}} \right) - \frac{{{J_2}}}{{{J_1}}}\frac{{\partial {u_r}}}{{\partial r}} = \varepsilon _{r\theta }^{\text{e}} - \frac{{{J_2}}}{{{J_1}}}\varepsilon _r^{\text{e}}。$

(50)

通过求解式（49），（50），可得到围岩塑性区径向位移和切向位移。

a）情况1

当 ${J_2} \ne 0$ （此时代表考虑孔口周边均匀切应力）时，围岩塑性区径向位移：

当 ${J_1} = - 1$ （此时对应 $A = 1$ ）时，

$u_r^{\text{p}} = {J_4}r + {J_5}{r^{ - 1}} - {J_3}\frac{{(1 + \nu )(1 - 2\nu )}}{E}r\ln r \text{；}$

(51)

当 ${J_1} \ne - 1$ （此时对应 $A \ne 1$ ）时，

$\begin{array}{l} u_r^{\text{p}} = {J_6}r + {J_7}{r^{{J_1}}} + \frac{{1 + \nu }}{E}\left\{ { - \frac{1}{2}\left[ {\left( {{J_1} + \frac{1}{{{J_1}}}} \right) + \left( {2 - {J_1} - \frac{1}{{{J_1}}}} \right)\nu } \right] \cdot } \right. \\ \left. {\left( { - {p_{\text{i}}} + \frac{{{J_3}}}{{{J_1} + 1}} + \frac{{{J_2}{\tau _{\text{i}}}}}{{{J_1} - 1}}} \right){{\left( {\frac{1}{{{r_{\text{i}}}}}} \right)}^{ - \left( {{J_1} + 1} \right)}}{r^{ - {J_1}}} + \frac{{{J_2}{\tau _{\text{i}}}}}{{{J_1} - 1}}\frac{{r_{\text{i}}^2}}{r}} \right\} 。\end{array}$

(52)

围岩塑性区切向位移：

当 ${J_1} = - 1$ （此时对应 $A = 1$ ）时，

$\begin{array}{l} u_\theta ^{\text{p}} = \left\{ {\frac{{(1 + \nu )(1 - 2\nu )}}{E} \cdot } \right.\left[ { - 2{p_{\text{i}}} + 2{J_3}\ln {r_{\text{i}}} - {J_2}{\tau _{\text{i}}} + (1 + \lambda ){p_0}} \right] - \\ \quad \quad \quad \quad 2{J_4}\left. \right\}r\theta + {h_1}(r) \text{；} \end{array}$

(53)

当 ${J_1} \ne - 1$ （此时对应 $A \ne 1$ ）时，

$\begin{array}{c} u_\theta ^{\text{p}} = \left[ {\frac{{1 + \nu }}{E} \cdot \left( { - 1 + \frac{1}{{{J_1}}} - \frac{2}{{{J_1}}}\nu + 2\nu } \right)\left( {\frac{{{J_3}}}{{{J_1} + 1}} - \frac{{1 + \lambda }}{2}{p_0}} \right)} \right. + \left( {\frac{1}{{{J_1}}} - 1} \right) \cdot \\ {J_6}\left. \right]r\theta + \left[ {\frac{{1 + \nu }}{E} \cdot \left( {1 + \frac{1}{{{J_1}}}} \right) \cdot \frac{{1 - \lambda }}{4}{p_0}\sin 2\theta } \right] \cdot r + {h_2}(r) 。 \end{array}$

(54)

式中： ${J_4}$ ， ${J_5}$ ， ${J_6}$ ， ${J_7}$ 为积分常数； ${h_1}(r)$ ， ${h_2}(r)$ 为只与r相关的函数。

b）情况2

当 ${J_2} = 0$ （此时代表不考虑孔口周边均匀切应力）时，围岩塑性区径向位移分别如下：

当 ${J_1} = - 1$ （此时对应 $A = 1$ ）时，

$\begin{array}{l} u_r^{\text{p}} = {J_{10}}r + {J_{11}}{r^{ - 1}} - {J_3}\frac{{(1 + \nu )(1 - 2\nu )}}{E}r\ln r + \\ \;\;\;\; \sum\limits_{w = 1}^{ + \infty } {\left[ {{V_{w,1}}\cos ({H_{w,1}}\ln r) + {V_{w,2}}\sin ({H_{w,1}}\ln r)} \right]\cos 2w\theta } \text{；} \end{array}$

(55)

当 ${J_1} \ne - 1$ （此时对应 $A \ne 1$ ）时，

$\begin{array}{l} u_r^{\text{p}} = {J_{12}}r + {J_{13}}{r^{{J_1}}} + \frac{{1 + \nu }}{E}\left\{ { - \frac{1}{2}\left[ {\left( {{J_1} + \frac{1}{{{J_1}}}} \right) + \left( {2 - {J_1} - \frac{1}{{{J_1}}}} \right)\nu } \right] \cdot } \right. \\ \;\;\;\;\;\;\;\; \left. {\left( { - {p_{\text{i}}} + \frac{{{J_3}}}{{{J_1} + 1}}} \right){{\left( {\frac{1}{{{r_{\text{i}}}}}} \right)}^{ - \left( {{J_1} + 1} \right)}}{r^{ - {J_1}}}} \right\} + \sum\limits_{w = 1}^{ + \infty } {{r^{\frac{{{J_1} + 1}}{2}}}} \cdot \\ \;\;\;\;\;\;\;\; \left[ {{V_{w,3}}\cos ({H_{w,2}}\ln r) + {V_{w,4}}\sin ({H_{w,2}}\ln r)} \right]\cos 2w\theta 。 \end{array}$

(56)

围岩塑性区切向位移分别如下：

当 ${J_1} = - 1$ （此时对应 $A = 1$ ）时，

$\begin{array}{l} u_\theta ^{\text{p}} = \left. {\left\{ {\frac{{(1 + \nu )(1 - 2\nu )}}{E} \cdot } \right.\left[ { - 2{p_{\text{i}}} + 2{J_3}\ln {r_{\text{i}}} + (1 + \lambda ){p_0}} \right] - 2{J_{10}}} \right\}r\theta + \\ \;\;\;\; \sum\limits_{w = 1}^{ + \infty } {\frac{1}{{2w}}} \left\{ {{V_{w,1}}\left[ {{H_{w,1}}\sin ({H_{w,1}}\ln r) - \cos ({H_{w,1}}\ln r)} \right] - } \right.{V_{w,2}} \cdot \\ \;\;\;\; \left. {\left[ {\sin ({H_{w,1}}\ln r) + {H_{w,1}}\cos ({H_{w,1}}\ln r)} \right]} \right\}\sin 2w\theta + {h_3}(r) \text{；} \end{array}$

(57)

当 ${J_1} \ne - 1$ （此时对应 $A \ne 1$ ）时，

$\begin{array}{l} u_\theta ^{\text{p}} = \left[ {\frac{{1 + \nu }}{E} \cdot \left( { - 1 + \frac{1}{{{J_1}}} - \frac{2}{{{J_1}}}\nu + 2\nu } \right)\left( {\frac{{{J_3}}}{{{J_1} + 1}} - \frac{{1 + \lambda }}{2}{p_0}} \right)} \right. + \left( {\frac{1}{{{J_1}}} - 1} \right) \cdot \\ \left. {{J_{12}}} \right]r\theta + \left[ {\frac{{1 + \nu }}{E} \cdot \left( {1 + \frac{1}{{{J_1}}}} \right) \cdot \frac{{1 - \lambda }}{4}{p_0}\sin 2\theta } \right] \cdot r + \sum\limits_{w = 1}^{ + \infty } {\frac{{{r^{\frac{{{J_1} + 1}}{2}}}}}{{4w{J_1}}}} \left\{ {{V_{w,3}} \cdot } \right. \\ \left[ {(1 - {J_1})\cos ({H_{w,2}}\ln r) - 2{H_{w,2}}\sin ({H_{w,2}}\ln r)} \right] + {V_{w,4}}\left[ {(1 - {J_1}) \cdot } \right. \\ \left. {\sin ({H_{w,2}}\ln r) + 2{H_{w,2}}\left. {\cos ({H_{w,2}}\ln r)} \right]} \right\}\sin 2w\theta + {h_4}(r) 。 \end{array}$

(58)

式中： ${H_{w,1}}$ ， ${H_{w,2}}$ 为关于 $w$ 的表达式； ${J_{10}}$ ， ${J_{11}}$ ， ${J_{12}}$ ， ${J_{13}}$ 为积分常数； ${h_3}(r)$ ， ${h_4}(r)$ 为只与 $r$ 相关的函数； ${V_{w,1}}$ ， ${V_{w,2}}$ ， ${V_{w,3}}$ ， ${V_{w,4}}$ 为待定系数。

2.3 塑性区半径解答

从2.1，2.2节可以看出，求解问题的关键在于塑性区半径 ${r_{\text{p}}}$ 。在两向不等压应力场下，从文献[]可知弹塑性交界线不是一个圆形，可取保角映射函数将z平面上的弹塑性交界线转换为 $\zeta$ 平面上的单位圆，进而圆内和圆外的区域分别表示塑性区和弹性区。如图 2所示。

图 2

$\zeta$ 平面上的弹塑性交界线

Figure 2. Elastic-plastic boundary in

$\zeta$ plane

下载: 全尺寸图片幻灯片

根据文献[8]，取保角映射函数为

$z = \omega (\zeta ) = \alpha \zeta {\left( {1 + \frac{\beta }{{{\zeta ^2}}}} \right)^\chi } 。$

(59)

式中： $\alpha$ ， $\beta$ ， $\chi$ 为控制弹塑性交界线的常数； $\zeta =$ $\xi + {\text{i}}\eta = \rho {{\text{e}}^{{\text{i}}\phi }}$ 为 $\zeta$ 平面上的复变函数， $\rho$ 为极径， $\phi$ 为极角， ${\text{i = }}\sqrt { - 1}$ 。

根据弹性力学中的复变函数解法，弹性区的应力可以采用两个解析函数 ${\varphi _{\text{e}}}(\zeta )$ 和 ${\psi _{\text{e}}}(\zeta )$ 表示为^[16]

${\varphi _{\text{e}}}(\zeta ) + \overline {{\varphi _{\text{e}}}(\zeta )} = \frac{{\sigma _r^{\text{e}} + \sigma _\theta ^{\text{e}}}}{2} \text{，}$

(60)

$\frac{{\overline {\omega (\zeta )} }}{{\omega '(\zeta )}}{\varphi '_{\text{e}}}(\zeta ) + {\psi _{\text{e}}}(\zeta ) = \frac{{\sigma _\theta ^{\text{e}} - \sigma _r^{\text{e}} + 2{\text{i}}\tau _{r\theta }^{\text{e}}}}{2}{{\text{e}}^{ - 2{\text{i}}\theta }} 。$

(61)

在弹塑性交界线处，存在

$\frac{{\sigma _r^{\text{e}} + \sigma _\theta ^{\text{e}}}}{2} = \frac{{\sigma _r^{\text{p}} + \sigma _\theta ^{\text{p}}}}{2} \text{，}$

(62)

$\frac{{\sigma _\theta ^{\text{e}} - \sigma _r^{\text{e}} + 2{\text{i}}\tau _{r\theta }^{\text{e}}}}{2} = \frac{{\sigma _\theta ^{\text{p}} - \sigma _r^{\text{p}} + 2{\text{i}}\tau _{r\theta }^{\text{p}}}}{2} 。$

(63)

在弹性区无穷远处，根据式（12）~（14）可得

$\frac{{\sigma _r^{\text{e}} + \sigma _\theta ^{\text{e}}}}{2} = - \frac{{1 + \lambda }}{2}{p_0} \text{，}$

(64)

$\frac{{\sigma _\theta ^{\text{e}} - \sigma _r^{\text{e}} + 2{\text{i}}\tau _{r\theta }^{\text{e}}}}{2}{{\text{e}}^{ - 2{\text{i}}\theta }}\left| {_{r \to + \infty }} \right. = - \frac{{1 - \lambda }}{2}{p_0} 。$

(65)

通过对 $A = 1$ 和 $A \ne 1$ 这2种情况分别来计算式（59）中的 $\alpha$ ， $\beta$ ， $\chi$ 。

a）情况1

当 ${J_1} = - 1$ （此时对应 $A = 1$ ）时，

$\begin{array}{l} \chi = 1 \text{，} \beta = \frac{{(1 - \lambda ){p_0}}}{{{J_3}}} \text{，} \\ \alpha = {r_{\text{i}}}\exp \left[ { - \frac{1}{{{J_3}}}\left( { - \frac{{1 + \lambda }}{2}{p_0} + \frac{{{J_2}{\tau _{\text{i}}}}}{2} + {p_{\text{i}}} + \frac{{{J_3}}}{2}} \right)} \right] 。 \end{array}$

(66)

当 ${\tau _{\text{i}}} = 0$ 且满足 $b = 0$ 和 $\varphi = {0^ \circ }{\text{ }}$ 时，式（66）中 $\alpha$ ， $\beta$ ， $\chi$ 取值与文献[5]中采用Tresca屈服准则相同。

b）情况2

当 ${J_1} \ne - 1$ （此时对应 $A \ne 1$ ）时，采用情况1求解常数 $\beta$ 和 $\chi$ 的方法，可得 $\chi$ 值、 $\alpha$ 与 $\beta$ 关系式分别为

$\chi = \frac{2}{{1 - {J_1}}} \text{，}$

(67)

$\begin{array}{l} - \frac{{{J_1} + 1}}{2}\left( { - {p_{\text{i}}} + \frac{{{J_3}}}{{{J_1} + 1}} + \frac{{{J_2}{\tau _{\text{i}}}}}{{{J_1} - 1}}} \right){\left( {\frac{1}{{{r_{\text{i}}}}}} \right)^{ - \left( {{J_1} + 1} \right)}}{\alpha ^{ - \left( {{J_1} + 1} \right)}}\beta \\ \quad \quad \quad \quad = - \frac{{1 - \lambda }}{2}{p_0} \text{，} \end{array}$

(68)

$\begin{array}{l} \frac{{1 + \lambda }}{2}{p_0} - \frac{{{J_3}}}{{{J_1} + 1}} + \frac{{1 - {J_1}}}{2}\left( { - {p_{\text{i}}} + \frac{{{J_3}}}{{{J_1} + 1}} + \frac{{{J_2}{\tau _{\text{i}}}}}{{{J_1} - 1}}} \right) \cdot \\ \quad \quad \quad \quad {\left( {\frac{1}{{{r_{\text{i}}}}}} \right)^{ - \left( {{J_1} + 1} \right)}}{R_0} = 0 。 \end{array}$

(69)

式中： ${R_0}$ 为与超几何函数相关的常数。

当 ${\tau _{\text{i}}} = 0$ 、 $b = 0$ 时且附录中的式（110）中的超几何函数只取第一项时（即取值为1），则式（67）~（69）中 $\alpha$ ， $\beta$ ， $\chi$ 取值与文献[]中采用Mohr-Coulomb强度准则相同。当超几何函数不仅仅取第一项（即取值不为1）时， $\alpha$ ， $\beta$ 值可通过式（68）、（69）并采用MATLAB编程进行求解。

将 ${\zeta _{\text{p}}} = {{\text{e}}^{{\text{i}}\phi }}$ 代入式（59），可得

$z = r{{\text{e}}^{{\text{i}}\theta }} = \alpha {{\text{e}}^{{\text{i}}\phi }}{(1 + \beta {{\text{e}}^{ - {\text{i2}}\phi }})^\chi } = \alpha {\rho ^\chi }{{\text{e}}^{{\text{i}}\left( {\phi + \chi \varepsilon } \right)}}。$

(70)

式中： $\rho = \sqrt {1 + 2\beta \cos 2\phi + {\beta ^2}}$ ；

$\cos \varepsilon = \frac{{1 + \beta \cos 2\phi }}{{\sqrt {1 + 2\beta \cos 2\phi + {\beta ^2}} }}。$

从式（70）可以看出，z平面上的弹塑性交界线处的塑性区半径为 $\alpha {\rho ^\chi }$ ，z平面上的极角 $\theta$ 与 $\zeta$ 平面上的极角 $\phi$ 的关系为 $\theta = \phi + \chi \varepsilon$ 。

2.4 求解流程

本文求解流程如图 3所示。

图 3 求解流程图

Figure 3. Flow chart for solutions

下载: 全尺寸图片幻灯片

特别指出：本文计算的塑性区半径 ${r_{\text{p}}}$ 在任意极角 $\theta$ 处均需满足 ${r_{\text{p}}} \geqslant {r_{\text{i}}}$ ，以保证柱形孔口周边的土体塑性区完全包围孔口。

3. 对比验证

为验证本文解的正确性，将本文解与文献[7，8]（复变函数法）、试验值^[19]进行对比分析。

3.1 本文解与复变函数解对比验证

当采用Tresca屈服准则时，取文献[]中的参数： ${r_{\text{i}}} = 1$ ， ${p_0} = c$ ， $\lambda {p_0} = 0.5c$ ， ${p_{\text{i}}} = 5c$ ， ${\tau _{\text{i}}} = 0$ 和 $c$ ， $\varphi = {0^ \circ }{\text{ }}$ ；当采用Mohr-Coulomb强度准则时，取 ${\tau _{\text{i}}} = 0$ ， $\varphi = {15^ \circ }{\text{ }}$ ，其他参数同Tresca屈服准则。另外，考虑到计算精度要求，取式（33）中 $k = 7$ （即取前7项）， ${k_1} = 24$ 。两种准则下的弹塑性交界线和极角 $\theta = {0^ \circ }{\text{ }}$ 时的应力对比结果如图 4，所示，考虑到对称性，，中弹塑性交界线仅取极角 $\theta$ 在0°∶90°区域的图形。

图 4 Tresca屈服准则

Figure 4. Tresca yield criterion

下载: 全尺寸图片幻灯片

图 5 Mohr-Coulomb强度准则

Figure 5. Mohr-Coulomb strength criterion

下载: 全尺寸图片幻灯片

从，中可以看出：当采用Tresca屈服准则时，本文解在 ${\tau _{\text{i}}} = c$ 时比文献[]（复变函数法）求得的弹塑性交界线增大了3.7%，而应力值是非常吻合的，而在 ${\tau _{\text{i}}} = 0$ 时求得的弹塑性交界线是相同的；当采用Mohr-Coulomb强度准则时，本文解和文献[]（复变函数法）求得的弹塑性交界线以及应力值均是相同的，并且在4.3节中，当采用 $\lambda = 1$ 进行位移分析时，位移值计算精度也非常高。

3.2 本文解与试验值对比验证

文献[]进行了9组不同埋深下的均匀砂土水平钻孔试验。本文以其中1组HB25为例，其基本参数：孔口直径 $D = 2{r_{\text{i}}} = 38$ mm，砂土密度 $\rho ' = 1696$ kg/m³，孔口深度与孔口直径比值 $H/D = 17.9$ ， $\lambda = 0.51$ ， $c = 5$ kPa（由于钻孔周围发生了入渗，从而考虑了黏聚力）， $\varphi = {46^ \circ }$ 。该试验测试了极角 $\theta = {270^ \circ }{\text{ }}$ 且 $r = 3{r_{\text{i}}}$ 的径向应力、切向应力增量值，通过与本文解（本文解采用 $b = 0$ ，在实际工程中可根据文献[]方法确定 $b$ 值）对比分析如图 6所示。

图 6 不同

${\tau _{\text{i}}}$ 下的本文解与试验值对比分析

Figure 6. Comparative analysis of proposed solutions and experimental values with different values of

${\tau _{\text{i}}}$

下载: 全尺寸图片幻灯片

从中可以看出：本文求得的径向应力增量 $\Delta {\sigma _r}$ 与试验值非常吻合，而求得的切向应力增量 $\Delta {\sigma _\theta }$ 比试验值略大，但从总体变化趋势来说较为吻合。同时由于 ${\tau _{\text{i}}}$ 与 ${p_{\text{i}}}$ 相比较小，故图 6中考虑切应力作用时与未考虑切应力时曲线变化不是特别明显。

4. 参数分析

本节进行参数分析时，取文献[]中的参数： ${r_{\text{i}}} = 1$ ， ${p_0} = c$ ， $\lambda {p_0} = 0.5c$ ， ${p_{\text{i}}} = 5c$ ， $\varphi = {15^ \circ }{\text{ }}$ ；另附加参数 $E = 100c$ ， $\nu = 0.3$ ，并取式（74）中 $w = 7$ （即取前7项）。考虑到对称性，本节分析仅取极角 $\theta$ 在0°∶90°区域的图形。

4.1 理论计算框架对计算结果的影响

从全文整体推导来看，本文将式（6）简化为式（38）时，会产生一定的相对误差，本节就这种简化产生的相对误差对计算结果的影响进行分析。

由于文献[3]给出了基于Tresca屈服准则时，考虑两向等压应力场和孔口剪切应力共同作用下弹性区、塑性区应力精确计算公式，但并未给出塑性区半径计算表达式（只需要在弹塑性交界线处，令弹性区和塑性区的径向正应力、切向正应力和切应力分别相等即可求得）。现将孔口周边不同切应力作用下，本文解与文献[3]中求得的塑性区半径、应力精确解进行对比分析。

当 $\lambda = 1$ ， ${p_{\text{i}}} = 5c$ ， $b = 0$ ， $\varphi =$ 0°，其他参数同前，在不同 ${\tau _{\text{i}}}$ 时，本文解与文献[3]求解的塑性区半径、柱形孔口处的应力精确解（其他位置处应力类似，由于篇幅限制在此不再赘述）对比分析如图 7所示。

图 7 不同

${\tau _{\text{i}}}$ 下的弹塑性交界线和应力分量（Tresca屈服准则）

Figure 7. Elastic-plastic boundary and stress components with different values

${\tau _{\text{i}}}$ (Tresca yield criterion)

下载: 全尺寸图片幻灯片

从中可以看出：在不同 ${\tau _{\text{i}}}$ 时，本文解与精确解弹塑性交界线变化趋势一致，最大相对误差为4.0%，而应力值是非常吻合的。因此从Tresca屈服准则角度来看，本文所作简化后计算精度是比较高的。

另外特别指出：当采用Mohr-Coulomb强度准则时，由于未见文献给出精确解，所以本文只给出本文解与文献[]（即 $b = 0$ ， ${\tau _{\text{i}}} = 0$ ， $\lambda = 1$ 情况下）精确解的对比，详见4.3节。

4.2 柱形孔口周边均匀切应力的影响

当 $\lambda = 0.5$ ， ${p_{\text{i}}} = 5c$ ， $b = 0$ ， ${\tau _{\text{i}}}$ 分别取0， $0.5c$ ， $c$ 时，其他参数同前，得到的弹塑性交界线、极角 $\theta = {0^ \circ }{\text{ }}$ 时的应力分量、柱形孔口处的径向位移（即 ${u_{r0}}$ ）和切向位移（即 ${u_{\theta 0}}$ ）如图 8所示。

图 8 不同

${\tau _{\text{i}}}$ 下的弹塑性交界线、应力分量和位移分量

Figure 8. Elastic-plastic boundary, stress components and displacement components with different values of

${\tau _{\text{i}}}$

下载: 全尺寸图片幻灯片

从可以看出：不同 ${\tau _{\text{i}}}$ 下的弹塑性交界线呈类椭圆形状，类椭圆的长轴方向与两向不等压应力场的较大值处一致，并且弹塑性交界线随 ${\tau _{\text{i}}}$ 增大呈均匀增大的趋势。从可以看出：在塑性区，不同 ${\tau _{\text{i}}}$ 下的切向正应力、切应力变化显著，而径向正应力基本重合；在弹性区，不同 ${\tau _{\text{i}}}$ 下的径向正应力、切向正应力、切应力基本重合。从可以看出：当 ${\tau _{\text{i}}}$ 时，柱形孔口处的径向位移在 ${0^ \circ } \leqslant \theta \leqslant {40^ \circ }$ 内基本无变化，而在 ${40^ \circ } < \theta \leqslant {90^ \circ }$ 内，随极角 $\theta$ 增大而减小；当 ${\tau _{\text{i}}} = 0$ 时，柱形孔口处的径向位移在 ${0^ \circ } \leqslant \theta$ $\leqslant {90^ \circ }$ 随极角 $\theta$ 增大而减小；柱形孔口处的切向位移（这里指绝对值大小）随极角 $\theta$ 呈先增大后减小的趋势，近似为正弦曲线，并且当 ${\tau _{\text{i}}} = 0$ ， $\theta$ 为0°，90°时，柱形孔口处的切向位移为0。

4.3 侧压力系数的影响

当 ${p_{\text{i}}} = 5c$ ， $b = 0$ ， ${\tau _{\text{i}}} = 0$ ， $\lambda$ 分别取0.50，0.75，1.00时，其他参数同前，得到的弹塑性交界线、极角 $\theta = {0^ \circ }{\text{ }}$ 时的应力分量、柱形孔口处的径向位移 ${u_{r0}}$ 和切向位移（ ${u_{\theta 0}}$ ）如图 9所示。

图 9 不同

$\lambda$ 下的弹塑性交界线、应力分量和位移分量

Figure 9. Elastic-plastic boundary, stress components and displacement components with different values of

$\lambda$

下载: 全尺寸图片幻灯片

从可以看出：不同 $\lambda$ 下的弹塑性交界线显著不同。并以 $\theta = {30^ \circ }{\text{ }}$ 为界分成两段；当 ${0^ \circ } \leqslant \theta \leqslant$ ${30^ \circ }{\text{ }}$ 时，弹塑性交界线随 $\lambda$ 增大水平向右移动；当 ${30^ \circ } < \theta \leqslant {90^ \circ }{\text{ }}$ 时，弹塑性交界线随 $\lambda$ 增大竖直向下移动，并且当 $\lambda = 1$ 时弹塑性交界线为圆形。因此在实际工程中，不能忽视侧压力系数 $\lambda$ 的影响。从可以看出：在塑性区，不同 $\lambda$ 下的径向正应力、切向正应力、切应力基本重合，这是由于在极角 $\theta = {0^ \circ }{\text{ }}$ 处的塑性区半径相差不大所导致的；在弹性区，切应力恒为0。从可以看出：柱形孔口处的径向位移以 $\theta = {40^ \circ }{\text{ }}$ 为界分成两段，当 ${0^ \circ } \leqslant \theta \leqslant {40^{ \circ {\text{ }}}}$ 时，径向位移随 $\lambda$ 增大而减小；当 ${40^ \circ } < \theta \leqslant {90^ \circ }{\text{ }}$ 时，径向位移随 $\lambda$ 增大而增大。柱形孔口处的切向位移（这里指绝对值大小）随 $\lambda$ 增大而减小。并且随 $\lambda$ 增大，径向位移和切向位移的数值比值也增大，即 $\lambda$ 越大，切向位移相对径向位移来说，越可以忽略不计。特别当 $\lambda = 1$ 时，本文方法求得的柱形孔口处的径向位移、切向位移分别为两个常数 $0.03{r_{\text{i}}}$ ，0，这与两向等压应力场时，假定柱形孔口均匀扩张，切向位移为0是吻合的，并且根据文献[]（即 $b = 0$ ， ${\tau _{\text{i}}} = 0$ ， $\lambda = 1$ 情况下）求得的径向位移也与 $0.03{r_{\text{i}}}$ 几乎相等。

5. 结论

（1）本文解给出了一种柱形孔扩张问题新的计算框架，不仅扩展了文献[7]采用Tresca屈服准则下求得的解，而且推导了考虑切应力下的径向位移和切向位移，体现了柱形孔扩张时的“非圆效应”。通过与文献[3]采用Tresca屈服准则并考虑切应力得出的精确解比较，弹塑性交界线最大相对误差为4.0%，而应力解非常吻合。

（2）由于考虑切应力可以进一步扩展塑性区半径，因此在水平定向钻井过程中，在达到相同塑性区半径情况下，考虑切应力影响可以减少扩孔压力。

（3）本文方法可以扩展应用到柱形孔压缩问题（比如隧道稳定性分析）以及其他本构模型（比如幂强化-理想塑性模型）中，这些将在后续进行研究。

（注：文中附录见本文电子版）

图 1 黄原胶的化学结构

Figure 1. Chemical structure of xanthan gum

下载: 全尺寸图片幻灯片

图 2 瓜尔豆胶的化学结构

Figure 2. Chemical structure of guar gum

下载: 全尺寸图片幻灯片

图 3 水泥-水玻璃稀释浆液凝结时间

Figure 3. Setting time of cement-sodium silicate slurry

下载: 全尺寸图片幻灯片

图 4 倒杯法测定凝结时间的示意图

Figure 4. Diagram of pouring cup method for determining setting time

下载: 全尺寸图片幻灯片

图 5 浆液抗分散性能试验装置示意图

Figure 5. Schematic diagram of slurry anti-dispersion test device

下载: 全尺寸图片幻灯片

图 6 改性水泥-水玻璃浆液的凝结时间

Figure 6. Setting time of modified cement-sodium silicate slurry

下载: 全尺寸图片幻灯片

图 7 改性水泥-水玻璃浆液的水化历程

Figure 7. Hydration process of modified cement-sodium silicate slurry

下载: 全尺寸图片幻灯片

图 8 不同水溶性植物胶对B液黏度时变性的影响

Figure 8. Effect of different water-soluble vegetable gums on viscosity evolution characteristics of liquid B

下载: 全尺寸图片幻灯片

图 9 改性水泥-水玻璃浆液结石体的抗压强度

Figure 9. Compressive strengths of modified cement-sodium silicate slurry paste matrix

下载: 全尺寸图片幻灯片

图 10 不同水溶性植物胶改性浆液结石体XRD图谱

Figure 10. XRD patterns of slurry paste matrix mixed with different water-soluble vegetable gums

下载: 全尺寸图片幻灯片

图 11 不同水溶性植物胶掺入的浆液红外光谱

Figure 11. Infrared spectra of slurries with different water-soluble vegetable gums

下载: 全尺寸图片幻灯片

图 12 浆液结石体的SEM-EDS (×2000)

Figure 12. SEM-EDS of grout paste matrix (×2000)

下载: 全尺寸图片幻灯片

图 13 华润水泥石灰石矿岩溶涌水示意图

Figure 13. Karst rushing water of China Resources cement limestone ore

下载: 全尺寸图片幻灯片

图 14 浆液跑浆特性

Figure 14. Grouting off characteristics of grout

下载: 全尺寸图片幻灯片

图 15 水溶性植物胶改性水泥-水玻璃浆液的封堵效果

Figure 15. Sealing effects of water-soluble vegetable gum-modified cement-sodium silicate slurry

下载: 全尺寸图片幻灯片

表 1 普通硅酸盐水泥的化学组成

Table 1 Chemical composition of ordinary portland cement (%)

类型	SiO₂	Fe₂O₃	Al₂O₃	CaO	MgO	LOI
OPC	19.45	4.42	5.84	61.72	4.38	0.56

下载: 导出CSV

表 2 改性水泥–水玻璃浆液抗分散性能试验结果

Table 2 Test results of dispersion resistance of modified cement-sodium silicate slurry

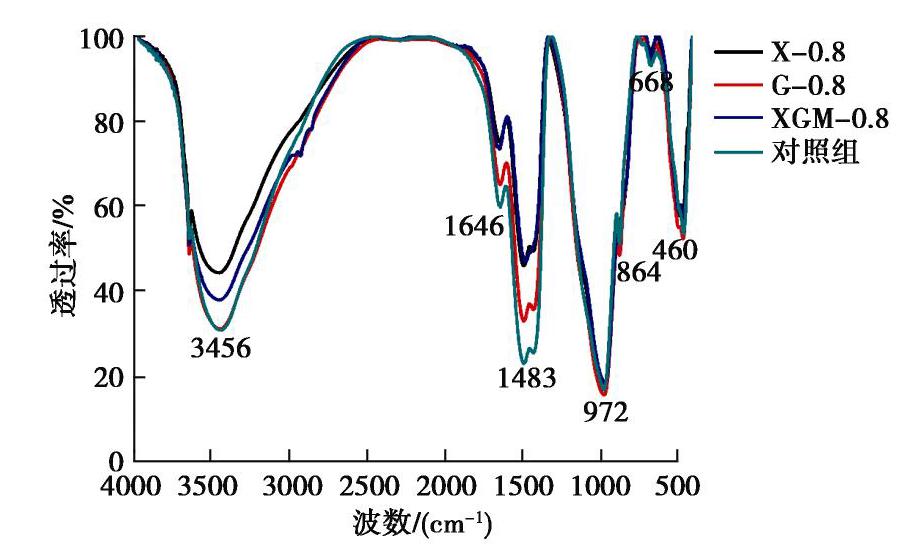
编号	名称	水溶性植物胶浓度/%	水玻璃掺量/%	W/C	C/S	R/%
1	X-0.8	0.6	60	1	3	80.2
2		0.8	60	1	3	82.0
3		1.0	60	1	3	83.8
4	G-0.8	0.6	60	1	3	91.2
5		0.8	60	1	3	96.4
6		1.0	60	1	3	93.2
7	XGM-0.8	0.6	60	1	3	84.8
8		0.8	60	1	3	87.6
9		1.0	60	1	3	89.2
10	对照组	0	60	1	3	75.8

下载: 导出CSV

表 3 EDS扫描的试样区域中的元素

Table 3 Elements in areas of specimens scanned by EDS

元素	X-0.8		G-0.8		XGM-0.8		对照组
元素	^#1	^#2	^#1	^#2	^#1	^#2	^#1	^#2
O	59.6	71.9	63.6	72.1	67.3	58.1	62.0	28.0
Si	11.0	3.2	9.8	3.1	8.2	2.2	10.2	1.7
Ca	16.5	15.1	13.8	14.7	10.0	32.5	17.4	59.5
注：^#1和^#2指的是图12中扫描电镜成像的位置。

下载: 导出CSV

参考文献(38)

[1]	李术才, 李树忱, 张庆松, 等. 岩溶裂隙水与不良地质情况超前预报研究[J]. 岩石力学与工程学报, 2007, 26(2): 217-225. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200702000.htm LI Shu-cai, LI Shu-chen, ZHANG Qing-song, et al. Forecast of the karst-fractured groundwater and defective geological condition[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(2): 217-225. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200702000.htm
[2]	张霄, 李术才, 张庆松, 等. 关键孔注浆方法在高压裂隙水封堵中的应用研究[J]. 岩石力学与工程学报, 2011, 30(7): 1415-1421. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201107016.htm ZHANG Xiao, LI Shu-cai, ZHANG Qing-song, et al. Application of key hole grouting method in high pressure fissure water plugging[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(7): 1415-1421. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201107016.htm
[3]	潘东东, 李术才, 许振浩, 等. 岩溶隧道承压隐伏溶洞突水模型试验与数值分析[J]. 岩土工程学报, 2018, 40(5): 828-836. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201805009.htm PAN Dong-dong, LI Shu-cai, XU Zhen-hao, et al. Model test and numerical analysis of water inrush from confined concealed karst caves in karst tunnels[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(5): 828-836. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201805009.htm
[4]	郑刚, 潘军, 程雪松, 等. 基坑开挖引起隧道水平变形的被动与注浆主动控制研究[J]. 岩土工程学报, 2019, 41(7): 1181-1190. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201907002.htm ZHENG Gang, PAN Jun, CHENG Xue-song, et al. Study on passive and grouting active control of horizontal deformation of tunnel caused by foundation pit excavation[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(7): 1181-1190. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201907002.htm
[5]	冯志强, 康红普, 杨景贺. 裂隙岩体注浆技术探讨[J]. 煤炭科学技术, 2005, 33(4): 63-66. https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ20050400I.htm FENG Zhi-qiang, KANG Hong-pu, YANG Jing-he. Discussion on grouting technology for fractured rock mass[J]. Coal Science and Technology, 2005, 33(4): 63-66. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ20050400I.htm
[6]	DALLYN P, EL-HAMALAWI A, PALMERI A, et al. Experimental testing of grouted connections for offshore substructures: a critical review[J]. Structures, 2015, 3: 90-108. doi: 10.1016/j.istruc.2015.03.005
[7]	HONG K. Typical underwater tunnels in the mainland of China and related tunneling technologies[J]. Engineering, 2017, 3(6): 871-879. doi: 10.1016/j.eng.2017.12.007
[8]	王玉钦, 冀焕军, 杨永利. 煤矿井下动水注浆堵水实践[J]. 煤炭科学技术, 2007, 35(2): 30-33. https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ200702008.htm WANG Yu-qin, JI Huan-jun, YANG Yong-li. Practices on dynamic water grouting and sealing in coal mine[J]. Coal Science and Technology, 2007, 35(2): 30-33. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ200702008.htm
[9]	李术才, 张霄, 张庆松, 等. 地下工程涌突水注浆止水浆液扩散机制和封堵方法研究[J]. 岩石力学与工程学报, 2011, 30(12): 2377-2396. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201112002.htm LI Shu-cai, ZHANG Xiao, ZHANG Qing-song, et al. Study on diffusion mechanism and plugging method of grouting slurry in underground engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(12): 2377-2396. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201112002.htm
[10]	李召峰, 李术才, 刘人太, 等. 富水破碎岩体注浆加固材料试验研究与应用[J]. 岩土力学, 2016, 37(7): 1938-1946. LI Zhao-feng, LI Shu-cai, LIU Ren-tai, et al. Experimental study and application of grouting reinforcement materials for water-rich broken rock mass[J]. Rock and Soil Mechanics, 2016, 37(7): 1938-1946. (in Chinese)
[11]	葛家良. 化学灌浆技术的发展与展望[J]. 岩石力学与工程学报, 2006, 25(增刊2): 3384-3392. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2006S2006.htm GE Jia-liang. Development and prospect of chemical grouting techniques[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(S2): 3384-3392. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2006S2006.htm
[12]	马哲, 庞浩, 杨元龙, 等. 化学灌浆材料的研究进展综述[J]. 广州化学, 2014, 39(1): 9-13. https://www.cnki.com.cn/Article/CJFDTOTAL-GZHX201401003.htm MA Zhe, PANG Hao, YANG Yuan-long, et al. Summary of research progress in chemical grouting materials[J]. Guangzhou Chemistry, 2014, 39(1): 9-13. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GZHX201401003.htm
[13]	SHA F, LI S C, LIU Ｒ T, et al. Experimental study on performance of cement-based grouts admixed with fly ash, bentonite, superplasticizer and water glass[J]. Construction and Building Materials, 2018, 161: 282-291.
[14]	商海星, 陆海军, 李继祥, 等. 裂隙岩体注浆结石体收缩变形与抗剪强度[J]. 科学技术与工程, 2016, 16(36): 231-235. https://www.cnki.com.cn/Article/CJFDTOTAL-KXJS201636040.htm SHANG Hai-xing, LU Hai-jun, LI Ji-xiang, et al. The shrinking and de-formation and shear strength of fractured rock grouting stone[J]. Science Technology and Engineering, 2016, 16(36): 231-235. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KXJS201636040.htm
[15]	吴克雄, 李顺凯, 杨钊, 等. 废弃泥浆改性同步注浆材料试验研究[J]. 科学技术与工程, 2017, 17(20): 277-281. https://www.cnki.com.cn/Article/CJFDTOTAL-KXJS201720048.htm WU Ke-xiong, LI Shun-kai, YANG Zhao, et al. Experimental study on the waste mud modified synchronous grouting materials[J]. Science Technology and Engineering, 2017, 17(20): 277-281. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KXJS201720048.htm
[16]	刘人太, 李术才, 张庆松, 等. 一种新型动水注浆材料的试验与应用研究[J]. 岩石力学与工程学报, 2011, 30(7): 1454-1459. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201107021.htm LIU Ren-tai, LI Shu-cai, ZHANG Qing-song, et al. Test and application of a new dynamic grouting material[J]. Journal of Rock Mechanics and Engineering, 2011, 30(7): 1454-1459. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201107021.htm
[17]	阮文军, 王文臣, 胡安兵. 新型水泥复合浆液的研制及其应用[J]. 岩土工程学报, 2001, 23(2): 212-216. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200102018.htm RUAN Wen-jun, WANG Wen-chen, HU An-bing. Development and application of new kind of cement composite grout[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(2): 212-216. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200102018.htm
[18]	李利平, 李术才, 张庆松, 等. 一种新型高分子注浆材料的试验研究[J]. 岩石力学与工程学报, 2010, 29(增刊1): 3150-3156. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2010S1082.htm LI Li-ping, LI Shu-cai, ZHANG Qing-song, et al. Experimental study of a new polymer grouting material[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S1): 3150-3156. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2010S1082.htm
[19]	王洪波, 张庆松, 刘人太, 等. 不良地质动水封堵加固材料试验及工艺研究[J]. 岩石力学与工程学报, 2017, 36(2): 3985-3991. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2017S2031.htm WANG Hong-bo, ZHANG Qing-song, LIU Ren-tai, et al. Experimental and technological study on unblocking geologic water blocking and strengthening materials[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(2): 3985-3991. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2017S2031.htm
[20]	王红喜, 张高展, 丁庆军, 等. 碱激发–工业废渣双液注浆材料性能研究[J]. 建筑材料学报, 2007, 10(3): 374-378. https://www.cnki.com.cn/Article/CJFDTOTAL-JZCX200703021.htm WANG Hong-xi, ZHANG Gao-zhan, DING Qing-jun, et al. Properties of two-liquid grouting materials for alkali-excited industrial wastes[J]. Journal of Building Materials, 2007, 10(3): 374-378. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZCX200703021.htm
[21]	宋雪飞. 粉煤灰改性水泥–水玻璃双液注浆性能试验研究[J]. 煤炭科学技术, 2014, 42(1): 143-150. https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ201401036.htm SONG Xue-fei. Experimental study on two-liquid grouting performance of fly ash modified cement-water glass[J]. Coal Science and Technology, 2014, 42(1): 143-150. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ201401036.htm
[22]	梁乃兴, 陈忠明. 注浆用水泥浆体性能研究[J]. 建筑材料学报, 2000, 3(3): 275-278. https://www.cnki.com.cn/Article/CJFDTOTAL-JZCX200003019.htm LIANG Nai-xing, CHEN Zhong-ming. Study on properties of cement paste for grouting[J]. Journal of Building Materials, 2000, 3(3): 275-278. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZCX200003019.htm
[23]	万志, 张蕾, 刘健, 等. 改性水泥–水玻璃注浆材料防渗性能试验研究[J]. 科学技术与工程, 2018, 18(19): 278-282. https://www.cnki.com.cn/Article/CJFDTOTAL-KXJS201819044.htm WAN Zhi, ZHANG Lei, LIU Jian, et al. Experimental study on impermeability of modified cement-sodium silicate grouting material[J]. Science and Technology and Engineering, 2018, 18(19): 278-282. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KXJS201819044.htm
[24]	刘军, 方惠琦, 贺鸿珠. 水下不分散混凝土的应用研究[J]. 建筑材料学报, 2000, 3(4): 360-365. https://www.cnki.com.cn/Article/CJFDTOTAL-JZCX200004012.htm LIU Jun, FANG Hui-qi, HE Hong-zhu. Application research of underwater non-dispersive concrete[J]. Journal of Building Materials, 2000, 3(4): 360-365. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZCX200004012.htm
[25]	陈沅江, 万秀峰. 外加剂对水泥–水玻璃浆液凝固特性的影响[J]. 硅酸盐通报, 2014, 33(7): 1847-1851. https://www.cnki.com.cn/Article/CJFDTOTAL-GSYT201407065.htm CHEN Yuan-jiang, WAN Xiu-feng. Effect of additives on the solidification characteristics of cement-water glass slurry[J]. Silicate Bulletin, 2014, 33(7): 1847-1851. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GSYT201407065.htm
[26]	KONG X M, EMMERLING S, PAKUSCH J, et al. Retardation effect of styrene-acrylate copolymer latexes on cement hydration[J]. Cem Concr Res, 2015, 75: 23-41.
[27]	SOWOIDNICH T, RACHOWSKI T, RÖßLER C, et al. Calcium complexation and cluster formation as principal modes of action of polymers used as superplasticizer in cement systems[J]. Cem Concr Res, 2015, 73: 42-50.
[28]	孔祥明, 卢子臣, 张朝阳. 水泥水化机理及聚合物外加剂对水泥水化影响的研究进展[J]. 硅酸盐学报, 2017, 42(2): 274-281. https://www.cnki.com.cn/Article/CJFDTOTAL-GXYB201702016.htm KONG Xiang-ming, LU Zi-chen, ZHANG Chao-yang. Research progress on hydration mechanism of cement and influence of polymer admixtures on cement hydration[J]. Journal of Portland, 2017, 42(2): 274-281. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GXYB201702016.htm
[29]	LI S C, ZHANG J, LI Z F, et al. Investigation and practical application of a new cementitious anti-washout grouting material[J]. Construction and Building Materials, 2019, 224: 66-67.
[30]	QI Y H, LI S C, LI Z F, et al. Effect of Xanthan on pore structure of cement slurry doped with sodium silicate[J/OL]. Materials Letters (2019). doi: 10.1016/j.matlet.2019.126736.
[31]	HOSSEIN H, KIANOUSH K D. Effective variables on production and structure of xanthan gum and its food applications: a review[J]. Biocatalysis and Agricultural Biotechnology, 2017, 10: 130-140.
[32]	ANUJ K, KUMMARA M R, SUNG S. Application of xanthan gum as polysaccharide in tissue engineering: a review[J]. Carbohydrate Polymers, 2018, 180: 128-144.
[33]	王元兰, 黄寿恩, 李忠海, 等. 黄原胶与瓜尔豆胶混胶黏度的影响因素及微结构研究[J]. 中国食品学报, 2015, 9(4): 119-123. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGSP200904031.htm WANG Yuan-lan, HUANG Shou-en, LI Zhong-hai, et al. Influencing factors and microstructure of viscosity of xanthan gum and guar gum[J]. Chinese Journal of Food Science, 2015, 9(4): 119-123. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGSP200904031.htm
[34]	袁敬强, 陈卫忠, 谭贤君, 等. 速凝浆液抗分散性质与凝胶性能试验研究[J]. 岩石力学与工程学报, 2015, 34(5): 961-967. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201505011.htm YUAN Jing-qiang, CHEN Wei-zhong, TAN Xian-jun, et al. Experimental study on the anti dispersive properties and gel properties of quick setting slurry[J]. Chinese Journal of rock mechanics and engineering, 2015, 34(5): 961-967. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201505011.htm
[35]	QI Y H, LI S C, LI Z F, et al. Hydration effect of sodium silicate on cement slurry doped with xanthan[J]. Construction and Building Materials, 2019, 223: 976-985.
[36]	李虎军, 王琪. 水溶性聚合物改性水泥的研究Ⅱ.水溶性聚合物对水泥水化过程的影响[J]. 功能高分子学报, 1999, 12(3): 276-280. https://www.cnki.com.cn/Article/CJFDTOTAL-GNGF199903009.htm LI Hu-jun, WANG Qi. Study on water-soluble polymer modified cement II. Effect of water-soluble polymer on hydration process of cement[J]. Journal of Functional Polymer, 1999, 12(3): 276-280. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GNGF199903009.htm
[37]	李应权. 弹性聚合物水泥材料组成、性能与结构的研究[D]. 北京: 北京工业大学, 2005. LI Ying-quan. Research of Composition, Properties and Structure on Elastic Polymer Modified Cement Based Material[D]. Beijing: Beijing University of Technology, 2005. (in Chinese)
[38]	JANSEN D, NEUBAUER J, GOETZ-NEUNHOEFFER F, et al. Change in reaction kinetics of a Portland cement caused by a superplasticizer-calculation of heat flow curves from XRD data[J]. Cem Concr Res, 2012, 42: 327-332.

施引文献

资源附件(0)

图(15) / 表(3)

计量

文章访问数: 345
HTML全文浏览量: 18
PDF下载量: 205
被引次数: 0

0. 引言
1. 基本假定与基本方程
1.1 基本假定
1.2 基本方程
2. 弹塑性解答
2.1 弹性区应力和位移解答
2.2 塑性区应力和位移解答
2.3 塑性区半径解答
2.4 求解流程
3. 对比验证
3.1 本文解与复变函数解对比验证
3.2 本文解与试验值对比验证
4. 参数分析
4.1 理论计算框架对计算结果的影响
4.2 柱形孔口周边均匀切应力的影响
4.3 侧压力系数的影响
5. 结论

0. 引言
1. 基本假定与基本方程
1.1 基本假定
1.2 基本方程
2. 弹塑性解答
2.1 弹性区应力和位移解答
2.2 塑性区应力和位移解答
2.3 塑性区半径解答
2.4 求解流程
3. 对比验证
3.1 本文解与复变函数解对比验证
3.2 本文解与试验值对比验证
4. 参数分析
4.1 理论计算框架对计算结果的影响
4.2 柱形孔口周边均匀切应力的影响
4.3 侧压力系数的影响
5. 结论

参考文献(38)

施引文献

资源附件(0)

水溶性植物胶改性水泥–水玻璃封堵材料试验研究 English Version

作者简介: 李召峰(1986—),男,博士(后),副教授,主要从事地下工程灾害治理及注浆材料的研发工作。E-mail：lizf@sdu.edu.cn

计量

出版历程

Experimental study of water-soluble vegetable gum-modified cement-sodium silicate plugging materials

0. 引言

1. 基本假定与基本方程

1.1 基本假定

1.2 基本方程

2. 弹塑性解答

2.1 弹性区应力和位移解答

2.2 塑性区应力和位移解答

2.3 塑性区半径解答

2.4 求解流程

3. 对比验证

3.1 本文解与复变函数解对比验证

3.2 本文解与试验值对比验证

4. 参数分析

4.1 理论计算框架对计算结果的影响

4.2 柱形孔口周边均匀切应力的影响

4.3 侧压力系数的影响

5. 结论

计量

出版历程

目录

0. 引言

1. 基本假定与基本方程

1.1 基本假定

1.2 基本方程

2. 弹塑性解答

2.1 弹性区应力和位移解答

2.2 塑性区应力和位移解答

2.3 塑性区半径解答

2.4 求解流程

3. 对比验证

3.1 本文解与复变函数解对比验证

3.2 本文解与试验值对比验证

4. 参数分析

4.1 理论计算框架对计算结果的影响

4.2 柱形孔口周边均匀切应力的影响

4.3 侧压力系数的影响

5. 结论

作者简介:
李召峰(1986—),男,博士(后),副教授,主要从事地下工程灾害治理及注浆材料的研发工作。E-mail：lizf@sdu.edu.cn