0.   引言

煤层开采过程中上覆岩层一般可划分为“三带”^[1],由下至上依次为垮落带、裂隙带以及弯曲下沉带。采空区垮落带一般指由采矿引起的上覆岩层破坏并向采空区垮落的岩层带,又称冒落带,根据实验室实测其孔隙率高达30%～45%^[2]。由于垮落带孔隙率高,渗透率大,邻近煤层卸压瓦斯、含水层或地表水涌入采空区使其蕴含着大量的瓦斯及水资源。采空区垮落带压实孔隙演化特征不仅影响着矿井水及瓦斯资源的高效抽采利用,还影响着残煤氧化自燃,威胁着工作面的安全生产^[3-6]。因此,准确掌握采空区垮落带破碎煤岩体压实过程中的破碎机制及孔隙演化特征对煤矿安全高效生产、采空区水瓦斯等资源存储利用、环境生态保护等具有重要的意义。

采空区垮落带可以视为由破碎煤岩体组成的多孔介质,随着工作面的持续推进,造成上覆岩层的不断下沉压实采空区垮落带,垮落带自身的应力、密度、孔隙率、渗透率等参数均会发生变化^[7]。在采空区垮落带受开采扰动过程中,垮落带内破碎岩体的再次损伤破碎、孔隙结构的调整以及破碎岩体的挤压变形是影响采空区垮落带孔隙及应力变化的主要原因^[8]。因此,掌握采空区垮落带破碎煤岩体在压实过程中的破碎演化特征,对于掌握垮落带内应力–孔隙等演化特征至关重要。然而,由于采空区含有大量的水及有毒有害气体,同时为了防止工作面漏风、残煤自燃等危害,采空区垮落带一般处于封闭状态。因此,目前仅限于实测采空区垮落带内的压实应力,而对于垮落带内煤岩体的破碎特征的观测很难实现^[9-10]。

对于采空区垮落带压实过程中的孔隙结构特征的研究大多处于实验室尺度。且已有的实验室研究多集中于破碎煤岩样压实过程中的应力、应变等因素对渗透特性的影响^[11-13]。由于试验条件的限制,对于压实过程中破碎岩样内部的孔隙结构特征涉及较少。随着现代装备的提升,已经将CT扫描运用于采空区破碎岩样或者颗粒土压实过程中的孔隙结构获取,并基于二值化算法进行孔隙率的定量表征,但仍然很难实现全过程实时对破碎岩样的定位与量化分析^[14-16]。

随着数值模拟手段的发展,由于其具有成本低、变量可控以及量化分析等特点,已经成为研究岩石力学性质的主要手段。而通过颗粒结构和细观本构模型对材料力学行为进行表征的颗粒离散元法,提供了连接岩石细观结构与宏观特性的桥梁,成为研究岩石物理力学性质的有力工具^[17-18]。颗粒破碎对颗粒集合体的力学响应有着显著的影响。离散元法为从不同尺度上研究颗粒破碎对颗粒集合体力学特性的影响提供了一条有效的方法。基于DEM的颗粒破碎模拟经过近二十年的发展,已经得到了广泛的应用并取得了丰富的研究成果,为从细观尺度研究可破碎颗粒及其集合体的力学响应和机理提供了有效的途径^[19-21]。但目前对于颗粒材料压实的数值模拟主要研究对象是堆石料及粗粒土的破碎。

为了进一步研究采空区垮落带煤岩体在压实过程中的破碎结构对破碎煤岩样模型应力及孔隙特征的影响。本文基于离散元数值模拟方法,给出了破碎颗粒初始不接触的模拟方法,反演得出煤岩样对应的颗粒球体参数与黏结参数,进一步模拟分析了破碎煤岩样压实过程中的破碎特征以及煤岩比例和组合结构对破碎特征的影响,量化分析了破碎煤岩样的破碎率演化特征。

1.   数值模型建立

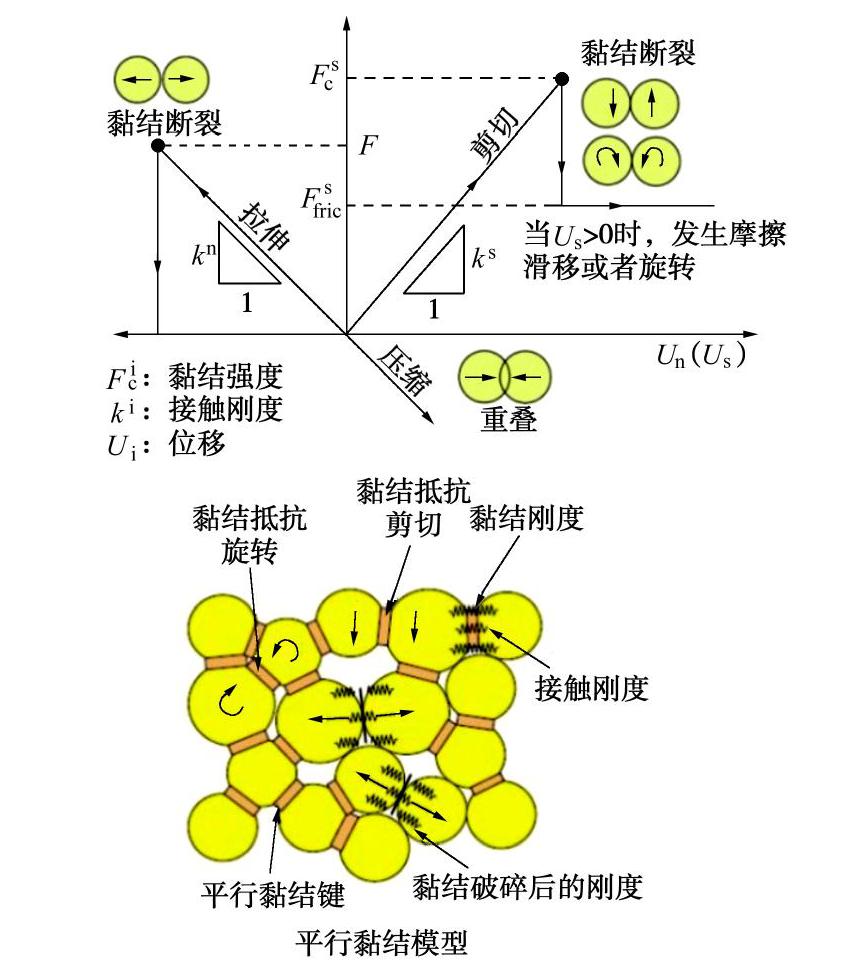
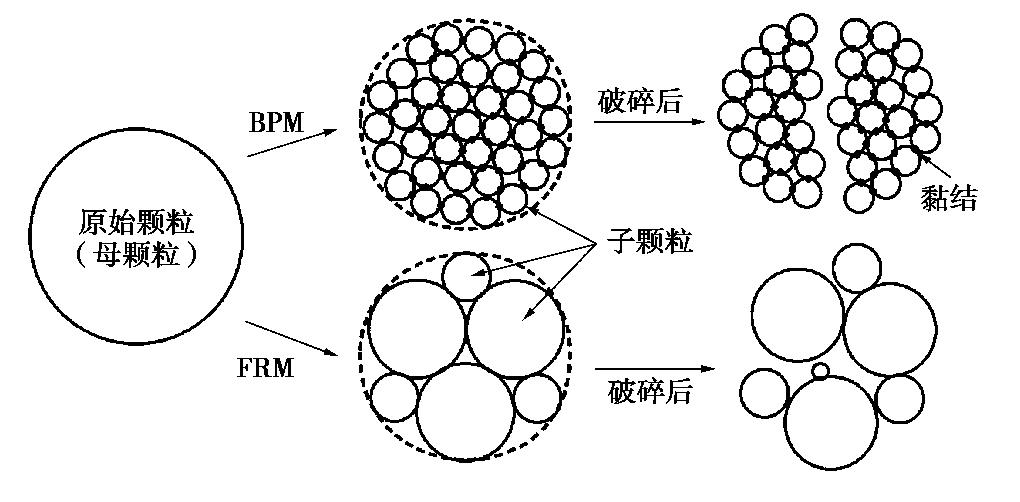
常用的基于离散元的岩石力学模拟软件主要有UDEC以及PFC。UDEC中常用Voronoi多边形模型进行实验室及现场岩石力学特征的模拟,取得了良好的效果。但是在上述模型中,不规则多边形不能进一步破碎,且裂隙发育必须沿着事先设置的多边形块体边界^[22]。这显然很难符合采空区垮落带煤岩体在压实过程中的再破碎特征。在采空区压实过程中,垮落破碎的煤岩体随着压实应力的增加将再次发生破碎。而同样基于离散元的数值模拟软件PFC自带的颗粒簇模型结合平行黏结力学模型能够模拟块体在压实过程中不断破碎的特征。基于此,本文采用PFC数值模拟进行破碎煤岩样压实的数值模拟研究。现阶段基于离散元模拟颗粒破碎主要包括两种方法,即基于颗粒黏结模型（BPM）和基于碎片替换法（FRM）的颗粒破碎模拟方法,两种方法具体的破碎过程如图1所示。基于BPM的颗粒破碎模拟方法能够一定程度上模拟颗粒破碎行为,能够较好的再现可碎颗粒集合体的复杂力学响应^[19-23],因此,本文采用颗粒黏结模型进行破碎煤岩样的力学模拟。颗粒黏结模型采用的本构模型为平行黏结模型,模型的强度主要取决于颗粒黏结强度以及接触强度。在应力超过黏结体的强度时,黏结体将发生剪切或者拉破坏,进而降低颗粒簇以及整个模型的强度,具体如图2所示,但不会影响其它区域黏结体的状态。

图  1  两种模拟颗粒再次破碎的方法^[19]

Figure  1.  Illustration of two particle breakage simulation methods

下载: 全尺寸图片 幻灯片

图  2  平行黏结模型力学参数及本构关系^[24]

Figure  2.  Micro-parameters and illustration of yielding process for micro-bonding^[24]

下载: 全尺寸图片 幻灯片

1.1   子颗粒粒径设计

采空区垮落带煤岩体在压实过程中逐步破碎,为了克服颗粒黏结模型子颗粒无法进一步破碎的问题,本文岩样子颗粒粒径根据Rosin-Rammler级配公式进行生成,具体的公式如下：

式中,D_pRR和n_RR这两个参数用来确定颗粒级配曲线,本文选择D_pRR=0.9722和n_RR=1.8185用来生成破碎岩样子颗粒粒径,参数由破碎岩样在加载至200 MPa时的粒径分布拟合获得。煤样子颗粒粒径则采用均匀粒径生成,平均粒径为0.5 mm。根据级配公式,采用FISH语言按照式（1）建立了相应级配的破碎煤岩样模型。

1.2   颗粒力学参数校准

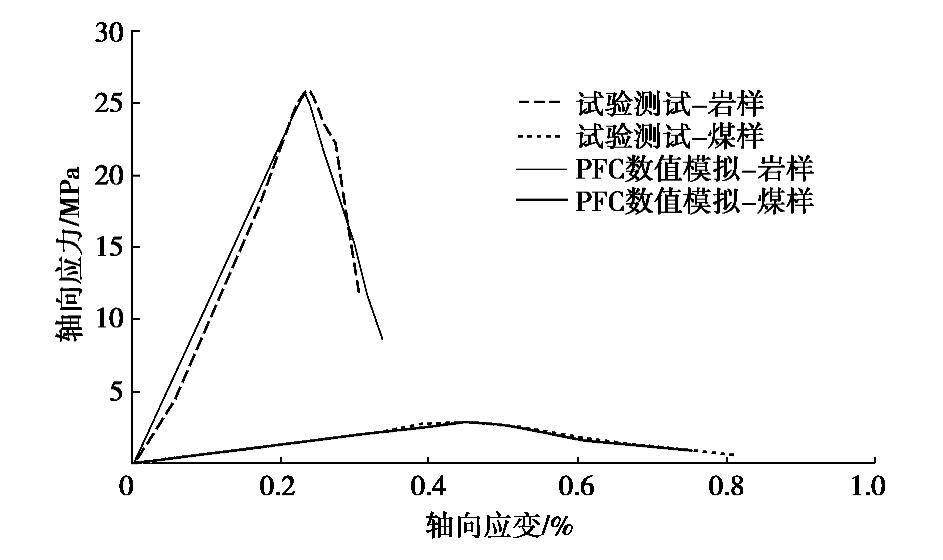
颗粒黏结模型的力学参数主要分为两类：控制颗粒弹性变形的体积模量和剪切模量以及控制颗粒黏结强度的内聚力、抗拉强度和内摩擦角。因此,在使用颗粒黏结模型分析前首先需要确定准确的力学参数。现阶段对于颗粒力学参数确定的方法主要是反演煤岩样的单轴抗压力学试验,本文经过反演后的煤样及岩样的力学参数见表1所示。针对单轴抗压强度的模拟结果与试验结果如图3所示。由图3可以看出,煤岩样的模拟应力应变曲线与实验室实测结果的匹配性非常好,表明所选参数的准确性。因此,本文所采用的模拟参数以及模型可以进一步用于采空区破碎煤岩样压实的数值模拟。

表  1  破碎煤岩样数值模拟参数

Table  1.  Numerical simulation parameters of breaking coal and rock mass

岩体类别	实验室测试结果			数值模拟参数
	E/GPa	抗拉强度/MPa	σc/MPa	pb_kn/(GPa·m-1)	pb_ks/(GPa·m-1)	pb_coh /MPa	pb_ten /MPa	pb_fa/(°)
煤体	0.65	0.27	2.83	1.00	0.50	0.5	1.0	20
岩体	10.21	2.89	25.91	15.8	12.6	8.97	6.59	38

下载: 导出CSV 

| 显示表格

图  3  煤岩样单轴压缩试验与数值模拟对比结果

Figure  3.  Comparison between laboratory and numerical simulation of coal and rock mass UCS tests

下载: 全尺寸图片 幻灯片

1.3   破碎煤岩样模型的建立

首先生成50 mm×100 mm的单轴压缩模型,模型内部颗粒级配与单轴压缩模型相同。然后随机从该试件中按照特定粒径选取颗粒簇直接进行分组,并设置选取的颗粒簇不存在重复区域。之后将未选择的部分直接删除,建立墙体,让选取的颗粒簇根据自身重力下降接触直至运算平衡,具体过程如图4所示。这样建模可以实现颗粒簇与颗粒簇之间不存在黏结力,能够完成模拟破碎煤岩样压缩试验,且能够模拟破碎煤岩样压缩过程中的进一步破碎。

图  4  破碎煤岩样模型生成步骤

Figure  4.  Generation steps of broken coal and rock samples

下载: 全尺寸图片 幻灯片

1.4   试验方案设计

在实际情况下,特别对于煤层开采产生的采空区而言,垮落带为直接顶岩体与工作面残余煤体的混合破碎煤岩体。垮落带内破碎岩体一般位于破碎煤体的上部,且比例要大于破碎煤体。因此,为了研究不同煤岩比例,不同煤岩样组合结构对破碎煤岩样的应力应变强度及其煤岩破碎特征的影响,本文在上文研究基础上,模拟了不同煤岩比例、不同煤岩相对位置的压缩试验。破碎煤岩样的比例见表2。其中不同比例的破碎煤岩组合体的组合结构为上部破碎岩体,下部破碎煤体,具体如图5所示,其中不同煤岩位置的Z2破碎煤岩样完全随机混合在一起,具体如图5（b）所示。

表  2  破碎煤岩样组合模型煤岩比例

Table  2.  Coal-rock ratio of broken coal and rock sample model

岩石类别	C1	R1	Z1	Z2	Z3	Z4
煤体	21	0	9	9	6	3
岩体	0	21	12	12	15	18

下载: 导出CSV 

| 显示表格

图  5  煤岩颗粒组合结构

Figure  5.  Composite structure of broken coal and rock samples

下载: 全尺寸图片 幻灯片

2.   模拟结果分析

2.1   应力应变曲线

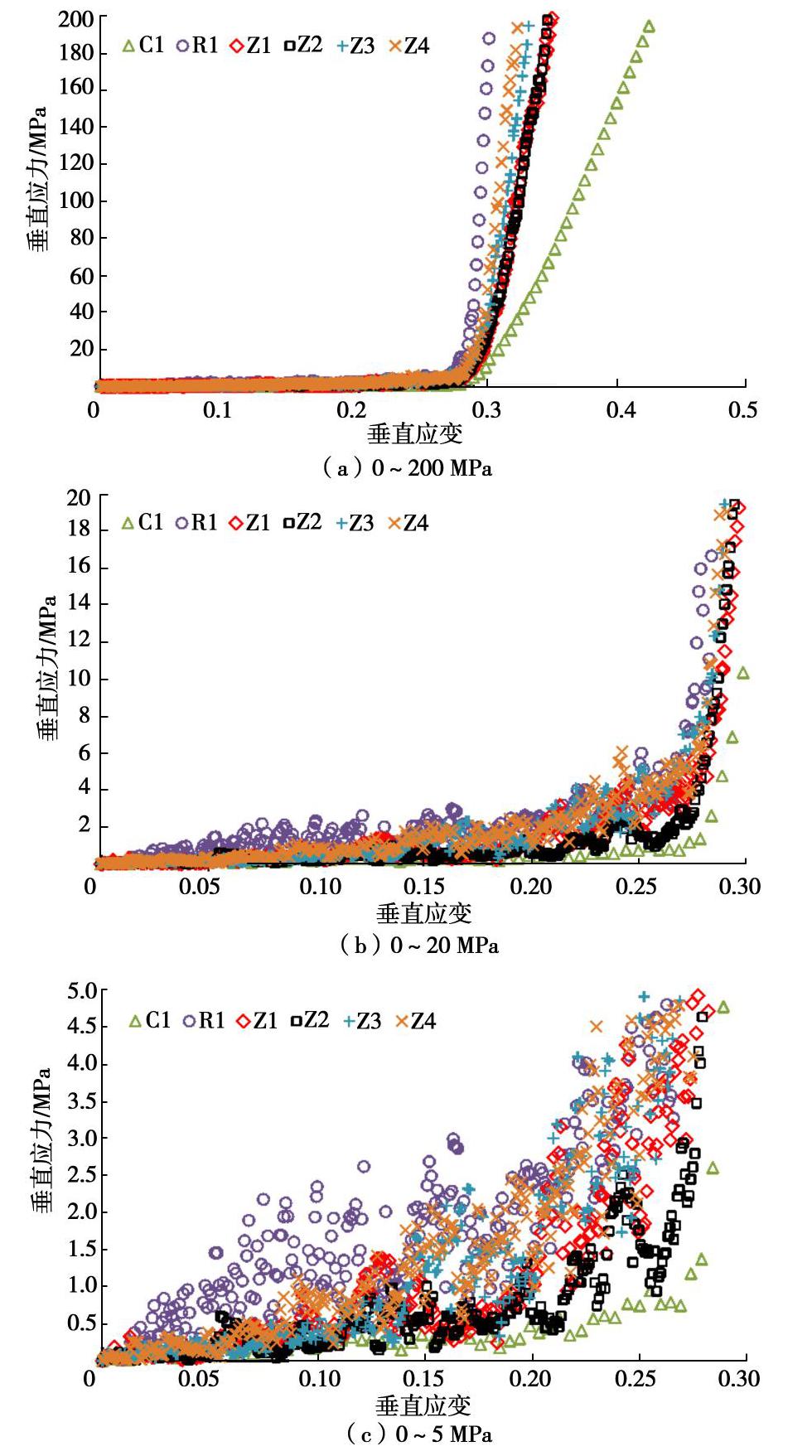
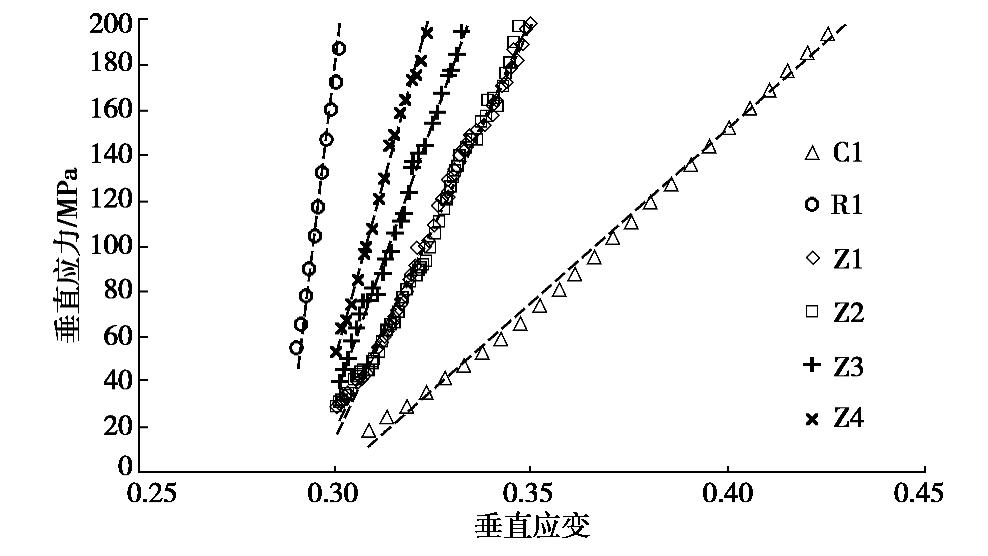
由于破碎煤岩样在生成和自重压实过程中会出现较大孔隙结构,导致初始孔隙率相差较大。为了解决这一问题,本文实时监测上压板的应力,当压板应力出现0时,则在这之前的应力数据不计入,认为之前破碎煤岩并未均匀压实。而垂直应变则采用之后的垂直位移比上此时破碎煤岩样的高度。本试验的加载速度与单轴压缩的加载速度一致,为0.002 mm/s。为了更全面的观测应力应变情况,本文破碎煤岩样加载至200 MPa时停止加载。这要高于实际情况下采空区的压实应力（埋深800 m,压实应力将近20 MPa）。不同煤岩样比例的压实应力应变曲线如图6所示。

图  6  不同煤岩组合比例模型应力应变曲线

Figure  6.  Stress-strain curves of broken coal and rock samples with different strengths

下载: 全尺寸图片 幻灯片

由图6可以看出,不同破碎煤岩样压实曲线在低应力段呈现明显指数式上升,在应变达到某一值后,应力应变曲线基本上呈线性增长。不同组合比例煤岩样的应变曲线存在明显的区别,破碎煤岩样中岩样比例越大,在直线段的应力应变曲线斜率越大。同时,对比煤岩比例相同,但组合结构不同的Z1与Z2可以看出在直线段的斜率基本相同,这表明直线段斜率并不受煤岩组合结构的影响,主要受煤岩组合比例的影响。对于低应力阶段的应力应变曲线,岩样比例的升高使得应力应变曲线更加靠上,但曲线的波动更为明显。

为了进一步获得应力应变曲线的分界点对应的应变以及应力应变曲线对应的公式,本文根据文献中关于采空区破碎煤岩体压实应力及应变的公式,对模拟的应力应变曲线进一步分析。针对长壁工作面垮落带压实过程中的应力应变压实特征,Yavuz^[25]提出了定量描述采空区压实应力应变的公式：

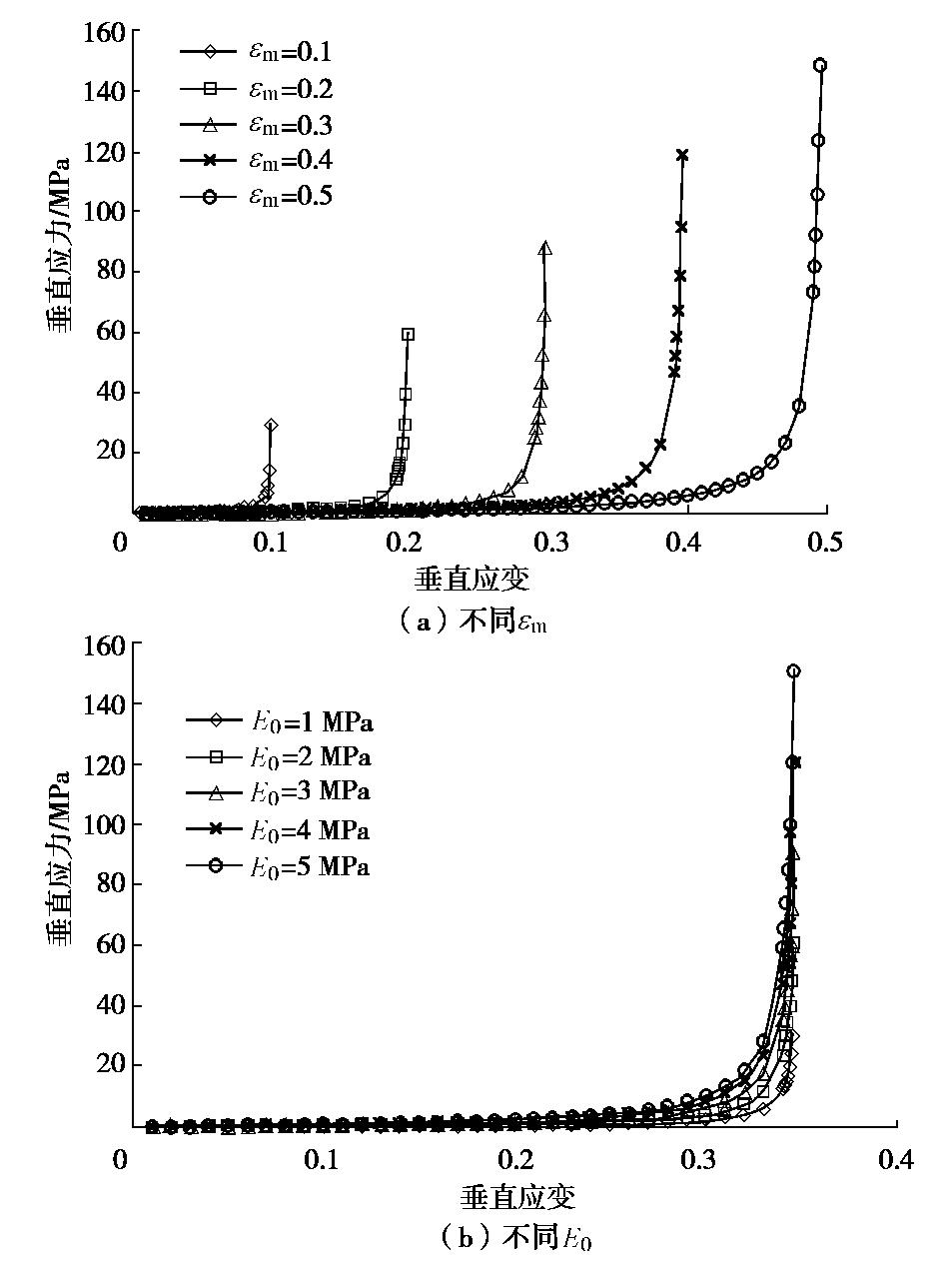
式中 ${\sigma }_{\text{c}}$为压实应力（MPa）；E₀为破碎煤岩样初始弹性模量（MPa）；$\epsilon$为当前垂直应变；${\epsilon }_{\text{m}}$为最大垂直应变,${\phi }_{\text{m}}$是模型的总孔隙率,${\phi }_{\text{p}}$为单颗粒的孔隙率。由式（2）可以看出,影响应力应变曲线的主要参数是E₀以及${\epsilon }_{\text{m}}$,图7（a）,（b）分别为E₀控制在3 MPa时,不同${\epsilon }_{\text{m}}$以及${\epsilon }_{\text{m}}$控制在0.35,不同E₀条件下的应力应变曲线。

图  7  最大应变ε_m与E₀对应力应变曲线的影响

Figure  7.  Effects of ε_m and E₀ on stress-strain curves

下载: 全尺寸图片 幻灯片

由图7可以看出,最大垂直应变控制曲线的变化趋势,而初始弹性模量则只影响应力的大小,且在应变靠近最大垂直应变时,初始弹性模量对应力升高的贡献要明显小于应变。因此,最大垂直应变对破碎煤样的应力应变曲线起控制作用。采用式（2）对不同组和比例破碎煤样的应力应变曲线进行拟合,拟合结果见表3,应力应变曲线的拟合段为应变0至计算获得的${\epsilon }_{\text{m}}$范围内。

表  3  破碎煤岩样应力应变曲线拟合结果

Table  3.  Fitting results of stress-strain curves of broken coal and rock samples

编号	C1	R1	Z1	Z2	Z3	Z4
实测φ0	0.401	0.405	0.405	0.405	0.405	0.405
拟合${\epsilon }_{\text{m}}$	0.301	0.295	0.302	0.302	0.302	0.303
拟合E0	0.565	2.56	1.58	1.48	1.99	2.29
R2	0.981	0.978	0.994	0.985	0.995	0.989

下载: 导出CSV 

| 显示表格

由表3拟合参数可以看出,除了岩石的拟合${\epsilon }_{\text{m}}$相对较小以为,其他模型基本相等。这进一步说明煤岩比例与组合结构对${\epsilon }_{\text{m}}$影响较小。除此之外,随着破碎煤岩样中岩样的组合比例升高,拟合E₀值也逐渐升高,这主要由于岩样比例的升高促使模型整体的弹性模量增加。在应变超过最大垂直应变后,破碎煤岩样的应力应变曲线呈现明显的线性特征,具体不同破碎煤岩组合比例的应力应变曲线的拟合结果如图8以及表4所示。

图  8  不同煤岩组合比例模型直线段应力应变曲线

Figure  8.  Stress-strain curves in linear section of broken coal and rock samples with different coal-rock ratios

下载: 全尺寸图片 幻灯片

表  4  不同煤岩组合比例直线段应力应变曲线拟合结果

Table  4.  Fitting results of stress-strain curves in linear section of broken coal and rock samples

编号	C1	R1	Z1	Z2	Z3	Z4
拟合斜率	1.54	14.12	3.62	3.60	4.96	6.29
R2	0.989	0.991	0.992	0.989	0.992	0.990

下载: 导出CSV 

| 显示表格

由图8及表4可以看出,在应变超过${\epsilon }_{\text{m}}$后,应力应变的线性相关性基本在0.99左右。同时,破碎煤岩样中岩样比例越大,直线段斜率也就越大。具有同样煤岩比例与不同组合结构的Z1与Z2的斜率基本相等。这说明直线段的斜率只与煤岩组合比例有关,进一步可以说明直线段斜率与初始颗粒的强度有关。

2.2   破碎结构分布特征

在定量分析煤岩样破碎特征中,常用的颗粒破碎指标有B_e及B_g^[26]。但这些指标基本上是基于整个模型的破碎指标。由于本文采用的数值模拟进行计算,数值模拟的优势是能够定位到每个初始破碎煤岩样的破碎情况,本文的破碎率的计算方法为

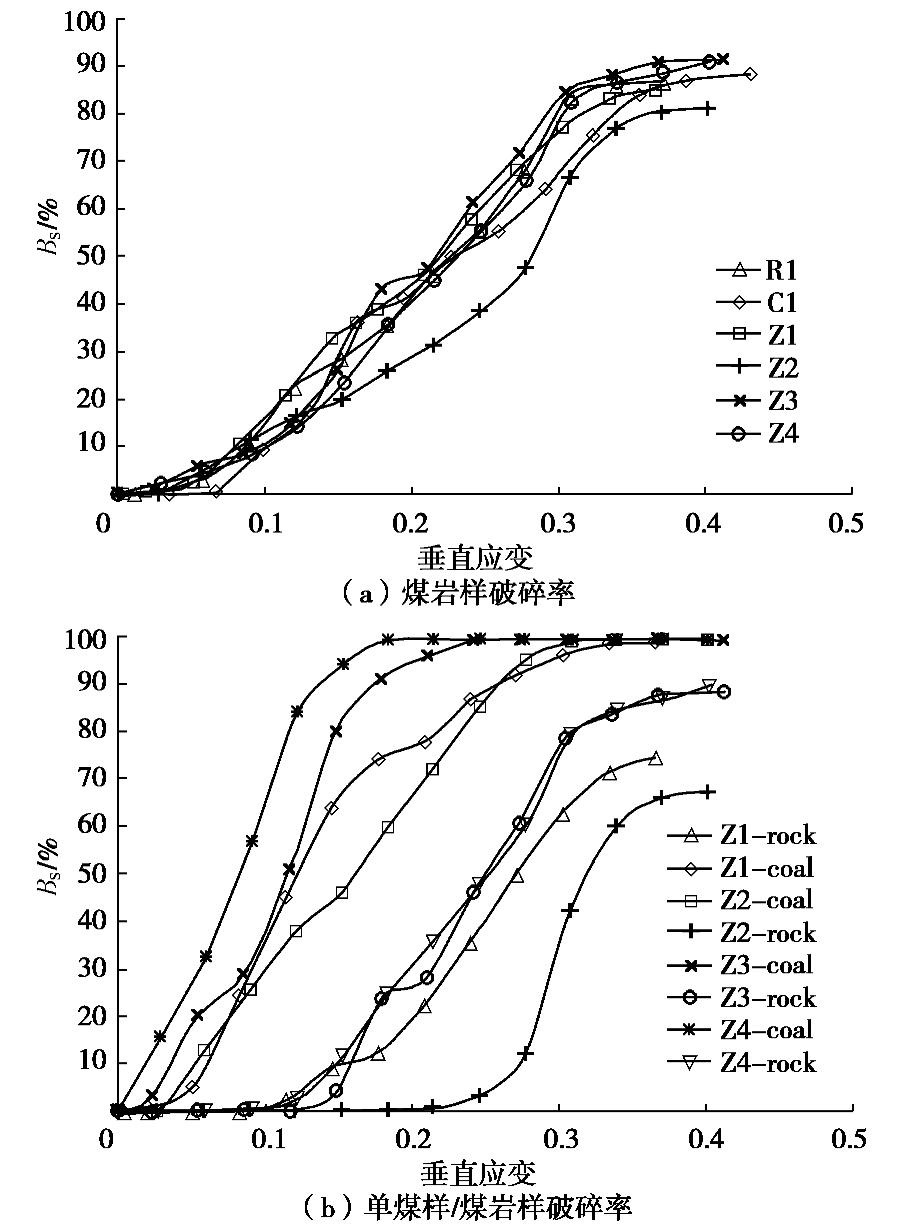
式中,S_max是煤岩样破碎后最大的颗粒簇粒径,S_I是破碎煤岩样原始粒径,根据式（4）,监测了模型中21个破碎煤岩样每个颗粒的破碎情况,分别取平均值获得模型的整体破碎率,若模型为煤岩组合颗粒,则再分别取破碎煤样平均值以及破碎岩样平均值,具体如图9所示。

图  9  不同煤岩比例破碎煤岩样模型破碎率–应变曲线

Figure  9.  Evolution of B_s in BCRSs with different coal-rock ratios

下载: 全尺寸图片 幻灯片

由图9可以看出,不同煤岩比例的破碎煤岩样破碎率随着垂直应变的增加,变化趋势基本一致,呈明显的S型分布。在应变达到${\epsilon }_{\text{m}}$后,破碎率逐渐趋于稳定。这表明煤岩样中煤岩比例对破碎率–垂直应变曲线特征影响不大。但其中Z2的破碎率应变曲线要明显低于其他几条曲线,特别是与其同样组合比例的Z1曲线。这表明当煤岩样比例相同时,煤岩样组合结构的不同对破碎煤岩样的破碎率产生明显的影响。而对于同一个破碎煤岩样,内部煤样的破碎率要明显大于岩样的破碎率。在组合结构情况相同的时候,煤样的比例越小,破碎煤样的破碎率越大,岩样的破碎率越小。而对于煤岩比例相同的Z1与Z2,Z2中岩样的破碎率要明显低于Z1的破碎率。这主要由于优先破碎的煤样对周围破碎岩样形成卸力缓冲作用,能够在岩样附近形成一个保护圈。具体如图10所示,根据PFC自带的fragment命令绘制出Z1与Z2破碎模型在加载过程中的破碎特征,图中将最小单颗粒直接隐去。

图  10  不同组合煤岩样结构加载破碎情况

Figure  10.  Particle fragmentation during loading process with different composite structures

下载: 全尺寸图片 幻灯片

由图10可以看出,随着应变的增加,在应变达到9%左右,煤样颗粒簇已发生明显的破碎,岩样则基本完好。随着应变的继续增加,煤样破碎更加严重,在应变达到15%左右时,基本不存在完整的破碎煤样,而Z1与Z2的岩样则产生了明显的区别。Z1中岩样已经开始出现破碎情况,而Z2岩样基本上没有破碎情况。当应变达到24%左右时,Z1破碎煤岩样靠近上部的岩样破碎已十分严重,只有中部以及靠近破碎煤样的岩样颗粒完整性较好。而Z2破碎煤岩样在应变达到24.61%时,基本上仍未开始破碎,只有位于顶部的岩样出现较小的破碎。当应变超过${\epsilon }_{\text{m}}$时,Z1与Z2破碎煤岩样中的岩样均发生大规模的破碎,但Z2破碎煤岩样的大颗粒岩样数目以及整体破碎率仍要明显小于Z1。而从破碎煤岩样Z1的破碎情况可以看出,在煤岩交界处的岩样完整性要优于上部岩样。综合Z1与Z2破碎煤岩样在加载过程中的破碎情况可以看出,在破碎煤岩样中煤样优于岩样破碎,煤样的破碎使得应力释放,从而造成周边岩样以及整个模型的应力减小。除此之外,煤样的破碎对周边岩样具有让压填充作用,降低岩样破碎率,这由Z2破碎煤岩样以及Z1煤岩交界处的岩样可以看出。

2.3   破碎率模型建立

由图9可以看出,破碎煤岩样的破碎率与应变大体呈S型曲线分布。运用S型曲线函数chapman函数,假设a小于等于100,当应变等于0时,破碎率等于0,获得对应的拟合函数公式（5）,该函数的破碎率在（0～a）%之间,利用该函数对上述破碎煤岩样破碎率进行拟合,具体拟合结果见表5。

表  5  不同煤岩组合比例模型破碎率–应变拟合结果

Table  5.  Breaking rate-strain fitting results of broken coal and rock samples with different coal-rock ratios

类别	a	b	c	(lnc)/b	R2
C1	100	8.2142	3.9779	0.168094	0.9923
R1	100	7.0472	2.3958	0.123981	0.9682
Z1	100	8.1576	3.3146	0.146898	0.9951
Z2	100	7.5754	4.5457	0.199881	0.9686
Z3	100	10.6665	5.6772	0.162795	0.9931
Z4	100	10.3432	6.3497	0.178708	0.9915
Z1煤	99.9503	14.5229	3.8591	0.092987	0.9976
Z1岩	98.0438	10.8329	12.4752	0.23297	0.9964
Z2煤	100	12.6659	4.0291	0.110023	0.9853
Z2岩	68.3351	41.7328	180502.0101	0.290024	0.9987
Z3煤	99.9998	21.0125	5.9714	0.085044	0.9878
Z3岩	97.1357	14.4950	22.5708	0.215016	0.9935
Z4煤	99.9999	23.7269	3.7703	0.055935	0.9900
Z4岩	100	12.5439	14.2782	0.211954	0.9958

下载: 导出CSV 

| 显示表格

由表5可以看出,除了Z2岩样的曲线的a值只有68.3351,远小于合理值100,表明Z2试件中岩样的破碎率要远小于其他模型。而对于不同煤岩比例的拟合参数可以看出,很难直接对比判断破碎率的差别,这主要由于不同组合破碎煤岩的破碎率–应变曲线相差不大（图9）。为了进一步量化对比破碎率曲线的演化特征,本文结合S曲线单调递增,且增速先增大后减小的特点,假设在破碎率增速达到最大值时对应的应变越小,其越容易破碎。根据计算可得破碎率最大增速对应的应变为x=(lnc)/b,具体计算结果见表5。由表可以看出,对于单一介质而言,破碎煤样颗粒的破碎率增速要略大于破碎岩样,这与破碎煤岩样中煤样的破碎情况相差较大。这主要由于即使破碎煤样强度要小于破碎岩样,但相同应变条件下岩样的应力更大。但对于组合破碎煤岩样而言,破碎煤岩样所受应力基本相等。除此之外,由于煤样的优先破碎卸压,降低了岩样的应力,使得岩样的破碎率降低。纵观模型的整体破碎率演化特征可以看出,其增速最大值对应的应变相差并不大,整体范围在0.123～0.199,这由图9同样可以看出,在组合结构相同的情况下,基本上是煤样比例越高,破碎率增速越快。而对于组合煤岩样中的岩样与煤样的破碎率演化特征则出现明显的区别。煤样的破碎率增速最大值对应的应变要远小于岩样,这表明煤样要明显先与岩样破碎,且煤样比例越小,煤样破碎率升高越快。

3.   结论

（1）数值反演了煤岩样单轴抗压试验,获得了能够匹配煤岩样的球体及接触参数。创新性的利用PFC自带的颗粒黏结模型提出了垮落带煤岩样压实再破碎的模拟方法,同时给出了岩样模拟过程中最小颗粒粒径的级配方程,实现了垮落带破碎煤岩样压实过程中的破碎模拟。

（2）破碎煤岩样在压实过程中的应力应变曲线以最大垂直应变${\epsilon }_{\text{m}}$分为两段,第一段的压实应力随着应变的增加呈指数式增加,并且符合传统的采空区压实应力应变演化曲线,同时拟合给出了指数段应力计算公式。在应变超过${\epsilon }_{\text{m}}$后,应力呈线性增加,直线段斜率与破碎煤岩样中岩样的比例呈正比,即岩样比例越大,直线段斜率越大,但破碎煤岩样的岩样比例对${\epsilon }_{\text{m}}$基本没有影响。

（3）在应变小于${\epsilon }_{\text{m}}$,破碎煤岩样在加载过程中不断发生破碎导致应力呈锯齿状上升,且岩样强度越大,应力波动越剧烈。进一步提出了颗粒破碎率B_s用于描述破碎煤岩样在压实过程中的破碎情况。得出模型破碎率随着应变的增加呈S型上升,在应变大于${\epsilon }_{\text{m}}$后,煤岩样基本不再发生破碎。煤岩样组合比例对其破碎率–应变曲线影响较小。但在相同煤岩比例下,煤岩组合结构不同对模型的破碎率影响较大。在破碎煤岩样加载过程中,破碎煤样优先于岩样破碎,进而对其周边破碎岩样产生卸压充填作用,大幅度降低了岩样的破碎率。

（4）给出了破碎煤岩样破碎率–应变拟合模型,得出了破碎煤岩样破碎率–应变公式。通过破碎率公式提出破碎率增长最大速度对应的应变值定量分析了煤岩比例对破碎率的影响。在相同组合结构情况下,煤样的比例越高,整体煤岩样破碎率增长越快。而对于组合破碎煤样而言,煤岩样中煤样的比例越低,煤样的破碎率增加越快。

4.   展望

本文采用离散元数值模拟研究了垮落带破碎煤岩样在压实过程中的应力、孔隙结构及破碎演化特征,分析了煤岩组合比例及组合结构对煤岩组合颗粒破碎压实特征的影响。但在实际情况下,采空区破碎煤岩体的形状并不是球体,尺寸也要远远大于模拟尺寸,且各级尺寸均存在。很显然,本文模拟过程中并未考虑破碎煤岩样的形状和大小,这需要在本文模拟的基础上进一步提升^[27]。除此之外,加载方式对颗粒破碎情况同样存在影响^[28],采空区垮落带应力条件并不是单一的均匀加载^[8],采动应力是非均匀的加载方式,而研究这种应力状态下的破碎情况也将是下一步的工作。