0.   引言

地震动强度参数（intensity measure,IM）是表征地震动强度的指标,包含着大量和地震动特性相关的信息。在结构抗震分析中,不同地震动强度参数在评估同一场地相同结构的地震响应时存在较大的差异性。因此如何根据合理的地震动强度参数来选择和调整实测地震记录进行结构地震动力响应分析,一直是结构工程抗震研究所面临的一个难点。

已有研究表明,当采用合适的IM和结构地震响应指标（engineering demand parameter,EDP）时,可以减少结构动力响应分析计算结果的离散性,提高计算效率,因此,选用合理的地震动强度参数对结构动力响应分析至关重要。已有研究多用基于有效性（efficiency）和充分性（sufficiency）两方面来衡量所选用的IM指标在评价结构地震响应的适用性。Riddell^[1]选取单自由度（single degree of freedom, SDOF）系统为研究对象,采用90条地震动记录,对23个地震动强度参数和4个结构地震响应变量进行研究,结果表明：与地震动峰值位移相关的地震动强度参数对长周期结构的地震响应有显著影响。Padgett等^[2]选取多跨简支钢梁桥为研究对象,基于人工合成地震记录和真实地震记录进行了桥梁结构地震响应研究,研究结果表明,地表峰值加速度（PGA）和基本周期对应的加速度反应谱,S_a(T₁,5%),是合成地震动记录中效果最佳的,而累积绝对速度（CAV）是所选真实地震动中最佳的。叶列平等^[3]选取60条原始地震动,采用33个地震动强度参数,基于弹塑性SDOF系统和多自由度（MDOF）系统进行了结构的非线性时程分析,结合结构的代表性地震响应指标,研究了不同的地震动强度参数与不同结构地震响应指标的相关性,发现采用单一地震动指标不适合作为结构地震响应的唯一标准,应采用复杂的多参数指标对结构地震响应进行合理评价。

增量动力分析（incremental dynamic analysis, IDA）方法是近年来逐渐发展起来的一种动力非线性分析方法,其分析结果可以反映出结构随地震强度增加的损伤演化过程^[4]。基于IDA的结构地震响应分析方法已成为结构抗震性能评估常用的方法之一,但该方法在选择地震记录时缺乏统一标准,且由于影响地震动的参数很多,不同的地震动强度参数对结构弹塑性地震响应的影响十分复杂,同时在现有研究中,人们多关注于地震动强度指标与地上结构地震响应指标的相关性,对于地上结构有关地震动强度参数的选取相关学者做了大量的研究,提供了不少参考指标,而对于地铁地下车站结构的地震响应与地震动强度参数的研究有限。基于此,本文以日本大开地铁车站为原型,选取22个地震动强度参数,考虑近场地震动输入的不确定性,通过增量动力分析（IDA）方法对土-结构体系进行非线性动力时程分析,从有效性（efficiency）、实用性（practicality）和效益性（proficiency）3方面对所选地震动强度参数进行综合评估。本文对地铁地下车站结构抗震分析选取合理的地震动强度参数提供一定参考意义。

1.   地震动强度参数选择

合理的地震动强度参数IM是预测结构响应和评价结构地震功能可恢复能力的重要基础,应能反映结构地震响应指标或损伤指标。目前常用的地震动强度参数有与结构独立的参数,如累计绝对速度（CAV）、Arias强度（AI）、均方根加速度a_rms、PGA、地表峰值速度PGV等；也有与结构相关参数,如谱加速度S_a、谱速度S_v、谱位移S_d等两类。由于地震动输入具有很强的随机性,导致结构的结果分析在很大程度上依赖于地震动输入,采用不同的地震动强度参数所得到的分析结果往往不尽相同。

为了确定地震激励下结构反应的评估而要选择最佳的IM,本文在此共选取了22个地震动参数指标,如表1所示,分为加速度型指标、速度型指标、位移型指标和谱相关型指标4种。在表1中,a(t)是地表地震动的加速度时程,v(t)是地表地震动的速度时程,d(t)是地表地震动的位移时程,g是重力加速度,t_f是地震动持时,t_d是地震动有效强震持时,其中t_d=t₂-t₁,t₁和t₂分别为5%和95%AI值对应的时刻,T₁是土-地下结构相互作用体系的基本周期。

表  1  本文选用的地震动强度参数

Table  1.  Intensity measures used in analysis

类别	编号	名称	定义	类别	编号	名称	定义
加速度相关型	1	峰值加速度	PGA=max|a(t)|	谱相关型	13	结构基本周期谱加速度	$S_a(T_1\text{, }\xi =0.05)$
	2	Arias强度	$\text{AI}=\frac{\text{π}}{2g}{\displaystyle {\int }_0^{t_f}{a}^2(\text{t})}d\text{t}$		14	结构基本周期谱速度	$S_v(T_{\text{1}}\text{, }\xi =0.05)$
	3	累计绝对速度	$CAV={\displaystyle {\int }_0^{{\text{t}}_f}\left|\text{a}(\text{t})\right|}d\text{t}$		15	结构基本周期谱位移	$S_d(T_1\text{, }\xi =0.05)$
	4	均方根加速度	$a_{rms}=\sqrt{\frac{1}{t_d}{\displaystyle {\int }_{{\text{t}}_1}^{{\text{t}}_2}{a}^2(t)}\text{d}t}$		16	加速度谱强度	$ASI={\displaystyle {\int }_{0.1}^{0.5}{\text{S}}_a(\text{T},5\%)}d\text{T}$
	5	复合加速度	${\text{I}}_a=PGA\cdot {\text{t}}_d^{1/3}$		17	速度谱强度	$VSI={\displaystyle {\int }_{0.1}^{2.5}{\text{S}}_V(\text{T},5\%)}d\text{T}$
	6	特征强度	${\text{I}}_c={({\text{a}}_{rms})}^{3/2}\sqrt{{\text{t}}_d}$		18	位移谱强度	$DSI={\displaystyle {\int }_{2.0}^{5.0}{\text{S}}_d(\text{T},5\%)}d\text{T}$
	7	加速度平方积分	${\text{a}}_{sq}={\displaystyle {\int }_0^{{\text{t}}_f}{\text{a}}^2(\text{t})}d\text{t}$
速度相关型	8	峰值速度	PGV=max|v(t)|	位移相关型	19	峰值位移	PGD=max|d(t)|
	9	均方根速度	${\text{v}}_{rms}=\sqrt{\frac{1}{{\text{t}}_d}{\displaystyle {\int }_{{\text{t}}_1}^{{\text{t}}_2}{\text{v}}^2(\text{t})}d\text{t}}$		20	均方根位移	${\text{d}}_{rms}=\sqrt{\frac{1}{{\text{t}}_d}{\displaystyle {\int }_{{\text{t}}_1}^{{\text{t}}_2}{\text{d}}^2(\text{t})}d\text{t}}$
	10	速度平方积分	${\text{v}}_{sq}={\displaystyle {\int }_0^{{\text{t}}_f}{\text{v}}^2(\text{t})}d\text{t}$		21	位移平方积分	${\text{d}}_{sq}={\displaystyle {\int }_0^{{\text{t}}_{\text{f}}}{\text{d}}^2(\text{t})}d\text{t}$
	11	复合速度	${\text{I}}_v=PG{V}^{2/3}\cdot {\text{t}}_d^{1/3}$		22	复合位移	${\text{I}}_d=PGD\cdot {\text{t}}_d^{1/3}$
	12	Fajfar强度	$FI=PGV\cdot {\text{t}}_d^{0.25}$

下载: 导出CSV 

| 显示表格

2.   计算模型与地震动记录选取

2.1   计算模型与参数

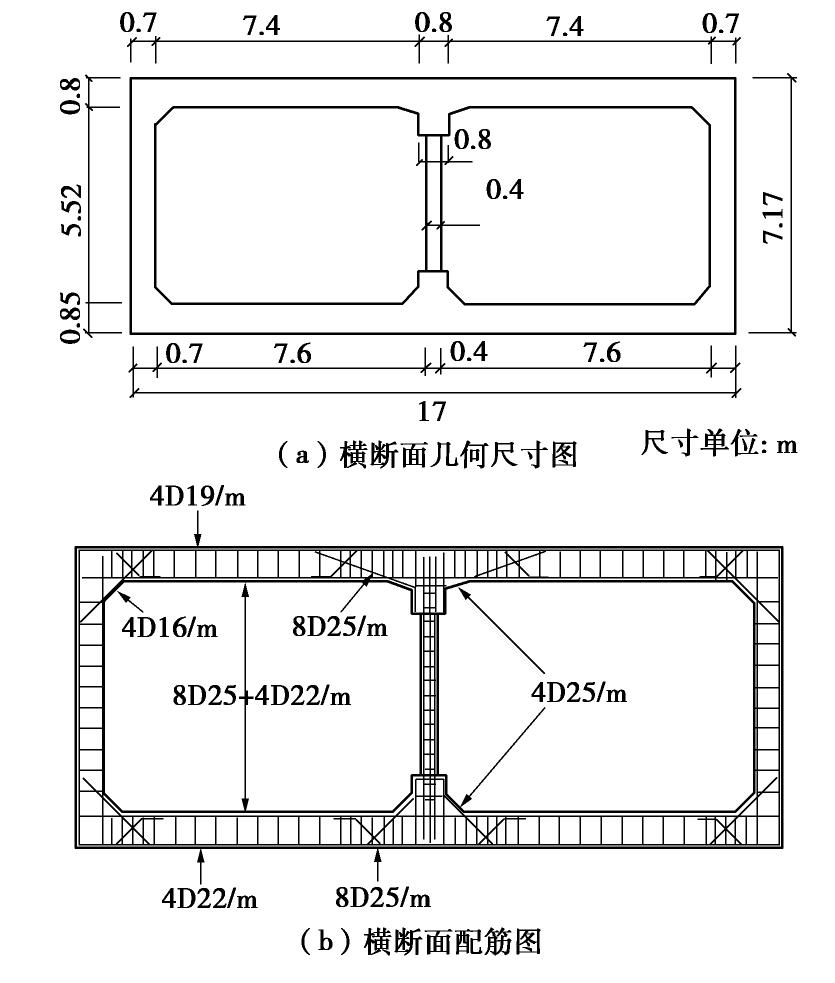
本文选取1995年阪神地震中遭到严重破坏的大开车站进行实例分析,其横断面尺寸和配筋如图1所示^[5]。

图  1  大开车站横断面详图

Figure  1.  Cross-sectional details of Daikai station

下载: 全尺寸图片 幻灯片

大开车站结构埋深4.8 m,所处场地主要由全新世砂土和更新世黏土组成,该场地的土层情况及其物理力学参数如表2所示。经计算该场地土层等效剪切波速为v_se=192 m/s,根据中国《城市轨道交通结构抗震设 计规范》（GB 50909—2014）^[6]对场地类别的划分,该场地属于Ⅱ类场地,相当于日本抗震规范的中硬土场地。虽然中国的抗震规范依靠场地覆盖土层厚度和等效剪切波速来进行场地划分,而日本规范则依据场地特征周期T_g^[7],但究其根本均依赖场地等效剪切波速,因此本文分析结果对国内工程也具有一定参考价值。

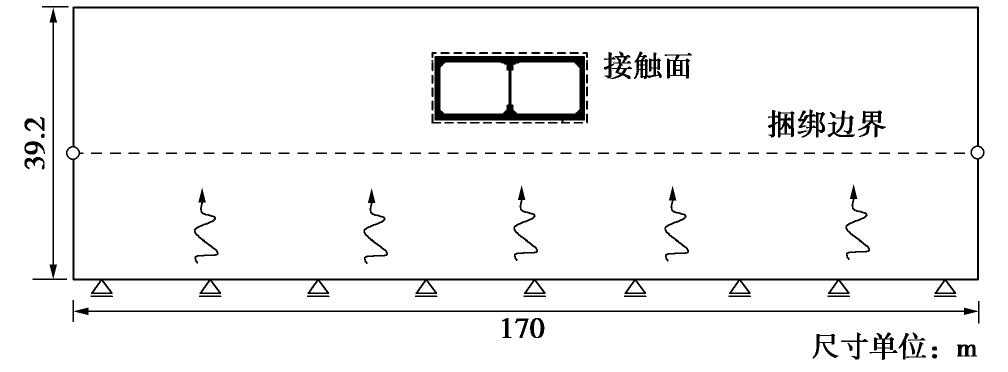
表  2  土层的性质

Table  2.  Properties of soils

土层信息	土层深度/m	密度/(kg·m-3)	剪切波速/(m·s-1)	泊松比	黏聚力/kPa	内摩擦角/(°)
人工填土	0~1.0	1900	140	0.33	20	15
全新世砂土	1.0~5.1	1900	140	0.32	1	40
全新世砂土	5.1~8.3	1900	170	0.32	1	40
更新世黏土	8.3~11.4	1900	190	0.40	30	20
更新世黏土	11.4~17.2	1900	240	0.30	30	20
更新世砂土	17.2~39.2	2000	330	0.26	1	40

下载: 导出CSV 

| 显示表格

采用通用有限元软件ABAQUS对大开车站横断面进行地震反应分析,土-结构系统的有限元模型如图2所示。对本文所建土-结构系统有限元模型进行模态分析,得到土-地下结构模型体系的基本周期T₁=0.51 s。建模时结构采用两节点线性梁单元（B21）,周围土体采用四节点二次减缩积分平面应变单元（CPE4R）。土体采用Drucker-Prager弹塑性模型,该模型可以用来模拟土、岩石等摩擦型材料,可考虑材料各向同性硬化或软化以及材料阻尼效应,可以较好的描述岩土介质的力学行为^[8]。结构采用C30混凝土材料,弹性模量取2.4×10⁴ MPa,密度取为2.5×10³ kg/m³。在二维平面应变分析时,考虑到中柱在车站纵向是等间距（3.5 m）分布,为保证等效前后截面的抗弯刚度、抗剪刚度、抗压刚度及截面质量均不改变,故等效后的中柱弹性模量取7.0×10³ MPa,密度取为7.14×10² kg/m³。为了尽可能消除边界效应对地下结构地震反应的影响,场地的计算宽度应取地铁车站结构宽度的5倍以上为宜^[9],本文的模型地基的宽度取170 m,工程基岩地面位于地下39.2 m。模型的底部在竖直方向进行约束,在模型两侧边设置捆绑边界（equal-displacement boundary）^[10],强制侧面边界上所对应点的位移相同,该边界适用于成层分布土层的弹塑性分析问题,并把地震动记录作为平面剪切波在土体底部输入。考虑土-结构之间黏结、滑移和脱开,采用接触面对法模拟土和结构之间的接触效应,接触面法向采用“硬接触”,切向接触采用库仑摩擦模型,摩擦系数µ为0.4^[11]。土体按照数值模拟精度要求离散,单元网格尺寸小于1/10～1/8波长^[12],在这里取土体单元网格尺寸为1 m。

图  2  土-结构相互作用有限元模型

Figure  2.  Finite element model for soil-structure interaction system

下载: 全尺寸图片 幻灯片

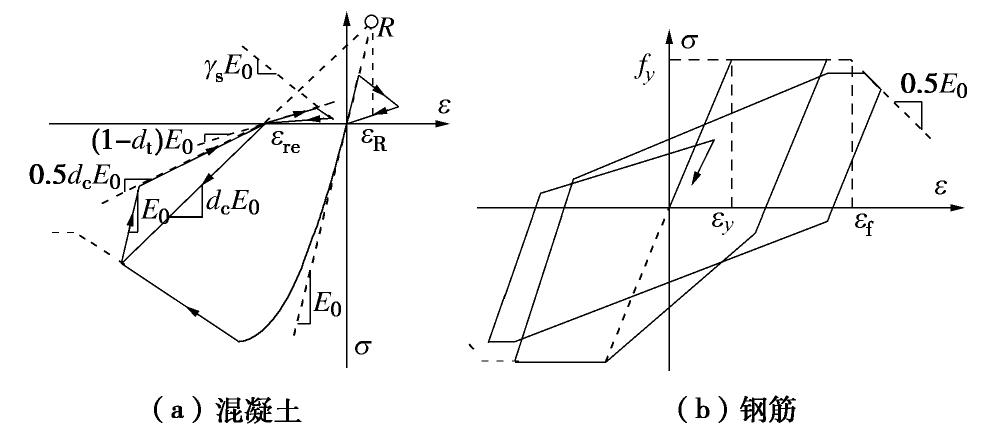
考虑到结构的非线性,在此使用基于ABAQUS开发的一组材料单轴滞回本构模型PQ-Fiber^[13],主要用于在钢筋混凝土结构、钢结构等的弹塑性时程分析中定义杆系结构的材料本构单元。采用ABAQUS中的铁木辛柯梁单元B21,通过*rebar关键字在梁单元中插入“钢筋”,可以模拟钢筋的力学行为。其中,钢筋采用考虑随动硬化弹塑性本构的USteel02模型,混凝土材料本构选用PQ-Fiber截面纤维模型中的混凝土模型UConcrete02,该模型能够考虑混凝土的抗拉强度。混凝土和钢筋非线性本构关系如图3所示,材料参数如表3所示。

图  3  混凝土和钢筋非线性本构关系

Figure  3.  Nonlinear constitutive models for concrete and reinforcement

下载: 全尺寸图片 幻灯片

表  3  钢筋及混凝土材料参数

Table  3.  Material parameters of steel rebar and concrete

材料	密度ρ/(kg·m-3)	弹性模量E/GPa	泊松比$\nu$	屈服强度fy/MPa	轴心受压强度fc0/MPa	轴心受拉强度ft/MPa	极限受压强度fu/MPa	峰值压应变εc0	极限压应变εcu
混凝土	2500	24	0.15	—	14.3	2.1	12.2	0.002	0.0038
钢筋	7800	200	0.3	235	—	—	—	—	—

下载: 导出CSV 

| 显示表格

依据上述参数建立土-结构模型,采用阪神地震中神户气象台和神户大学的时程记录作为输入地震动,为了证明数值模拟的合理性,将所得结果与李洋^[14]和杜修力等^[15]两者的计算分析结果进行了对比,如表4所示,当相同的土和结构模型采用不同的本构模型时,所得结果会有偏差,但是误差不大,证明本文所用模型的合理性。

表  4  计算结果对比

Table  4.  Comparison of calculated results

类别	本构模型		输入地震动	层间位移角/%	误差/%	峰值剪应力/(kN·m-1)	误差/%
	土体	结构
李洋(3D)	Mohr-Coulomb 模型	弹塑性模型	神户大学	1.00	—	250	—
本文结果(2D)	Drucker-Prager模型	PQ-Fiber模型		0.90	10.0	211	15.6
杜修力等(3D)	弹塑性本构 模型	弹塑性模型	神户气象台	1.20	—	283	—
本文结果(2D)	Drucker-Prager模型	PQ-Fiber 模型		1.00	16.7	269	4.95

下载: 导出CSV 

| 显示表格

2.2   地震动记录选取

鉴于地震动特性是影响地下结构地震反应的关键因素^[16],不同特性的地震动会引起结构不同的破坏现象,同时根据对已有的近场地震动的研究表明：近场地震动与远场地震动的特性有很大差异,近场地震动下的结构相对于远场地震动的结构破坏更为严重,且近场地震动是地震造成的地面运动中最复杂的,与断层破裂过程、滑动方向及速度、断层面上位错的发展过程等众多因素相关^[17]。近年来发生的近场地震动,如美国的Northridge地震（1994）、日本的Kobe地震（1995）、台湾Chi-Chi地震（1999）、台湾花莲地震（2018）等都证实了结构在这种类型的地震动下将会产生更严重的破坏。本文从PEER强震记录数据库^[18]（http://peer.Berkeley.edu/nga）中根据矩震级大于6.5级,震中距小于10 km选取了6组水平向近断层地震记录数据。所选的地震记录信息见表5,图4为所选12条地震记录的加速度反应谱曲线。本文以此获得的地震记录为基础对不同地震动强度指标与结构响应指标的关联性进行研究。

表  5  本文选用的近断层地震记录

Table  5.  Near-fault ground motion records

编号	地震	台站	震级Mw	震中距/km	地震动分量	PGA/g	PGV/(cm·s-1)	总时间/s
1	Kobe, Japan,1995	Kobe University	6.9	0.92	KBU000	0.276	55.3	32
2					KBU090	0.312	30.9
3	Kobe, Japan,1995	KJMA	6.9	0.94	KJM000	0.834	91.1	32
4					KJM090	0.630	76.1
5	Kobe, Japan,1995	Port Island(0m)	6.9	3.31	PRI000	0.348	90.6	42
6					PRI090	0.290	51.1
7	Kobe, Japan,1995	Takatori	6.9	1.47	TAK_000	0.618	120	40
8					TAK_090	0.671	123
9	Imperial Valley-06	El Centro Array #5	6.53	3.95	H-E05_140	0.529	48.9	32
10					H-E05_230	0.383	96.9
11	Erzican,Turkey,1999	Erzincan	6.69	4.38	ERZ-NS	0.387	107	21
12					ERZ-EW	0.496	78.1

下载: 导出CSV 

| 显示表格

图  4  地震加速度反应谱曲线 (阻尼比=0.05)

Figure  4.  Acceleration response spectra of selected ground motions (damping ratio = 0.05)

下载: 全尺寸图片 幻灯片

3.   地震动强度参数评价

在基于性能的地震工程计算中,地震动强度参数与结构地震响应指标的选择直接决定着计算分析过程中的计算量以及结果的精度。合理的结构地震响应指标能较真实反映地震作用下结构的损伤状态,例如地上结构一般常选用最大层间位移角θ_max作为反映结构破坏程度的工程需求参数。对于地下车站结构,许成顺等^[19]研究表明：在水平地震作用下,结构中柱与侧墙的水平相对变形相差不大；结构中柱底部由于构件截面较小最先达到其极限承载力,是承载力验算的关键截面。同时根据庄海洋等^[20]对地下结构响应指标的定义和相关取值,本文在此选取地铁车站顶底板水平相对位移,中柱底部的轴力、弯矩和剪力作为结构地震响应指标,计算时均选取动力时程结果的绝对值最大值。

为了考虑地震动强度对土-结构系统随机地震反应的影响,对上述12条地震动记录进行调幅,每条地震动记录的计算峰值加速度按比例调整,将土体底部输入的地震动峰值分别调整为0.05g～1.0g,共180条地震动记录（每个调整的PGA水平下包括12条记录）分别作用于二维土-结构有限元模型,通过IDA分析,可对结构在地震作用下的反应从弹性到弹塑性直到结构动力失稳做出全面的评估,同时能够反映出结构在不同强度等级地震下的地震需求能力和整体抗倒塌能力,能够体现出结构的强度、刚度及变形的变化过程。根据地震动强度参数的评价标准：有效性、实用性和效益性对上述弹塑性有限元模型的动力反应结果进行综合评价分析。

3.1   有效性

地震动强度参数的有效性是指,能够使在指定的地震动强度条件下工程需求参数结果的离散性相对较小,从而在不降低精度的前提下,减少分析所需的地震动记录数量和非线性动力时程分析次数^[21],在此可通过条件对数标准差β来判别。选择一个有效的地震动强度参数能够使在指定的地震动强度条件下结构反应的离散性相对较小,从而在不降低精度的前提下,减少估计条件概率P（EDP│IM）和用于进行结构易损性分析时所需要的地震动数量和非线性分析次数^[21]。

Cornell等^[22]指出：结构地震响应指标与地震动强度参数之间近似满足指数关系,其关系式形式如式（1）所示。该关系式得到了国内外研究人员的广泛认可,在此本研究也采用该关系式研究合理的地震动强度参数。

由于式（1）满足一元线性回归模型,可采用最小二乘法原理对获得的n个离散点（IM_i,EDP_i）进行回归分析,进而获得ln(IM)与ln(EDP)的经验回归直线,并得到条件对数标准差如下：

式中,n表示非线性动力时程分析的次数。对于一个地震动参数IM来说,其值越小,结构响应的离散性越小,所选地震动强度参数的有效性越高,反之则越差。

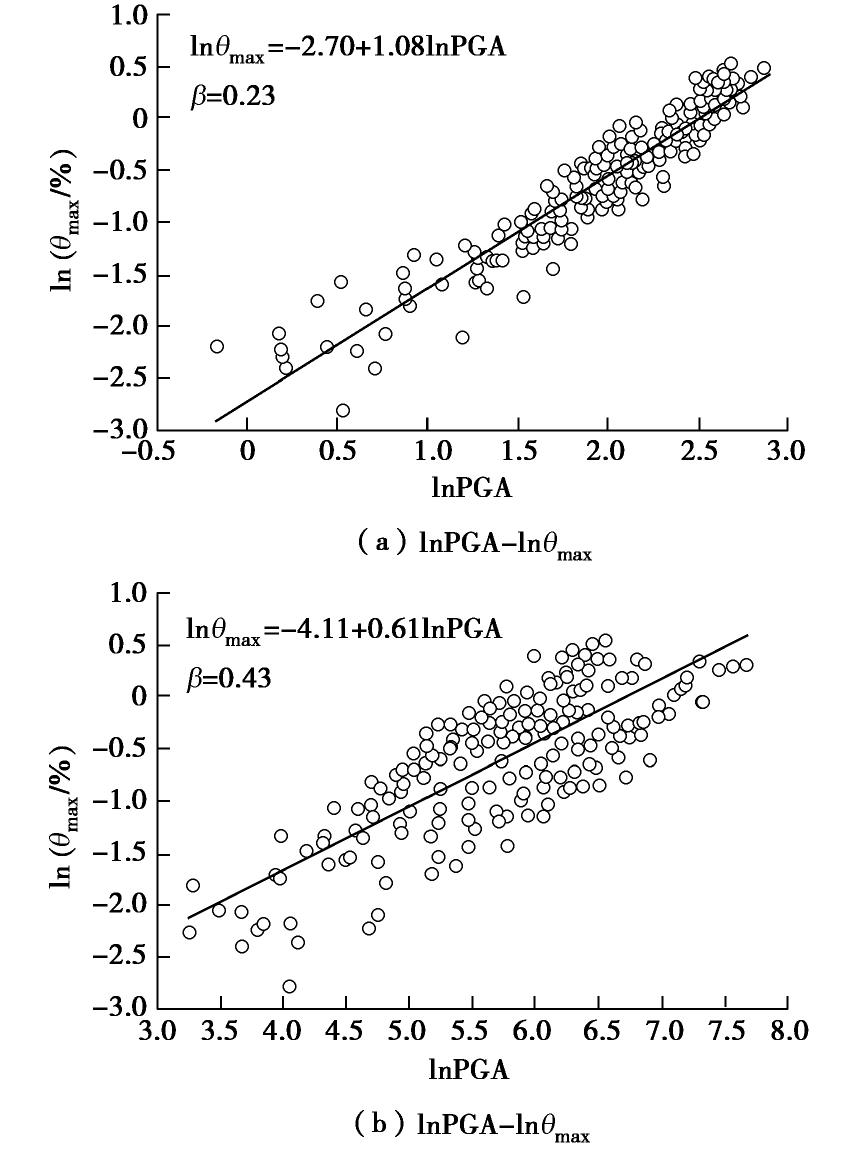
图5通过数据离散和线性回归方程得出了地震激励下地铁车站中柱的最大层间位移角θ_max关于地表峰值加速度PGA、速度谱强度VSI和地表峰值位移PGD的有效程度,直观的展现了结构地震响应指标与地震动强度参数的有效性,由图5可知,lnPGA-lnθ_max的离散性最小（β=0.23）,说明PGA的有效性最好；VSI有效性次之（β=0.37）,PGD的有效性最差（β=0.43）。由于PGD指的是地表的绝对位移,并不直接表征地下结构顶底板位置处所在土层的相对位移,故PGD的有效性较差。此外,土-地下结构相互体系可以看成是一个广义结构。对于一个广义结构的横断面来说,峰值加速度与结构的受力水平具有较明显的相关性,故在此PGA所得结果的离散性更小。

图  5  不同地震动强度参数有效性的比较

Figure  5.  Comparison of efficiency of different IMs

下载: 全尺寸图片 幻灯片

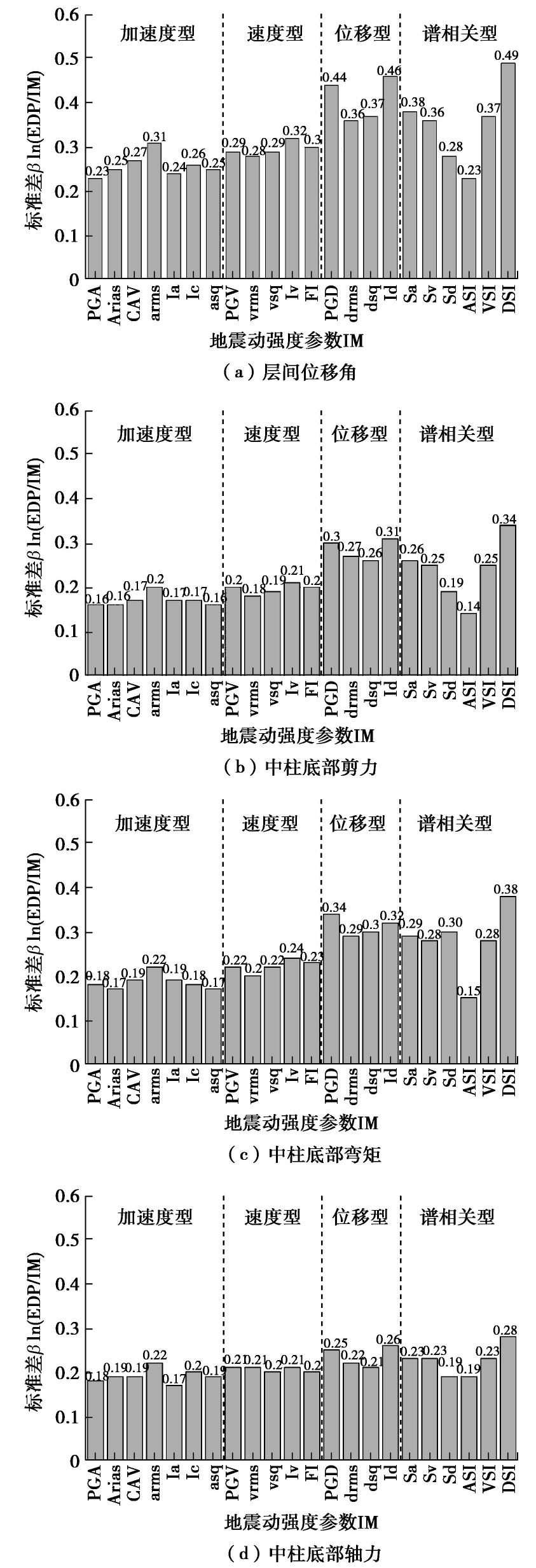
图6展示了表1中不同地震动强度参数的条件对数标准差β值。统计结果表明：①采用结构中柱底部轴力和剪力为EDP时,结果的离散性较小,以层间位移角为EDP时,结果的离散性最大。②对于层间位移角来说,加速度型指标、速度型指标和位移型指标的对结构响应的离散性整体从左往右呈现逐渐增大的趋势,且在谱相关型指标β值中,加速度谱强度ASI离散性最小,最适合作为谱相关型的IM。对于弯矩、轴力和剪力来说,以加速度型指标、速度型指标、位移型指标和谱相关型指标为IM,计算结构响应的离散性整体变化不大。③对不同的EDP而言,前3个最有效的IMs分别是ASI,PGA,I_a,以PGA和I_a为代表的加速度型指标和以ASI为代表的谱相关型指标均适用于预测地铁地下结构在地震作用下的结构响应,不适合作为预测结构在地震作用下的地震动强度参数有弹性加速度反应谱S_a、速度反应谱S_d和位移谱强度DSI。

图  6  不同地震动强度参数与结构地震响应指标的有效性计算结果

Figure  6.  Results of efficiency of different IMs and EDPs

下载: 全尺寸图片 幻灯片

3.2   实用性

实用性是指地震动强度参数与工程需求参数的关联敏感性^[23]。若某一地震动强度参数实用性不强,表明结构地震响应指标受该地震动强度参数变化的影响较小。实用性的量化指标通常取式（2）中的线性回归系数b来判断^[24]。b值越大,表明该地震动强度参数的变化对结构地震需求参数的影响越大,实用性越高；若b值趋于0,表明该地震动强度参数的变化对结构地震需求参数的无影响,图7阐明了IM之间实用性的相对关系。

图  7  不同地震动强度参数与结构地震响应指标的实用性计算.结果

Figure  7.  Results of practicability of different IMs and EDPs

下载: 全尺寸图片 幻灯片

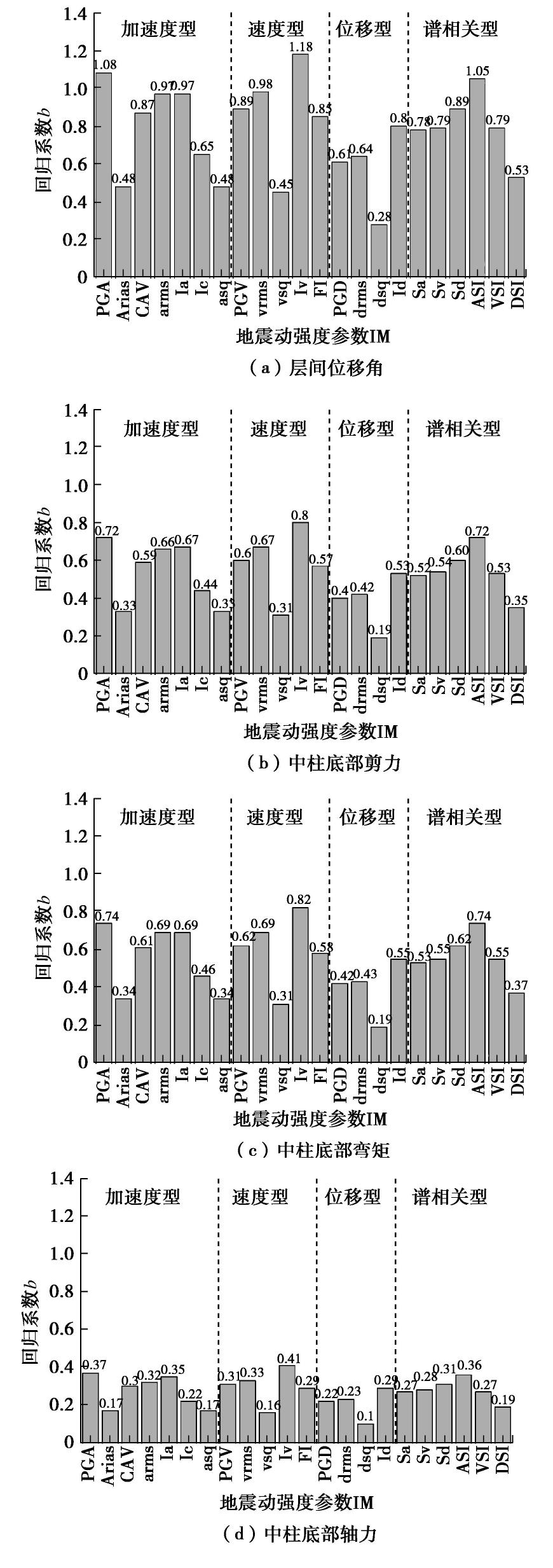
图7给出当各个地震动强度参数为自变量时,回归方程中的回归系数b。统计结果表明：①对于不同的结构地震响应指标,实用性最好的前5个IMs分别依次是I_v,PGA,ASI,I_a和a_rms,实用性最差的前3个IMs依次是d_sq,v_sq和a_sq。从实用性的角度看,近场地震动下以PGA,I_a和a_rms为代表的加速度型指标、以I_v为代表的速度型指标和以ASI为代表的谱相关型指标均适用于预测地铁地下结构在地震作用下的结构响应,这些地震动强度参数的变化对结构地震响应造成的影响较小；②针对同一个地震动参数,不同结构响应指标的情况,可以看出层间位移角更适合作为结构地震响应指标,其次是剪力和弯矩,最后是轴力。

3.3   效益性

效益性指标$\zeta$^[24]是综合考虑有效性和实用性的指标,是线性回归的对数标准差${\text{β}}_{\ln (EDP|IM)}$和线性回归系数b的比值,即

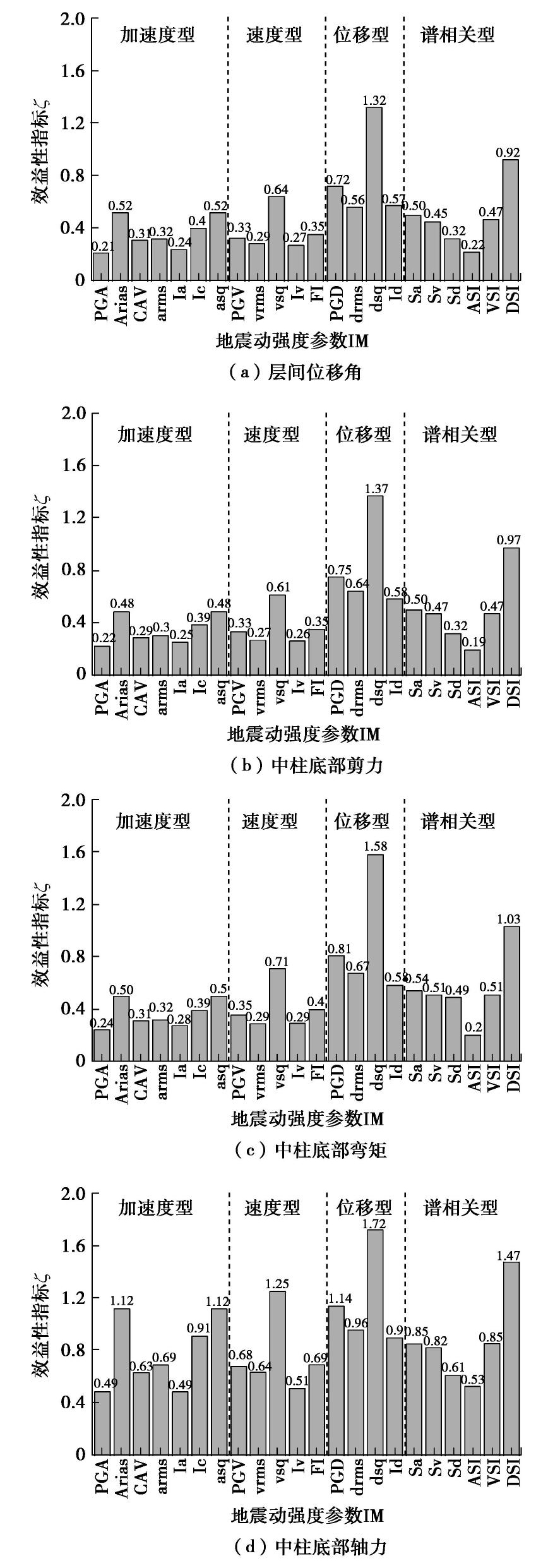
显然$\zeta$值越小,意味着对应的地震动参数的效益性越高。单纯的分别使用有效性和实用性去衡量IM,将会导致对某一个IM的适用性评价存在偏差,而使用效益性指标可以对有效性和实用性这两个评价标准进行平衡。各个地震动强度参数与4个结构地震响应指标在近场地震动激励下的效益性评价结果如图8所示。由图8可以看出,①对于结构响应指标来说,层间位移角、剪力和弯矩的效益性相差不大,而轴力与各地震动参数的效益相关性最差,说明地震动强度参数的变化对结构地震需求参数的影响较小,不宜作为结构地震响应指标；②对于地震动参数来说,从整体上来看,加速度型指标和速度型指标的效益性最好,谱相关型指标效益性次之,位移型指标效益性较差,在22个IM中,效益性最好的地震动参数是峰值加速度PGA和加速度谱强度ASI,d_sq在4种不同的结构响应参数中的效益性最差,说明其不适用于预测地铁地下结构在地震作用下的结构响应。

图  8  不同IM与EDP的效益性计算结果

Figure  8.  Results of proficiency of different IMs and EDPs

下载: 全尺寸图片 幻灯片

4.   结论

本文围绕适用于地铁地下车站的地震动强度参数展开研究,以大开车站为研究对象,通过引入IDA方法到地下结构的动力响应评价中,采用近场地震动进行非线性动力时程分析,得到不同强度地震动作用下结构体系的动力响应。分别对22个地震动强度参数和结构地震响应指标进行对数线性回归分析,从有效性、实用性和效益性3个方面对不同的地震动参数进行评价,得到了以下结论：

（1）根据有效性、实用性和效益性的综合评价结果,以PGA和I_a为代表的加速度型地震动参数和以ASI为代表的谱相关型地震动参数更适合用于预测单层双跨地铁车站结构在地震作用下的动力响应,同时层间位移角、中柱底部剪力和弯矩更适合作为地铁地下结构的动力响应指标。

（2）在地震作用下的4种地震动强度参数中,从有效性来看,加速度型指标的有效性要强于速度型指标、位移型指标和谱相关型指标,表明加速度型指标下得到的结构响应的离散性最小；从实用性来看,加速度型指标和速度型指标的实用性要强于位移型指标和谱相关型指标,表明加速度型指标和速度型指标下得到的结构地震响应受该地震动强度参数变化的影响较小。

（3）本文的分析中仅考虑单层双跨的单一地铁车站,随着地铁地下结构形式越来越复杂,在后续研究中还需开展不同构造形式的地铁车站和不同场地条件下地下结构地震响应与地震动参数间的相关规律研究,以得到普适性的结论。