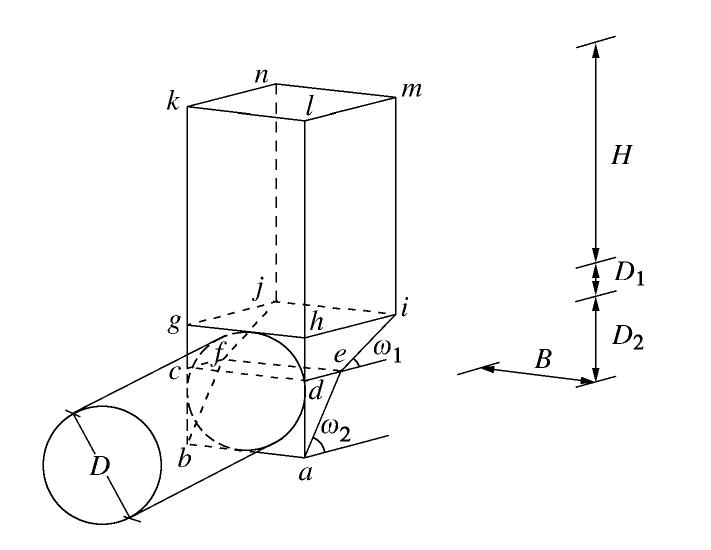
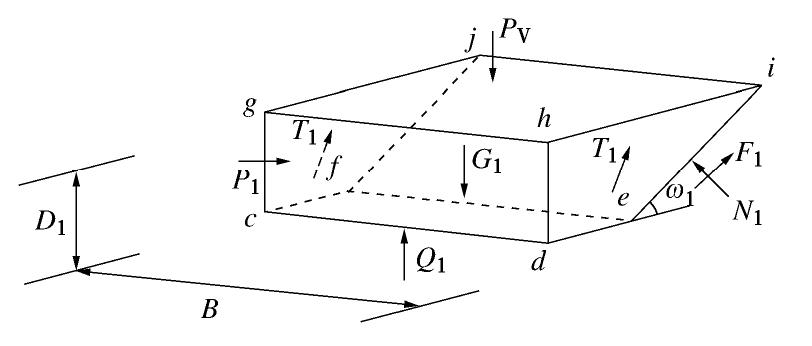
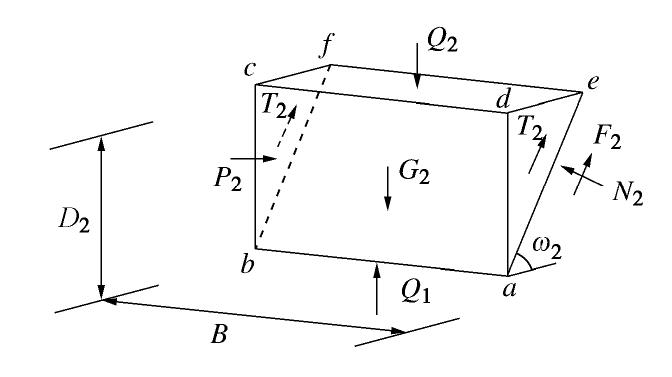
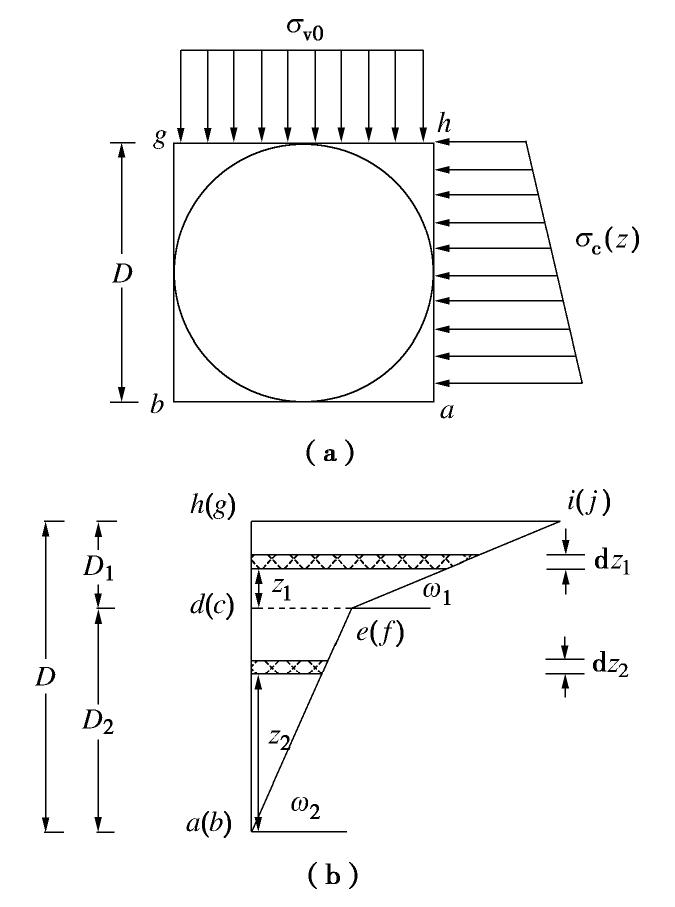
Model tests on stability and ultimate support pressure of shield tunnel in sand-gravel composite stratum
-
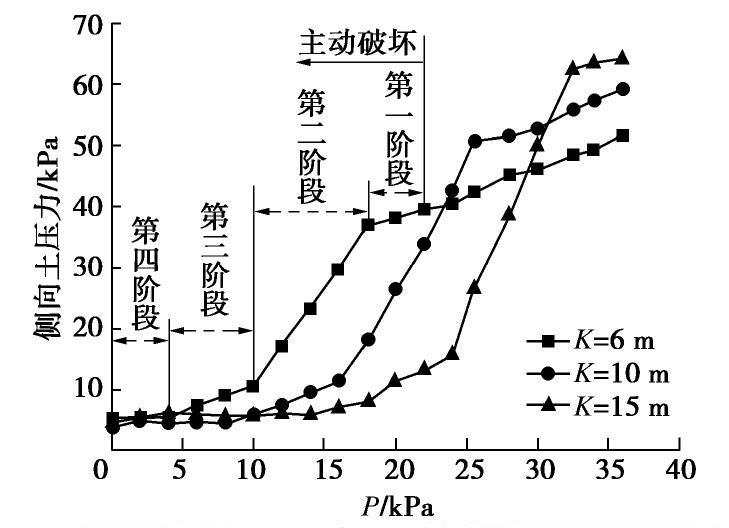
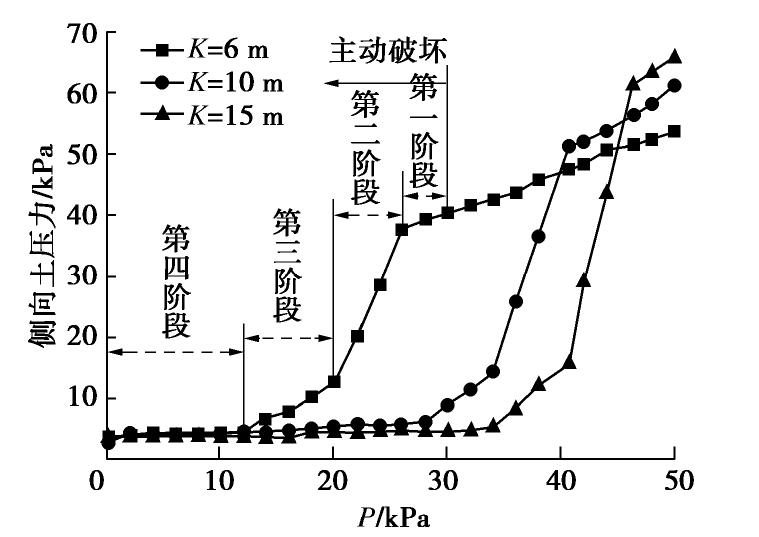
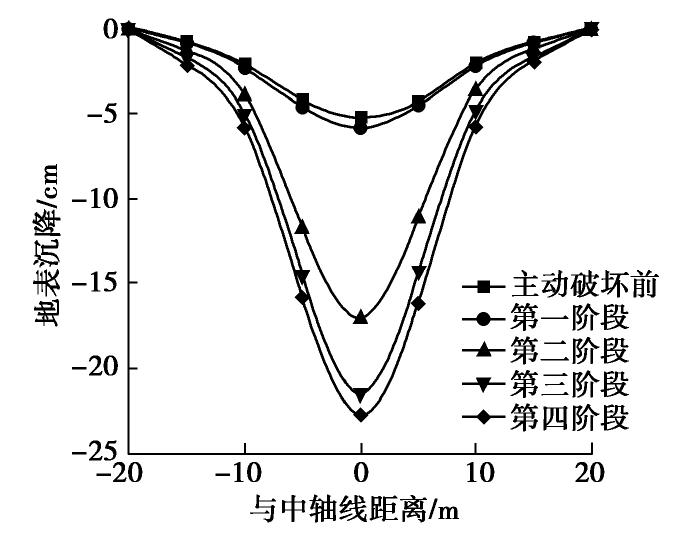
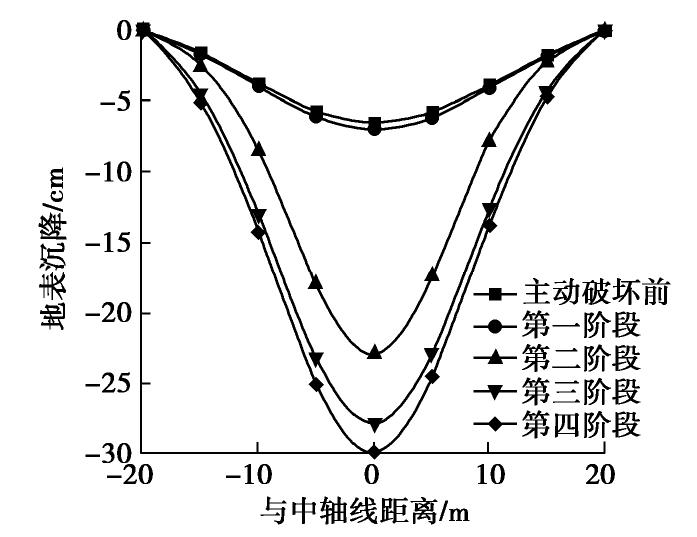
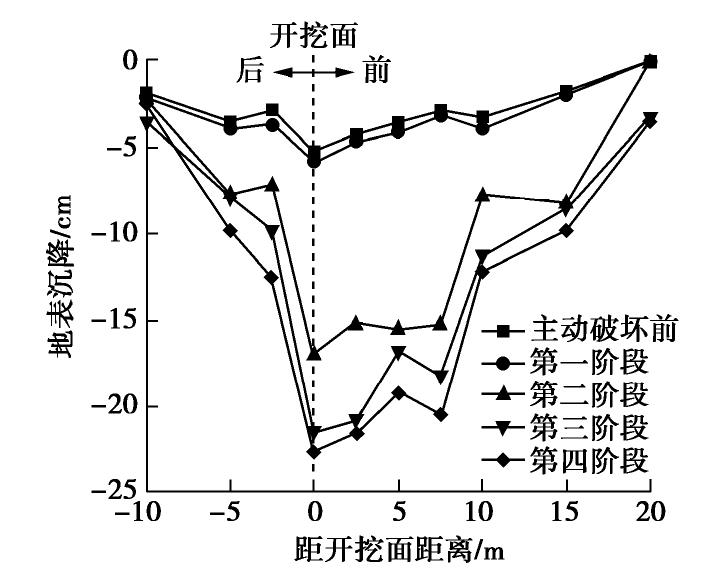
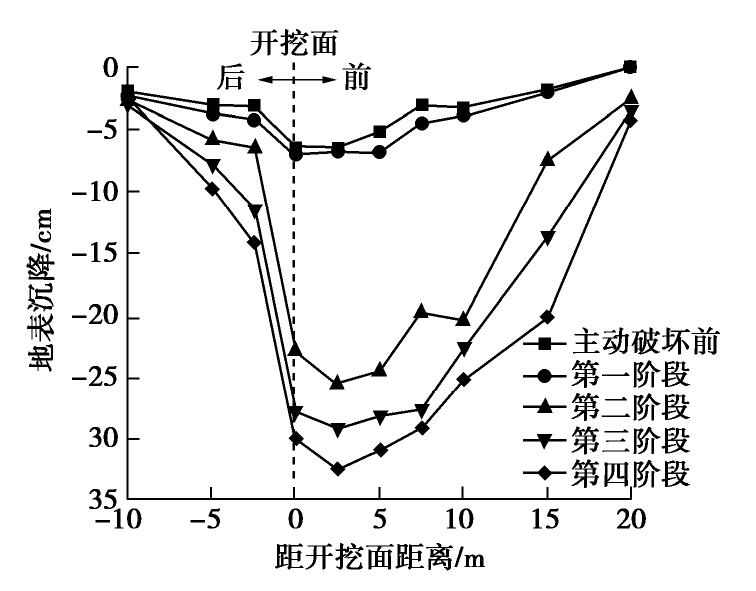
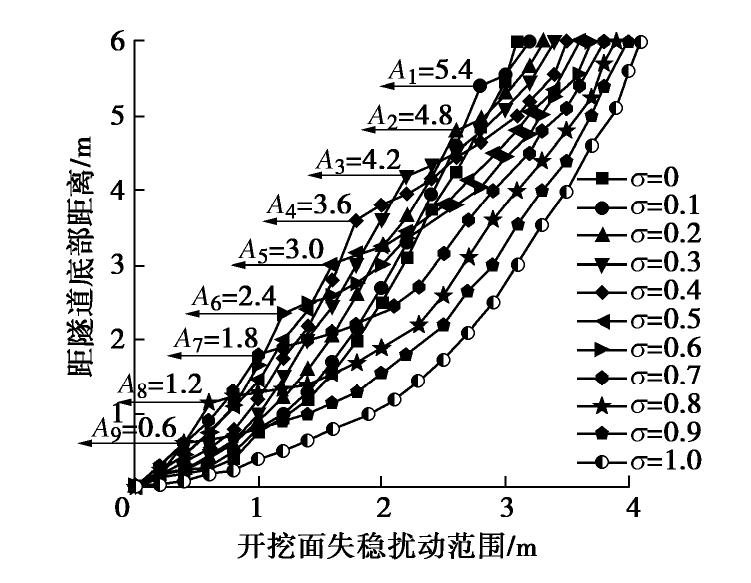
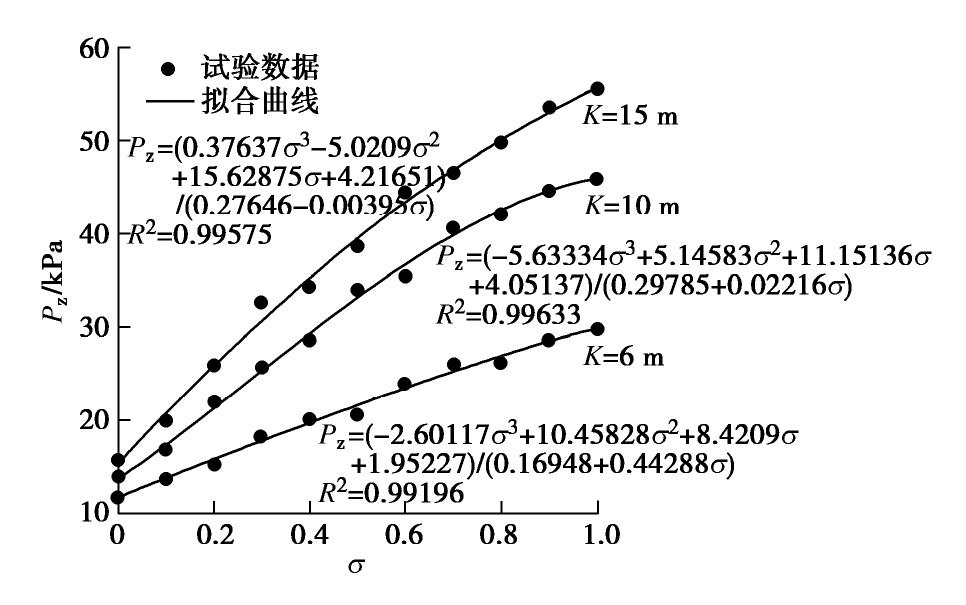
摘要: 砂-砾复合地层盾构掘进时支护力过小极易导致开挖面前方土体发生主动破坏,造成地表沉降。定义砂-砾复合地层σ（盾构开挖面内粉细砂高度与盾构机刀盘直径的比值）,并通过试验分析了σ对极限支护力、地表沉降和开挖面失稳扰动范围的影响；基于模型试验和筒仓理论,建立了适用于砂-砾复合地层的盾构隧道开挖面极限支护力计算模型,将σ引入模型中并推导出其计算公式。研究结果表明：①随着开挖面支护力的减小,开挖面发生主动破坏时侧向土压力-支护力曲线表现出不敏感阶段、快速下降阶段、缓慢下降阶段、稳定阶段4个阶段的规律；②破坏时σ越大,越不利于地表沉降控制；③与传统模型相比较,通过试验得知破坏面近似为折线,更贴合砂-砾复合地层的变形破坏模式；④极限支护力随着σ的增大呈近似线性的函数关系增长,覆土深度较大时,应充分重视σ对极限支护力带来的影响；⑤埋地层中,覆土深度对极限支护力的影响更加明显,需引起重视。研究结果对确定砂-砾复合地层开挖面的极限支护力有重要的指导意义。Abstract: For the shield-tunneling in sand-gravel composite stratum, if the support force is too small, it will easily lead to active destruction of soils in front of the excavation face and cause surface settlement. A parameter for the sand-gravel composite stratum is defined, that is the ratio of height of silty fine sand in excavation face to the cutter diameter of shield machine. Its effects on the ultimate support force, surface settlement and disturbance range of excavation face instability are analyzed. Based on the model tests and the silo theory, a computational model for the ultimate support force of excavation face of shield tunnels is established. It is introduced into the model, and the relevant formula is derived. The results show that: (1) With the decrease of the support force of the excavation face, the lateral earth pressure-support force curve exhibits the laws of insensitive stage, rapid declining stage, slow declining stage and stable stage. (2) The larger the value of σ is, the less conducive the control of surface settlement is. (3) Compared with that by the traditional model, the failure surface being approximately a broken line by the proposed method is more suitable for the deformation and failure mode of sand-gravel composite stratum. (4) The ultimate support force increases in an approximate linear functional relationship with the increase of σ. When the depth of overburden is large, the effects ofσ on the ultimate support force should be paid more attention to. (5) In the shallow stratum, the effects of overburden depth on the ultimate support force are more obvious, and need to be paid attention to. The research results have important guiding significance to determining the ultimate support force of excavation face in sand-gravel composite stratum.
-
0. 引言
对于河湖库的清淤以及各种海洋工程的修建、维护不可避免地产生大量的疏浚泥[1]，在沿海地区经常将疏浚泥作为填料，用于围海吹填造陆工程[2-3]。中国通常采用水力方式进行疏浚，其优点是连续作业、效率高、成本低，符合中国基本国情[4]。水力式疏浚产生的疏浚泥具有含水率高、压缩性高、强度低等特点，工程性质差[5-6]。工程实践中发现，真空预压法加固高含水率疏浚泥经常在排水板附近形成土桩，远离排水板的区域加固作用不明显[7-9]。一些研究者将真空排水固结技术处理大面积疏浚泥效果不佳归结于土颗粒径向移动，富集于排水板附近形成透水性差的致密区，从而导致排水淤堵[9-10]。
关于真空作用下高含水率疏浚泥的颗粒迁移试验研究见之报道不多，开展真空压力作用下不同含水率疏浚泥颗粒迁移性状的试验研究具有科学意义和应用价值。本研究采用室内模型试验，针对具有不同液限的疏浚泥开展不同初始含水率条件下的真空固结试验，分析真空作用下高含水率疏浚泥颗粒迁移性状与关键控制因素。
1. 试验装置与试验方案
1.1 试验装置
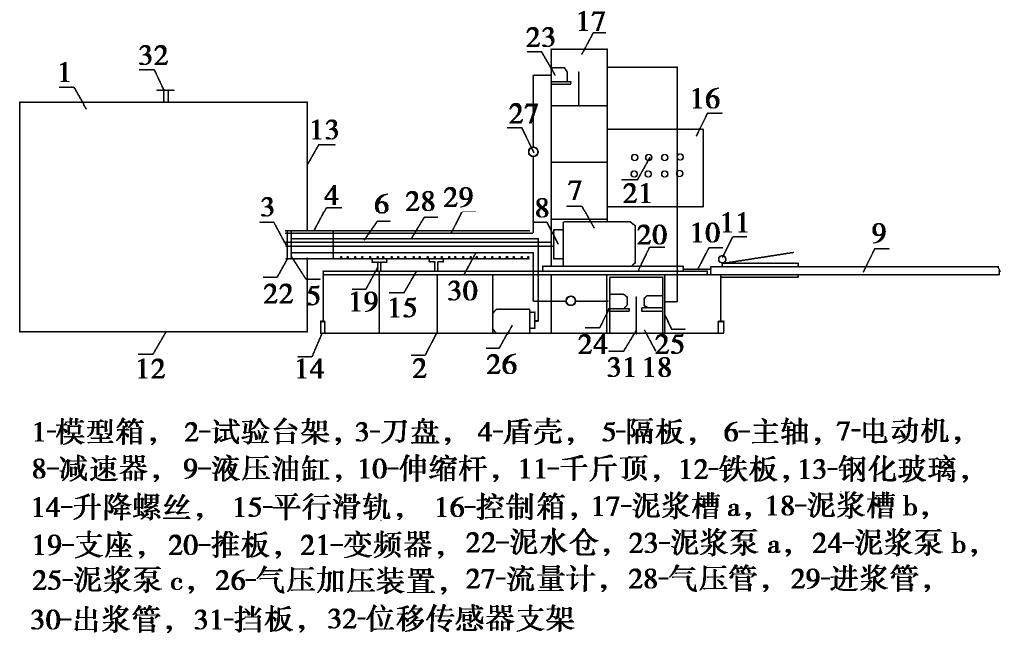
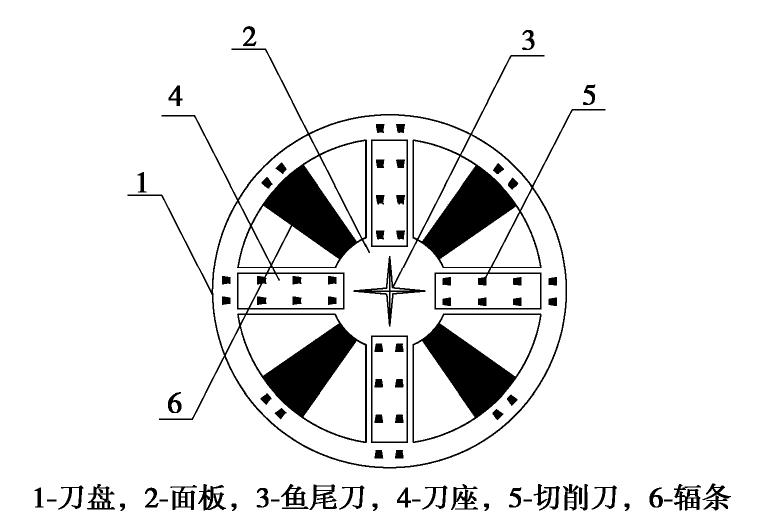
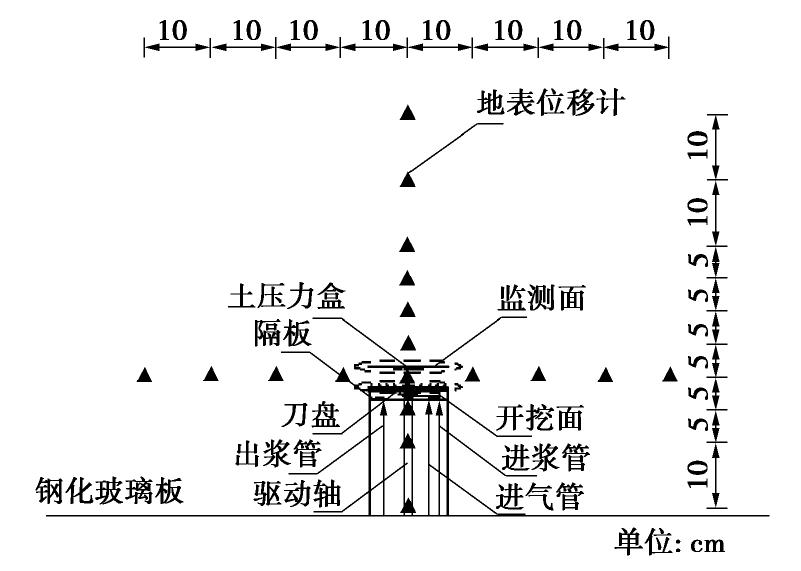
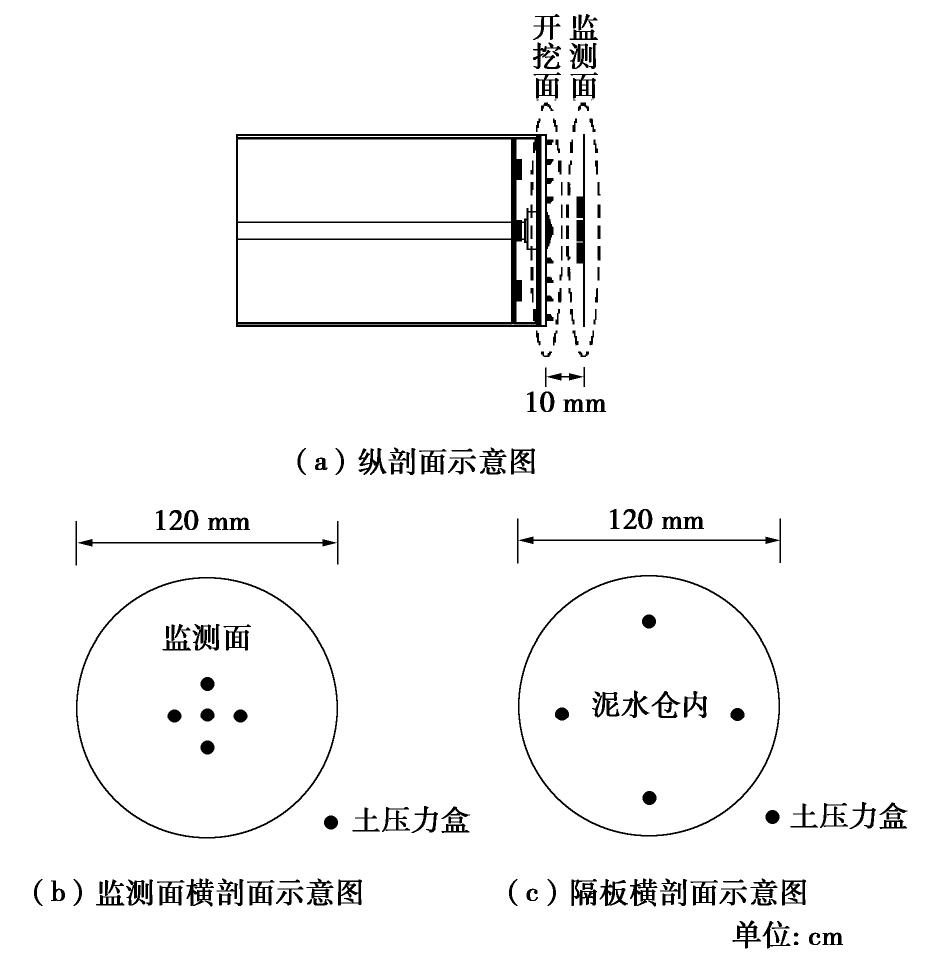
本研究自主研发了高含水率疏浚泥真空固结模型试验装置，如图 1所示。试验装置由三部分组成：真空泵、水气压力平衡装置和试样室。真空泵用于施加真空负压；水气压力平衡装置用于收集水气并且上方安装压力表能随时监控施加的真空负压值，保证压力恒定；试样室的高度为16 cm，内直径为6.3 cm的有机玻璃环，顶部为可以上下活动的有机试样盖，有机试样盖顶部与水气压力平衡装置通过管道相连，底部与透水石相连，试样顶部与透水石相连为排水边界，试样室下方底座装有真空压力表，监测试样底部受到的真空负压值。真空加载试验前先将水气压力平衡装置抽真空，使其内部真空压力达到试验所需真空负压值，然后打开水气平衡装置与试样间的阀门，对试样进行加载，并保持水气平衡装置内压力恒定，试样固结过程中的水经过真空导管进入水气平衡装置中。
1.2 试样
本文使用两种不同的疏浚泥：一种取自于福州市大学城的旗山湖，称为旗山湖疏浚泥；另一种取自于温州市瓯飞一期工程，称为温州疏浚泥，试样液限根据《土工试验方法标准：GB/T50123—2019》，使用碟式液限仪测定，塑限采用滚搓法测定，相对质量密度通过比重瓶法测定，颗粒级配根据ASTM D422-63标准使用细筛与H151比重计进行测定。温州疏浚泥的液限为63.3%，塑限为26.1%；旗山湖疏浚泥的液限为35.6%，塑限为18.6%。两种土样主要由细颗粒组成，其中温州疏浚泥的黏粒含量（d < 0.005 mm）和粉粒含量（d: 0.075~0.005 mm）分别为46.1%和49.5%，旗山湖疏浚泥的黏粒含量和粉粒含量分别为33.9%和58.4%。图 2为两种土样的塑性图，可以看出两种土均位于A线上方，旗山疏浚泥为低液限黏土，温州疏浚泥为高液限黏土。
1.3 试验方案
针对旗山湖疏浚泥和温州疏浚泥，制备不同的初始含水率试样，分别为液限的1.5倍、2.0倍、2.5倍、3.0倍和4.0倍左右，如表 1所示。将搅拌均匀的试样慢慢倒入高16 cm的有机玻璃套环中，试样安装完成后施加100 kPa的真空荷载，真空固结变形稳定后，拆开试样室获得距离上部排水边界1~2 cm处的上部试样，以及距离底部不排水边界1~2 cm处的下部试样，并将上、下部试样分别自然风干后进行颗粒分析试验。
表 1 疏浚泥真空固结试验方案Table 1. Test programs for investigated clays旗山湖疏浚泥 温州疏浚泥 wL/% w0/% w0/wL wL/% w0/% w0/wL 35.6 53.40 1.50 64.3 129.10 2.01 35.6 72.30 2.03 64.3 161.36 2.51 35.6 89.42 2.51 64.3 191.40 2.98 35.6 107.00 3.00 64.3 258.51 4.02 35.6 141.97 3.99 2. 试验结果
图 3（a），（b）给出了温州疏浚泥在真空固结后不同试样高度的颗粒分布曲线对比分析结果，发现初始含水率（w0）为液限（wL）的2.0倍和2.5倍时，真空固结后上部和下部试样的颗粒分布曲线基本一致，并且与真空固结前试样的颗粒分布曲线基本重叠，说明初始含水率为液限的2.0倍和2.5倍时，温州疏浚泥在真空作用下没有发生颗粒迁移。当初始含水率为液限的3.0倍时，真空固结后温州疏浚泥上部试样的颗粒分布曲线向上移动，下部试样向下移动，说明较小粒径的颗粒发生了迁移，向排水面方向富集，如图 3（c）所示。由图 3（d）可见，当初始含水率为液限的4.0倍时，上部与下部试样的颗粒分布曲线差异变大，说明随着w0/wL的增大，颗粒迁移现象逐步显著。
![]()
图 3 温州疏浚泥真空加载后试样上、下部分颗分曲线Figure 3. Particle segregation behaviour of Wenzhou clay under vacuum pressure同样的规律可见于旗山湖疏浚泥，当w0/wL = 1.5，2.0，2.5时，旗山湖疏浚泥在真空作用下没有发生颗粒迁移，如图 4（a）~（c）所示。当初始含水率为3.0倍和4.0倍液限含水率时，较小粒径的颗粒向排水面迁移，颗粒迁移的程度随着初始含水率与液限比值的增大而愈发明显，如图 4（d），（e）所示。
![]()
图 4 旗山湖疏浚泥真空加载试样上、下部分颗分曲线Figure 4. Particle migration behaviour of Qishanhu clay under vacuum pressure3. 颗粒组分变化规律
疏浚泥颗分分布通常具有宽广的级配，如本文采用的两种疏浚泥颗粒大小变化范围为1.0~ < 0.001 mm。因此，为了简单清晰地探讨真空固结过程疏浚泥颗粒迁移性状，按照土力学的颗粒组成划分方法，将土颗粒划分3个粒组：黏粒（d < 0.005 mm）、粉粒（0.075 mm > d > 0.005 mm）和砂粒（d > 0.075 mm），两种疏浚泥在真空作用后不同部位各粒组含量变化如图 5，6所示。当含水率很低时土体为密实固态，真空作用下土颗粒不会发生迁移，因此将真空固结前试样的不同颗粒含量数据显示于w0/wL= 0处，用于比较分析。
![]()
图 5 温州疏浚泥不同部位各粒组含量分布Figure 5. Change of grain size with initial state for Wenzhou clay![]()
图 6 旗山湖疏浚泥不同部位各粒组含量分布Figure 6. Change of grain size with initial state for Qishanhu clay图 5显示了温州疏浚泥试样初始含水率为2倍和2.5倍液限含水率时，经过真空固结后上部和下部的颗粒组成变化很小，黏粒含量变化范围在42.1%~42.3%范围内，粉粒含量变化范围为51.5%~51.7%，与真空固结前颗分组分基本一致；当初始含水率为3.0倍液限时，离排水面较近的上部试样黏粒含量为45.5%，粉粒含量为48.5%，而离排水边界较远的下部试样黏粒含量为41.7%，粉粒含量为52.7%；当初始含水率为4.0倍液限时，上部和下部试样的黏粒含量和粉粒含量的差距进一步加大，离排水面较近的上部试样黏粒含量为47.1, %，粉粒含量为47.5%，而离排水边界较远的下部试样黏粒含量为34.5%，粉粒含量为59.9%。
图 6显示了福州旗山湖疏浚泥试样初始含水率为1.5倍、2倍和2.5倍液限含水率时，真空固结前后的颗粒组成含量基本没有变化，黏粒含量分布于33.9%附近，粉粒含量分布于58.4%附近；当初始含水率为3.0倍液限时，离排水面较近的上部试样黏粒含量为34.9%，粉粒含量为57.5%，而离排水边界较远的下部试样黏粒含量为33.7%，粉粒含量为59.4%；当初始含水率为4.0倍液限时，上部和下部试样的黏粒含量和粉粒含量的差距加大，离排水面较近的上部试样黏粒含量为35.9%，粉粒含量为56.8%，而离排水边界较远的下部试样黏粒含量为30.7%，粉粒含量为61.3%。
以上结果说明，当初始含水率小于2.5倍液限含水率时，没有发生颗粒迁移现象；当初始含水率大于3.0倍液限含水率后，黏粒向排水面富集，导致距离排水边界较近区域的上部试样黏粒质量含量增多，粉粒含量减小，而距离排水边界较远区域的下部试样黏粒质量含量减小，粉粒含量增大。同时也可以看出，粗颗粒总含量很小，颗粒迁移对其相对含量的影响很小。
初始含水率为3倍和4倍液限试样在真空加载后由于黏粒和粉粒相对含量的变化，从图 4，5可以看出，颗粒迁移导致颗粒分布曲线的斜率发生相应的变化，本文引入等效不均匀系数Cur = d60/d30用于分析颗粒分布曲线斜率的变化规律，d30作为有效粒径，表示小于该粒径的土含量占总质量的30%，d60表示小于该粒径的土含量占总质量的60%，为控制粒径。等效不均匀系数Cur变大，表明试样的粒径大小相差越悬殊。图 7（a）显示温州疏浚泥初始含水率为2.0倍和2.5倍液限含水率试样真空固结后的不均匀系数浮动范围15.47~15.88，与真空固结前试样等效不均匀系数15.87基本一致。当初始含水率为3.0倍和4.0倍液限含水率试样真空固结后等效不均匀系数为8.24~19.78，真空固结前后等效不均匀系数发生显著变化。图 7（b）显示旗山湖疏浚泥试样初始含水率为1.5倍、2.0倍和2.5倍液限含水率试样真空固结前后等效不均匀系数变化很小，分布于7.14~7.42范围内；3.0倍和4.0倍液限含水率固结后试样等效不均匀系数变化很大，分布于4.92~10.57。
![]()
图 7 等效不均匀系数随着w0/wL的变化Figure 7. Change of nonuniformity coefficient with initial state4. 发生颗粒迁移的临界初始状态与变化规律
土体的液性指数或者更为简单的初始含水率与液限比值经常用于定量描述初始状态对饱和重塑土力学性状的影响，文献[6，11，12]给出重塑土不固结不排水剪切强度随着初始含水率与液限比值的增大而减小的结论。本研究采用初始含水率与液限比值描述真空作用下颗粒迁移性状，图 8给出了离排水面不同距离的上部试样黏粒含量与下部试样黏粒含量的比值随w0/wL的变化，可以发现，两种具有不同物理性质（包括液塑限和颗粒分布）的高含水率疏浚泥，发生颗粒迁移的临界初始状态值均为w0/wL = 2.7。初始状态小于临界值，没有发生颗粒迁移；当w0/wL大于临界值，黏粒向排水面附近富集。以上结果表明，真空作用下疏浚泥是否发生颗粒迁移与疏浚泥的强度密切相关。
图 9给出了上部试样和下部试样的等效不均匀系数比值随w0/wL的变化，可以发现，等效不均匀系数比值发生变化的临界初始状态与上部试样黏粒含量与下部试样黏粒含量的比值的临界初始状态基本一致，大约为w0/wL = 2.7。另外，从图 8还可以发现，当w0/wL大于发生颗粒迁移临界值，上部试样黏粒含量与下部试样黏粒含量的比值随w0/wL变化的斜率越大，该斜率可以代表颗粒迁移的显著程度，说明液限高的温州疏浚泥随着w0/wL的增大，颗粒迁移显著程度要大于液限低的旗山湖疏浚泥，也就是液限越高，一旦发生颗粒迁移，在排水通道附近发生黏粒富集的现象越明显。
![]()
图 9 试样上部和下部等效不均匀系数的比值Figure 9. Ratios of upper to lower nonuniformity coefficients of clay samples应该明确指出，本研究仅限于两种不同液限的疏浚泥开展初始状态对真空作用下颗粒迁移性状的试验研究，关于发生颗粒迁移的初始状态临界值w0/wL，以及颗粒迁移程度随w0/wL的变化规律需要更多的试验数据予以验证完善。同时，今后需要进一步开展不同试样高度和不同起始真空压力下的颗粒迁移性状试验研究与现场实例研究，分析不同尺度下不同排水距离的颗粒迁移性状和真空加固效果。
5. 结论
本研究基于自行研制的高含水率疏浚泥真空固结模型装置，针对两种不同液限的疏浚泥开展不同初始状态对真空作用下颗粒迁移性状的试验研究，得出如下3点结论。
（1）真空作用下高含水率疏浚泥是否发生颗粒迁移的临界阈值取决于疏浚泥的初始含水率与液限的比值，说明真空作用下发生颗粒迁移的阈值与疏浚泥不固结不排水强度密切相关。
（2）当初始含水率与液限比值小于临界阈值，真空作用下高含水率疏浚泥基本不会发生颗粒迁移。
（3）当初始含水率与液限比值大于临界阈值，真空作用下黏粒向排水面附近聚集，富集程度随着初始含水率与液限比值的增大而增大。
-
![]()
图 7 开挖面侧向土压力-支护力曲线（
σ =0.3）Figure 7. Lateral earth pressure-supporting force curves of excavation face（
σ =0.3）![]()
图 8 开挖面侧向土压力-支护力曲线（
σ =0.7）Figure 8. Lateral earth pressure-supporting force curves of excavation face（
σ =0.7）![]()
图 13 开挖面失稳扰动范围与
σ 值的关系曲线Figure 13. Relationship between disturbance range of excavation face instability and value of
σ ![]()
图 15 粉细砂地层楔形体受力示意图
Figure 15. Schematic diagram of stress of wedge in fine sand formation
![]()
图 16 圆砾地层楔形体受力示意图
Figure 16. Schematic diagram of stress of wedge in round gravel formation
![]()
图 17 楔形体竖向应力计算示意图
Figure 17. Schematic diagram of vertical stress calculation of wedge
表 1 土层物理力学参数
Table 1 Physical and mechanical parameters of soil layers
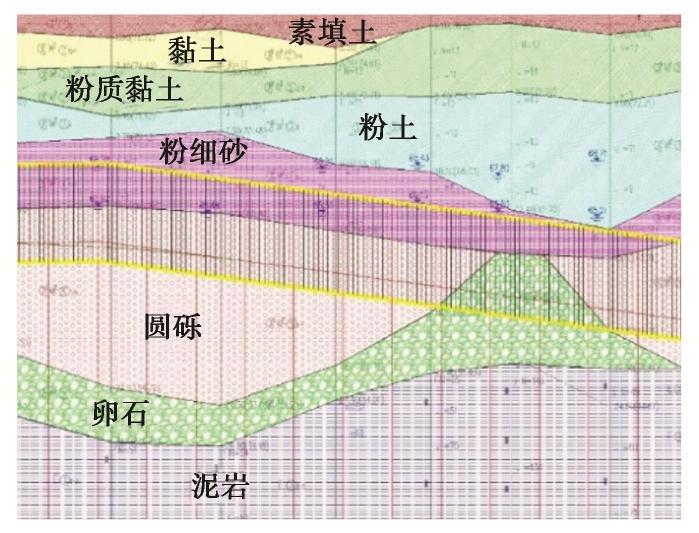
土层编号 土层名称 重度/(kN·m-3) 黏聚力/kPa 内摩擦角/(°) 压缩模量 ①2 素填土 19.6 15.0 10.0 9 ②2-1 黏土 19.4 50.0 11.6 24 ②2-2 粉质黏土 19.9 45.0 13.0 21 ③1 粉土 19.7 16.0 15.0 12 ④1-1 粉细砂 20.1 0 21.0 10 ⑤1-1 圆砾 20.8 0 35.0 25 ⑤1-2 卵石 21.0 0 37.0 25 ⑦1-2 泥岩 20.6 65 18.0 50 
下载: 导出CSV
表 2 土体围岩物理力学参数
Table 2 Physical and mechanical parameters of soils
围岩类别 重度/(kN·m-3) 压缩模量/MPa 黏聚力/kPa 内摩擦角/(°) 粉细砂层 原型 20.1 10.00 0 21 模型 15.4 0.15 0 21 圆砾层 原型 20.8 25.00 0 35 模型 16.0 0.38 0 35
下载: 导出CSV
-
[1] 袁大军, 沈翔, 刘学彦, 等. 泥水盾构开挖面稳定性研究[J]. 中国公路学报, 2017, 30(8): 24-37. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201708003.htm YUAN Da-jun, SHEN Xiang, LIU Xue-yan, et al. Study on stability of excavation face of mud-water shield[J]. China Journal of Highway and Transport, 2017, 30(8): 24-37. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201708003.htm
[2] HORN M. Horizontal earth pressure on perpendicular tunnel face[C]//Proceedings of the Hungarian National Conference of the Foundation Engineer Industry Hungarian, 1961, Budapest.
[3] JANSSEN H A. Versuche fiber getreidedruck in silozellen[J]. Zeitschrift des Vereins DeutscherIngenieure, 1895, 39(35): 1045-1049.
[4] JANCSECZ S, STEINER W. Face support for a large mix-shield in heterogeneous ground conditions[C]//Proceeding of the 7 th International Symposium on Tunneling. London: Taylor and Francis, 1994.
[5] ANAGNOSTOU G, KOVARI K. The face stability of slurry-shield-driven tunnels[J]. Tunneling and Underground Space Technology, 1994, 9(2): 165-174. doi: 10.1016/0886-7798(94)90028-0
[6] ANAGNOSTOU G, KVOARL K. Face stability conditions with Earth-Pressure-BalancedShields[J]. Tunneling and Underground Space Technology, 1996, 11(2): 165-173. doi: 10.1016/0886-7798(96)00017-X
[7] 赵明华, 毛韬, 牛浩懿, 等. 上硬下软地层盾构隧道开挖面极限支护力分析[J]. 湖南大学学报(自然科学版), 2016, 43(1): 103-109. https://www.cnki.com.cn/Article/CJFDTOTAL-HNDX201601014.htm ZHAO Ming-hua, MAO Tao, NIU Hao-jin, et al. Extreme supporting force analysis of shield tunnel excavation faces in upper and lower soft stratum[J]. Journal of Hunan University (Natural Science), 2016, 43(1): 103-109. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HNDX201601014.htm
[8] 陈仁朋, 李君, 陈云敏, 等. 干砂盾构开挖面稳定性模型试验研究[J]. 岩土工程学报, 2011, 33(1): 117-122. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201101022.htm CHEN Ren-peng, LI Jun, CHEN Yun-min, et al. Experimental study on stability of excavated face of dry sand shield tunneling[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 117-122. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201101022.htm
[9] 吕玺琳, 曾盛, 王远鹏, 等. 饱和圆砾地层盾构隧道开挖面稳定性物理模型试验[J]. 岩土工程学报, 2019, 41(增刊2): 129-132. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2019S2034.htm LU Xi-lin, ZENG Sheng, WANG Yuan-peng, et al. Physical model test of stability of excavation face of shield tunnel in saturated cobbledstratum[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(S2): 129-132. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2019S2034.htm
[10] 宋洋, 张维东, 王贺平, 等. 浅覆地层盾构开挖面被动破坏极限支护力及破坏模式研究[J]. 防灾减灾工程学报, 2019, 39(5): 748-754. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK201905008.htm SONG Yang, ZHANG Wei-dong, WANG He-ping, et al. Research on the passive support limit and failure mode of the passive damage of shallow shield shield excavation face[J]. Journal of Disaster Prevention and Mitigation Engineering, 2019, 39(5): 748-754. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK201905008.htm
[11] 王士民, 陈兵, 王先明, 等. 盾构隧道二次衬砌合理施作时机模型试验研究[J]. 岩土工程学报, 2020, 42(5): 882-891. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202005014.htm WANG Shi-min, CHEN Bing, WANG Xian-ming, et al. Model test research on the reasonable operation timing of secondary lining of shield tunnel[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(5): 882-891. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202005014.htm
[12] PECK R B. Deep excavations and tunneling in soft ground[C]//Proceeding of 7th International Conference on Soil Mechanics and Foundation Engineering, 1969, Mexico.
[13] 秦建设. 盾构施工开挖面变形与破坏机理研究[D]. 南京: 河海大学, 2005. QIN Jian-she. Study on Deformation and Failure Mechanism of Shield Excavation Face[D]. Nanjing: Hohai University, 2005. (in Chinese)
[14] LEE I M, LEE J S, NAM S W. Effect of seepage force on tunnelface stability reinforced with multi-step pipe grouting[J]. Tunnelling and Underground Space Technology, 2004, 19(6): 51-565.
[15] T ERZAUHI K. Theoretical Soil Mechanics[M]. New York: John Wiley and Sons, 1943: 66-76.
[16] SCHMIDT B. Discussion on “Earth pressure at rest related to stress history”[J]. Canadian Ueotechnical Journal, 1996, 3(4): 239-242.
计量
- 文章访问数: 327
- HTML全文浏览量: 12
- PDF下载量: 143
