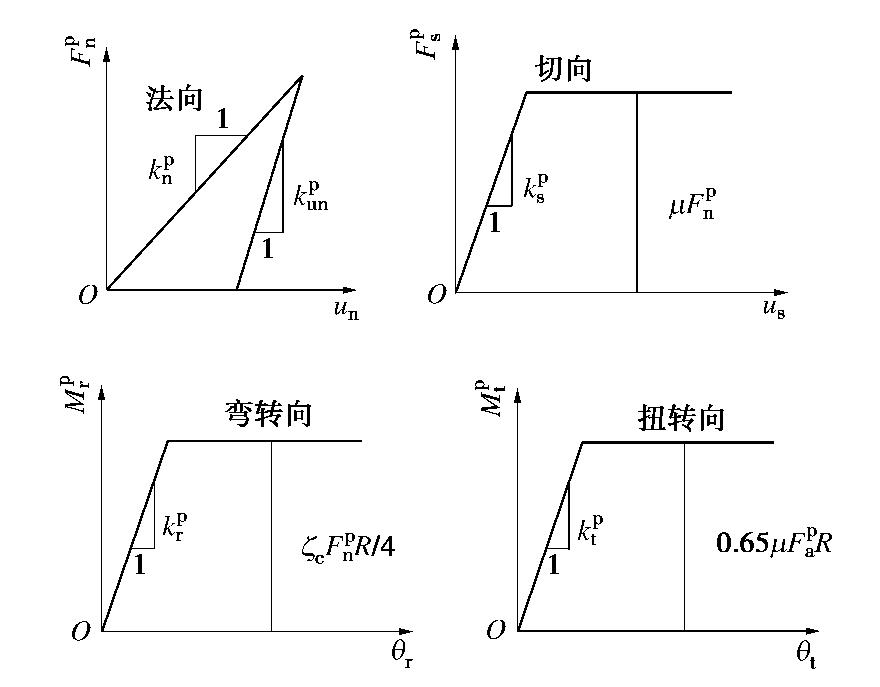
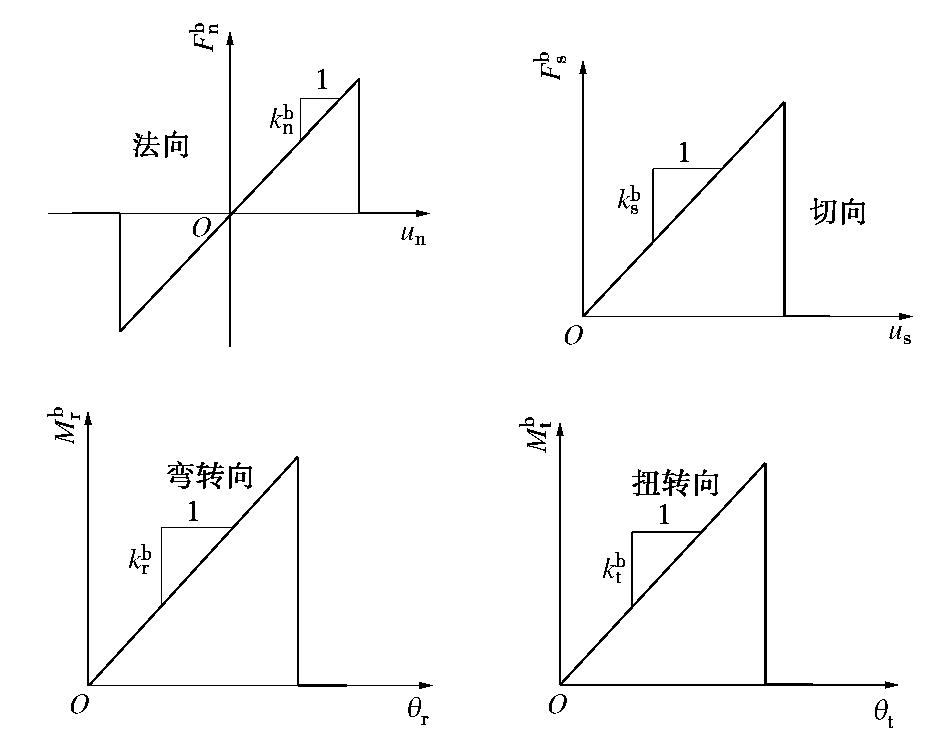
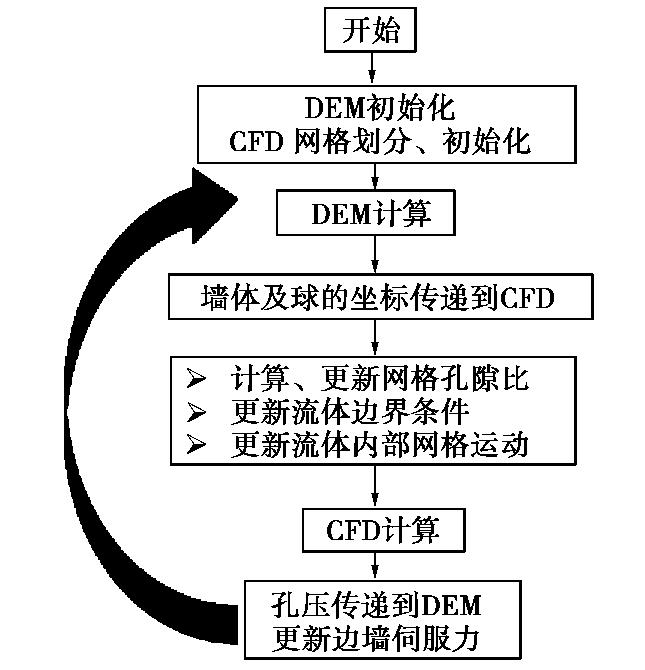
CFD-DEM simulation of microbially treated sands under undrained consolidated cyclic triaxial tests
-
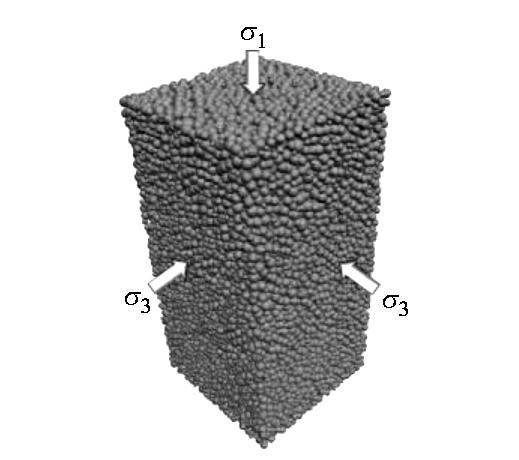
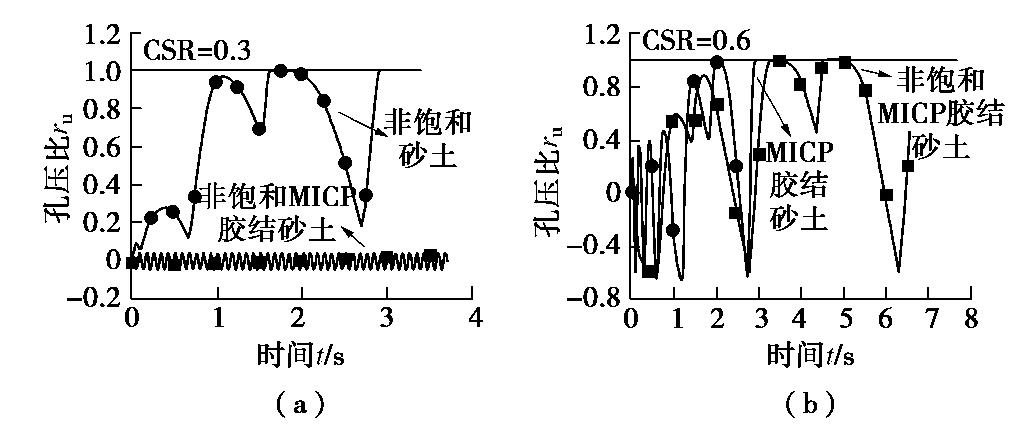
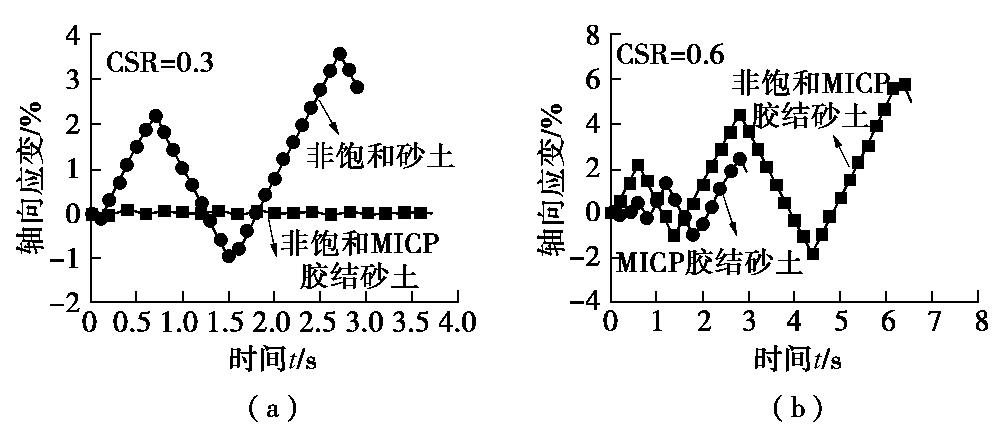
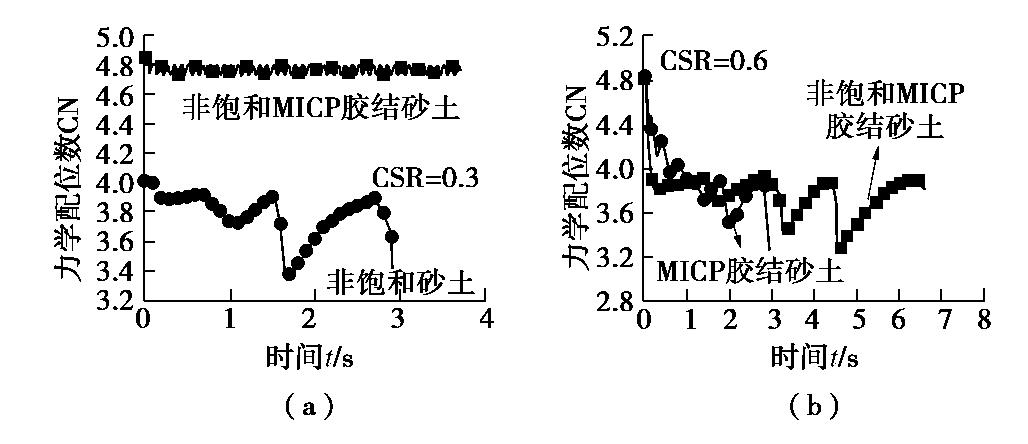
摘要: 微生物诱导碳酸钙沉积是一种新型的地基处理技术,处理后的土体可以看成一种结构性土。首先,在已有三维含颗粒抗转动和抗扭转模型及三维胶结破坏准则的基础上,通过考虑颗粒碰撞接触过程中颗粒本身的塑性变形及率相关性的接触黏滞阻尼,建立考虑循环荷载作用下的三维胶结模型;然后,参考已有研究,建立了反硝化反应在加固砂土中的时效性关系。并引入CFD-DEM耦合程序,用以模拟分析不同胶结含量以及不同气泡含量下,微生物处理砂土在固结不排水循环剪切试验中的力学特性;最后,从宏微观角度分析生物胶结与生物气泡对砂土抗液化性能的影响及其作用机理。研究表明,胶结和气泡共同存在对抗液化能力的提升并没有起到“1+1=2”的效果;胶结的存在提高了非饱和砂土的抗液化能力,明显抑制孔压比和轴向应变的发展,力学配位数得到了提升;而气泡的存在却降低了胶结砂土的抗液化能力,使得胶结砂土达到初始液化的振次减少,轴向应变向受拉方向大幅增长,力学配位数下降明显。
-
关键词:
- 微生物诱导碳酸钙沉积 /
- CFD-DEM耦合 /
- 不排水循环三轴剪切 /
- 地基液化 /
- 离散单元法
Abstract: The microbially induced calcite precipitation is a promising technology to improve ground, and the treated soil can be regarded as the structural one. In this study, firstly, based on the three-dimensional (3D) contact model for granulates incorporating rolling and twisting resistances and 3D bonds failure criteria, and considering both the slight plastic deformation of particles during collisions and the rate-dependency, a cyclic bonded contact model is established. A time-dependent relationship is then proposed to describe the denitrification reaction in reinforced sand. Next, the mechanical responses of microbially treated sands at different cementation and bubble contents are investigated by the coupled CFD-DEM in undrained-consolidated cyclic triaxial tests. The effects of biological bond and biological bubbles on the liquefaction resistance of sands are analyzed in link with the mechanism from macroscopic and microscopic scales. The results show that the coexistence of cementation and bubble does not increase the liquefaction resistance as expected in the form of "1+1=2". The presence of cementation enhances the liquefaction resistance of unsaturated sands evidenced by the decrease of excess pore water pressure ratio and axial strain, and the increase of coordination number. However, the presence of bubbles reduces the liquefaction resistance of cemented sands, where the number of cycles to the initial liquefaction decreases, the axial strain increases significantly in the tensile direction, and the coordination number decreases significantly. -
0. 引言
颗粒破碎是指颗粒处于足够大应力下发生断裂产生更小颗粒的现象。颗粒破碎会改变砂土的微观结构,从而显著影响砂土的力学和物理特性。颗粒破碎现象广泛存在于钙质砂等易破碎岩土体和高土石坝、桩基工程等高应力条件的相关工程领域,研究岩土材料的颗粒破碎问题具有十分重要的意义[1-4]。
目前岩土领域对颗粒破碎的研究已取得一定进展。Coop等[5]通过试验,证明了颗粒破碎的有限性,即破碎不可能无限发展下去,最终会到达一种基本稳定的状态即分形状态。试验和理论研究表明固体材料破碎的最终态满足分形规律。受加载条件等因素的影响,分形维数α虽略有差异,基本在理论值2.5左右[6-8]。颗粒破碎受到诸多因素影响,如荷载类型、矿物组成、孔隙比、颗粒形状等。就单颗粒而言,如钙质砂和堆石料,破碎是由于内部裂隙的扩展与贯通,颗粒尺寸越大所含有裂隙越多,强度越低,并且单颗粒强度大致服从Weibull分布[9-10]。从群颗粒角度而言,级配较好的土体,颗粒之间接触面多,颗粒相互咬合,在荷载作用下的破碎越少[11]。颗粒破碎会导致土体内摩擦角的降低、临界状态线下移,土体抗剪强度降低。为了研究此现象,出现了许多基于临界状态理论的颗粒破碎本构模型研究[12-14]。颗粒的破碎同样影响土体其它性质。如颗粒破碎产生的细小颗粒能显著降低土体的渗透系数[15]。基于离散元等方法的颗粒破碎数值模拟与试验结果得到的颗粒破碎规律类似[16-17]。此外模拟结果表明发生破碎后颗粒形状的演化存在一定规律性[18]。
另一方面,颗粒的形状也能影响土体的力学性质,如Xiao等[19]通过试验验证,土体颗粒整体越接近球形,土体的内摩擦角越低,反映为土体抗剪强度的降低。颗粒形状的几何分析可分成3个尺度:颗粒整体尺度,如长径比和球形度;局部尺度,如圆度;表面结构,如粗糙度[20]。本文采用长径比、凸度、球形度和圆度描述颗粒的几何形状。图 1(a)~(d)展示了这4类形状参数的定义。长径比是用来描述颗粒形状的常用参数,球形颗粒长径比为1,颗粒越细长越接近0;凸度是描述颗粒密实程度参数,颗粒越紧实,内凹面积越小,凸度值越接近1;球形度量化了颗粒与理想球体的接近程度,理想球体球形度为1;圆度是量化颗粒棱角的参数,棱角越少则越接近1[21-22]。有学者指出颗粒破碎会显著改变颗粒的形状[23-24]。目前针对形状演化的研究多集中在数值模拟方面,缺少对天然土体颗粒形状演化规律系统的试验研究。本文研究了两种典型的砂土材料在侧限压缩条件下的变形特性、粒径和形状演化的规律,探究颗粒破碎与形状的联系,为考虑颗粒形状和粒径两方面研究破碎创造条件。
1. 试验设计
1.1 试验材料
试验所用钙质砂取自南海,主要成分为碳酸钙,由海洋软体动物的遗体和残骸经过海洋作用形成,为典型的海源性砂土,具有粗糙多孔、棱角较多、疏松易碎等特点。石英砂为福建标准砂,其颗粒由岩石碎裂、搬运、磨蚀等风化作用形成,主要成分为二氧化硅,为陆源性岩土材料。试验前将两种材料清洗烘干,并用筛分法取出0.8~1.0 mm粒径的颗粒。
两种材料的物理性质和初始平均形状如表 1所示。由于两种材料的颗粒形状不同,即使二者具有相似的不均匀系数和曲率系数,但孔隙比差异较大。两种砂颗粒的扫描电子显微镜图(SEM)和初始粒径分布如图 1(e)所示,两者形状和孔隙的差异较明显。
表 1 试验用砂土物理性质和初始形状Table 1. Physical properties and initial shapes of test sand类别 emin emax Gs d50 /μm Cu Cc Ar Cx Sp Rn 钙质砂 0.98 1.37 2.74 903 1.32 1.02 0.675 0.949 0.794 0.214 石英砂 0.61 0.88 2.67 909 1.27 1.00 0.734 0.968 0.823 0.251 注:emin,emax为最小、最大孔隙比;Gs为相对密度;d50为累计质量为50%时对应颗粒直径;Cu为不均匀系数;Cc为曲率系数;Ar,Cx,Sp,Rn为初始形状分布累计达50%质量时对应形状参数值。 1.2 试验设备
侧限压缩加载仪器为MTS万能试验机,如图 2(a)所示,最大量程为100kN,应力位移数据自动采集,可预设程序自动循环加载。试验中采用位移控制,加载速率为0.15 mm/min,确保试样受到准静态加载[30]。轴向力加载至目标值后位移不发生变化则认为试样达到稳定。
颗粒粒径和形状的检测装置采用SYMPATEC公司生产的激光粒度仪(QICPIC),如图 2(b)所示。工作原理如图 2(c)所示:在测试过程中,仪器通过控制高压气流将颗粒吹散,形成稳定的颗粒流,通过高分辨、高帧率相机,获得颗粒运动中的二维图像进行分析。所采用的M7镜头,形状有效识别范围为38~2888 μm,最小像素点5.5 μm2。该仪器可在不产生二次破碎的情况下对颗粒粒径和形状进行精准分析[22, 26]。所得数据为颗粒的二维图像,相比筛分法更为精确,采用最小弦长对颗粒粒径进行评估与筛分法最为接近。由于图像识别精度问题,该设备对微小颗粒形状识别效果较差。并且土体中粉粒的形状对于土体的影响较为次要,对颗粒形状进行分析时已将小于75 μm颗粒排除在外。
1.3 试验方案
现有研究表明,粗粒土在侧限压缩条件下存在明显的屈服点[27],本试验实测0.8~1.0 mm单粒径钙质砂屈服点σCy为2 MPa,石英砂屈服点σQy为12 MPa。因为矿物成分和内部结构的差异,两种颗粒材料的单颗粒强度差别较大,采用相同的应力水平产生的破碎量差异较大,不能分析比较。所以此处定义终止应力比值β=σu/σy,其中σu为加载的终止应力。两种砂土颗粒形状的差异很大,导致无法采用相同的初始孔隙比进行压缩,所以试验控制初始相对密实度Dr=80%。本试验采用试样的高度与直径比值为0.75以减小拱效应的影响[15],圆柱体试样尺寸如图 2(a)。压缩后破碎颗粒进行重新排布再次压缩会使得破碎进一步发展,本试验也将破碎后颗粒是否重排考虑在内,颗粒重排组在每次加载完成后完全取出,重新填装进行下次加载;循环加载的试样则保持一次加载后状态,卸载之后再加载,重复至相应次数。试样加载信息如表 2所示。
表 2 试验组信息及编号Table 2. Information and number of samples钙质砂 β 加载情况 石英砂 β 加载情况 C0 0 不加载 Q0 0 不加载 C1 2 1次加载 Q1 1 1次加载 C2 4 1次加载 Q2 2 1次加载 C3 8 1次加载 Q3 3 1次加载 C4 12 1次加载 Q4 4 1次加载 C5 12 4次循环加载 Q5 4 4次循环加载 C6 12 2次重排加载 Q6 4 2次重排加载 C7 12 4次重排加载 Q7 4 4次重排加载 2. 压缩特性
如图 3(a),(b)所示,两种砂土压缩过程中,孔隙比e随轴向应力σa的增加而降低。两种砂分别加载至不同的终止轴向应力,压缩曲线重合度较高。在轴向应力为对数-孔隙比为线性的坐标系下,压缩曲线曲率值最大点所对应的轴向应力即为此种砂土的屈服点,即有上述钙质砂和石英砂的屈服点。两种材料的压缩曲线均满足由直到曲,最后线性稳定的特征。根据经典土力学,土体的一维压缩曲线符合下式[8]:
e=e′−Cclgσa, (1) 式中,e′为直线在纵坐标轴的截距,Cc为压缩指数,为土体的经验常数。根据此公式对两种砂土的压缩曲线末端进行拟合,得出所用钙质砂压缩指数为0.587,石英砂则为0.520。随着轴向应力的增加初始孔隙比对土体压缩特性的影响会逐渐降低[28],由此可见钙质砂相比石英砂具有更高的可压缩程度。C5和C7展示了钙质砂颗粒不重排与颗粒重排条件下的压缩曲线。C7曲线每次初始值的不同,表明试样颗粒破碎后进行的重排会使得密实状态下孔隙比低于初始状态,同时最终孔隙比低于不进行重排颗粒的孔隙比。不重排循环压缩同样会使得孔隙比降低,但程度较小。加载—卸载的循环过程中土体表现出明显的弹性特征,钙质砂和石英砂压缩后卸载回弹的弹性模量E,分别稳定在2.0 GPa和2.4 GPa,接近完全卸载时弹性模量会降低。
3. 粒径演化
如图 3(c), (d)所示钙质砂和石英砂的粒径累计分布曲线。随着终止轴向应力的增加,粒径分布曲线左移,小粒径颗粒增多。同时重新排布土体的再次加载会使得破碎进一步发展,这一现象在两种砂土中都十分明显。C4和C5曲线接近说明不进行颗粒重排的钙质砂试样在加载卸载循环中破碎几乎不再发展,而Q4和Q5存在差距表明对于石英砂不进行重新排布的循环加载卸载同样会使得破碎进一步发展。
为更好地描述颗粒破碎程度,许多学者通过粒径分布曲线定义了量化破碎量的方法[29-32]。在此引入Einav定义的相对破碎率[31]。以分形维数α=2.5的曲线为颗粒破碎的最终级配,确定方式为[33]
F(d)=(d/dM)3−α, (2) 式中,d为某一直径,F(d)为小于直径d颗粒百分比,dM为最大粒径。相对破碎率Br定义为
Br=Bt/Bp, (3) 其中,Bp为破碎潜能,Bt为总破碎。两者取值如图 4(a)所示,破碎潜能为最终级配和初始级配围成的面积值、总破碎为当前级配与初始级配围成的面积值。石英砂相对破碎率随终止应力比线性增加,但增幅逐步降低,钙质砂在β≥2时具有同样的规律。石英砂和钙质砂增加相同倍数的屈服应力时,石英砂发生的破碎要多于钙质砂。已有研究发现颗粒相对破碎率与单位体积塑性功Wp近似存在双曲线关系[34],
Br=a×Wp/(b+Wp), (4) 式中,a,b均为拟合系数。单位体积塑性功采用下式简化计算:
Wp=∫σadεa−EΔεa2, (5) 其中,dεa为轴向应变增量,E为砂土卸载回弹弹性模量,Δεa为卸载回弹轴向应变。图 4(c)展示了单位体积塑性功与相对破碎率的关系,可以看出二者具有明显的双曲线函数关系。钙质砂相对石英砂在相同单位体积塑性功时具有更多的破碎量。
4. 形状演化
通过QICPIC对加载后两种砂土进行检测,得出如图 5所示的形状参数累计分布演化图。从图 5(a)~(d)中可以看出,钙质砂的长径比、球形度和圆度累计曲线均发生了明显的右移,表明颗粒的最大、最小费雷特直径差值减小;颗粒图像趋向于圆形,颗粒本身趋向于球形;颗粒局部棱角减少。相反,凸度曲线变化有限,即颗粒内凹面积并没有太大变化。凸度对钙质砂是一个对颗粒破碎变化不敏感的形状参数。从图 5(e)~(h)中可以看出,石英砂的圆度变化规律与钙质砂相同。长径比和球形度的分布曲线同样有右移趋势,但与钙质砂不同的是石英砂的变化并不是单调右移,表现为先减少后增加。而石英砂的凸度表现为减少的趋势。为了更好的量化形状参数的变化趋势,定义砂土试样的整体形状值S,如图 5(i)所示,形状分布曲线左侧围成的面积值即为整体形状值。
根据对整体形状值S的定义,绘制整体形状值与相对破碎的关系如图 6所示。钙质砂除凸度的整体形状值基本不变外,其余整体形状值均随着破碎率的增加而增长。钙质砂整体形状值与相对破碎率有较强的双曲线关系,如长径比整体形状值满足
SCAr=a×Br/(b+Br)+ArC0, (6) 式中,SCAr为长径比整体形状值,下标为长径比,上标C代表钙质砂,a,b为拟合参数,ArC0为钙质砂初始长径比整体形状值,其他形状参数同理。因Br与S具有较好的对应关系,由此可根据破碎情况估计形状变化程度。
石英砂的整体形状值除圆度持续增加外,长径比和球形度的整体形状值先下降后上升,凸度下降至稳定。四者均近似满足二次函数关系,如长径比整体形状值满足
SQAr=a×Br2+b×Br+ArQ0, (7) 式中,上标Q对应石英砂。石英砂在较大破碎后整体形状值上升,原因是颗粒的重新排布造成的破碎进一步发展,为更好地说明这一问题,对破碎进行颗粒尺度的分析。
颗粒的破碎可以按照破碎后形成的颗粒质量比例分为破裂、磨碎和磨损[35],如图 7(a)所示。破裂会产生许多大小相近的子颗粒;磨碎会产生一个与原来颗粒大小相近的颗粒和许多较小颗粒;磨损是从原颗粒上脱离一些细小颗粒。石英砂颗粒初始形状较为规则,在磨碎破坏掉部分棱角之后,轴向压力逐渐增加至颗粒破裂,产生一些具有棱角的子颗粒,造成长径比和球形度的整体形状值的降低。随后试样被压实,破碎产生更多的接触面使得Br增长减缓。后续颗粒重新排布降低了颗粒间的接触面积,使不规则颗粒的棱角容易形成应力集中,发生磨碎破坏使得子颗粒更为规则。这一过程表现为长径比和球形度呈现下凸的抛物线形式。相反,由于钙质砂初始形状的不规则,破碎后产生的子颗粒的形状相比于原颗粒并没有变得不规则,所以在荷载作用下多种破坏模式并存,使得颗粒总体的形状总是趋向于规则,表现为增长逐步放缓的双曲线函数。不同加载程度下钙质砂(C0,C3,C7)和石英砂(Q0,Q3,Q7)的电镜图片如图 7(b)所示,由此可见随着位体积塑性功的增加,颗粒粒径减小,破碎量增加。钙质砂颗粒的形状从图中可以看出向着更为规则发展。石英砂初步的破碎会产生一些具有棱角的子颗粒,随着破碎的进一步发展,子颗粒进一步破碎,会使得颗粒形状趋于规则。
由上述分析和试验结果可以提出一个关于颗粒形状变化的猜想:砂土颗粒在经历破碎之后, 颗粒形状会趋于一个稳定的区间,即形状演化的最终值。目前已有数值模拟研究得出这一结论[18],本试验研究已存在变化趋势,关于距离形状稳定区间还需要进一步试验研究。
5. 结论
本文通过对单粒径钙质砂和石英砂进行不同程度的侧限压缩试验,并且利用图像测量对颗粒的破碎与形状变化进行了分析。提出了土体的整体形状值S来量化颗粒的形状及形状演化,得到了3点结论。
(1)钙质砂和石英砂的侧限压缩会使孔隙比与应力的对数趋向线性关系。砂土的颗粒破碎率与单位体积塑性功具有显著的双曲线关系。在相同单位体积塑性功下钙质砂破碎多于石英砂。
(2)颗粒破碎过程中,颗粒粒径变化的同时颗粒形状也在发生明显的变化。不同的形状参数对形状变化的敏感程度不同。对于钙质砂,在凸度基本不变的同时,长径比、球形度和圆度都随破碎量的扩大而增加。石英砂的长径比和球形度随破碎先下降后上升,凸度先下降后稳定,圆度持续增加。
(3)采用砂土的整体形状值S能较好地量化颗粒形状、反映颗粒形状的变化趋势。钙质砂的整体形状值与相对破碎率呈现显著的双曲线关系,随破碎的增加形状参数增长放缓;石英砂则具有下凸的抛物线关系。
-
表 1 胶结颗粒模型微观参数
Table 1 Microscopic parameters of model for bond grains
组成 参数名称 数值 颗粒部分 颗粒模量Ep/Pa 3×108 颗粒法向与切向刚度比 ξ 1.5 颗粒摩擦系数 μ 0.5 颗粒抗转动系数 β 0.2 颗粒局部破损系数 ξc 2.1 颗粒法向接触加卸载刚度比 en 0.95 胶结部分 胶结半径比例系数 η (0.5)* 胶结模量Eb/Pa 2×108 胶结泊松比 νb 0.2 胶结抗拉强度 σt /Pa1.6×106 胶结抗压强度 σc /Pa8×107 黏滞阻尼 法向临界阻尼比 βn 0.6 切向临界阻尼比 βs 0.6 注: 胶结半径比例系数η 在标定过程中取0.5,在此后的模拟中为控制胶结含量的研究变量。表 2 数值模拟试样微生物处理过程时效性
Table 2 Time-dependent characteristics of microbial processing of numerical simulation samples
反应时间/d 微生物处理生成胶结 微生物处理生成气泡 胶结体积/mm3 胶结半径比例系数η 气泡体积/mm3 饱和度Sr/% 孔隙流体压缩系数C 0 0 0 0 100 4.5×10-7 2 0.718 0.231 2.46 98.3 3.87×10-5 表 3 微生物处理砂土循环三轴数值模拟工况与结果列表
Table 3 Simulation program and main results of cyclic triaxial compression tests on different microbial treatment time on sand
试样编号 模拟工况 模拟结果 土体种类 微生物处理时间/d 胶结半径比例系数η 孔隙流体压缩系数C 循环应力比CSR 破坏振次NL 破坏模式 L0 净砂 0 0 0.15 1 I.L. MU2-1 非饱和MICP胶结砂土 2 0.273 3.87×10-5 0.30 45+ — MU2-6 非饱和MICP胶结砂土 2 0.273 3.87×10-5 0.60 3 I.L. MP2-2 MICP胶结砂土 2 0.273 0.60 5 I.L. US2-4 非饱和砂土 2 3.87×10-5 0.30 2 I.L. -
[1] 沈珠江. 理论土力学[M]. 北京: 中国水利水电出版社, 2000. SHEN Zhu-jiang. Theoretical Soil Mechanics[M]. Beijing: China Water and Power Press, 2000. (in Chinese)
[2] GAO Y F, HANG L, HE J, et al. Mechanical behaviour of biocemented sands at various treatment levels and relative densities[J]. Acta Geotechnica, 2019, 14(3): 697-707. doi: 10.1007/s11440-018-0729-3
[3] WANG Y, SOGA K, DEJONG J T, et al. A microfluidic chip and its use in characterising the particle-scale behaviour of microbial-induced calcium carbonate precipitation (MICP)[J]. Géotechnique, 2019, 69(12): 1-9.
[4] INAGAKI Y, TSUKAMOTO M, MORI H, et al. A centrifugal model test of microbial carbonate precipitation as liquefaction countermeasure[J]. Japanese Geotechnical Journal, 2011, 6(2): 157-167. doi: 10.3208/jgs.6.157
[5] HAN Z G, CHENG X H, MA Q. An experimental study on dynamic response for MICP strengthening liquefiable sands[J]. Earthquake Engineering and Engineering Vibration, 2016, 15(4): 673-679. doi: 10.1007/s11803-016-0357-6
[6] 刘汉龙, 肖鹏, 肖扬, 等. MICP胶结钙质砂动力特性试验研究[J]. 岩土工程学报, 2018, 40(1): 38-45. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201801003.htm LIU Han-long, XIAO Peng, XIAO Yang, et al. Dynamic behaviors of MICP-treated calcareous sand in cyclic tests[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(1): 38-45. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201801003.htm
[7] REBATA-LANDA V, SANTAMARINA J C. Mechanical effects of biogenic nitrogen gas bubbles in soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(2): 128-137. doi: 10.1061/(ASCE)GT.1943-5606.0000571
[8] HE J. Mitigation of liquefaction of sand using microbial methods[D]. Singapore: Nanyang Technological University, 2013.
[9] CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 1979, 29(1): 47-65. doi: 10.1680/geot.1979.29.1.47
[10] KHOUBANI A, EVANS T M, MONTOYA B M. Particulate simulations of triaxial tests on bio-cemented sand using a new cementation model[C]//Proceedings of GeoChicago: Sustainability, Energy, and the Geoenvironment. Chicago, 2016: 1-10.
[11] FENG K, MONTOYA B M, EVANS T M. Discrete element method simulations of bio-cemented sands[J]. Computers and Geotechnics, 2017, 85: 139-150. doi: 10.1016/j.compgeo.2016.12.028
[12] ANDERSON J D, WENDT J. Computational Fluid Dynamics[M]. New York: McGraw-Hill, 1995.
[13] CHANG C Y, SCHMIDT J, DÖRENKÄMPER M, et al. A consistent steady state CFD simulation method for stratified atmospheric boundary layer flows[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 172: 55-67. doi: 10.1016/j.jweia.2017.10.003
[14] PAREKH J, RZEHAK R. Euler-Euler multiphase CFD-simulation with full Reynolds stress model and anisotropic bubble-induced turbulence[J]. International Journal of Multiphase Flow, 2018, 99: 231-245. doi: 10.1016/j.ijmultiphaseflow.2017.10.012
[15] EL SHAMY U, ZEGHAL M. A micro-mechanical investigation of the dynamic response and liquefaction of saturated granular soils[J]. Soil Dynamics and Earthquake Engineering, 2007, 27(8): 712-729. doi: 10.1016/j.soildyn.2006.12.010
[16] 蒋明镜, 张望城. 一种考虑流体状态方程的土体CFD-DEM耦合数值方法[J]. 岩土工程学报, 2014, 36(5): 793-801. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201405002.htm JIANG Ming-jing, ZHANG Wang-cheng. Coupled CFD-DEM method for soils incorporating equation of state for liquid[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(5): 793-801. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201405002.htm
[17] 蒋明镜. 现代土力学研究的新视野—宏微观土力学[J]. 岩土工程学报, 2019, 41(2): 195-254. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902002.htm JIANG Ming-jing. New paradigm for modern soil mechanics: Geomechanics from micro to macro[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(2): 195-254. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902002.htm
[18] JIANG M J, SHEN Z F, WANG J F. A novel three- dimensional contact model for granulates incorporating rolling and twisting resistances[J]. Computers and Geotechnics, 2015, 65: 147-163. doi: 10.1016/j.compgeo.2014.12.011
[19] 金树楼. 结构性砂土三维微观接触力学试验及离散元数值模拟[D]. 上海: 同济大学, 2016. JIN Shu-lou. Three Dimensional Experimental and Numerical Study on Micro- and Macro-mechanical Behaviors of Structural Sands[D]. Shanghai: Tongji University, 2016. (in Chinese)
[20] THORNTON C, CUMMINS S J, CLEARY P W. An investigation of the comparative behavior of alternative contact force models during inelastic collisions[J]. Powder Technology, 2013, 233(3): 30-46.
[21] SHEN Z F, JIANG M J, THORNTON C. DEM simulation of bonded granular material: Part I contact model and application to cemented sand[J]. Computers & Geotechnics 2016, 75: 192-209.
[22] 谭亚飞鸥. 考虑循环荷载的三维微观胶结模型及微生物处理砂土循环三轴CFD-DEM耦合模拟[D]. 上海: 上海理工大学, 2018. TAN Ya-fei-ou. A Novel Three-dimensional Bonded Contact Model Incorporating the Effect of Cyclic Loads and CFD-DEM Simulation of Microbially Treated Sands Under Undrained Consolidated Cyclic Triaxial Tests[D]. Shanghai: University of Shanghai for Science and Technology, 2018. (in Chinese)
[23] ZHANG A, JIANG M J. Numerical simulation of undrained triaxial tests for granular soil using a coupled CFD-DEM method with moving mesh[J]. Acta Geotechnica, 2019. (to be submitted)
[24] ZHAO T. Investigation of Landslide-induced Debris Flows by the DEM and CFD[D]. Oxford: University of Oxford, 2014.
[25] VAN PAASSEN L A, DAZA C M, STAAL M, et al. Potential soil reinforcement by biological denitrification[J]. Ecological Engineering, 2010, 36(2): 168-175.
[26] AL QABANY A, SOGA K, SANTAMARINA C, et al. Factors affecting efficiency of microbially induced calcite precipitation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(8): 992-1001.
[27] SCHUURMAN I E. The compressibility of an air/water mixture and a theoretical relation between the air and water pressures[J]. Géotechnique, 1966, 16(4): 269-281.
[28] 刘侃, 朱小军, 张帆舸, 等. 含气泡土的孔隙流体压缩系数计算分析[J]. 岩土工程学报, 2017, 39(增刊2): 120-123. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2017S2031.htm LIU Kan, ZHU Xiao-jun, ZHANG Fan-ge, et al. Calculation of coefficient of compressibility for air-water mixture in gassy soils[J]. Chinese Journal of Geotechnical Engineering,2017, 39(S2): 120-123. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2017S2031.htm
[29] DORSEY N E. Properties of Ordinary Water-Substance[M]. New York: Reinhold Publishing Corporation, 1940.
[30] FENG K, MONTOYA B M. Influence of confinement and cementation level on the behavior of microbial-induced calcite precipitated sands under monotonic drained loading[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2016, 142(1): 04015057.
[31] JIANG M J, KONRAD J M, LEROUEIL S. An efficient technique for generating homogeneous specimens for DEM studies[J]. Computers and Geotechnics, 2003, 30(5): 579-597.
[32] KUHN M R, RENKEN H E, MIXSELL A D, et al. Investigation of cyclic liquefaction with discrete element simulations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140(12): 04014075.
-
期刊类型引用(12)
1. 谢永晟,杨果岳,王阳,杨少光. 剪切速率对水泥胶结钙质砂强度及变形的影响. 湘潭大学学报(自然科学版). 2024(01): 83-91 .  百度学术
百度学术
2. 陈军浩,张艳娥,王刚,王恒. 不同固结路径下钙质砂固结排水强度性状研究. 岩土力学. 2024(08): 2290-2298 .  百度学术
百度学术
3. 肖汉清,赵斌,熊力,陈令,秦朗,刘杰. 往复荷载作用下滨海滩涂软基长期性能劣化机制试验研究. 河南科学. 2024(09): 1325-1333 .  百度学术
百度学术
4. 杨振杰,张凌凯. 北疆白砂岩力学特性及其微观机制试验研究. 水利水电科技进展. 2024(05): 94-102 .  百度学术
百度学术
5. 刘鑫,李飒,尹福顺,姚婷. 基于动态图像技术的南海钙质土颗粒形态特征研究. 岩土工程学报. 2023(03): 590-598 .  本站查看
本站查看
6. 王欲敏,赵梦珍,梁旭之,李菁若,周启伟. 西南地区路用石灰岩粗集料矿物组成和物理力学性质的关联性分析. 土木工程学报. 2023(06): 136-144 .  百度学术
百度学术
7. 蒋超,陈杰,蒋昌波,姚震,梁海,伍志元. 柱状珊瑚砂静水沉降试验研究. 海洋学报. 2023(04): 57-67 .  百度学术
百度学术
8. 李钒,陈远中,廖洁,夏冰,樊科伟. 颗粒形状对钙质砂最终级配影响的试验研究. 河海大学学报(自然科学版). 2023(04): 41-45+71 .  百度学术
百度学术
9. 施勇,贾献林,吕国儿,李宝建. 钙质砂最大最小孔隙比的确定及其影响因素分析. 地基处理. 2023(04): 293-298 .  百度学术
百度学术
10. 沈扬,马英豪,芮笑曦. 波浪荷载作用下饱和钙质砂孔压特性及累积损失能量试验研究. 岩土力学. 2023(08): 2195-2204 .  百度学术
百度学术
11. 白思凯,杨超,刘建宏. 基于钙质砂形态参数的神经网络模式识别研究. 工业建筑. 2023(S1): 657-660+599 .  百度学术
百度学术
12. 李洪成,曾荣,杨天圆,牛智有. 玉米籽粒冲击破碎特性试验研究. 农业工程学报. 2022(07): 29-37 .  百度学术
百度学术
其他类型引用(25)




 下载:
下载: