Analytical solution and application of unsteady flow model under suspended curtain
-
摘要: 临海地铁深基坑多采用截水联合排水的降水措施,基坑周围的地下水因受海水补给影响多呈非稳定流动性状。为此,建立悬挂式止水帷幕及固定补给下基坑承压含水层抽水数学模型,采用Laplace变换和有限Fourier余弦变换获得水位降深在Laplace空间域内的解,再用Stehfest数值反演法得到其在实际空间的解析解。最后通过退化解和数值模拟分别验证其正确性并讨论分析其影响因素,得到以下结论:抽水后期,地下渗流趋于稳定后,止水帷幕插入比越大,坑内抽水含水层水位降深越大,而坑外抽水含水层水位降深不断减小;当固定补给距离基坑越近,坑内抽水含水层水位达到稳定的时间越短,且达到稳定后水位降深越小;坑外抽水含水层水位降深受含水层各向异性影响明显。同时,定义了相对降深比对固定补给影响分3个区:高影响区、过渡区和低影响区。针对不同影响区提出相应设计及施工方案以确保基坑的止降水效果。Abstract: The deep foundation pits of nearshore subways mostly adopt the dewatering measures of cutting water and draining, and the groundwater around the foundation pits shows unstable flow behavior due to the influences of seawater recharge. Therefore, a mathematical model for the pumping of confined aquifer in a foundation pit under suspended water curtain and fixed recharge is established. The Laplace transform and finite Fourier cosine transform are used to obtain the solution of the water level drop in the Laplace space domain, and then the analytical solution is obtained by using the Stehfest numerical inversion method in practical space. Finally, the correctness of the degradation solution and numerical simulation are verified, and the influencing factors are discussed. The conclusions are drawn as follows: (1) At the later stage of pumping, after the underground seepage tends to be stable, the larger the insertion ratio of the waterproof curtain, the greater the depth of the water level of the pumped aquifer in the pit, and the deeper the water level of the pumped aquifer outside the pit decreases. (2) When the fixed recharge is closer to the foundation pit, the shorter the time for the water level of the pumped aquifer in the pit to reach stability, and the smaller the water level drops after reaching stability. (3) The drop in the water level of the pumped aquifer outside the pit is obviously affected by the anisotropy of the aquifer. At the same time, a relative depth ratio is proposed to divide the impact of fixed recharge into three zones: high impact zone, transition zone and low impact zone. The corresponding design and construction plans are proposed for different zones to ensure the dewatering effects of the foundation pit.
-
Keywords:
- confined water /
- suspended curtain /
- non-steady flow /
- analytical solution /
- recharge zone
-
0. 引言
随着城市地下空间的不断开发利用,基坑的体量、规模和开挖深度逐年增加。富水地层的深基坑常存在承压含水层,施工过程中极易出现坑底承压水突涌、结构上浮、周边地表沉降等问题。为确保基坑及周边环境的安全,需要开展相关的地下水控制设计。当前这些设计多基于地下水稳定井流设计理论。但是地下水非稳定井流更能反映实际地下水运动规律,且止水帷幕的设置改变原有的地下水渗流,使得地下水的流动变得更为复杂[1-2]。因此,有必要开展基坑工程中的地下水非稳定井流的研究。
Theis[3]首次推导出实用的地下水非稳定井流完整井的计算公式。Neuman等[4-5]给出了完整井和非完整井单井抽水作用下潜水含水层的水位降深变化的解析解答。这些研究初步建立了非稳定井流理论。在此基础上,近些年有学者对不同类型含水层的不同降水系统展开进一步的研究。如任红蕾等[6]建立沟渠附近潜水非稳定渗流模型,应用阶梯函数的Laplace变换求出模型解析解,得出潜水位变动速度随时间的变化规律。李炯等[7]建立了考虑堵塞效应的定水头非完整回灌井非稳定流模型,通过Laplace及有限余弦Fourier变换,Stehfest数值逆变换得出半解析解,为回灌堵塞评估与预测提供参考。余俊等[8]应用叠加原理和分离变量法研究水位波动下有封底基坑二维渗流场孔压响应,得出显式解析解。
目前关于非稳定流计算理论的初始假设都相对简单,如将承压含水层假设为无限延伸的含水层等[9-12]。这样的假设可使计算相对简便,但与实际工程环境并不相符。近年来已有一些关于补给边界的研究。李炳蔚等[13]采用复变函数和直线补给边界下承压完整井流公式,在半无限域中分析出条形域防渗墙上钻孔压水试验渗流参数。冯庆高等[14]结合工程实际构建了侧向有限延伸的典型弱透水层−承压水层系统中非完整井非稳定流计算模型。这些研究大多单纯考虑补给边界下的井流计算,并未考虑止水帷幕等围护结构的隔水作用。曾超峰等[15-16]通过室内模型试验发现存在阻隔效应时可适当减少坑内降水井的数量实现同样的降水效果,因此实际降水设计应当考虑止水帷幕对基坑附近渗流场的影响。近期已有学者[17]对止水帷幕下深基坑内涌水量展开研究。武永霞等[18]先通过数值模拟回归分析方法得出只回灌时帷幕两侧水位差的计算公式,然后叠加已有只考虑抽水时水位差计算公式,并分析了抽灌承压水时帷幕两侧产生水位差的相关因素。彭祎等[19]采用闸坝改进阻力系数法对传统计算公式进行修正,得到了定量计算悬挂式帷幕基坑涌水量和坑外水位降深的公式。但以上都是基于稳定井流的研究,无法反映基坑降水过程中含水层地下水的非稳定流动特性。
综上所述,为了充分考虑悬挂式止水帷幕及固定补给对基坑附近地下水流动的影响,本文建立了悬挂式止水帷幕及固定补给下基坑承压含水层抽水数学模型,推导了模型解析解。并对本文解的合理性进行退化和数值模拟验证。最后,基于解析解分析了止水帷幕插入比、固定补给、承压土层各向异性对承压含水层地下水渗流和水位变化的影响。基于此提出固定补给影响分区方法并介绍相关工程应用,为临海深基坑工程合理有效的止降水设计和施工提供理论支撑与参考。
1. 模型的基本假定与构建
1.1 模型的工程背景
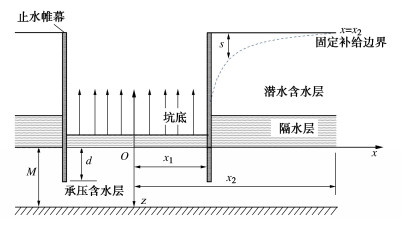
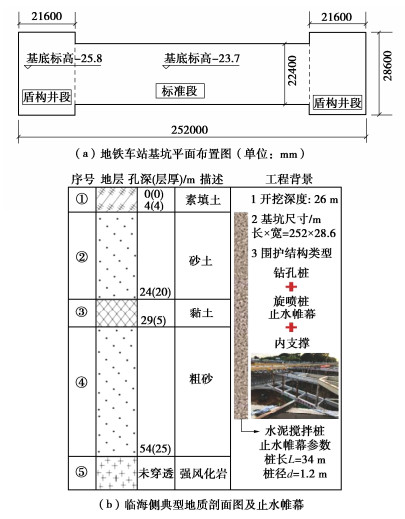
随着临海或临江地区城市地铁工程项目不断增多,涌现出大量紧邻水域环境施工的深基坑工程。此类项目的工程地质和水文地质条件中常存在透水性土层(如砂层、砾石层等)情况,地下水埋藏较浅(一般在1~3 m),地下水直接与海水(江水)发生水力联系。基坑降水措施多采用止水帷幕截水叠加坑内外降排水的联合方式。地铁车站主体结构埋深较大,止水帷幕通常需要穿越承压层,但其桩长又未能穿透不透水层。典型的地铁车站基坑平面布置、止水帷幕及地层分布见图 1和表 1。
表 1 土层分布及其特征Table 1. Distribution and characteristics of soil layers地层编号 岩性 平均厚度/m 含水层 ① 素填土 4 潜水层 ② 粗砂 20 潜水层 ③ 黏土 5 隔水层 ④ 粗砂 25 承压含水层 ⑤ 强风化岩 — 不透水层 由于临海地铁车站基坑平面呈长条形,长约252 m,标准段和盾构井的净宽分别为22.4,28.6 m,长宽比L/b≈10,因此可视为条形基坑。标准段和盾构井的基坑各自的埋深分别约为23.7,25.8 m。场地土层分布中第二、四层为粗砂,强透水层,考虑临海海水影响,此处存在固定补给,可假设为固定补给边界;基坑降水采用三轴搅拌桩止水帷幕,搅拌桩长34 m,未达到不透水层,可视为悬挂式止水帷幕。
1.2 基本假定及模型建立
图 2为悬挂式止水帷幕及固定补给下基坑承压含水层抽水二维轴对称计算模型。假定基坑为条形基坑,坐标原点O位于承压含水层顶板抽水井中心处,z轴向下为正。该模型主要采用以下假定:①不考虑上覆潜水含水层的水量补给;②承压含水层均质、各向异性、等厚;③x=x2处有固定补给,不考虑抽水井影响半径的影响;④抽水点位于承压含水层的顶部,考虑坑内井群降水,坑内承压水头线简化为水平线;⑤不考虑止水帷幕的厚度。
基坑宽度为2x1,承压含水层厚度为M,帷幕插入承压层的深度为d,坑内每延米抽水量为Q。
根据上述问题的描述和基本假定,建立相应的承压地下水渗流运动数学方程:
Kx∂2s(x,z,t)∂x2+Kz∂2s(x,z,t)∂z2=Ss∂s(x,z,t)∂t。 (1) 边界条件及初始条件为
s(x,z,0)=0, (2) ∂s(x1,z,t)∂x={0(0<z<d)−Q2Kx(M−d)(d<z<M), (3) s(x2,z,t)=0, (4) ∂s(x,0,t)∂z=0, (5) ∂s(x,M,t)∂z=0。 (6) 式中:t为时间(s);M为承压含水层厚度(m);d为止水帷幕插入承压含水层的深度(m);Q为每延米抽水井抽水量(m2/s);s为水头降深(m);Kx,Kz分别为承压含水层水平向和竖直向渗透系数(m/s);Ss为承压含水层储水率(m-1),表示水头变化1 m时从单位面积的含水层中释放的水量。
2. 模型的解析解及验证
2.1 模型的解析解
由悬挂式止水帷幕及固定补给下基坑承压含水层抽水计算模型可知,承压含水层水头降深s(x,z,t)为空间坐标x、z和时间t的函数。求解上述计算模型时,首先将模型进行Laplace变换:
¯s(x,z,p)=+∞∫0s(x,z,t)e−ptdt。 (7) 式中:p为Laplace变换变量。
根据初始条件(2),对方程(1)及边界条件(3)~(6)应用Laplace变换,得
Kx∂2¯s∂x2+Kz∂2¯s∂z2=Ssp¯s, (8) ∂¯s(x1,z,p)∂x={0(0<z<d)−Q2pKx(M−d)(d<z<M), (9) ¯s(x2,z,p)=0, (10) ∂¯s(x,0,p)∂z=0, (11) ∂¯s(x,M,p)∂z=0。 (12) 根据边界条件式(11),(12),对方程式(8)应用有限Fourier余弦变换,即
ˉsc=M∫0¯scos(nπzM)dz (n≠0), (13) ˉsc=M∫0¯sdz (n=0)。 (14) 当≠n≠0时,对方程(8)及边界条件(9),(10)应用式(13)变换,得
Kx∂2ˉsc∂x2−[Kz(nπM)2+Ssp]ˉsc=0, (15) ∂¯sc(x1,p)∂t=QM2Kx(M−d)npπsin(nπdM), (16) ˉsc(x2,p)=0。 (17) 方程(15)通解为
ˉsc=b1e−N1x+b2eN1x。 (18) 其中,N1=√[Kz(nπM)2+Ssp]1Kx,b1,b2为常数。
将边界条件(16)和(17)代入通解(18),分别可得
b1=−QMeN1x22nπKx(M−d)pN1β1sin(nπdM), (19) b2=QMe−N1x22nπKx(M−d)pN1β1sin(nπdM)。 (20) 其中,β1=eN1(x1−x2)+eN1(x2−x1),将b1,b2代入式(18)即可得到ˉsc。通过有限Fourier余弦逆变换求解:
¯s=1Mˉsc0+2M∞∑n=1ˉsccos(nπzM)。 (21) 对于ˉsc0,即当n=0重复上述步骤即可得
ˉsc0=Q[eN2(x2−x)−eN2(x−x2)]2KxpN2[eN2(x1−x2)+eN2(x2−x1)]。 (22) 其中,N2=√Ssp/Kx。令β2=eN2(x1−x2)+eN2(x2−x1),将式(18),(22)代入式(21),得
¯s=Q2KxpM[eN2(x2−x)−eN2(x−x2)N2β2+2M(M−d)π∞∑n=1eN1(x−x2)−eN1(x2−x)nN1β1cos(nπzM)sin(nπdM)]。 (23) 式(23)为水位降深s在Laplace空间域内的解。采用Stehfest数值反演方法对模型在实际空间的解求解[22]。Stehfest法逆变换形式如下:
s(x,z,t)=ln2tN∑i=1Vi¯s(x,z,p)。 (24) 式中:Vi为Stehfest数值逆变换法求和级数;p为经过Stehfest数值反演后取为ln2ti;N为偶数,一般取值范围为8~16。
将式(23)代入逆变换式(24),得
s(x,z,t)=Qx12KxMN∑i=1Vi{R1+2M(M−d)⋅Δ}。 (25) 式中,R1=e¯N2(x2−x)−e¯N2(x−x2)¯N2[e¯N2(x1−x2)+e¯N2(x2−x1)],¯N1= √[Kz(nπM)2+iSsln2/t]1x12Kx,¯N2=√iSsln2/x12Kxt,Δ=∞∑n=1R21ncos(nπzM)sin(nπdM),R2=e¯N1(x2−x)−e¯N1(x−x2)¯N1[e¯N1(x1−x2)+e¯N1(x2−x1)]。
式(25)即为悬挂式止水帷幕及固定补给下基坑承压含水层抽水计算模型解析解。
2.2 计算模型解析解的退化验证
若不考虑固定补给对坑承压含水层抽水计算的影响,即x2→∞,此时有
s(∞,z,t)=0。 (26) 式(25)可简化为
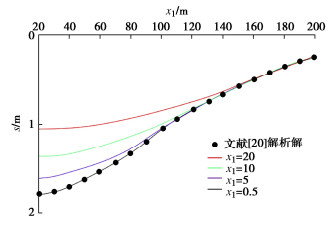
s∞=Qx12KxMN∑i=1Vi[e¯N2(x1−x)¯N2−2M(M−d)π⋅∞∑n=1e¯N1(x1−x)n¯N1cos(nπzM)sin(nπdM)]。 (27) 式(27)为仅考虑悬挂式止水帷幕影响的模型解析解。基于该公式,对基坑不同宽度下减压降水时坑外承压含水层中水头降深(z=0处)进行计算,结果见图 3。
由图 3可见,随着基坑宽度x1逐渐减小,水头降深s逐渐逼近文献[20]中承压含水层非完整井的解答,这表明式(25)可退化为与已知解的相同结果,验证了式(25)解析解的正确性和可靠性。
2.3 模型解析解的数值验证
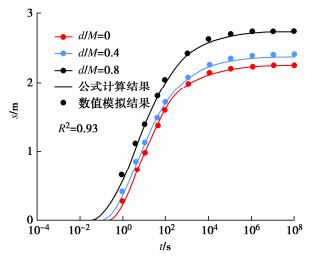
采用GeoStudio有限元软件中的Seep/W模块建立二维瞬态渗流数值模型进一步验证模型解析解的准确性。有限元模型的边界条件同上述模型的基本假定,各参数取值:Q=5×10-5 m2/s(每延米流量),M=20 m,x1=20 m,Ss=2×10-5 m-1,Kx=Kz=10-4 m/s。由于实际工程中止水帷幕的渗透系数远小于基坑土的渗透系数,为了加快计算收敛速度,将帷幕简化为不透水边界;对降水井定义为给定水头边界进行瞬态分析,即用12 d将基坑内水位降到设计水位后保持不变,模型左侧、基坑内含水土层底边界、含水土层顶边界均采用不透水边界,模型右侧设为透水边界。计算结果见图 4。
由图 4知,解析解的计算结果与数值模拟结果吻合较好,相关系数R2=0.93,进一步验证了式(25)解析解的正确性。
3. 模型影响因素分析与讨论
根据已建立的考虑悬挂式止水帷幕以及固定补给的基坑承压含水层抽水计算模型,分析不同影响因素下承压含水层地下水渗流和水位变化情况。在以下分析中,各参数取值为:Q=5×10-5 m2/s(每延米的流量),M=20 m,x1=20 m,Ss=2×10-5 m-1,Kx=Kz=10-4 m/s。
3.1 止水帷幕插入比的影响
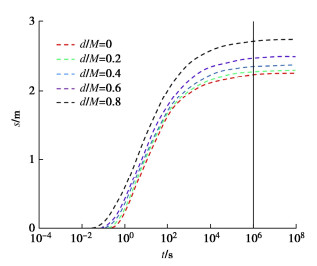
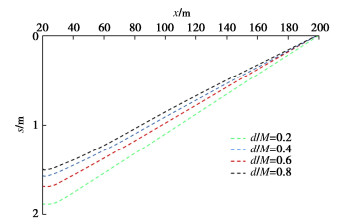
图 5为不同止水帷幕插入比情况下,当x2=200 m时,在x=x1,z=20 m处基坑内抽水含水层水位降深随时间变化的情况。其中止水帷幕插入比d/M分别为0,0.2,0.4,0.6,0.8。从图 5中可知,在抽水初期,止水帷幕插入比对基坑内降深的影响相对较小。这是因为抽水初期抽水对地下水渗流场的影响较小,受到边界环境的影响很小。当地下水流迅速向井口流动,影响范围进一步扩大,此时止水帷幕插入的作用体现出来。抽水后期(t=106 s后),当地下渗流趋于稳定时,止水帷幕插入比越大,坑内抽水含水层水位降深越大,且随着止水帷幕插入比的逐渐增大,坑内降深的增长幅度也不断增大。说明增大止水帷幕插入比可以很好地降低基坑内的水位。
图 6为坑内抽水含水层水位最终降深与不同止水帷幕插入比的关系。可以看出坑内抽水含水层水位降深随着止水帷幕插入深度的增加而不断增大。当止水帷幕插入比d/M > 0.6时,水头降深增大会更加显著。在实际基坑工程的止水帷幕设计时,建议开展止水帷幕插入比d/M的优化设计,使其不仅能满足坑内水位降深的要求,同时节约施工经济成本。
图 7为止水帷幕插入比d/M=0.2,0.4,0.6,0.8的情况下,当x2=200 m时,在t=106 s,z=0 m处基坑外抽水含水层水位降深空间分布情况。与基坑内水位变化相比,坑外水位降深受止水帷幕插入比变化的影响相对要小。这主要是因为在x=x2处的固定补给可以不断补给地下水。坑外抽水含水层水位降深随着止水帷幕插入比的增大不断减小,由于止水帷幕对渗流的阻断作用,当止水帷幕插入得越深,从坑外流入坑内的渗流路径越长,说明止水帷幕的阻断效果越好,坑外水位降深也越小。
3.2 固定补给的影响
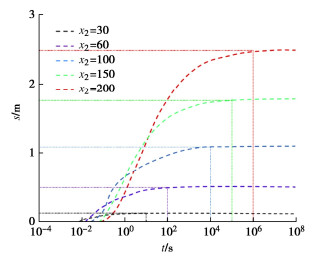
图 8为不同固定补给边界距离下,当d/M=0.6,x=x1时,在z=20 m处坑内抽水含水层水位降深随时间变化的情况。其中固定水头边界与基坑中心距离分别设定为30,60,100,150,200 m。从图 8中可知,坑外固定补给对坑内抽水降深影响很大。当固定补给距离基坑越近,坑内抽水含水层水位达到稳定的时间越短,且达到稳定后水位降深也越小。
当固定补给距离基坑中心30,60,100,150,200 m时,坑内含水层水位达到稳定所需时间分别约为10,102,104,105,106 s,稳定后的水位降深分别约为0.2,0.5,1.1,1.8,2.5 m;比较固定补给距离最近和最远(30,200 m)两种情况,稳定所需时间增加了105倍,稳定后的水位降深增大了12倍。这是因为当固定补给水源距离基坑越近时,基坑越容易得到边界固定补给,坑内水位受到补给量也越大,故坑内的水位降深越小;当固定补给水源距离基坑越远时,补给的延迟效应越大,故坑内降深达到稳定所需的时间越长。
图 9为当d/M=0.6,t=106 s时,固定补给与基坑中心距离分别为30,60,100,150,200 m,在z=0 m处基坑外抽水含水层水位降深空间分布情况。与无固定补给时(图 3)相比,固定补给源的补给效应“中和”了群井抽水形成的漏斗曲线,抽水含水层水位降深由原来的曲线分布变为趋近直线分布。固定补给距离为30 m时基坑外最大水位降深仅为0.1 m,而固定补给距离为200 m时,最大水位降深可增大到1.6 m。由此可见,固定补给对基坑外降深的影响很大。因此,实际工程中,如遇基坑周围存在近距离的固定补给时,不可忽略其对基坑降水的影响,必要时需采取相应处理措施(如阻断补给)。
3.3 土层各向异性的影响
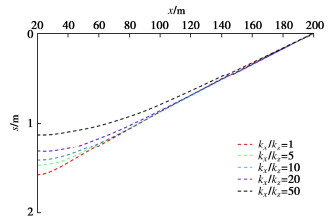
图 10为土层各向异性的情况下,在t=1 d,z=0 m处基坑外抽水含水层水位降深空间分布情况。其中渗透系数比Kx/Kz分别为1,5,10,20,50。计算结果表明,基坑外抽水含水层水位降深受含水层各向异性影响明显,且随含水层各向异性程度的增加,水位降深随之减小,最后趋于均匀。
4. 工程应用
4.1 补给影响区的划分
相对降深比Δ按下式定义:
Δ=(s0−s)/s0。 (28) 式中:s0为无固定补给时的最终降深,按式(27)计算降深值;s为存在固定补给时的计算降深,按式(25)计算降深值。
根据前文解析解编制了“临海基坑止降水设计及施工软件”,划分了补给影响区域并提出相应设计施工建议。补给区域划分流程如下,计算软件的界面见图 11:①收集工程区域地形地貌、岩土层分布情况、各岩土层计算参数及地下水分布情况。②输入基本参数及设计参数,计算不考虑补给时最终降深s0;当成层土时可概化成一层土,其等效渗透系数按各含水层厚度加权平均。③输入x2,计算补给距离下的计算降深s。④按式(28)计算相对降深比Δ;⑤根据相对降深比Δ,按表 2确定所属的补给区域及相应的设计施工建议。
表 2 补给区域划分方法及设计施工建议Table 2. Supply zoning method and suggestions for design or construction相对降深比Δ 补给区域 设计施工建议 Δ⩾50% 高影响区 隔断补给区域,如围堰或其他隔断措施 10%⩽Δ<50% 过渡区 调整设计参数,如抽水井设计抽水量、止水帷幕插入深度等 Δ<10% 低影响区 常规设计施工 当相对降深比Δ≥50%时,判断为“补给高影响区”,即固定补给源距离基坑较近且流量较大,其对基坑抽水影响极大,此时采用一般的降水措施难以保证坑内降水效果,实际工程可能需要采取隔断补给源的措施,如围堰施工等;当10%≤Δ < 50%时,判断为“补给过渡区”,即固定补给源距离基坑较远且流量较小,其对基坑抽水影响相对较小,但按常规降水设计大多不能取得较好的降水效果,可通过调整设计参数确保基坑降水效果,如增大基坑抽水井的设计抽水量或增加止水帷幕插入深度等;当Δ < 10%时,判断为“补给低影响区”,此时固定补给源通常距离基坑远且流量小,其对基坑抽水影响很小,可忽略不计,即等同于无固定补给,可按常规的基坑降水设计和施工。
4.2 补给分区的工程应用
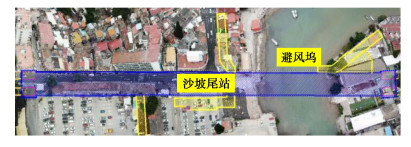
(1)厦门地铁南延段沙坡尾车站的基坑深度为22.85 m,基坑所处地层为杂填土、淤泥质粉质黏土、中粗砂、全风化花岗岩、散体状强风化花岗岩,其中淤泥质黏土土层厚度较厚,该地铁站下穿一与外海交接的避风坞(见图 12),水域宽60.0~100.0 m,河床底标高为-1.18~0.0 m,受每年不定时河道清淤的影响。基坑场地内分布有潜水和承压水,其中不透水层的淤泥质黏土土层厚度较厚。由于车站局部下穿避风坞,车站顶板距离避风坞底约1.5 m,对基坑抽水影响极大。计算得到相对降深比Δ=92%,判断属于“补给高影响区”,应采用措施隔断补给水源。最终选择施工期间先对避风坞进行围堰施工。
围堰堰身结构填筑开山土石,围堰外侧自坡顶向下坡率为1∶2.5,坡面自上而下依次为干砌块石300 mm,二片石300 mm。围堰内侧自坡顶向下至原泥面标高处坡率为1∶3,坡面依次为二片石200 mm,土工布(350 g/m2),最后回填黏性土。临海侧设置闸阀,围堰中埋设2根Ø2000 mm钢管联通海域侧与避风坞侧。
沙坡尾站基坑施工期间降水效果良好。车站施工完成后,拆除围堰,恢复避风坞原状。
(2)某滨海深基坑工程承压含水层厚度约为26.7 m[21],场地内分布有潜水和承压水,工程设计地下连续墙插入承压含水层深度11.0 m,为悬挂式止水帷幕。基坑中心至临海补给的最近距离为197.0 m。最初的设计抽水量为17.9 m3/h,此时计算得到相对降深比Δ=29%,判断属于“补给过渡区”,对基坑抽水影响相对较小。该工程对基坑抽水井的设计抽水量进行了调整,调整之后的抽水量为27.8 m3/h,调整后相对降深比Δ=7.8%,根据抽水井测得的实测降深与计算降深相差在8%以内,可满足基坑内的降水要求。
5. 结论
(1)建立了悬挂式止水帷幕及固定补给下基坑承压含水层抽水数学模型,计算模型考虑了止水帷幕以及固定补给的边界条件,并通过数值逆变换推导了相应的解析解。
(2)在抽水初期,止水帷幕插入比对坑内降深影响较小。但到抽水后期时,地下渗流趋于稳定后,止水帷幕插入比越大,坑内抽水含水层水位降深越大,而坑外抽水含水层水位降深不断减小。
(3)坑外固定补给对坑内抽水降深的影响出现在抽水中后期。当固定补给距离基坑越近,坑内抽水含水层水位达到稳定的时间越短,且达到稳定后水位降深越小。固定补给距离基坑越近,对坑内外的水位都会产生更大的影响。
(4)根据相对降深比将固定补给影响划分为补给的高影响区、过渡区和低影响区三个区域;高影响区建议采取隔断补给源措施,过渡区建议调整止降水设计参数;低影响区无需考虑补给影响。
利益冲突声明/Conflict of Interests:所有作者声明不存在利益冲突。All authors disclose no relevant conflict of interest.作者贡献/Authors' Contributions:陈东霞和杨雪菲推导分析了悬挂式止水帷幕的非稳定流模型解析解;陈东霞、杨雪霏和孟旭参与论文的写作和修改,杨明辉参与了论文讨论;陈波和袁博提供了工程实例资料。所有作者均阅读并同意最终稿件的提交。The analytical solution was derived and analyzed by CHEN Dongxia and YANG Xuefei. The manuscript was drafted and revised by CHEN Dongxia, YANG Xuefei and MENG Xu and was discussed with the participation of YANG Minghui. Engineering case data were provided by CHEN Bo and YUAN Bo. All the authors have read the last version of paper and consented for submission. -
表 1 土层分布及其特征
Table 1 Distribution and characteristics of soil layers
地层编号 岩性 平均厚度/m 含水层 ① 素填土 4 潜水层 ② 粗砂 20 潜水层 ③ 黏土 5 隔水层 ④ 粗砂 25 承压含水层 ⑤ 强风化岩 — 不透水层 表 2 补给区域划分方法及设计施工建议
Table 2 Supply zoning method and suggestions for design or construction
相对降深比Δ 补给区域 设计施工建议 Δ⩾50% 高影响区 隔断补给区域,如围堰或其他隔断措施 10%⩽Δ<50% 过渡区 调整设计参数,如抽水井设计抽水量、止水帷幕插入深度等 Δ<10% 低影响区 常规设计施工 -
[1] 黄娟, 和振, 余俊, 等. 考虑封底效应的圆形围堰渗流场解析解及应用[J]. 岩土工程学报, 2023, 45(12): 2510-2518. doi: 10.11779/CJGE20221101 HUANG Juan, HE Zhen, YU Jun, et al. Analytical solutions and application of circular cofferdams considering backseal effects[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(12): 2510-2518. (in Chinese) doi: 10.11779/CJGE20221101
[2] 余俊, 李东凯, 和振, 等. 带有两端防渗墙坝基的各向异性渗流解析解[J]. 岩土力学, 2023, 44(8): 2381-2388. YU Jun, LI Dongkai, HE Zhen, et al. Analytical solution of anisotropic seepage in dam foundation with anti-seepage walls at both ends[J]. Rock and Soil Mechanics, 2023, 44(8): 2381-2388. (in Chinese)
[3] THEIS C V. The relation between the lowering of the Piezometric surface and the rate and duration of discharge of a well using ground-water storage[J]. Eos, Transactions American Geophysical Union, 1935, 16(2): 519-524. doi: 10.1029/TR016i002p00519
[4] NEUMAN S P, WITHERSPOON P A. Applicability of current theories of flow in leaky aquifers[J]. Water Resources Research, 1969, 5(4): 817-829. doi: 10.1029/WR005i004p00817
[5] NEUMAN S P, WITHERSPOON P A. Theory of flow in a confined two aquifer system[J]. Water Resources Research, 1969, 5(4): 803-816. doi: 10.1029/WR005i004p00803
[6] 任红蕾, 陶月赞, 林飞, 等. 排水期沟渠附近潜水非稳定流解析解及参数反演[J]. 水利学报, 2022, 53(1): 117-125. REN Honglei, TAO Yuezan, LIN Fei, et al. Analytical solution and parameter inversion of transient seepage model of groundwater near ditch during drainage period[J]. Journal of Hydraulic Engineering, 2022, 53(1): 117-125. (in Chinese)
[7] 李炯, 李明广, 詹红兵, 等. 考虑井周堵塞效应的定水头非完整回灌井流模型[J]. 岩土工程学报, 2024, 46(1): 207-215. doi: 10.11779/CJGE20221085 LI Jiong, LI Mingguang, ZHAN Hongbing, et al. Model for well hydraulics of constant-head injection using a partially penetrating well considering clogging in well vicinity[J]. Chinese Journal of Geotechnical Engineering, 2024, 46(1): 207-215. (in Chinese) doi: 10.11779/CJGE20221085
[8] 余俊, 张志中, 郑靖凡, 等. 水位波动条件下有封底基坑渗流场孔压解析解[J]. 岩土力学, 2023, 44(12): 3415-3423. YU Jun, ZHANG Zhizhong, ZHENG Jingfan, et al. Analytical solution of pore pressure in seepage field of foundation pit with a sealed bottom under water level fluctuation[J]. Rock and Soil Mechanics, 2023, 44(12): 3415-3423. (in Chinese)
[9] 吴纲, 孙红月, 陈永珍, 等. 完整井定降深抽水非稳定流水位流量近似解[J]. 岩石力学与工程学报, 2017, 36(12): 3095-3101. WU Gang, SUN Hongyue, CHEN Yongzhen, et al. An approximate solution of unsteady flow under fixed-drop pumping[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(12): 3095-3101. (in Chinese)
[10] 王旭东, 殷宗泽, 宰金珉, 等. 柱坐标系下地下水非稳定流模拟的有限层法[J]. 岩土工程学报, 2009, 31(1): 15-20. doi: 10.3321/j.issn:1000-4548.2009.01.002 WANG Xudong, YIN Zongze, ZAI Jinmin, et al. Finite layer method for numerical simulation of unsteady groundwater flow in cylindrical coordinate system[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(1): 15-20. (in Chinese) doi: 10.3321/j.issn:1000-4548.2009.01.002
[11] 彭祎, 成建梅, 马郧, 等. 二元结构含水层悬挂式帷幕深基坑降水计算方法研究[J]. 工程勘察, 2021, 49(6): 38-45. PENG Yi, CHENG Jianmei, MA Yun, et al. Study on calculation method of dewatering in deep excavation with suspended cut-off curtain in dual aquifer[J]. Geotechnical Investigation & Surveying, 2021, 49(6): 38-45. (in Chinese)
[12] 葛晓永, 张姝伊, 陈征, 等. 悬挂式止水帷幕圆形基坑承压含水层地下水非稳定流计算[J]. 水资源与水工程学报, 2022, 33(1): 178-183. doi: 10.11705/j.issn.1672-643X.2022.01.25 GE Xiaoyong, ZHANG Shuyi, CHEN Zheng, et al. Calculation of non-steady groundwater flow in confined aquifer of a circular excavation pit with suspended waterproof curtain[J]. Journal of Water Resources and Water Engineering, 2022, 33(1): 178-183. (in Chinese) doi: 10.11705/j.issn.1672-643X.2022.01.25
[13] 李炳蔚, 吴吉春. 防渗墙钻孔压水试验渗流参数研究[J]. 岩石力学与工程学报, 2016, 35(2): 396-402. LI Bingwei, WU Jichun. Study of seepage parameters measured in water pressure test inside boreholes in cut-off wall[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(2): 396-402. (in Chinese)
[14] 冯庆高, 蔡兵华, 冯晓腊, 等. 侧向有限越流承压含水层中非完整井非稳定流模型及解析解[J]. 岩土力学, 2021, 42(1): 168-176. FENG Qinggao, CAI Binghua, FENG Xiaola, et al. Analytical solutions of transient flow model for a partially penetrating well in a finite leaky confined aquifer system[J]. Rock and Soil Mechanics, 2021, 42(1): 168-176. (in Chinese)
[15] 曾超峰, 张祖浩, 高文华, 等. 坑外群桩阻隔效应对基坑内抽水引发变形影响机制[J]. 岩土工程学报, 2023, 45(11): 2378-2386. doi: 10.11779/CJGE20220255 ZENG Chaofeng, ZHANG Zuhao, GAO Wenhua, et al. Barrier effects of surrounding group piles on deformation of foundation pits induced by dewatering[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(11): 2378-2386. (in Chinese) doi: 10.11779/CJGE20220255
[16] 曾超峰, 蔡钢, 朱龙, 等. 考虑既有地铁车站阻隔效应的基坑抽水致沉模型试验研究[J]. 岩石力学与工程学报, 2023, 42(10): 2566-2577. ZENG Chaofeng, CAI Gang, ZHU Long, et al. Laboratory-scale model test on settlement incurred by foundation pit dewatering considering the barrier effect of pre-existing metro station[J]. Chinese Journal of Rock Mechanics and Engineering, 2023, 42(10): 2566-2577. (in Chinese)
[17] 李瑛, 陈东, 刘兴旺, 等. 悬挂式止水帷幕深基坑减压降水的简化计算方法[J]. 岩土力学, 2021, 42(3): 826-832, 862. LI Ying, CHEN Dong, LIU Xingwang, et al. Simplified calculation method of decompression dewatering for deep excavation with suspended waterproof curtain[J]. Rock and Soil Mechanics, 2021, 42(3): 826-832, 862. (in Chinese)
[18] 武永霞, 沈水龙. 悬挂式止水帷幕下基坑内外抽灌承压水的计算方法[J]. 岩土工程学报, 2023, 45(9): 1971-1978. doi: 10.11779/CJGE20220564 WU Yongxia, SHEN Shuilong. Method for calculating pumping and recharging confined water inside and outside excavations under suspended waterproof curtain[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(9): 1971-1978. (in Chinese) doi: 10.11779/CJGE20220564
[19] 彭祎, 成建梅, 马郧, 等. 基于改进阻力系数法的悬挂式帷幕基坑渗流计算[J]. 地质科技通报, 2021, 40(4): 179-186. PENG Yi, CHENG Jianmei, MA Yun, et al. Seepage calculation of foundation with suspended curtain based on improved resistance coefficient method[J]. Bulletin of Geological Science and Technology, 2021, 40(4): 179-186. (in Chinese)
[20] 杨天行. 地下水流向井的非稳定运动的原理及计算方法[M]. 北京: 地质出版社, 1980. YANG Tianxing. Principle and Calculation Method of Unsteady Movement of Groundwater Flowing to Wells[M]. Beijing: Geological Publishing House, 1980. (in Chinese)
[21] 武永霞. 基坑止水帷幕对含水层渗流作用的计算方法研究[D]. 上海: 上海交通大学, 2016. WU Yongxia. Method of Barrier Effect of Waterproof Curtain on Groundwater Seepage during Dewatering in Aquifers[D]. Shanghai: Shanghai Jiao Tong University, 2016. (in Chinese)
-
其他相关附件



 下载:
下载: