重塑超固结饱和黏土蠕变试验与蠕变模型

胡敏云; 肖斌; 陆雨珂; 张雨惠; 张勇

doi:10.11779/CJGE2023S10040

重塑超固结饱和黏土蠕变试验与蠕变模型 English Version

胡敏云^{1, 2,},
肖斌^{1, 3},
陆雨珂⁴,
张雨惠¹,
张勇^1, ,

1.
浙江工业大学土木工程学院, 浙江杭州 310023
2.
中国水利水电科学研究院, 北京 100048
3.
浙江同济科技职业学院, 浙江杭州 311231
4.
浙江工业大学工程设计集团有限公司, 浙江杭州 310014

基金项目:

国家自然科学基金项目 51878616

浙江省基础公益研究计划项目 LHY19E090002

详细信息

作者简介:
胡敏云(1970—)，女，博士，教授，主要从事特殊土力学特性与模型方面的研究工作。E-mail: humy@iwhr.com

通讯作者:
张勇, E-mail: zhangyong@zjut.edu.cn

中图分类号: TU432
计量
- 文章访问数: 224
- HTML全文浏览量: 39
- PDF下载量: 73
出版历程
- 收稿日期: 2023-07-04
- 网络出版日期: 2023-11-23
- 刊出日期: 2023-10-31

Creep tests and creep model for reconstituted over-consolidated saturated clay

HU Minyun^{1, 2,},
XIAO Bin^{1, 3},
LU Yuke⁴,
ZHANG Yuhui¹,
ZHANG Yong^1, ,

1.
College of Civil Engineering, Zhejiang University of Technology, Hangzhou 310023, China
2.
China Institute of Water Resources and Hydropowver Research, Beijing 100048, China
3.
Zhejiang Tongji Vocational College of Science and Technology, Hangzhou 311231, China
4.
Zhejiang University of Technology Engineering Design Group., Ltd., Hangzhou 310014, China

摘要

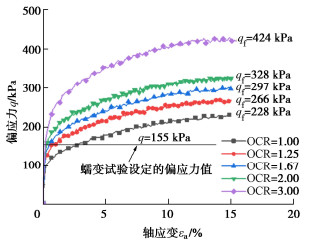
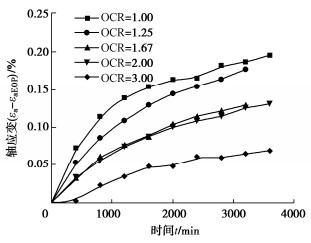
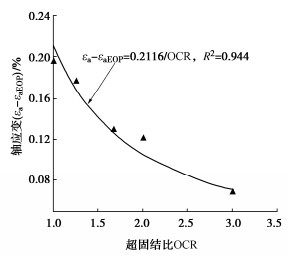
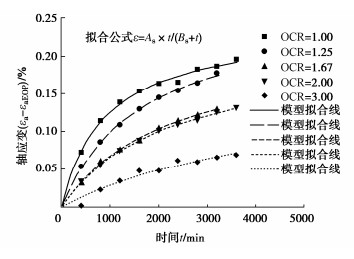
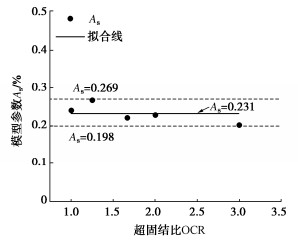
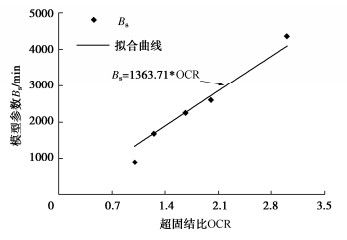
摘要: 采取杭州地区黏土制备重塑超固结土样（OCR=1.00，1.25，1.67，2.00，3.00）进行三轴剪切蠕变试验，研究超固结饱和黏土的时间变形特性和蠕变模型，对模型参数取值进行了分析。结果表明，重塑超固结饱和黏土的应力应变曲线具有应变硬化特征，在恒定偏应力下土样的时间变形曲线具有双曲线特征；超固结比越大，施加偏应力初始阶段试样中产生的超静孔压越小，试样变形进入蠕变阶段的时间越早，且在一定时间内试样的蠕变量发展越小。基于“孔压消散法”确定了超固结土的蠕变起始时间，采用双曲线蠕变模型可以高度拟合超固结饱和黏土剪切蠕变发展规律，曲线拟合分析表明：在相同的偏应力下，不同超固结比试样的最终蠕变量大致相等，但是超固结比越大时，土样蠕变发展越缓慢，表现为双曲线蠕变模型参数A_s在超固结比变化时几乎保持为常量，参数B_s则随超固结比的增大近似呈线性增长。
- 超固结饱和黏土 /
- 三轴蠕变试验 /
- 蠕变模型 /
- 模型参数
Abstract: The triaxial shear creep tests are carried out on the reconstituted over-consolidated clay samples (OCR=1.00, 1.25, 1.67, 2.00, 3.00) from Hangzhou, China. The time-dependent deformation characteristics and creep model for the over-consolidated saturated clay are studied, and the values of model parameters are analyzed. The results show that the stress-strain curve of the reconstituted over-consolidated saturated clay has strain-hardening characteristics. The time-deformation curves of the over-consolidated clays under constant deviator stress are of hyperbolic characteristics. The larger the over-consolidation ratio, the smaller the excess pore pressure generated at the initial stage of the deviator stress application, the earlier the creep stage starts, and the smaller the creep evolution of the sample within a certain time. Based on the "pore pressure dissipation method", the t_EOP of the over-consolidated clay is determined. The hyperbolic creep model can highly fit the shear creep curves of the over-consolidated saturated clay. The curve fitting analysis shows that under the same deviator stress, the final creep values of the samples with different over-consolidation ratios are roughly equal. However, the larger the over-consolidation ratio, the slower the creep development of clay. The hyperbolic creep model parameter A_s almost remains constant when the over-consolidation ratio changes, while the parameter B_s approximately linearly increases with the increase of the over-consolidation ratio.
- over-consolidated saturated clay /
- triaxial creep test /
- creep model /
- model parameter

HTML全文

0. 引言

多元复合地基可同时拥有多种增强体的特性，故其在道路、机场、码头等软土地基处理的工程中被广泛应用^[1-3]。常见的多元复合地基处理形式有塑料排水板联合水泥搅拌桩复合地基、长板-短桩复合地基、散体材料桩联合不透水桩复合地基等。多元复合地基固结理论是预测复合地基沉降和沉降控制设计的基础，对其固结理论的研究也愈发得到学者们的重视。

多元复合地基具有地基形式多样化、边界条件复杂化、土体及增强体材料差异较大等特点，使得相关的理论研究还处于发展阶段。Zhang等^[4-5]建立了将塑料排水板联合粉喷桩复合地基等效为均质土体的多元复合地基固结解析解；陈蕾等^[6]建立了以排水板为中心，将粉喷桩等效为不透水环位于单元外围的多元复合地基固结的解析解和数值解；刘吉福^[7]认为复合地基中的排水桩和不透水桩均存在孔压，且假定孔压随深度成比例变化；Ye等^[8-9]建立以水泥搅拌桩为中心，将排水板等效为环状排水墙位于单元外围的模型，并假定土体中的水流由单元中心向外围排水墙发生渗流；Zhang等^[10]同样采用排水墙的方法建立了长板-短桩复合地基固结解析解；杨涛等^[11]建立了考虑碎石桩为恒井阻时在瞬时荷载作用下的碎石桩-不排水桩复合地基固结解析解；Lu等^[12-13]提出3种多元复合地基模型，建立了考虑排水板为恒井阻时塑料排水板联合不透水桩复合地基固结解析解。上述研究均未考虑排水板或砂井的淤堵效应。

随着固结的发展，排水体将产生淤堵效应，已有部分学者对其展开研究。Deng等^[14-15]假定排水板的井阻随时间及随时间和深度同时增大，研究了排水板单一复合地基的固结特性；郭霄等^[16]基于Deng等^[15]变井阻假定，推导了竖井地基等应变条件下径向固结的控制方程及解析解；江文豪等^[17]同样基于Deng等^[15]变井阻假定，推导了考虑土体中径-竖向渗流的砂井地基固结理论。现有关于淤堵效应的研究均以竖井地基为模型，多元复合地基固结理论均未考虑淤堵效应。

本文在现有研究的基础上，考虑排水板的淤堵效应，假定其井阻随时间和深度同时衰减，推导了该问题的固结控制方程及4种常见荷载下的解析解答，该解答同时将排水板的涂抹作用、水泥搅拌桩的扰动效应以及土体的竖向与径向渗流考虑在内。然后，通过与现场案例进行对比，验证了本文的正确性。最后，基于解析解答分析井阻效应、井阻因子、附加应力沿深度分布形式对多元复合地基的固结度及孔压的影响。

1. 计算模型

1.1 模型的建立

在实际工程中，多元组合桩复合地基大多以三角形、矩形等规则形式布置，模型单元可以塑料排水板或水泥搅拌桩为中心划分单元，本文以卢萌盟等^[13]提出的适用于多桩型任意排列形式布置的模型C为研究对象。如所示，在三角形布置方式下，以塑料排水板为中心进行单元划分，单元外围同时包含 ${n_{\text{d}}}$ 个塑料排水板和 ${n_{\text{p}}}$ 个水泥搅拌桩，按面积等效的原则，外围排水板和水泥搅拌桩的等效个数均为1个，模型单元中心及外围均有排水板，因此模型中的孔隙水沿径向同时存在向内和向外的双向渗流。为复合地基等效单元的计算模型，单元中心排水板的涂抹区为半径 $r$ 在 ${r_{\text{d}}}\sim{r_{{\text{s1}}}}$ 之间的环形影响区，该涂抹区土体的渗透系数为 ${k_{{\text{s1}}}}$ ；由单元外围的排水板引起的涂抹作用和水泥搅拌桩施工造成的扰动效应共同作用的影响区为半径 $r$ 在 ${r_{{\text{s2}}}}\sim{R_e}$ 之间的环形影响区，该影响区土体的渗透系数为 ${k_{{\text{s2}}}}$ ；半径 $r$ 在 ${r_{{\text{s1}}}}\sim{r_{{\text{s2}}}}$ 间为未扰动的土体，其渗透系数为 ${k_{\text{h}}}$ 。

图 1 地基单元划分与等效模型

Figure 1. Selection of typical units and equivalent model

下载: 全尺寸图片幻灯片

图 2 复合地基计算模型

Figure 2. Model for composite foundation

下载: 全尺寸图片幻灯片

单元中心排水板按环形等效原则^[18]进行等效，即排水板的周长和面积在等效前后均保持不变的情况下，将排水板等效为环状排水体。表达式如下：

${r_{\text{d}}} = \frac{{\omega + b}}{{\text{π }}}\text{，}$

(1)

$\omega b = \zeta {\text{π }}r_{\text{d}}^2。$

(2)

式中： ${r_{\text{d}}}$ 为中心排水板的等效半径； $\omega$ ， $b$ 分别为排水板的宽度和厚度； $\zeta$ 为排水板的面积折减系数，通过该参数来保证等效后环形排水体的截面积与排水板的截面积相同。面积折减系数可表示为

$\zeta = \frac{{{\text{π }}\omega b}}{{{{(\omega + b)}^2}}}。$

(3)

中心排水板引起的涂抹区的半径和渗透系数与单个排水板引起的涂抹区的半径和渗透系数的值相同，即 ${r_{{\text{s1}}}}{\text{ = }}{r_{{\text{sd}}}}$ ， ${k_{{\text{s1}}}}{\text{ = }}{k_{{\text{sd}}}}$ 。由单元外围排水板引起的涂抹作用和水泥搅拌桩施工造成的扰动效应共同作用的影响区的面积为 ${n_{\text{d}}}$ 个塑料排水板的涂抹区面积和 ${n_{\text{p}}}$ 个水泥搅拌桩扰动区的面积之和，计算式如下：

${r_{{\text{s2}}}} = \sqrt {R_{\text{e}}^2 - {n_{\text{d}}}(r_{{\text{sd}}}^2 - r_{\text{d}}^2) - {n_{\text{p}}}(r_{{\text{sp}}}^2 - r_{\text{p}}^2)} 。$

(4)

式中： ${n_{\text{d}}}$ 和 ${n_{\text{p}}}$ 分别为单元外围塑料排水板和水泥搅拌桩的数量； ${R_{\text{e}}}$ 为影响区半径； ${r_{\text{p}}}$ 为单个水泥搅拌桩的半径； ${r_{{\text{s1}}}}$ 为单元中心排水板引起的扰动区的外半径； ${r_{{\text{s2}}}}$ 为单元外围影响区的内半径； ${r_{{\text{sd}}}}$ 和 ${r_{{\text{sp}}}}$ 分别为单个排水板引起的涂抹区和单个水泥搅拌桩引起的扰动区的半径。

对于外围排水板引起的涂抹作用和水泥搅拌桩施工造成的扰动效应共同作用下的渗透系数 ${k_{{\text{s2}}}}$ ，按面积的加权平均值计算，计算式如下：

${k_{{\text{s2}}}} = \frac{{{n_{\text{d}}}{k_{{\text{sd}}}}(r_{{\text{sd}}}^2 - r_{\text{d}}^2) + {n_{\text{p}}}{k_{{\text{sp}}}}(r_{{\text{sp}}}^2 - r_{\text{p}}^2)}}{{{n_{\text{d}}}(r_{{\text{sd}}}^2 - r_{\text{d}}^2) + {n_{\text{p}}}(r_{{\text{sp}}}^2 - r_{\text{p}}^2)}} \text{，}$

(5)

式中， ${k_{{\text{sd}}}}$ 和 ${k_{{\text{sp}}}}$ 分别为单个排水板引起的涂抹区和单个水泥搅拌桩引起的扰动区的渗透系数。

由复合地基等效单元的计算模型可得，影响区半径为

$R_{\text{e}}^2 = \frac{{{A_{\text{n}}} - {A_{{\text{d1}}}} - {A_{{\text{p1}}}}}}{{\text{π }}} 。$

(6)

式中： ${A}_{\text{n}}=\text{π}{R}_{\text{n}}^{2}；{A}_{\text{d1}}={n}_{\text{d}}\omega b；{A}_{\text{p1}}={n}_{\text{d}}\text{π}{r}_{\text{p}}^{2}$ ； ${A_{\text{n}}}$ ， ${A_{{\text{d1}}}}$ 和 ${A_{{\text{p1}}}}$ 分别为计算单元、单元外围排水板和单元外围水泥搅拌桩的面积； ${R_{\text{n}}}$ 为计算单元的半径。

结合式（1），（2），（6）可得

$R_{\text{e}}^2 = R_{\text{n}}^2 - \zeta {n_{\text{d}}}r_{\text{d}}^2 - {n_{\text{p}}}r_{\text{p}}^2。$

(7)

1.2 基本假定

（1）土体为饱和土，土颗粒和孔隙水不可压缩，土体的变形源于孔隙水的排出。

（2）等应变条件成立，即土体、排水板和水泥搅拌桩的竖向变形相等。

（3）土体及排水板中的渗流服从达西定律。

（4）考虑排水板的淤堵效应随时间和围压的增大而增大，因此假定排水板渗透系数 ${k_{{\text{Dd}}}}$ 随时间指数衰减，且同时随深度线性衰减，即

${k_{{\text{Dd}}}} = {k_0}\left( {{\theta _1} - {\theta _2}\frac{z}{H}} \right){{\text{e}}^{ - {\theta _3}t}}。$

(8)

式中： ${k_{\text{0}}}$ 为塑料排水板的初始渗透系数； ${\theta _1}$ ， ${\theta _2}$ ， ${\theta _3}$ 为常数，且 ${\theta }_{1}＞0$ ， $0 \leqslant {\theta _2} \leqslant {\theta _1}$ （为了确保渗透系数为正）， ${\theta _3} \geqslant 0$ ； ${\theta _1}$ 和 ${\theta _2}$ 用来描述排水板排水能力随深度的变化，即井阻的深度影响因子； ${\theta _3}$ 用来描述排水板排水能力随时间的变化，即井阻的时间影响因子。

（5）排水板满足流量连续相等假定，即沿径向流入中心排水板和外围排水板的水量等于沿竖向流出的水量。式（9）表示中心排水板流量连续相等的假定，式（10）表示单元外围排水板流量连续相等的假定，具体表达式如下；

${\left. {\left[ {2{\text{π }}r\frac{{{k_{\text{r}}}(r)}}{{{\gamma _{\text{w}}}}}\frac{{\partial {u_{\text{s}}}}}{{\partial r}}} \right]} \right|_{r = {r_{\text{d}}}}} = - \frac{{\zeta {\text{π }}r_{\text{d}}^2}}{{{\gamma _{\text{w}}}}}\frac{\partial }{{\partial z}}\left( {{k_{{\text{Dd}}}}\frac{{\partial {u_{\text{d}}}}}{{\partial z}}} \right)\text{，}$

(9)

${\left. {\left[ {2{\text{π }}r\frac{{{k_{\text{r}}}(r)}}{{{\gamma _{\text{w}}}}}\frac{{\partial {u_{\text{s}}}}}{{\partial r}}} \right]} \right|_{r = {R_{\text{e}}}}} = \frac{{{n_{\text{d}}}\zeta {\text{π }}r_{\text{d}}^2}}{{{\gamma _{\text{w}}}}}\frac{\partial }{{\partial z}}\left( {{k_{{\text{Dd}}}}\frac{{\partial {u_{\text{d}}}}}{{\partial z}}} \right) 。$

(10)

式中： $r$ 为径向坐标； ${k_{\text{r}}}(r)$ 为桩周土体的水平渗透系数； ${u_{\text{s}}}$ 和 ${u_{\text{d}}}$ 分别为土体和排水板内任意一点任一时刻的超静孔压； ${\gamma _{\text{w}}}$ 为水的重度。

2. 控制方程的推导及解答

2.1 控制方程的推导

首先，中心排水板与土体界面的超孔隙水压力相等，即

$\left.u_{\mathrm{s}}(r, z, t)\right|_{r=r_{\mathrm{d}}}=u_{\mathrm{d}} \quad 。$

(11)

另外，多元复合地基的外部荷载由 ${n_{\text{d}}} + 1$ 个塑料排水板、 ${n_{\text{p}}}$ 个水泥搅拌桩和土体共同承担，即

${\overline \sigma _{\text{d}}}{A_{\text{d}}} + {\overline \sigma _{\text{p}}}{A_{\text{p}}} + {\overline \sigma _{\text{s}}}{A_{\text{s}}} = \sigma {A_{\text{n}}} 。$

(12)

式中： $\sigma =\sigma (z，t)$ 为荷载在地基内引起的附加应力； ${\overline \sigma _{\text{d}}}$ ， ${\overline \sigma _{\text{p}}}$ 和 ${\overline \sigma _{\text{s}}}$ 分别为排水板、水泥搅拌桩和土体任意深度的总平均应力； ${A_{\text{d}}}$ ， ${A_{\text{p}}}$ ， ${A_{\text{s}}}$ 和 ${A_{\text{n}}}$ 分别为塑料排水板、水泥搅拌桩、土体和地基单元的截面积； ${A_{\text{d}}} = \zeta ({n_{\text{d}}} + 1){\text{π }}r_{\text{d}}^2$ ， ${A_{\text{p}}} = {n_{\text{p}}}{\text{π }}r_{\text{p}}^2$ ， ${A_{\text{s}}} = {\text{π }}(R_{\text{e}}^2 - r_{\text{d}}^2)$ ， ${A_{\text{n}}} =$ ${\text{π }}R_{\text{n}}^2 = {A_{\text{p}}} + {A_{\text{d}}} + {A_{\text{s}}}$ 。

由假设（2）可知，等应变假设可表达为

$\frac{{{{\overline \sigma }_{\text{d}}} - {u_{\text{d}}}}}{{{E_{\text{d}}}}} = \frac{{{{\overline \sigma }_{\text{p}}}}}{{{E_{\text{p}}}}} = \frac{{{{\overline \sigma }_{\text{s}}} - {{\overline u }_{\text{s}}}}}{{{E_{\text{s}}}}} = {\varepsilon _z} 。$

(13)

式中： ${E_{\text{d}}}$ ， ${E_{\text{p}}}$ 和 ${E_{\text{s}}}$ 分别为塑料排水板、水泥搅拌桩和土体的压缩模量，在计算中通常假定 ${E_{\text{d}}} = {E_{\text{s}}}$ ； ${\varepsilon _z}$ 为复合地基任一深度处的竖向应变； ${\overline u _{\text{s}}}$ 为土体沿径向的平均超静孔压，可表示为

${\overline{u}}_{\text{s}}=\frac{1}{\text{π}({R}_{\text{e}}^{2}-{r}_{\text{d}}^{2})}{\displaystyle {\int }_{{r}_{\text{d}}}^{{R}_{e}}2\text{π}r{u}_{\text{s}}(r\text{，}z\text{，}t)}\text{d}r 。$

(14)

垂直应变率可由式（12），（13）得

$\frac{{\partial {\varepsilon _z}}}{{\partial t}} = \frac{1}{{{E_{{\text{com}}}}}}\left[ {\frac{{\partial \sigma }}{{\partial t}} - \frac{{\partial \overline u }}{{\partial t}}} \right] \text{，}$

(15)

式中， ${E_{{\text{com}}}}$ 为复合地基的复合压缩模量， $\overline u$ 为地基任一深度处的平均孔隙水压力。其中

$\begin{aligned} E_{\text {com }}= & \frac{E_{\mathrm{p}} A_{\mathrm{p}}+E_{\mathrm{d}} A_{\mathrm{d}}+E_{\mathrm{s}} A_{\mathrm{s}}}{A_{\mathrm{n}}} \\ & =\frac{n_{\mathrm{p}} N_{\mathrm{pd}}^2 Y_{\mathrm{ps}}+\zeta\left(n_{\mathrm{d}}+1\right) Y_{\mathrm{ds}}+N^2-1}{N^2+\zeta n_{\mathrm{d}}+n_{\mathrm{p}} N_{\mathrm{pd}}^2} E_{\mathrm{s}}, \end{aligned}$

(16)

$\overline u = \frac{{{u_{\text{d}}}{A_{\text{d}}} + {{\bar u}_{\text{s}}}{A_{\text{s}}}}}{{{A_{\text{n}}}}} = \frac{{\zeta ({n_{\text{d}}} + 1){u_{\text{d}}} + ({N^2} - 1){{\overline u }_{\text{s}}}}}{{{N^2} + \zeta {n_{\text{d}}} + {n_{\text{p}}}N_{{\text{pd}}}^2}} \text{，}$

(17)

其中，

${N}_{\text{pd}}=\frac{{r}_{\text{p}}}{{r}_{\text{d}}}\text{，}N=\frac{{R}_{\text{e}}}{{r}_{\text{d}}}\text{，}{Y}_{\text{ps}}=\frac{{E}_{\text{p}}}{{E}_{\text{s}}}\text{，}{Y}_{\text{ds}}=\frac{{E}_{\text{d}}}{{E}_{\text{s}}} 。$

参考谢康和等^[19]的研究，土体的固结方程可统一写为

$\frac{1}{r}\frac{\partial }{{\partial r}}\left[ {\frac{{{k_{\text{r}}}(r)}}{{{\gamma _{\text{w}}}}}r\frac{{\partial {u_{\text{s}}}}}{{\partial r}}} \right] + \frac{{{k_{\text{v}}}}}{{{\gamma _{\text{w}}}}}\frac{{{\partial ^2}{{\overline u }_{\text{s}}}}}{{\partial {z^2}}} = - \frac{{\partial {\varepsilon _z}}}{{\partial t}} \text{，}$

(18)

式中， ${k_{\text{v}}}$ 为土体的平均竖向渗透系数。

参考Lu等^[20]研究，利用边界条件式（9）~（11）对式（18）沿径向积分，并联立式（14），（15），（17）可得关于土体中超静孔压的3个偏微分方程，即本文的求解方程：

${\overline u _{\text{s}}} = {u_{\text{d}}} - \frac{{{\lambda _1}{\theta _2}{k_{\text{0}}}}}{{{\lambda _4}}}{{\text{e}}^{ - {\theta _3}t}}\frac{{\partial {u_{\text{d}}}}}{{\partial z}} + \frac{{{\lambda _1}}}{{{\lambda _4}}}{k_{{\text{Dd}}}}\frac{{{\partial ^2}{u_{\text{d}}}}}{{\partial {z^2}}} \text{，}$

(19)

$\overline u = {\lambda _8}{u_{\text{d}}} + {\lambda _7}{{\text{e}}^{ - {\theta _3}t}}\frac{{\partial {u_{\text{d}}}}}{{\partial z}} + {\lambda _3}{k_{{\text{Dd}}}}\frac{{{\partial ^2}{u_{\text{d}}}}}{{\partial {z^2}}} \text{，}$

(20)

$\begin{gathered} \lambda_1 k_{\mathrm{Dd}} \frac{\partial^4 u_{\mathrm{d}}}{\partial z^4}+\lambda_2 \mathrm{e}^{-\theta_3 t} \frac{\partial^3 u_{\mathrm{d}}}{\partial z^3}+\lambda_3 k_{\mathrm{Dd}} \frac{\partial^3 u_{\mathrm{d}}}{\partial z^2 \partial t}+\lambda_7 \frac{\partial^2 u_{\mathrm{d}}}{\partial z \partial t}+\lambda_8 \frac{\partial u_{\mathrm{d}}}{\partial t}+ \\ \left(\lambda_4+\lambda_5 \mathrm{e}^{-\theta_3 t}+\lambda_6 k_{\mathrm{Dd}}\right) \frac{\partial^2 u_{\mathrm{d}}}{\partial z^2}-\lambda_7 \theta_3 \mathrm{e}^{-\theta_3 t} \frac{\partial u_{\mathrm{d}}}{\partial z}=\frac{\partial \sigma}{\partial t} 。\;\;\;\;\;\;\;\;\;\;\;\;\;\; \end{gathered}$

(21)

其中，

$\begin{array}{ll} \lambda_1=-\frac{k_{\mathrm{v}} F_{\mathrm{c}} E_{\mathrm{com}}}{\gamma_{\mathrm{w}}\left(N^2-1\right)}, & \lambda_2=-\frac{3 \theta_2 k_0 k_{\mathrm{v}} F_{\mathrm{c}} E_{\mathrm{com}}}{H \gamma_{\mathrm{w}}\left(N^2-1\right)}, \\ \lambda_3=\frac{F_{\mathrm{c}}}{N^2+\zeta n_{\mathrm{d}}+n_{\mathrm{p}} N_{\mathrm{pd}}^2}, & \lambda_4=-\frac{k_{\mathrm{v}} E_{\mathrm{com}}}{\gamma_{\mathrm{w}}}, \\ \lambda_5=-\frac{\theta_3 k_0 E_{\mathrm{com}} \zeta\left(1-n_{\mathrm{d}}\right)}{H \gamma_{\mathrm{w}}\left(N^2-1\right)}, & \lambda_6=\lambda_3 \theta_3-\frac{\zeta E_{\mathrm{com}}\left(1-n_{\mathrm{d}}\right)}{\gamma_{\mathrm{w}}\left(N^2+1\right)}, \\ \lambda_7=-\frac{\theta_2 k_0 F_{\mathrm{c}}}{N^2+\zeta n_{\mathrm{d}}+n_{\mathrm{p}} N_{\mathrm{pd}}^2}, & \lambda_8=\frac{\zeta\left(n_{\mathrm{d}}+1\right)+N^2+1}{N^2+\zeta n_{\mathrm{d}}+n_{\mathrm{p}} N_{\mathrm{pd}}^2} 。 \end{array}$

式中， ${F_{\text{c}}}$ 表达式的推导参考文献[13]。

2.2 控制方程的解答

假定复合地基顶部透水（孔压为零），底部不透水（流速为零），故竖向边界条件可以写为

$\left.\begin{array}{l} \left.\bar{u}(z, t)\right|_{z=0}=0,\left.\quad u_{\mathrm{d}}(z, t)\right|_{z=0}=0, \\ \left.\frac{\partial \bar{u}(z, t)}{\partial z}\right|_{z=H}=0,\left.\quad \frac{\partial u_{\mathrm{d}}(z, t)}{\partial z}\right|_{z=H}=0 。 \end{array}\right\}$

(22)

在初始时刻，外部荷载由复合地基的平均孔压承担，则初始条件为

$\left.\bar{u}(z, t)\right|_{t=0}=\sigma(z, 0)=\sigma_0 \quad,$

(23)

式中， ${\sigma _0}$ 为初始附加应力。

本文采用分离变量法对非齐次方程式（21）进行求解，假设其解为

${u_{\text{d}}}(z,t) = \sum\limits_{m = 1}^\infty {{T_m}(t)\sin \left( {\frac{M}{H}z} \right)} \text{，}$

(24)

其中，

$M = \frac{{2m - 1}}{2}{\text{π }}\;\;\;\;\;\;\;\;\;\;\;\;(m = 1,2,3, \cdot \cdot \cdot ) 。$

将式（24）代入式（21），然后在式两边同时乘以 $\sin (Mz/H)$ ，并在[0，H]上对 $z$ 进行积分，同时利用傅里叶级数的正交性得

${T_m}^\prime (t) + {G_m}(t){T_m}(t) = {Q_m}(t) \text{，}$

(25)

其中，

${G_m}(t) = \frac{{{L_m}{{\text{e}}^{ - {\theta _3}t}} - {\lambda _4}{{\left( {\frac{M}{H}} \right)}^2}}}{{\frac{{{\lambda _7}}}{H} + {\lambda _8} - {\lambda _3}{K_m}{{\text{e}}^{ - {\theta _3}t}}}} \text{，}$

(26)

${Q}_{m}(t)=\frac{\frac{2}{H}{\displaystyle {\int }_{0}^{H}\frac{\partial \sigma (z\text{，}t)}{\partial t}}\mathrm{sin}\left(\frac{M}{H}z\right)\text{d}z}{\frac{{\lambda }_{7}}{H}+{\lambda }_{8}-{\lambda }_{3}{K}_{m}{\text{e}}^{-{\theta }_{3}t}} \text{，}$

(27)

其中，

$\begin{gathered} K_m=k_0\left(\theta_1-\frac{\theta_2}{2}\right)\left(\frac{M}{H}\right)^2, \\ L_m=\left[\lambda_1\left(\frac{M}{H}\right)^2-\lambda_6\right] K_m-\left(\frac{\lambda_2}{H}+\lambda_5\right)\left(\frac{M}{H}\right)^2-\frac{\lambda_7 \theta_3}{H} 。 \end{gathered}$

将式（24）代入式（20），然后式两边同乘以 $\sin (Mz/H)$ ，并在[0，H]上对 $z$ 进行积分，结合初始条件式（23），利用傅里叶级数的正交性得

${T}_{m}(0)=\frac{\frac{2}{H}{\displaystyle {\int }_{0}^{H}\sigma (z\text{，}0)\mathrm{sin}\left(\frac{M}{H}z\right)\text{d}z}}{\frac{{\lambda }_{7}}{H}+{\lambda }_{8}-{\lambda }_{3}{K}_{m}} 。$

(28)

结合 ${T_m}(0)$ 的值，由常微分方程理论得式（25）的解为

${T_m}(t) = \frac{{\left[ {{P_m} + {S_m}(t)} \right]{{\text{e}}^{{\beta _m}t}}}}{{{{\left( {\frac{{{\lambda _7}}}{H} + {\lambda _8} - {\lambda _3}{K_m}{{\text{e}}^{ - {\theta _3}t}}} \right)}^{{\gamma _m}}}}} \text{，}$

(29)

其中，

${\beta _m} = \frac{{{\lambda _4}}}{{\frac{{{\lambda _7}}}{H} + {\lambda _8}}}{\left( {\frac{M}{H}} \right)^2} \text{，}$

(30)

${\gamma _m} = \frac{{{L_m}}}{{{\lambda _3}{\theta _3}{K_m}}} - \frac{{{\beta _m}}}{{{\lambda _3}}} \text{，}$

(31)

${P}_{m}=\frac{2{\displaystyle {\int }_{0}^{H}\sigma }(z\text{，}0)\mathrm{sin}\left(\frac{M}{H}z\right)\text{d}z}{H{\left(\frac{{\lambda }_{7}}{H}+{\lambda }_{8}-{\lambda }_{3}{K}_{m}\right)}^{1-{\gamma }_{m}}} \text{，}$

(32)

$\begin{aligned} S_m(t)= & \frac{2}{H} \int_0^t\left(\frac{\lambda_7}{H}+\lambda_8-\lambda_3 K_m \mathrm{e}^{-\theta_3 \tau}\right) \mathrm{e}-\beta_m \tau . \\ & \int_0^H \frac{\partial \sigma(z, \tau)}{\partial \tau} \sin \left(\frac{M}{H} z\right) \mathrm{d} z \mathrm{~d} \tau \end{aligned}$

(33)

结合式（19），（20），（24），（29）可得任意荷载作用下任一深度处排水板内的超静孔压、土体的平均超静孔压、复合地基的平均超静孔压以及复合地基总平均固结度如下（其中复合地基总平均固结度按应力定义计算）：

${u_{\text{d}}} = \sum\limits_{m = 1}^\infty {\left\{ {\frac{{\left[ {{P_m} + {S_m}{\text{(}}t{\text{)}}} \right]{{\text{e}}^{{\beta _m}t}}\sin \left( {\frac{M}{H}z} \right)}}{{{{\left( {\frac{{{\lambda _7}}}{H} + {\lambda _8} - {\lambda _3}{K_m}{{\text{e}}^{ - {\theta _3}t}}} \right)}^{{\gamma _m}}}}}} \right\}} \text{，}$

(34)

$\begin{aligned} & \bar{u}_{\mathrm{s}}=\sum\limits_{m=1}^{\infty}\left\{\frac{\left[P_m+S_m(t)\right] \mathrm{e}^{\beta_m t}}{\left(\frac{\lambda_7}{H}+\lambda_8-\lambda_3 K_m \mathrm{e}^{-\theta_3 t}\right)^{\gamma_m}} .\right. \\ & \left.\left[\sin \left(\frac{M}{H} z\right)-\frac{\lambda_1 \theta_2 k_0}{\lambda_4} \mathrm{e}^{-\theta_3 t} \cos \left(\frac{M}{H} z\right)-\frac{\lambda_1}{\lambda_4} k_{\mathrm{Dd}} \sin \left(\frac{M}{H} z\right)\right]\right\}, \end{aligned}$

(35)

$\begin{aligned} & \bar{u}=\sum\limits_{m=1}^{\infty}\left\{\frac{\left[P_m+S_m(t)\right] \mathrm{e}^{\beta_m t}}{\left(\frac{\lambda_7}{H}+\lambda_8-\lambda_3 K_m \mathrm{e}^{-\theta_3 t}\right)^{\gamma_m}} .\right. \\ & \left.\left[\lambda_8 \sin \left(\frac{M}{H} z\right)+\lambda_7 \frac{M}{H} \mathrm{e}^{-\theta_3 t} \cos \left(\frac{M}{H} z\right)-\lambda_5\left(\frac{M}{H}\right)^2 k_{\mathrm{Dd}} \sin \left(\frac{M}{H} z\right)\right]\right\}, \end{aligned}$

(36)

$\begin{gathered} U(t)=\frac{\int_0^H[\sigma(z, t)-\bar{u}(z, t)] \mathrm{d} z}{\int_0^H \sigma_{\mathrm{u}}(z) \mathrm{d} z}=\frac{\int_0^H \sigma(z, t) \mathrm{d} z}{\int_0^H \sigma_{\mathrm{u}}(z) \mathrm{d} z}- \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\ \frac{1}{\int_0^H \sigma_{\mathrm{u}}(z) \mathrm{d} z} \sum\limits_{m=1}^{\infty}\left\{\frac{\left[P_m+S_m(t)\right] \mathrm{e}^{\beta_m t}}{\left(\frac{\lambda_7}{H}+\lambda_8-\lambda_3 K_m \mathrm{e}^{-\theta_3 t}\right)^{\gamma_m}} \cdot\right. \\ \left.\left\{\lambda_8 \frac{H}{M}-\lambda_5 k_0 \theta_1 \frac{M}{H}-(1)^m\left[\lambda_7 \frac{M}{H} \mathrm{e}^{-\theta_3 t}+\lambda_5 \frac{k_0 \theta_1}{H}\left(\frac{M}{H}\right)^2\right]\right\}\right\} 。 \end{gathered}$

(37)

瞬时荷载、线性荷载、多级瞬时荷载和多级线性荷载4种常见荷载形式下解答的推导参考文献[]，其中 ${\beta _m}$ 按式（30）计算。

2.3 解答的验证

通过对解答进行退化研究，从理论方面验证本文解答的有效性。

（1）当 ${\theta _3}{\text{ = }}0$ 时，本文关于复合地基任意荷载下的总平均固结度的表达式（37）可退化为考虑排水板的井阻仅随深度变化时任意荷载作用下的总平均固结度的解答，即

$\begin{gathered} U(t)=\frac{{\displaystyle {\int }_{0}^{H}\left[\sigma (z，t)-\overline{u}(z，t)\right]\text{d}z}}{{\displaystyle {\int }_{0}^{H}{\sigma }_{\text{u}}(z)\text{d}z}}=\frac{{\displaystyle {\int }_{0}^{H}\sigma (z，t)\text{d}z}}{{\displaystyle {\int }_{0}^{H}{\sigma }_{\text{u}}(z)\text{d}z}}-\;\;\;\;\;\;\\ \frac{1}{\int_0^H \sigma_{\mathrm{u}}(z) \mathrm{d} z} \sum\limits_{m=1}^{\infty}\left\{\frac{\left[P_m+S_m(t)\right] \mathrm{e}^{\beta_m t}}{\left(\frac{\lambda_7}{H}+\lambda_8-\lambda_3 K_m\right)^{\gamma_m}} \cdot\right. \\ \left.\left\{\lambda_8 \frac{H}{M}-\lambda_5 k_0 \theta_1 \frac{M}{H}-(-1)^m\left[\lambda_7 \frac{M}{H}+\lambda_5 \frac{k_0 \theta_1}{H}\left(\frac{M}{H}\right)^2\right]\right\}\right\} 。 \end{gathered}$

(38)

（2）当 ${\theta _1} = 1$ ， ${\theta _2} \to 0$ ， $\sigma (z，t)={\sigma }_{\text{u}}g(t)$ 时，式（37）可退化为白垚等^[21]考虑排水板井阻仅随时间变化情况时任意荷载作用下多元复合地基的总平均固结度的解答，即

$\begin{aligned} & U(t)=g(t)-\sum\limits_{m=1}^{\infty}\left\{\frac{\left[P_m+S_m(t)\right] \mathrm{e}^{\beta_m t}}{\sigma_{\mathrm{u}}\left(\frac{\lambda_7}{H}+\lambda_8-\lambda_3 K_m \mathrm{e}^{-\theta_3 t}\right)^{\gamma_m}} .\right. \\ & \left.\left\{\lambda_8 \frac{H}{M}-\lambda_5 k_0 \frac{M}{H}-(-1)^m\left[\lambda_7 \frac{M}{H} \mathrm{e}^{-\theta_3 t}+\lambda_5 \frac{k_0}{H}\left(\frac{M}{H}\right)^2\right]\right\}\right\} . \end{aligned}$

(39)

（3）继续令 ${\theta _3} \to 0$ ，式（39）可退化为考虑排水板为恒井阻时任意荷载作用下的多元复合地基的总平均固结度的解答^[13]，即

$U(t) = g(t) - \sum\limits_{m = 1}^\infty {\frac{2}{{{M^2}}}} \left[ {\frac{{{\sigma _0}}}{{{\sigma _{\text{u}}}}}{{\text{e}}^{{\beta _m}t}} + {{\text{e}}^{{\beta _m}t}}\int\limits_0^t {\frac{{{\text{d}}g(\tau )}}{{{\text{d}}\tau }}{{\text{e}}^{ - {\beta _m}\tau }}{\text{d}}\tau } } \right] 。$

(40)

（4）继续令 $t \to 0$ ， ${r_{\text{d}}} \to 0$ ， ${r_{\text{p}}} \to 0$ ，且当外部荷载为瞬时施加时，式（40）可退化为Terzaghi^[22]天然地基一维固结解答：

$U(t){\text{ = }}1 - \sum\limits_{m = 1}^\infty {\frac{2}{{{M^2}}}{{\text{e}}^{ - {M^2}{T_{\text{v}}}}}} \text{，}$

(41)

式中， ${T_{\text{v}}}$ 为土体的竖向时间因子， ${T_{\text{v}}} = {c_{\text{v}}}t/{H^2}$ ，其中 ${c_{\text{v}}}$ 为土体的竖向固结系数， ${c_{\text{v}}} = {k_{\text{v}}}{E_{\text{s}}}/{\gamma _{\text{w}}}$ 。

通过将本文解答经退化研究可得，在不同条件下本文解答可退化为已有的解析解答，这从理论的角度对本文解答的正确性进行了验证。同时，上述学者的解答可视为本文解答的特例，故本文解答具有更好的适用性。

3. 固结性状分析

本节利用本文解答对多元复合地基的固结性状进行参数敏感性分析。排水板采用市面常见的规格型，宽100 mm，厚4 mm，此排水板按照环形等效原则得其面积折减系数约为0.116。本文的对比采用径向时间因子 ${T_{\text{h}}} = {k_{\text{h}}}{E_{{\text{com}}}}t/(4R_{\text{n}}^2{\gamma _{\text{w}}})$ 为横坐标。计算参数取值见表 1。

表 1 模型参数取值表

Table 1. Values of model parameters

H/m	H/R_n	r_d/m	r_p/m	r_sd/r_d	r_sp/r_p	k_sd/k_h	k_sp/k_h	k_v/(10^-9m·s^-1)	k_h/k_v	k₀/(10^-5m·s^-1)	k₀/(10^-5m·s^-1)	E_s/MPa	E_p/E_s	E_d/E_s	σ₀/kPa	σ_B/kPa	σ_T/kPa	${\theta _1}$	${\theta _2}$	${\theta _3}$ /(10^-7 1·s^-1)	T_h
13	10	0.033	0.25	2	3	1/3	0.3	1.63	2	5.5	5.5	1.68	50	1	10	10	25	1	0.01	2.6	1
注：表中 ${\sigma _{\text{T}}}$ 和 ${\sigma _{\text{B}}}$ 分别为复合地基顶面和底面处的附加应力值。

下载: 导出CSV

| 显示表格

图 3，4分别为考虑排水板不同井阻效应下复合地基的平均孔压随时间消散的曲线和固结度的对比曲线，包括卢萌盟等^[13]考虑排水板为恒井阻的多元复合地基解、本文推导的考虑排水板井阻随深度变化、井阻随时间变化、以及井阻随时间和深度同时变化4种情况下的对比。由图 3，4可得，复合地基的孔压消散和地基固结最快和最慢的情况分别为考虑恒井阻和井阻随时间和深度同时变化的情况；相比于恒井阻的情况，考虑井阻随时间和深度同时变化时复合地基的孔压消散速率减慢的趋势可看作单一因素减慢趋势的叠加；考虑井阻随深度变化对复合地基孔压消散的影响随着固结的发展逐渐减弱，而考虑井阻仅随时间变化对复合地基的孔压消散影响则随着固结的发展而增大。

图 3 不同井阻效应下复合地基的平均孔压随时间消散的曲线

Figure 3. Curves of average pore pressure of composite foundation dissipating with time under different well resistance effects

下载: 全尺寸图片幻灯片

图 4 不同井阻效应下复合地基总平均固结度的对比

Figure 4. Comparison of total average consolidation degrees of composite foundation under different well resistance effects

下载: 全尺寸图片幻灯片

图 5，6分别为不同附加应力下复合地基的平均孔压沿深度的分布曲线和对地基固结度的影响曲线图。由图 5可得，本文假设地基底面为不透水面，地基深处的孔隙水压力明显大于上部地基的水压力，表明地基深处的孔隙水压力消散要远慢于上部地基，并且在复合地基顶面的附加应力越大，地基深处的孔隙水压力消散越快。由图 6可得，在假定地基表面为透水面而底面为不透水面时，地表处的附加应力值越大地基的固结越快。

图 5 不同附加应力沿深度分布形式下复合地基的平均孔压沿深度的分布曲线

Figure 5. Distribution curves of average pore pressure along depth of composite foundation with different additional stress distribution forms along depth

下载: 全尺寸图片幻灯片

图 6 不同附加应力沿深度分布形式对复合地基总平均固结度的影响

Figure 6. Influences of different additional stress distribution forms along depth on total average consolidation degree of composite foundation

下载: 全尺寸图片幻灯片

~分别为不同 ${\theta _1}$ 、 ${\theta _2}$ 和 ${\theta _3}$ 值对多元复合地基总平均固结度的影响曲线。由~可得，随着塑料排水板的井阻因子 ${\theta _1}$ 的增大，复合地基的固结曲线左移，表明复合地基的固结速率增大；井阻因子 ${\theta _2}$ 对复合地基固结影响甚微，随着井阻因子 ${\theta _2}$ 增大，复合地基的固结速率稍有减小；增大塑料排水板的井阻因子 ${\theta _3}$ 对于固结前期影响甚微，但对于后期固结速率影响较大，复合地基固结后期的固结速率随 ${\theta _3}$ 增大而减小，且当 ${\theta _3}$ 较大时，多元复合地基在固结后期由于径向排水明显减弱，仅通过竖向渗流继续固结，也可达到复合地基完全固结。

图 7 不同

${\theta _1}$ 值对固结度的影响

Figure 7. Influences of different values of

${\theta _1}$ on consolidation degree

下载: 全尺寸图片幻灯片

图 8 不同

${\theta _2}$ 值对固结度的影响

Figure 8. The effect of different

${\theta _2}$ values on the degree of consolidation

下载: 全尺寸图片幻灯片

图 9 不同

${\theta _3}$ 值对固结度的影响

Figure 9. Influences of different values of

${\theta _3}$ on consolidation degree

下载: 全尺寸图片幻灯片

图 10~分别为复合地基深度在H/2时排水板的井阻因子 ${\theta _1}$ 、 ${\theta _2}$ 和 ${\theta _3}$ 对复合地基的平均超静孔压消散的影响曲线。由~可得，随着 ${\theta _1}$ 的减小， ${\theta _2}$ 和 ${\theta _3}$ 的增大，复合地基的平均超静孔压消散速率减慢。经对比后发现，对复合地基的平均孔压消散的影响最明显的是 ${\theta _3}$ ，其次是 ${\theta _1}$ ，然后是 ${\theta _2}$ 。

图 10 不同

${\theta _1}$ 值对复合地基的平均孔压消散的影响

Figure 10. Influences of different values of

${\theta _1}$ on dissipation of average pore pressure of composite foundation

下载: 全尺寸图片幻灯片

图 11 不同

${\theta _2}$ 值对复合地基的平均孔压消散的影响

Figure 11. Influences of different values of

${\theta _2}$ on dissipation of average pore pressure of composite foundation

下载: 全尺寸图片幻灯片

图 12 不同

${\theta _3}$ 值对复合地基的平均孔压消散的影响

Figure 12. Influences of different values of

${\theta _3}$ on dissipation of average pore pressure of composite foundation

下载: 全尺寸图片幻灯片

4. 工程案例分析

Zhang等^[23]在临连高速的CK0+850—CK1+500段进行了塑料排水板联合粉喷桩的多元复合地基现场试验。排水板和粉喷桩按三角形布置，间距为1.8 m，长度均为10.5 m，排水板宽100 mm，厚4 mm，该复合地基 ${n_{\text{p}}} = 1$ 。试验段路堤可视为两个加载阶段，第一阶段为77 d内匀速填筑至4 m；第二阶段为4 d匀速填筑至6 m，之后保持不变。该加载过程简化为二级线性加载。试验中给出的基本参数及取值如表 2所示。

表 2 基本参数及取值

Table 2. Basic parameters and values

H/m	R_n/m	r_d/m	r_p/m	A_sd/A_d	k_v/(10^-9 m·s^-1)	k_h/k_v	k_h/k_sd	k_d/(10^-6m³·s^-1)	E_s/MPa	E_p/E_s
10.5	1.039	0.033	0.25	9	1.61	2	3	35	1.25	9.4

下载: 导出CSV

| 显示表格

图 13为本文考虑排水板的淤堵随时间和深度同时变化的解答、白垚等^[21]考虑淤堵仅随时间变化的多元复合地基的解答、卢萌盟等^[13]考虑排水板为恒井阻的多元复合地基的解答与Zhang等^[23]现场实测值的对比。由图 13可得，在固结前期，固结曲线与实测值均较为吻合，但随着固结的发展，卢萌盟等^[13]解答固结最快，其次是白垚等^[21]的解答，最后是考虑淤堵随时间和深度同时变化的解答，且本文的工况下与现场实测值拟合最好，这是由于本文考虑了排水板的淤堵效应，因此固结后期排水速率明显减小。实际上，在试验进行到102 d，即固结度为75%左右时，在较短时间内路堤高度从4 m填筑至6 m，荷载短时间内增大，卢萌盟等^[13]未考虑淤堵效应的解答相应地产生了固结加快的响应，而实测值与本文的解答则未产生明显加快的现象。产生此现象的原因为：随着固结的发展，排水板会产生土颗粒堵塞排水通道，导致排水板的井阻变大，排水功效降低，因此固结速率也不会产生加快的预期效果。

图 13 固结度的理论解和实测值的对比

Figure 13. Comparison between theoretical solutions and measured values of consolidation degree

下载: 全尺寸图片幻灯片

5. 结论

本文推导了考虑排水板淤堵效应随时间和深度同时变化的多元组合桩复合地基的固结理论。假定排水板的渗透系数随时间呈指数型衰减且沿深度呈线性衰减，同时将排水板的涂抹效应、水泥搅拌桩的扰动效应以及土体的竖向和径向渗流考虑在内，通过推导得出多元复合地基的固结控制方程及其解答，最后对该多元复合地基的固结性状进行对比分析，得到以下4点结论。

（1）本文解答可退化到多种已有工况解答，从理论和必要性上证明了解答的合理性；另外，通过与现场试验实测数据对比，进一步验证了本文解答的有效性与精确性。

（2）相比于恒井阻的情况，考虑井阻随时间和深度同时变化时复合地基的孔压消散和固结减慢，且减慢的趋势可看作单一影响因素减慢趋势的叠加；考虑井阻随深度分布变化对复合地基的孔压消散和固结的影响随着固结的发展逐渐减弱，而考虑井阻仅随时间变化对复合地基的孔压消散和固结的影响则随着固结过程而增大。

（3）多元复合地基深处的孔压要明显大于上部地基的孔压，即地基深处的孔压消散较慢；地表处的附加应力越大，复合地基的固结速率越大，地基深处的孔压消散越快。

（4）当 ${\theta _1}$ 减小或 ${\theta _2}$ 增大时，多元复合地基的平均孔压消散速率和固结速率均减小； ${\theta _3}$ 的增大对多元复合地基的平均孔隙水压力消散速率和后期固结速率的减小有显著影响；当 ${\theta _3}$ 较大时，由于径向固结减弱，固结后期地基仅靠竖向渗流达到完全固结。

图 1 不同超固结比试样的应力应变曲线

Figure 1. Stress-strain curves for over-consolidated clay in CU test

下载: 全尺寸图片幻灯片

图 2 偏应力加载过程响应曲线

Figure 2. Response curves during deviatoric stress loading process

下载: 全尺寸图片幻灯片

图 3 不同超固结比试样的蠕变曲线

Figure 3. Creep deformations of samples with different over-consolidation ratios

下载: 全尺寸图片幻灯片

图 4 蠕变量与超固结比的关系（t=4320 min）

Figure 4. Relationship between over-consolidation ratio and creep deformation of samples

下载: 全尺寸图片幻灯片

图 5 超固结土双曲线蠕变模型拟合曲线

Figure 5. Fitting of shear creep curves of samples with different over-consolidation ratios

下载: 全尺寸图片幻灯片

图 6 模型参数A_s与超固结比OCR关系

Figure 6. Relationship between model parameters A_s and OCR

下载: 全尺寸图片幻灯片

图 7 模型参数B_s与超固结比OCR关系

Figure 7. Relationship between model parameters B_s and OCR

下载: 全尺寸图片幻灯片

表 1 原状土的基本物理性质指标

Table 1 Index parameters of intact soil samples

取土深度/m	G_s	含水率w/kPa	天然密度 $\rho$ /(g·cm^-3)	液限w_L/%	塑限 w_P/%	塑性指数I_p	液性指数I_L
15~25	2.72	36.21	1.87	40.27	20.26	20.01	0.79

下载: 导出CSV

表 2 超固结土三轴试验方案

Table 2 Test schemes of over-consolidated ratio

试样编号	OCR	σ'_c/kPa	σ'₀/kPa	q/kPa	K
①	1.00	200	200	155	0.68
②	1.25	250	200	155	0.58
③	1.67	334	200	155	0.52
④	2.00	400	200	155	0.47
⑤	3.00	600	200	155	0.37
注：σ'_c为试样先期有效固结压力；σ '₀为初始有效围压；q为偏应力，q=σ₁-σ₃；K为蠕变偏应力和剪切强度q_f的比值。

下载: 导出CSV

表 3 剪切蠕变双曲线模型参数

Table 3 Fitting parameters of hyperbolic creep model

超固结比	偏应力/ kPa	A_s/%	B_s/min	相关系数R²/%
1.00	155	0.2397	904.33	99.64
1.25	155	0.2659	1685.06	99.89
1.67	155	0.2202	2248.02	99.78
2.00	155	0.2279	2602.10	99.74
3.00	155	0.2011	4352.29	95.64

下载: 导出CSV

参考文献(12)

[1]	王者超, 乔丽苹, 李术才. 荷载水平和孔隙比对土次压缩性质影响研究[J]. 土木工程学报, 2013, 46(1): 112-118. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201301013.htm WANG Zhechao, QIAO Liping, LI Shucai. Influences of load level and void ratio on secondary compressibility of soil[J]. China Civil Engineering Journal, 2013, 46(1): 112-118. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201301013.htm
[2]	曾玲玲, 洪振舜, 刘松玉, 等. 重塑黏土次固结性状的变化规律与定量评价[J]. 岩土工程学报, 2012, 34(8): 1496-1500. http://www.cgejournal.com/cn/article/id/14669 ZENG Lingling, HONG Zhenshun, LIU Songyu, et al. Variation law and quantitative evaluation of secondary consolidation behavior for remolded clays[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(8): 1496-1500. (in Chinese) http://www.cgejournal.com/cn/article/id/14669
[3]	YIN J H. Non-linear creep of soils in oedometer tests[J]. Géotechnique, 1999, 49(5): 699-707. doi: 10.1680/geot.1999.49.5.699
[4]	SINGH A, MITCHELL J K. General stress-strain-time function for soils[J]. Journal of the Soil Mechanics and Foundations Division, 1968, 94(1): 21-46. doi: 10.1061/JSFEAQ.0001084
[5]	MESRI G, FEBRES-CORDERO E, SHIELDS D R, et al. Discussion: shear-stress-strain time behaviour of clays[J]. Géotechnique, 1982, 32(4): 407-411. doi: 10.1680/geot.1982.32.4.407
[6]	XIAO B, HU M Y, ZHOU P J, et al. Creep behavior of saturated clay in triaxial test and a hyperbolic model[J]. Geofluids, 2021: 1-12.
[7]	高彦斌. 超固结土一维次压缩特性实验研究[C]// 2004年度上海市土力学与岩土工程学术年会. 上海, 2004. Yanbin. Experimental study on one-dimensional compression characteristics of over-consolidated soil[C]// 2004 Annual Conference of Soil mechanics and Geotechnical Engineering in Shanghai. Shanghai, 2004. (in Chinese))
[8]	韩剑, 姚仰平, 尹振宇. 超固结度对超固结饱和黏土不排水蠕变特性的影响研究[J]. 岩土工程学报, 2018, 40(3): 426-430. doi: 10.11779/CJGE201803005 HAN Jian, YAO Yangping, YIN Zhenyu. Influences of overconsolidation ratio on undrained creep behavior of overconsolidated saturated clay[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(3): 426-430. (in Chinese) doi: 10.11779/CJGE201803005
[9]	YIN J H, ZHU J G, GRAHAM J. A new elastic viscoplastic model for time-dependent behaviour of normally and overconsolidated clays: theory and verification[J]. Canadian Geotechnical Journal, 2002, 39(1): 157-173. doi: 10.1139/t01-074
[10]	胡亚元, 杨平, 余启致. 超固结土次固结系数的时间效应[J]. 中国公路学报, 2016, 29(9): 29-37. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201609003.htm HU Yayuan, YANG Ping, YU Qizhi. Time effect of secondary consolidation coefficient of over-consolidated soil[J]. China Journal of Highway and Transport, 2016, 29(9): 29-37. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201609003.htm
[11]	土工试验方法标准: GB/T 50123—2019[S]. 北京: 中国计划出版社, 2019. Standard for Soil Test Method: GB/T 50123—2019[S]. Beijing: China Planning Press, 2019. (in Chinese)
[12]	肖斌. 重塑粉质黏土的蠕变特性及蠕变模型研究[D]. 杭州: 浙江工业大学, 2017. XIAO Bin. Study on Creep Characteristics and Creep Model of Reconstituted Silty Clay[D]. Hangzhou: Zhejiang University of Technology, 2017. (in Chinese)

施引文献

资源附件(0)

图(7) / 表(3)

计量

文章访问数: 224
HTML全文浏览量: 39
PDF下载量: 73
被引次数: 0

0. 引言
1. 计算模型
1.1 模型的建立
1.2 基本假定
2. 控制方程的推导及解答
2.1 控制方程的推导
2.2 控制方程的解答
2.3 解答的验证
3. 固结性状分析
4. 工程案例分析
5. 结论

重塑超固结饱和黏土蠕变试验与蠕变模型 English Version

作者简介: 胡敏云(1970—)，女，博士，教授，主要从事特殊土力学特性与模型方面的研究工作。E-mail: humy@iwhr.com

通讯作者: 张勇, E-mail: zhangyong@zjut.edu.cn

计量

出版历程

Creep tests and creep model for reconstituted over-consolidated saturated clay

0. 引言

1. 计算模型

1.1 模型的建立

1.2 基本假定

2. 控制方程的推导及解答

2.1 控制方程的推导

2.2 控制方程的解答

2.3 解答的验证

3. 固结性状分析

4. 工程案例分析

5. 结论

计量

出版历程

目录

0. 引言

1. 计算模型

1.1 模型的建立

1.2 基本假定

2. 控制方程的推导及解答

2.1 控制方程的推导

2.2 控制方程的解答

2.3 解答的验证

3. 固结性状分析

4. 工程案例分析

5. 结论

作者简介:
胡敏云(1970—)，女，博士，教授，主要从事特殊土力学特性与模型方面的研究工作。E-mail: humy@iwhr.com

通讯作者:
张勇, E-mail: zhangyong@zjut.edu.cn