降水条件下抗滑桩-锚杆加固边坡的离心模型试验研究

张泽蔚; 刘素嘉; 张嘎

doi:10.11779/CJGE2023S10036

降水条件下抗滑桩-锚杆加固边坡的离心模型试验研究 English Version

清华大学水沙科学与水利水电工程国家重点试验室, 北京 100084

基金项目:

清华大学自主科研计划课题

国家自然科学基金重点项目 52039005

详细信息

作者简介:
张泽蔚(2003—)，男，本科，主要从事边坡工程方面的研究。E-mail: zhang-zw21@mails.tsinghua.edu.cn

中图分类号: TV22
计量
- 文章访问数: 105
- HTML全文浏览量: 23
- PDF下载量: 46
出版历程
- 收稿日期: 2023-07-04
- 网络出版日期: 2023-11-23
- 刊出日期: 2023-10-31

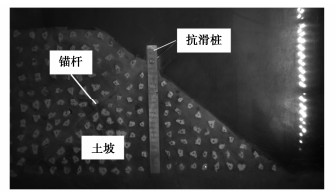
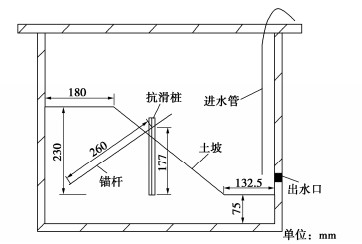
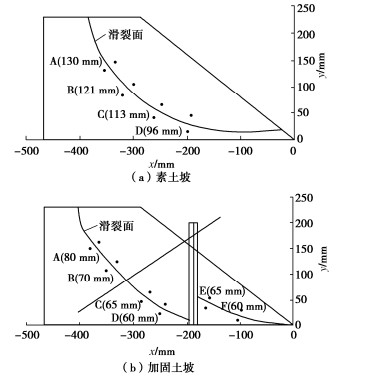
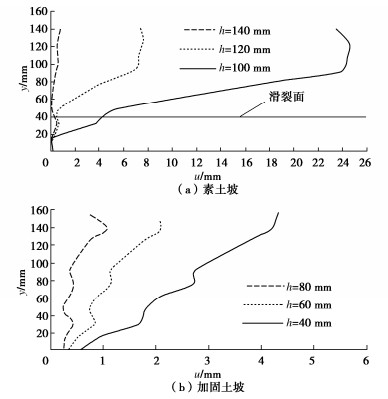
Centrifuge modeling of anti-slide piles with anchored bolt-reinforced slopes under drawdown conditions

State Key Laboratory of Hydroscience and Engineering, Tsinghua University, Beijing 100084, China

摘要

摘要: 锚杆抗滑桩是一种加固边坡的有效结构。本文进行了水位下降条件下素土坡与锚杆抗滑桩组合结构加固土坡的离心模型试验，测量了边坡的位移场变化，分析了锚杆抗滑桩的行为以及土体的变形特性。试验结果表明，锚杆抗滑桩加固导致边坡位移显著减小、改变了滑裂面连续性，并使得坡体破坏表现出显著渐进性。水位下降条件下锚杆抗滑桩加固土坡的破坏过程与变形局部化表现出显著的耦合特性。锚杆抗滑桩结构使得边坡变形均匀化，阻挡了桩侧土体滑动，从而延迟了边坡破坏。
- 边坡 /
- 抗滑桩 /
- 锚杆 /
- 离心模型试验 /
- 桩土相互作用
Abstract: The anti-slide pile with anchored bolt is an effective structure for reinforcing side slopes. The centrifugal model tests are conducted to compare the unreinforced slope with the anchor-pile-reinforced one under drawdown conditions. The histories of displacement of slopes are measured. The behavior of the anti-slide pile with anchored bolt and the distribution of strain of soil are analyzed. The test results show that the anti-slide pile with anchored bolt significantly reduces the displacement of landslide, changes the continuity of slip surface and causes obvious progressive failure behavior. Under the drawdown conditions, the failure process of the anchor-pile-reinforced slope exhibits significant coupling with the deformation localization. The anti-slide pile with anchored bolt homogenizes slope deformation and resists the displacement of soil, therefore delaying the failure of side slopes.
- side slope /
- anti-slide pile /
- anchored bolt /
- centrifugal model test /
- soil-structure interaction

HTML全文

0. 引言

三峡库岸滑坡事故频发，主要是由于季节性强降雨和库区水位剧烈变化的联合作用^[1]。库岸边坡如果在历史上发生过滑坡灾害，无论是否发生新滑坡，依照确定性分析理论，计算的安全系数一般略大于临界值1.0，属于潜在重大地质灾害源。单凭安全系数作为评价指标，不能真实反映库岸老滑坡当前的稳定状态。因此，基于非饱和土理论、不确定性原理，分析库岸边坡的稳定性，逐渐得到学术界和工程界的重视。

李梦姿等^[2]、傅方等^[3]、邓志平等^[4]分别从抗拉强度、地震荷载作用、地层变异性及岩土参数变异性等角度，对边坡展开稳定性分析。蒋水华等^[5]通过修正Green-Ampt入渗模型，在非饱和土边坡稳定性分析中，探讨了岩土参数空间变异性与降雨入渗作用。

考虑Soil-Water Characteristic Curve (SWCC)模型及的参数影响，Rahimi等^[6]研究了SWCC模型参数变化对边坡稳定性的影响。唐栋等^[7]通过数值模拟方法，研究了SWCC模型参数拟合值的变化对边坡渗流以及稳定性的影响。王林等^[8]提出了基于室内土工试验数据的SWCC模型贝叶斯比选和参数校准方法。

考虑饱和渗透系数的空间变异性，Vanmarcke^[9]将工程地质勘察剖面视作二维空间分布的随机场，模拟岩土参数的空间变异性。Gui等^[10]采用饱和渗透系数随机场，对大坝的渗流和稳定性开展了分析。Srivastava等^[11]将饱和渗透系数视为对数正态分布的随机场变量，研究了边坡稳态渗流和稳定性。Zhu等^[12]采用快速Fourier变换技术，生成边坡饱和渗透系数的随机场，开展了稳定性分析。

三峡库区石榴树包老滑坡位于湖北省巴东县，2020年遭遇了极端降雨。在前期研究中，将黏聚力、内摩擦角、杨氏模量和饱和渗透系数视为空间统计相关的随机场变量，基于边坡勘察数据和长期监测数据，采用贝叶斯理论，校准了随机场统计特征，并开展了老滑坡的稳定性分析。在夏季低水位和暴雨的联合作用下，得出了边坡稳定性满足可靠度要求的结论^[13]。但是，此次特大暴雨还伴随着库区水位骤升陡降，因此从水力参数（土水特征曲线和饱和渗透系数）的联合作用出发，讨论非饱和渗透系数随机场统计特征，在边坡稳定性分析中的控制效应尤为重要。

综上所述，首先根据有限的SWCC试验数据和先验知识，采用贝叶斯方法, 校准SWCC模型参数，并量化不同SWCC模型估计的不确定性。再使用随机场理论，描述饱和渗透系数，联合随机（场）统计特征讨论非饱和渗透系数空间变异性对边坡稳定性的影响。

1. 非饱和土边坡稳定性分析理论

土水特征曲线SWCC可以描述土体中含水率与基质吸力之间的变化关系，因而成为研究非饱和土力学的基本工具。

1.1 土水特征曲线与渗透系数

目前有多种方法拟合或者预测理论土水特征曲线SWCC。如Van Genuchten-Mualem（VGM）模型^[14]、Van Genuchten-Burdine（VGB）模型^[15]、Van Genuchten（VG）模型^[16]和Fredlund-Xing（FX）模型^[17]是4种比较常用的SWCC理论模型。

以VG模型对应的非饱和渗透系数为例，通过体积含水率 $\theta$ 和饱和土渗透系数 ${k_{\text{s}}}$ ，可以计算非饱和渗透系数。如采用幂函数形式，表示非饱和土体积含水率 $\theta$ 与基质吸力 $\psi$ 之间的关系^[16]：

$\theta = {\theta _{\text{r}}} + \frac{{{\theta _{\text{s}}} - {\theta _{\text{r}}}}}{{{{\left[ {1 + {{\left( {\frac{\psi }{a}} \right)}^n}} \right]}^m}}} 。$

(1)

式中： ${\theta _{\text{s}}}$ 为饱和体积含水率； ${\theta _{\text{r}}}$ 为残余体积含水率； $\psi$ 为基质吸力； $\alpha$ ， $n$ 和 $m$ 均为拟合参数。非饱和渗透系数 ${k_{\text{w}}}(\psi )$ 和基质吸力 $\psi$ 之间的关系为^[16]

${k_{\text{w}}}(\psi ) = {k_{\text{s}}}\frac{{{{\left[ {1 - {{{\text{(}}\psi /a{\text{)}}}^{n - 1}}{{\left[ {1 + {{{\text{(}}\psi /a{\text{)}}}^n}} \right]}^{ - m}}} \right]}^2}}}{{{{\left[ {1 + {{{\text{(}}\psi /a{\text{)}}}^n}} \right]}^{{m \mathord{\left/ {\vphantom {m 2}} \right. } 2}}}}} \text{，}$

(2)

式中， ${k_{\text{s}}}$ 为饱和渗透系数， ${k_{\text{w}}}(\psi )$ 为当前基质吸力 $\psi$ 对应的非饱和渗透系数。

1.2 非饱和土的剪切强度

SWCC模型描述了基质吸力 $\psi$ 与饱和度 ${S_{\text{r}}}$ （或饱和含水率 $\theta$ ）之间的关系，非饱和渗流理论则描述了非饱和渗透系数 ${k_{\text{w}}}(\psi )$ 随着土体饱和度 ${S_{\text{r}}}$ 不断变化的规律。3个水力参数之间相互关联，并最终影响非饱和土的抗剪强度 ${\tau _{\text{f}}}$ ^[18]，进而影响边坡的稳定性。

${\tau _{\text{f}}} = c' + (\sigma - {u_{\text{a}}})\tan \varphi ' + \frac{{\theta - {\theta _{\text{r}}}}}{{{\theta _{\text{s}}} - {\theta _{\text{r}}}}}({u_{\text{a}}} - {u_{\text{w}}})\tan \varphi ' \text{，}$

(3)

式中， ${\tau _{\text{f}}}$ 为非饱和土的抗剪强度， $c'$ 为有效黏聚力， $\varphi '$ 为有效内摩擦角， $\sigma$ 为总应力。岩土参数 $c'$ 和 $\varphi '$ 虽然也受到非饱和土基质吸力 $\psi$ 的影响，但为了深入研究水力参数的空间变异性，暂不考虑岩土参数的不确定性。水力参数的变异性通常比岩土参数的变异性要大，因此，本文联合SWCC模型参数的随机统计特征和饱和渗透系数的随机场统计特征，研究非饱和渗透系数 ${k_{\text{w}}}(\psi )$ 的空间变异性。

1.3 非饱和土边坡稳定性分析

考虑渗流的非饱和土边坡稳定性分析理论主要包括边坡降雨浸润和库区水位波动作用下的瞬态渗流分析和边坡稳定性分析。

（1）瞬态渗流分析

Richards^[19]提出了非饱和土孔隙水瞬态流动的控制方程：

$\frac{\partial }{{\partial {x_1}}}\left( {{k_{{\text{w}},{x_1}}}(\psi )\frac{{\partial H}}{{\partial {x_1}}}} \right) + \frac{\partial }{{\partial {x_2}}}\left( {{k_{{\text{w}},{x_1}}}(\psi )\frac{{\partial H}}{{\partial {x_2}}}} \right){\text{ + }}\frac{\partial }{{\partial {x_3}}}\left( {{k_{{\text{w}},{x_1}}}(\psi )\frac{{\partial H}}{{\partial {x_3}}}} \right) + q \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= {m_{\text{w}}}{\gamma _{\text{w}}}\frac{{\partial H}}{{\partial t}} = \frac{{\partial \theta }}{{\partial t}} 。$

(4)

式中： ${k_{{\text{w}},{x_1}}}(\psi )$ ， ${k_{{\text{w}},{x_2}}}(\psi )$ 和 ${k_{{\text{w}},{x_3}}}(\psi )$ 分别为多孔介质在 ${x_1}$ ， ${x_2}$ （水平方向）和 ${x_3}$ （竖直方向）上的非饱和渗透系数，它们是关于基质吸力 $\psi$ 的函数； $H$ 为总水头； $q$ 为边界流量； $t$ 为渗流时间； ${\gamma _{\text{w}}}$ 为水的重度； ${m_{\text{w}}}$ 为容水能力，

${m_{\text{w}}} = - \frac{{\partial \theta }}{{\partial ({u_{\text{a}}} - {u_{\text{w}}})}} 。$

(5)

若已知土水特征曲线SWCC和基质吸力 $\psi$ 与非饱和渗透系数 ${k_{\text{w}}}(\psi )$ 之间的函数，即可求解式（4）的偏微分方程。

（2）非饱和土边坡稳定性分析

采用数值计算软件GeoStudio 2012，开展非饱和土边坡稳定性分析。在渗流条件下，采用Morgenstern- Price极限平衡法^[20]，计算非饱和土边坡稳定性的安全系数 ${F_{\text{s}}}$ 。

2. 边坡可靠度分析方法

在考虑渗流作用的非饱和土边坡稳定性分析理论中，根据室内土工试验数据和先验知识，利用贝叶斯理论，校准SWCC模型参数的随机统计特征。然后根据饱和渗透系数 ${k_{\text{s}}}$ 的随机场统计特征，联合离散化非饱和渗透系数 ${k_{\text{w}}}(\psi )$ ，开展边坡稳定性可靠指标计算。

2.1 SWCC模型参数校准的贝叶斯方法

为了减小结果误差，王林等^[8]采用Markov Chain Monte-Carlo（MCMC）方法，对SWCC模型参数开展反演分析，将贝叶斯方法应用于模型优化选择。刘源^[21]则提出采用adaptive Bayesian updating subset Simulation方法进行SWCC模型参数的反演分析，以提高模型优化选择的计算效率和精度。以下采用MCMC方法^[8]开展研究。

先通过室内土工试验方法，获取石榴树包老滑坡残积土的SWCC试验数据 ${{\boldsymbol{z}}_b}$ ，数据包含N个数据点 $(S_{{\text{e}},i}^{\text{m}},{\psi _i})$ 。其中， $S_{_{{\text{e}},i}}^{\text{m}}$ 表示第i个基质吸力Ψ_i(i = 1，2，…，N)对应的饱和度测试值。VGM，VGB，VG和FX模型 ${M}_{j}（j = \text{ }1,\text{ }2,\text{ }\cdots ,{N}_{\text{m}}）$ 对应的SWCC模型参数为 ${\boldsymbol{\varTheta }}{\text{ = [}}a,n,m,\sigma {\text{]}}$ ，包括模型参数（如FX模型的拟合参数 ${a_{{\text{fx}}}}$ ， ${n_{{\text{fx}}}}$ 和 ${m_{{\text{fx}}}}$ ）及模型测试值 $S_{_{{\text{e}},i}}^{\text{m}}$ 与拟合值 ${S_{{\text{e}},i}}$ 间的误差（如FX模型的误差标准差 ${\sigma _{\varepsilon ,{\text{fx}}}}$ ）。然后采用联合均匀分布描述先验信息，采用MCMC模拟方法计算模型参数的后验统计结果，通过后验概率密度函数 $p\left( {{{\boldsymbol{\varTheta }}_k}|{{\boldsymbol{z}}_b},{M_j}} \right)$ 量化第k次抽样模型参数 ${{\boldsymbol{\varTheta }}_k}$ 的不确定性。最后根据后验概率 $P（{M}_{j}|{z}_{b}）$ 计算SWCC模型 ${M_j}$ 的不确定性，并量化不同SWCC模型的备选概率。

2.2 随机场理论

通常采用正态分布（均值 $\mu$ 和标准差 $\nu$ ）描述随机场变量 $z(x)$ 的随机性，采用试验变异函数 ${\gamma ^*}(h)$ 描述其空间变异性：

${\gamma ^*}(h) = \frac{1}{{2{N_h}}}\sum\limits_{i = 1}^{{N_h}} {{{[z({x_i} + h) - z({x_i})]}^2}} \text{，}$

(6)

式中， $h$ 为滞后距， ${N_h}$ 为在 $({x_i},{x_i}{\text{ + }}h{\text{)}}$ 空间距离之间用来计算变异函数样本值的数据对。

球状变异函数具有简洁性和鲁棒性，常用于理论变异函数的研究：

$\gamma (h) = \left\{ \begin{array}{l} {C_0} + {C_1}\left[ {1.5\left( {\frac{h}{a}} \right) - 0.5{{\left( {\frac{h}{a}} \right)}^{\text{3}}}} \right]\;\;\;\;(0 \leqslant h \leqslant a) \hfill \\ {C_0} + {C_1}\;\;\;\;\;\;\;\;\;\;\;\;(h > a) \hfill \\ \end{array} \right. \text{，}$

(7)

式中， ${C_0}$ 为块金值， ${C_0}{\text{ + }}{C_1}$ 为基台值（即方差）， $\alpha$ 为相关距离（即变程），变异函数样本值可通过回归拟合方法，得到理论变异函数。

随机场变量 $Z(x)$ 在三维空间中的各向异性统计特征，可由加权的滞后距h表示：

$h = \sqrt {{{\left( {\frac{{{h_1}}}{{{\eta _1}}}} \right)}^2} + {{\left( {\frac{{{h_2}}}{{{\eta _2}}}} \right)}^2} + {{\left( {\frac{{{h_2}}}{{{\eta _3}}}} \right)}^2}} 。$

(8)

式中： ${\eta _1}$ 恒等于1.0； ${\eta _2}$ ， ${\eta _3}$ 分别为第二相关距离比率和第三相关距离比率，计算值分别为其对应方向上的相关距离 ${a_2}$ ， ${a_3}$ 除以主相关距离 ${a_1}$ 。

序贯高斯模拟算法在地统计学中的应用已经取得较好的研究成果^[22]。对于某一研究区域D，先将其离散化成K个随机单元，然后再序贯处理每个单元中点的赋值。求解普通Kriging方程组得到该单元的均值和方差，建立该单元处随机变量的正态分布，抽样得到该单元的一个样本值。

例如，已知某空间随机场的均值 $\mu$ 、方差 ${\nu ^2}$ 和自变异函数为γ(h)，那么利用条件数据 $z(x)$ ，预测结点 ${x_0}$ 的均值和方差为

$\mu ({x_0}) = \sum\limits_{i = 1}^n {{\lambda _i} \cdot z(} {x_i}) \text{，}$

(9)

${\nu ^2}({x_0}) = \sum\limits_{i = 1}^n {{\lambda _i}\gamma (} {x_i} - {x_0}) + \zeta \text{，}$

(10)

式中， $n$ 为结点 ${x_0}$ 的相邻观测值，通常取 $n = 10$ 。

插值系数 ${\lambda _i},i = 1, \cdots ,n$ 和拉格朗日系数 $\zeta$ 可由最小方差估计的普通Kriging方法方程组确定^[23]：

$\sum\limits_{i = 1}^n {{\lambda _i}{\gamma _1}({x_i} - {x_j})} + \zeta = {\gamma _2}({x_0} - {x_j}) \\ \;\;\;\;\;\;\;\;\;\;\; \left( {i,j = 1,2, \cdots ,n,{\text{ }}\sum\limits_i^n {{\lambda _i} = 0} } \right) \text{，}$

(11)

式中， ${x_i}$ 和 ${x_j}$ 为未知点 ${x_{\text{0}}}$ 周围的样本点， $\gamma$ 为滞后距为 $h = {x_i} - {x_j}$ 的变异函数。

根据计算得到 ${x_0}$ 处的均值 $\mu ({x_0})$ 和方差 ${\nu ^2}({x_0})$ ，建立单元中点处随机变量的正态概率分布。抽样得到样本值 $z({x_0})$ ，以及原始勘察数据 $z(x)$ 作为后续抽样的条件数据。空间离散域 $D$ 将由 $K$ 个相继的步骤产生。

饱和渗透系数 ${k_{\text{s}}}$ 整体上满足对数正态分布特征。现有原始数据 $[{k_{\text{s}}}({x_j}),j = 1,2, \cdots n]$ 经自然对数变换后，数据 $[z({x_j}),j = 1,2, \cdots ,n]$ 服从正态概率分布：

$p[z({x_j})] = \frac{1}{{\sqrt {2{\text{π }}} \nu ({x_0})}}{{\text{e}}^{ - {{[z({x_j}) - \mu ({x_0})]}^2}/2{\nu ^2}({x_0})}} 。$

(12)

通过随机场序贯高斯模拟方法，生成饱和渗透系数 ${k_{\text{s}}}$ 的空间分布值。数值计算模型中的滑坡体每个岩土单元都将获得一个对数正态分布的饱和渗透系数 ${k_{\text{s}}}$ ^[13]。另一方面，基于SWCC模型参数的后验统计特征，生成随机的土水特征曲线，采用式（1），（2），联合模拟滑坡体的非饱和渗透系数 ${k_{\text{w}}}(\psi )$ 随机场。

2.3 可靠指标计算方法

将非饱和渗透系数 ${k_{\text{w}}}(\psi )$ 随机场作为非饱和GeoStudio 2012土边坡稳定性分析的输入参数，通过的SEEP/W模块和SLOPE/W模块，计算边坡的安全系数 ${F_{\text{s}}}$ ，采用Monte-Carlo模拟算法，计算边坡的失效概率 ${P_{\text{f}}}$ （或可靠指标 $\beta$ ）。边坡安全系数 ${F_{\text{s}}}$ 的极限状态函数表示为

$G = {F_{\text{s}}} - {\text{1}} \text{，}$

(13)

式中， ${F_{\text{s}}}$ 为最危险滑动面的安全系数， ${P_{\text{f}}}$ 为极限状态函数 $G \leqslant 0$ 的失效概率。

对于不同SWCC模型 ${M_j}$ ， $j = 1,2,3, \cdots ,{N_{\text{m}}}$ ，采用Monte-Carlo模拟算法，生成 ${N_{\text{P}}}$ = 100000个随机样本 ${{\boldsymbol{\varTheta }}_k}$ ，并生成相应的土水特征曲线。联合饱和渗透系数 $k_{\text{s}}^{}$ 的空间随机场离散值，合成边坡稳定性分析中的非饱和渗透系数 ${k_{\text{w}}}(\psi )$ ，计算得到100000个边坡安全系数 ${F_{\text{s}}}$ 值。采用式（14），（15）计算条件失效概率 $P[{F_{\text{s}}} < 1|{M_j},{{\boldsymbol{z}}_b}{\text{,}}{k_{\text{w}}}(\psi )]$ 以及 $P[{F_{\text{s}}} < 1|{{\boldsymbol{z}}_b}{\text{,}}{k_{\text{w}}}(\psi )]$ 。

$[{F_{\text{s}}} < 1|{M_j},{{\boldsymbol{z}}_b}{\text{,}}{k_{\text{w}}}(\psi )] \\ = \frac{{\displaystyle \sum _{k = 1}^{{N}_{\text{P}}}I[{F}_{\text{s}}|{\boldsymbol{\varTheta }}_{k},{M}_{j},{z}_{b}\text{,}{k}_{\text{w}}(\psi )]}}{{N}_{\text{P}}}\text{ }\text{，}$

(14)

$P[{F_{\text{s}}} < 1|{{\boldsymbol{z}}_b}{\text{,}}{k_{\text{w}}}(\psi )] \\ = \frac{{\displaystyle \sum _{j = 1}^{{N}_{\text{m}}}{\displaystyle \sum _{k = 1}^{{N}_{\text{P}}}I[{F}_{\text{s}}|{\boldsymbol{\varTheta }}_{k},{M}_{j},{z}_{b},{k}_{\text{w}}(\psi )]}}P\left({M}_{j}|{z}_{b}\right)}{{N}_{\text{P}}}\text{ }。$

(15)

$P[{F_{\text{s}}} \lt 1|{M_j},{{\boldsymbol{z}}_b}{\text{,}}{k_{\text{w}}}(\psi )]$ 表示SWCC模型 ${M_j}$ 在给定室内土工试验数据z_b和非饱和渗透系数随机场 ${k_{\text{w}}}(\psi )$ 的条件下，非饱和土边坡稳定性的失效概率。由所有SWCC模型 ${M_j}$ 的参数 ${{\boldsymbol{\varTheta }}_k}$ ， $k = 1, \cdots ,{N_{\text{P}}}$ 的后验样本计算对应的 ${F_{\text{s}}}$ 值，并统计非饱和土边坡的失效概率， $P[{F_{\text{s}}} \lt 1|{{\boldsymbol{z}}_b}{\text{,}}{k_{\text{w}}}(\psi )]$ 是综合SWCC备选模型的非饱和土边坡失效概率。

不同SWCC模型 ${M_j}$ 对应安全系数 ${F_{\text{s}}}$ 的均值 $E[{F_{\text{s}}}|{M_j},{{\boldsymbol{z}}_b}{\text{,}}{k_{\text{w}}}(\psi )]$ 和方差 ${\text{Var}}[{F_{\text{s}}}|{M_j},{{\boldsymbol{z}}_b}{\text{,}}{k_{\text{w}}}(\psi )]$ 为

$E({F_{\text{s}}}|{M_j},{{\boldsymbol{z}}_b}) \approx \mu _{{F_{\text{s}}}}^j = \frac{1}{{{N_{\text{P}}}}}\sum\limits_{k = 1}^{{N_{\text{P}}}} {F_{\text{s}}^k} \text{，}$

(16)

${\text{Var}}({F_{\text{s}}}|{M_j},{{\boldsymbol{z}}_b}) \approx \sigma _{{F_{\text{s}}}{,_j}}^2 = \frac{1}{{{N_{\text{P}}} - 1}}\sum\limits_{k = 1}^{{N_{\text{P}}}} {{{\left( {F_{\text{s}}^k - \mu _{{F_{\text{s}}}}^j} \right)}^2}} \text{，}$

(17)

式中， $\mu _{{F_{\text{s}}}}^j$ 和 $\sigma _{{F_{\text{s}}}{,_j}}^2$ 分别为模型 ${M_j}$ ，参数 ${{\boldsymbol{\varTheta }}_k}$ 值相应安全系数 $F_{\text{s}}^k$ 的平均值和方差。

如所示，模块一根据室内土工试验数据 ${{\boldsymbol{z}}_b}$ ，采用贝叶斯方法校准SWCC模型参数。模块二采用随机场理论，描述饱和渗透系数的空间变异性，并开展随机单元离散化赋值。利用模块一SWCC模型参数随机统计特征和模块二饱和渗透系数的随机场统计特征，联合生成非饱和渗透系数 ${k_{\text{w}}}(\psi )$ 的空间分布。模块三采用极限平衡法与经典Monte-Carlo算法模拟边坡的失效概率或可靠指标，综合评估库岸老滑坡的稳定性。

图 1 非饱和土边坡稳定性计算流程图

Figure 1. Flow chart of stability analysis of slopes of unsaturated soils

下载: 全尺寸图片幻灯片

3. 非饱和土库岸老滑坡稳定性分析

得到石榴树包老滑坡残积土的SWCC室内土工试验及模型参数的后验分布结果后，开展边坡稳定性的数值分析。最后根据《水利水电工程结构可靠性设计统一标准：GB50199—2013》，对2020年夏季石榴树包老滑坡稳定性做出评估。

3.1 石榴树包老滑坡的工程概况

石榴树包老滑坡位于湖北省巴东县黄蜡石村，该村落位于三峡库区上游约55 km处。图 2为地质剖面图，潜在滑坡体积为11.8×10⁶ m³，面积约0.25 km²，宽度为350~470 m，高程为60~350 m，坡度为25°~30°。基岩主要由三叠纪中期形成的泥灰岩和石灰岩组成，滑坡体由松散的残积土组成。通过课题组前期的现场勘察，发现石榴树包老滑坡的结构和物质成分复杂，但由于长年累月的风化作用和雨水冲刷，大量碎石已被风化成土体，被强降雨形成的地表径流携带至坡脚。

图 2 SWCC模型的试验数据和拟合曲线

Figure 2. Laboratory test data and fitting models of SWCC

下载: 全尺寸图片幻灯片

在石榴树包老滑坡上，现场取样残积土，立即用保鲜膜将土样包裹、运输。然后进行土的烘干法和环刀法试验，得到石榴树包边坡土的天然含水率为20.80%，干密度为1.66 g/cm³。土体筛分试验以及液塑限联合测定法的试验结果表明，土体的液限w_L为32.5%，塑限w_P为21.6%，塑性指数I_P为10.9。塑性指数I_P小于17而大于10。所以石榴树包边坡土在分类上为粉质黏土，并夹杂着由岩层破碎形成的碎石。

3.2 校准SWCC模型参数

基于压力板仪试验，得到低吸力段的试验数据；采用蒸汽平衡法，得到高吸力段试验数据。采用4种SWCC模型，拟合石榴树包老滑坡残积土的土水特征曲线，如图 2所示。

采用MCMC模拟方法，生成4个SWCC模型参数的 ${N_{\text{P}}}$ = 100000个随机样本。采用Metropolis-Hastings (M-H)算法，挑选服从参数 ${{\boldsymbol{\varTheta }}_k}$ 的后验分布样本，收敛到稳态的Markov Chain后，统计分析随机样本，求得参数 ${{\boldsymbol{\varTheta }}_k}$ 的后验统计特征^[9]。采用R语言编写贝叶斯算法程序，输入土水特征曲线的试验数据、先验信息和备选的SWCC模型，计算模型参数 ${\boldsymbol{\varTheta }}$ 的后验概率密度函数，先验信息的参数取值范围来自参考文献[]，其中 ${\alpha _{{\text{vgm}}}}$ ， ${\alpha _{{\text{vgb}}}}$ ， ${\alpha _{{\text{vg}}}}$ 和 ${\alpha _{{\text{fx}}}}$ 取值为(0 kPa，300 kPa]， ${n_{{\text{ vgm}}}}$ 取值为(1, 10]， ${n_{{\text{ vgb}}}}$ 取值为(2, 10]， ${n_{{\text{ vg}}}}$ 和 ${n_{{\text{ fx}}}}$ 取值为(0, 10]， ${m_{{\text{ vg}}}}$ 和 ${m_{{\text{ fx}}}}$ 取值为(0, 10]。~给出 ${N_{\text{P}}}$ = 100000个MCMC随机样本统计的后验概率密度函数。表示SWCC模型参数 $\alpha$ 的后验分布，红色的直方图为随机样本统计的频数分布，黑色曲线是拟合的概率密度函数Probabilistic Density Function (PDF)曲线。

图 3 SWCC模型参数

$\alpha$ 的后验分布

Figure 3. Posterior distributions of SWCC model parameter

$\alpha$

下载: 全尺寸图片幻灯片

图 4 SWCC模型参数n的后验分布

Figure 4. Posterior distributions of SWCC model parameter

$n$

下载: 全尺寸图片幻灯片

图 5 SWCC模型VG和FX参数m的后验分布

Figure 5. Posterior distributions of SWCC model (i.e., VG and FX) parameter

$m$

下载: 全尺寸图片幻灯片

图 6 SWCC模型误差

$\sigma$ 的后验分布

Figure 6. Posterior distributions of SWCC model error

$\sigma$

下载: 全尺寸图片幻灯片

对于4个SWCC模型，模型参数的后验统计值也不尽相同，表明 ${\boldsymbol{\varTheta }}$ 的后验统计特征受到SWCC备选模型的影响。采用贝叶斯方法计算SWCC备选模型概率 $P（{M}_{j}|{z}_{\text{b}}）$ 的结果，从大到小依次为FX > VG > VGB > VGM，分别是52.04%，25.56%，12.27%和10.13%。因此，根据土水特征曲线试验数据和先验信息，石榴树包老滑坡残积土最优的SWCC是FX模型。

3.3 非饱和土边坡稳定性的数值分析

图 7为石榴树包老滑坡的数值计算模型，边坡确定性分析的岩土参数和水力参数取值和课题组前期研究保持一致^[13]。数值计算模型的前缘设置为降雨和水位的混合边界（蓝色线段表示），采用完全入渗流速边界，即根据实际降雨强度设定的入渗流速。其具体取值，可根据不同工况下的库区水位波动和日降雨量确定，并在滑坡体内设置3个变形监测点。

图 7 数值计算模型

Figure 7. Numerical model

下载: 全尺寸图片幻灯片

2020年第5波洪峰经过三峡时的水文情况如图 8所示，将第5波洪峰所在的整个8月作为数值模拟的时间范围。库区水位从最低145 m到最高175 m的30 m高度作为水位升降范围。降雨等级取300 mm/d的特大暴雨，水位升、降取4 m/d的变化速度。根据以上水文监测数据和数值模拟假设的降雨及水位变化条件，共设计了降雨，水位变化以及降雨联合水位变化3种计算工况。若老滑坡在假设的极端工况下，依然可保持较大的安全系数，则说明不存在滑坡风险；否则应开展边坡的可靠性分析，综合评估老滑坡的稳定性。

图 8 2020年三峡库区第5波洪峰水文图

Figure 8. Hydrograph of fifth wave of flood arriving at Three Gorges Reservoir in 2020

下载: 全尺寸图片幻灯片

SWCC模型FX备选概率最高，为52.04%。因此确定性边坡稳定性分析采用FX模型。降雨作用下，为了保证总降雨量一定且降雨集中在汛期，前期设计为无雨工况，所以在这段时间内安全系数无变化。当边坡遇到特大暴雨降雨，安全系数在一开始迅速降低，最终降雨工况下安全系数为1.029，但特大暴雨和水位骤升陡降联合作用下库岸边坡的安全系数变化幅度显然更大。刚开始时，随着水位的骤然上升，由于存在指向滑坡体内的动水压力，边坡的安全系数较初始水位145 m的数值呈现增大趋势，由初始的1.128增大至1.228。当库区水位保持175 m最高位时，安全系数回落至1.203，并趋于稳定。在水位下降和降雨联合作用阶段，边坡的安全系数快速降低至1.028，如图 9所示。由此判断，石榴树包老滑坡的确定性分析的安全系数略大于临界状态值1.0, 老滑坡有激活的风险。

图 9 边坡安全系数变化图

Figure 9. Variation of factor of safety of slopes

下载: 全尺寸图片幻灯片

3.4 非饱和土边坡稳定性可靠度分析

石榴树包老滑坡确定性分析的安全系数最小值仅为1.026，预示着边坡处于临界状态，需开展非饱和土边坡稳定性的可靠度分析。饱和渗透系数 $k_{\text{s}}^{}$ 的随机统计特征来自于参考文献[]，均值 ${\mu _{{k_{\text{s}}}}}$ = 2.04 m/d，标准差 ${v_{{k_{\text{s}}}}}$ = 0.29 m/d。另外，随机场统计特征主相关距离 ${a_{\text{1}}}$ 与坡面平行（倾角为27.5°），相关距离 ${a_{\text{1}}}$ ， ${a_2}$ 和 ${a_3}$ 互相垂直。假设 ${a_{\text{1}}}$ 和 ${a_2}$ 的值取为20 m，第三相关距离比率 ${\eta _3}$ 取为0.2，即 ${\eta _{{k_{\text{s}}}}}$ = 0.2。潜在滑坡单元体将被赋予非饱和渗透系数的随机场统计特征，单元最大边长尺寸为2.0 m，不大于第三相关距离 ${a_3}$ 的一半，保证离散化的随机场可以描述非饱和渗透系数 ${k_{\text{w}}}(\psi )$ 的空间变异性。图 10给出结合SWCC模型参数随机统计特征的非饱和渗透系数空间离散化赋值示例。

图 10 非饱和渗透系数随机场离散化赋值

Figure 10. Spatial discretization of unsaturated hydraulic conductivity

下载: 全尺寸图片幻灯片

非饱和土边坡稳定性失效概率的计算结果表明VGM、VGB、VG和FX模型对应的失效概率在1.36×10^-4~3.06×10^-3变化。如图 11所示，分别为7.94×10^-4，1.36×10^-4，1.67×10^-3和3.06×10^-3。显然FX模型的失效概率最大，安全系数均值 ${\mu _{{F_{\text{s}}}}}$ = 1.065；VGB模型的失效概率最小，安全系数均值 ${\mu _{{F_{\text{s}}}}}$ = 1.082。综合考虑SWCC模型不确定性的失效概率为2.12×10^-3。

图 11 SWCC模型对应边坡稳定性安全系数的PDF曲线

Figure 11. PDFs of factor of safety of 4 SWCC models

下载: 全尺寸图片幻灯片

如所示，安全系数可靠指标在2.70~4.27变化，FX模型对应的可靠指标最小， $\beta = {\text{2}}.{\text{741}}$ ，VGB模型对应的可靠指标最大， $\beta = {\text{3}}.{\text{641}}$ 。图中的红色虚线表示综合4个SWCC模型计算得到的边坡稳定性可靠指标 $\beta = {\text{2}}.{\text{86}}0$ ，蓝色虚线是将非饱和渗透系数简化考虑为随机变量（即 ${\mu _{{k_{\text{s}}}}}$ = 2.04 m/d，标准差 ${v_{{k_{\text{s}}}}}$ = 0.29 m/d）得到的计算结果，可靠指标 $\beta = {\text{2}}.{\text{349}}$ 。

图 12 不同SWCC模型的可靠指标

Figure 12. Reliability indices of 4 SWCC models

下载: 全尺寸图片幻灯片

结果表明，如将非饱和渗透系数作为随机变量，计算得到的可靠指标 $\beta$ 不能满足《水利水电工程结构可靠性设计统一标准：GB 50199—2013》的要求（ $\beta \lt {\text{2}}.{\text{7}}0$ ）。而考虑非饱和渗透系数空间变异性的边坡稳定性可靠度分析方法表明，虽然石榴树包老滑坡的安全系数比较低，但是稳定性可靠指标大于规范要求（ $\beta \gt {\text{2}}.{\text{7}}0$ ）。因此石榴树包老滑坡在未来遭遇类似2020年暴雨和水位骤升陡降等极端工况作用，不采取加固措施也可以保持边坡稳定。

4. 总结与展望

以土水特征曲线的室内土工试验数据为基础，采用贝叶斯方法比选理论模型和校准模型参数。考虑土水特征曲线的随机统计特征和饱和渗透系数的随机场统计特征，描述非饱和渗透系数的空间变异性。基于非饱和渗透系数随机场，开展石榴树包老滑坡稳定性的可靠度分析，主要得出以下3点结论。

（1）基于土水特征曲线的试验数据，采用贝叶斯方法得出VGM、VGB、VG和FX理论模型后验发生概率，分别为10.13%，12.27%，25.56%和52.04%，最优的理论土水特征曲线是FX模型。

（2）2020年第5波洪峰过境时，开展石榴树包老滑坡的确定性数值模拟分析，水位骤升陡降和降雨联合作用下库岸老滑坡的安全系数最小，不满足边坡稳定性要求。

（3）将非饱和渗透系数简化考虑为随机变量，边坡稳定性的可靠指标 $\beta$ 不能满足规范要求（ $\beta$ < 2.70）。而考虑非饱和渗透系数随机场统计特征时，边坡稳定性可靠度分析结果满足规范要求（ $\beta$ > 2.70），无需采取额外的边坡工程加固措施，建议继续开展边坡的长期健康监测。

图 1 加固土坡模型照片

Figure 1. Photo of reinforced slope model

下载: 全尺寸图片幻灯片

图 2 加固土坡模型示意图

Figure 2. Schematic view of reinforced slope model

下载: 全尺寸图片幻灯片

图 3 素土坡与加固土坡破坏过程

Figure 3. Failure process of unreinforced and reinforced slopes

下载: 全尺寸图片幻灯片

图 4 加固土坡点对相对位移

Figure 4. Relative displacements of point couples in reinforced slope

下载: 全尺寸图片幻灯片

图 5 y=120 mm最大剪应变水平分布

Figure 5. Horizontal distribution of maximum shear strain at y= 120 mm

下载: 全尺寸图片幻灯片

图 6 x = -210 mm水平位移竖向分布，

Figure 6. Vertical distribution of horizontal displacement at x = -210 mm

下载: 全尺寸图片幻灯片

图 7 水位h = 40 mm水平位移水平分布

Figure 7. Horizontal distribution of horizontal displacement at water level h = 40 mm

下载: 全尺寸图片幻灯片

参考文献(10)

[1]	李寻昌, 门玉明, 王娟娟. 锚杆抗滑桩体系的群桩、群锚效应研究现状分析[J]. 公路交通科技, 2005, 22(增刊2): 56-59. https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK2005S2014.htm LI Xunchang, MEN Yuming, WANG Juanjuan. Analysis on researche reality of the effects of pile groups and anchor groups in anchor anti-slide piles[J]. Journal of Highway and Transportation Research and Development, 2005, 22(S2): 56-59. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK2005S2014.htm
[2]	刘英朴, 门玉明, 蔺兴淼, 等. 锚杆抗滑桩内力计算的初参数法研究[J]. 水文地质工程地质, 2005, 32(6): 57-60. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG200506013.htm LIU Yingpu, MEN Yuming, LIN Xingmiao, et al. The initial parameter method study on the internal force calculation of anchor anti-slide pile[J]. Hydrogeology and Engineering Geology, 2005, 32(6): 57-60. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG200506013.htm
[3]	DONG X G, LI Z, CUI Z Z, et al. Stability analysis of the pile-prestressed anchor composite structure based on failure mode[J]. Engineering Failure Analysis, 2022, 137: 106223. doi: 10.1016/j.engfailanal.2022.106223
[4]	WANG C T, WANG H, QIN W M, et al. Experimental and numerical studies on the behavior and retaining mechanism of anchored stabilizing piles in landslides[J]. Bulletin of Engineering Geology and the Environment, 2021, 80(10): 7507-7524. doi: 10.1007/s10064-021-02391-3
[5]	HUANG Y, XU X, LIU J J, et al. Centrifuge modeling of seismic response and failure mode of a slope reinforced by a pile-anchor structure[J]. Soil Dynamics and Earthquake Engineering, 2020, 131: 106037. doi: 10.1016/j.soildyn.2020.106037
[6]	郑颖人, 唐晓松. 库水作用下的边(滑)坡稳定性分析[J]. 岩土工程学报, 2007, 29(8): 1115-1121. doi: 10.3321/j.issn:1000-4548.2007.08.001 ZHENG Yingren, TANG Xiaosong. Stability analysis of slopes under drawdown condition of reservoirs[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(8): 1115-1121. (in Chinese) doi: 10.3321/j.issn:1000-4548.2007.08.001
[7]	LIU S J, LUO F Y, ZHANG G. Centrifuge model tests on pile-reinforced slopes subjected to drawdown[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2020, 12(6): 1290-1300. doi: 10.1016/j.jrmge.2020.02.006
[8]	LIU S J, LUO F Y, ZHANG G. Pile reinforcement behavior and mechanism in a soil slope under drawdown conditions[J]. Bulletin of Engineering Geology and the Environment, 2021, 80(5): 4097-4109. doi: 10.1007/s10064-021-02191-9
[9]	LUO F Y, ZHANG G. Progressive failure behavior of cohesive soil slopes under water drawdown conditions[J]. Environmental Earth Sciences, 2016, 75(11): 1-12.
[10]	ZHANG G, HU Y, ZHANG J M. New image analysis-based displacement-measurement system for geotechnical centrifuge modeling tests[J]. Measurement, 2009, 42(1): 87-96. doi: 10.1016/j.measurement.2008.04.002

施引文献

资源附件(0)

图(7)

计量

文章访问数: 105
HTML全文浏览量: 23
PDF下载量: 46
被引次数: 0

0. 引言
1. 非饱和土边坡稳定性分析理论
1.1 土水特征曲线与渗透系数
1.2 非饱和土的剪切强度
1.3 非饱和土边坡稳定性分析
2. 边坡可靠度分析方法
2.1 SWCC模型参数校准的贝叶斯方法
2.2 随机场理论
2.3 可靠指标计算方法
3. 非饱和土库岸老滑坡稳定性分析
3.1 石榴树包老滑坡的工程概况
3.2 校准SWCC模型参数
3.3 非饱和土边坡稳定性的数值分析
3.4 非饱和土边坡稳定性可靠度分析
4. 总结与展望

0. 引言
1. 非饱和土边坡稳定性分析理论
1.1 土水特征曲线与渗透系数
1.2 非饱和土的剪切强度
1.3 非饱和土边坡稳定性分析
2. 边坡可靠度分析方法
2.1 SWCC模型参数校准的贝叶斯方法
2.2 随机场理论
2.3 可靠指标计算方法
3. 非饱和土库岸老滑坡稳定性分析
3.1 石榴树包老滑坡的工程概况
3.2 校准SWCC模型参数
3.3 非饱和土边坡稳定性的数值分析
3.4 非饱和土边坡稳定性可靠度分析
4. 总结与展望

参考文献(10)

施引文献

资源附件(0)

降水条件下抗滑桩-锚杆加固边坡的离心模型试验研究 English Version

作者简介: 张泽蔚(2003—)，男，本科，主要从事边坡工程方面的研究。E-mail: zhang-zw21@mails.tsinghua.edu.cn

计量

出版历程