0.   引言

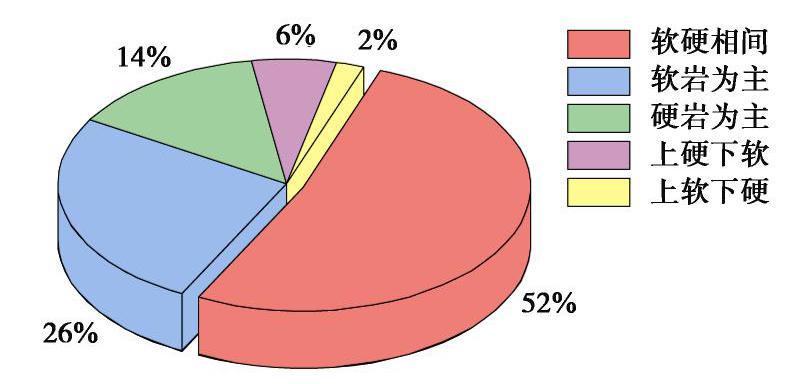
反倾边坡通常被视为比较稳定,但近年来,西部地区已发现许多大型深层倾倒变形体,最大倾倒深度甚至达到了300 m^[1],且可进而转变为大型滑坡,如锦屏水文站倾倒体,直接导致了两岸形成深度远超220 m的巨型滑坡^[2]。笔者统计了中国西部山区50个较大规模倾倒体的岩体结构（图1）,发现具有软硬互层结构的样本占比达52%,可见该结构对倾倒变形的形成具有重要影响。因此,针对软硬互层反倾边坡的变形破坏机理的研究尤为必要。

图  1  倾倒变形体岩体结构统计

Figure  1.  Statistics of rock mass structures of toppling slope

下载: 全尺寸图片 幻灯片

目前,物理模型试验与数值模拟仍是反倾边坡研究中最常用的方法^[3]。倾倒变形属典型的重力时效变形过程,常用的试验方法有底摩擦试验^[4-5]和离心模型试验两种,相比之下,离心试验通过高速旋转的离心力形成远大于模型自重的重力场^[6],对边坡施加体力,具有更显著的优越性。Adhikary等^[7]通过离心模型试验对比研究了脆性与延性材料模型边坡的倾倒变形机理；汪小刚等^[8]以龙滩水电站左岸边坡为原型,通过两种材料模型的离心试验得出反倾边坡破裂面为双折线型；吴昊等^[9]以平板玻璃为相似材料,开展不同坡角、倾角组合下的多组离心模型试验,认为可通过位移矢量的方向来确定破裂面位置；蒋金阳^[10]则通过离心模型试验验证了苗尾水电站右坝肩倾倒体支护结构的有效性。但离心试验成本高昂,限制了其在研究中的广泛应用。

数值模拟在反倾边坡研究中应用比较广泛,如Orr等^[11]采用有限差分法研究了西澳大利亚州露天金矿边坡的倾倒变形机理；Leandro等^[12]通过有限单元法详细研究了西班牙某露天矿边坡上部倾倒、下部滑移的组合变形机理；Coggan等^[13]通过离散元法研究了英国Delabola采石场板岩边坡的深层倾倒机理；孙东亚等^[14]则通过DDA法研究倾倒变形机理,并讨论了Goodman等提出的经典破坏模式的合理性。反倾边坡破裂面的形成与岩层的断裂过程联系密切,而离散元法可模拟岩层的变形与破裂,在反倾边坡研究中具有独特的优势^[15-16]。

综上,现有成果仍较少考虑软硬互层结构的影响,且弯曲倾倒变形机制复杂,单一手段难以全面合理地分析。本文采取物理模拟与数值模拟相结合的思路,首先通过地质结构简化的理想化离心模型试验,采用位移测量系统与图像处理获得边坡位移场及变形特征,并以此校核数值模型参数,对离心试验过程进行模拟计算,得到与物理试验基本一致的破裂面演化及位移特征。而后通过点对分析,对倾倒变形不同阶段的力学机制进行了探讨。通过对离心模型试验与离散元数值模拟结果的对比、融合,较全面地分析了软硬互层反倾边坡倾倒变形破坏机制。

1.   离心模型试验

1.1   试验设备

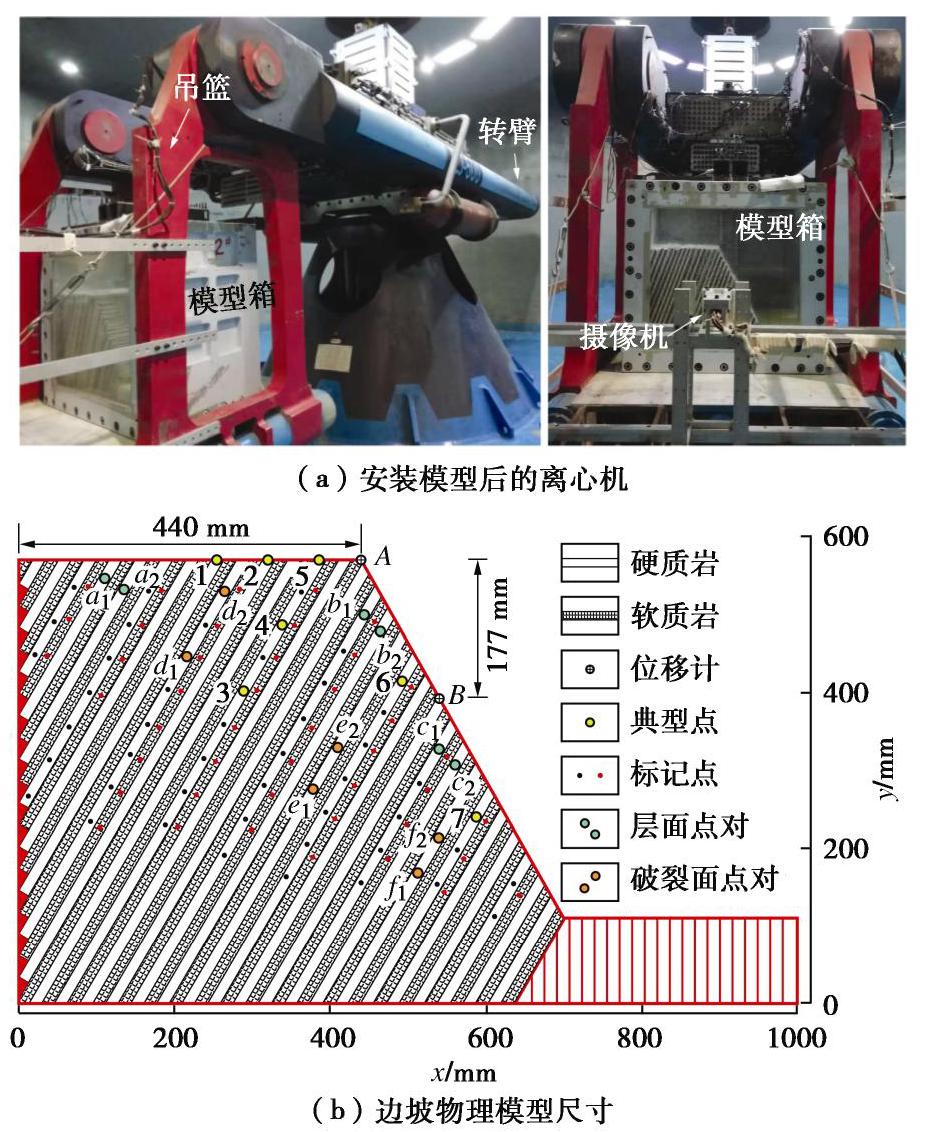
试验采用地质灾害防治与地质环境保护国家重点实验室（成都理工大学）的TLJ-500型土工离心机（图2（a））。主要由主机、900 kw直流电机、直流调速装置、加速度控制系统、主控台、测量系统、电视监视通讯系统及模型箱等组成,最大容量500 g·t,有效半径4.5 m,主机采用单吊斗、不对称臂结构。通过动态信号测量系统采集位移、加速度等动态变化量,采集间隔设置为1 s,并通过监视系统采集高清图像,摄像机布置在转臂上,分辨率大于600 ppi。

图  2  试验设备与边坡物理模型

Figure  2.  Geotechnical centrifuge and physical model for slope

下载: 全尺寸图片 幻灯片

1.2   试验模型及条件

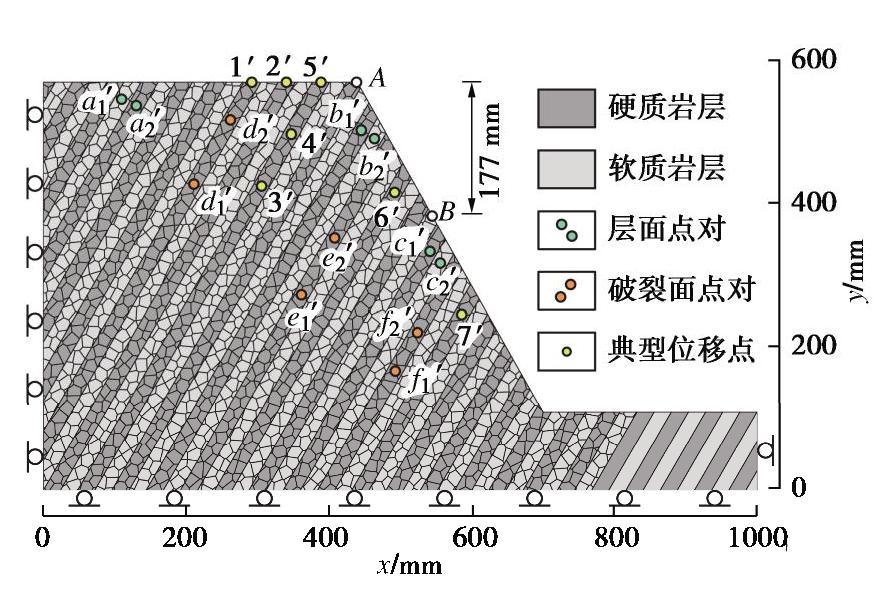
以苗尾水电站右坝肩倾倒体^[10]中软硬互层段岩层为原型,其软质绢云母片岩平均层厚为1 m。假设软硬岩层等厚,对原型缩小简化,根据试验设备尺寸,设计岩层模板单层厚1 cm,从而确定试验几何相似比为C_l=100,需满足下列相似判据^[17]：

式中 C_σ为应力相似常数；C_γ为重度相似常数；C_l为几何尺寸相似常数；C_ε为应变相似常数；C_μ为泊松比相似常数；C_φ为内摩擦角相似常数；C_E为弹性模量相似常数；C_c为黏聚力相似常数。根据边坡模拟范围及试验设备尺寸,取C_l=100,C_γ=1,由相似判据得C_σ= C_γC_l= C_E = C_c= 100,C_φ= C_μ = 1。

模型主要考虑软硬互层岩体结构,在边坡宏观尺寸上没有严格意义的原型边坡,根据模型箱尺寸,最终预堆砌模型尺寸为70 cm×55 cm×57 cm,相当于高57 m的原型边坡。

相似材料以石英砂为骨料,石膏和水泥为黏结剂,使用浓度2%的硼砂做缓凝剂,原料易得、操作简便,强度可调范围大。最终配比见表1,通过100 mm×50 mm试样单轴压缩试验,测得硬岩材料抗压强度为10 MPa,软岩材料为0.3 MPa。

表  1  相似材料最终配比

Table  1.  Final ratios of similar materials

相似材料	石英砂	石膏	水泥	水	重晶石
硬岩	1	0.600	0.050	0.400	0
软岩	1	0.350	0.025	0.613	1

下载: 导出CSV 

| 显示表格

模型边坡倾角为60°,坡角为60°,采用砌筑法,预制试块模板尺寸为60 cm×10 cm×1 cm或40 cm×10 cm×1 cm,待其干燥硬化后进行切割和堆砌。软岩材料脱模前需静置3 h以上,硬岩静置30 min,所有材料需在阴凉通风处静置30 d。模型尺寸如图2（b）所示,在坡顶和坡表中部布置两个位移计,并在岩层上设置若干典型标记点（DX点）,通过图像处理提取更加丰富的位移数据。

1.3   试验过程

离心模型试验流程为：制作材料模板→模板养护和切割→装配边坡模型→传感器连接与调试→试验加载→记录边坡破坏形态并收集分析试验数据。加载方案为：①离心加速度由0逐渐加载至30g,并在30g保持稳态旋转5 min；②加速度由30g逐渐加载至50g,并在50g稳态旋转5 min；③加速度由50g逐渐加载至90g,并保持稳态旋转5 min。边坡在加载进行至约550 s时发生整体失稳,此时的离心加速度约为40g。

2.   离散元数值模型的构建

2.1   材料模型与参数确定

数值模拟使用UDEC6.0软件,为实现较真实的岩层断裂,通过泰森网格预置层内随机裂隙,考虑计算效率,网格最大边长设为15 mm。

层面采用面接触–库仑滑移模型（joint model area）,需要5个参数^[18]：节理黏聚力c_j、节理摩擦角${\phi }_{\text{j}}$、节理抗拉强度${\sigma }_{\text{tj}}$、节理法相刚度k_n、节理剪切刚度k_s。其中${\sigma }_{\text{tj}}$,c_j和${\phi }_{\text{j}}$结合物理模型参数,并参考Adhikary等^[7]的离心试验取值,k_n值采用Diederichs等^[19]推导的方程估算：

式中,E_rm和E分别为岩体和完整岩石的弹性模量,s为节理间距。

层内微节理采用面接触–具有残余强度的库仑滑移模型（joint model ss）,该模型适用于描述内部开裂^[20],需要8个参数：黏聚力c_ij、内摩擦角φ_ij、抗拉强度${\sigma }_{\text{it}}$及其残余值$c_{\text{ijres}}$,${\phi }_{\text{ijres}}$,${\sigma }_{\text{ijres}}$,节理法向刚度k_in和剪切刚度k_is。前6个参数代表完整岩石的强度,接触法向刚度k_in使用Cho等^[21]提出的公式确定：

式中,∆Z_min为垂直方向上与接触面相邻区域的最小宽度,K和G为别为块体的体积模量和剪切模量^[18]。通过多次试算与校核,最终参数见表2。

表  2  数值模型材料参数

Table  2.  Material parameters of numerical model

材料	密度ρ/(kg·m-3)	法相刚度$\frac{k_{\text{in}}}{k_{\text{n}}}/{10}^9$	剪切刚度$\frac{k_{\text{is}}}{k_{\text{s}}}/{10}^9$	黏聚力$\frac{c_{\text{ij}}}{k_{\text{j}}}/({10}^4\text{Pa})$	抗拉强度$\frac{{\sigma }_{\text{it}}}{{\sigma }_{\text{t}}}/({10}^6\text{Pa})$	内摩擦角$\frac{{\phi }_{\text{ij}}}{{\phi }_{\text{j}}}$/(°)	残余摩擦角φijres/(°)
硬岩	2850	28	25	3.4×102	2.5	23	18
软岩	2250	14	12	1.4×102	1.1	15	10
层面	—	8	7.5	1.5	0	12	—

下载: 导出CSV 

| 显示表格

2.2   数值试验方案

数值模型与物理模型等尺寸（图3）,软硬岩层等厚,为保证计算效率,层厚适当增大至15 mm。坡面位移点A,B的位置与物理模型相同,以便对比。

图  3  边坡数值模型

Figure  3.  Numerical slope model of centrifugal tests

下载: 全尺寸图片 幻灯片

模型底部固定y方向速度为0,两侧固定x方向速度为0,坡顶与坡面为自由边界。首先计算至自重平衡（1g）,之后模拟离心机加载过程,间隔2g对边坡逐级增加重力荷载。每级加载分配足够的时步,保证稳定的模型响应。

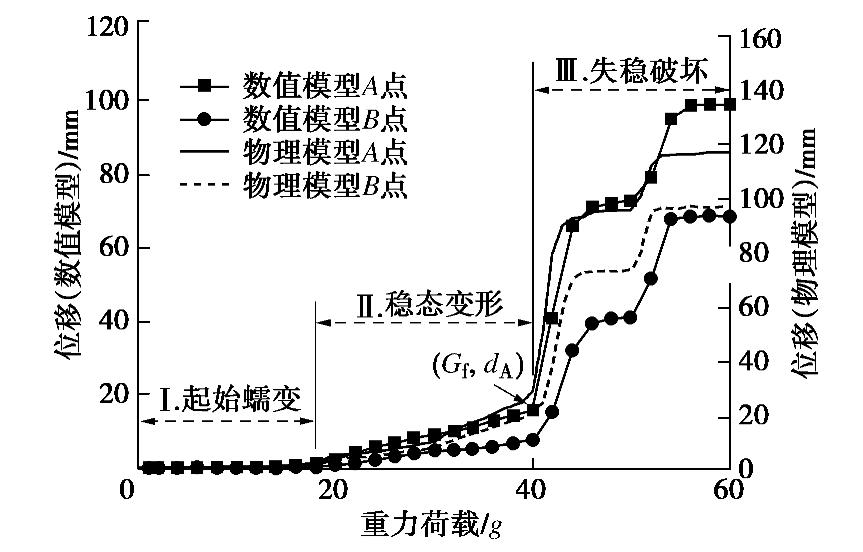
2.3   竖向位移对比

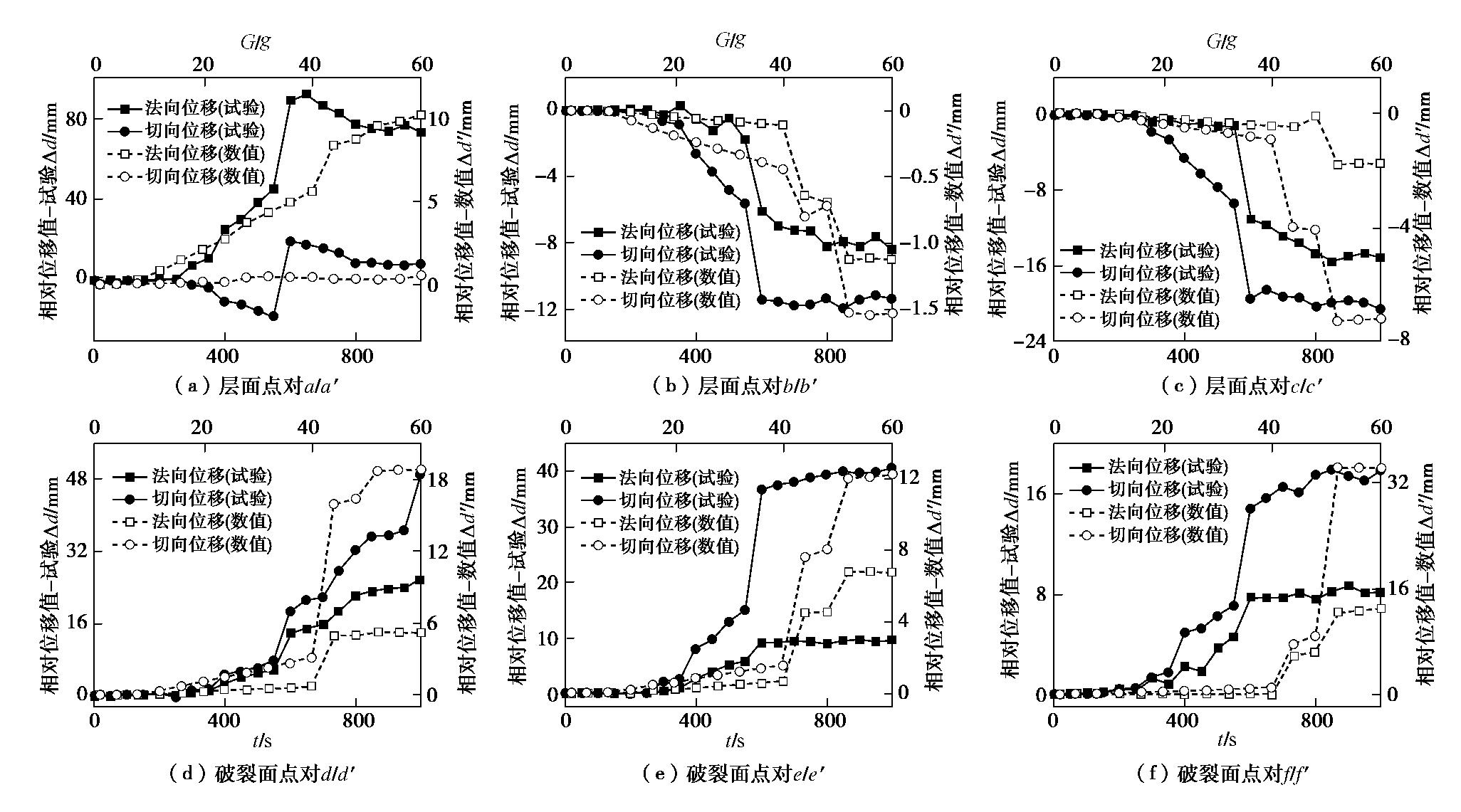
对比数值与试验关键位移点的位移–荷载曲线（图4）,二者变化趋势高度吻合,验证了模拟的可行性。

图  4  位移曲线对比

Figure  4.  Comparison of displacement curves

下载: 全尺寸图片 幻灯片

根据位移曲线,将倾倒变形过程分为3个阶段：①起始蠕变阶段,约18g之前,坡体内应力迅速调整,整体位移极小,各部位无可见变形,位移场由坡顶向周围均匀递减,无明显指向性；②稳态变形阶段,边坡在重力作用下持续倾倒变形,18g～40g,位移曲线斜率增大,位移近似线性增大；③失稳破坏阶段,约40g之后,位移急剧增大,边坡发生整体破坏。

3.   反倾边坡变形破坏特征

3.1   物理模型破坏特征

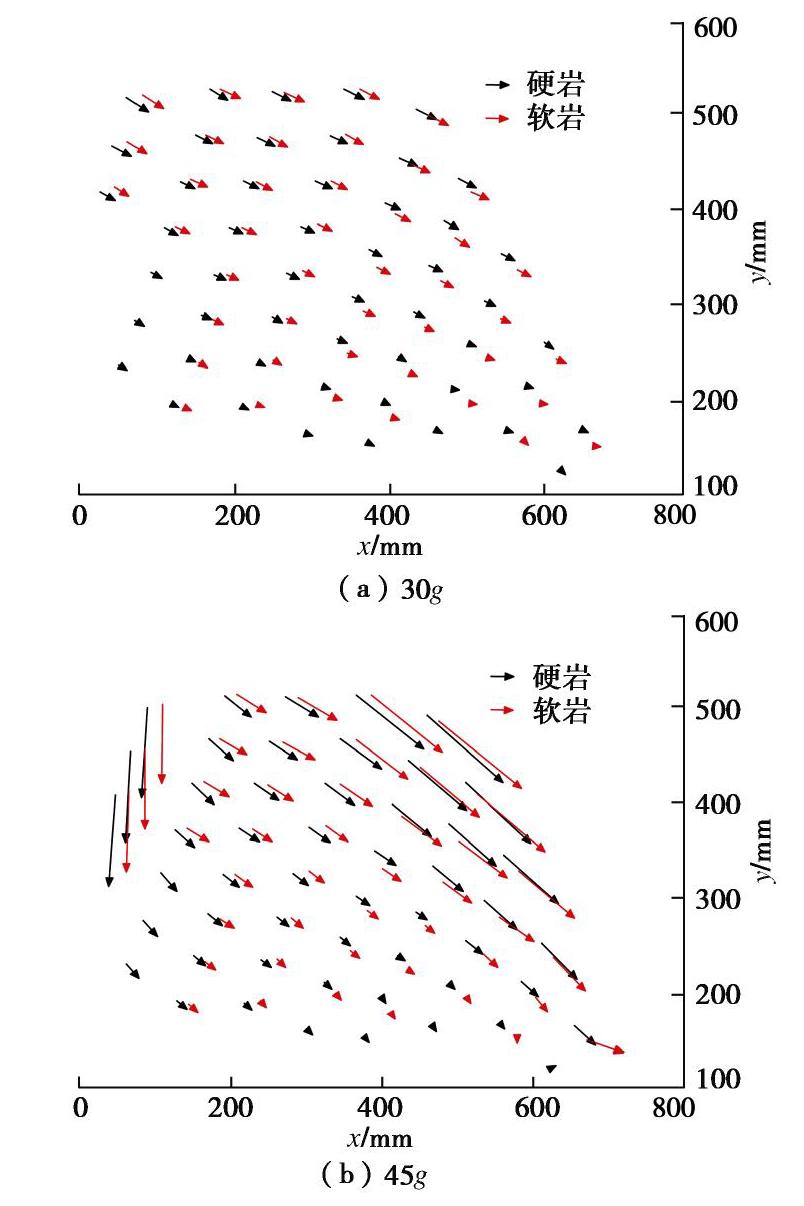
图5为试验典型时刻边坡变形图。进入稳态变形阶段后,岩层持续缓慢蠕变,变形过程中后缘最先出现较明显的拉张脱层（图5（a））,坡脚岩层则发生轻度弯曲（图5（b））。位移矢量图（图6（a））表明,边坡各处变形较均匀,坡顶位移稍大,矢量方向越靠前部偏转越大,此阶段岩层内部尚无明显可见的拉张裂缝；40g后,持续的弯曲使岩层达到材料抗弯极限,坡脚处首先出现少量层内拉裂纹,之后快速向坡内延伸,45g时,破裂面已贯通整个坡体,岩层折断,破裂面处岩层内的拉张裂缝明显（图5（c））,边坡已整体失稳,各记录点位移曲线显著阶跃（图4）。相同岩层位移矢量由内到外递增,且坡表矢量方向偏转显著（图6（b））,说明越靠外部弯曲程度更大；而在垂直岩层方向,过坡顶岩层位移最大,向前后两侧递减；继续加载至50g时,后缘处前期暂态稳定的岩层发生局部折断,造成位移曲线二次阶跃。变形体中前部的变形和断裂更加显著,60g时破裂面中下部已形成贯穿多层的拉裂缝,存在剪切错动趋势,并保持至加载结束（90g）。

图  5  典型时刻物理模型变形图

Figure  5.  Deformations of physical model at typical time

下载: 全尺寸图片 幻灯片

图  6  物理模型位移矢量图

Figure  6.  Displacement vectors of physical model

下载: 全尺寸图片 幻灯片

图5（c）还可见,45g时,硬岩中裂隙明显,但相邻软岩中却无明显裂隙,至60g后,坡体中下部才出现同时贯穿软硬岩的拉裂缝（图5（f））,且大多数软岩位移矢量的大小及偏转角均略小于相邻硬岩点（图6）,可见硬岩首先折断破坏。这是由于硬岩模量大,发生破坏的应变小,导致软岩承力之前硬岩已率先破坏。另一方面,软岩裂缝产生晚,能较长期地保持一定连续性,有利于岩体充分弯曲,从而形成深层倾倒变形。

加载结束后（90g）,边坡破裂面呈弧形（图5（d））,与单一岩性反倾边坡的直线型破面^[7,20]存在明显差异。坡体内存在两条整体破裂面,均呈弧形,最底层破裂面（P₁）为变形底界,其下岩体未变形。自下而上的第二条破裂面（P₂）为本次试验的主失稳面,试验结束后拆开模型可见（图5（e））,该破裂面已接近完全贯通。两面之间岩体变形较弱,在P₂以上岩体垮落前可保持相对稳定。此外,前部发育局部次级破裂面（P₃）,未贯通至坡顶,但随加载进行,P₃的形成会使坡脚岩体首先脱离母体而形成空腔,使上部岩体失去支撑,加速边坡整体变形。

3.2   数值模型变形破坏演化

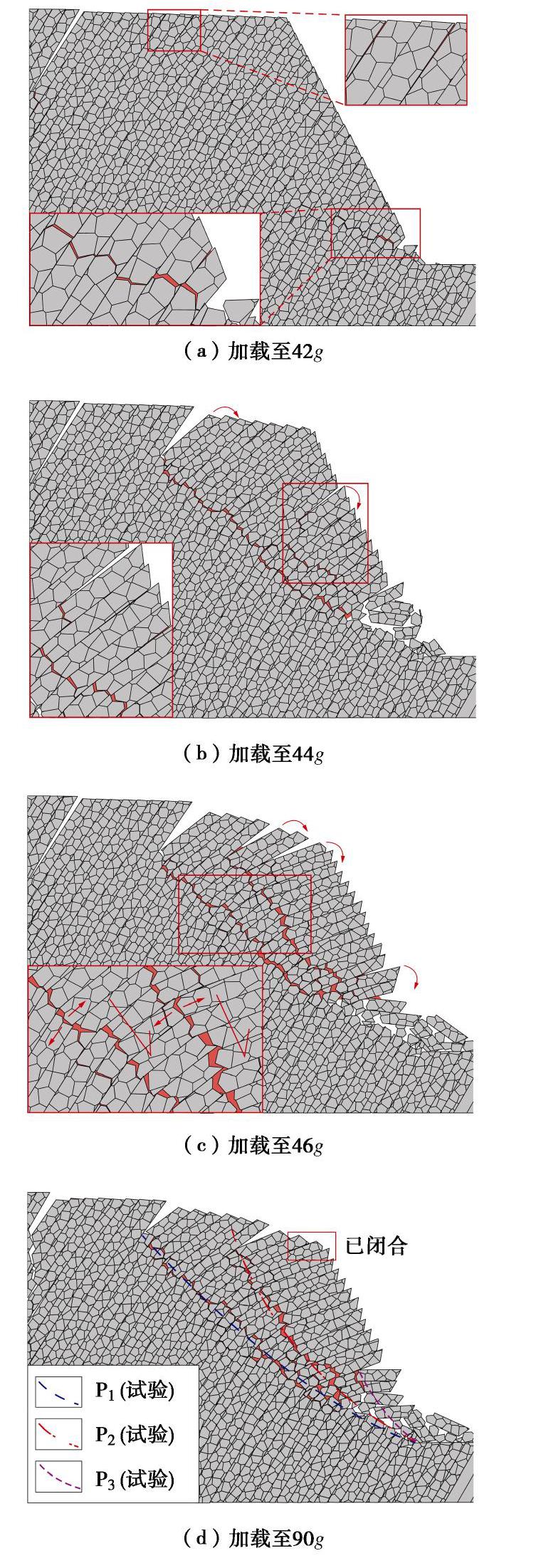
数值模型更好地展现了破裂面的演化过程（图7）。边坡在稳态变形阶段（18g～40g）,位移近似线性增大,后缘拉裂缝持续增大,岩体轻度弯曲,坡顶及坡表可见轻微的相对错动。42g时,坡脚岩体在持续的弯曲下,已出现局部裂隙（图7（a））。44g时,底层破裂面（${\text{P}}_1^{\prime }$）贯通（图7（b））,岩体快速倾倒,坡脚岩体完全折断,脱离母体,形成空腔,加剧上部变形,并导致自空腔末端延伸出第二破裂面（${\text{P}}_2^{\prime }$）。

图  7  数值模型变形破坏图

Figure  7.  Deformation and failure of numerical model

下载: 全尺寸图片 幻灯片

46g时,边坡位移达到第一个峰值,此时${\text{P}}_2^{\prime }$已贯通至坡顶（图7（c））,造成该面以上岩体更加强烈的变形,坡脚更多岩体在上部岩体的持续挤压下弯曲折断,堆积于坡前。之后坡体短暂稳定,至52g时坡脚空腔以上岩体再次折断,${\text{P}}_2^{\prime }$后缘局部悬挑岩层发生骨牌式折断,位移曲线小幅跃升。

将物理模型破裂面投影至数值模型变形图上（图7（d））,可见二者位置及形态高度吻合。以破裂面为界,可将P₃以上视为极强倾倒区Q₁,最先失稳垮落；将P₂和P₃之间岩体视为强倾倒区Q₂；P₁与P₂之间则为弱倾倒区Q₃。数值模型的P₃面更加明显,且已有较多岩体脱离母体。据此可推测,Q₁岩体全部坠覆后,Q₂岩体失去支撑,逐渐垮落,之后Q₃岩体重复该过程,失稳垮落呈渐进后退式。该结果与黄润秋等^[2]通过现场调查得出的倾倒体变形分区特征类似。

4.   边坡位移特征分析

4.1   边坡位移–速率–加速度时程分析

以各点x,y方向的合位移及其速率和加速度（图8）来进一步分析变形过程。数值模型不同部位位移关系与试验基本一致,仅坡脚处由于数值模型岩层破坏后期已脱离母体,位移量明显大于其他位置。变形体不同部位位移趋势接近（图8（a）,（d））,同一岩层上（点DX-3,DX-4,DX-5）越靠近外侧位移越大,水平方向上（点DX-1,DX-2,DX-5）约靠近临空面位移越大,垂向上（点DX-5,DX-6,DX-7）越靠近坡顶位移较大。边坡变形符合“叠合悬臂梁”式变形特征^[17,22]。

图  8  边坡位移–速率–加速度时程曲线

Figure  8.  Time-history curves of slope displacement-rate-acceleration

下载: 全尺寸图片 幻灯片

物理模型合位移速率及加速度曲线（图8（b）,（c））表明,阶段Ⅰ中d,v,a均几乎为零；而进入稳态变形阶段后,位移量匀速增长,速率基本保持稳定,但又并非完全恒定,而是在小范围内波动,整体呈缓慢增大趋势,这是由于随岩板的持续弯曲变形,岩体重力方向逐渐与岩层面法向合并,整体缓慢加速变形。此阶段变形主要受重力驱动,发生累进性破坏。

变形后期（接近40g）,岩体内部裂隙扩展并逐渐贯通,岩层抗弯强度降低,潜在破裂面进入最终的孕育阶段,边坡整体变形明显。破裂面贯通后（40g）,d,v,a曲线均发生明显突变,岩层加速倾倒,坡体后缘形成拉陷区,边坡整体失稳。破坏后位移速率及加速度迅速降低,可见破坏是在短时间内迅速完成的。

数值模型各点的位移速率及加速度变化趋势均与物理模型类似（图8（e）,（f））,区别在于其稳态变形阶段的v,a曲线更加平滑理想,整体呈直线形,虽变化量值很小,但局部仍表现出与试验类似的缓慢增大的速率变化趋势。数值模型二次破坏位移量更大,因此,其v,a曲线的二次波动更加显著。

4.2   点对分析边坡破坏特性

点对分析可定量确定滑裂面形成路径和性质^[23]。层面点对a,b,c（图2（b）,图3）的法向位移反映岩体沿层面法向的拉张或压缩,切向位移则反映沿层面方向的相对错动；根据破裂面形态,选择预置在其两侧的标记点作为破裂面点对d,e,f（图2（b）,图3）,其法向和切向位移分别指示沿破裂面法向的拉压和沿破裂面的剪切错动。层面点对相对位移通过下式解算：

式中,∆x,∆y分别为点对中各点x,y方向的绝对位移,${\alpha }_j$为对应时刻的层面倾角。破裂面点对计算以破裂面为基准,计算方法类似。

由图9可知,在起始变形阶段（试验300 s之前,数值模拟18g之前）,点对a～f相对位移均很小,表明坡体各部位基本无变形,破裂面尚未发育。整体上,进入稳态变形阶段后,法向和切向位移曲线逐渐离散；对于层面点对,图9（a）可见,后上部点对a/$a^{\prime }$此阶段法向位移明显大于切向,且均匀增大,说明此处的变形以沿层面法向的拉张为主,岩层间的相对错动较弱,破裂面贯通后,该处法向位移出现了明显的跃升；而坡体中前部点对b/$b^{\prime }$,c/$c^{\prime }$的两条曲线均为负值（图9（b）,（c））,点对下侧点的位移小于上侧点,说明层面法向上发生压缩变形,切向上剪切错动,越靠上的岩层向边坡临空面的位移越大；破坏前中前部点对二曲线均近似线性增大,切向位移的增速和量值均明显大于法向,说明边坡中前部变形以层间剪切错动为主；破裂面贯通后,两曲线以近相同的速率快速增大,岩体几乎同时发生了沿层面的压缩和错动破坏,可以推断此处的岩体为压剪性破坏；c/$c^{\prime }$的相对位移量值明显大于上部的b/$b^{\prime }$,说明坡脚处岩体压剪变形更强烈,并逐渐导致岩板产生压致拉裂破坏,表现在变形图上该处岩层拉裂隙明显较多。

图  9  点对相对位移曲线

Figure  9.  Relative displacement curves of point couples

下载: 全尺寸图片 幻灯片

对于破裂面点对（图9（d）,（e）,（f））,各点对曲线均为正值,表明沿破裂面法向的变形均为拉张破坏；稳态变形阶段,点对d,e,f的两条曲线以相近的速率近线性增大,说明在破裂面整体为拉–剪复合破坏；边坡整体失稳后,上部仍以拉–剪破坏为主,而中下部则过渡为剪切错动占优,表现在变形上,此处已出现贯穿多层软硬岩的裂缝。

4.3   弯曲倾倒形成机制

融合离心试验与数值模拟结果,对软硬互层反倾边坡的变形破坏机制进行概括：

（1）起始蠕变阶段：加载初期,边坡在离心超重力场作用下达到力学平衡,坡体各处位移极小,整体无可见变形,坡内位移场分布无明显指向性,位移、速度、加速度等均接近零值,边坡整体稳定。

（2）稳态变形阶段：岩体在重力作用下向临空面方向持续变形,变形量近似稳态增长,坡体上部以拉张变形为主,伴随轻微的层间错动；而坡体中前部变形以压剪变形为主；潜在破裂面附近岩体为拉张–剪切复合变形；该阶段是一个相对长期的重力时效变形过程,工程中遇到的倾倒斜坡大多处于该阶段^[17],该阶段的临界位移等变形特征对指导反倾边坡的监测预警有重要意义,值得进一步探究。

（3）失稳破坏阶段：岩层在重力弯矩作用下持续累积变形,达到抗弯极限后即发生折断,首先发生在坡脚,此处岩层弯曲曲率最大；之后破裂面自下而上快速延伸至坡顶,形成下缓上陡的弧形拉–剪性破裂面。随加载持续,变形体内将逐渐由深至浅发育多级破裂面。坡脚岩体发生压致拉裂破坏,并逐渐与母岩脱离。破裂面附近岩体的切向位移已显著大于法向,变形区彻底失稳,边坡整体过渡为剪切-滑移破坏。

5.   倾角、坡角及材料参数的影响

5.1   对破坏模式的影响

倾角和坡角的组合关系对反倾边坡的变形破坏具有显著影响。图10给出了9种较典型组合下的边坡变形破坏图,不难发现,倾角和坡角的组合直接影响边坡的破坏,具体表现为倾角$\alpha$和坡角$\beta$之和大于等于120°时,边坡才会发生显著的倾倒破坏,而当二者之和小于120°时,边坡在加载至200g时仍仅存在局部变形,因此,可认为此种边坡稳定性较好。但需要指出的是,本文模拟基于理想化模型,而实际边坡通常存在复杂的节理裂隙,若坡内存在贯通性良好的横向节理裂隙,则不排除此类边坡发生较大规模剪切滑移的可能性。

图  10  不同倾角、坡角时的边坡破坏模式

Figure  10.  Failure modes of slope at different dip and slope angles

下载: 全尺寸图片 幻灯片

当倾角、坡角之和大于等于120°时,整体上各组合下的破坏模式类似（图10）,坡脚浅层破裂面以上的岩体首先失稳坠覆,与母体脱离,而后逐级向坡内扩展,直至底层破裂面以上的变形体全部折断坠覆。

5.2   单因素敏感性分析

由图10还可发现,不同倾角、坡角组合下,反倾边坡破坏的难易程度及变形体量差异明显,为此,以边坡破裂面贯通时的临界破坏荷载G_f和底层破裂面平均倾角${\gamma }_{\text{f}}$为评价指标进行单因素敏感性分析。G_f反映破坏的难易程度,${\gamma }_{\text{f}}$则可反映岩体变形规模。

（1）倾角、坡角的影响

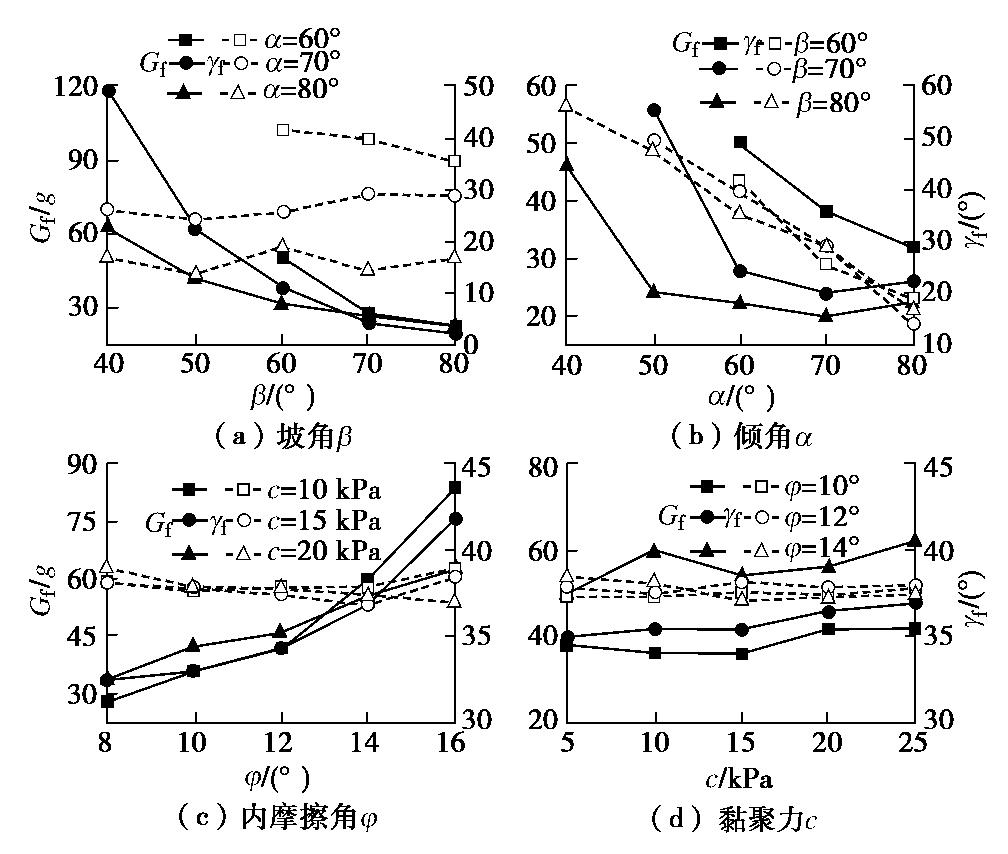
保持其他参数不变,分别改变坡角和倾角,以分析二者对G_f和${\gamma }_{\text{f}}$的敏感性。由图11可见,坡角$\beta$对G_f的影响最显著,表现为随$\beta$增大而幂函数减小（图11（a））,说明反倾边坡的稳定性与坡角直接相关,坡角越大,边坡越容易失稳。坡角一定时,G_f随倾角$\alpha$增大同样逐渐减小（图11（b））,倾角较小时减小相当迅速,但当倾角较大时,G_f的波动程度明显减小,且在倾角80°时,G_f出现了小幅回升,说明大倾角明显不利于反倾边坡稳定性,边坡在倾角约70°时最易破坏。

图  11  坡角、倾角及层面c、φ值对边坡稳定的影响

Figure  11.  Effects of slope angle, dipangle, c and φ on slope stability

下载: 全尺寸图片 幻灯片

对破裂面倾角${\gamma }_{\text{f}}$而言,坡角对其影响较小,其关系曲线（图11（a））仅小幅波动。但${\gamma }_{\text{f}}$与倾角关系密切,其随$\alpha$的增大线性减小（图11（b））,说明${\gamma }_{\text{f}}$主要受岩层倾角控制,岩层倾角越大,破裂面倾角越小,即变形岩体规模越大,因而当反倾边坡倾角较大时更容易发育深层倾倒现象。

（2）层面参数的影响

层面参数对反倾边坡稳定性有重要影响^[22],固定边坡倾角和坡角均为60°,分别研究层面黏聚力c和摩擦角φ的影响。结果表明,破坏荷载G_f受层面参数影响明显,特别是层面φ值（图11（c））,呈高度的线性正相关,且波动范围较大。层面c值影响较小,但G_f同样随c的增大而逐渐增大。

对破裂面倾角${\gamma }_{\text{f}}$而言,图11（c）,（d）表明其受层面参数影响较小,${\gamma }_{\text{f}}$与层面c,φ值的关系曲线均接近水平,因而二者对边坡变形规模及破坏模式的影响不明显。

6.   反倾边坡加固措施探讨

反倾边坡的破坏模式具有特殊性,基于前文研究,提出以下适用于反倾边坡的加固建议。

（1）削坡整形

坡角对反倾边坡的破坏具有显著影响,破坏荷载随坡角的减小幂函数增大,且在坡角与岩层倾角之和小于120°时,很难发生破坏。因此,在边坡场区条件允许时,削坡减载是对此类边坡十分有效的处理方法。

（2）坡脚堆载

反倾边坡的破坏首先发生在坡脚,呈自下而上的渐进后退式破坏。坡脚发生的局部破坏极大的加速了上部岩体的倾倒失稳,因此,可在坡脚堆载,增大坡脚破坏的难度,从而使边坡整体稳定性增加。但当岩层倾角极大时,边坡可能自堆载体顶部向坡内延伸形成破坏,此时应适当结合削坡或锚固等措施。

（3）层面加固

反倾边坡岩层的倾倒伴随着明显的层间相对错动及局部的强烈拉张,数值模拟表明,当层面c、φ值增大时,破坏荷载将显著增大。因此,对于实际边坡,若采用工程手段增大岩层间的黏结,使岩体的整体性增强,岩层间难以产生拉张和相对错动,进而难以弯曲折断,从而可使边坡整体稳定性提高。可采用层面注浆、预应力锚杆（索）等加固方法。

实际反倾边坡通常结构复杂,存在多种复杂结构面,可能存在多种破坏模式,需因地制宜,具体分析,融合采用多种加固方式,保障边坡安全。

7.   结论

本文针对软硬互层岩质反倾边坡,综合大型离心模型试验与离散元数值模拟结果,对倾倒变形机理进行了专题研究。得出以下4点结论。

（1）离心模型试验可以较好地模拟反倾边坡的破坏过程,其变形可分为起始变形、稳态变形、失稳破坏3个阶段：起始阶段变形微小；稳态变形阶段,边坡整体向临空面等速蠕变,为重力时效累积变形过程；失稳破坏阶段,坡脚岩层首先达到其抗弯极限而折断,破裂面快速贯通至坡顶,边坡整体失稳。

（2）离散元模拟得到的位移曲线、破裂面位置及形态、整体变形特征等与试验吻合度较高,验证了数值模拟的有效性。坡体内发育多级弯折带,均呈弧形,下缓上陡；根据变形程度以破裂面为界将变形体分为极强倾倒区、强倾倒区、弱倾倒区。

（3）点对分析表明,坡体后上部岩体以拉张破坏为主,中前部则为沿层面的压剪性破坏；破裂面为拉张–剪切复合破坏,整体式失稳后,逐渐过渡为剪切–滑移破坏,最终变形体渐进后退式垮落。

（4）反倾边坡的变形破坏受倾角、坡角组合关系影响显著,二者之和小于120°时极难破坏；坡角越大,边坡越易破坏；倾角越大,破裂面倾角越小,即变形岩体规模越大；层面参数φ对边坡稳定性影响较大。