基于区间参数反演的重力坝非概率可靠性分析

魏博文; 占良红; 李火坤; 徐镇凯

doi:10.11779/CJGE202002014

基于区间参数反演的重力坝非概率可靠性分析 English Version

南昌大学建筑工程学院,江西　南昌330031

基金项目:

国家自然科学基金项目 51779115

国家自然科学基金项目 51869011

国家自然科学基金项目 51879126

江西省水利厅科研课题 201820YBKT29

江西省青年科学重点项目 20192ACB21022

江西省杰出青年基金项目 2018ACB21018

南昌大学研究生创新专项资金项目 CX2018052

详细信息

作者简介:
魏博文（1981— ）,男,副教授,博士生导师,主要从事数值安全监控及水工结构方面的科研工作。E-mail：bwwei@ncu.edu.cn

通讯作者:
李火坤, E-mail：lihuokun@126.com

中图分类号: TV642.3
计量
- 文章访问数: 0156
- HTML全文浏览量: 0
- PDF下载量: 0118
出版历程
- 收稿日期: 2018-09-27
- 网络出版日期: 2022-12-07
- 刊出日期: 2020-01-31

Non-probabilistic reliability analysis of gravity dams based on inversion of interval parameters

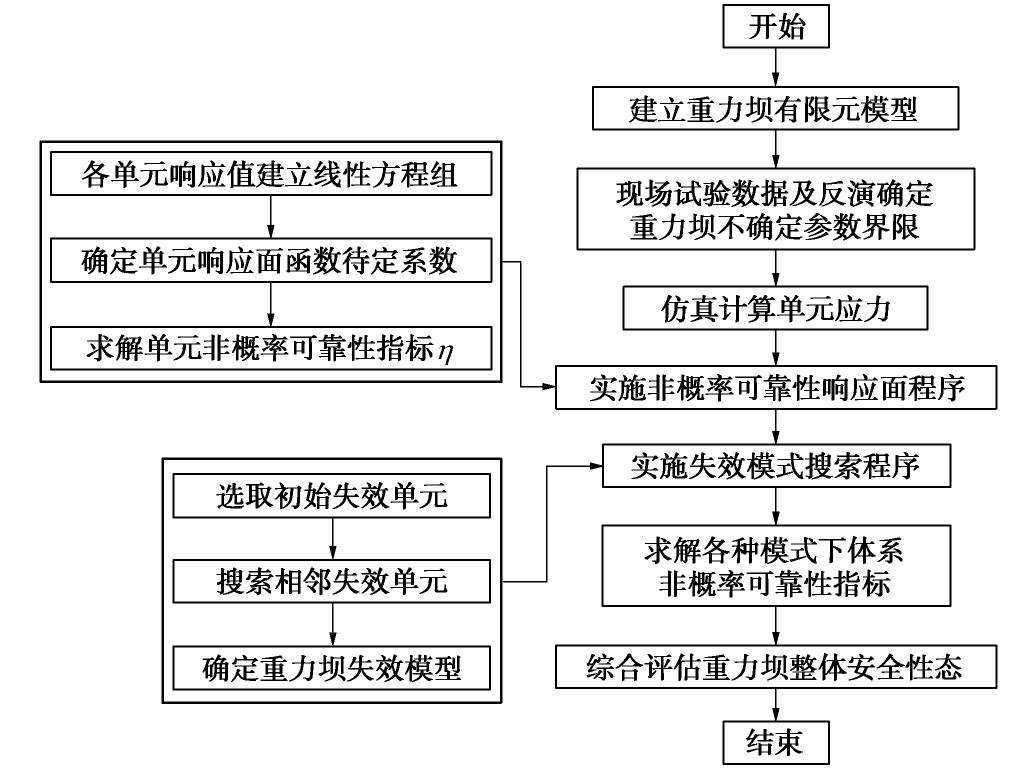
School of Civil Engineering and Architecture, Nanchang University, Nanchang 330031, China

摘要

摘要: 传统概率可靠性分析方法应用重力坝结构性能和服役性态评估过程中,其受不确定参数严格随机性、计算结果对参数过敏感性及其功能函数高度非线性等多因素制约。提出了基于区间参数的重力坝单元和体系非概率可靠性（Nonprobabilistic Reliability,NR）分析方法。首先,充分依据重力坝原型监测资料、数学模型和物理模型计算成果获取重力坝区间参数的界限,综合运用区间数学和NR等理论和方法,构建了基于区间参数的重力坝单元与体系NR计算模型,发展了一种基于响应面方法的重力坝NR指标（NR-η）计算方法。其次,从重力坝系统可能失效路径及失效模式入手,剖析单一和多重失效模式下重力坝体系的安全性。最后,通过某重力坝工程表明：方法能够有效地揭示重力坝局部和整体可靠状态,计算结果符合重力坝运行特点前提下与该大坝服役背景状况高度吻合。
- 重力坝 /
- 非概率可靠性 /
- 区间参数 /
- 失效模式 /
- 服役可靠度
Abstract: In the evaluation of structural performance and service behavior of gravity dams, the traditional probabilistic reliability analysis method is restricted by many factors, such as strict randomness of uncertain parameters, oversensitivity of calculated results and high nonlinearity of function function. A non-probabilistic reliability (NR) analysis method for gravity dam elements and system based on the interval parameters is proposed. First, according to the prototype monitoring data and the achievements of physical and mathematical models for gravity dams, the interval parameter boundary of the gravity dam is obtained. A NR model based on the interval parameters is established, and a method for calculating NR index (NR-η) based on response surface method is developed by using the interval mathematics and NR theory. Then, the safety of the gravity dam system in single and multiple failure modes is analyzed from the possible failure paths and modes. Finally, based on a gravity dam, the results indicate that the proposed method can effectively reveal the local and overall reliable states of the gravity dam. The calculated results are in good agreement with the background conditions of the dam under the premise of the operating characteristics of the gravity dam.
- gravity dam /
- non-probabilistic reliability /
- interval parameter /
- failure mode /
- service reliability

HTML全文

图 1 失效模式搜索示意图

Figure 1. Schematic diagram of failure mode search

下载: 全尺寸图片幻灯片

图 2 重力坝体系NR-η_s计算流程

Figure 2. Flow chart of NR-η_s evaluation for gravity dam system

下载: 全尺寸图片幻灯片

图 3 重力坝有限元模型

Figure 3. Finite element model for gravity dam

下载: 全尺寸图片幻灯片

图 4 环境量监测曲线

Figure 4. Graph of environmental variables

下载: 全尺寸图片幻灯片

图 5 D35水平位移实测值、拟合值及残差值曲线

Figure 5. Actual values, fitted values and residuals curves of horizontal displacement of D35

下载: 全尺寸图片幻灯片

图 6 单元NR- $η_{e}$ 分布云图

Figure 6. Contour map of NR- $η_{e}$ for dam elements

下载: 全尺寸图片幻灯片

图 7 坝体单元NR- $η_{e}$ 统计图

Figure 7. Statistical graph of NR- $η_{e}$ for dam body elements

下载: 全尺寸图片幻灯片

图 8 初始失效单元

Figure 8. Initial failure elements

下载: 全尺寸图片幻灯片

图 9 初始单元失效模式

Figure 9. Failure modes for initial elements

下载: 全尺寸图片幻灯片

图 10 组合单元失效模式

Figure 10. Failure modes for combination elements

下载: 全尺寸图片幻灯片

表 1 水压分量拟合系数

Table 1 Fitting coefficients of water pressure component

系数	a₁₁	a₁₂	a₁₃	a₂₁-a₁₁	a₂₂-a₁₂	a₂₃-a₁₃
D35	0.44253	-0.01015	0.00014	0.10270	-0.00295	0.00002
注：各系数定义参考文献[26]。

下载: 导出CSV

表 2 参数界限反演结果

Table 2 Inversion results of interval parameters

水压调整系数区间值		弹性模量区间值/GPa
$X_{I}$	$Y_{I}$	$E_{c I}^{}$	$E_{r I}^{}$
[0.858, 0.936]	[0.898, 0.982]	[18.02, 19.66]	[14.37, 15.71]
注： $X_{I}^{} = E_{c0} / E_{c I}^{}$ 和 $Y_{I} = E_{r0} / E_{r I}^{}$ 。

下载: 导出CSV

表 3 主要区间参数界限

Table 3 Boundaries of main interval parameters

荷载	材料参数	界限范围	均值	离差
荷载	扬压力系数α	[0.28, 0.32]	0.30	0.02
坝体	混凝土抗拉强度f_t/MPa	[1.40, 1.70]	1.55	0.15
	混凝土抗压强度f_c/MPa	[16.00, 18.50]	17.25	1.25
	坝体弹性模量E_c/GPa	[18.02, 19.66]	18.84	0.82
岩基	岩基抗拉强度f_t′/MPa	[1.12, 1.44]	1.28	0.16
	岩基抗压强度f_c′/MPa	[14.60, 17.20]	15.90	1.30
	岩基弹性模量E_r/GPa	[14.37, 15.71]	15.04	0.67
岩基面	滑移面摩擦系数f_′	[0.82, 1.08]	0.95	0.13
岩基面	滑移面凝聚力c′/MPa	[0.80, 0.96]	0.88	0.08
注：上游水位为正常蓄水位定值,混凝土重度取定值γ_c = 2350 kg·m^-3。

下载: 导出CSV

表 4 各失效模式下NR-η

Table 4 NR-η of each failure mode

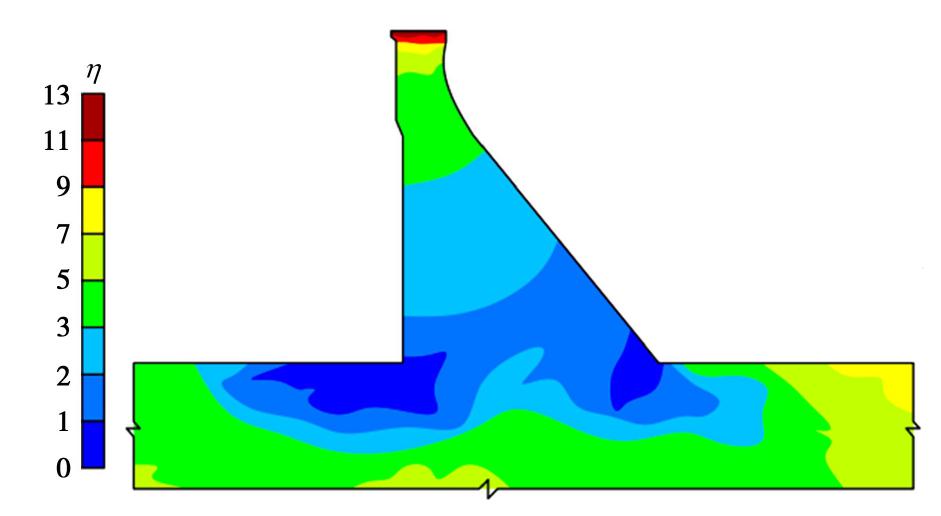
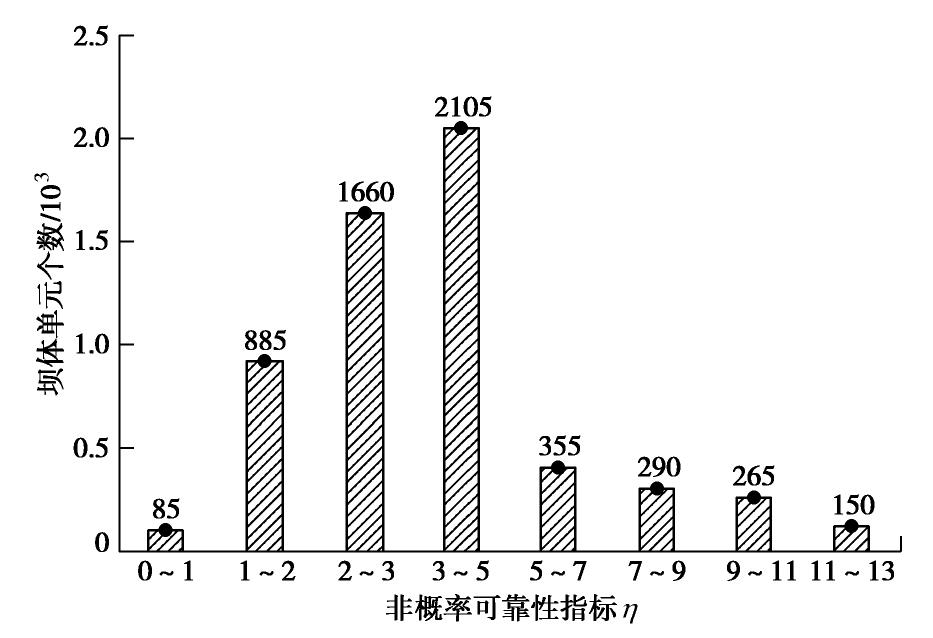
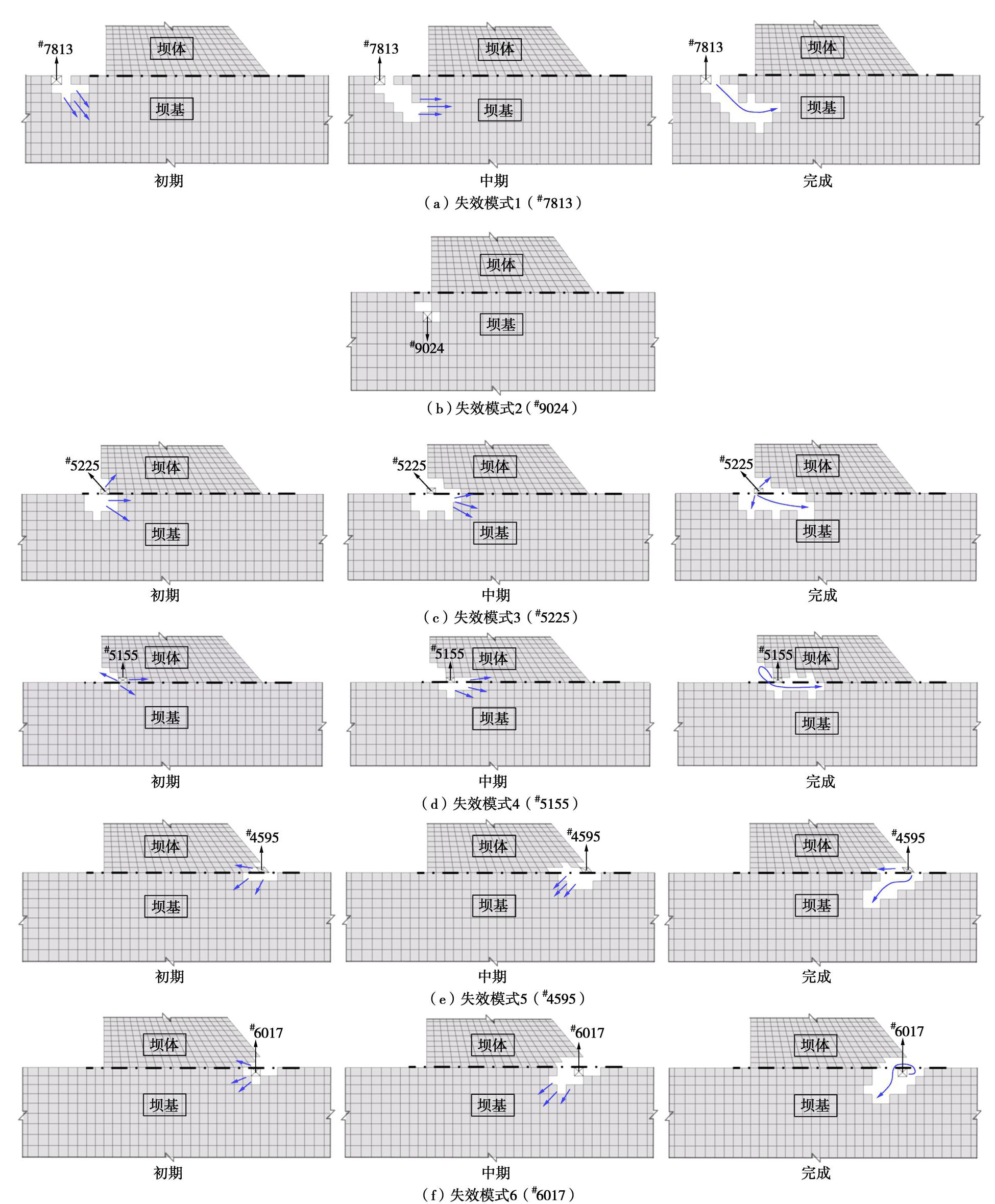
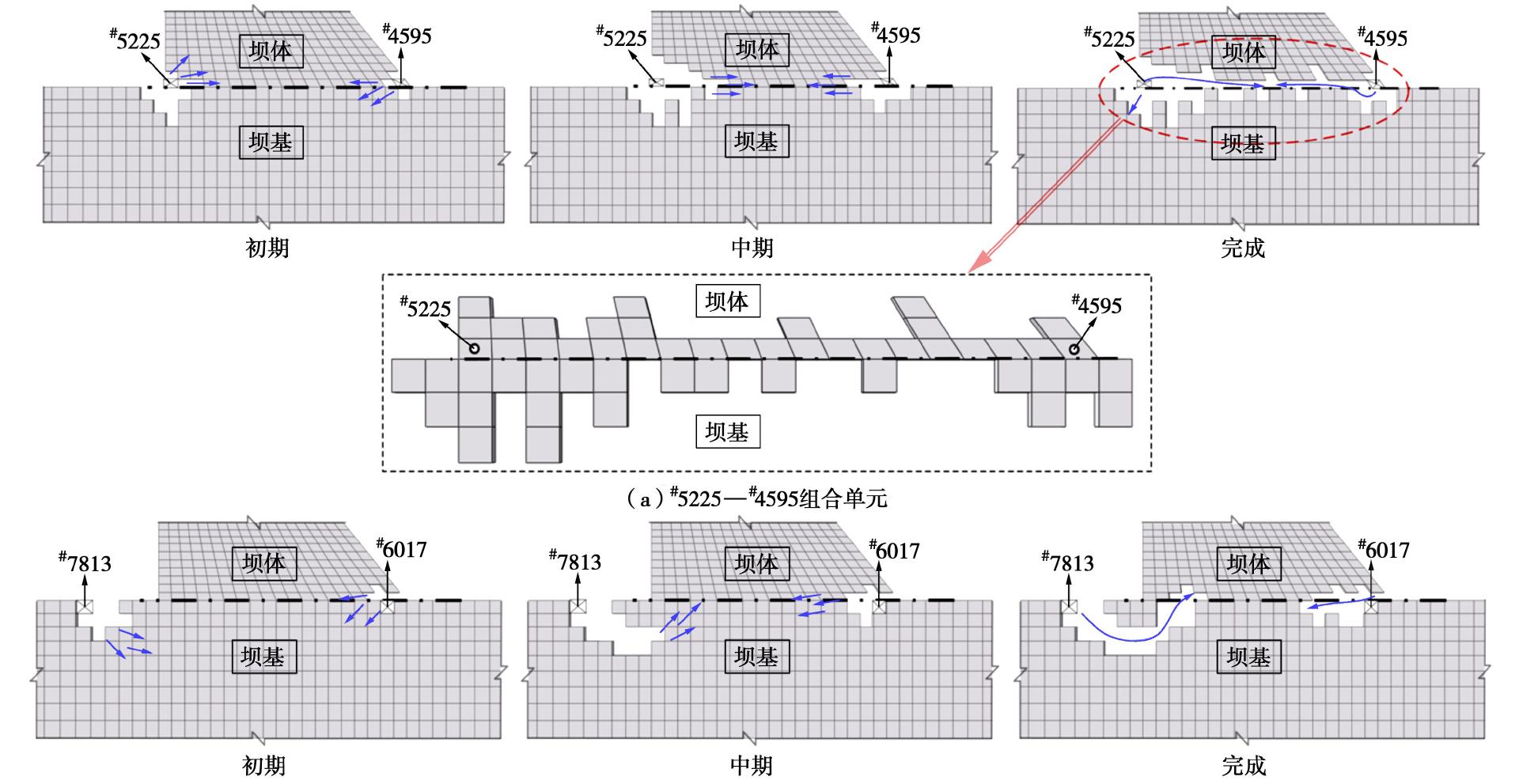
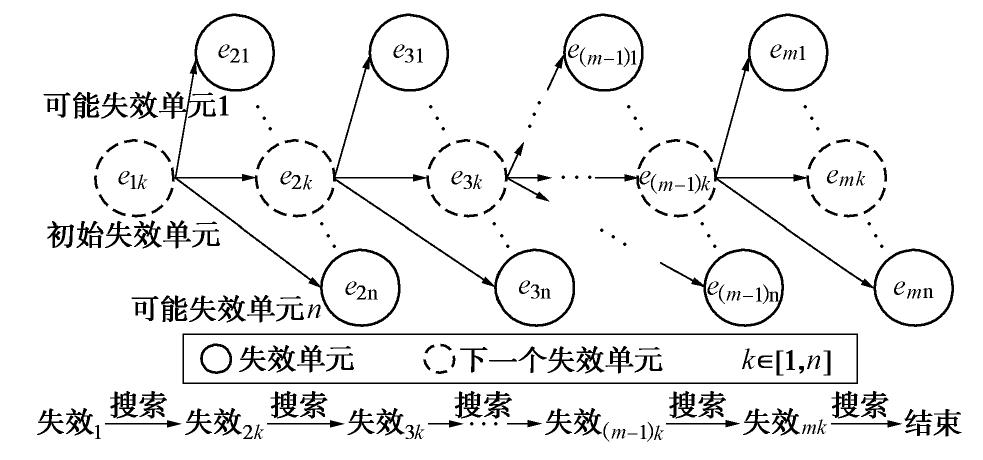
失效模式	失效模式1	失效模式2	失效模式3	失效模式4	失效模式5	失效模式6	^#5225—^#4595	^#7813—^#6017
NR-η	0.916	1.301	0.854	0.872	0.914	0.919	0.732	0.835

下载: 导出CSV

参考文献(28)

[1]	张社荣, 王超, 孙博. 重力坝层间抗滑稳定体系的动力可靠度分析方法[J]. 岩土力学, 2012, 33(10): 263-268, 302. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201210042.htm ZHANG She-rong, WANG Chao, SUN Bo. Dynamic reliability analysis method of anti-sliding stability between layers of gravity dams[J]. Rock and Soil Mechanics, 2012, 33(10): 263-268, 302. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201210042.htm
[2]	王刚, 秦净净, 管莉莉. 基于遗传算法的重力坝多滑面稳定可靠度分析[J]. 岩石力学与工程学报, 2016(增刊1): 3153-3161. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2016S1064.htm WANG Gang, QIN Jing-jing, GUAN Li-li. Reliability analysis on stability of gravity dam foundation over multiple sliding planes based on GA[J]. Chinese Journal of Rock Mechanics and Engineering, 2016(S1): 3153-3161. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2016S1064.htm
[3]	HARIRI-ARDEBILI M A, POURKAMALI-ANARAKI F. Support vector machine based reliability analysis of concrete dams[J]. Soil Dynamics & Earthquake Engineering, 2018, 104: 276-295.
[4]	顾冲时, 苏怀智, 刘何稚. 大坝服役风险分析与管理研究述评[J]. 水利学报, 2018, 49(1): 26-35. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201801005.htm GU Chong-shi, SU Huai-zhi, LIU He-zhi. Review on service risk analysis of dam engineering[J]. Journal of Hydraulic Engineering, 2018, 49(1): 26-35. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201801005.htm
[5]	YAKOV B H. A non-probabilistic concept of reliability[J]. Structural Safety, 1994, 14(4): 227-245. doi: 10.1016/0167-4730(94)90013-2
[6]	BEN-HAIM Y, ELISHAKOFF I. Discussion on: A non-probabilistic concept of reliability[J]. Structural Safety, 1995, 17(3): 195-199. doi: 10.1016/0167-4730(95)00010-2
[7]	QIU Z, CHEN S, ELISHAKOFF I. Non-probabilistic eigenvalue problem for structures with uncertain parameters via interval analysis[J]. Chaos Solitons & Fractals, 1996, 7(3): 303-308.
[8]	QIU Z, ELISHAKOFF I. Antioptimization of structures with large uncertain-but-non-random parameters via interval analysis[J]. Computer Methods in Applied Mechanics & Engineering, 1998, 152(3): 361-372.
[9]	GANZERLI S, PANTELIDES C P. Optimum structural design via convex model superposition[J]. Computers & Structures, 2000, 74(6): 639-647.
[10]	KANG Z, LUO Y, LI A. On non-probabilistic reliability-based design optimization of structures with uncertain-but-bounded parameters[J]. Structural Safety, 2011, 33(3): 196-205. doi: 10.1016/j.strusafe.2011.03.002
[11]	LUO Y, KANG Z, LUO Z, et al. Continuum topology optimization with non-probabilistic reliability constraints based on multi-ellipsoid convex model[J]. Structural & Multidisciplinary Optimization, 2009, 39(3): 297-310.
[12]	罗阳军, 亢战, 蔡坤. 考虑非概率可靠性的结构柔顺度拓扑优化设计[J]. 计算力学学报, 2011, 28(6): 821-826. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJG201106002.htm LUO Yang-jun, KANG Zhan, CAI Kun. A compliance based topology optimization design of structures considering non-probabilistic reliability[J]. Chinese Journal of Computational Mechanics, 2011, 28(6): 821-826. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSJG201106002.htm
[13]	刘国梁, 陈建军, 马洪波. 一种基于非概率可靠性的结构水平集拓扑优化[J]. 工程力学, 2012, 29(6): 58-62. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201206010.htm LIU Guo-liang, CHEN Jian-jun, MA Hong-bo. Structural topological optimization for non-probability reliability in level set method[J]. Engineering Mechanics, 2012, 29(6): 58-62. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201206010.htm
[14]	JIANG C, HAN X, LU G Y, et al. Correlation analysis of non-probabilistic convex model and corresponding structural reliability technique[J]. Computer Methods in Applied Mechanics & Engineering, 2011, 200(33): 2528-2546.
[15]	BAI Y C, HAN X, JIANG C, et al. A response-surface- based structural reliability analysis method by using non-probability convex model[J]. Applied Mathematical Modelling, 2014, 38(15/16): 3834-3847.
[16]	苏国韶, 郝俊猛. 复杂工程结构非概率可靠度分析的高斯过程动态响应面法[J]. 应用基础与工程科学学报, 2015(4): 750-762. https://www.cnki.com.cn/Article/CJFDTOTAL-YJGX201504010.htm SU Guo-shao, HAO Jun-meng. Gaussian process based dynamic response surface method of non-probabilistic reliability analysis for complicated engineering structure[J]. Journal of Basic Science and Engineering, 2015(4): 750-762. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YJGX201504010.htm
[17]	KANG Z, ZHANG W. Construction and application of an ellipsoidal convex model using a semi-definite programming formulation from measured data[J]. Computer Methods in Applied Mechanics & Engineering, 2016, 300: 461-489.
[18]	袁慕勇, 陆廷春, 徐宝松, 等. 基于非概率方法的碾压混凝土重力坝可靠度计算[J]. 三峡大学学报(自然科学版), 2013, 35(6): 29-33. https://www.cnki.com.cn/Article/CJFDTOTAL-WHYC201306009.htm YUAN Mu-yong, LU Ting-chun, XU Bao-song, et al. Reliability calculation of rcc gravity dam based on non-probabilistic method[J]. Journal of China Three Gorges University (Natural Sciences), 2013, 35(6): 29-33. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-WHYC201306009.htm
[19]	张勇, 赖国伟, 程睿, 等. 高拱坝的非概率可靠性分析[J]. 中国农村水利水电, 2008(5): 62-65. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNSD200805018.htm ZHANG Yong, LAI Guo-wei, CHENG Rui, et al. Non-probabilistic reliability analysis of high arch dams[J]. China Rural Water and Hydropower, 2008(5): 62-65. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNSD200805018.htm
[20]	方砚兵, 苏永华, 肖旺, 等. 基于子区间法的隐式功能函数非概率可靠性方法研究[J]. 岩土力学, 2017, 38(4): 1171-1178, 1187. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201704032.htm FANG Yan-bing, SU Yong-hua, XIAO Wang, et al. Non-probabilistic reliability model for implicit performance function based on subinterval method[J]. Rock and Soil Mechanics, 2017, 38(4): 1171-1178, 1187. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201704032.htm
[21]	赵明华, 蒋冲, 曹文贵. 基于区间理论的挡土墙稳定性非概率可靠性分析[J]. 岩土工程学报, 2008, 30(4): 467-472. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200804001.htm ZHAO Ming-hua, JIANG Chong, CAO Wen-gui. Non-probabilistic reliability analysis of retaining walls based on interval theory[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(4): 467-472. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200804001.htm
[22]	俞茂宏. 岩土类材料的统一强度理论及其应用[J]. 岩土工程学报, 1994, 16(2): 1-10. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC402.000.htm YU Mao-hong. Unified strength theory for geomaterials and lts applications[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(2): 1-10. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC402.000.htm
[23]	HU J, MA F H, WU S H. Nonlinear finite-element-based structural system failure probability analysis methodology for gravity dams considering correlated failure modes[J]. Journal of Central South University of Technology, 2017, 24(1): 178-189.
[24]	徐强, 陈健云, 李静, 等. 基于贝叶斯理论的大坝体系可靠度计算方法[J]. 大连理工大学学报, 2011, 51(1): 84-89. https://www.cnki.com.cn/Article/CJFDTOTAL-DLLG201101017.htm XU Qiang, CHEN Jian-yun, LI Jing, et al. Calculation method for system reliability of dam based on Bayes theory[J]. Journal of Dalian University of Technology, 2011, 51(1): 84-89. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DLLG201101017.htm
[25]	魏博文, 徐镇凯, 李火坤, 等. 基于GA-APSO混合罚模型的混凝土坝力学参数优化反演[J]. 中南大学学报(自然科学版), 2015, 46(11): 4211-4217. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201511031.htm WEI Bo-wen, XU Zhen-kai, LI Huo-kun, et al. Optimization inversion for mechanical parameters of concrete dam based on GA-APSO mixed penalty model[J]. Journal of Central South University (Science and Technology), 2015, 46(11): 4211-4217. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201511031.htm
[26]	QIN X, GU C, CHEN B, et al. Multi-block combined diagnosis indexes based on dam block comprehensive displacement of concrete dams[J]. Optik-International Journal for Light and Electron Optics, 2017, 129: 172-182.
[27]	夏雨, 张仲卿, 赵小莲, 等. 基于可能失效模式的拱坝安全度评价[J]. 应用力学学报, 2011, 28(3): 313-317. https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX201103020.htm XIA Yu, ZHANG Zhong-qing, ZHAO Xiao-lian, et al. Safety analysis of arch dam based on possible failure modes[J]. Chinese Journal of Applied Mechanics, 2011, 28(3): 313-317. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX201103020.htm
[28]	徐强, 李静, 陈健云, 等. 非平稳地震动过程中混凝土重力坝受拉失效路径可靠度分析[J]. 工程力学, 2011, 28(3): 123-128. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201103019.htm XU Qiang, LI Jing, CHEN Jian-yun, et al. Concrete gravity dam reliability analysis on tension failure path under non-stationary ground motion processes[J]. Engineering Mechanics, 2011, 28(3): 123-128. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201103019.htm

施引文献(28)

期刊类型引用(12)

1.	李贝贝. 强动压巷道底板变形破坏特征及控制技术研究. 山东煤炭科技. 2025(01): 1-4+11 . 百度学术
2.	毕智强，于振亚，张涛. 深井动压软岩巷道底鼓变形破坏机理与防治技术. 陕西煤炭. 2025(04): 84-88+113 . 百度学术
3.	伊丙鼎. 煤层水仓围岩变形破坏特征及控制技术研究. 煤炭工程. 2024(03): 117-123 . 百度学术
4.	肖同强，王泽源，刘发义，代晓亮，赵帅，余子豪. 深部强动压巷道底鼓控制机理及技术研究. 采矿与安全工程学报. 2024(04): 666-676 . 百度学术
5.	丁维波，王丹影，闫医慧. 回采巷道底鼓机理及防治技术研究. 煤炭技术. 2024(08): 23-27 . 百度学术
6.	朱国保，董垠枫. 非均质围岩隧道断面的施工关键技术研究. 四川建筑. 2024(05): 200-201 . 百度学术
7.	耿铭，孙静. 厚硬顶板悬顶致灾机理及切顶控制技术研究. 工矿自动化. 2024(11): 132-141 . 百度学术
8.	柴敬，韩志成，雷武林，张丁丁，马晨阳，孙凯，翁明月，张有志，丁国利，郑忠友，张寅，韩刚. 回采巷道底鼓演化过程的分布式光纤实测研究. 煤炭科学技术. 2023(01): 146-156 . 百度学术
9.	吕情绪，曹军，高亮. 重复采动回采巷道变形机理及稳定控制. 中国矿业. 2023(05): 96-103 . 百度学术
10.	丁自伟，王少轩，王庆阳，王耀声，王春斌，李军岐，邸广强，李亮. 软岩巷道底鼓机理及其稳定性控制研究. 煤炭工程. 2023(07): 102-109 . 百度学术
11.	吕志强，黄亚军，景明，徐啸川. 深部软岩巷道变形破坏机理及支护技术. 能源与环保. 2023(11): 280-286 . 百度学术
12.	杨晓炜. 深部软岩大断面巷道大变形控制技术研究. 能源与环保. 2023(11): 312-318 . 百度学术