0.   引言

天然海床、边坡由于沉积作用的影响，其内部土体结构排列呈现原生各向异性，这通常用颗粒排列取向，粒间接触方向或内部孔隙结构（统称组构）来表征^[1-3]。已有的试验和细观力学分析表明：组构各向异性及其演化对于砂土的抗剪强度以及剪胀特性有显著的影响^[4-9]。在此基础上，有学者提出了一些考虑组构各向异性的弹塑性^{[8, 10-11]}或亚塑性模型^[12]，其中多为共轴模型。

组构各向异性不仅显著影响砂土单元特性，对砂土地基的承载特性也有重要影响。前人研究主要聚焦各向异性砂土地基上的浅基础承载力问题^[13-18]。1g模型试验结果表明，同一相对密实度但不同沉积角砂土地基上的浅基础承载力差异可达25%^[14]。Kimura等^[15]的离心机试验也显示出类似的结果：不同沉积方向浅基础承载力系数差异达15%^[14]。Guo等^[16]基于直剪试验的理论分析表明：如砂土强度各向异性考虑不当，采用经典的承载力理论，会高估浅基础的承载力系数达8倍。数值研究方面，Gao等^[17]和Chaloulos等^[18]基于各向异性临界状态本构模型计算发现：忽略组构的影响时，会导致砂土地基上浅基础承载力被高估30%。上述数值模拟基于组构各向异性砂土本构模型，但未考虑非共轴塑性流动，而较难模拟出不同组构沉积角下浅基础周围的非对称剪切破坏面。同时，上述模拟尚未对砂土应变局部化进行数值处理，导致浅基础承载力计算结果存在明显的网格依赖性^[19-22]。现有试验和数值模拟大多针对浅基础，鲜有关于埋置基础（如板锚基础）在各向异性海床中承载特性的研究。

本文围绕砂土组构各向异性对板锚上拔承载特性影响这一目标，基于砂土各向异性临界状态理论框架^[8]，引入考虑组构各向异性及演化的非共轴流动法则，建立了砂土各向异性非共轴本构模型，并嵌入三维有限元程序ABAQUS；通过引入正则化技术，降低了砂土应变局部化导致的网格依赖性。基于不同路径下砂土单元试验和砂土海床中平板锚上拔离心机试验，验证了该模型的适用性。在此基础上，通过开展参数分析，揭示了砂土组构各向异性及演化对板锚上拔承特性的影响；并定量评价了忽略组构各向异性时，数值模拟和极限平衡分析对砂土中板锚上拔承载力的预测误差。

1.   考虑各向异性演化的非共轴砂土本构模型及数值实现

1.1   各向异性临界状态理论框架

大量砂土单元试验结果表明，砂土力学行为与其状态相关。砂土状态相关变量包括孔隙比$e$、应力水平$p{\text{'}}$、组构各向异性程度$A$。经典状态相关砂土理论框架只以孔隙比$e$、应力$p{\text{'}}$作为状态变量。该理论框架无法描述砂土在相同$e$和$p{\text{'}}$条件下，因组构各向异性$A$不同而表现出的显著力学行为差异。

针对这一局限，Li等^[8]提出了各向异性临界状态理论框架（anisotropic critical state theory, 也即ACST）。在ACST框架中，砂土的状态由$e$，$p{\text{'}}$，$A$三者共同决定；同时，将组构各向异性程度$A$及其演化引入到屈服函数、硬化法则、剪胀方程、塑性模量等的表达式中，为统一描述砂土在不同组构各向异性和加载方向耦合下的力学行为提供了理论框架。

在ACST框架中，各向异性系数$A$被定义为组构张量${\boldsymbol{F}_{ij}}$和加载方向张量${\boldsymbol{n}_{ij}}$的第一联合不变量：

式中：${\boldsymbol{F}_{ij}}$为对称的二阶偏张量，表征材料内结构的各向异性；$ \boldsymbol{n}_{ij}^F $为单位二阶偏张量，表征组构各向异性的方向单位二阶偏张量，表征组构张量的方向；${\boldsymbol{n}_{ij}}$为单位偏张量，表征加载方向。标量值$N = \boldsymbol{n}_{ij}^F{\boldsymbol{n}_{ij}}$表征织物各向异性取向和加载方向之间的相对差异，范围为-1~1。达到临界状态时，张量各向异性联合不变量$A$趋于其归一化临界状态值1，组构张量方向朝向加载方向。

对于有自然沉积的砂土，本文在描述初始组构各向异性时采用Li等^[8]对砂土等横观各向同性的定义（假设沉积轴为z轴），砂土的初始的组构各向异性可以被表示为

式中，${F_{\text{0}}}$为初始的组构各向异性。当土样的沉积方向与参考坐标系不一致时，可以通过正交变换得到${\boldsymbol{F}_{ij}}$。

1.2   各向异性非共轴砂土本构模型

本文在ACST理论框架下，以Gao等^[10]的砂土共轴各向异性模型为基础模型，引入了考虑组构各向异性的非共轴塑性流动法则，建立了各向异性非共轴砂土本构模型，旨在：①改进现有共轴各向异性模型针对不同加载方向时（尤其是单剪）砂土力学响应的预测效果，②克服现有共轴各向异性模型无法模拟不同组构沉积角海床中垂直受荷基础周围土体的非对称破坏面的问题。下面对本文非共轴模型进行简述，重点介绍本文非共轴各向异性模型与基础模型^[10]的改进之处。

本文模型与基础模型等^[10]相比，主要改进在于构造并引入了能考虑组构各向异性的非共轴流动法则。本模型则采用非相关联流动法则，其中塑性势函数$g$在应力比空间下可以被表示为

式中：R为应力比不变量，$R = \sqrt {\frac{3}{2}{r_{ij}}{r_{ij}}} $，r_ij为应力比张量，${\boldsymbol{r}_{ij}} = \frac{{{\boldsymbol{s}_{ij}}}}{{p'}} = \frac{{{{\boldsymbol{\sigma} '}_{ij}} - p'{\delta _{ij}}}}{{p'}}$，${\boldsymbol{s}_{ij}}$为偏应力张量，${\boldsymbol{\sigma} '_{ij}}$为应力张量，$p'$为有效应力和${\delta _{ij}}$是Kronecker delta符号；$g(\theta )$为罗德角的插值函数（表 1）；$H$为硬化参数，主要依赖于砂土的状态及摩擦角（表 1）。

表  1  本文的公式

Table  1.  Proposed equations

描述	控制方程	模型参数
弹性模量	$G = {G_0}\frac{{{{(2.97 - e)}^2}}}{{1 + e}}\sqrt {p{\text{'}}{p_{\text{a}}}} $	弹性模量${G_0}$
	$K = G\frac{{2(1 + \nu )}}{{3(1 - 2\nu )}}$	泊松比$\nu $
组构张量	${\boldsymbol{F}_{ij}} = \left( {\begin{array}{*{20}{c}} {{F_z}}&0&0 \\ 0&{{F_x}}&0 \\ 0&0&{{F_y}} \end{array}} \right) = \sqrt {\frac{2}{3}} \left( {\begin{array}{*{20}{c}} {{F_{\text{0}}}}&0&0 \\ 0&{ - \frac{{{F_{\text{0}}}}}{2}}&0 \\ 0&0&{ - \frac{{{F_{\text{0}}}}}{2}} \end{array}} \right)$	初始组构各向异性参数${F_{\text{0}}}$
各向异性变量	$A = {\boldsymbol{F}_{ij}}{\boldsymbol{n}_{ij}} = \boldsymbol{Fn}_{ij}^F{\boldsymbol{n}_{ij}} = FN$
组构演化	${\text{d}}{\boldsymbol{F}_{ij}} = L{k_{\text{f}}}({\boldsymbol{n}_{ij}} - {\boldsymbol{F}_{ij}}){e^A}$	组构演化参数${k_{\text{f}}}$
屈服面方程	$f = \frac{R}{{g(\theta )}} - H{e^{ - {k_{\text{h}}}{{\left( {A - 1} \right)}^2}}} = 0$	硬化参数${k_{\text{h}}}$
剪胀方程	$D = \frac{{{\text{d}}\varepsilon _{{\text{ii}}}^{\text{p}}}}{{\sqrt {\frac{2}{3}{\text{d}}e_{ij}^{\text{p}}{\text{d}}e_{ij}^{\text{p}}} }} = \frac{{{d_1}}}{{{M_{\text{c}}}g(\theta )}}\left[ {1 + \frac{R}{{{M_{\text{c}}}g(\theta )}}} \right]\left[ {{M_{\text{c}}}g(\theta ){e^{m\zeta }} - R} \right]$	三轴压缩临界状态应力比${M_{\text{c}}}$ 剪胀参数$ {d}_{1}，m $
流动法则	${\text{d}}e_{ij}^{\text{p}} = L{m_{ij}}$, ${m_{ij}} = \frac{{m_{ij}^{{\text{co}}} + m_{ij}^{{\text{nc}}}}}{{m_{ij}^{{\text{co}}} + m_{ij}^{{\text{nc}}}}}$
	$m_{ij}^{{\text{co}}} = \frac{{\frac{{\partial g}}{{\partial {r_{ij}}}} - \frac{{\partial g}}{{\partial {r_{mn}}}}{\delta _{mn}}\frac{{{\delta _{ij}}}}{3}}}{{\frac{{\partial g}}{{\partial {r_{ij}}}} - \frac{{\partial g}}{{\partial {r_{mn}}}}{\delta _{mn}}\frac{{{\delta _{ij}}}}{3}}}$(共轴部分)
	$m_{ij}^{{\text{nc}}} = k(1 - A){F_{ij}}$（非共轴部分）	非共轴参数$k$
硬化法则	${\text{d}}H = L{r_{\text{h}}} = L\frac{{G({c_{\text{h}}} - e)}}{{p'}}\left[ {\frac{{{M_{\text{c}}}g(\theta ){e^{ - n\zeta }}}}{R} - 1} \right]$
塑性模量	${K_{\text{p}}} = \frac{R}{{g(\theta )}}\left\{ {\frac{{G(1 - {c_{\text{h}}}e)}}{{p'H}}\left[ {\frac{{{M_{\text{c}}}g(\theta ){e^{ - n\zeta }}}}{R} - 1} \right] + 2{k_{\text{h}}}{k_{\text{f}}}{{(1 - A)}^2}} \right\}$	硬化参数${c_{\text{h}}}$，$n$
$e - {\left( {\frac{{p{\text{'}}}}{{{p_{\text{a}}}}}} \right)^\xi }$空间的临界状态线	${e_{\text{c}}} = {e_{{\Gamma }}} - {\lambda _{\text{c}}}{\left( {\frac{{p{\text{'}}}}{{{p_{\text{a}}}}}} \right)^\xi }$	临界状态线在$e - {\left( {\frac{{p{\text{'}}}}{{{p_{\text{a}}}}}} \right)^\xi }$空间的截距、斜率、参数$ \text{ }{e}_{\text{Γ}}，{\lambda }_{\text{c}}，\xi $
	$\zeta = e - {e_{\text{c}}} - {e_{\text{A}}}(A - 1)$	状态相关参数${e_{\text{A}}}$

下载: 导出CSV 

| 显示表格

通过假定偏平面空间中存在一个非相关联流动法则，塑性偏应变增量${\text{d}}e_{ij}^{\text{p}}$可表示为

式中：$L$为加载因子；$\left\langle {} \right\rangle $为麦考利符号；当$L > 0$时，$\left\langle L \right\rangle = L$，当$L \leqslant 0$时，$\left\langle L \right\rangle = 0$；${m_{ij}}$为塑性偏应变流动方向，包含与应力共轴的流动方向$m_{ij}^{{\text{co}}}$和组构各向异性诱发的非共轴的流动方向$m_{ij}^{{\text{nc}}}$两部分：

与应力共轴的流动方向$m_{ij}^{{\text{co}}}$表达式为

与应力非共轴的流动方向$m_{ij}^{{\text{nc}}}$的表达式构造为

式（7）的构造主要基于前人的试验和离散元模拟结果^[10]，能描述以下关键物理机制：①砂土剪切时塑性流动方向不只与应力张量主方向相关，还取决于加载过程中组构各向异性的演化；②在剪切初期，砂土塑性应变张量增量的主方向与主应力增量方向不共轴。随着剪切的进行，${\boldsymbol{F}_{ij}}$逐渐向加载方向演化，使非同轴分量越来越小。③达临界状态时，非共轴塑性应变增量消失，此时，${\boldsymbol{F}_{ij}}$与${\boldsymbol{n}_{ij}}$相同，即得到$A{\text{ = }}1$。在式（7）中引入各向异性组构变量是为了考虑砂土体的非共轴流动不只与组构各向异性相关，还与土体的加载方向和组构各向异性方向的偏离程度即各向异性变量$A$相关。Wang等^[11]在研究非共轴流动时也引入了类似的组构状态变量以及组构张量的影响。当组构方向与加载方向接近时，其非共轴各向异性会显著减小。当土体发生应力旋转时（即受非比例载荷），土体由于非同轴方向所产生的塑性应变增量会显著增加，达到临界状态时，由于非共轴所导致的应变会最终消失（处于完全塑性状态），并完全变为同轴下的塑性应变流动^[11]。当然，非共轴流动法则同时考虑组构状态变量和组构张量的影响可能值得商榷，需在将来的研究中进一步改进。

与Gao等^[10]模型相比，本文模型提出了一种能考虑组构各向异性的非共轴流动法则，旨在能用一套材料参数合理预测同一种砂土在三轴压缩、三轴伸长、单剪加载条件下的试验结果；本文模型在组构演化时采用指数型演化表达，该组构演化率更符合细观试验和离散元模拟结果。在有限元模型数值实现时，将非局部化理论应用于临界状态各向异性砂土模型中，有效地解决砂土应变软化材料的网格依赖性问题。除了上述非共轴流动法则，本文模型的屈服函数、硬化法则、剪胀方程、塑性模量都与组构各向异性及其演化相关。表 1总结了本文模型的数学表达式。

1.3   各向异性砂土模型的非局部化及数值实现

为了模拟边界值问题（如砂土海床中的板锚上拔），本文的各向异性砂土模型被嵌入三维有限元平台ABAQUS（基于用户自定义材料子程序UMAT）。本模型采用Sloan等^[23]提出的显式应力积分方法，计算得到每一应变增量步下的应力增量。根据Sloan等^[23]的建议，相对误差根据分段误差进行校正检验，然后在每个子步中进行迭代校正。计算中，屈服面容许误差取0.001 kPa，每一个子增量步误差为10^-5。为了尽量消除砂土本构计算受网格构型变化的影响，本文引入了Hughes等^[24]提出的大应变数值积分方法。

为最大程度消除数值计算中砂土应变局部化导致的网格依赖性问题，针对本文各向异性砂土模型采取了非局部化处理。传统正则化技术只将非局部化应用到线性相关的软化材料模型^[19-21]，而不适用于状态相关砂土本构等复杂模型。本文的正则化技术主要针对与状态相关的砂土本构模型，在数值计算时采用以状态相关参数（孔隙比增量）作为非局部变量的非局部化技术^[22]。局部的孔隙比增量${\text{d}}e$表示为非局部化体应变${\text{d}}{\varepsilon _{{\text{vn}}}}$的函数：

式中，e为孔隙比。

本文模拟中，采用了该技术来计算每个积分点的局部体应变增量，并进行非局部平均，然后在该自增量步结束时进行孔隙比的更新。本构模型的非局部化体应变增量基于下式计算获得，每一子增量步结束后，

对孔隙比进行相应更新：

式中：N为非局部平均的积分点的总数；${w_i}$为有限元中第i个积分点的加权函数；${v_i}$，${\text{d}}{\varepsilon _{{\text{v}}i}}$为有限元网格中第i个积分点的体积和局部体积应变增量。加权函数被表示为

式中，l为依赖于砂土粒径的内结构长度；${r_i}$为当前积分点与第𝑖个高斯积分点之间的距离。结果表明，上述加权函数比高斯正态分布函数能得到更好的非局部化结果。

2.   各向异性非共轴砂土模型验证：单元体试验验证

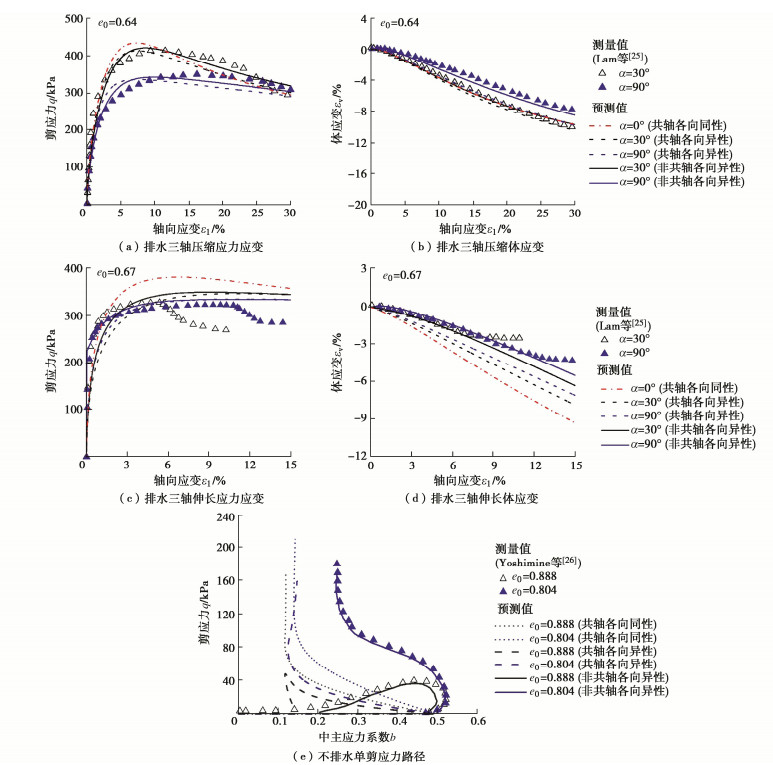
为了验证本文非共轴各向异性砂土模型效果，选取了同一种砂（丰浦砂）在三种不同应力路径（单剪、三轴压缩、三轴伸长等）下的试验结果^[25-26]。模型参数基于三轴压缩试验结果标定获得，并用于预测三轴压缩、单剪加载条件下的试验结果（模型参数详见表 2）。

表  2  本构模型参数

Table  2.  Parameters of constitutive model

参数		丰浦砂基于各向异性性模型	丰浦砂基于各向同性模型	UWA石英砂基于各向异性模型
弹性参数	G0	125	125	135
	$\nu $	0.1	0.1	0.05
临界状态参数	${M_{\text{c}}}$	1.25	1.25	1.296
	$ {e}_ \mathit{\Gamma } $	0.934	0.934	0.812
	${\lambda _{\text{c}}}$	0.02	0.02	0.0189
	$\xi $	0.7	0.7	0.7
剪胀参数	${d_1}$	0.2	0.2	1
	m	5	5	3.5
组构参数	${e_{\text{A}}}$	0.095	—	0.045
	${k_{\text{f}}}$	4.8	—	3
	${F_{\text{0}}}$	0.45	—	0.35
非共轴参数	k	0.5	—	0.4
硬化参数	${c_{\text{h}}}$	1.4	1.4	0.45
	${k_{\text{h}}}$	0.03	0.03	0.03
	n	3	3	2

下载: 导出CSV 

| 显示表格

图 1（a），1（b）分别显示了不同组构倾角的丰浦砂（沉积角α₀为30°，90°）在排水三轴压缩路径下的应力-应变、轴应变-体应变关系的试验和模型预测结果。预测值分别用非共轴各向异性模型（模型）、共轴各向异性模型（模型退化得到）和各向同性模型（模型退化得到）3个模型计算得到。可以看出，非共轴各向异性模型能合理预测α_o为30°，90°的试验结果。即便不考虑非共轴，对计算结果影响不显著；这是由于三轴压缩时主应力方向与各向异性组构张量方向接近，$ 非同轴 $相关塑性偏应变分量较小。如果不考虑组构各向异性，模型无法用一套参数统一预测α₀为30°，90°时的试验结果。

图  1  丰浦砂试验与模拟结果对比

Figure  1.  Comparison between model simulations and test data on Toyoura sand

下载: 全尺寸图片 幻灯片

图 1（c），1（d）显示了不同组构倾角的丰浦砂（沉积角α₀为30°，90°）在排水三轴伸长路径下的应力-应变、轴应变-体应变关系的试验和模型预测结果。可以看出，非共轴各向异性模型能较好预测α₀为30°，90°的试验结果。如不考虑非共轴，模型预测的体应变相比试验结果可高估54%。这是因为三轴伸长时，非同轴相关塑性偏应变分量较三轴压缩时增大。如不考虑各向异性，并基于三轴压缩数据标定的模型参数，预测三轴伸长试验结果时偏差显著。

图 1（e）显示了丰浦砂在不排水单剪时的中主应力系数与剪切应力的关系。可以看出，如果忽略非共轴或组构各向异性中的任一因素，模型预测都与实测结果有显著差异；非共轴各向异性模型能合理预测不同密实度砂土的不排水单剪试验结果。

综上，模型由于同时考虑了组构各向异性、非共轴及两者的耦合效应，能用一套材料参数合理预测同一种砂土在三轴压缩、三轴伸长、单剪加载条件下的试验结果。由于上述加载路径往往同时存在于边界值问题中（如板锚上拔问题），因此有必要在数值模拟中同时考虑砂土的组构各向异性和非共轴效应。

3.   各向异性非共轴砂土模型验证：离心机模型锚板上拔实验

3.1   砂土海床中锚板上拔有限元模拟

为了验证各向异性砂土本构及其非局部化后的数值模型，对Hao等^[27]在同一种砂土海床中4个不同埋深的锚板上拔离心机实验进行了预测比对。

试验所用砂为UWA石英砂，其最小和最大孔隙比分别为0.516，0.703。平均粒径为0.25 mm，不均匀系数为1.87。每个试验都采用干砂，砂土海床在1g条件下用落雨法制备，得到其初始相对密实度为85%~88%。每个试验都采用圆形铝制锚板，其模型厚度为2 mm，直径为20 mm（表示厚度为0.04 m，直径为0.4 m的等效圆形锚）。4个试验中，圆形锚板的嵌深比（埋深与直径之比）分别为3，6，9，12。

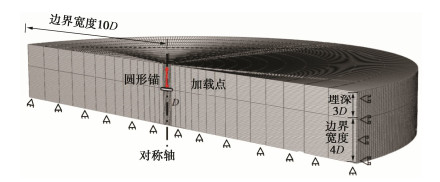
有限元模拟时采用三维模型进行模拟，典型有限元网格（埋深比为3）如图 2所示。为消除边界效应的影响，锚板右侧边界长度取10D，锚板底部的边界长度取4D^[28]。

图  2  典型锚板上拔离心机试验的有限元模型网格

Figure  2.  Mesh details along with boundary conditions used in simulation of plate anchor

下载: 全尺寸图片 幻灯片

有限元模拟时采用模型尺寸的平板锚进行模拟，模拟时初始分析步设为自然重力下地应力平衡，并将锚板中心处的相对密实度设为85%，而后模拟离心机重力上升的过程，待超重力上升到20g，地表沉降稳定后，对锚板中心施加向上的位移直至0.4D。

数值计算采用本文提出的各向异性非共轴模型（模型参数见表 2）。假设锚板上覆土体的重度为16 kN/m³，初始土压力系数${k_0}$设置为0.5。因此在数值模拟时，锚板表面与砂土的接触设置不考虑下部土体与平板锚之间的粘结力，仅考虑接触摩擦，界面摩擦系数设为0.7 (tan35$^\circ $)。根据Gao等^[10]的建议，由落雨法制得的砂样，F₀可以直接根据不排水三轴试验初始时刻的dq/dp的值标定，其表达式为${F_{\text{0}}} = \frac{{\sqrt 6 }}{{{\text{d}}q{\text{/d}}p - 1}}$。初始的组构张量系数F₀被假定为0.35^[9]。

根据Mallikarachchi等^[21]的建议，数值计算时颗粒材料的内部特征长度l通常大于10d₅₀。考虑锚板的半径为0.2 m，在计算时颗粒材料内部长度l取为0.2 m，以消除锚板区域范围内的应力集中。

为了探究网格尺寸对于平板锚上拔承载力的影响，本文比对了局部化网格和非局部化正则化网格技术的两种不同模拟结果。现选取不同的网格数目对于埋深为3D的锚泊基础进行网格依赖性分析。参数分析所采用的网格数分别为938，3193，6214，9826。

3.2   非局部正则化技术对网格依赖性的影响

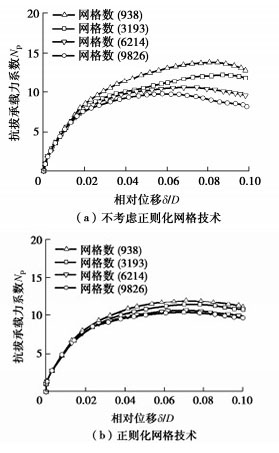
图 3（a）为未考虑非局部正则化技术得到的锚泊基础（H/D=3，${D_{{\text{r0}}}}$=0.85）承载力位移曲线。图中锚板的承载力系数为$ {N}_{\text{P }} $(${N_{\text{P}}} = \frac{{{q_{\text{u}}}}}{{\gamma AH}}$)，$\gamma $为砂土体的单位重度，$A$为圆形锚的面积，$H$为平板锚的嵌入深度。从图中可得，不考虑非局部化的数值解高度依赖于网格，当网格数目增加10倍（从938增加至9826），承载力系数峰值下降了38%（图 3（a））。且当网格数目从6214增加到9826时，承载力系数仍变化了18%。

图  3  网格尺寸对平板锚承载力的影响

Figure  3.  Effects of mesh size on bearing capacity of plate anchor predicted by anisotropic model

下载: 全尺寸图片 幻灯片

图 3（b）显示了考虑非局部技术预测的上拔力-位移关系（H/D=3，${D_{{\text{r0}}}}$=0.85）。随着网格尺寸的减小，承载力出现很强的收敛性，网格之间的差异对于模拟结果影响不显著。当网格数目增加10倍（从938增加至9826），平板锚的承载力系数仅降低10%左右。且当网格数目大于6214后，承载力系数几乎不再变化。

3.3   砂土海床中板锚上拔离心试验验证

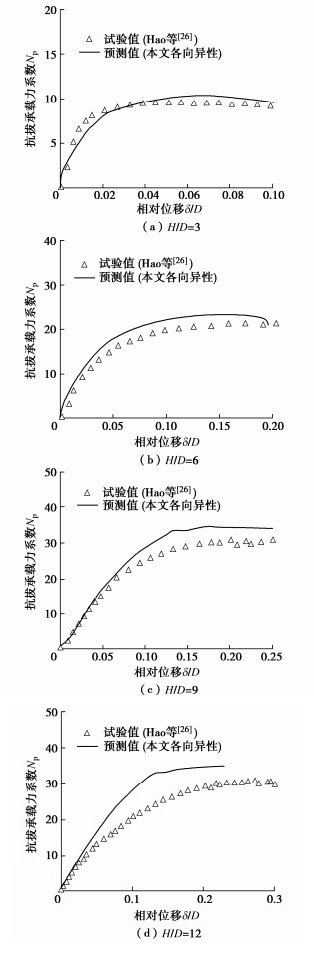
图 4（a）~4（d）比较了板锚不同嵌深比下离心机试验和两种模型（共轴各向同性模型、非共轴各向异性模型）的预测结果。本文非共轴各向异性模型能合理预测不同嵌入深度下的平板锚上拔承载力发挥系数与上拔位移间的关系。该模型准确描述了两个试验规律：承载力系数随H/D的增加而增大；达到上拔峰值力所需的位移随H/D的增加而增大。

图  4  UWA硅砂20g下平板锚上拔试验

Figure  4.  Comparison of simulated and measured mobilised N_p for circular anchors in UWA silica sand at H/D = 3, 6, 9 and 12

下载: 全尺寸图片 幻灯片

4.   砂土海床沉积角对锚板上拔承载特性的影响研究

4.1   各向异性砂土海床中板锚上拔典型响应

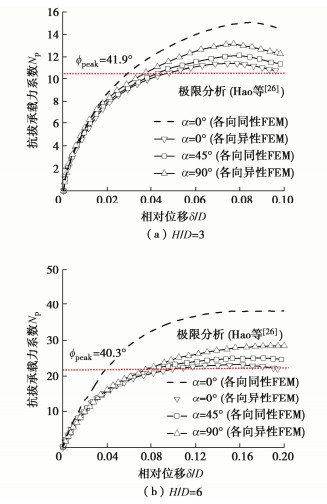
为了分析组构各向异性及演化对板锚上拔承载特性的影响，基于本文各向异性模型，模拟了不同组构沉积海床（沉积角α₀为0°，45°，90°）中平板锚的上拔。网格划分如图 2所示。初始的组构张量模长F₀定为0.35（针对自由沉积海床）。模型参数采用UWA砂的参数，详见表 2。针对上述工况，对比了基于非共轴各向异性模型（本文模型）、共轴各向同性模型（本文模型退化获得）的数值分析结果、以及基于极限平衡法的计算结果。极限平衡法采用Hao等^[27]提出的圆形锚上拔承载力计算公式，假定剪切破坏面与竖直方向的夹角为剪胀角，通过计算板锚上覆土重以及剪切破坏面两侧的剪切强度，获得板锚上拔承载力。

图 5（a），5（b）分别显示了各向异性砂土海床中不同埋深（H/D为3，6）板锚的上拔响应。结果表明，对两种不同的埋深，板锚的上拔承载力都随沉积角α_o的增大而变大。当海床沉积角α₀从0°变大到90°时，H/D为3，6的板锚上拔承载力分别增大了20%和27%。组构沉积角为45°海床的承载力则介于两者之间。这说明尽管上述3种工况中，砂土海床的应力水平$p{\text{'}}$和孔隙比$e$相同，但板锚上方土体发挥的峰值摩擦角不同；3种工况中砂土组构各向异性及演化速率的差异是主要原因。

图  5  不同组构沉积角下的承载力位移曲线（D_r0=0.85）

Figure  5.  Bearing capacity-displacement relationship for a plate anchor in sand with different bedding plane orientations

下载: 全尺寸图片 幻灯片

图 5也显示，如果忽略组构各向异性影响，并基于三轴压缩数据标定模型参数，会使模型预测结果高出试验值50%~100%。这是因为各向同性模型在满足三轴压缩预测条件下，会高估其他路径下（如三轴伸长、单剪）的砂土强度^[16]。图 6以H/D=3的板锚工况为例，对比了各向同性、各向异性模型计算获得的板锚达峰值上拔抗力时土中摩擦角发挥值云图。可以看出，相比于各向异性模型，各向同性模型所计算的剪切破坏面上土体摩擦角发挥值更高，且板锚上覆剪切区域更大。因此，各向同性模型显著高估了板锚上拔承载力（图 5）。如图 5所示，采用Hao等^[27]的各向同性的极限平衡法由于在分析时只考虑了密实度的影响，并且对于整个海床模型采用统一的经验摩擦角和剪胀角，虽然能合理预测自然沉积下的砂土海床锚板上拔承载力时，但低估了不同沉积角对于平板锚上拔承载力的影响。

图  6  H/D=3各向异性平板锚承载力峰值时刻摩擦角云图

Figure  6.  Contours of peak friction angle by different models

下载: 全尺寸图片 幻灯片

4.2   组构各向异性及演化对平板锚承载特性影响

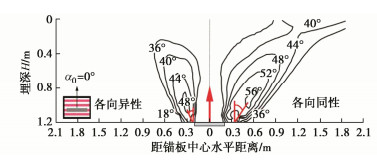
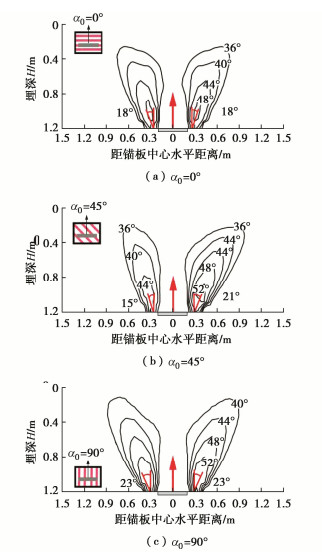
为了解释图 5中不同沉积角海床中板锚板锚上拔承载特性的不同，图 7（a）~7（c）分别显示了α₀为0°，45°，90°计算工况中，板锚达峰值上拔抗力时土中摩擦角发挥值云图。可以看出，板锚两侧剪切破坏面上的发挥摩擦角随α₀增大而增大。从定量上看，当初始沉积角α₀从0°增加到90°时，剪切破坏面上摩擦角最大发挥值从48°增加至52°；剪切面与垂直面的夹角从18°增加至23°。综上，砂土海床α₀增大导致更高的发挥摩擦角，更大的板锚上覆剪切区，导致高α₀砂土海床中板锚承载能力增强（图 5）。

图  7  不同组构海床中承载力峰值时刻板锚两侧发挥摩擦角云图

Figure  7.  Contours of peak friction angle with different bedding plane orientations

下载: 全尺寸图片 幻灯片

由于本文模型考虑非共轴流动法则（式（4）~（7）），实现了对倾斜组构海床中垂直上拔板锚两侧剪切破坏区域的非对称模拟。这是对共轴各向异性砂土模型较难模拟出上述现象（Gao等^[17]和Chaloulos等^[18]）的改进。

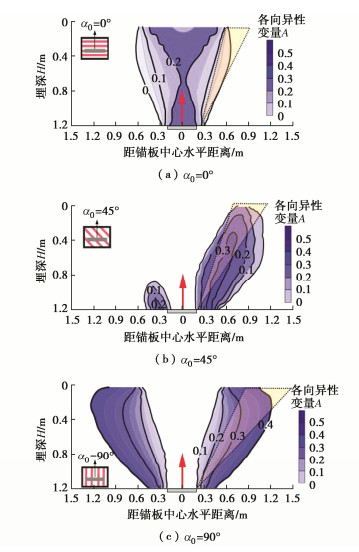
板锚上覆土体摩擦角的发挥值与其组构各向异性演化程度密切相关。为了进一步揭示两者关系，图 8（a），8（b），8（c）分别显示了平板锚上拔力达峰值时，不同组构沉积角海床中（α₀为0°，45°，90°）各向异性变量A的分布云图。每个图中，虚线阴影区域对应板锚侧面的剪切破坏区（基于图 7获得）。

图  8  不同组构海床中峰值时刻板锚两侧各向异性变量云图

Figure  8.  Contours of anisotropy variable with different bedding plane orientations

下载: 全尺寸图片 幻灯片

图 8显示，海床初始组构倾角α₀从0°增大到90°时，板锚侧面剪切破坏区内各向异性变量A均值从0.05增加至0.3。这说明，海床初始组构倾角越大，其剪切破坏区内组构演化越快，所以α₀=90°工况中锚周土体发挥摩擦角最快接近峰值强度（图 7），从而表现出最大上拔承载力（图 5）。当初始沉积角为45°时，如图 8（b）所示，由于初始沉积方向为45°沉积，并不沿锚板中心对称分布。因此在上拔时组构各向异性与剪切错动方向较为一致的右侧演化远高于左侧的各向异性演化，并最终导致了锚板的滑动摩擦角云图非均匀分布。在右侧剪切破坏区上，其单元的组构各向异性方向与剪切方向更为接近，演化速率远大于左侧剪切带上的单元，其各向异性变量在承载力峰值时刻最大值达到0.3，而左侧则为0.2，且左侧单元在剪切带内的各向异性正值范围较小。两侧的组构非均匀共轴演化导致了承载力介于0°~90°，且云图呈现出非对称规律。

传统的各向异性本构模型在流动法则中忽略了各向异性的影响，导致其在砂质海床中数值模拟时很难产生非对称破坏。而本文模型引入了考虑组构各向异性的非共轴塑性流动法则，因此在模拟时会由于初始海床组构颗粒排列不对称，进而产生非共轴应变，并最终导致了模拟结果的非对称破坏。

5.   结论

本文围绕砂土组构各向异性对板锚上拔承载特性影响这一目标，基于砂土各向异性临界状态理论框架，引入了考虑组构各向异性及演化的非共轴流动法则，建立了砂土各向异性非共轴本构模型，并嵌入三维有限元程序ABAQUS；通过引入正则化技术，降低了砂土应变局部化导致的网格依赖性。基于不同路径下砂土单元试验和砂土海床中平板锚上拔离心机试验，验证了该模型的适用性。在此基础上，通过开展参数分析，揭示了砂土组构各向异性及演化对板锚上拔承特性的影响；并定量评价了忽略组构各向异性时，数值模拟和极限平衡分析对砂土中板锚上拔承载力的预测误差。得出4点结论。

（1）同一应力水平和密实度下，平板锚的上拔峰值承载力随海床组构沉积角α_o的增大而提高。在锚板上拔受拉时，越靠近锚板边缘的点，其所受的剪切力越大，各向异性演化速率越快，并且最早达到临界状态。因此高α₀海床中的砂土组构演化更快、导致峰值摩擦角更高。

（2）由于本文模型考虑非共轴塑性流动法则，实现了对倾斜组构海床中垂直上拔板锚两侧剪切破坏区域的非对称模拟。这是对基于共轴各向异性砂土模型的数值分析不能模拟上述现象的改进。

（3）基于三轴压缩所标定的各向同性的砂土本构模型会高度平板锚的上拔承载力。这是由于在计算时忽略组构各向异性影响，因为各向同性模型在满足三轴压缩预测条件下会高估其他路径下（如三轴伸长、单剪）的砂土强度。

（4）传统极限平衡分析法由于在设计时不考虑组构各向异性的影响，只能合理预测初始沉积角为α₀= 0°时的锚板承载力。沉积角为α₀为45°，90°时的平板锚，极限平衡法会远远低估其上拔承载力。设计时建议适当考虑组构各向异性的影响。