0.   引言

随着中国交通隧道的快速发展，穿越活动断层隧道不断涌现，高地震烈度区地震与断层错动对隧道结构的安全稳定性造成极大影响。因此，如何提高穿越活动断层隧道的结构抗震性能受到广泛关注。

为了提高隧道结构抗震性能，国内外学者对隧道地震响应展开了广泛研究。现有规范^[1-2]规定隧道位于断层破碎带等地段的结构，抗震设防长度应根据地形、地质条件确定，但并未分级给出具体抗震加强长度。随着国内外学者的深入研究，现有震害分区方法主要是通过现场震害及破坏特征进行分区。对于破坏机理及特征，国内外学者展开了大量研究，刘学增等^[3]研究发现逆断层错动情况下，隧道最终破坏为逆断层下的剪切破坏，主要表现为变形缝两侧隧道衬砌脱落和纵向裂缝，认为影响区集中在2倍洞径区域。武世燕^[4]对大梁隧道震后灾害特征进行研究后发现，断层核心区变形破坏严重，严重震害主要分布在出口段约350 m范围内。汪振等^[5]对断层错动展开研究后发现，隧道横断面在正断面错动下呈压缩变形状态，并认为隧道衬砌在断面滑动面周围8 m长范围内属于完全破坏状态。唐浪洲等^[6]对不同走滑断层错动量下小角度斜交穿越断裂面铁路隧道进行研究，发现走滑断层错动量大于0.6 m后，隧道结构开始破坏。何川等^[7]通过振动台模型试验对跨断层破碎带隧道动力响应进行研究，发现隧道断层带段围岩具有较大加速度响应特性，衬砌具有最大应力峰值，更容易发生破坏。崔光耀等^[8]对汶川地震公路隧道震害调查资料统计分析，指出隧道洞口浅埋段震害影响向深埋段延伸一定距离。对于影响区分区，田四明等^[9]基于震害调查结果，通过理论分析，将活动断裂带影响区划分为强烈影响段及一般影响段，并建议分区设防。周栋等^[10]对青海门源地震震害调查资料进行分析后发现隧道震害主要集中在断层影响范围，严重破坏段约350 m，占全长5.33%，较严重段占全长15.96%，其余段落总体轻微。尹超^[11]研究发现，断层错动情况下，右旋走滑时衬砌拉伸破坏范围较大，左旋走滑时衬砌压缩破坏范围较大，隧道衬砌破坏区间为断层面前后90 m左右。张锴^[12]基于隧道横断面相对变形率提出穿越活动断层隧道的地震作用纵向影响区，认为穿越断层破碎带隧道主要影响区为4.5倍洞径。孙风伯^[13]针对穿越活动断裂带山岭隧道开展系统性研究，分析了断层错动影响范围并确定了隧道纵向设防范围。对于能量法，崔光耀等^[14]通过对隧道破坏过程的能量分析，获得隧道结构的可释放应变能公式，提出跨活跃断层隧道的抗错断设计思路。曲宏略等^[15]采用基于能量释放率的分析方法对断层影响下的隧道震害进行研究，认为断层宽度为10 m的能量释放影响范围为60 m。马至刚等^[16]提出一种基于HHT和边际谱的能量识别方法对隧道结构损伤变形特性进行研究，并利用能量阐明隧道结构的地震损伤变形发展过程和破坏特性。Zhang等^[17]从可释放弹性应变能角度建立跨断层隧道纵向影响分区，并得到了跨断层隧道节段式衬砌最优抗减震措施。

以上研究主要集中在穿越断层隧道的震害特征及震害机理、基于震害程度的影响分区方法、能量法在隧道抗错设计方面的应用等方面，但在利用能量原理进行穿越活动断层隧道震害影响分区方面的研究鲜有报道。本文以龙洞子F5断层段为依托，基于能量理论，研究了地震和断层错动作用下的隧道能量响应，建立了地震和断层错动作用下能量曲线的计算方法，提出了基于能量原理的穿越活动断层隧道震害影响分区方法，并依托龙洞子和龙溪隧道现场震害进行验证。研究成果可为穿越活动断层隧道抗震设防设计提供参考。

1.   穿越活动断层隧道能量响应理论

1.1   地震和断层错动作用下的能量方程

对于穿越活动断层隧道二衬，根据结构位移、阻尼和质量等参数可建立多自由度系统方程

式（1）结合结构位移$u(t)$进行积分可得

式（2）以能量的形式表示：

式中：${E_{\text{k}}}$为结构动能；${E_{\text{D}}}$为阻尼能；${E_{\text{S}}}$为应变能；${E}_{地震}$代表地震位移输入能量；${E}_{错动}$代表断层错动输入能量。

因此，由式（2），（3）可得

1.2   隧道结构稳定性的能量准则

当隧道结构受到地震和断层错动作用时，隧道结构的动能、阻尼能、应变能等能量将被内部非线性恢复力消耗或吸收。

当输入能量等于内部变形引起的能量和部分耗损的能量情况下，结构处于平衡状态，当输入能量较大时，多余的能量将转化为其它形式能量并消耗，结构再次回到平衡状态。因此，结构的动态平衡状态可以表示为

式（9）中，${\boldsymbol{F}_{{\text{ext}}}}(t)$为瞬时外力矢量，${\boldsymbol{F}_{\text{int} }}(t)$为瞬时内力矢量。

结构动力、阻尼力和地震动力视为瞬时外力矢量，恢复力视为瞬时内力矢量，即

因此，在地震和断层错动作用下，瞬时外力矢量所做的瞬时功和顺时内力矢量所做的累计功可以表示为

则，结构所受瞬时外力和内力所做功的差可表示为

绝热过程中，外力矢量和内力矢量所做的功代表了结构的能量变化，结构内部能量可由外力矢量功和内力矢量功的差值得到，公式表达为

此外，结构的总输入能量可由${E_{\text{I}}}$表示，即${E_{\text{I}}} =$ ${E}_{地震}+{E}_{错动}$，当外部输入能量小于结构内部能量时，结构处于不稳定状态，此时结构会吸收“额外”能量以补偿输入能量。因此，基于能量的结构动态稳定准则为

进一步，得到结构动态稳定函数为

对于式（16）离散化以便于计算，则：

同时外力所做功离散化，则：

2.   龙洞子F5断层地震响应能量曲线

2.1   工程概况

龙洞子隧道位于龙洞子山庙子坪至龙溪石灰窑场一带。隧道为双线隧道，左洞长度为1070 m，右洞长度为1042 m。

F5断层为龙溪断层派生次级正断层，为活动性断层。F5断层上下盘均为梁山组灰黑色炭质泥岩，为Ⅳ级围岩。断层破碎带宽约10 m，倾角75°，呈半胶结碎裂结构，为V级围岩。

隧道结构初支采用25 cm厚的C25喷射混凝土，二衬采用45 cm厚的C25模筑混凝土。

2.2   计算模型

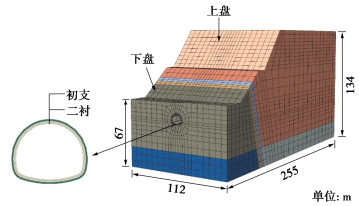
为研究穿越活动断层隧道震害影响区分区，建立计算模型（图 1）。隧道出口段埋深11.7 m，纵向开挖长度为255 m，隧道底部基岩厚度为20 m，左右侧宽度为50 m模型宽度为112 m，断层破碎带宽度为10 m，断层倾角75°。隧道断面长为11.8 m，高为10 m。下盘长度为45 m，上盘长度为200 m，下盘高度为67 m，上盘高度为134 m。模型遵循弹塑性屈服准则和Mohr-Coulomb准则。

图  1  计算模型

Figure  1.  Computational model

下载: 全尺寸图片 幻灯片

假定土体为黏弹性体，模型边界条件设置为：静力计算时模型四周以及底部采用静态边界约束，上部无约束；动力计算时，模型底部采用固定边界，四周采用自由场边界，上部无约束。

考虑到断层错动具有一定倾角，正断层错动通过固定上下盘左右方向，并赋予上下盘垂直速度和远离断层方向的水平速度，以实现强制位错，断层错距为20 cm。

2.3   计算参数

围岩参数根据地质勘测资料确定，在动力荷载下，计算模型主要参数见表 1所示。

表  1  计算参数

Table  1.  Computational parameters

材料	重度/ (kN·m-3)	弹性模量/ GPa	泊松比	内摩擦角/ (°)	黏聚力/MPa
上下盘Ⅳ级围岩	22	2.5	0.3	35	0.5
破碎带Ⅴ级围岩	20	1.0	0.4	25	0.2
Ⅱ级围岩(基岩)	25	20	0.2	50	1.5
初支	22	23	0.2	—	—
二衬	25	28	0.2	—	—

下载: 导出CSV 

| 显示表格

2.4   动力荷载及监测面布置

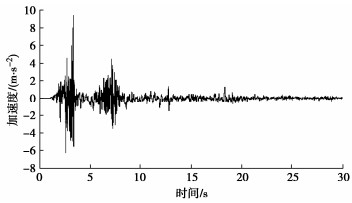
本文地震加速度波选择采用汶川地震荷载数据，以Ⅺ度地震烈度标准化，持续时长30 s，在模型底部输入三方向加速度荷载。采用瑞利阻尼，临界阻尼比为5%，滤波及基线校正后地震加速度时程曲线如图 2（以X方向为例）所示。

图  2  加速度时程曲线（X方向）

Figure  2.  Time-history curves of acceleration (X direction)

下载: 全尺寸图片 幻灯片

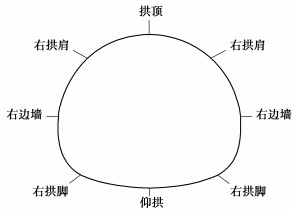
选取断层破碎带中心断面为监测断面，监测点选取隧道拱顶、左右拱肩、左右边墙、左右拱脚及仰拱等8个测点，监测点如图 3所示。

图  3  监测点布置

Figure  3.  Arrangement of monitoring points

下载: 全尺寸图片 幻灯片

2.5   能量响应分析

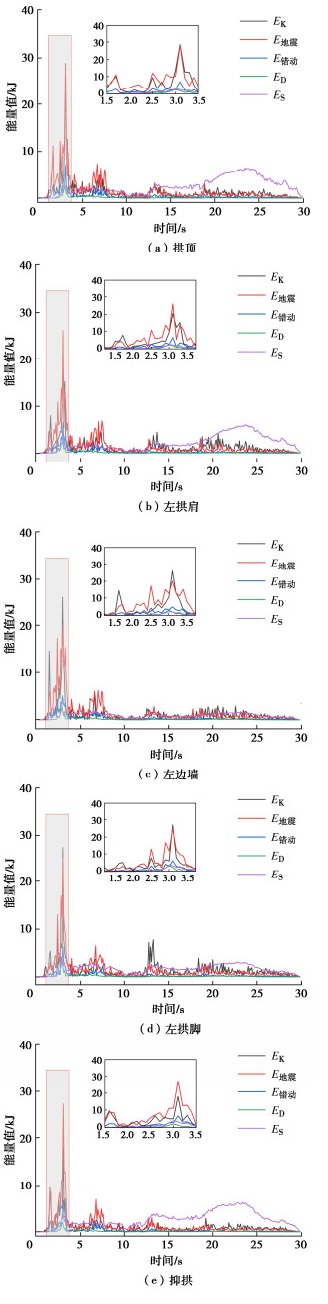
提取1/2结构各监测点的位移、速度、加速度等参数，计算各监测点能量，分析其能量响应，各监测点包含的能量分量如图 4所示，各测点能量峰值见表 2所示。

图  4  能量响应曲线

Figure  4.  Curves of energy response

下载: 全尺寸图片 幻灯片

表  2  监测点能量峰值

Table  2.  Peak energy values at monitoring points (单位：kJ)

能量	拱顶	左拱肩	左边墙	左拱脚	仰拱
结构动能	28.7	20.5	26.1	27.3	18.1
地震输入能	28.2	26.1	20.1	25.1	27.3
错动输入能	7.05	6.52	5.03	6.29	6.82
阻尼能	2.41	2.31	2.04	2.27	2.13
应变能	6.51	5.94	2.21	3.85	6.26

下载: 导出CSV 

| 显示表格

由图 4可知，各测点结构动能、地震输入能、错动输入能、阻尼能在2.5~3.5 s内达到峰值，在7~8 s内存在次波峰，应变能E_s的波峰出现在23~24 s附近。结构动能、地震输入能、错动输入能、阻尼能在地震前10 s内变化剧烈，此时隧道结构处于剧烈震荡状态。与图 2中展示地震加速度时程曲线符合，具体表现为，在2~4 s内变化幅度最显著，在前10 s内能量波动频繁。

由表 2可知，各测点结构动能峰值、地震输入能峰值、错动输入能峰值、应变能峰值差距较大，阻尼能峰值相近。整体来看，结构动能峰值、阻尼能峰值和应变能峰值小于总输入能量（E_I）峰值，其中总输入能量峰值等于地震输入能量与错动输入能量之和。拱顶结构动能峰值为28.7 kJ，总输入能峰值为28.2+7.05=35.25 kJ，阻尼能峰值为2.41 kJ，应变能峰值为6.51 kJ，均大于各其它部位能量峰值，说明在地震作用和断层错动情况下，拱顶处能量响应大于其它位置，拱顶处能量变化剧烈，较其它位置更易发生震害。

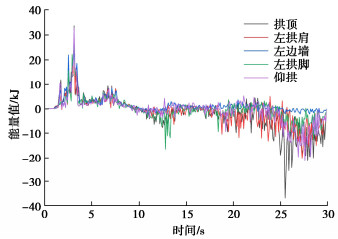
为准确评估地震运动过程中结构状态的变化，引入动力稳定函数$S(t)$，由式（16）~（20）计算地震过程动力稳定函数，绘制动态稳定函数曲线图如图 5所示。

图  5  动态稳定函数曲线

Figure  5.  Curves of dynamic stability function

下载: 全尺寸图片 幻灯片

由图 5可知，结构在前10 s内$S(t)＞0$，表明结构整体在前10 s暂未失稳，同时稳定性处于先增加后降低状态，在10 s左右出现$S(t)＜0$，说明此时结构的稳定性发生变化，开始破坏，出现裂缝。在10~18 s左右，除左拱脚位置出现较大幅度能量波动外，其余位置能量值整体变化较为平稳，表明此时其它位置裂缝尚未加速发育，左拱脚位置能量值快速变化，在12~13 s内裂隙迅速发育。其余位置能量值在18 s左右负值逐渐变大，说明此时隧道除左拱脚以外，其他位置裂缝发育加速。拱顶处负峰值最大，负峰值为36.8 kJ，出现在25.5 s左右。左边墙能量值整体基本不变化，表明左边墙较少发育裂缝，左边墙相比其他位置更为稳定。

为评估地震运动过程中结构动态稳定，定义结构破坏率为监测点能量稳定函数$S(t)＜0$累计时长与地震波持时30 s的比值，破坏率计算公式如下所示。

各监测点破坏率计算结果见表 3所示（以左侧为例）。

表  3  监测点破坏率

Table  3.  Damage rates at monitoring points

监测点位置	拱顶	左拱肩	左边墙	左拱脚	仰拱
破坏率	56.67%	53.0%	26.33%	50.33%	43.66%

下载: 导出CSV 

| 显示表格

由表 3可知，拱顶处破坏率最大，左拱肩处破坏率次之，左边墙破坏率最小，说明隧道顶部能量稳定函数$S(t)＜0$累计时长更长，隧道顶部处于不稳定状态时长更长。隧道破坏率顶部与底部较大，边墙较小，说明隧道顶部与底部容易发生震害，裂缝由顶部与底部向左右边墙延伸。由于拱顶破坏率最大，因此本文后续研究主要围绕拱顶展开。

2.6   震害影响分区

为研究穿越活动断层隧道震害影响分区，需沿隧道纵向布置多个监测断面。

（1）监测断面布置

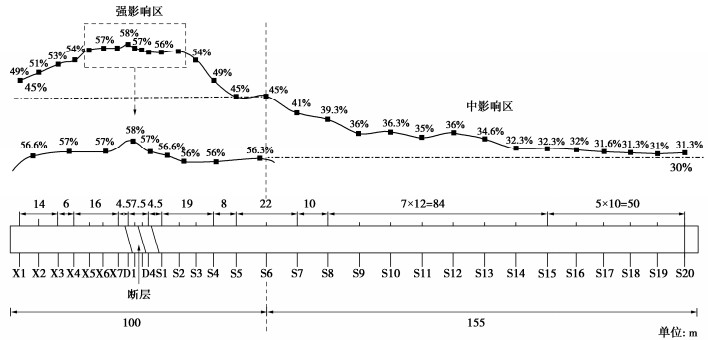
计算模型下盘设置7个监测断面（X1~X7），断层设置4个监测面（D1~D4），上盘设置20个监测断面（S1~S20），监测面布置如图 6所示。

图  6  隧道纵向破坏率及震害影响分区图

Figure  6.  Longitudinal damage rate and seismic impact zones of tunnel

下载: 全尺寸图片 幻灯片

（2）计算结果及分析

计算各监测面拱顶处破坏率并绘制隧道纵向破坏率变化图，隧道纵向破坏率变化图如图 6所示。

由图 6可知，破坏率随着与断层距离加大而降低，破坏率在监测面D1处达到最大，断层区监测面D1~D4破坏率分别为58%，57%，56.6%，56%，断层处隧道破坏率最大处出现在离下盘最近监测面（监测面D1），隧道最小破坏率为31%，出现在监测面S19处。下盘段隧道最大破坏率为57%，破坏率在49%以上段长度为39 m，上盘最大破坏率为56.3%，破坏率在49%以上段长度为22.65 m。距断层中心位置约8 m处，下盘破坏率为57%，上盘破坏率为56%。下盘距断层中心位置23.8 m处（监测面X4处）破坏率与上盘距断层中心位置21.25 m处（监测面S3处）破坏率相同，均为54%，下盘距断层中心位置44 m处（监测面X1）处破坏率与上盘距断层中心位置27.65 m处（监测面S4）相同，均为49%，下盘破坏率下降5%经过3个监测面，长度为20.2 m，上盘下降相同大小破坏率只经过1个破坏面，长度为6.4 m，此段内下盘破坏率降低速度（0.25%/m）小于上盘破坏率降低速度（0.78%/m），由上述可知，距离断层中心位置相同距离情况下隧道下盘破坏率大于上盘，下盘破坏情况较上盘相比较为严重，原因是隧道洞口效应的影响较大。上下盘同时遭受错动和地震惯性力影响，但由于下盘位于洞口段，且处于错动和洞口效应的叠加区，下盘承受地震惯性力大于上盘，下盘所受地震动影响要强于上盘。

隧道在上盘处破坏率下降速度呈先快后慢趋势，监测面S1~S5处破坏率下降速度最快，破坏率由56.3%降低至45%，破坏率下降了11.3%，经过4个监测面，长度为27.6 m，破坏率下降速度为0.41%/m。监测面S5~S9处下降速度放缓，破坏率由45%降低至36%，破坏率下降了9%，共经过4个监测面，长度为45.465 m，破坏率下降速度为0.20%/m。监测面S9~S20处破坏率基本停止下降。此时最终破坏率为31.3%。上盘破坏率及破坏率下降速度逐渐降低的原因可能是因为随着上盘与断层破碎带距离的增加，隧道埋深逐渐增加所受的地震惯性力及地震动影响逐渐下降，隧道逐渐处于安全环境。

隧道洞口段X1~X3埋深为11.7 m，断层中心位置埋深33.2 m，S1处埋深为40 m，S3处埋深为41.6 m，S4处埋深为49.3 m，S4处破坏率为49%，由此可知，当隧道埋深小于50 m时，该段隧道破坏率较大，说明隧道所承受地震惯性力作用较强，因此，本模型地震惯性力影响范围主要为监测面X1~S4，长度为71.65 m。

基于隧道纵向破坏率变化图，综合考虑错动、地震惯性力和洞口效应的影响，出于保守考虑，建立穿越活动断层隧道震害影响区分区标准，拟定分区标准见表 4所示。

表  4  震害影响区分区标准

Table  4.  Criteria for seismic impact zones

分区	强影响区	中影响区	弱影响区	无影响区
破坏率	$\partial$≥45%	45%＞$\partial$≥30%	30%＞$\partial$≥10%	10%＞$\partial$

下载: 导出CSV 

| 显示表格

由表 4可知，拟定穿越活动断层隧道以45%破坏率为强影响区和中影响区分界点，强影响区与中影响区在监测面S6处交界，强影响区范围为X1~S6。中影响区与弱影响区分界点为30%破坏率。弱影响区与无影响区分界点为10%，无影响区破坏率小于10%。本论文计算模型应用影响分区标准后，震害影响区分区如图 6所示。

由图 6可知，本次研究建立的隧道模型处于强影响区和中影响区，暂未出现弱影响区和无影响区，本隧道模型强影响区为洞口至监测面S6处，强影响区长度为100 m，S6处埋深为73.15 m，强影响区主要受地震惯性力、洞口效应、地震和断层错动作用的综合影响。中影响区为模型余下部分，中影响区长度为155 m，S7~S20处埋深为79 m，中影响区主要受地震和断层错动的影响。

3.   现场震害分析及分区方法验证

以龙洞子隧道为例，进行现场震害分析，并结合龙溪隧道震害情况进行分区方法验证。

3.1   龙洞子F5断层段震害统计及分析

龙洞子隧道隧址区地震设防烈度为Ⅶ度。汶川地震中，龙洞子隧道实际地震烈度为Ⅺ度，该隧道F5断层错动20 cm。

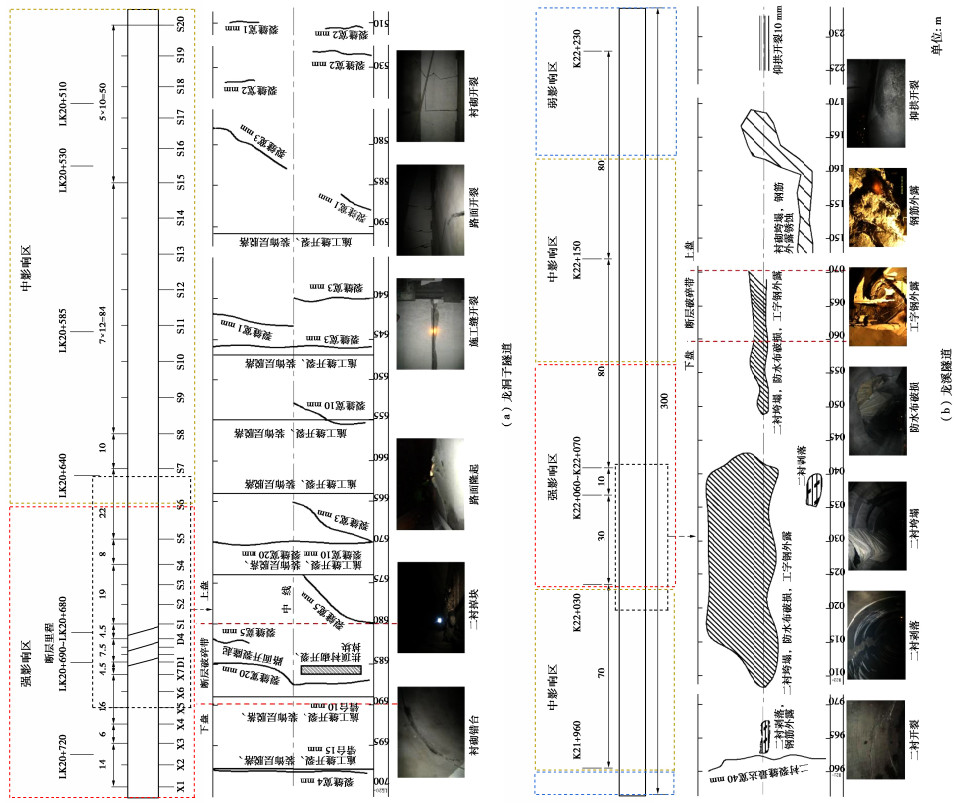
F5断层现场震害统计范围为：下盘45 m（延伸至出口），断层破碎带10 m，上盘200 m，单洞255 m，双洞共计510 m。该段震害类型主要有：衬砌开裂、路面开裂、衬砌错台、路面错台、路面隆起以及二衬掉块等。通过实地调查、绘制震害展布图、统计各震害类型长度及震害比例，对其震害情况进行分析。龙洞子隧道F5断层段震害类型如图 7所示，震害统计情况见表 5所示。

图  7  震害类型

Figure  7.  Types of seismic damage

下载: 全尺寸图片 幻灯片

表  5  震害统计

Table  5.  Statistics of seismic damage

震害 类型	震害长度/m	震害 比例		震害 类型	震害长度/m	震害 比例
A	155	30.39%		E	68	13.33%
B	159	31.18%		F	12	2.35%
C	47	9.22%		G	207	40.59%
D	69	13.52%		—	—	—
注：G为震害总长度；震害比例为震害长度比统计隧道长度，F5断层附近的统计隧道长度为510 m。

下载: 导出CSV 

| 显示表格

当破坏率∂≥45%时为强影响区，破坏率45%＞∂≥30%时为中影响区，强影响区和中影响均极易出现震害，故统计强影响区和中影响区两区段不同震害类型的现场实际震害比例，在一定范围内，破坏率越高，震害比例越大，二者正相关。

由表 5可知，龙洞子隧道F5断层段震害以衬砌及路面开裂为主，二衬掉块长度为12 m，震害比例为2.35%，衬砌错台长度为47 m，震害比例为9.22%。龙洞子隧道F5断层段震害总长度达207 m，震害长度比例为40.59%，震害严重。

3.2   分区方法验证

（1）龙洞子隧道F5断层

龙洞子隧道F5活动断层段震害展布图如图 8（a）所示。

图  8  穿越活动断层隧道震害展布图

Figure  8.  Seismic damages in tunnels crossing active faults

下载: 全尺寸图片 幻灯片

由图 8（a）可知，龙洞子隧道F5断层影响区出现多条裂缝，裂缝走向基本为环向或斜向，隧道在穿越活动断层段隧道集中出现多种震害，如里程LK20+675~LK20+700（断层破碎带里程为LK20+ 680~+690）部分出现施工缝开裂，装饰层错落，错台15 mm，路面出现的最宽裂缝宽度为20 mm，二衬开裂掉块，路面隆起。隧道强影响区的洞口段出现较多类型震害，如里程LK20+718~727出现施工缝开裂，装饰层脱落，裂缝宽度为5 mm。强影响区上盘段出现5 mm宽斜裂缝。上述说明隧道强影响区下盘段震害强于强影响区上盘段，说明洞口效应的影响较大，洞口段处于错动和洞口效应的叠加区，破坏严重。隧道中影响区出现的震害类型随着远离活跃断层而逐渐减少，裂缝长度与宽度也逐渐下降。如里程LK20+577~+592出现斜裂缝，里程LK20+530及里程LK20+510附近出现1~2 mm宽短裂缝。随着距断层距离逐渐增大，出现的裂缝长度减小，裂缝宽度也减小。

综上所述，衬砌错台、二衬掉块、路面隆起等强震害类型集中出现于断层破碎带区域。在分区范围内，随着隧道远离断层破碎带，隧道逐渐处于安全状态，震害类型及强度逐渐降低。龙洞子隧道F5断层震害情况较好的验证了本文隧道震害影响区分区标准。

（2）龙溪隧道F8断层

以相同方法对龙溪隧道包括F8断层在内的K21+950~K22+250进行震害影响分区，分区长度共300 m，分区结果如图 8（b）所示。

由图 8（b）可知，龙溪隧道F8断层影响区震害严重，大面积出现二衬垮塌现象，二衬剥落、二衬开裂、仰拱开裂等多种震害均有发生。二衬垮塌集中发生在强影响区内，二衬剥落易发生在中影响区，弱影响区内出现二衬以及仰拱开裂现象。其中，大面积二衬垮塌现象出现在里程K22+010~+045段，该段跨越

强影响区与中影响区分界（里程K22+030），一半位于强影响区，另一半位于中影响区。断层破碎带出现二衬垮、防水布破损以及工字钢外露现象，结构受损严重。里程K21+960~970和K22+150~170两段位于中影响区，二衬垮塌面积减小，隧道受震害影响有所降低。隧道在弱影响区如里程K21+950~960以及K22+225~235仅出现裂缝，震害强度进一步降低。龙溪隧道F8断层震害情况较好的验证了本文隧道震害影响区分区标准。

因此，本文所提出的能量响应计算理论可较好的评价穿越活动断层隧道在遭受地震作用和断层错动下的地震响应，所建立的穿越活动断层隧道震害分区标准可较好地应用于穿越活动断层隧道震害影响分区。

4.   结论

（1）基于能量准则可以有效检测穿越活动断层隧道的地震不稳定性。当输入能量小于固有能量时隧道开始发生破坏，借助动态稳定函数还可确定穿越活动断层隧道开始出现裂缝时间。

（2）穿越活动断层隧道拱顶处能量响应最大，破坏率最大。拱顶处动能峰值为28.7 kJ，地震输入能峰值为28.2 kJ，阻尼能峰值为2.41 kJ，应变能峰值为6.51 kJ。破坏率为56.67%，拱肩、拱脚次之，边墙最小。隧道在10 s左右失稳出现裂缝。穿越活动断层隧道断层破碎带处破坏率最大，破坏率最大为58%。随着距离破碎带距离的增加，破坏率逐渐降低。

（3）根据隧道纵向破坏率图，建立穿越活动断层隧道震害影响区分区标准，以破坏率45%及以上区段为断层强影响区，以破坏率30%~45%区段为中影响区。以破坏率10%~30%区段为弱影响区，破坏率10%以下区段为无影响区。

（4）根据现场震害资料，龙洞子隧道F5断层段震害以衬砌及路面开裂、错台以及路面隆起为主，二衬掉块长度为12 m，震害比例为2.35%，衬砌错台长度为47 m，震害比例为9.22%。龙洞子隧道F5断层段震害总长度达207 m，震害长度比例为40.59%，整体震害严重。

（5）结合龙洞子隧道F5断层段和龙溪隧道F8断层段的汶川地震现场震害验证了本文基于能量原理的穿越活动断层隧道震害影响分区方法。因此，本文所提出的能量响应计算理论可较好的评价穿越活动断层隧道在遭受地震作用和断层错动下的地震响应，所建立的穿越活动断层隧道震害分区标准可较好地应用于穿越活动断层隧道震害影响分区，具有一定可靠性和推广性。