Resilience evolution of shield tunnel structures under ground surcharge
-
摘要: 韧性理论的提出和发展为盾构隧道结构性能评估提供了新思路。在提出考虑历史最大变形的衬砌性能指标基础上,建立包含管片、接头和非线性土弹簧的精细化三维有限元分析模型,研究了地面堆卸载作用下,不同埋深盾构隧道结构响应特征和韧性演化规律。结果表明:地面堆载下拱顶、拱底内弧面受拉,拱腰外弧面受拉,受错缝拼装影响,结构内力和损伤集中于边环纵缝相邻的中环管片处;卸载阶段隧道水平收敛减小,完全卸载后的残余变形随堆载量增加而增大,相同水平收敛情况下浅埋隧道卸载后变形恢复率大;隧道结构韧性随着水平收敛的增大快速降低,而缩短响应时间、提高修复措施效率可以提升隧道结构韧性;将隧道结构韧性分为4个等级,当结构进入极低韧性阶段时,应采取更加高效快速的综合修复方案,同时避免造成结构的二次损伤。Abstract: The proposition and development of the resilience theory provide a new way for the performance evaluation of shield tunnel structures. On the basis of the proposed lining performance index considering the maximum historical deformation, a refined 3D finite element model including segments, joints, and nonlinear soil springs is established. The structural response and resilience evolution of shield tunnels with different buried depths under surcharge and unloading are studied. The results show that under the ground surcharge, the inner surfaces at the arch crown and arch bottom, as well as the outer surface at the arch waist, are tensioned. Affected by staggered joints, the structural internal force and damage are more concentrated in the segment of the central ring adjacent to the longitudinal joint of the side ring. At the unloading stage, the horizontal convergence of the tunnel decreases, and the residual deformation after complete unloading increases with the increase of the surcharge. Under the same horizontal convergence, the deformation recovery rate of the shallow burial tunnels after unloading is greater. The resilience of the tunnel structures decreases quickly with the increase in the horizontal tunnel convergence, and shortening response time and improving the efficiency of repair measures can help enhance the resilience of the tunnel structures. While the resilience of the tunnel structures is divided into four levels, more efficient, rapid and comprehensive repair measures should be adopted to avoid the secondary damage to the structures when entering the extremely low resilience stage.
-
Keywords:
- shield tunnel /
- resilience /
- ground surcharge /
- lining performance /
- horizontal convergence
-
0. 引言
盾构隧道因其拼装式管片结构特点,对周边施工扰动高度敏感,极易受地面堆载、基坑开挖等因素影响产生较大结构变形,进而产生接缝渗漏水、混凝土开裂掉块、管片错台等结构病害[1-4]。据不完全统计,目前全国管片破损里程累计已超过60 km,运营期盾构隧道结构安全已成为影响城市交通基础设施可持续发展的重要因素之一。
准确评估盾构隧道的结构性能是保证隧道结构安全的前提,目前研究中主要针对某一时刻隧道承载能力进行评估[5-6],较少关注扰动全过程隧道结构性能时变演化规律。韧性理论的提出和发展,极大丰富了基础设施安全评价的维度。Shadabfar等[7]将目前主要的基础设施韧性评估模型分为两类,基于显式性能函数的确定性评估模型和考虑不确定性因素影响的概率评估模型。在盾构隧道运维期韧性评估中,确定性模型应用的较广,例如Huang等[8]基于隧道水平收敛提出韧性指标,并在地面堆载案例中评估了隧道在扰动-加固全过程的韧性演变规律。林星涛等[9]、Lin等[10]结合隧道收敛、位移等变形指标提出了多次扰动下盾构隧道韧性评估理论模型。Zhang等[11]开展了隧道纵向接头足尺试验,并分析了隧道纵向接头的韧性发展规律[11]。但盾构隧道结构韧性指标的力学机理和演化规律尚不明确,限制了其在工程中的推广应用。
因此,本文建立了考虑历史最大变形的衬砌性能指标,并通过三维精细化有限元模型研究了堆卸载全过程不同埋深隧道衬砌性能和结构韧性的演化规律。
1. 盾构隧道韧性指标建立
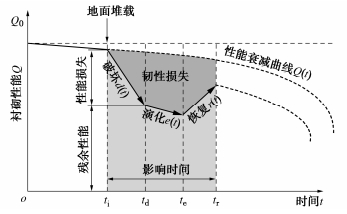
以地面堆载这种典型施工扰动为例,图 1为典型的隧道韧性评价框架[8-10],其中横坐标轴为时间t,纵坐标轴为隧道衬砌性能指标Q。受耐久性等因素影响,隧道性能下降曲线为Q(t)。ti为堆载开始时刻,ti~tr为堆载影响时间。其中,ti~td段为堆载引起隧道性能降低曲线d(t),td~te段为堆载发生后、措施采取前隧道性能的演化曲线e(t),te~tr段为采用修复措施后,隧道性能的恢复曲线r(t)。
地面堆载下隧道结构韧性定义为
Re = Sd+Se+Srtr−ti, (1) 其中,权重系数Sd,Se,Sr分别定义为
Sd=∫tdtid(t)dt∫tdtiQ(t)dt, (2) Se=∫tetde(t)dt∫tetdQ(t)dt, (3) Sr=∫trter(t)dt∫trteQ(t)dt。 (4) 确定合适的隧道性能指标Q是合理评估隧道结构韧性的关键。研究表明,地面堆载主要引起隧道横截面的变形,而隧道水平收敛作为反映衬砌结构性能的关键指标,可通过三维激光扫描、自动化全站仪进行监测,并且和接缝张开、螺栓应力等存在明显的相关性。此外,盾构隧道在受到历史因素影响产生较大变形时,管片结构发生的损伤不可恢复。即使采取注浆等回调措施减小结构变形,衬砌的承载能力仍会收到历史因素的影响而降低,结构性能函数应当考虑历史最大变形的影响。因此隧道性能指标定义为水平收敛的函数,表达式为
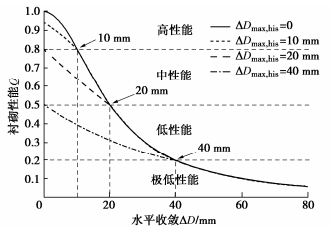
Q(t)={11+2.5×10−4(ΔD(t)+ΔDmax, his2)2 (ΔD(t)≤ΔDmax, his)11+2.5×10−4ΔD(t)2 (ΔD(t)>ΔDmax, his), (5) 式中:Q(t)为衬砌性能指标;ΔD(t)为隧道当前水平收敛值;ΔDmax, his为隧道历史水平收敛最大值(mm)。
图 2为根据式(5)绘制的衬砌性能Q随水平收敛ΔD的变化曲线。衬砌性能分为高、中、低和极低4个等级,其中高—中性能的分界点10 mm和中—低性能分界点20 mm分别为《城市轨道交通结构安全保护技术规范:CJJ/T202—2013》中规定的预警值和控制值[12]。根据已有的错缝拼装足尺管片试验和数值仿真结果[13],当隧道水平收敛超过40 mm后进入变形快速发展阶段,此时衬砌性能降为极低。
当采取回调措施使隧道水平收敛减小时,衬砌性能有一定程度的恢复,但无法完全恢复至初始状态。根据图 2中不同历史最大收敛变形下的衬砌性能曲线可知,当衬砌性能下降至某一等级时,通过变形回调措施最多能使性能恢复至上一等级。例如,处于低性能等级的衬砌(Q=0.2~0.5),性能恢复的上限为中性能(Q=0.5~0.8)。
2. 地面堆载下盾构隧道荷载-结构模型
将实际工况简化为两个阶段,第一阶段将初始水土压力和地面堆载等效为作用在隧道表面的为荷载,计算作用在隧道表面的附加应力;第二阶段将地层约束简化为非线性土弹簧,同时考虑管片螺栓和钢筋的影响,建立精细化的盾构隧道荷载-结构模型,分析地面堆载下隧道结构性能和韧性演化规律。
2.1 隧道结构模型
(1)管片环有限元模型
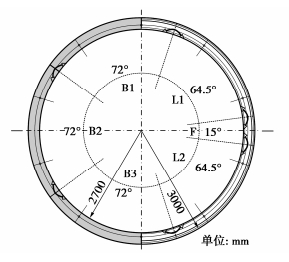
以深圳地铁1号线典型管片为研究对象,管片环结构如图 3所示。管片环外径6.0 m,厚度0.3 m,由3个标准块(B1、B2和B3),两个邻接块(L1和L2)以及1个封顶块(F)组成。管片接头采用M24螺栓连接,环间采用错缝拼接。
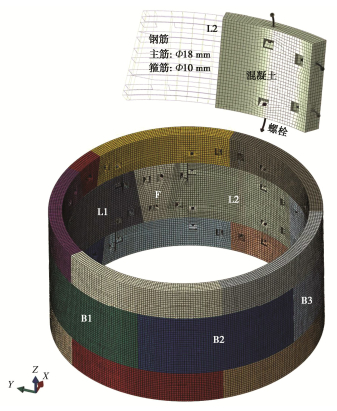
如图 4所示,建立包含混凝土管片、钢筋和螺栓的三环精细化有限元模型(1个整环+2个半环)。考虑到止水垫、压力垫等对结构整体受力模式影响较小,因此忽略上述部件,将环缝和纵缝接头简化为平面,以降低计算代价。模型的单元采用C3D8R,钢筋单元采用T3D2。
(2)材料参数
管片混凝土强度等级为C50,采用CDP本构模型,参数根据《混凝土结构设计规范:GB50010—2010)》确定[14],密度ρ为2400 kg/m3,弹性模量E为30 GPa,泊松比ν为0.2,膨胀角为40°,偏心率为0.1,fb0/fc0为1.16,K为0.6667,黏性参数为0.0005。其余参数见表 1。钢筋等级为HRB400,屈服强度400 MPa,极限强度500 MPa。螺栓采用8.8级高强螺栓,屈服强度640 MPa,极限强度800 MPa,未考虑螺栓预紧力的影响[15]。
表 1 C50混凝土CDP模型参数Table 1. CDP model parameters of C50 concrete屈服应力(压)/MPa 塑性应变 屈服应力(拉)/MPa 开裂应变 18.9 0 2.73 0 24.3 9.00×10-5 2.42 2.00 25.9 0.00012 2.02 5.00×10-5 28.5 0.00018 1.70 8.00×10-5 32.9 0.00048 1.45 0.0001 33.6 0.00072 1.26 0.00012 33.1 0.00091 1.12 0.00014 28.5 0.00155 1.01 0.00016 23.1 0.00221 0.91 0.00018 15.6 0.00344 0.78 0.00021 11.4 0.00457 0.46 0.00038 9.2 0.00548 0.39 0.00046 (3)相互作用
采用面-面接触模拟混凝土-混凝土、混凝土-螺栓之间的接触行为。法向为硬接触,切向罚函数,管片间的摩擦系数为0.5,螺栓和混凝土间的摩擦系数为0.3。接触面设置为有限滑动,允许值为0.005。螺栓端头和手孔采用绑定约束[15]。
(4)模型验证
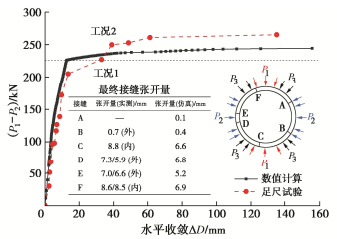
以深圳地铁1号线三环错缝管片环足尺加载试验进行算例验证。管片模型和荷载工况参见文献[16-18],如图 5所示,数值计算和足尺试验实测的水平收敛和接缝张开量变化规律一致,证明了所建立的隧道模型的准确性。在卸载工况2下,数值仿真的水平收敛增长速率明显快于足尺试验实测值,最终接缝张开量小于实测值。数值分析产生误差的主要原因包括:①采用的边界条件不能完全反映实际情况;②本构模型及参数与实际情况存在差异;③对管片接头进行了简化等。
2.2 结构荷载
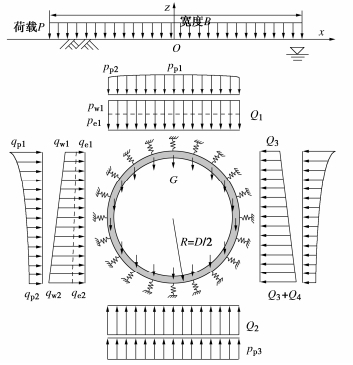
图 6为作用在隧道表面的结构荷载。隧道拱顶的竖向力为Q1,包含顶部所受的土压力pe1和孔隙水压力pw1;隧道顶部和底部所受的水平力分别为Q3和Q3+Q4,qe1和qe2分别为隧道顶部和底部的水平土压力,qw1和qw2为对应的孔隙水压力。G为隧道结构自重荷载,Q2为隧道底部的竖向反力。水土荷载具体计算方法可以参考文献[19]。
考虑地面堆载在隧道正上方、并且沿隧道纵向长条状分布的情况,荷载宽度B,大小为P,可简化为平面应变问题。本文参考Gao等[20]的研究,采用Flamant解的竖向附加应力ppz、水平附加应力qpx:
ppz=2π ∫B2−B2Pz3[z2+(x−ε)2]2dε, (6) qpx=2π ∫B2−B2Pz(x−ε)2[z2+(x−ε)2]2dε, (7) 计算隧道顶部和两侧的附加应力分布,并用多项式拟合后施加在有限元模型的隧道边界上。堆载卸除时,将对应的附加荷载减小至0。
2.3 土弹簧
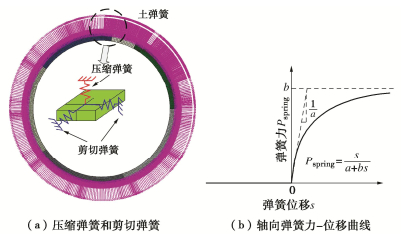
地层简化为与隧道相连的地弹簧,如图 7所示,在数值模型中,衬砌外表面的每个节点连接1个压缩弹簧和2个剪切弹簧。忽略土体受拉特性,因此压缩弹簧不承受拉力,受压段采用双曲非线性弹簧,弹簧力-位移关系如图 7(b)所示。根据节点周围的单元面积计算出压缩弹簧的刚度,剪切弹簧刚度取为压缩弹簧刚度的1/3[15]。本文重点探讨隧道结构损伤对隧道鲁棒性和恢复性的影响,未考虑土体塑性影响。
2.4 计算工况
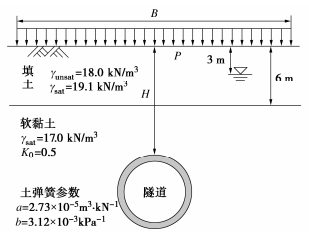
图 8为本文的算例。地层分填土层和软黏土层,填土层厚度6 m,天然重度为18.0 kN/m3,饱和重度为19.1 kN/m3;软黏土层饱和重度为17.0 kN/m3,水平侧压力系数K0=0.5,地下水位深度为3 m。隧道埋深为H,正上方作用有宽度B=12 m,大小P的长条形堆载。表 2汇总了计算工况,考虑浅埋H=D和深埋H=3D两种情况。计算分3个步骤:第一步施加水土压力和结构自重;第二步施加地面堆载;第三步卸除地面堆载。土弹簧参数根据文献[21]中淤泥质黏土参数选取,考虑到堆载工况下影响隧道断面安全的主要变形因素为水平收敛,地层水平抗力起控制性作用,因此,参数a,b主要通过扁铲侧胀试验等反演获得。
表 2 计算工况Table 2. Calculation conditions序号 H/m 堆载/kPa S01 6 0→180→0 S02 0→225→0 S03 0→252→0 S04 0→279→0 S05 0→288→0→256 D01 18 0→315→0 D02 0→396→0 D03 0→450→0 D04 0→477→0 D05 0→486→0→436 3. 堆卸载全过程隧道结构响应特征
3.1 衬砌整体变形
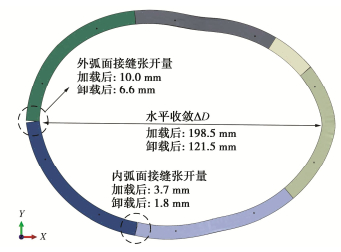
以工况S05为例分析地面堆卸载全过程衬砌结构响应。图 9为工况S05中间环的整体变形,在地面堆载P=288 kPa(对应16 m填土高度)作用下,隧道向扁椭圆形状发展,堆载后的水平收敛值为198.5 mm;由于堆载量较大,卸载阶段隧道变形难以完全恢复,完全卸载后的水平收敛为121.5 mm,恢复率仅为38.8%。堆载引起了拱顶和拱底内弧面接缝张开,最大张开位置为左侧拱底,堆载完张开量为3.7 mm,完全卸载后恢复至1.8 mm;两侧拱腰处外弧面张开,最大张开位置位于左侧拱腰,堆载完张开量为10.0 mm,完全卸载后恢复至6.6 mm。由于模型的边环和中间环封顶块位置全部位于右上位置,右半环接缝数量多,刚度较弱,并且在大变形阶段土弹簧刚度衰减较快,因此右半环整体变形相对较大。
3.2 衬砌结构内力
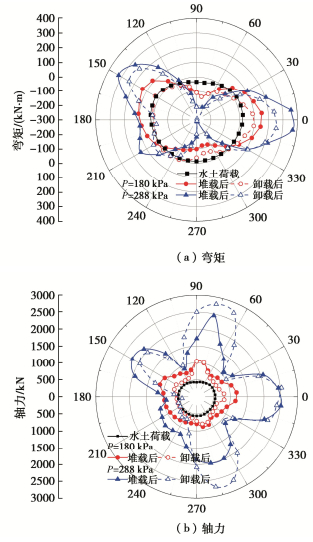
图 10为隧道埋深6 m时中间环管片的弯矩和轴力变化图,其中弯矩以外侧受拉为正,轴力以受压为正。在初始水土压力作用下,拱顶、拱底内弧面受拉,两侧拱腰外弧面受拉;拱顶处轴力较小,其余位置轴力基本一致。而地面堆载会引起管片内力的显著增大。拱顶、拱底位置进一步受压,两侧拱腰处进一步受拉。由于接缝处刚度整体偏弱,受到管片错缝拼装的影响,弯矩在环缝间传递,导致边环接缝对应位置(0°,64.5°,79.5°,144°,216°,288°)的中间环管片弯矩值大幅增加,中间环接缝位置(28.5°,43.5°,108°,180°,252°,324°)的管片弯矩值相对较小。随着堆载增大,接头刚度减弱,导致弯矩进一步向管片集中。轴力的变化趋势和弯矩较为类似,在拱顶、拱底和两侧拱腰轴力增长较为明显。受错缝拼装影响,边环接缝处对应的中环轴力大幅增加,中环接缝位置附近的轴力增长幅度较小,差值随着地面堆载的增加而增大。
当堆载全部卸除时,两侧拱腰弯矩减小。P=180 kPa工况下,卸载后拱底弯矩减小,拱顶弯矩几乎不变;P=288 kPa工况下,卸载前后拱底弯矩几乎不变,拱顶弯矩显著增加。卸载引起拱腰处的轴力整体减小。堆载P=180 kPa工况下,拱顶、拱底的轴力几乎不变,而堆载P=288 kPa工况下,拱顶、拱底的轴力显著增加。当堆载值较大时,隧道拱顶受压下凹成“M形”,拱顶接缝张开量快速增大,边环拱顶接头承载能力大幅降低,侧向水土压力集中作用于中环拱顶的管片上,造成局部弯矩和轴力进一步增加。
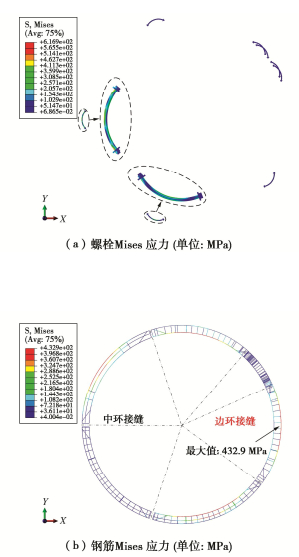
图 11为S05工况堆载后中间环螺栓和钢筋的应力云图,可以看出由于中间环大部分接缝位于斜向位置,张开量不大,因此螺栓未达到屈服应力640 MPa。左侧拱腰处外弧面张开量较大,引起螺栓外侧受拉较为明显;左侧拱底处内弧面张开量较大,因此螺栓主要为内侧受拉。拱顶、拱底内侧和拱腰外侧钢筋整体受力较大,但在中间环接缝处,由于接头可以产生较大变形,钢筋受力不大;在边环接缝位置,受错缝拼装弯矩传递效应的影响,钢筋内力显著增加。钢筋Mises应力最大值出现在右侧拱腰处,发生受拉屈服。
3.3 衬砌结构损伤
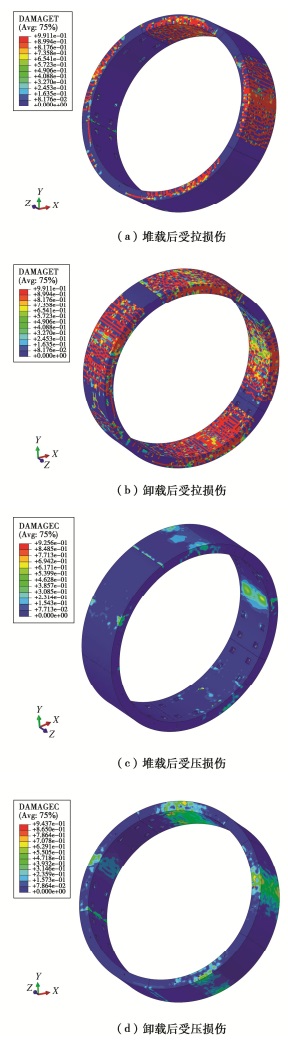
图 12为工况S05堆卸载全过程中间环的损伤分布云图。
拱顶、拱底的内弧面和两侧拱腰的外弧面产生较大的受拉损伤,而拱顶、拱底外弧面和拱腰内弧面的受压损伤较大,受错缝拼装影响损伤集中于边环接缝对应的位置,这与管片内力和钢筋应力的结果一致。卸载阶段管片损伤进一步发展。特别是受拉损伤贯穿拱顶和拱腰位置。主要原因是结构在加载阶段已发生较大的塑性变形和损伤,并且接头承载能力的丧失导致卸载时结构应力重分布。
4. 堆卸载全过程隧道韧性演化规律
4.1 衬砌性能曲线
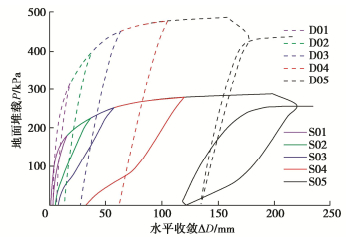
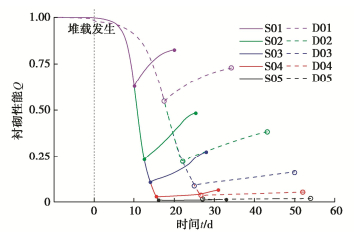
图 13为不同埋深条件下,隧道水平收敛随地面堆载的变化曲线。加载阶段随着水平收敛值逐渐增大,拱腰处土弹簧提供的水平反力逐渐趋近于极限值,结构侧向约束力的增长难以支撑竖向堆载的增加,导致变形速率逐渐增大直至结构失稳。相同地面堆载条件下,深埋隧道相比浅埋隧道的水平收敛增量更小,这是因为堆载宽度有限,随着深度增大,地面堆载引起的附加荷载逐渐减小。
当地面堆载完全卸除时,隧道结构水平收敛无法完全恢复,存在一定的残余变形,并且随着堆载值的增加,完全卸载后的残余变形增大。由于模型未考虑土体塑性变形,因此残余变形可以认为是隧道管片、接头塑性和结构内力重分布引起的结构塑性变形。另外,如S05和D05所示,当堆载使结构接近极限状态时,卸载初期结构水平收敛仍会持续增大,这与郑光辉等[17]、王康任等[18]整环足尺试验实测曲线一致。原因是极限状态下,隧道接头已发生很大的塑性变形,此时卸载将会引起结构内力的调整,使变形进一步发展。S05和D05两组工况卸载完再加载时隧道极限荷载均有减小,表明初次加卸载循环已经使结构发生较为严重的损伤,使结构极限承载力有所降低。浅埋隧道卸载-再加载的滞回圈更大,表明结构耗能更大,在卸载-再加载段的损伤更加严重。
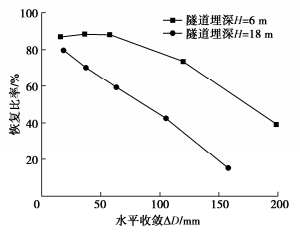
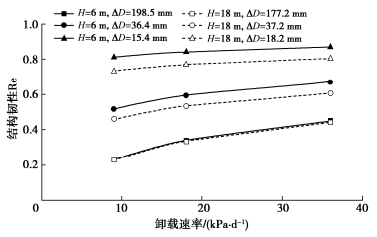
图 14为加载至不同水平收敛值后,卸载引起的隧道水平收敛恢复比率。隧道埋深H=6 m,当水平收敛小于60 mm时,卸载后水平收敛的恢复比率稳定在90%左右,随着水平收敛值进一步增大至198.5 mm,恢复比率逐渐下降至38.8%;隧道埋深H=18 m时,当水平收敛从18.2 mm增大至158.2 mm时,卸载后恢复比率从80%下降至15%。深埋隧道初始水土荷载更大,结构损伤后变形更难恢复。
假定堆载速率vld、卸载速率vud均为18 kPa/d(对应土层高度1 m/d),绘制如图 15所示的衬砌性能演化曲线。在初始水土压力施加完毕后,t=0为堆载开始时间,堆载、卸载总时长相等。堆载初期衬砌性能下降较慢,随着堆载量逐渐增加,衬砌性能快速下降,浅埋隧道相比深埋隧道衬砌性能下降更早,速率也更快。卸载阶段衬砌性能有所恢复,并且当堆载量较小时,衬砌性能恢复到较高水平。随着堆载量逐渐增大,衬砌性能恢复程度有所降低。当衬砌水平收敛增大至接近极限时(超过150 mm),卸载使衬砌性能几乎无恢复。在堆载使衬砌性能降低相同幅度的情况下,卸载后埋深较浅的隧道性能恢复幅度更大。
4.2 隧道结构韧性曲线
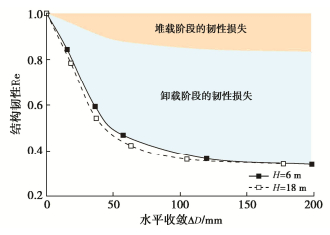
图 16为堆载、卸载速率均为18 kPa/d下的隧道结构韧性随堆载后水平收敛的变化曲线。随着堆载引起水平收敛值增大,隧道结构韧性显著下降。不同埋深下的隧道结构韧性变化趋势类似,但埋深较大时韧性较低。图中阴影部分分别表示堆载和卸载阶段韧性损失的占比,随着堆载引起的水平收敛值增大,堆载、卸载阶段的韧性损失均有所增加;由于卸载阶段衬砌性能处于较低水平且无法完全恢复,卸载阶段的韧性损失更大。
(1)响应时间对韧性的影响
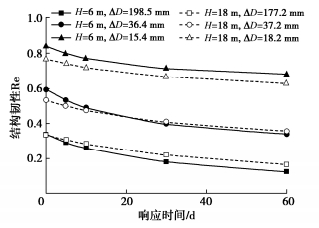
假定响应时间内衬砌性能保持不变,图 17为响应时间(灾害发生后到采取措施之间的时间)对隧道结构韧性的影响曲线。随着响应时间增加,隧道结构韧性显著降低,当响应时间超过60 d时,隧道结构韧性降幅约为0.2。响应时间对埋深较浅的隧道韧性影响较大,这是由于埋深较浅的隧道对堆载更加敏感,响应时间在总影响时间的占比更大。此外,响应时间内周围地层持续变形、衬砌内部损伤累积发展等因素会造成隧道结构韧性进一步下降,因此建立应对突发状况的快速响应机制十分重要。
(2)卸载速率对韧性的影响
保持堆载速率为18 kPa/d不变,图 18为卸载速率对隧道结构韧性的影响曲线。当卸载速率增加时,结构韧性逐渐提高,即快速修复对提升结构韧性有利,并且堆载荷载越大,卸载速率对结构韧性的影响越显著。这是因为随着堆载增大,结构损伤更加严重,恢复能力降低,卸载阶段持续越长,对结构韧性的影响越大。
4.3 韧性指标分级
结合上述分析结果,将地面堆载下隧道结构韧性分为4个级别:①高韧性(Re≥0.9):结构变形不超过规范预警值,衬砌性能整体位于高性能区间,结构恢复性能好,结构处于安全状态。②中韧性(0.8≤Re<0.9):结构变形未超过规范控制值,在外部作用影响时段内,衬砌性能整体处于高、中性能区间,结构安全风险低,应及时卸除地面堆载,一般无需进行结构加固;③低韧性(0.6≤Re<0.8)。结构变形超过规范控制值,在外部作用影响时段内,衬砌性能整体处于中、低性能区间,恢复性能变差,韧性指标加速下降,结构安全风险高。应尽快卸除地面堆载,并采取必要的地层和结构加固措施。④极低韧性(Re<0.6):结构变形大幅超过规范控制值,变形快速发展,在外部作用影响时段内,衬砌性能处于极低性能区间,恢复能力大幅减弱至丧失,此时进行侧向注浆、顶部卸载时可能造成隧道结构的二次损伤。应结合地层、结构情况,尽快采取合理的综合加固修复措施。
需要注意的是,本文采用的韧性指标阈值为基于结构性能曲线,通过有限元进行各工况的计算获得,更加合理的阈值取值则需要通过大量理论计算和工程案例反演来完善。
5. 结论
本文提出了地面堆载下盾构隧道衬砌性能指标,并通过三维精细化有限元模型,研究了不同埋深盾构隧道在地面堆卸载过程中结构响应和韧性演化规律,得到以下4点结论。
(1)建立了考虑历史最大变形的衬砌性能指标,以水平收敛0~10,10~20,20~40, > 40 mm将衬砌性能分为高性能、中性能、低性能和极低性能4个等级。
(2)堆载阶段,拱顶、拱底内弧面和拱腰外弧面产生受拉损伤,拱腰内弧面产生受压损伤,受错缝拼装影响,边环接缝对应的中间环位置损伤更为集中。
(3)卸载阶段隧道结构水平收敛无法完全恢复,并且随着堆载值的增加,完全卸载后的残余变形增大,浅埋隧道卸载后水平收敛恢复量大于深埋隧道。当隧道水平收敛接近极限值时,卸载或侧向注浆可能造成结构的二次损伤。
(4)快速响应并采取高效修复措施有利于提高隧道韧性。随着隧道性能的降低,对加固修复措施合理性及时效性要求更高,大变形下多种加固方式对隧道结构的影响规律有待进一步研究。
-
表 1 C50混凝土CDP模型参数
Table 1 CDP model parameters of C50 concrete
屈服应力(压)/MPa 塑性应变 屈服应力(拉)/MPa 开裂应变 18.9 0 2.73 0 24.3 9.00×10-5 2.42 2.00 25.9 0.00012 2.02 5.00×10-5 28.5 0.00018 1.70 8.00×10-5 32.9 0.00048 1.45 0.0001 33.6 0.00072 1.26 0.00012 33.1 0.00091 1.12 0.00014 28.5 0.00155 1.01 0.00016 23.1 0.00221 0.91 0.00018 15.6 0.00344 0.78 0.00021 11.4 0.00457 0.46 0.00038 9.2 0.00548 0.39 0.00046 表 2 计算工况
Table 2 Calculation conditions
序号 H/m 堆载/kPa S01 6 0→180→0 S02 0→225→0 S03 0→252→0 S04 0→279→0 S05 0→288→0→256 D01 18 0→315→0 D02 0→396→0 D03 0→450→0 D04 0→477→0 D05 0→486→0→436 -
[1] 邵华, 黄宏伟, 张东明, 等. 突发堆载引起软土地铁盾构隧道大变形整治研究[J]. 岩土工程学报, 2016, 38(6): 1036-1043. doi: 10.11779/CJGE201606009 SHAO Hua, HUANG Hongwei, ZHANG Dongming, et al. Case study on repair work for excessively deformed shield tunnel under accidental surface surcharge in soft clay[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(6): 1036-1043. (in Chinese) doi: 10.11779/CJGE201606009
[2] 朱旻, 陈湘生, 王雪涛. 盾构隧道衬砌结构性能演化分析与思考[J]. 工程力学, 2022, 39(3): 33-50. ZHU Min, CHEN Xiangsheng, WANG Xuetao. Analysis and thinking on structural performance evolution of shield tunnel lining[J]. Engineering Mechanics, 2022, 39(3): 33-50. (in Chinese)
[3] 梁荣柱, 曹世安, 向黎明, 等. 地表堆载作用下盾构隧道纵向受力机制试验研究[J]. 岩石力学与工程学报, 2023, 42(3): 736-747. LIANG Rongzhu, CAO Shian, XIANG Liming, et al. Experimental investigation on longitudinal mechanical mechanism of shield tunnels subjected to ground surface surcharge[J]. Chinese Journal of Rock Mechanics and Engineering, 2023, 42(3): 736-747. (in Chinese)
[4] 王如路, 张冬梅. 超载作用下软土盾构隧道横向变形机理及控制指标研究[J]. 岩土工程学报, 2013, 35(6): 1092-1101. http://cge.nhri.cn/cn/article/id/15080 WANG Rulu, ZHANG Dongmei. Mechanism of transverse deformation and assessment index for shield tunnels in soft clay under surface surcharge[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(6): 1092-1101. (in Chinese) http://cge.nhri.cn/cn/article/id/15080
[5] LI X J, LIN X D, ZHU H H, et al. Condition assessment of shield tunnel using a new indicator: the tunnel serviceability index[J]. Tunnelling and Underground Space Technology, 2017, 67: 98-106. doi: 10.1016/j.tust.2017.05.007
[6] CHEN X Q, LI X J, ZHU H H. Condition evaluation of urban metro shield tunnels in Shanghai through multiple indicators multiple causes model combined with multiple regression method[J]. Tunnelling and Underground Space Technology, 2019, 85: 170-181. doi: 10.1016/j.tust.2018.11.044
[7] SHADABFAR M, MAHSULI M, ZHANG Y, et al. Resilience-based design of infrastructure: review of models, methodologies, and computational tools[J]. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering, 2022, 8(1): 03121004. doi: 10.1061/AJRUA6.0001184
[8] HUANG H W, ZHANG D M. Resilience analysis of shield tunnel lining under extreme surcharge: characterization and field application[J]. Tunnelling and Underground Space Technology, 2016, 51: 301-312. doi: 10.1016/j.tust.2015.10.044
[9] 林星涛, 陈湘生, 苏栋, 等. 考虑多次扰动影响的盾构隧道结构韧性评估方法及其应用[J]. 岩土工程学报, 2022, 44(4): 591-601. doi: 10.11779/CJGE202204001 LIN Xingtao, CHEN Xiangsheng, SU Dong, et al. Evaluation method for resilience of shield tunnel linings considering multiple disturbances and its application[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(4): 591-601. (in Chinese) doi: 10.11779/CJGE202204001
[10] LIN X T, CHEN X S, SU D, et al. An analytical model to evaluate the resilience of shield tunnel linings considering multistage disturbances and recoveries[J]. Tunnelling and Underground Space Technology, 2022, 127: 104581. doi: 10.1016/j.tust.2022.104581
[11] ZHANG Y J, SAADAT Y, HUANG H W, et al. Experimental study on deformational resilience of longitudinal joint in shield tunnel lining[J]. Structure and Infrastructure Engineering, 2022: 1-12.
[12] 城市轨道交通结构安全保护技术规范: CJJ/T 202—2013[S]. 北京: 中国建筑工业出版社, 2014. Technical Code for Protection Structures of Urban Rail Transit: CJJ/T 202—2013[S]. Beijing: China Architecture & Building Press, 2014. (in Chinese)
[13] LIU X, ZHANG Y M, BAO Y H. Full-scale experimental investigation on stagger effect of segmental tunnel linings[J]. Tunnelling and Underground Space Technology, 2020, 102: 103423. doi: 10.1016/j.tust.2020.103423
[14] 混凝土结构设计规范: GB50010—2010[S]. 2015. Code for Design of Concrete Structures: GB50010—2010[S]. 2015. (in Chinese)
[15] SU D, CHEN W J, WANG X T, et al. Numerical study on transverse deformation characteristics of shield tunnel subject to local soil loosening[J]. Underground Space, 2022, 7(1): 106-121. doi: 10.1016/j.undsp.2021.07.001
[16] 刘钊. 复杂工况条件下错缝拼装盾构管片变形性能试验与仿真分析研究[D]. 北京: 中国铁道科学研究院, 2017. LIU Zhao. Shield Segment Deformation Performance Test and Simulation Analysis under Complicated Working Condition[D]. Beijing: China Academy of Railway Sciences, 2017. (in Chinese)
[17] 郑光辉, 庞小朝, 王康任. 基于整环足尺试验的盾构隧道破坏机制及纵缝外弧面变形分析[J]. 隧道建设(中英文), 2021, 41(S2): 165-171. ZHENG Guanghui, PANG Xiaochao, WANG Kangren. Failure mechanism of shield tunnel based on full-scale experiment and analysis of longitudinal joint's outboard deformation[J]. Tunnel Construction, 2021, 41(S2): 165-171. (in Chinese)
[18] 王康任, 庞小朝, 刘树亚, 等. 复杂荷载条件下错缝拼装盾构隧道受力性能及结构安全指标研究[J]. 现代隧道技术, 2018, 55(增刊2): 588-598. WANG Kangren, PANG Xiaochao, LIU Shuya, et al. Study on mechanical performances and structural safety index of stagger-jointed shield tunnel under complex load conditions[J]. Modern Tunnelling Technology, 2018, 55(S2): 588-598. (in Chinese)
[19] 魏纲, 洪文强, 魏新江, 等. 偏心堆载引起的盾构隧道横向受力理论计算[J]. 中南大学学报(自然科学版), 2019, 50(7): 1645-1654. WEI Gang, HONG Wenqiang, WEI Xinjiang, et al. Theoretical calculations of transverse force on shield tunnel caused by eccentric load[J]. Journal of Central South University (Science and Technology), 2019, 50(7): 1645-1654. (in Chinese)
[20] GAO X, WANG H N, JIANG M J. Analytical solutions for the displacement and stress of lined circular tunnel subjected to surcharge loadings in semi-infinite ground[J]. Applied Mathematical Modelling, 2021, 89: 771-791. doi: 10.1016/j.apm.2020.07.061
[21] 王洪新, 李雪强, 杨石飞, 等. 应用于基坑围护结构变形计算的非线性土体弹簧模型及参数研究[J]. 岩土工程学报, 2020, 42(6): 1032-1040. doi: 10.11779/CJGE202006006 WANG Hongxin, LI Xueqiang, YANG Shifei, et al. Nonlinear soil spring model and parameters for calculating deformation of enclosure structure of foundation pits[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(6): 1032-1040. (in Chinese) doi: 10.11779/CJGE202006006
-
期刊类型引用(7)
1. 张陈龙,张东明,黄忠凯,黄宏伟. 考虑地震强度不确定性的车站韧性评估方法. 岩土工程学报. 2025(01): 164-172 .  本站查看
本站查看
2. 赵千,陈湘生,胡明伟,韩凯航,苏栋. 基于网络演化的城市轨道交通系统关键站点识别. 市政技术. 2025(02): 1-9 .  百度学术
百度学术
3. 姜海波. 盾构隧道结构有限元计算中的外荷载模拟方式研究. 市政技术. 2025(03): 209-214 .  百度学术
百度学术
4. 董侨 ,杜豫川 ,郭猛 ,黄优 ,贾彦顺 ,蒋玮 ,金娇 ,李峰 ,刘成龙 ,刘鹏飞 ,刘状壮 ,罗雪 ,吕松涛 ,马涛 ,沙爱民 ,单丽岩 ,司春棣 ,王朝辉 ,王大为 ,肖月 ,徐慧宁 ,杨旭 ,张久鹏 ,张园 ,朱兴一. 中国路面工程学术研究综述·2024. 中国公路学报. 2024(03): 1-81 .  百度学术
百度学术
5. 刘力英,杨春山,喻志远,欧振锋. 附加荷载作用下隧道结构力学响应与韧性演化特征. 现代隧道技术. 2024(05): 167-173+233 .  百度学术
百度学术
6. 林双燕,魏纲,徐天宝,金子原,周彦臣. 堆载下折叠加固盾构隧道受力特性研究. 低温建筑技术. 2024(12): 97-101 .  百度学术
百度学术
7. 王剑宏,夏志鹏,杨华,孟立夫,牛余朋. 海底盾构隧道结构韧性安全性能评价研究. 土木工程学报. 2024(S1): 65-71 .  百度学术
百度学术
其他类型引用(4)
-
其他相关附件



 下载:
下载: