0.   引言

实际工程中的岩土类材料处于复杂的应力状态，对于其中一个立方体单元而言，不仅荷载大小会随时间变化，同时荷载的方向也会处于时变状态^[1]。从主应力观察的角度出发，当土单元体的沉积方向与外荷作用方向不一致时，则主应力空间的破坏面随应力主轴发生旋转，应力主轴旋转将会导致岩土体产生明显的塑性变形，最终导致结构破坏。主应力轴旋转在实际工作状态中的岩土体中随处可见，比如黄土路基地层中的土单元体受到交通荷载作用；水库的堤坝下的土体单元，随着蓄水及放水的变化，堤坝下地基土体单元也承受着主应力轴旋转作用等。另一方面，从微观结构观察的角度看，土颗粒在天然沉积或人工填筑过程中，受重力的作用颗粒之间相互滑动，往往会呈现出一定的排列规律，在水平方向上颗粒的长轴方向通常平行于沉积方向，形成稳定排列状态，表现为显著的横观各向同性，故可以把土视为横观各向同性、纵观各向异性的材料^[2]。通过大量的现场和室内试验测试表明，采用横观各向同性土体来描述原状水平场地是适宜的。

外荷载作用下，土颗粒之间的接触方式发生改变，原有的定向排列状态被打乱，形成另一种定向排列状态，在宏观上表现为应力诱导各向异性特性。各向异性对于岩土材料应力–应变关系的影响在实际岩土工程中具有现实的工程背景，比如土石坝工程中的黄土单元体，在大主应力方向加荷所产生的小主应力方向的侧向变形，与小主应力方向加荷引起大主应力方向的侧向应变有很大差异，这就意味着两个方向的泊松比有很大差异，而目前土石坝有限元计算所采用模型参数多依据常规三轴试验结果，泊松比是大主应力方向加荷测得的，数值较大，而在水库蓄水时，水荷载是在小主应力方向施加，实际泊松比要小的多。各向异性对实际工程的变形和稳定性同样具有较大影响。王林等^[3]开展常规三轴试验分析东京地区沉积软岩3个方向的变形和强度特性差异，表明现场水平方向的弹性模量和抗压强度要比垂直方向的大约30%。Oda等^[4]通过微观量测发现，土体沉积时颗粒长轴定向排列形成的这种沉积结构在后期加载过程中变化甚微，该模型试验也证实，不考虑地基土的强度时，各向异性可能会导致过高估计地基承载力30%~50%，使得工程设计偏于危险。殷宗泽^[5]针对面板堆石坝中堆石体侧膨胀性对面板受力影响的有限元分析表明，堆石体泊松比由0.1变化到0.4时，面板中的拉应力将增加40%左右，其中各向异性是引起堆石体侧膨胀性发生变化的主要因素之一。

显然，将岩土材料视为均质、各向同性的材料，在此基础上，将其在某个特定应力水平条件下表现出的复杂的应力状态和应变状态借助于各向同性理论进行简单描述，而忽视材料的各向异性影响，将会得到与实际不符的计算结果，也将导致实际工程无法容忍的灾变结果。

适应于一般应力条件下的各向异性强度准则应该能够反映中主应力的影响，同时反映应力空间域的空间面变化。现有的各向同性强度准则中Matsuoka等^[6]提出的空间滑动面(SMP)准则和Lade-Duncan准则^[7]对中主应力对强度影响描述较好的准则之一。且空间滑动面准则具有明确的物理意义^[8]。宋美娜^[9]在广义非线性强度理论基础上加入一个各向异性参数，得到主应力空间的强度变化规律。李学丰等^[10]采用宏细观相结合的方法，沿用Li等^[11]和Dafalias等^[12]提出的采用组构张量和应力张量联合定义反映各向异性程度的各向异性状态变量，提出了一个新的各向异性状态变量，然后将该变量应用到广义Mohr-Coulomb（M-C）各向同性破坏准则中形成一个各向异性破坏准则，使用多组各向异性砂土试验以验证破坏准则和该方法的合理性。虽然这些准则的提出具有一定的理论基础，但大多缺乏试验支撑，模型参数复杂，因此对实际的各向异性材料模拟过程中还存在很多的缺陷。姚仰平等^[13]通过分析横观各向同性土的经验规律，克服了组构张量法应用于三轴压缩条件下的不足，建立了峰值强度表达式，进而建立横观各向同性强度准则，并通过Santa Monica海滩砂土和San Francisco海湾黏土真三轴试验数据验证了该准则的合理性。同年，姚仰平等^[14]为反映各向异性的影响，改进应力张量提出各向异性土的破坏准则。而后，又在修正剑桥模型的基础上，通过引入统一硬化参数，建立UH模型及UH系列模型^[15-16]。该准则和本构模型的提出主要是通过各向异性转换应力的方法对不同方向的应力分量修正的思路，而本文则是通过研究八面体面主应力空间域强度变化与空间滑动面以及应力状态三者之间的关系，推广空间滑动面概念，提出一种考虑岩土材料的空间滑动面随着空间应力域应力条件变化的横观各向同性破坏准则。该准则不再受主应力空间和物理空间限制，可以对一般应力状态下的横观各向同性岩土材料的强度变化规律进行描述，为实际工程问题分析中考虑横观各向同性提供理论参考。

1.   基于空间面变化的横观各向同性土强度参数

1.1   应力空间域的应力状态变化

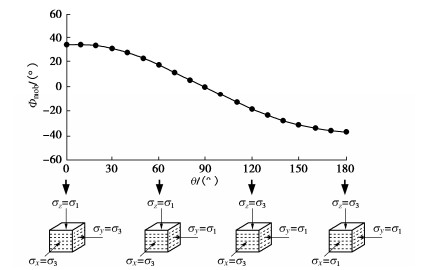
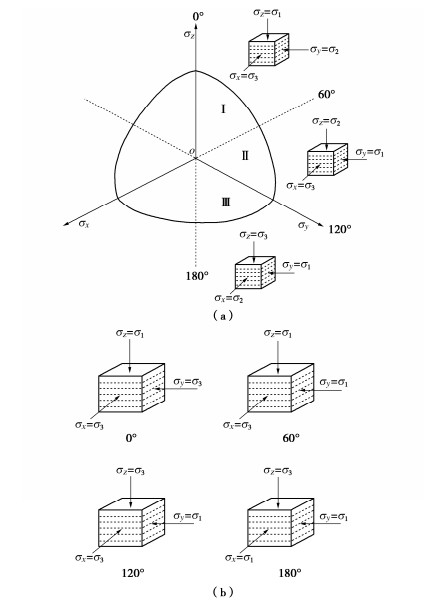
考虑实际物理空间与应力空间的有效对应，对反映结构性土各向异性与强度、变形特性之间的内在关系，揭示各向异性的数学描述和物理意义等有着至关重要的影响。故采用坐标（$z，y，x$）来表征天然沉积作用影响的原状土物理空间方位，如（${\sigma }_{z}，$ ${\sigma }_{y}，{\sigma }_{x}$）分别表示与沉积面垂直的面为Z轴方向作用主应力、与沉积面平行的面为正交Y轴方向作用主应力和与沉积面平行的另一面为正交X轴方向作用主应力，它们所代表的沉积面与应力状态可以绘制在八面体应力空间内。对于横观各向同性土，如图 1（a）所示，应力主轴${\sigma }_{z}，{\sigma }_{y}，{\sigma }_{x}$将π平面空间分割为3个象限，若定义顺时针方向径向偏角$\theta$为正，Ⅰ，Ⅱ，Ⅲ象限可分别表示为$\theta \in [{0}^{\circ }，{60}^{\circ }]$，$\theta \in [{60}^{\circ }，{120}^{\circ }]$和$\theta \in [{120}^{\circ }，{180}^{\circ }]$，显然地，3个象限所对应的应力条件可表示为Ⅰ（${\sigma _z} \gt {\sigma _y} \gt {\sigma _x}$），Ⅱ（${\sigma _y} \gt {\sigma _z} \gt {\sigma _x}$），Ⅲ（${\sigma _y} \gt {\sigma _x} \gt {\sigma _z}$）。图 1（b）给出对应象限土的应力状态与沉积面关系。例如：应力主轴${\sigma _z}$正、负半轴分别代表径向偏角$\theta =$0°和$\theta =$180°，对应大主应力${\sigma _1}$作用于垂直沉积面${\sigma _z}$方向的三轴压缩应力状态和小主应力${\sigma _3}$作用于垂直沉积面${\sigma _z}$方向的三轴挤伸应力状态；应力主轴${\sigma _x}$负半轴代表径向偏角$\theta =$60°，对应小主应力${\sigma _3}$作用于沉积面${\sigma _x}$方向的三轴挤伸应力状态；应力主轴${\sigma _y}$正半轴代表径向偏角$\theta =$120°，对应大主应力${\sigma _1}$作用于沉积面${\sigma _y}$方向的三轴压缩应力状态。

图  1  主应力状态与八面体应力空间的关系

Figure  1.  Relationship between principal stress state and spatial domain of octahedral stress

下载: 全尺寸图片 幻灯片

1.2   空间滑动面与应力状态关系

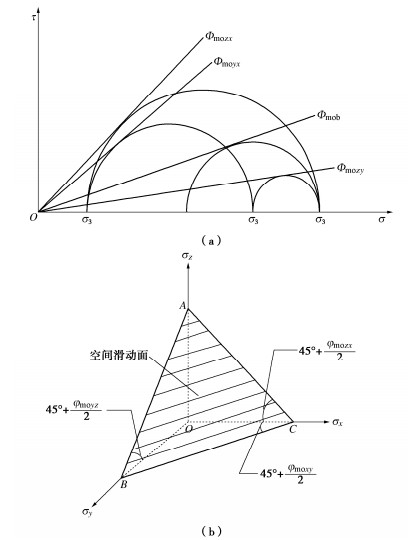
岩土材料强度破坏时主应力单元内存在一个潜在空间滑动面，往往通过假定该面上的应力条件服从特定的规律而建立强度准则。常见的描述各向同性材料的Drucker-Prager弹塑性模型的屈服准则，确立的滑动面方向余弦为$(\sqrt{3}/3，\text{ }\sqrt{3}/3，\text{ }\sqrt{3}/3)$，其滑动面为静法向滑动面，滑动面形态不随破坏应力${\sigma }_{1}，{\sigma }_{2}，{\sigma }_{3}$和材料特性变化而变化；Mohr-Coulomb准则确立的滑动面方向余弦为$(\mathrm{cos}[{45}^{\circ }+\varphi /2]，\text{ }0，\text{ }\mathrm{cos}[{45}^{\circ }-\varphi /2])$，其滑动面为动法向滑动面，滑动面形态仅与材料抗剪强度有关；而SMP强度准则由于具有明确的物理意义且考虑了中主应力的影响被广泛应用于实际工程中，它所确立的滑动面方向余弦为$\left(\sqrt{\frac{{I}_{3}}{{\sigma }_{1}{I}_{2}}}，\sqrt{\frac{{I}_{3}}{{\sigma }_{2}{I}_{2}}}，\sqrt{\frac{{I}_{3}}{{\sigma }_{3}{I}_{2}}}\right)$，其滑动面同样为动法向滑动面，滑动面形态仅随破坏应力${\sigma }_{1}，$ ${\sigma }_{2}，{\sigma }_{3}$变化而变化，与材料特性无关。而实际各向异性土单元的空间滑动面达到极限平衡状态时所处的应力状态不仅与土体性质和应力状态有关，同时所处应力状态随着应力空间变化。例如：轴对称压缩条件下滑动面与主应力夹角为${45^ \circ } + \varphi /2$，轴对称挤伸条件下滑动面与主应力夹角改变为${45^ \circ } - \varphi /2$，当滑动面与主应力夹角为45°为八面体面，因此广义空间滑动面与主应力轴夹角并非定值，而是在${45^ \circ } + \varphi /2$~${45^ \circ } - \varphi /$$2$内变化。

1.3   基于空间滑动面变化的横观各向同性强度参数确定

空间滑动面准则是物体所处应力状态的综合表征，有明确的物理意义^[8]，其表达式的获得是基于两个重要假定：①空间滑动面与${\sigma _i}o{\sigma _j}$平面交线为直线；②空间滑动面与${\sigma _i}o{\sigma _j}$平面交线与应力主轴${\sigma _i}{\sigma _j}$组成的三角形的夹角为$\frac{{{\rm{ \mathsf{ π} }}}}{4} + \frac{{{\varphi _{ij}}}}{2}$（$i, j = 1, 2, 3$）。基于这两个假定得到空间滑动面上的剪应力和法向应力之比为某一常数（$\frac{{{\tau _{{\text{SMP}}}}}}{{{\sigma _{{\text{SMP}}}}}} = {k_{\text{f}}}$），认为材料发生强度破坏。显然，这两个假定与实际土体非线性强度特性不符，仅反映了材料强度的中主应力效应以及三维空间摩擦效应，本文沿用SMP准则材料破坏取决于最大剪应力比${(\tau /\sigma )_{\max }}$的思想，在其考虑中主应力效应的基础上，充分考虑不同应力状态下Mohr圆的切线角，丰富了SMP准则在反映空间域单一强度变化的缺陷，以期反映实际土体非线性强度特性。故将不同应力状态下Mohr圆的切线角为最大强度发挥角${\varPhi _{{\text{mob}}}}$，${\varPhi _{{\text{mob}}}}$为反映应力条件和材料特性的综合参量，考虑不同应力状态下${\sigma _z} - {\sigma _y}$，${\sigma _y} - {\sigma _x}$，${\sigma _z} - {\sigma _x}$应力平面可以得到对应的强度发挥角${\varPhi _{{\text{mozy}}}}$，${\varPhi _{{\text{moyx}}}}$，${\varPhi _{{\text{mozx}}}}$，见图 2（a）。定义与最大主应力面呈$\frac{{{\rm{ \mathsf{ π} }}}}{4} + \frac{{{\varPhi _{{\text{mob}}}}}}{2}$角的面，为最大强度发挥面，则不同应力域的3个最大强度发挥面在空间内所形成的3条线形成的一个平面，为空间强度发挥面，见图 2（b）。定义综合参量表达式为

图  2  空间滑动面示意图

Figure  2.  Schematic diagram of generalized space plane

下载: 全尺寸图片 幻灯片

式中，$\varphi$为材料特性参数，为土的内摩擦角，可通过垂直于沉积面方向${\sigma _z}$作用大主应力${\sigma _1}$的常规三轴试验直接获得，$\theta$为所述应力空间域内与应力状态和Lode角${\theta _\sigma }$相关的径向偏角，$\cos \theta$为反映土应力条件的参数，可通过几何坐标换算确定。将通过综合反映应力条件和材料特性的参量${\varPhi _{{\text{mob}}}}$反映材料空间滑动面变化这一特性。

1.4   各向异性参量的确定方法与分析

（1）横观各向同性参量与破坏应力的关系

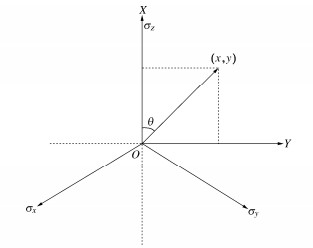
应力轴${\sigma }_{x}，{\sigma }_{y}，{\sigma }_{z}$构成的坐标系$({\sigma _z}, {\sigma _y}, {\sigma _x})$，将其投影至二维坐标$(X，Y)$（图 3），可得空间中一点可表示为

图  3  应力空间示意图

Figure  3.  Diagram of principal stress space

下载: 全尺寸图片 幻灯片

矢径

此时$\cos \theta$可表示为

由此可知，${\varPhi _{{\text{mob}}}}$的取值范围为${\varPhi _{{\text{mob}}}} \in \left[ { - \varphi , \varphi } \right]$，则${45^ \circ } + \varphi /2$表示土体处于压缩应力状态，${45^ \circ } - \varphi /2$表示土体处于挤伸应力状态。

（2）横观各向同性参量与应力状态的关系

土体复杂应力状态下发生主应力轴旋转，且旋转对强度的影响非常显著，体现在不同空间域内强度破坏点显著差异，通过采用横观各向同性综合参量可以很好得模拟土体横观各向同性强度特性。如图 1所示，对于空间域Ⅰ，Ⅱ，Ⅲ为垂直于沉积面方向${\sigma _z}$分别作用${\sigma }_{1}，{\sigma }_{2}，{\sigma }_{3}$所对应的应力状态，随着$\theta$从0°到180°范围变化，分别经历轴对称压缩应力状态（$\theta =$0°）、纯剪应力状态（$\theta =$90°）以及挤伸状态（$\theta =$180°）等。对于黄土真三轴试验结果，图 4表示了横观各向同性综合参量$\varPhi$随$\theta$角的变化规律，${\varPhi _{{\text{mob}}}}$随$\theta$角的增大而减小，然而并非表示空间域破坏强度越低，而是代表空间域内不同应力状态。

图  4  横观各向同性参数${\varPhi _{{\text{mob}}}}$随径向偏角$\theta$变化

Figure  4.  Variation of anisotropic parameter ${\varPhi _{{\text{mob}}}}$ with radial declination $\theta$

下载: 全尺寸图片 幻灯片

2.   空间滑动面变化的横观各向同性破坏准则

由此可以看出，横观各向同性材料，$\frac{{{\rm{ \mathsf{ π} }}}}{4} + \frac{{{\varPhi _{{\text{mob}}}}}}{2}$不再为常数，它与应力条件$\sigma$和材料参数$\varphi$有关。可以说，基于空间滑动面强度理论考虑了不同应力空间域的应力条件对空间发挥面的影响，该空间发挥面在物理空间内由应力状态决定，可以认为最大强度发挥面即为应力空间中的优势滑动面或强度薄弱面，不难看出，最大强度发挥面与主应力轴夹角越小，材料的强度也就越低。

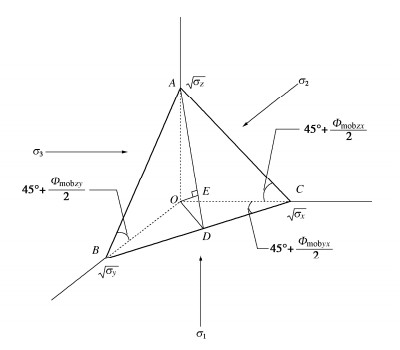
依据Mohr-Coulomb强度理论给出的土材料的剪切破坏形态，滑动剪切面与大主应力面夹角为$\frac{{{\rm{ \mathsf{ π} }}}}{4} + \frac{{{\varPhi _{{\text{mob}}}}}}{2}$（轴对称压缩条件下${\varPhi _{{\text{mob}}}} = \varphi$），这一结论也被大量常规土工测试结果所证实，而实际工程土体往往受到三向主应力作用的影响，此时它的滑动剪切面就不再为一个二维平面，而自然地拓展为三维空间滑动面，依据Mohr-Coulomb准则，同时考虑三个主应力平面内出现滑动破坏，空间面交线与应力主轴作用面之间的夹角表示为$\frac{{{\rm{ \mathsf{ π} }}}}{4} + \frac{{{\varPhi _{{\text{mob}}}}}}{2}$。因此对横观各向同性岩土材料空间滑动面进行几何应力分析，如图 5。依据土剪切破坏时空间滑动面上剪应力和法向应力之比为常数，则横观各向同性空间滑动面正应力和剪应力可表示为

图  5  空间滑动面上的应力

Figure  5.  Stresses on spatial mobilized plane

下载: 全尺寸图片 幻灯片

进而，得到考虑空间面变化的各向异性强度准则更为普通的形式：

该准则对于横观各向同性土在常规三轴条件下（${\sigma _y} = {\sigma _x}$且${\sigma _2} = {\sigma _3}$），同时考虑以上两个主应力平面内出现滑动破坏，确定的破坏面与主应力方向关系可表示为

式中，${K_\varPhi } =$${\tan ^2}\left( {{{45}^ \circ } + \frac{{{\varPhi _{{\text{mob}}}}}}{2}} \right)$${\tan ^2}\left( {{{45}^0} + \frac{{{\varPhi _{mob}}}}{2}} \right)$。

故式（7）可以化简为

式中，${k_{\text{f}}} = \frac{{\sqrt 2 }}{3}\frac{{k - 1}}{{\sqrt k }}$，需要指出的是，这里的$k$为轴对称压缩条件下的土体应力条件的参数$\theta$和内摩擦角$\varphi$，该条件下$\theta$的余弦值为1，故$k = {\tan ^2}$${45^ \circ } + \frac{\varphi }{2}$。

该空间面随主应力夹角改变而变化，实际上反映了应力空间域内土的横观各向同性特性。当土单元中的空间滑动面受介质内的微观结构控制，不随主应力变化而变化时，则不同应力条件下空间滑动面形态有所不同，对应不同应力空间域有不同应力条件，反映应力条件和材料特性的综合参量${\varPhi _{{\text{mob}}}}$随之改变，由此建立了能够反映空间滑动面变化的横观各向同性强度特性准则。

该准则同样可以延伸到预测黏聚特性的材料，对于$c \ne 0$的情况通过坐标平移进行转化，即${\hat \sigma _j} = {\sigma _j} + \frac{c}{{\tan \varphi }}$，$j = 1, 2, 3$。

3.   准则的试验验证及讨论

3.1   横观各向同性准则的参数讨论

本文采用的横观各向同性强度准则中有3个参数，即土体内摩擦角$\varphi$，径向偏角$\theta$，横观各向同性综合参量${\varPhi _{{\text{mob}}}}$。其中第1个参数$\varphi$通过垂直于沉积面方向${\sigma _z}$作用大主应力${\sigma _1}$的常规三轴试验可以确定，$\varphi$为三轴压缩时土的内摩擦角。其中第2个参数径向偏角$\theta$，用来表征空间域位置，是主应力的函数。

横观各向同性3个区间域对应不同的主应力状态，此时的中主应力参数、罗德角等会在不同区间域出现对应的取值，将分别进行讨论：

（1）区间域I有${\sigma _1} > {\sigma _2} \geqslant {\sigma _3}$，则有

根据罗德角定义，有

式中，$b{\text{ = }}\frac{{{\sigma _2} - {\sigma _3}}}{{{\sigma _1} - {\sigma _3}}}$。

联立式（10），（11），可以建立径向偏角$\theta$和罗德角${\theta _\sigma }$关系式：

（2）区间域Ⅱ有${\sigma _2} > {\sigma _1} \geqslant {\sigma _3}$，有

根据罗德角定义，同样有

式中，$b{\text{ = }}\frac{{{\sigma _1} - {\sigma _3}}}{{{\sigma _2} - {\sigma _3}}}$。

联立式（13）、（14），可以建立区间域Ⅱ的径向偏角$\theta$和罗德角${\theta _\sigma }$关系式：

（3）区间域Ⅲ有${\sigma _2} \geqslant {\sigma _3} > {\sigma _1}$，有

根据罗德角定义，同样有

式中，$b{\text{ = }}\frac{{{\sigma _3} - {\sigma _1}}}{{{\sigma _2} - {\sigma _1}}}$。

联立式（16）、（17），可以建立区间域Ⅲ的径向偏角$\theta$和罗德角${\theta _\sigma }$关系式：

由此可知，罗德角${\theta _\sigma }$和文中定义径向偏角$\theta$均是与中主应力相关的参数，若在区域Ⅰ中，其变化范围为-30°≤${\theta _\sigma }$≤30°，0°≤$\theta$≤60°和0≤b≤1。且在三轴压缩（${\sigma }_{1} > {\sigma }_{2}，{\sigma }_{2}={\sigma }_{3}$）时，$b = 0$，${\theta _\sigma } =$-30°，$\theta =$0°；且在三轴拉伸（${\sigma }_{1}={\sigma }_{2}，{\sigma }_{2} >$ ${\sigma _3}$）时，$b = 1$，${\theta _\sigma } =$0°，$\theta =$60°。若区间域Ⅱ、Ⅲ中，径向偏角$\theta$变化范围分别为60°≤$\theta$≤120°和120°≤$\theta$≤180°。且在三轴压缩（${\sigma }_{2} > {\sigma }_{1}，{\sigma }_{1}=$ ${\sigma _3}$）时，$b = 0$，${\theta _\sigma } =$-30°，$\theta =$120°；且在三轴拉伸（${\sigma }_{2}={\sigma }_{3}，{\sigma }_{3} > {\sigma }_{1}$）时，$b = 1$，${\theta _\sigma } =$30°，$\theta =$180°。

第3个横观各向同性综合参量${\varPhi _{{\text{mob}}}}$，为上两参数的关系式，用于反映应力条件和材料特性，由此可见并非定值。

3.2   横观各向同性强度准则破坏面讨论

本文提出的基于空间面变化的横观各向同性强度准则则是考虑了不同应力域强度破坏面变化，是由应力条件和材料特性参数共同确定的三维空间摩擦准则，如图 6（a），（b）所示。在应力空间中，该准则确定的应力空间破坏面有如下特征：①空间面沿应力主轴${\sigma _z}$呈对称分布；②八面体面的截面随摩擦角的增大向外扩展，形状由圆向平滑圆角的抹圆三角形变化；③区间域Ⅲ中破坏强度相较常规三轴压缩条件下强度值有所降低；④空间面形态与材料摩擦角有着密切关系，摩擦角越大材料的摩擦强度越大，轴对称挤伸条件下破坏强度中心偏移愈显著，压缩强度与挤伸强度差异愈明显，表明空间面中心轴相对静水压力轴发生偏转越明显，横观各向同性特性越明显；⑤在${{\rm{ \mathsf{ π} }}}$平面上Mohr-Coulomb准则及本文提出的基于空间面变化的横观各向同性强度准则的图形在原点收缩为零，故遵循摩擦准则，即当约束力为零时，强度为零。

图  6  偏平面上的空间面变化的横观各向同性破坏准则

Figure  6.  Cross-isotropic failure criteria on deviatoric plane under rotation of principal stress space

下载: 全尺寸图片 幻灯片

3.3   试验验证

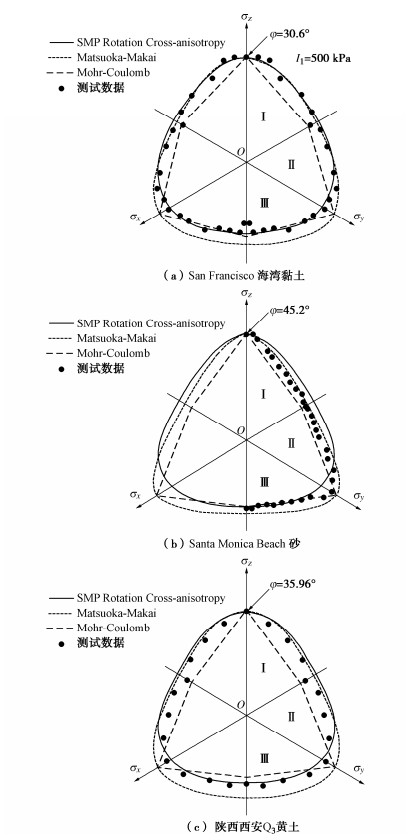
本文选用的横观各向同性土试验结果进行基于空间面变化的横观各向同性准则的验证，分别为San Francisco海湾黏土、Santa Monica Beach砂和陕西西安Q₃黄土的真三轴试验结果。

图 7（a）为Kirkgard和Lade对San Francisco海湾黏土八面体面内的真三轴试验结果，结果表现出较强的横观各向同性差异，试验得到竖向作用大主应力，水平向作用小主应力的轴对称压缩摩擦角${\varphi _{\text{f}}} =$ 30.6°。图 7（b）为A V Abelev和P V Lade对Santa Monica Beach砂真三轴排水试验结果，试验得到竖向作用大主应力，水平向作用小主应力的轴对称压缩摩擦角${\varphi _{\text{f}}} =$45.2°。图 7（c）为许萍等^[17]对陕西西安白鹿原Q₃原状黄土，沿试样竖向沉积面方向分别施加大、中、小主应力，进行了不同固结围压常中主应力比值的固结排水真三轴试验结果，试验得到竖向作用大主应力，水平向作用小主应力的轴对称压缩摩擦角${\varphi _{\text{f}}} =$35.96°。图中给出了Mohr-Coulomb和Matsuoka- Nakai各向同性破坏准则和本文的基于空间面变化的横观各向同性破坏准则的对比模拟。可以看出（a）、（c）两类岩土材料破坏面在区间域Ⅰ内，Matsuoka-Nakai各向同性破坏准则和本文提出的横观各向同性准则均可以反映试验结果，但区间域Ⅲ内，由于土体的沉积方向与加载方向不一致，主应力空间的破坏面随应力主轴发生偏转，该域的土材料破坏强度中心偏移，而本文提出的横观各向同性准则能够在3个应力域内较好地反映破坏强度。（b）材料具有较大摩擦强度，其破坏面在应力空间域Ⅰ，Ⅱ内Matsuoka-Nakai各向同性破坏准则与试验接近，本文的基于空间面变化的横观各向同性较大的估计了材料破坏强度, 而区间域Ⅲ内本文提出的横观各向同性准则能很好地反映该应力路经下三轴挤伸试验结果。

图  7  横观各向同性破坏准则比较

Figure  7.  Comparison between test results and failure criteria for cross-anisotropic loess

下载: 全尺寸图片 幻灯片

4.   结论

本文基于空间滑动面强度理论，在对八面体主应力空间域强度变化与空间滑动面、应力状态三者关系进行了分析研究的基础上，基于各向异性土的强度发挥角随着应力域的应力状态和材料特性变化的假定定义一个综合反映应力条件和材料特性的各向异性参量，沿用SMP准则材料破坏取决于最大剪应力比${{\text{(}}\tau /\sigma {\text{)}}_{\max }}$的思想，同时考虑3个主应力空间面发生滑动破坏的情况，建立了一个考虑岩土材料空间滑动面变化的横观各向同性强度准则表达式，得出4点结论。

（1）定义的各向异性参量通过应力空间投影简单获得，且具有明确的物理意义，即表征应力空间域的不同应力状态。

（2）建立横观各向同性破坏准则确立的破坏面形态由圆逐渐向平滑圆角的抹圆三角形变化，且沿应力主轴呈轴对称分布；破坏强度随着材料摩擦角的增大而增大，且轴对称压缩条件下破坏强度与挤伸条件下强度差异愈明显，即空间面中心轴相对静水压力轴发生偏转越明显。

（3）通过与现有不同类型土的真三轴试验结果对比表明，建立的基于空间面变化的横观各向同性破坏准则可以较好地反映材料的强度特性规律性变化，特别对主应力轴发生偏转时应力域的强度预测具有较好的适用性。

（4）建立横观各向同性破坏准则反映了岩土材料的空间滑动面随着空间应力域应力条件变化特征，表达式的获得同时考虑了一般应力条件（${\sigma }_{x}，{\sigma }_{y}，$${\sigma _z}$）和主应力条件（${\sigma }_{1}，{\sigma }_{2}，{\sigma }_{3}$），一定程度上可以近似反映真实的三维应力状态的不确定性，但对于反映三维应力空间的普适性，考虑无穷多映射仍需开展进一步工作。