土石料粒径与级配的图像智能识别研究

刘禹杉; 孙淼军; 吴帅峰; 张丽雅; 孙黎明

doi:10.11779/CJGE2023S10051

土石料粒径与级配的图像智能识别研究 English Version

1.
中国水利水电科学研究院流域水循环模拟与调控国家重点实验室, 北京 100048
2.
中国电建集团华东勘测设计研究院有限公司, 浙江杭州 311100

基金项目:

浙江省“尖兵”研发攻关计划项目 2022C03009

中国电建集团重点科技项目 DJ-ZDXM-2019-3

详细信息

作者简介:
刘禹杉(1997—)，女，工程师，主要从事水利工程信息化方面的研究工作。E-mail: wusf@iwhr.com

通讯作者:
吴帅峰, E-mail: wusf@iwhr.com

中图分类号: TU43
计量
- 文章访问数: 259
- HTML全文浏览量: 58
- PDF下载量: 86
出版历程
- 收稿日期: 2023-07-04
- 网络出版日期: 2023-11-23
- 刊出日期: 2023-10-31

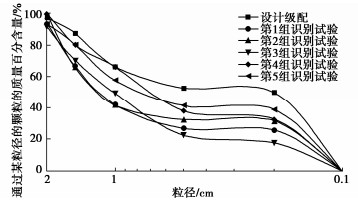
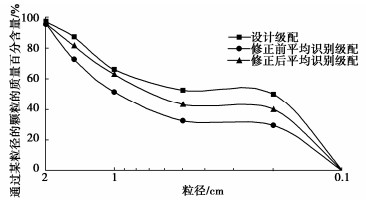
Intelligent image recognition of particle size and gradation of earth-rock

1.
State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin, China Institute of Water Resources and Hydropower Research, Beijing 100048, China
2.
Power China Huadong Engineering Corporation, Hangzhou 311100, China

摘要

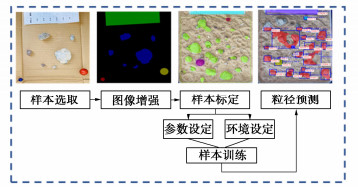
摘要: 土石料的级配直接影响着土石坝的质量与防渗，为解决传统人工筛分和目测超粒径剔除的低效率与随机性。采用基于MaskRCNN算法的图像识别技术，从标准球体的图像识别入手，研究了不同组别粒径下识别球体数量与真实数量间的关系，提出了将颗粒平面识别向空间体积扩展的椭球计算方法，建立了基于指数函数的图像识别与级配之间的转换方法。采用该方法应用于碎石料和砂石料的粒径与级配识别中，相关系数均提升10%以上，级配曲线所反映的C_u，C_c准确度最高提升35.26%。该研究为土石料级配的图像识别提供了新方法。
- 土石料 /
- 级配 /
- 图像识别 /
- 颗粒轮廓 /
- 空间转换
Abstract: The gradation of soil and stone materials directly affects the quality and anti-seepage of earth-rock dams. In order to solve the low efficiency and randomness of the traditional manual screening and the visual removal of oversized particles, the image recognition technology based on the MaskRCNN algorithm is used to start with the image recognition of standard spheres, and the relationship between the number of recognized spheres and the real number under different groups of particle sizes is studied. The ellipsoid calculation method that extends particle plane recognition to space volume is proposed, and the transformation method between the image recognition and the gradation based on the exponential function is established. By applying this method to the identification of particle size and the gradation of crushed stone and gravel, the correlation coefficient increases by more than 10%, and the accuracy of C_u and C_c reflected by the gradation curve is up to 35.26%. This stud may provide a new method for the image recognition of soil and stone gradation.
- earth-rock /
- gradation /
- image recognition /
- particle profile /
- spatial conversion

HTML全文

0. 引言

土体裂缝是岩土工程中常见的隐患和引起破坏的主要原因之一^[1]。在土质心墙坝中,坝顶裂缝和黏土心墙裂缝最为常见,坝顶裂缝一般是由于坝壳与心墙模量的差异、蓄水期水压力以及上游坝壳湿化变形等原因引起的,此类裂缝严重影响坝体的长期稳定性^[2]；而心墙裂缝主要是由于填料局部碾压不实、不均匀沉降和干缩等原因引起的,此类裂缝降低了心墙的防渗性能,在快速蓄水时可能会引起水力劈裂进而导致坝体渗漏甚至失稳^[3]。在城市垃圾填埋场的压实黏土衬垫系统中,在环境的影响下极易产生干缩裂缝,此类裂缝在上覆荷载作用下若发生扩展可能会引发渗漏问题进而导致衬垫系统失效^[4]。研究土体既有裂缝起裂和扩展问题具有重要的工程意义和实用价值。

当土体内存在宏观裂缝时,在外荷载作用下将会导致裂缝尖端产生应力集中,可从材料断裂角度对其进行分析。自Skempton等^[5]建议用断裂力学的概念解释含裂缝硬黏土边坡的失稳过程以来,人们对土体断裂问题给予了一定关注^[6-7],在纯拉、纯剪或拉剪应力状态下的土体断裂问题中研究相对较多,即I型、II型和I-II复合型裂缝问题,而实际工程中岩土体大多处于压剪应力状态,但压剪作用下土体既有裂缝的开裂问题鲜有关注。

在岩石断裂领域,压剪裂缝问题研究较多,但尚未形成统一认识。虽然剪切断裂常在地震断层中发现,但对于剪切裂缝的产生条件、机理以及剪切断裂韧度测试方法仍未统一^[8-9],目前更多的还是以压剪-张拉断裂研究为主^[10]。前人对受压裂缝的K_I存在过不同观点：①将压剪裂缝认为是受压闭合的,考虑了裂缝间的摩擦力,但并未注意到对于闭合裂缝K_I不复存在,仍将K_I进行变号处理^[11-13]；②将压剪裂缝认为是非闭合的,将K_I变号处理,但却考虑了裂缝间的摩擦效应^{[8, 14]}。实质上这是由于未区分裂缝形态导致的,对于压剪闭合裂缝,原始的裂缝面无法相互侵入,因此K_I = 0^[15]；对于压剪非闭合裂缝,认为压应力对裂缝张开有抑制作用,此时将其改变符号,即K_I < 0。即便如此,仍存在传统断裂力学理论无法解释的试验现象,例如,根据传统理论计算得到的压剪闭合裂缝张拉起裂角为恒定值70.5°。许多试验表明,无论裂缝闭合与否,张拉起裂角与裂缝倾角、裂缝长度均存在关系^[16]。随着学者们的逐渐探索,T应力对计算结果的影响被学者们所重视^[17]。岩石材料的断裂过程区尺寸较一般脆性材料（如玻璃、陶瓷等）更大,T应力的影响相对更大,因此不可忽略。此外,裂缝形态也会对断裂行为产生影响^[18]。

压实黏土碾压不实产生的弱面常被认为是心墙土体裂缝产生的原因之一^[19],前人采用断裂力学分析心墙开裂问题时通常将其裂缝考虑成非闭合形态,认为导致其开裂的应力状态为拉剪作用^[20]。然而,碾压弱面多处于闭合接触状态,研究闭合裂缝在压剪应力作用下的开裂行为具有实际意义。

鉴于此,采用理论分析和试验验证的研究手段,查明了压实黏土闭合裂缝的断裂特性,验证了考虑T应力的压剪闭合裂缝张拉断裂准则在压实黏土中的适用性,揭示了压实黏土中闭合裂缝压剪张拉断裂机制,并讨论了非闭合与闭合裂缝的差异化断裂行为。

1. 压剪裂缝尖端应力场及压剪张拉断裂准则

1.1 传统断裂力学理论

经典I-II复合型裂缝尖端应力场如下式所示

${\begin{cases} σ_{r} = \frac{1}{2 \sqrt{2 π r}} [K_{I} \cos \frac{θ}{2} (3 - \cos θ) + K_{II} \sin \frac{θ}{2} (3 \cos θ - 1)], \\ σ_{θ} = \frac{1}{2 \sqrt{2 π r}} \cos \frac{θ}{2} [K_{I} (1 + \cos θ) - 3 K_{II} \sin θ], \\ τ_{r θ} = \frac{1}{2 \sqrt{2 π r}} \cos \frac{θ}{2} [K_{I} \sin θ + K_{II} (3 \cos θ - 1)], \end{cases}$

(1)

式中, $σ_{r}$ , $σ_{θ}$ , $τ_{r θ}$ 分别为径向应力、周向应力、剪应力,K_I和K_II分别代表I型、II型应力强度因子,r,θ为极径和极角,开裂角的正负取决于K_II方向（图1）。

图 1 裂缝尖端应力场及裂缝起裂方向定义

Figure 1. Stress field at crack tip and definition of crack initiation direction

下载: 全尺寸图片幻灯片

对于图2所示的双向受压的中心斜裂缝模型。

图 2 双向压缩作用下中心斜裂缝的应力场

Figure 2. Stress field of inclined crack under biaxial compression

下载: 全尺寸图片幻灯片

裂缝面受力状态如下式所示：

${\begin{cases} σ_{T} = - σ (\cos^{2} β + λ \sin^{2} β), \\ σ_{N} = - σ (\sin^{2} β + λ \cos^{2} β), \\ τ_{N} = - σ (1 - λ) \sin β \cos β, \end{cases}$

(2)

式中,β为裂缝与竖直方向的夹角, $λ$ 为侧压力系数。

压剪作用下,非闭合裂缝的应力强度因子常写为

${\begin{cases} K_{I} = σ_{N} \sqrt{π a} = - σ (\sin^{2} β + λ \cos^{2} β) \sqrt{π a}, \\ K_{II} = τ_{N} \sqrt{π a} = - σ (1 - λ) \sin β \cos β \sqrt{π a} 。 \end{cases}$

(3)

裂缝闭合后,应力场主要由K_II控制,此时需考虑裂缝面摩擦效应（一般认为闭合裂缝面上的黏聚力c很小,常将其忽略）,裂缝面所受剪应力采用有效剪应力表示。由于剪应力方向变化导致摩擦力方向也会相应改变,因此闭合裂缝的应力强度因子表示为

${\begin{cases} K_{I} = 0, \\ K_{II} = τ_{eff} \sqrt{π a} = [\begin{array}{l} 0 (| τ_{N} | \leq μ | σ_{N} |) \\ - (τ_{N} - μ σ_{N}) \sqrt{π a} (| τ_{N} | > μ | σ_{N} |) \end{array} 。 \end{cases}$

(4)

1.2 考虑T应力的断裂力学理论

Williams等^[21]最早将裂缝尖端应力场采用无限级数展开项表示：

$σ_{i, j} = A_{1} r^{- 1 / 2} f_{_{i j}}^{1} (θ) + A_{2} r^{0} f_{_{i j}}^{2} (θ) + A_{3} r^{1 / 2} f_{_{i j}}^{3} (θ) + \dots$ 。

(5)

式中第一项为奇异项（r^-0.5项）,占据主导地位；第二项为非奇异项（r⁰项）,即常数项,第三项及后续项为r高阶项,传统理论通常写为式（1）形式。

Smith等^[17]系统性地研究了T应力对材料断裂行为的影响,提出了广义最大周向应力准则（GMTS准则）,广泛运用于I-II复合型断裂问题（裂缝受拉剪应力）。在压剪作用下,裂缝尖端K场、T场有所差异。

目前为止,针对T应力存在形式有以下几种观点：①考虑平行于裂缝面的T_x^[22]。②由于裂缝闭合,不仅考虑了平行于裂缝面的T_x,还考虑了垂直于裂缝面的T_y,T_y < 0^[23]。③不仅考虑了T_x和T_y,还考虑了T_y对闭合裂缝产生的摩擦作用,即T_xy^[18]。其中,观点①适用于非闭合裂缝,应力状态可为压剪或拉剪；观点②和③适用于压剪闭合裂缝,但观点②忽略了T_y对闭合裂缝产生的摩擦作用。对于岩土体材料,闭合裂缝面存在一定的摩擦作用,忽略T_xy对计算结果存在一定影响。

考虑T应力后,压剪闭合裂缝尖端应力场为

${\begin{cases} σ_{r} = \frac{K_{II}}{2 \sqrt{2 π r}} \sin \frac{θ}{2} (3 \cos θ - 1) + T_{x} \cos^{2} θ + T_{y} \sin^{2} θ + \\ T_{x y} \sin 2 θ, \\ σ_{θ} = - \frac{3 K_{II}}{2 \sqrt{2 π r}} \sin θ \cos \frac{θ}{2} + T_{x} \sin^{2} θ + T_{y} \cos^{2} θ - \\ T_{x y} \sin 2 θ, \\ τ_{r θ} = \frac{K_{II}}{2 \sqrt{2 π r}} \cos \frac{θ}{2} (3 \cos θ - 1) + \frac{1}{2} (T_{y} - T_{x}) \sin 2 θ + \\ T_{x y} \cos 2 θ, \end{cases}$

(6)

${\begin{cases} T_{x} = - σ {(cos}^{2} β + λ \sin^{2} β), \\ T_{y} = - σ (\sin^{2} β + λ \cos^{2} β), \\ T_{x y} = - μ σ (\sin^{2} β + λ \cos^{2} β) 。 \end{cases}$

(7)

1.3 压剪闭合裂缝张拉断裂准则

最大周向应力准则（MTS准则）在评价裂缝张拉起裂中运用最为广泛：裂缝尖端周向应力 $σ_{θ}$ 达到临界值时,将沿着最大周向应力的方向扩展。起裂角θ₀和最大周向应力 $σ_{θ}_{\max}$ 由下式可得

$\frac{\partial σ_{θ}}{\partial θ} = 0, \begin{matrix} \end{matrix} \frac{\partial^{2} σ_{θ}^{}}{\partial θ^{2}} ＜ 0, \begin{matrix} \end{matrix} (σ_{θ}_{\max} = σ_{θ_{0}}) 。$

(8)

基于传统理论,压剪闭合裂缝发生张拉起裂时最大周向应力为

$σ_{θ}_{\max} = - \frac{3}{2 \sqrt{2 π r_{c}}} K_{II} \sin θ_{0} \cos \frac{θ_{0}}{2} 。$

(9)

考虑T应力后,压剪闭合裂缝发生张拉起裂时最大周向应力为

$\begin{matrix} σ_{θ}_{\max} = - \frac{3 K_{II}}{2 \sqrt{2 π r_{c}}} \sin θ_{0} \cos \frac{θ_{0}}{2} + T_{x} \sin^{2} θ_{0} + \\ T_{y} \cos^{2} θ_{0} - T_{x y} \sin 2 θ_{0} \end{matrix}$ ,

(10)

将式（9）,（10）代入式（8）即可进行断裂分析。

1.4 裂缝尖端临界尺寸r_c和相对临界尺寸α

考虑T应力后,裂缝尖端临界尺寸r_c在计算时均无法回避。一般地,r_c常被认为是材料的特征属性。在岩石断裂领域,常采用式（11）进行经验估算^[24]：

$r_{c} = \frac{1}{2 π} {(\frac{K_{IC}}{σ_{t}})}^{2}$ 。

(11)

Ayatollahi等^[25]针对几种典型岩石材料,采用GMTS准则结合式（11）得到的理论预测值与试验结果匹配程度较好。因此,该公式目前被许多学者推广运用于岩石I-II复合型断裂研究中。

式（11）是否适用于压实黏土并未有所报道,此外,对于压剪裂缝而言,其裂缝尖端的K场和T场均存在差异,采用式（11）合理性尚无依据。因此,后文根据试验结果反分析得到了压实黏土的r_c,并对该公式存在的问题进行了讨论。

从式（10）可发现,考虑T应力后,裂缝长度和临界尺寸共同影响最大周向应力,为此,引入相对临界尺寸 $α = \sqrt{2 r_{c} / a}$ ,将其化简为

$\begin{matrix} {(σ_{θ})}_{\max} = - \frac{3 τ_{eff}}{2 α} \sin θ_{0} \cos \frac{θ_{0}}{2} + T_{x} \sin^{2} θ_{0} + \\ T_{y} \cos^{2} θ_{0} - T_{x y} \sin 2 θ_{0} \end{matrix}$ 。

(12)

有学者认为 $α$ 也是材料的特征属性^[26],实质上将其认为是一定裂缝尺度情况下的特征属性更为合适。

2. 含中心裂缝压实黏土单轴压缩试验

2.1 试验材料及试验方法

为查明压实黏土压剪断裂特性并验证压剪张拉起裂准则的适用性,开展了含中心裂缝压实黏土单轴试验。试验土料选自重庆某建筑工地,液限w_P为50%,W_L为30%。根据土料的击实曲线,含水率取16.6%,干密度取1.66 g/cm³。压实黏土强度特性如表1所示,根据Wang等^[27]研究成果,采用了半圆弯曲、直裂缝半圆弯曲试样,分别测定了土体的抗拉强度和断裂韧度；采用直剪试验测定了土体的抗剪强度。

表 1 试验土料强度特性

Table 1. Strength properties of test clay

K_IC/(kPa·m^0.5)	σ_t /kPa	c/kPa	φ/(°)
17	62	68	22

下载: 导出CSV

| 显示表格

含裂缝试样的制备过程如下：如图3所示,在自制的立方体容器中预先放置中心裂缝垫块（厚度在2.5 mm左右）,通过旋转垫块,即可使得含非闭合裂缝压实黏土试样在击实过程中形成,试样尺寸为100 mm×100 mm×100 mm。由于垫块存在,无法采用普通击实锤,需采用更小的击实工具进行局部击实。

图 3 含中心裂缝压实黏土试样制备

Figure 3. Preparation of compacted clay sample with inclined crack

下载: 全尺寸图片幻灯片

以往关于土体中闭合裂缝的预制鲜有报道,在岩石、混凝土断裂研究中,常采用预埋钢片或内部充填材料等方法实现闭合裂缝预制。对于第一种方法,裂缝面和钢片间很可能存在一定空隙^[28],故本文采用了充填方法预制了土体的闭合裂缝。本文充填材料选用石蜡,待非闭合裂缝试样制备完成后,将加热后的液相石蜡通过漏斗倒入非闭合裂缝中,待石蜡从液相转变为固相后,即可完成闭合裂缝的预制。

根据石蜡基本特性,其体积膨胀系数为0.76× 10^-3/℃,熔点为52℃。在实验室条件下（室温20℃）其液相和固相转变的温差为32℃。考虑极端情况,假定温差为80℃,计算得到其体积收缩率为6%,线收缩率为2%。对于本文试样尺寸,石蜡从液相转变为固相时厚度方向上的收缩量仅为0.06 mm左右,石蜡冷缩作用对试验结果的影响可忽略。通过后文结果也可知,在闭合裂缝端部起裂前,石蜡和土体必然完全接触。在试验前对10个试样进行了摩擦试验^[29],测定了压实黏土与固相石蜡之间的摩擦系数μ,平均值为0.38。

待含中心裂缝压实黏土试样制备完后,将其放置于仪器加载板,于加载板涂抹凡士林减小摩擦,以0.8 mm/min加载速率进行等应变加载,采用高速摄像仪对试样破坏过程进行图像捕捉,荷载位移曲线由数据采集器接收传输至计算机。

2.2 单向受压条件下裂缝面应力分布状态

如图4所示,在单向受压状态（λ = 0）,无论裂缝闭合与否,裂缝面压应力均随β增大而增大,有效剪应力随β增大先增大后减小。随着μ增大,有效剪应力逐渐减小,最大剪应力对应的β逐渐减小,在一定倾角范围有效剪应力为0,即K_II = 0。

图 4 单向受压时裂缝面受力状态

Figure 4. Stress distribution on crack surface under uniaxial compression

下载: 全尺寸图片幻灯片

2.3 试验方案

试验方案如表2所示。

表 2 试验方案

Table 2. Test schemes

类型	裂缝倾角β/(°)	无量纲裂缝长度2a/W
闭合	0,15,30,45,60,75	0.5
闭合	45	0.2,0.35,0.65
非闭合	15,30,45,60	0.5
注：W为试样的边长,100 mm。

下载: 导出CSV

| 显示表格

为查明闭合裂缝试样的压剪断裂特性,前两组试验方案中分别考虑了6种裂缝倾角、4种裂缝长度开展了试验。第三组试验方案针对4种裂缝倾角的非闭合裂缝试样进行了对照试验,探究了非闭合、闭合裂缝差异化断裂行为。此外,试验前对不含裂缝的完整试样进行了单轴试验,峰值应力为300 kPa。

3. 压剪作用下压实黏土的断裂性状

3.1 闭合裂缝起裂特征

（1）裂缝倾角的影响

图5为不同倾角时闭合裂缝的典型起裂特征。

图 5 裂缝倾角对闭合裂缝起裂特征的影响（2a/W = 0.5）

Figure 5. Effects of β on initiation characteristics of closed cracks

下载: 全尺寸图片幻灯片

当β = 0°时,闭合裂缝面上压应力和有效剪应力均为0,属于压剪应力状态的临界状态。但从试验现象来看,在试样的加载过程中观察到了端部的张拉起裂现象,起裂方向与预制裂缝方向一致。随着荷载逐渐施加,在裂缝端部以外区域会产生局部微裂隙。

当β = 75°时,裂缝面有效剪应力为0,压剪比趋于无穷大。在裂缝以外局部区域首先出现局部张拉微裂隙,随后逐步发育扩展至预制闭合裂缝中部区域。在应力达到峰值之后,由于试样中的微裂隙逐渐发育,其在闭合裂缝端部附近也会出现明显的张拉裂隙,但其开裂机制并不是由压剪闭合裂缝端部应力集中导致。

当β = 15°,30°,45°和60°时,闭合裂缝的起裂模式基本类似,均是在端部出现翼型张拉裂缝,然后张拉裂缝逐渐朝大主应力方向（单轴加载方向）扩展。在β = 30°和45°时,部分试样的裂缝端部出现了次生剪切裂缝,与光滑的翼型张拉裂缝不同,剪切裂缝往往较为粗糙,且伴随着局部碎屑剥落现象。从图5中可发现,宏观剪切裂缝并不是一条光滑的直线,而是类似于锯齿状的波浪线,在细观层面,宏观剪切裂缝是由许多拉伸微裂隙贯通形成的^[29]。此外,在β = 45°时,还观察到混合型拉剪裂缝,其发展过程是端部先产生剪切裂缝,随后转变为张拉裂缝。

（2）裂缝长度的影响

图6为不同裂缝长度的闭合裂缝起裂特征。

图 6 裂缝长度对闭合裂缝起裂特征的影响（β = 45°）

Figure 6. Effects of 2a on initiation characteristics of closed cracks

下载: 全尺寸图片幻灯片

当2a/W = 0.2时,翼型张拉裂缝逐渐扩展至贯穿试样,加载至一定时,裂缝端部以外局部区域会出现一些张拉微裂隙。当2a/W = 0.35～0.65时,在翼型张拉裂缝扩展过程中,大部分试样都出现了次生裂缝,且次生剪切裂缝占多数,扩展方向与预制裂缝共面或近似共面。当次生剪切裂缝发展过程受阻时,可能会转变为张拉裂缝,如图6中2a/W = 0.5试样产生的混合拉剪裂缝。除2a/W = 0.2外,试样的最终破坏面多为带擦痕的剪切破裂面,在2a/W = 0.65时尤为明显。

3.2 非闭合裂缝起裂特征

如图7所示,与闭合裂缝试样类似,非闭合裂缝试样均是在端部首先产生翼型张拉裂缝。在β = 15°时翼型裂缝将扩展至裂缝端部,贯通试样。在β = 30°,45°,60°时,翼型裂缝扩展的同时,部分试样的裂缝端部会出现次生剪切裂缝。不过,次生剪切裂缝的方向存在一定差异,当β = 30°和45°时,剪切断裂面基本与预制裂缝近似共面,但β = 60°时存在一定夹角。

图 7 非闭合裂缝起裂特征（2a/W = 0.5）

Figure 7. Initiation characteristics of open cracks

下载: 全尺寸图片幻灯片

试样的最终破坏模式存在一定差异,在β = 15°时基本为翼型张拉裂缝扩展至贯通导致试样破坏,在β = 30°和60°时,试样破坏时破裂面通常表现为：一侧翼型张拉裂缝扩展至贯通,一侧剪切裂缝扩展至贯通。而β = 45°时,多为剪切裂缝扩展,然后与局部剪切带贯通导致试样破坏。

根据试样的断裂特征,总结如下：当β = 15°～60°时（裂缝面有效剪应力不为0）,无论裂缝闭合与否,裂缝端部均首先出现翼型张拉断裂,说明张拉断裂为压剪作用下压实黏土的起裂模式；裂缝倾角、裂缝长度对闭合裂缝起裂特征影响显著；裂缝倾角一定时,非闭合裂缝和闭合裂缝张拉起裂角存在明显差异。

3.3 张拉起裂角

图8（a）为2a/W = 0.5时不同裂缝倾角下闭合、非闭合裂缝的张拉起裂角试验结果。

图 8 裂缝张拉起裂角试验结果

Figure 8. Test and theoretical values of tensile initiation angle

下载: 全尺寸图片幻灯片

随着裂缝倾角增加,无论裂缝闭合与否,张拉起裂角均逐渐增加,非闭合裂缝的起裂角相对更大些。传统理论计算得到的闭合裂缝张拉起裂角恒等于70.5°,非闭合裂缝起裂角恒大于70.5°,与试验结果均存在较大差距。

基于压剪闭合裂缝的张拉断裂准则,计算得到了不同相对临界尺寸α时的理论曲线（μ = 0.38）,如图8（b）所示。从图中可知,α = 0.4理论曲线与闭合裂缝试验值吻合相对良好,根据 $α = \sqrt{2 r_{c} / a}$ 反算得到本文压实黏土的r_c为2 mm左右。

进一步,将r_c = 2 mm代入 $α = \sqrt{2 r_{c} / a}$ 得到不同裂缝长度对应的 $α$ 值,进而可计算得到β = 45°时不同裂缝长度对应的起裂角理论值。如图8（c）所示,张拉起裂角的理论值和试验值随裂缝长度增大呈线性增大趋势,与试验结果趋势类似。

3.4 峰值应力和起裂应力

图9给出了不同裂缝长度时的峰值应力和起裂应力的影响曲线（β = 45°）。随着裂缝长度增加,起裂应力随裂缝长度呈线性减小趋势,峰值应力随裂缝长度增加呈台阶式下降趋势。

图 9 裂缝长度对闭合裂缝试样峰值应力和起裂应力的影响

Figure 9. Effects of crack length on peak stress and initiation stress of closed crack samples

下载: 全尺寸图片幻灯片

从图10可知,在β = 15°～60°时,随着裂缝倾角增加,闭合裂缝的峰值应力先减小后增加,在β = 30°最小,而非闭合裂缝的峰值应力逐渐减小。

图 10 裂缝倾角对含裂缝试样峰值应力的影响

Figure 10. Effects of angles on peak stress of fracture samples

下载: 全尺寸图片幻灯片

从图11可知,随着裂缝倾角增加,闭合裂缝和非闭合裂缝的起裂应力均是先减小后增加,起裂应力均在β = 45°最小。当裂缝倾角相同时,闭合裂缝的起裂应力和峰值应力均大于非闭合裂缝。

图 11 裂缝倾角对含裂缝试样起裂应力的影响

Figure 11. Effects of angles on initiation stress of fracture samples

下载: 全尺寸图片幻灯片

对于非闭合裂缝试样,不同倾角时的峰值应力均小于无裂缝试样的峰值应力（300 kPa）,体现了缺陷对材料强度的弱化效应。但多数闭合裂缝试样比无裂缝试样的峰值应力更大,主要是因为本文中采用了石蜡模拟闭合裂缝,相当于在缺陷中增加了比土体强度更大的材料。在β = 30°,45°时较为特殊,试样的破坏模式多为剪切破坏,由于石蜡与黏土界面剪切强度较黏土更低,峰值应力相对较低些。

对于闭合裂缝试样,许多学者常采用滑动裂纹模型进行分析其峰值应力变化规律^[28]：在裂隙体材料一定、裂隙长度不变的情况下,即裂隙面上有效剪应力最大时,裂隙体模型承载能力最低。根据图4可知,当μ = 0.38时,峰值应力最小值对应β = 35°,本文闭合裂缝试样最小峰值应力出现在β = 30°,与理论值接近。但对于非闭合裂缝试样,由于其几何特征难以量化,无法准确定量分析其峰值应力变化规律^[28]。

4. 讨论

4.1 压剪作用下压实黏土闭合裂缝的起裂机理

如图12（a）所示,采用传统理论时,裂缝尖端最大周向应力随β增大先增大后减小,呈典型的抛物线状,最大值出现在β = 35°附近。随着 $α$ 增大,最大周向应力的变化规律不变,但其数值逐渐减小。

图 12 　α对裂缝尖端最大周向应力的影响（μ = 0.38）

Figure 12. Effects of α on maximum tangential stress of crack tip

下载: 全尺寸图片幻灯片

如图12（b）所示,考虑T应力后,最大周向应力随 $β$ 增大的变化规律并不一致,且最大值对应的 $β$ 也不是定值,而是随着 $α$ 增大逐渐增大。当 $α$ 增大至一定时,部分 $β$ 对应的最大周向应力并不为正值,即表示此时不会发生张拉断裂。

根据以上分析,可解释图11中裂缝长度对闭合裂缝起裂应力的影响机制：在压剪应力比一定时,裂缝长度越大（相对临界尺寸α越小）,导致周向应力越大,即在发生张拉起裂所需要的应力更小。

根据3.3节中的分析结果,2a/W = 0.5时（裂缝长度为2a= 50 mm）对应相对临界尺寸α为0.4左右,反算得到的r_c约为2 mm。从图12可知,α = 0.4时,采用传统理论和考虑T应力的闭合裂缝压剪断裂准则可得,最小起裂强度对应的裂缝倾角β分别为35°和43°。结合图11试验结果,β = 45°时闭合裂缝起裂应力最小,说明了压剪闭合裂缝张拉断裂准则的合理性。

此外,当α = 0.4时, $β$ = 15°～60°均存在正的周向应力,试验现象也出现了明显的张拉断裂。当β = 0°和75°时,裂缝尖端的周向应力均为0,无法产生张拉起裂,本文β = 75°试样观察到类似现象。不过β = 0°时则与理论存在差异,预制裂缝端部出现了与原裂缝近似共面的张拉裂缝,原因主要是裂缝受压导致裂缝端部产生与裂缝面垂直的拉应力^[30]。

4.2 临界尺寸r_c经验公式的适用性

根据表2中的强度指标,采用式（11）计算得到的r_c值为12 mm,而根据试验结果反分析得到的r_c值为2 mm左右,经验值是实际值的6倍,差异显著。进一步,将经验值r_c = 12 mm代入 $α = \sqrt{2 r_{c} / a}$ ,本文2a/W = 0.5试样对应的α为1.0。从图12（b）可发现,当α = 1.0时,在β = 15°和30°时裂缝尖端最大周向应力小于0,不存在拉应力,然而本文试验结果中却出现了明显的张拉裂缝。由此说明,式（11）并不适用。

在I-II复合型断裂问题中,以Ayatollahi为代表的许多学者^{[25, 31]}认为,采用经验公式（11）得到的GMTS准则理论曲线与试验值通常较为接近,近年来被广泛运用于PMMA、沥青混凝土、岩石等材料的断裂分析。然而本文中采用式（11）得到的理论结果与试验结果差距甚远,为探讨该问题,笔者进行了讨论。

图13给出了单轴拉伸时裂缝的起裂角理论曲线（GMTS准则）和单轴压缩时光滑闭合裂缝的起裂角理论曲线（本文准则）。不难发现,压剪作用下α对起裂角的影响较拉剪作用下敏感得多,尤其是裂缝倾角较小时。根据Wang等^[27]统计,岩石材料K_IC/σ_t通常在0.1～0.2,根据式（11）得r_c经验值为1.6～6.4 mm。取岩石最大值r_c = 6.4 mm,根据本文对比结果,假定r_c的经验值为真实值的6倍,当裂缝长度2a为50 mm时, $α$ 的经验值和真实值差距 $Δ α$ 为0.4左右。从图13可知,在拉剪应力状态时, $Δ α$ = 0.4引起的起裂角差异在5°左右,而在压剪应力状态时,其最大差异则超过了20°。对于断裂准则的验证,通常根据试验数据点是否“接近”理论曲线来判断,10°以内的起裂角差异并不明显。此外,材料r_c基数越小, $Δ α$ 也会变小。

图 13 不同应力状态下α对起裂角的影响

Figure 13. Effects of α oninitiation angle under different stress states

下载: 全尺寸图片幻灯片

综上可知,由于拉剪应力作用下 $α$ 对起裂角的影响并不敏感,故采用式（11）得到的GMTS理论曲线通常与试验值较为接近。然而压剪作用下 $α$ 对起裂角的影响相对更敏感,且K_IC/σ_t受到测试方法的影响,采用经验公式（11）估算得到的r_c存在较大不确定性,难以获得满意的预测结果。现阶段只有通过试验证实的方法,进而获取满足要求的r_c。由于在裂缝倾角较小时 $α$ 对结果影响更敏感,今后试验中只需取β = 10°,20°,30°3种典型角度即可快速确定r_c的取值范围。

4.3 非闭合与闭合裂缝的差异化断裂行为解释

经典复合型断裂研究中并不涉及裂缝闭合问题,通常将其视为数学裂缝（宽度趋于0）,以裂缝端部起裂为前提假设建立相应的断裂准则。

如前文所述,压剪裂缝通常被考虑成非闭合和闭合两种情况,其中,对K_I变号处理实际上仍是将压剪非闭合裂缝认为是数学裂缝,并未考虑其几何特性。也就是说,从裂缝形态上看,光滑闭合裂缝和非闭合裂缝区别仅在于接触与否,但两者的K_I存在明显差异。

本文尝试性地引入T应力（只考虑T_x）,建立了非闭合裂缝压剪张拉断裂准则,其中,非闭合裂缝周向应力可表示为

$σ_{θ} = \frac{1}{2 \sqrt{2 π r}} \cos \frac{θ}{2} [K_{I} (1 + \cos θ) - 3 K_{II} \sin θ] + T_{x} \sin^{2} θ$ ,

(13)

结合式（3）,（7）,（8）,即可进行断裂分析。

图14中给出了两种理论计算得到的闭合裂缝和非闭合裂缝的起裂角理论曲线。为进行对比讨论,选取本文2a = 50 mm,β = 15°～60°的闭合、非闭合裂缝试验结果。同时,增加了Bobet经典石膏单轴试验结果^[32],其试验中同时考虑了闭合、非闭合裂缝试样,相关参数如下：2a = 12.7 mm,r_c = 0.22 mm（ $α$ = 0.26）,闭合裂缝面摩擦系数μ = 0.3。

图 14 非闭合裂缝和光滑闭合裂缝的张拉起裂角

Figure 14. Initiation angles of open cracks and smoothly closed cracks

下载: 全尺寸图片幻灯片

对于闭合裂缝试验结果,考虑T应力的闭合裂缝压剪张拉断裂准则均能与Bobet和本文结果吻合良好,充分说明了其合理性。此外,图14（a）,（b）中均给出了光滑闭合裂缝的理论曲线,相对于粗糙闭合裂缝,其起裂角明显更大。

考虑T_x后,非闭合裂缝的起裂角理论曲线也得到了改善,在β = 0°～45°范围起裂角明显较传统理论曲线更小,但整体上仍比光滑闭合裂缝的起裂角更大,且随着β增大差距越大。虽然从裂缝形态上来看,非闭合裂缝（数学裂缝）无限接近光滑闭合裂缝,但两者理论结果的差异是显著的。

此外,考虑T应力的非闭合裂缝起裂角理论曲线与Bobet石膏试验结果吻合程度良好,但与本文试验数据吻合程度较差。主要原因是：室内断裂试样的非闭合裂缝通常存在一定张开度,与数学裂缝的假设存在差异。此外,过大的张开度不仅会影响裂缝尖端周向应力大小,而且还会影响其起裂位置^[28]。本文试样裂缝宽度为2.5 mm,而Bobet试验中仅为0.1 mm,更贴近数学裂缝的假设,故其试验值与理论值吻合较好。

5. 结论

（1）无论裂缝闭合与否,压剪作用下裂缝端部总是首先出现翼型张拉裂缝。裂缝倾角增大,非闭合裂缝和闭合裂缝的起裂角均逐渐增大,非闭合裂缝起裂角相对更大些；裂缝倾角一定时,裂缝长度越大,闭合裂缝起裂角越大。

（2）闭合裂缝试样的峰值、起裂应力均随裂缝倾角增加先减小后增大,分别在β = 30°和45°达到最小；随着裂缝长度增加,闭合裂缝的峰值应力和起裂应力均逐渐减小。对于非闭合裂缝试样,随着裂缝倾角增加,峰值应力逐渐减小,起裂应力则先减小后增大。

（3）基于考虑T应力的闭合裂缝压剪张拉起裂准则,解释了裂缝倾角、裂缝长度对张拉起裂角、起裂应力的影响规律。通过试验反分析,本文压实黏土试样的临界尺寸r_c为2 mm左右,与经验公式 $r_{c} =$ ${(2 π)}^{- 1} {(K_{IC} / σ_{t})}^{2}$ 得到的12 mm存在较大差异。

（4）压剪作用下 $α$ 对断裂行为的影响较拉剪作用下敏感得多,采用经验公式计算r_c存在较大不确定性。关于r_c的取值方法尚无合理的理论依据,采用试验证实的方式是现阶段唯一有效手段。

（5）引入T应力,尝试性地建立了非闭合裂缝的压剪张拉起裂准则,讨论了非闭合裂缝与闭合裂缝的差异化断裂行为。通过与Bobet经典石膏试验、本文试验结果对比分析可知,由于室内断裂试样的非闭合裂缝往往存在一定宽度,与理论假设中的数学裂缝不吻合,导致理论值与试验值存在差异。

图 1 训练识别过程

Figure 1. Training identification process

下载: 全尺寸图片幻灯片

图 2 土石颗粒识别近似转换

Figure 2. Approximate transformation for identification of soil-rock particle

下载: 全尺寸图片幻灯片

图 3 标准球体设计级配曲线

Figure 3. Design gradation curve of standard sphere

下载: 全尺寸图片幻灯片

图 4 标准球体识别试验

Figure 4. Identification tests on standard ball

下载: 全尺寸图片幻灯片

图 5 试验识别与设计级配在各粒径下倍数关系

Figure 5. Relationship between test identification and design gradation under each particle size

下载: 全尺寸图片幻灯片

图 6 空间修正后识别试验级配曲线对比

Figure 6. Comparison of gradation curves of identification tests after spatial correction

下载: 全尺寸图片幻灯片

图 7 碎石料5组识别试验

Figure 7. Five groups of identification tests on crushed stone

下载: 全尺寸图片幻灯片

图 8 碎石土修正模型的应用

Figure 8. Application of modified model for gravelly soil

下载: 全尺寸图片幻灯片

图 9 砂石料5组识别试验

Figure 9. Five groups of identification tests on sand and gravel

下载: 全尺寸图片幻灯片

图 10 砂石料修正模型的应用

Figure 10. Application of modified model for sand and gravel

下载: 全尺寸图片幻灯片

参考文献(10)

[1]	杨玉生, 赵剑明, 王龙, 等. 级配特征对筑坝砂砾料填筑标准的影响[J]. 水利学报, 2019, 50(11): 1374-1383. doi: 10.13243/j.cnki.slxb.20190547 YANG Yusheng, ZHAO Jianming, WANG Long, et al. Influence of gradation characteristics on filling standard of sand gravel material for dam construction[J]. Journal of Hydraulic Engineering, 2019, 50(11): 1374-1383. (in Chinese) doi: 10.13243/j.cnki.slxb.20190547
[2]	汤洪洁, 杨正权. 高土石坝筑坝材料特性的认识与思考[J]. 水利规划与设计, 2019(1): 125-129. doi: 10.3969/j.issn.1672-2469.2019.01.035 TANG Hongjie, YANG Zhengquan. Understanding and thinking on the characteristics of dam materials for high earth-rock dams[J]. Water Resources Planning and Design, 2019(1): 125-129. (in Chinese) doi: 10.3969/j.issn.1672-2469.2019.01.035
[3]	朱晟, 钟春欣, 郑希镭, 等. 堆石体的填筑标准与级配优化研究[J]. 岩土工程学报, 2018, 40(1): 108-115. doi: 10.11779/CJGE201801010 ZHU Sheng, ZHONG Chunxin, ZHENG Xilei, et al. Filling standards and gradation optimization of rockfill materials[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(1): 108-115. (in Chinese) doi: 10.11779/CJGE201801010
[4]	ZHANG S L, WU G J, YANG X G, et al. Digital image-based identification method for the determination of the particle size distribution of dam granularmateria[J]. KSCE Journal of Civil Engineering, 2018, 22(8): 2820-2833. doi: 10.1007/s12205-017-0304-8
[5]	张国英, 邱波, 刘冠洲, 等. 基于图像的原矿碎石粒度检测与分析系统[J]. 冶金自动化, 2012, 36(3): 47-50. https://www.cnki.com.cn/Article/CJFDTOTAL-YJZH201203018.htm ZHANG Guoying, QIU Bo, LIU Guanzhou, et al. Image-based volume modeling and particle size analysis system of crushed ore[J]. Metallurgical Industry Automation, 2012, 36(3): 47-50 (in Chinese https://www.cnki.com.cn/Article/CJFDTOTAL-YJZH201203018.htm
[6]	HAN D, ZHU J H, LI L L. et al. Verification andapplication of two-dimensional slice identificationmethod in three-dimensional mesostructure under different aggregate gradations and packing algorithms[J]. Construction and Building Materials, 2016, 102(1): 843-851.
[7]	雷雨萌, 陈祖煜, 于沭, 等. 基于深度阈值卷积模型的土石料级配智能检测方法研究[J]. 水利学报, 2021, 52(3): 369-380. doi: 10.13243/j.cnki.slxb.20200499 LEI Yumeng, CHEN Zuyu, YU Shu, et al. Intelligent detection of gradation for earth-rockfill materials base on Deep Otsu Convolutional Neural Network[J]. Journal of Hydraulic Engineering, 2021, 52(3): 369-380. (in Chinese) doi: 10.13243/j.cnki.slxb.20200499
[8]	LEE J R J, SMITH M L, SMITH L N. New approach to the three-dimensional quantification of angularity using image analysis of the size and form of coarse aggregates[J]. Engineering Geology, 2007, 91(2): 254-264.
[9]	SEZGIN M, SANKUR B. Survey over image thresholding techniques and quantitative performance evaluation[J]. Journal of Electronic Imaging, 2004, 13(1): 146-168. doi: 10.1117/1.1631315
[10]	黄鹏, 郑淇, 梁超. 图像分割方法综述[J]. 武汉大学学报(理学版), 2020, 66(6): 519-531. doi: 10.14188/j.1671-8836.2019.0002 HUANG Peng, ZHENG Qi, LIANG Chao. Overview of image segmentation methods[J]. Journal of Wuhan University (Natural Science Edition), 2020, 66(6): 519-531. (in Chinese) doi: 10.14188/j.1671-8836.2019.0002

施引文献(24)

期刊类型引用(10)

1.	朱才辉，周小松，乔建伟，李鑫磊. 孔内深层强夯法处理湿陷性黄土地基试验研究. 自然灾害学报. 2025(01): 217-229 . 百度学术
2.	张子萱，曹宝花，韩泽敏，许江波，程芳卉，陈绍华，侯鑫敏，詹皓辰. PFC3D颗粒流模拟纳米黏土改良黄土三轴试验. 岩土工程技术. 2024(03): 365-373 . 百度学术
3.	杨智慧，李珊花. 基于PFC~(2D)的水泥土单轴压缩试验及细观数值模拟. 中外公路. 2023(01): 189-193 . 百度学术
4.	刘欢，张庆文，连晓兰，朱孟龙，聂广影. 非饱和绢云母片岩残积土一维压缩变形规律. 科学技术与工程. 2021(03): 1131-1137 . 百度学术
5.	李涛，蒋明镜，李立青. 非饱和重塑黄土应变控制等应力比试验三维离散元分析. 水利与建筑工程学报. 2021(02): 36-41 . 百度学术
6.	蒋明镜，王优群，卢国文，张鹏. 非饱和重塑与结构性黄土平面应变试验三维离散元模拟. 水利与建筑工程学报. 2021(02): 1-5+18 . 百度学术
7.	李瑶，伏映鹏，廖红建，吕龙龙，董琪. 考虑吸力作用的非饱和土离散元模型及细观参数影响分析. 岩土工程学报. 2021(S1): 246-250 . 本站查看
8.	米文静，张爱军，刘争宏，刘宏泰. 黄土自重湿陷变形的多地层离心模型试验方法. 岩土工程学报. 2020(04): 678-687 . 本站查看
9.	蒋明镜. 现代土力学研究的新视野——宏微观土力学. 岩土工程学报. 2019(02): 195-254 . 本站查看
10.	蒋明镜，张浩泽，李涛，张鹏. 非饱和重塑与结构性黄土等向压缩试验离散元分析. 岩土工程学报. 2019(S2): 121-124 . 本站查看

其他类型引用(14)

资源附件(0)

图(10)

计量

文章访问数: 259
HTML全文浏览量: 58
PDF下载量: 86
被引次数: 24

0. 引言
1. 压剪裂缝尖端应力场及压剪张拉断裂准则
1.1 传统断裂力学理论
1.2 考虑T应力的断裂力学理论
1.3 压剪闭合裂缝张拉断裂准则
1.4 裂缝尖端临界尺寸rc和相对临界尺寸α
2. 含中心裂缝压实黏土单轴压缩试验
2.1 试验材料及试验方法
2.2 单向受压条件下裂缝面应力分布状态
2.3 试验方案
3. 压剪作用下压实黏土的断裂性状
3.1 闭合裂缝起裂特征
3.2 非闭合裂缝起裂特征
3.3 张拉起裂角
3.4 峰值应力和起裂应力
4. 讨论
4.1 压剪作用下压实黏土闭合裂缝的起裂机理
4.2 临界尺寸rc经验公式的适用性
4.3 非闭合与闭合裂缝的差异化断裂行为解释
5. 结论

0. 引言
1. 压剪裂缝尖端应力场及压剪张拉断裂准则
1.1 传统断裂力学理论
1.2 考虑T应力的断裂力学理论
1.3 压剪闭合裂缝张拉断裂准则
1.4 裂缝尖端临界尺寸r_c和相对临界尺寸α
2. 含中心裂缝压实黏土单轴压缩试验
2.1 试验材料及试验方法
2.2 单向受压条件下裂缝面应力分布状态
2.3 试验方案
3. 压剪作用下压实黏土的断裂性状
3.1 闭合裂缝起裂特征
3.2 非闭合裂缝起裂特征
3.3 张拉起裂角
3.4 峰值应力和起裂应力
4. 讨论
4.1 压剪作用下压实黏土闭合裂缝的起裂机理
4.2 临界尺寸r_c经验公式的适用性
4.3 非闭合与闭合裂缝的差异化断裂行为解释
5. 结论

参考文献(10)

施引文献

资源附件(0)

土石料粒径与级配的图像智能识别研究 English Version

作者简介: 刘禹杉(1997—)，女，工程师，主要从事水利工程信息化方面的研究工作。E-mail: wusf@iwhr.com

通讯作者: 吴帅峰, E-mail: wusf@iwhr.com

计量

出版历程

Intelligent image recognition of particle size and gradation of earth-rock

0. 引言

1. 压剪裂缝尖端应力场及压剪张拉断裂准则

1.1 传统断裂力学理论

1.2 考虑T应力的断裂力学理论

1.3 压剪闭合裂缝张拉断裂准则

1.4 裂缝尖端临界尺寸rc和相对临界尺寸α

2. 含中心裂缝压实黏土单轴压缩试验

2.1 试验材料及试验方法

2.2 单向受压条件下裂缝面应力分布状态

2.3 试验方案

3. 压剪作用下压实黏土的断裂性状

3.1 闭合裂缝起裂特征

3.2 非闭合裂缝起裂特征

3.3 张拉起裂角

3.4 峰值应力和起裂应力

4. 讨论

4.1 压剪作用下压实黏土闭合裂缝的起裂机理

4.2 临界尺寸rc经验公式的适用性

4.3 非闭合与闭合裂缝的差异化断裂行为解释

5. 结论

期刊类型引用(10)

其他类型引用(14)

计量

出版历程

目录

0. 引言

1. 压剪裂缝尖端应力场及压剪张拉断裂准则

1.1 传统断裂力学理论

1.2 考虑T应力的断裂力学理论

1.3 压剪闭合裂缝张拉断裂准则

1.4 裂缝尖端临界尺寸rc和相对临界尺寸α

2. 含中心裂缝压实黏土单轴压缩试验

2.1 试验材料及试验方法

2.2 单向受压条件下裂缝面应力分布状态

2.3 试验方案

3. 压剪作用下压实黏土的断裂性状

3.1 闭合裂缝起裂特征

3.2 非闭合裂缝起裂特征

3.3 张拉起裂角

3.4 峰值应力和起裂应力

4. 讨论

4.1 压剪作用下压实黏土闭合裂缝的起裂机理

4.2 临界尺寸rc经验公式的适用性

4.3 非闭合与闭合裂缝的差异化断裂行为解释

5. 结论

作者简介:
刘禹杉(1997—)，女，工程师，主要从事水利工程信息化方面的研究工作。E-mail: wusf@iwhr.com

通讯作者:
吴帅峰, E-mail: wusf@iwhr.com

1.4 裂缝尖端临界尺寸r_c和相对临界尺寸α

4.2 临界尺寸r_c经验公式的适用性

1.4 裂缝尖端临界尺寸r_c和相对临界尺寸α

4.2 临界尺寸r_c经验公式的适用性