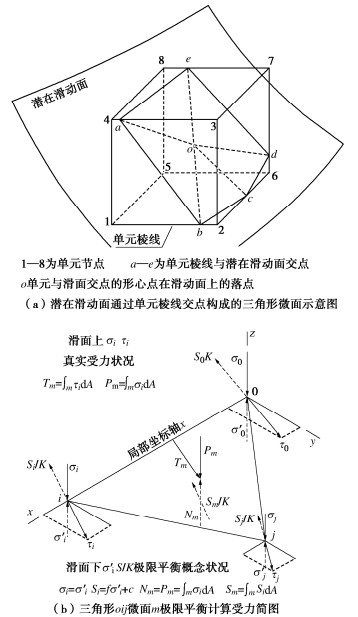
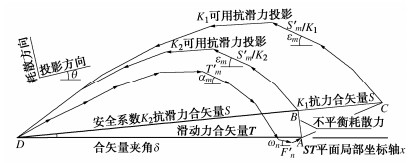
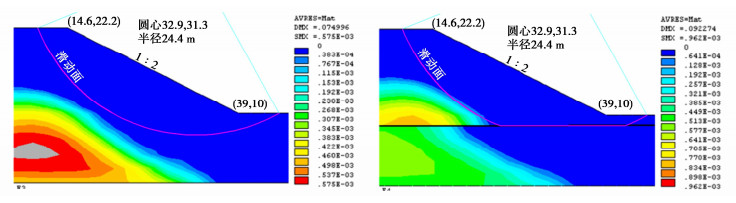
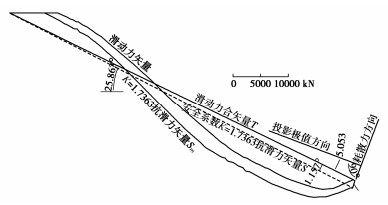
Theoretical model for limit equilibrium anti-sliding stability of stress vectors on three-dimensional sliding surface based on projection direction extreme principle
-
摘要: 根据投影方向极值原理揭示的复杂滑动面切向应力合矢量非共线不平衡特征，且其滑动势能比在平衡研究投影方向具有极大、耗散方向势能极小，针对三维滑动面节点应力状态差异使微面内的切向滑动力与抗滑力作用方向存在微小差异，构建三维复杂滑动面切向应力合成矢量在投影-耗散正交极值方向的塑性极限平衡抗滑稳定计算理论模型。完成理论模型的三维拓展，并给出理论模型具体计算方法步骤。通过典型稳定算题的微面切向滑动力与抗滑力势能比极值特性曲线和计算极值点的吻合程度证明理论模型的合理可靠性。并且依典型算例探讨了有限元应力场影响因素的变化对理论模型解的敏感性。矢量理论模型是抗滑稳定力学基础理论创新性的研究成果，具有重大理论发展推进作用和工程实际使用经济价值。Abstract: According to the projection direction extreme principle, in which the unbalance characteristics of non-collinear forces formed by tangential stress vectors on the complex sliding surface are revealed and the sliding potential energy ratio of the unbalance stress vectors in the equilibrium direction has the maximum, and minimum potential energies in the dissipation direction, in view that the difference of the stress state of the joints on the three-dimensional sliding surface leads to slight difference between direction of the tangential sliding force and that of the anti-sliding force in the micro-element plane, a theoretical model for calculating the stability of a three-dimensional complex sliding surface against sliding in the plastic limit equilibrium is proposed in the direction of the projection-dissipation orthogonal extreme. The three-dimensional expansion for the theoretical model is completed, and the concrete calculation steps of the theoretical model are given. The reasonable reliability of the model is proved by the curve of the extreme value of potential energy ratio between tangential sliding force and anti-sliding force on the sliding surface of typical stability problems and the degree of agreement between the calculated extreme point and the model. The sensitivity of the change of the factors affecting the finite element stress field to the solution of the theoretical model is also discussed. The vector theoretical model is an innovative research on the basic mechanics theory of anti-slide stability, which is of important theoretical development and practical economic value.
-
0. 引言
近年来，为实现“双碳”目标并随着“海洋强国”战略的实施，中国海上风电发展迅速。海上风电结构由于其特殊的服役条件，在风、浪等长期环境动荷载的联合下，结构会产生显著的动力响应。过大的振动不仅对结构造成损伤，甚至还会影响发电机组的正常运行，开展海上风电结构动力特性的研究具有重要意义。
自振频率和阻尼比是反映结构动力特性的重要模态参数[1-4]。国内外有关海上风电结构动力特性的研究集中在通过理论分析及数值建模方面，由于对环境荷载及地质条件的简化，研究成果存在一定局限性和失真现象等。随着海上测试手段完善，以原位测试进行结构振动信号收集，并通过一定数学算法进行模态参数识别研究的方式越来越受到广大学者们重视。Häckell等[1]针对德国5 MW海上三脚架支撑风电结构，提出了通过数据驱动随机子空间方法和向量自回归方法获取结构模态和运行状态参数的分析模型。依据实测数据，Álamo等[2]研究了桩-土相互作用对海上单桩基础动态特性的影响，结果表明表层土体特性对桩-土系统的固有频率和阻尼比变化起到主导作用。Bassett等[3]实测了2.3 MW风电结构开机与稳定运行状态下的结构加速度数据，通过小波分解方法获得了结构振动响应特征。Weijtjens等[4]通过对比利时单桩基础海上风电结构进行了1年的观测数据研究，发现结构自振频率和阻尼比受风电结构运行条件的影响很大。
复合筒型基础作为一种新的海上风电基础结构型式，因陆上建造成本低、海上安装快、抗倾覆能力强、适用多种地质及水深条件等特点，具有较高的发展潜力，目前已成功应用于江苏响水、大丰、如东以及广东阳江等地海上风场。蔡正银等[5]、Zhu等[6]、练继建等[7]和Ding等[8]对中国复合筒型基础的沉贯特性及静力承载特性等开展了一系列的数值分析、室内试验及原位观测研究，取得了丰富成果，而关于复合筒型基础海上风电结构在环境激励作用下动力特性的研究还相对有限，长期的原位观测数据较为匮乏，结构模态参数与环境激励间的相关性缺乏深入分析。
为此，本文以江苏如东复合筒型基础海上风电结构为研究对象，采取原位测试获取结构长期振动数据，利用集合经验模态分解-模拟退火算法及随机子空间算法分别进行测试数据的降噪与结构模态参数的识别，重点研究了结构模态参数与环境激励的相关性，并初步就结构频率的时变性进行了讨论。
1. 如东地区海上风电结构原位测试
1.1 气象、水文和地质条件
江苏如东风电场场址处65 m高度的年平均风速为7.2 m/s，年平均风功率密度为356 W/m2，全年有效风时为7941 h，主风向为东南风，东南东方向的风向频率最大，如东气象站多年风向玫瑰图如图 1（a）所示。全年中波浪主要为东方向，出现频率为34.21%，其次为东南东方向，频率为19.27%，如图 1（b）所示。全年最大有效波高出现北东向，为3.43 m，最大波高为6.36 m。次强浪向为北东向和东南东向，最大有效波高均在3 m左右。测试期间测点处的平均海水深16.5 m，潮位差约4.2 m，平均流速0.87 m/s。
工程地质资料表明，测试风电结构位置处的浅部土层自上而下依次为松散—稍密的粉砂夹粉土（厚度约3.0 m）、淤泥质粉质黏土（厚度约6.3 m）及淤泥质粉质黏土夹粉土（厚度约2.4 m）。现场静力触探和室内试验成果等表明基础深度范围内具有“上硬下软”的地层结构特性，土体基本参数见表 1。
表 1 试验场地土层基本参数Table 1. Basic mechanical parameters of in-situ tests土层名称 ρ/(g·cm-3) Es /MPa c/kPa φ/(°) 粉砂夹粉土 2.01 11.38 3.6 33.7 淤泥质粉质黏土 1.80 3.09 14.4 11.6 淤泥质粉质黏土夹粉土 1.85 3.31 14.5 11.8 注：ρ为天然密度，Es为压缩模量，c为黏聚力，φ为内摩擦角。 1.2 海上风电结构形式
以如东某近海风电场的一台筒型基础风电结构进行振动加速度测试，该风电结构离岸约61.0 km，额定功率为4.0 MW，额定转速为11.2 r/min，切入和切出风速分别为3 m/s和25 m/s，额定风速为10.2 m/s。由图 2可知，该海上风电整机结构由上部结构（叶片、轮毂和机舱）、塔筒和基础3部分组成。叶片直径为146.0 m，轮毂高度为95.0 m，上部结构（叶片、轮毂和机舱）质量约为255 t。塔筒为3段式安装，塔筒之间通过法兰连接，质量约为270 t。
如图 3所示，基础为复合筒型基础，总高42.5 m，泥面下部筒体高度10.0 m，底面直径32.0 m，筒壁厚度为0.02 m，分仓板厚0.025 m，筒体顶部浇筑有0.5 m厚混凝土层；泥面以上的结构为主筒体和撑杆，主筒体直径为5.5 m，壁厚为30~85 mm；撑杆直径为1.2~2.0 m，壁厚为25~35 mm。主筒体通过6根撑杆与筒体相连接，基础总质量约为2136t。
1.3 监测方案及参数
如图 2所示，在塔筒内壁共设置5个加速度测点，距离筒型基础上部筒身分别为15，25，50，75，90 m。原位观测采用1C302型电容式三向加速度传感器，该传感器轴向灵敏度175 mV/g，最大量程5g。采用DH2002在线监测分析系统进行动态采集，数据采集频率为50 Hz，数据通过4G信号无线传输至远程接收终端。值得注意的是，如图 2所示，考虑到机舱旋转造成的影响，安装在塔筒上的传感器测得的响应会有变化，因此，有必要根据偏航数据进行坐标转换，具体方法可参考文献[9]，不再赘述。
2. 海上风电结构模态参数识别方法
2.1 基于EEMD-SAA的数据降噪
集合经验模态分解（ensemble empirical mode decomposition，EEMD）是在原始信号上叠加若干次白噪声进行辅助分析，将多次分解后的固有模态函数平均值作为最终的（Intrinsic Mode Function）IMF分量，以解决经验模态分解（empirical mode decomposition，EMD）存在的模态混叠缺陷现象[10]。算法基本过程为：
步骤1：在原始信号基础上加入白噪声信号：
xi(t)=x(t)+gi(t)。 (1) 式中：xi(t)为加入噪声后的信号；x(t)为原始信号；gi(t)为白噪声信号。
步骤2：对xi(t)信号进行EMD分解，获取IMF分解分量：
xi(t)=m∑j=1aij(t)+ri(t)。 (2) 式中：aij(t)为第i次分解中的第j个IMF分解分量；m为IMF分解分量个数，ri(t)为残差余项。
步骤3：对各次加入噪声分解得到的IMF分解分量求均值得到最终的IMF分量，以抵消噪声对分解结果的影响：
ai(t)=1NN∑i=1aij(t)。 (3) 式中：N为加入噪声的次数。
模拟退火算法（simulated annealing algorithm, SAA）是一种全局优化方法，可以高效避免陷入局部最优解并最终趋于全局最优解，具有较强的全局收敛性、适应性和鲁棒性。EEMD算法的关键在于所加入白噪声信号的幅值和次数。过大或过小的白噪声幅值和次数都可能导致出现模式混叠现象[10]，因此本文引入SAA算法实现EEMD算法中白噪声信号参数的优化选择，实施步骤如下：
步骤1：构建极值点分布特性评价函数：
F(x)=N1∑i=1[Pmax (4) 式中：Pmax，Pmin为极大值点和极小值点位置系数；i，j是第i个极大值点和第j个极小值点；N1，N2是极大值和极小值数量。
步骤2：利用SAA算法寻优EEMD中白噪声幅值e的最优解。
步骤3：依据如下公式，计算白噪声加入次数：
\ln e + \frac{\beta }{2}\ln N = 0 。 (5) 式中：e为白噪声幅值；β为分解误差；N为次数。
2.2 基于SSI算法的模态参数提取
自该风电结构运行日起，提取风电结构工作状态下210 d内的550组测试文件。为更好地反映模态参数的时变性，每个测试文件均截取相同时长的不间断数据信息并进行EEMD-SAA联合降噪处理，以方便进行对比分析。需要注意的是，数据的截取时长会对识别结果造成一定影响，参照前人研究成果[9]，数据时长选取为20 min。
采用随机子空间算法（stochastic subspace identification，SSI）进行模态参数识别，其具有识别精度高、抗干扰性强及鲁棒性强等特点[11]，实施步骤如下：
步骤1：采用降噪数据构造Hankel矩阵，即Y=Yp/Yf，其中下标p表示“过去”，下标f表示“未来”。
步骤2：构造Toeplitz矩阵形式的协方差矩阵T1/i，即T1/i= Yf YpT。
步骤3：对矩阵T1/i进行奇异值分解得到观测矩阵Oi和控制矩阵Mi，计算公式为
\boldsymbol{T}_{1 / i}=\boldsymbol{U}_i \boldsymbol{S}_i \boldsymbol{V}_i=\boldsymbol{O}_i \boldsymbol{M}_i 。 (6) 式中：Si为主奇异值对角阵；Ui和Vi分别为左、右奇异矢量矩阵。
步骤4：计算系统状态矩阵A：
\boldsymbol{A}=\boldsymbol{O}_i^{+} \boldsymbol{T}_{2 / i+1} \boldsymbol{M}_i^{+}=\boldsymbol{S}_i^{-1 / 2} \boldsymbol{U}_i^{\mathrm{T}} \boldsymbol{T}_{2 / i+1} \boldsymbol{V}_i \boldsymbol{S}_i^{-1 / 2} 。 (7) 式中：上标+表示伪逆运算。
步骤5：对系统状态矩阵A进行特征值分析以得出模态参数，设时间间隔为 \Delta t ，特征值为zi，zi对应的第i个连续时间特征值为 {\lambda _i} ，则有 {\lambda _i} =ln zi/ \Delta t 。系统的固有频率和阻尼比则为
{f}_{i}=\frac{\left|{\lambda }_{i}\right|}{2{\rm{\mathsf{π}}}}\text{，}{\xi }_{i}\text{=}-\frac{\mathrm{Re}({\lambda }_{i})}{\left|{\lambda }_{i}\right|} 。 (8) 式中：fi为固有频率； {\xi _i} 为阻尼比；“Re”表示取实部。
3. 测试结果分析
3.1 风电结构振动加速度结果
图 4为低（3~5 m/s）、中（9~11 m/s）及高（15~17 m/s）3种风速范围下的塔筒顶部顺风向的加速度典型测试结果时程图。塔筒顶部加速度振动幅度与风速等级密切相关，但各时间点振动加速度峰值均未超过风机厂商限定值±0.08g，风电结构处于安全状态。
![]()
图 4 塔筒顶部#5测点典型测试结果Figure 4. Partial test results of structural acceleration at measuring point No. 5图 5为各位置测点顺风向加速度峰值与对应平均风速关系图。加速度峰值均随平均风速的增大近似呈线性增长，塔筒顶部与下部加速度差异值随着风速增大而明显增长。此外#4和#5测点监测结果的差异较小，加速度峰值交叉出现，说明存在塔筒中上部加速度大于塔筒顶部加速度值的现象，塔筒中上部段受机组发电机运行的显著影响。
3.2 模态参数时序分布特性
为说明结构整体响应规律及对比分析，图 6给出了利用塔筒下部和顶部两点加速度时序数据，识别得到的机舱径向及切向两个方向的基本模态频率和阻尼比。由图中的数据时序分布可以看出，不同测点时序数据识别得到的结果均表现出一定离散性和随机性。
模态频率方面，在机舱切向方向波动范围为0.294~ 0.320 Hz，在机舱径向方向波动范围为0.296~0.321 Hz；阻尼比方面，结构在机舱切向方向波动范围为1.65%~4.50%，在机舱径向方向波动范围为1.65~4.72%。
为避免风电结构在运行过程中发生共振，需保证整机运行在合理的安全频率范围内，本风电结构设计采用“软-刚”理念[9]，即结构频率需限制在1倍频的风轮旋转频率和3倍频的风轮旋转频率之间。根据设计资料，本风电结构频率允许波动范围为0.27~0.35 Hz，结合测试结果可知测试期间的风电结构模态频率均处于设计允许范围。
图 7为模态频率和阻尼比的分布直方图。由图可知，不同测点的模态频率及阻尼比分布区间基本一致，说明结构整体未发生不协调振动变形。模态频率及阻尼比均近似服从正态分布，且底部测点数据的拟合优度更高。综合两测点结果来看，径向频率主要集中在0.308~0.315 Hz，径向阻尼比主要集中在2.75%~3.5%；切向频率主要集中在0.302~0.306 Hz，切向阻尼比主要集中在2.25%~3.0%。此外，由测试数据可知径向方向的模态参数均大于切向方向，表明机舱径向方向为风电结构的主要振动方向。
3.3 频率与环境激励相关性
前述可知，采用不同数据序列识别的模态参数离散明显，从模态参数随环境激励的变化角度进行统计分析更具有准确性和科学性。风和浪荷载是影响海上风电结构振动响应的主要环境激励[7-9]。考虑到实际风和浪荷载的复杂性，为便于分析，在此分别选取平均风速及有效波高来代表风及浪的荷载激励。
分别统计反演数据样本对应的平均风速及有效波高平均值，并绘制二者与模态频率关系，如图 8所示。总体来看，不同测点处的径向和切向频率随风速变化趋势较为一致，且数据具有一定离散性，可能是受风向、温度及浪荷载等因素的耦合作用影响。
![]()
图 8 不同风速和波高下的结构模态频率Figure 8. Modal frequencies at different wind speeds and wave heights从图 8（a），（b）中可以看出，模态频率与风速之间呈负相关，且随着风速升高，模态频率的离散性有降低趋势，说明风荷载为控制风电结构振动特性的关键荷载。从图 8（c），（d）中可看出，与风速相关性不同，模态频率与波高之间没有表现出明显的相关性，且随着波高的变化，模态频率的离散性基本没有变化，说明波浪荷载对结构模态频率的影响较弱。此外，对比不同高程处结构模态频率的散点图，可以看出，相较于位于塔筒顶部的#5测点，塔筒低处#1测点的切向频率与径向频率的差值有所降低，二者数据重叠量明显增多。
为了进一步说明模态频率与风速等级的相关性，按风速范围1 m/s的间隔，将模态频率分组统计。其中，考虑到风速大于14 m/s的数据样本量有限，将其合并为1组，最终数据被划分为12组。
图 9给出了12组风速范围下径向频率和切向频率随风速变化的箱型图。总体而言，在相同风速范围时，不同测点处机舱径向频率的均值明显大于切向频率，切向频率的离散性略大于径向频率。从均值上看，当风速小于7 m/s时，结构径向和切向频率值随着风速增大发生微弱波动；当风速位于7~12 m/s时，结构径向和切向频率随着风速增大而发生近似线性减小；当风速大于12 m/s时，结构径向和切向频率值基本稳定，随着风速增大而发生小幅值波动，这主要是因为风速大于12 m/s的数据样本量较少，不足以精确反映出高风速情况下的结构模态参数分布特性。从离散性上看，结构径向和切向频率的离散程度随着风速增大呈现略有下降趋势。从测点位置上看，底部#1测点结果的离散性略高于顶部#5测点。
3.4 阻尼比与环境激励相关性
分别绘制结构阻尼比与数据样本对应时长范围的平均风速、有效波高的关系，如图 10所示。
![]()
图 10 不同风速和波高下的结构模态阻尼比Figure 10. Damping ratios at different wind speeds and wave heights实际结构模态阻尼比是结构材料阻尼、气动力阻尼、土体阻尼和基础辐射阻尼的共同作用结果[12]。从图 10（a），（b）可以看出，不同测点的径向阻尼比与风速呈正相关，且随着风速升高，其相关性有变强的趋势；而模态切向阻尼比与风速间的相关性相对较差，且其离散性受风速波动的影响不大，这是因为径向方向为主要振动方向，强烈的筒-土相互作用使得土体辐射阻尼效应得以充分发挥[12]，最终改变了结构模态径向阻尼比。相反的，切向方向非主振方向，土与筒型基础的相对位移较弱，辐射阻尼效应总体水平较低。
从图 10（c），（d）可以看出，不同测点的径向及切向阻尼比与波高的相关性均较差，表明波浪荷载非结构模态阻尼的主要影响因素。为更好地展现径向阻尼比与风速的相关性，绘制12组风速范围下径向阻尼比随风速变化的箱型图。
由图 11可知，风速范围位于3~6 m/s内的结构径向阻尼比均值呈上下波动趋势；当风速大于6 m/s时，结构径向阻尼比均值大体上呈波动上升趋势。从离散性上看，径向阻尼比的离散度随风速增大而发生小幅值波动，其基本不受风速变化的影响。此外，#1测点处的径向阻尼比整体大于#5测点。这可能是#1测点更靠近塔筒底部，受土体阻尼作用的影响更显著。
![]()
图 11 不同风速下的结构阻尼比箱型图Figure 11. Box diagram of modal damping ratio at different wind speeds4. 结构频率时变性的讨论
为研究结构频率的时变性，分别给出了8~9 m/s及13~14 m/s平均风速范围下结构径向频率随时间的变化趋势，如图 12所示。
随着测试时间推移，不同测点处的结构频率均出现一定程度退化。自测试开始至约第150 d（第375组数据）间，结构频率维持在较高的衰减速度；而第150 d后的结构频率衰减速度放缓，部分风速范围对应的结构频率在测试后期进入了平稳发展阶段。
实际上，本文研究的结构基频是结构特性、地基土特性、筒基础与地基土的接触作用特性3方面的综合体现。结构疲劳损伤、地基土弱（硬）化亦或筒-土接触作用的变化均会导致结构频率发生一定程度的改变。海洋环境下的结构疲劳损伤为渐变累积过程，结构损伤程度与时间呈正相关。前人的研究成果表明[13]：结构损伤会导致模态参数降低，且降低速率随损伤程度的增加而增大，即结构损伤导致的模态参数退化主要发生在后期阶段，这与本文中结构频率退化集中在初期阶段的规律并不同。因此，本文中的结构频率退化现象可排除结构损伤的影响，主要反映土体对筒型基础整体约束能力的下降。结合场地工程地质条件，从筒-土接触作用角度，分析可能有以下两种情况单独或同时发生：
（1）筒-土界面刚度弱化作用：如前文所述，场地表层为松散-稍密的粉砂夹粉土，砂-筒界面附近一定范围的土体在长期循环剪切作用下会发生土颗粒重新排列，形成剪切带[14]。剪切带累积收缩导致筒-土界面刚度的持续弱化：这是因为循环剪切作用下，处于高位势的砂土颗粒降低到较低位势的状态，部分小颗粒进入到大颗粒间的孔隙，进而导致松砂出现剪缩[15]。室内砂与钢板的循环剪切试验还表明，钢板-土界面弱化主要发生在初始阶段，随着循环次数的增加，钢板-土界面弱化速率不断降低并趋于平缓[16]，这与本文中结构频率退化速率随时间推移而降低的规律一致。
（2）海底潮流冲刷作用：测试风电结构的基础处于复杂水文环境下，不可避免会出现一定程度的冲刷掏蚀现象。而冲刷作用一方面直接降低了筒-土接触面积，另一方面增加了风电结构裸露于地基土体外的长度，导致结构自振周期增大[17-18]，这与本文中结构频率随时间推移而降低的现象相符。另外，本场地浅部的粉砂夹粉土层工程性能差，抗潮流冲刷能力弱，这与本文中结构频率快速退化阶段相对应；而地基深部为淤泥质粉质黏土层，抗潮流冲刷能力较强，符合本文中结构频率缓慢退化阶段的变化特征。
5. 结论与展望
本文以江苏如东复合筒型基础海上风电结构为研究对象，基于210 d的加速度监测数据，识别了550组不同环境激励下的结构模态参数，主要得到以下4点结论。
（1）结构模态参数总体服从正态分布，径向频率主要集中在0.308~0.315 Hz，径向阻尼比主要集中在2.75%~3.5%，切向频率主要集中在0.302~0.306 Hz，切向阻尼比主要集中在2.25%~3.0%，测试期间结构加速度和频率均处于设计允许范围。
（2）结构模态频率与风速之间呈负相关，且风速大于7 m/s后，相关性随着风速增大略有增加，离散性出现一定程度降低；结构模态频率与波高之间相关性始终较差，风荷载为风电结构振动特性的关键控制荷载。
（3）结构切向阻尼比和径向阻尼比随风荷载的变化规律不同，模态径向阻尼比与风速呈正相关，且随着风速升高，相关性有变强的趋势；而模态切向阻尼比与风速间的相关性较差，离散性受风速的影响不大。
（4）结构频率随时间推移出现了一定程度的退化，退化主要集中在测试期间的前150 d，反映出筒-土接触作用的减弱，可能表现为筒-土界面刚度弱化或海底潮流冲刷现象，后续可开展现场工作进行验证。
-
![]()
图 1 滑动面任意点的真实应力状况与极限平衡受力计算简图
Figure 1. Real stress states of any point on slip surface and calculation of limit equilibrium forces
![]()
图 2 滑面通过单元三角形微面矢量极限平衡计算简图
Figure 2. Calculation of vector limit equilibrium on triangle micro-plane of sliding surface over element
![]()
图 3 三角形微面矢量力在合矢量平面的投影示意图
Figure 3. Projection sketch of vector forces of triangular micro-plane in resultant vector plane
![]()
图 5 有限元网格及水平位移云图
Figure 5. Finite element meshes and nephogram of horizontal displacement
![]()
图 6 椭球滑动面对称面处无软夹层情况、有软夹层情况等效塑性应变云图
Figure 6. Equivalent plastic strain nephogram of ellipsoidal sliding surface without and with soft strata on symmetric plane
![]()
图 8 随投影方向角变化的安全系数、势能、势能比曲线
Figure 8. Curves of factor of safety, potential energy and potential energy ratio with respect to projection direction
![]()
图 9 楔体算例1与算例2有限元剖分网格图
Figure 9. Finite element meshes of wedges (example 1 and example 2)
![]()
图 10 楔体1对称材料、楔体1非对称材料、楔体2结构面单元的等效塑性应变云俯视图
Figure 10. Top views of equivalent plastic strain nephogram for wedge 1 (symmetric material), wedge 1 (asymmetric material) and wedge 2 in soft rock elements
![]()
图 11 楔体算例2合矢量平面内的矢量平衡图
Figure 11. Vector equilibrium of wedge 2 in resultant vector plane
![]()
图 12 楔体算例2随投影方向变化的安全系数、势能曲线
Figure 12. Variation of curves of factor of safety and potential energy of wedge 2 with projection direction
表 1 椭球滑动面土层力学参数
Table 1 Mechanical parameters of soil on ellipsoidal surface
参数 内摩擦角φ/(°) 黏聚力c/(kN·m-2) 重度/(kN·m-3) 弹性模量E/kPa 泊松比μ 剪胀角/(°) 土层 20 28.74 18.84 5.0×104 0.30 4 软层 10 0. 18.84 2.0×103 0.25 2 
下载: 导出CSV
表 2 椭球滑动面两种情况抗滑稳定计算结果
Table 2 Calculated results of stability of ellipsoidal sliding surface in two cases
计算方法 情况1无软夹层 情况2有软夹层 安全系数 与本文Kλ相比/% 安全系数 与本文Kλ相比/% Zhang-X极限平衡法[6] 2.122 -2.08 1.553 -14.13 Hungr简化Bishop法[6] 2.167 +0.04 1.620 -9.41 陈祖煜极限平衡法[2-3] 2.187 +0.96 1.640 -8.08 郑宏滑面极限平衡法[7-8] 2.140 -1.22 1.706 -3.89 Lam通用极限平衡法[9] — 1.603 -10.57 Huang极限平衡法[10] — 1.665 -6.46 Jiang主滑向极限平衡法[11] 2.127 -1.84 1.766 -0.37 极限分析上限法[3, 12] 2.262 +4.24 1.717 -3.23 应力数值解代数和法[13] — 1.607 -10.30 有限元应力主滑向极限平衡法[14] 2.226 +2.69 1.730 -2.46
下载: 导出CSV
表 3 矢量理论模型计算结果
Table 3 Calculation results of vector theoretical model
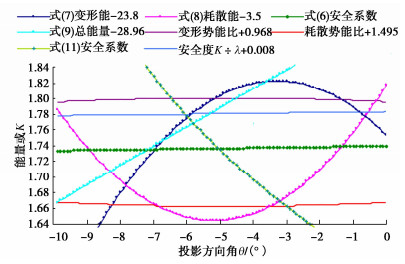
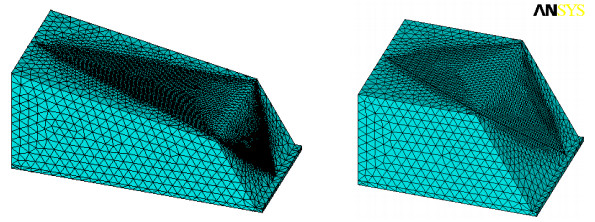
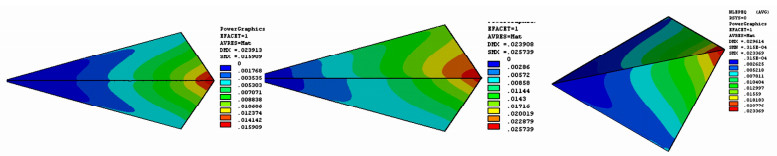
参数 本文矢量理论解 滑动力合矢量倾角和合矢量夹角δ 投影极值方向倾角和投影极值方向角θ 应力代数和法安全系数 滑面通过单元数和三角形微面数 情况1无软夹层 Kλ=2.1661，K=2.0546，λ=0.9485 倾角24.5607°，夹角δ=2.8630° 倾角32.8839°，θ=-8.3232° 代数和法K=2.1006，与本文Kλ相比为-3.12% 单元1606个，微面6420个 情况2有软夹层 Kλ=1.7725，K=1.7363，λ=0.9796 倾角25.8634°，夹角δ=1.1573° 倾角20.8109°，θ=-5.0528° 代数和法K=1.7404，与本文Kλ相比为-1.84% 单元1684个，微面6776个
下载: 导出CSV
表 4 楔体几何形体特征
Table 4 Geometric features of wedges
部位 楔体算例1 楔体算例2 倾向/(°) 倾角/(°) 倾向/(°) 倾角/(°) 左结构面 115 45 120 40 右结构面 245 45 240 60 顶面 180 10 180 0 坡面 180 60 180 60 楔体坡高/m 64.89 98.4
下载: 导出CSV
表 5 模型物理力学参数
Table 5 Physical and mechanical parameters of models
算例工况 内摩擦角φ/(°) 黏聚力c/(kN·m-2) 重度/(kN·m-3) 弹性模量E/kPa 泊松比 \nu 剪胀角/(°) 楔体1对称工况左右结构面 20 50 25.48 1.0×105 0.25 4 弹性岩体 25.48 5.0×106 0.20 楔体1非对称工况左结构面 20 50 25.48 1.0×105 0.25 4 右结构面 10 30 25.48 1.0×105 0.25 3 楔体2左右结构面相同 30 50 26.0 1.0×105 0.25 4 弹性岩体 26.0 5.0×106 0.20
下载: 导出CSV
表 6 楔体抗滑稳定算例计算结果
Table 6 Calculated results of anti-sliding stability of wedges
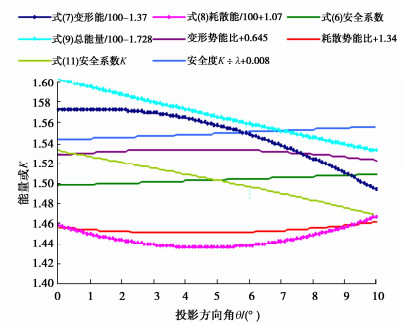
计算方法 楔体1材料对称 楔体1材料非对称 楔体2交线倾向11.3380° 安全系数 投影倾角/(°) 与本文比较/% 安全系数 投影倾角/(°) 与本文比较/% 安全系数 投影倾角/(°) 与本文比较/% 楔体极限平衡[15, 16] 1.5578 22.9098 +10.17 1.1815 22.9098 -7.91 1.6400 28.9964 +4.30 陈祖煜简化极限平衡法[2] 1.556 22.9098 +10.06 1.167 22.9098 -9.25 — 郑宏滑面严格平衡法[8] — 1.636 +4.07 极限平衡法[11] — 1.629 +3.66 主滑向应力代数和[14] — 1.497 -4.84
下载: 导出CSV
表 7 矢量理论模型计算结果
Table 7 Calculation results of vector theoretical model
参数 楔体1材料对称 楔体1材料非对称 楔体2交线倾向11.3380° 安全系数 投影倾角 安全系数 投影倾角 安全系数 投影倾角 本文矢量理论模型解 Kλ=1.3994 40.2520° Kλ=1.2750 28.7662° Kλ=1.5694 42.2410° 安全系数K和程度系数λ K=1.3365 λ=0.9551 K=1.2384 λ=0.9713 K=1.5034 λ=0.9580 合矢量夹角δ和投影倾向 δ=2.5649° 倾向0° δ=1.6438° 倾向1.6267° δ=2.3986° 倾向16.7218° 滑动力矢量倾角和倾向 倾角39.7084° 倾向0° 倾角29.1022° 倾向3.1532° 倾角44.0963° 倾向10.4716° 代数和法安全系数K K=1.3392 -4.50% K=1.2375 -3.03% K=1.4978 -4.78% 滑面通过单元和微面数 单元11616个 微面46493个 单元6936个 微面28014个
下载: 导出CSV
表 8 单元剖分尺寸对理论模型解的影响
Table 8 Influences of element size on solution of theoretical model
单元类型及尺寸 3 m四面体 3 m六面体 4 m六面体 5 m六面体 安全度系数Kλ 1.5711（+0.108%） 1.5694（0.0%） 1.5703（+0.057%） 1.5712（+0.115%） 安全系数K 1.5055 1.5034 1.5045 1.5054 程度系数λ 0.9582 0.9580 0.9581 0.9581 三角形微面数 28014 16417 10742 结构面单元数 13673 6936 4056 2646 单元总数 135732 342623 190545 127207 注：括号内数字为相对于3 m六面体单元的安全度系数Kλ变化率。
下载: 导出CSV
表 9 弹性模量变化对理论模型解的影响
Table 9 Influences of change of elastic modulus on solution of theoretical model
变化部位 弹性模量乘数 0.50 0.75 1.00 1.25 1.50 仅结构面 安全度系数Kλ 1.6042（+2.06%） 1.5858（+0.92%） 1.5712 1.5592（-0.77%） 1.5497（-1.39%） 程度系数λ 0.9623 0.9599 0.9581 0.9566 0.9553 仅岩体 安全度系数Kλ 1.5330（-2.49%） 1.5555（-1.01%） 1.5712 1.5825（+0.71%） 1.5920（+1.31%） 程度系数λ 0.9535 0.9562 0.9581 0.9595 0.9608 结构面
及岩体安全度系数Kλ 1.5711 1.5711 1.5712 1.5711 1.5712 程度系数λ 0.9581 0.9581 0.9581 0.9581 0.9584 注：括号内数字为相对于弹性模量乘数1.00的安全度系数Kλ变化率。
下载: 导出CSV
表 10 泊松比变化对理论模型的影响
Table 10 Influences of Poisson's change on solution of theoretical model
部位 泊松比μ μ=0.15 0.20 0.25 0.30 0.350 结构面 安全度系数Kλ 1.5849（+0.86%） 1.5787（+0.75%） 1.5712（0.0%） 1.5619（-0.60%） 1.4827（-1.29%） 程度系数λ 0.9601 0.9593 0.9581 0.9571 0.9559 岩体 安全度系数Kλ 1.5577（-0.87%） 1.5712（0.0%） 1.5856（+0.91%） 1.6016（+1.90%） 1.6171（+2.84%） 程度系数λ 0.9570 0.9581 0.9593 0.9609 0.9622 两者同比例 泊松比乘数 0.75μ 0.8μ 1.0μ 1.2μ 1.4μ 安全度系数Kλ 1.5685（-0.17%） 1.5689（-0.15%） 1.5712（0.0%） 1.5750（+0.24%） 1.5805（+0.59%） 程度系数λ 0.9584 0.9584 0.9581 0.9581 0.9583 注：括号内数字为相对于结构面泊松比μ=0.25、岩体泊松比μ=0.20的安全度系数Kλ变化率。
下载: 导出CSV
表 11 剪胀角变化对理论模型解影响
Table 11 Influences of change of dilatancy angle on theoretical model
剪胀角 0° 2° 4° 6° 8° 安全度系数Kλ 1.5800（+0.56%） 1.5753（+0.26%） 1.5712（0.0%） 1.5681（-0.20%） 1.5646（-0.42%） 安全系数K 1.5207 1.5126 1.5054 1.4997 1.4935 程度系数λ 0.9625 0.9602 0.9581 0.9564 0.9546 注：括号内数字为相对于剪胀角4°的安全度系数Kλ变化率。
下载: 导出CSV
表 12 不同塑性准则对理论模型解的影响
Table 12 Influences of different plastic criteria on solution of theoretical model
塑性准则 等底面积D-P 外接圆D-P 弹性 安全度系数Kλ 1.5712 1.4200（-10.64%） 1.2960（-21.23%） 安全系数K 1.5054 1.3315 1.1801 程度系数λ 0.9581 0.9397 0.9106 滑动力合矢量/(104 kN) 292.525 306.053（+4.42%） 321.222（+8.93%） 滑动力合矢量倾角/(°) 44.1091 48.5751 51.6391 抗滑力合矢量/(104 kN) 439.202 405.907（-8.20%） 379.014（-10.63%） 合矢量夹角/(°) 2.3900 3.5533 5.1188 极值方向倾角/(°)
极值方向倾向/(°)42.3137
16.560146.8366
20.854551.4313
19.4447注：括号内数字为相对于等底面积D-P准则的变化率。
下载: 导出CSV
-
[1] DUNCAN J M. State of the art: limit equilibrium and finite-element analysis of slopes[J]. Journal of Geotechnical Engineering, 1996, 122(7): 577-596. doi: 10.1061/(ASCE)0733-9410(1996)122:7(577)
[2] 陈祖煜, 弥宏亮, 汪小刚. 边坡稳定三维分析的极限平衡方法[J]. 岩土工程学报, 2001, 23(5): 525-529. http://cge.nhri.cn/article/id/10783 CHEN Zuyu, MI Hongliang, WANG Xiaogang. A three-dimensional limit equilibrium method for slope stability analysis[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(5): 525-529. (in Chinese) http://cge.nhri.cn/article/id/10783
[3] 陈祖煜. 土质边坡稳定分析: 原理·方法·程序[M]. 北京, 中国水利水电出版社, 2003. CHEN Zuyu. Soil Slope Stability Analysis: Theory, Methods and Programs[M]. Beijing: China Water Power Press, 2003: 335-376. (in Chinese)
[4] 孙建生. 基于有限元应力载荷宏观刚性滑裂面极限平衡抗滑稳定计算理论[J]. 岩石力学与工程学报, 2018, 37(4): 862-875. SUN Jiansheng. Theoretical model of stability calculation of macro-rigid sliding planes with FEM stress load based on limit equilibrium[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(4): 862-875. (in Chinese)
[5] 孙建生. 投影方向极值原理的滑裂面应力矢量极限平衡抗滑稳定计算理论[J]. 计算力学学报, 2023, 40(1): 93-104. SUN Jiansheng. Theoretical model of limit equilibrium anti-sliding stability of stress vector on sliding planes based on projection direction extreme principle[J]. Chinese Journal of Computational Mechanics, 2023, 40(1): 93-104. (in Chinese)
[6] XING Z. Three-dimensional stability analysis of concave slopes in plan view[J]. Journal of Geotechnical Engineering, 1988, 114(6): 658-671. doi: 10.1061/(ASCE)0733-9410(1988)114:6(658)
[7] 郑宏. 严格三维极限平衡法[J]. 岩石力学与工程学报, 2007, 26(8): 1529-1537. doi: 10.3321/j.issn:1000-6915.2007.08.002 ZHENG Hong. A rigorous three-dimensional limit equilibrium method[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(8): 1529-1537. (in Chinese) doi: 10.3321/j.issn:1000-6915.2007.08.002
[8] ZHENG H. Eigenvalue problem from the stability analysis of slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(5): 647-656. doi: 10.1061/(ASCE)GT.1943-5606.0000071
[9] LAM L, FREDLUND D G. A general limit equilibrium model for three-dimensional slope stability analysis[J]. Canadian Geotechnical Journal, 1993, 30(6): 905-919. doi: 10.1139/t93-089
[10] HUANG C C, TSAI C C. New method for 3D and asymmetrical slope stability analysis[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(10): 917-927. doi: 10.1061/(ASCE)1090-0241(2000)126:10(917)
[11] JIANG Q H, ZHOU C B. A rigorous method for three-dimensional asymmetrical slope stability analysis[J]. Canadian Geotechnical Journal, 2018, 55(4): 495-513. doi: 10.1139/cgj-2017-0317
[12] CHEN Z Y, WANG X G, HABERFIELD C, et al. A three-dimensional slope stability analysis method using the upper bound theorem[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(3): 369-378. doi: 10.1016/S1365-1609(01)00012-0
[13] STIANSON J R, FREDLUND D G, CHAN D. Three-dimensional slope stability based on stresses from a stress-deformation analysis[J]. Canadian Geotechnical Journal, 2011, 48(6): 891-904. doi: 10.1139/t11-006
[14] 苏振宁. 三维边坡稳定有限元极限平衡法研究及应用[D]. 大连: 大连理工大学, 2021. SU Zhennin. Research and Application of Finite Element Limit Equilibrium Method for Three-Dimensional Slope Stability[D]. Dalian: Dalian University of Technology, 2021. (in Chinese)
[15] HOEK E, BRAY J D. Rock Slope Engineering[M]. 3rd ed. Boca Raton: CRC Press, 1981.
[16] 陈祖煜. 岩质边坡稳定分析: 原理·方法·程序[M]. 北京: 中国水利水电出版社, 2005. CHEN Zuyu. Rock Slope Stability Analysis: Theory, Methods and Programs[M]. Beijing: China Water & Power Press, 2005. (in Chinese)
[17] CHEN Z Y, MI H L, ZHANG F M, et al. A simplified method for 3D slope stability analysis[J]. Canadian Geotechnical Journal, 2003, 40(3): 675-683. doi: 10.1139/t03-002
[18] 赵尚毅, 郑颖人, 刘明维, 等. 基于Drucker-Prager准则的边坡安全系数定义及其转换[J]. 岩石力学与工程学报, 2006, 25(增刊1): 2730-2734. ZHAO Shangyi, ZHENG Yingren, LIU Mingwei, et al. Definition and transformation of slope safety factor based on Drucker-Prager criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(S1): 2730-2734. (in Chinese)
[19] 孙建生. 挡土墙土压力研究的错误倾向[J]. 岩土工程学报, 2016, 38(7): 1324-1329. doi: 10.11779/CJGE201607021 SUN Jiansheng. Error tendency for studying earth pressure on retaining walls[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(7): 1324-1329. (in Chinese) doi: 10.11779/CJGE201607021
[20] 孙建生. "矢量和法" 抗滑稳定计算模型的力学概念错误[J]. 岩土工程学报, 2021, 43(5): 975-980. doi: 10.11779/CJGE202105024 SUN Jiansheng. Mechanical concept errors in anti-sliding stability computational model of "vector sum method"[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(5): 975-980. (in Chinese) doi: 10.11779/CJGE202105024
[21] 孙建生. 关于"稳定安全系数计算公式中荷载与抗力错位影响探讨"的质疑[J]. 岩土工程学报, 2021, 43(11): 2146. doi: 10.11779/CJGE202111024 SUN Jiansheng. Query about "Discussion of dislocation phenomena of resistance and load in formula for stability safety factor"[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(11): 2146. (in Chinese) doi: 10.11779/CJGE202111024
计量
- 文章访问数: 297
- HTML全文浏览量: 44
- PDF下载量: 95
