Similarity optimization of reduced-scale model tests on break of homogeneous clay dam due to overtopping
-
摘要: 为进一步研究土石坝漫顶溃坝模型与原型之间的相似性问题，从均质黏土坝在水流冲刷作用下的起动极限状态分析入手，提出调整筑坝压实度来降低缩尺模型坝的抗冲刷能力，进而达到漫顶溃坝过程相似性优化的设想。基于黏土的抗剪强度及黏聚力会随着压实度的降低呈非线性减小，以某土石坝工程的漫顶溃坝分析为原型，开展了不同压实度和几何比尺条件下的均质黏土坝相似漫顶流槽试验。结果表明：采用与原型黏土坝相同筑坝密实度的模型坝溃决过程与原型完全不相似，模型与原型之间的差异性会随着几何比尺的增加而愈发明显；适当减小黏土模型坝的压实度能够显著提升模型坝与原型在溃坝形态、溃决时间等溃坝过程相似性。Abstract: The reduced-scaled physical model test under the conventional gravity of 1g is an important and common method for analyzing failure of embankment dams due to overtopping. However, the similarity of the overtopping failure process between the prototype embankment dam and the scaled model is a lasting technical problem to be resolved. Based on the incipient limit state analysis of homogeneous clay dams under the action of overtopping flow, the idea of adjusting the compaction degree of the model dam is proposed to reduce its erosion resistance so that the similarity optimization on the overtopping failure process of the homogeneous clay dam can be achieved. The shear strength and cohesion of clay decrease nonlinearly with the decrease of compaction degree. Taking the dam break of an actual embankment dam as the prototype, similar hydraulic flume tests on break of homogeneous clay dams due to overtopping are conducted with different compaction degrees and geometric scales. The results show that the breaching process of the model dam with the same compactness as the prototype is completely different from that of the prototype, and the difference between the model and the prototype will become more significant with the decrease of the geometric scale. Appropriately reducing the compaction degree of the model clay dam can significantly improve the similarity between the model and the prototype in breach processes such as breach morphology and time.
-
Keywords:
- overtopping /
- dam break /
- homogeneous clay /
- reduced-scale model test /
- inception /
- compaction degree
-
0. 引言
城市化进程的快速发展导致地下空间的开发和利用不断增加，由此出现了许多深大基坑。城市大多建于第四纪松散沉积物之上，其下分布有水位高、厚度大的承压含水层。为防止承压水突涌给基坑带来的风险，常采用降水的方式来降低承压水水位。基坑降水使得土体固结，从而可能导致地面沉降、地面塌陷、建筑物开裂等环境问题的产生。因此，一般采用止水帷幕以减少降水对环境的影响。由于承压含水层厚度大，止水帷幕造价高，大多数工程采用悬挂式止水帷幕。
在环境保护要求较高的地区基坑降水时，悬挂式止水帷幕不足以有效控制地面沉降，地下水回灌作为一种比较经济的措施在工程中得到了广泛应用[1-3]。如上海汉中路枢纽站开挖降水过程中，在需保护建筑物周边布设了6口回灌井进行回灌后，坑内降水并未引起建筑物沉降[4]。当抽水井和回灌井共同工作时，坑内抽水使得坑内承压水位降至安全水位以下，以确保基坑的安全；坑外回灌使得其周边构筑物下承压水位下降较少，从而达到保护环境的目的。而抽水和回灌的效果最直观的表现在于基坑内外的水位变化上。一般情况下，开挖降水过程中基坑内观测井能够实时观测承压水的水位。然而，在实际工程中，因施工场地限制，布设的坑外观测井较少，而且在施工过程中坑外观测井经常遭受破坏、掩埋等，无法正常工作。在这些因素下，能够用于监测坑外水位的观测井很少，甚至没有。
目前常用数值分析法模拟计算抽灌水过程中基坑内外地下水的分布情况[5-6]。但是，建立数学模型比较复杂，现场工程师不能直接应用。工程现场的工程师更愿意使用简单实用的公式快速计算现场的水位差。Pujades等[7]提出了承压含水层中长条形构筑物（水平方向或垂直方向完全隔断含水层）两侧水位差的计算方法，该方法不考虑源汇项。Shen等[8]提出了悬挂式止水帷幕下基坑内降水时止水帷幕两侧的水位差的计算方法，在已知坑内水位的前提下可获得坑外的最大水位降深；该方法仅考虑了基坑内抽水的情况，并未考虑坑外回灌。因此本文的目的为探明回灌作用下止水帷幕两侧水位差与止水帷幕插入承压含水层深度、含水层各向异性、含水层厚度及天然水力梯度间的关系，进而提出一种能直接计算基坑内外抽灌承压含水层止水帷幕两侧水位差的计算方法。
1. 帷幕-井作用机理
基坑内外抽灌水可看作是抽水和回灌的叠加。关于悬挂式止水帷幕下基坑内抽水时帷幕-井作用机理，已有很多文献进行过详细的论述，此处不再赘述。
图 1为基坑外回灌时止水帷幕对渗流场阻挡示意图。回灌时，若无止水帷幕，则承压含水层水位线为具有轴对称性质的连续曲线，如图 1曲线hrn (由于对称性，此处仅显示含止水帷幕一侧水位)；当存在止水帷幕时，承压含水层水位线变为不连续曲线(曲线hr)。与无止水帷幕作用下相比，由于止水帷幕的阻挡作用，基坑外靠近回灌井一侧水位雍高，基坑内水位降低，基坑外远离回灌井一侧水位降低。
![]()
图 1 回灌时止水帷幕对承压含水层阻隔剖面图Figure 1. Barrier effects of waterproof curtain during recharging图 2为抽灌作用下止水帷幕对承压含水层阻隔剖面图。图 2中所示基坑中心有一口抽水井抽取承压水，止水帷幕的存在使得基坑内外承压水位出现水位差，且以抽水井为对称轴对称分布(曲线hp)。当在基坑外某一侧承压含水层中布设回灌井进行回灌时，水位的分布发生了变化，不再对称分布(曲线hrp)。且在非完整井和止水帷幕的附近均出现了三维流。由于止水帷幕的阻挡作用，回灌水主要进入了坑外承压含水层中，另有部分回灌水通过止水帷幕下方进入基坑，进入基坑的回灌水有小部分通过远离回灌井的止水帷幕下方流出基坑。而水位的抬升量与灌入的水量密切相关，整体来看，基坑内外水位均有所抬升。靠近回灌井一侧，水位抬升比较大；远离回灌井一侧，水位抬升比较小。
![]()
图 2 抽灌时止水帷幕对承压含水层阻隔剖面图Figure 2. Barrier effects of waterproof curtain during pumping and recharging2. 基于数值模拟的帷幕两侧水位差的计算方法
2.1 基坑内抽水
关于悬挂式止水帷幕下基坑内降水，Wu等[9]研究中已详细分析了承压水位沿含水层竖直方向的分布特征。图 3为不同止水帷幕深度下，抽水稳定后帷幕两侧承压含水层水位降深沿含水层深度的分布。在含水层顶部，基坑内水位降深最大，基坑外水位降深最小；在含水层底部，坑内外水位降深与含水层顶部相反。即沿含水层纵向深度，止水帷幕两侧的水位差逐渐减小。造成这种差异的主要原因是：离止水帷幕底板越远，承压水通过止水帷幕下方进入基坑时其渗流路径越长。根据Darcy定律，渗流路径越长，水位的变化越小，即含水层顶部坑外水位降深最小。
![]()
图 3 抽水作用下含水层竖向深度与水位降深关系图Figure 3. Relationship between longitudinal depth and drawdown in confined aquifer under pumping基于上述承压水位的分布特性，Shen等[8]通过Darcy定律和对大量数值模拟的结果分析获得了基坑内抽水时止水帷幕两侧最大水位降深差的计算公式。公式表明，水位差Δhp与止水帷幕插入承压含水层的深度、承压含水层的水平及垂向渗透系数、止水帷幕的宽度和承压含水层的厚度有关。具体如下：
Δhp={inLb(1.32bbd(kxkz)58(10b)0.3668lnb−0.852bLb+bbd1−bbd+1) (bbd<0.25)inLb(√18ln(6b1.1bd(1−bbd)2.23)(kxkz)58(10b)0.3668lnb−0.852bLb+bbd1−bbd+1) (bbd≥0.25)， (1) 式中：in为止水帷幕未进入承压含水层时其两侧的水力梯度；Lb为止水帷幕的宽度；b为承压含水层的厚度；bbd为止水帷幕插入承压含水层的相对厚度；kx，kz分别为承压含水层的水平向和垂向渗透系数。
2.2 基坑外回灌
（1）止水帷幕两侧水位差的形成
地下水的回灌可以看作是抽水的逆过程，区别在于，坑内抽水时坑外承压水通过止水帷幕下方进入基坑；而回灌时回灌水经靠近回灌井的止水帷幕（第一道）进入基坑，之后部分回灌水经远离回灌井的止水帷幕（第二道）流出基坑。由于渗流路径不同，故两道止水帷幕两侧的水位差明显不同（图 1所示）。止水帷幕产生的水位差，一方面是渗流面积减少引起的，用srbi表示；一方面是渗流方向和渗流路径的改变引起的，用srbo表示。srbi和srbo如下所示：
srbi=Δhrb−Δhrn， (2) srbo=Δhrt−Δhrb， (3) Δhrn=irnLb。 (4) 式中：Δhb为止水帷幕两侧含水层底部的水位差；Δhrt为止水帷幕两侧含水层顶板水头差；Δhrn为止水帷幕未进入承压含水层时，止水帷幕两侧的水头差；irn为止水帷幕未进入承压含水层回灌时止水帷幕两侧水力梯度。
当回灌井为完整井时，可根据Thiem[10]公式（式（5））计算irn。当回灌井为非完整井时，如果rb≥1.5b，则用式（5）计算irn；若rb < 1.5b，则irn根据Kozeny[11]经验公式（式（6））进行计算：
irn=Qrw2π TLBln(1+LBrb), (5) irn=1DQw2π TLbln(rb0rb)， (6) D=bsb(1+7√rw2bs⋅cosπ bs2b)。 (7) 当srbi，srbo和Δhrn确定后，则可以采用下式计算出回灌作用下止水帷幕两侧的水位差：
Δhr=srbo+srbi+irnLb。 (8) 由于止水帷幕的存在，srbi和srbo难以直接用解析计算公式进行计算。因此借助数值模拟法，不同止水帷幕下水位的分布规律，将数值计算结果进行回归分析，进而得出srbi和srbo的值。为使计算结果具有一般性，将srbi和srbo无量纲化，其无量纲形式分别为
srbid=srbi/(irnLb)， (9) srbod=srbo/(irnb)。 (10) 无量纲形式表明srbid和srbod与回灌井过滤器的长度无关。第一道、第二道止水帷幕两侧无量纲形式水位差分别用s1rbid和s1rbod，s2rbid和s2rbod表示。
（2）数值计算模型
a）分析范围及网格划分
为获得基坑外回灌时止水帷幕两侧的水位差的计算公式，采用三维有限差分软件Visual Modflow建立数学模型，分析采用圆形基坑（见图 5）。基坑半径为18 m，止水帷幕宽度为1 m。假设在基坑外距离止水帷幕15 m处有一口回灌井，回灌量为300 m3/d。土层的分布以上海典型地层为依据，水文地质情况自上而下分别为：潜水层；第Ⅰ相对隔水层；承压含水层及第Ⅱ相对隔水层。止水帷幕在承压含水层的相对位置如图 4所示。
模型在水平方向以基坑中心点为中心向外扩展，以消除边界条件对计算结果的影响，分析范围为830 m×820 m。水平方向网格从基坑向外由密到疏，竖直方向地面以下44 m。要分析srbid和srbod与止水帷幕插入承压含水层深度间的关系，将承压含水层在竖直方向细化，划分为20层，其它土层各划分为1层，故网格在竖直方向共分为29层。图 5为网格剖分图，图中不同颜色代表不同的土层。
b）模型参数
模型中计算参数见表 1。土层厚度基于上海500 kV世博变电工程，承压含水层渗透系数及储水率来源于该工程抽水试验报告[12]，其它土层参数取值基于室内试验。止水帷幕起隔水作用，其渗透系数取值为10-9 m/s。
表 1 模型计算参数Table 1. Model parameters土层名称 水文地质 厚度/m kx/(m·d-1) Kz/(m·d-1) Ss/m-1 ②粉质黏土 Aq0 3 8×10-4 5×10-4 1×10-6 ③淤泥质粉质黏土 5 5.1×10-4 2.7×10-4 1×10-6 ④淤泥质黏土 7 2.4×10-4 1.4×10-4 1×10-6 ⑤1-1黏土 AdI 5 3.03×10-3 1.74×10-3 1×10-6 ⑤1-2粉质黏土 6 2.5×10-4 1.17×10-3 1×10-6 ⑥粉质黏土 4 2.8×10-4 1.5×10-4 1×10-6 ⑦粉砂 AqI 10 3.6 3.6 6×10-5 ⑧粉质黏土 AdII 4 8×10-4 5×10-4 1×10-6 注：kx，kz分别为水平渗透系数和垂向渗透系数，Ss为储水率。 c）边界和初始条件
模型中初始潜水含水层和第Ⅰ相对隔水层水位取为地面下-1 m，承压含水层和第Ⅱ相对隔水层水位取为地面下-7 m。边界远离回灌井，故四周采用定水头边界条件，其水位同初始条件；底部为隔水边界。回灌井为模型的唯一源汇项；过滤器位于承压含水层中，长度为10 m。此外，基坑内外各有2个计算点，计算点在止水帷幕的两侧。
（3）帷幕两侧承压含水层水位竖向分布规律
通过建立的三维模型计算回灌作用下承压含水层竖向深度水位的抬升。为和抽水下的水位降深作比较，计算中⑦粉砂层垂向渗透系数取为0.6 m/d。为使计算结果具有一般性，采用无量刚形式。无量纲水位抬升sd为模型计算出的水位变化量s与特征水位抬升量sc的比值，其中sc计算公式如下：
sc=Qrw/(2π T)。 (11) 变换后的无量纲形式不再受承压含水层厚度、土层导水系数及回灌量的影响。
图 6为回灌作用下含水层竖向深度与水位抬升的关系图。由图 6可知，止水帷幕插入承压含水层的深度越大，基坑外水位抬升量越大，基坑内越小。在承压含水层的上部和下部，止水帷幕深度对水位抬升量的影响较小；止水帷幕上方20%含水层厚度的范围内，水位变化较大。比较图 3，6发现，基坑内抽水时止水帷幕对基坑内外水位差影响程度远大于基坑外回灌。
![]()
图 6 回灌作用下含水层竖向深度与水位抬升关系图Figure 6. Relationship between longitudinal depth and drawdown in confined aquifer under recharging（4）帷幕两侧水位差与止水帷幕深度关系
改变止水帷幕插入承压含水层的深度，共计20个工况，计算每种工况下止水帷幕两侧的水位差，即C1与C2、C3与C4之间的水位差，并根据式（9），（10）转化为无量纲形式。
图 7为止水帷幕插入承压含水层的相对深度bbd与帷幕两侧无量纲水位差间的关系。图 7中s1rbid0，s2rbid0分别为回灌水经过第一道和第二道止水帷幕因渗流面积减少引起的水位差；s1rbod0，s2rbod0分别为第一道和第二道止水帷幕因渗流方向和渗流路径的改变引起的水位差。由图 7可知，止水帷幕插入承压含水层的相对深度bbd越大，s1rbid0和s2rbid0越大。当bbd ≤ 0.85时，bbd越大，s1rbod0和s2rbod0越大；当bbd > 0.85时，bbd越大，s1rbod0和s2rbod0越小。图中的点可用指数函数进行拟合，拟合曲线的相关系数R2分别为0.997和0.998，拟合公式如下所示：
s1rbid0=0.5b1.4bdeb2bd(1−bbd)0.28， (12) s1rbod0=2.5b1.3bde−b1.6bd(1−bbd)0.05， (13) s2rbid0=0.5b1.1bdeb0.8bd(1−bbd)0.31， (14) s2rbod0=2.8b1.85bde−b1.6bd(1−bbd)0.08。 (15) ![]()
图 7 帷幕两侧无量纲水位差与bbd关系图Figure 7. Relationship between dimensionless water level difference and bbd上述公式表明，无量纲水位差仅与止水帷幕插入承压含水层的相对深度有关。
（5）影响因素分析
式（12）~（15）是基于各向同性含水层且以含水层厚度为10 m的圆形基坑为前提。因此需讨论含水层的各向异性、含水层厚度及止水帷幕形状对计算结果的影响。
a）含水层各向异性
将含水层各向同性时分析所得曲线（图 7）作为标准曲线，分别计算承压含水层水平向渗透系数kx分别是3倍、6倍和10倍垂向渗透系数kz的情况下，止水帷幕两侧水位差与止水帷幕插入承压含水层深度之间的关系。计算过程中，更改垂向渗透系数，其它参数保持不变。图 8给出了含水层各向异性对第一道止水帷幕两侧水位差的影响。从图 8可以看出，不同垂向渗透系数下，所得曲线与标准曲线不重合；且相同止水帷幕深度下，kz越小，s1rbid1越小，s1rbod1越大。
![]()
图 8 含水层各向异性对s1rbid和s1rbod的影响Figure 8. Effects of aquifer anisotropy on s1rbid and s1rbodb）含水层厚度
更改含水层的厚度，其它参数保持不变。分别计算b=8 m，b=16 m，b=20 m和b=30 m时，止水帷幕两侧水位差与止水帷幕插入承压含水层深度之间的关系。b=8 m时，回灌井过滤器长度为8 m，其它条件下均为10 m。图 9给出了含水层厚度对第一道止水帷幕两侧水位差的影响。从图 9中可以看出，当含水层厚度b大于10 m时，相同止水帷幕深度下，s1rbid及s1rbod均随含水层厚度增加而减小；当b小于10 m时，含水层厚度对计算结果几乎无影响。此外，当bbd≤0.5时，含水层厚度对s1rbid影响较小；当bbd≤0.25时，含水层厚度对s1rbod影响较小。
![]()
图 9 含水层厚度对s1rbid和s1rbod的影响Figure 9. Effects of aquifer thickness on s1rbid and s1rbodc）止水帷幕形状
以上计算结果是基于圆形基坑获得的，改变基坑的形状，即改变止水帷幕的形状。假设基坑为矩形，长度为50 m，宽度为36 m；其它参数保持不变。计算矩形基坑在不同止水帷幕深度下帷幕两侧的水位差。图 10分别给出了矩形基坑和圆形基坑下第一道止水帷幕两侧水位差与止水帷幕插入承压含水层深度之间的关系。由图 10可知，当bbd≤0.85时，止水帷幕形状对s1rbid无影响；当bbd＞0.85时，止水帷幕形状对s1rbid影响较小。当bbd≤0.6时，止水帷幕形状对s1rbod无影响；当bbd＞0.6时，止水帷幕形状对s1rbid影响较小。总体来说，止水帷幕形状对止水帷幕两侧水位差的影响很小。
![]()
图 10 止水帷幕形状对s1rbid和s1rbod的影响Figure 10. Effects of aquifer thickness on s1rbid and s1rbod含水层各向异性、含水层厚度及止水帷幕形状对第二道止水帷幕两侧水位差的影响具有相似的规律。
（6）止水帷幕两侧水位差的计算
如果要利用式（12）~（15）计算无量纲水位差，则需要对含水层各向异性和含水层厚度进行修正，修正后图 8和图 9中的所有计算点应落在标准曲线附近。
修正无量纲水位差并代入式（8）~（10）后，可得到回灌作用下止水帷幕两侧水位差的计算公式，具体如下：
第一道止水帷幕两侧水位差：
Δh1r=i1rnLB[52b1.3bde−b1.6bd(1−bbd)0.05(kxkz)720(10b)0.032lnb−0.78bLB+12b1.4bdeb2bd(1−bbd)0.28(kxkz)−514(10b)0.3lnb−0.3+1]。 (16) 第二道止水帷幕两侧水位差：
Δh2r=i2rnLB[2.8b1.85bde−b1.6bd(1−bbd)0.08(kxkz)47100i2rnb+12b1.1bdeb0.8bd(1−bbd)0.31(kxkz)−310(10b)0.23lnb−0.1+1]。 (17) 式中：i1rn和i2rn分别为止水帷幕未进入承压含水层时两道止水帷幕两侧的水力梯度。
2.3 坑内外抽灌共同作用
止水帷幕作用下基坑内抽水基坑外回灌时，止水帷幕两侧的水位差可以看作是抽水引起的水位差和回灌引起的水位差的叠加。第一道止水帷幕对回灌水的作用表现为止水帷幕两侧坑外水位的雍高大于坑内，即增加了止水帷幕两侧的水位差；第二道止水帷幕对回灌水的作用与第一道止水帷幕相反，减少了止水帷幕两侧的水位差。因此第一道及第二道止水帷幕两侧水位差的解析计算公式分别为
Δh1=Δhp + Δh1r， (18) Δh2=Δhp−Δh2r。 (19) 如果抽水井和回灌井是完整井，则式（1），（16）和（17）中in，i1rn和i2rn可以通过式（5）进行计算；如果抽灌井为非完整井，则可采用式（6）进行计算。此外，如果有多口井抽水或回灌水，只需将每口井在止水帷幕两侧产生的in，i1rn和i2rn进行叠加，即所提出的计算公式可以用于多口井抽水及回灌。
3. 工程应用
相关文献中没有发现止水帷幕作用下基坑内外抽灌地下水的工程实例，故选择现场抽水试验工程。通过数值模拟方法对工程实测数据进行反演，确定含水层的水文地质参数。在同一数值模型下，假设基坑内有抽水井抽水基坑外有回灌井进行回灌，将数值模拟计算结果与上述提出的回归公式法所得结果进行比较，对所提出的计算方法进行验证。
3.1 工程概况
上海市某轨道交通地下区间风井基坑工程（Wu等[13]），基坑长49 m，宽22.5 m，开挖深度28.15 m；采用地下连续墙作为围护结构，地下连续墙宽1.2 m，深48.6 m。基坑平面布置图如图 11所示。该工程位于上海正常土层分布区，在65 m深度范围内，分布有潜水含水层和承压含水层，厚度分别为21.1，37.7 m。土层地质剖面图如图 12所示。
3.2 抽水试验
为获得承压含水层的渗透系数，在基坑开挖前进行了抽水试验。试验井平面如图 11所示。其中W1为抽水井，井深50 m，过滤器长17 m，井径为273 mm；G1为观测井，井深43 m，过滤器长10 m。试验期间，抽水井抽水量为744 m3/d。Wu等[13]通过数值模拟分析法获得了承压含水层的水文地质参数（图 12）。
3.3 结果分析
假设基坑外有一口回灌井（图 11），回灌井井结构同抽水井。基坑内抽水井以744 m3/d的抽水量抽水2 d后，开启基坑外回灌井，回灌井回灌量为360 m3/d。抽灌共同作用时间为3 d。分别应用本文提出的回归公式法和数值法分析计算C1和C2及C3和C4两侧的水位差。
（1）回归公式法
根据图 12，⑦1砂质粉土及⑦2粉细砂水平向渗透系数分别为2.6，3.6 m/d，垂向渗透系数分别为0.6，1.1 m/d；故承压含水层水平向与垂向加权平均渗透系数比为3.4 m/d，导水系数T为131 m2/d。本工程承压含水层的顶板埋深为27.6 m，地下连续墙进入承压含水层的相对深度bbd为0.55。由图 11可知，抽水井和回灌井与各计算点的距离小于1.5倍承压含水层厚度，因此在计算抽水井或回灌井引起的水位降深时，需要考虑井的非完整性，采用Kozeny经验公式计算。将相关数值代入式（6），（7）后，可计算出单独抽水和单独回灌时地下连续墙两侧计算点间的天然水力梯度，如表 2所示。
表 2 解析计算相关数值Table 2. Relevant values of proposed methodQw/(m3·d-1) r1/m r2/m r3/m r4/m i1ni1rn i2ni2rn 744 7.21 8.06 15.20 16.55 0.139 0.106 -360 9.53 8.49 27.65 28.90 0.070 0.027 说明：Qw为抽灌水量，r1，r2，r3和r4分别为抽水井或回灌井距离计算点C1、C2、C3和C4的距离，i1n，i2n，i1rn和i2rn分别为计算点C1和C2、C3和C4间在无止水帷幕下抽水和回灌时的天然水力梯度。
根据式（1），（16）和（17）分别计算出基坑内单独抽水及单独回灌作用下引起的C1与C2、C3与C4间的水位差。将计算结果带入式（18），（19)中，可获得由抽灌共同作用引起的C1与C2、C3与C4间的水位差。表 3列出了相关计算结果。
表 3 回归公式法计算结果Table 3. Calculated results by proposed method条件 位置 符号 数值/m 抽水引起的水位差 C1、C2间 Δh1p 13.77 C3、C4间 Δh2p 10.51 回灌引起的水位差 C1、C2间 Δh1r 2.02 C3、C4间 Δh2r 1.02 抽灌共同引起的水位差 C1、C2间 Δh1 15.79 C3、C4间 Δh2 9.49 （2）数值分析法
采用三维非稳定流数值模拟方法计算抽灌作用下地下连续墙两侧的水位差。模型分析范围及计算参数基于文献Wu等[13]。图 13为抽灌水5 d后承压含水层的水位等值线图。由图 13可知，计算点C1与C2间的水位差为14.09 m，C3与C4间的水位差为11.39 m。
将回归公式法计算结果与数值计算结果进行比较发现，回归公式法计算的C1与C2间的水位差略大于数值法，C3与C4间的水位差略小于数值法。这是由于计算天然水力梯度时，不同计算点的水位降深使用相同的非完整井不完整系数。总体来说，两种方法计算结果比较接近，表明本文提出的计算公式是合理的。
4. 结论
（1）基坑内外抽灌水时止水帷幕对渗流场的影响机制在于渗流方向和渗流路径改变引起的止水帷幕一侧水位壅高，一侧水位降低；以及渗流面积减少引起的帷幕两侧水位差的增大。
（2）基坑外回灌井进行回灌时，止水帷幕两侧水位抬升量在承压含水层不同深度处有所不同，在含水层顶部水位变化最大，在含水层底部水位变化最小；止水帷幕深度对帷幕两侧水位差的影响小于坑内抽水。
（3）通过数值模拟分析法对不同止水帷幕下帷幕两侧的水位差进行了回归分析，获得了基坑外回灌承压含水层时，回灌水流经第一道和第二道止水帷幕时，两道帷幕两侧水位差的计算公式。
（4）获得了基坑内外抽灌地下水时止水帷幕两侧水位差的计算公式，该公式考虑止水帷幕插入深度、含水层各向异性、含水层厚度及抽水井和回灌井参数。
（5）将提出的计算方法应用到了一个的工程实例中，并将其计算结果与数值计算结果进行了对比，结果验证了计算公式的合理性。
-
![]()
图 1 团聚体在漫顶水流冲刷下的极限平衡状态
Figure 1. Limit equilibrium state of agglomerate under scouring of overtopping water
![]()
图 5 95%压实度模型坝的漫顶过程(λl=200)
Figure 5. Overtopping process of model dam at compaction degree of 95% (λl=200)
![]()
图 6 85%压实度模型坝的漫顶过程(λl=150)
Figure 6. Overtopping process of model dam at compaction degree of.85% (λl=150)
![]()
图 7 黏土模型坝漫顶溃坝时间反算的原型结果
Figure 7. Derived prototype failure interval results of clay dam by similarity law
表 1 试验参数换算方式
Table 1 Conversion method for test parameters
物理量 几何比尺 时间 流速 流量 重度 含水率 相似比 λl λl0.5 λl0.5 λl2.5 — 1 
下载: 导出CSV
表 2 流槽模型试验方案
Table 2 Experimental scheme of model tests in flume
压实度Dc/% 几何比尺λl 100 150 200 300 95 — — √ — 90 √ — √ √ 85 √ √ √ √ 80 — √ — √ 注：“√”表示该组试验将进行，“—”表示该组试验未进行。
下载: 导出CSV
表 3 流槽试验的时间表
Table 3 Interval results of flume tests
几何比尺λl 时间
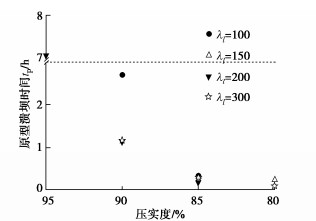
参数压实度/% 95 90 85 80 100 t0 — 5 min33 s 3 min10 s — t1 — 21 min45 s 5 min5 s — tm — 16 min12 s 1 min 55 s — tp — 162 min 19 min10 s — 150 t0 — — 4 min55 s 2 min40 s t1 — — 6 min35 s 3 min47 s tm — — 1 min40 s 1 min7 s tp — — 20 min25 s 13 min41 s 200 t0 3 min40 s 4 min52 s 8 min32 s — t1 > 34 s 9 min40 s 9 min12 s — tm > 30 s 4 min48 s 40 s — tp > 420 s 67 min53 s 9 min26 s — 300 t0 — 2 min45 s 2 min56 s 2 min20 s t1 — 6 min50 s 3 min55 s 2 min40 s tm — 245 s 59 s 20 s tp — 70 min44 s 17 min2 s 5 min46 s 注：t0代表漫顶时刻，t1代表溃坝时刻，tm=t1-t0代表溃坝间隔时间，tp代表计算原型结果。
下载: 导出CSV
-
[1] LUCAS-BORJA M E, PITON G, YU Y, et al. Check dams worldwide: objectives, functions, effectiveness and undesired effects[J]. CATENA, 2021, 204: 105390. doi: 10.1016/j.catena.2021.105390
[2] ASHRAF M, SOLIMAN A H, EL-GHORAB E, et al. Assessment of embankment dams breaching using large scale physical modeling and statistical methods[J]. Water Science, 2018, 32(2): 362-379. doi: 10.1016/j.wsj.2018.05.002
[3] MORRIS M W, HASSAN M A A M, VASKINN K A. Breach formation: field test and laboratory experiments[J]. Journal of Hydraulic Research, 2007, 45(S1): 9-17.
[4] ZHOU G G D, ZHOU M J, SHRESTHA M S, et al. Experimental investigation on the longitudinal evolution of landslide dam breaching and outburst floods[J]. Geomorphology, 2019, 334: 29-43. doi: 10.1016/j.geomorph.2019.02.035
[5] ZHANG J Y, FAN G, LI H B, et al. Large-scale field model tests of landslide dam breaching[J]. Engineering Geology, 2021, 293: 106322. doi: 10.1016/j.enggeo.2021.106322
[6] 张建云, 李云, 宣国祥, 等. 不同粘性均质土坝漫顶溃决实体试验研究[J]. 中国科学(E辑: 技术科学), 2009, 39(11): 1881-1886. https://www.cnki.com.cn/Article/CJFDTOTAL-JEXK200911017.htm ZHANG Jianyun, LI Yun, XUAN Guoxiang, et al. Experimental study on overflow breakage of homogeneous earth dams with different viscosity[J]. Science in China (Series E (Technological Sciences)), 2009, 39(11): 1881-1886. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JEXK200911017.htm
[7] HUNT S L, HANSON G J, COOK K R, et al. Breach widening observations from earthen embankment tests[J]. Transactions of the ASAE, 2005, 48(3): 1115-1120. doi: 10.13031/2013.18521
[8] FELICIANO CESTERO J A, IMRAN J, CHAUDHRY M H. Experimental investigation of the effects of soil properties on levee breach by overtopping[J]. Journal of Hydraulic Engineering, 2015, 141(4): 04014085-1-04014085-14.
[9] 罗优, 陈立, 郝婕妤, 等. 均质土石坝不同因素与漫顶破坏模式的内在联系[J]. 武汉大学学报(工学版), 2014, 47(5): 610-614. https://www.cnki.com.cn/Article/CJFDTOTAL-WSDD201405006.htm LUO You, CHEN Li, HAO Jieyu, et al. Impact of different factors on dam break mode of homogeneous earth-rock dams[J]. Engineering Journal of Wuhan University, 2014, 47(5): 610-614. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-WSDD201405006.htm
[10] BRIAUD J L, CHEN H C, GOVINDASAMY A V, et al. Levee erosion by overtopping in New Orleans during the Katrina Hurricane[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134(5): 618-632. doi: 10.1061/(ASCE)1090-0241(2008)134:5(618)
[11] 张红武, 刘磊, 卜海磊, 等. 尾矿库溃坝模型设计及试验方法[J]. 人民黄河, 2011, 33(12): 1-5. https://www.cnki.com.cn/Article/CJFDTOTAL-RMHH201112003.htm ZHANG Hongwu, LIU Lei, BU Hailei, et al. Test and design of tailings dam model[J]. Yellow River, 2011, 33(12): 1-5. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-RMHH201112003.htm
计量
- 文章访问数: 117
- HTML全文浏览量: 30
- PDF下载量: 12
