FDEM simulation for granular materials based on exact scaling and coarse granulation
-
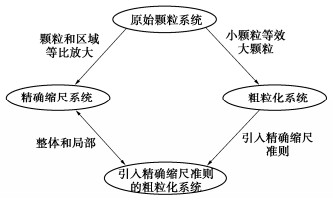
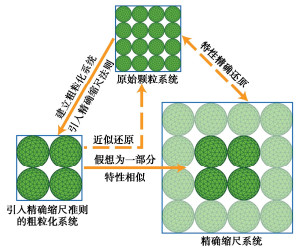
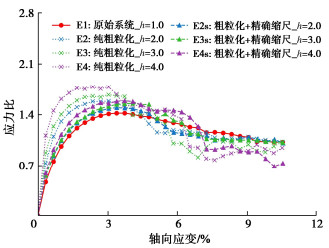
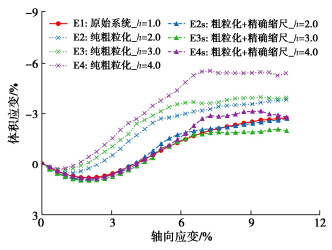
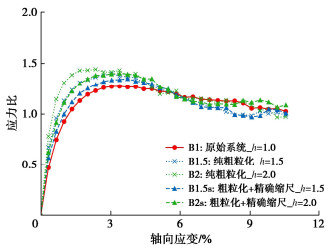
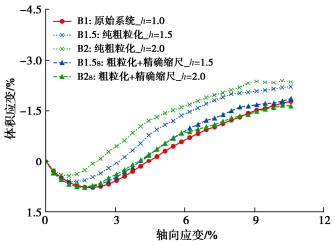
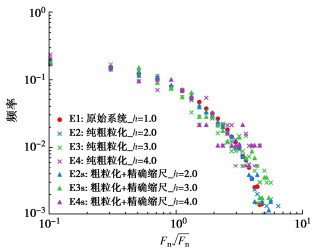
摘要: 颗粒材料具有非连续、离散性等特征，在进行数值模拟时面临着较大的计算压力。通过将精确缩尺准则和粗粒化方法引入到连续-离散耦合（combined finite-discrete element method, FDEM）方法中，旨在为加速基于FDEM的颗粒材料数值模拟提供一种解决方案。基于精确缩尺和粗粒化等理论，推导了FDEM中应遵循的精确缩尺准则，在此基础上分别进行了等粒径颗粒体系及二元颗粒体系的三轴剪切数值试验。试验结果表明，在未引入精确缩尺准则时，粗粒化模型表现的力学响应特征会发生改变，结果出现失真，因此必须对粗粒化模型参数进行修正。引入精确缩尺准则后，粗粒化模型的力学响应特征会得到补正。试验结果论证了FDEM引入精确缩尺准则和粗粒化方法的有效性，即能在近似原始颗粒体系的条件下大幅度提升采用FDEM进行颗粒材料数值模拟的计算效率。基于数值试验结果进行了宏细观力学分析，宏观应力变形和细观接触力相互映证，揭示了精确缩尺和粗粒化方法的细观力学机理。
-
关键词:
- 颗粒材料 /
- 连续-离散耦合分析方法 /
- 精确缩尺 /
- 粗粒化 /
- 计算效率
Abstract: The particle materials are characterized by discontinuity and dispersion, so they face great computational pressure in numerical simulation. The exact scaling criterion and coarse-grained method are introduced into the combined finite-discrete element method (FDEM) to provide a solution for accelerating the numerical simulation of granular materials based on the FDEM. Based on the theories of exact scaling and coarse granulation, the exact scaling criteria for the FDEM are derived. On this basis, the numerical triaxial shear tests for equal diameter particle system and binary particle system are carried out respectively. The test results show that without the introduction of the exact scaling criteria, the mechanical response characteristics of the coarse-grained model will change, resulting in distortion, and the parameters of the coarse-grained model need to be corrected. After the introduction of the exact scaling criteria, the mechanical response characteristics of the coarse-grained model are corrected. The test results demonstrate the effectiveness of introducing the exact scaling criteria and coarse granulation method into the FDEM. It can greatly improve the computational efficiency of numerical simulation of granular materials using the FDEM under the similar conditions to the original particle system. Based on the numerical test results, the macroscopic stress deformation and mesoscopic contact force are correlated, and the micromechanical mechanism of the exact scaling and coarse-grained methods is revealed.-
Keywords:
- granular material /
- FDEM /
- exact scaling /
- coarse granulation /
- computational efficiency
-
0. 引言
岩土热导率作为表征岩土介质热传导能力的重要热物性参数，特别是近年来随着中国双碳目标提出以及能源结构调整（地热、天然气水合物等地质能源开发比重增加），其研究日益受到国内外学者的关注[1]。但是，由于部分岩土试样获取困难，热导率直接测试所需设备和环境复杂，导致原位/室内试验测试周期与成本较高。因此，大量学者转而尝试分析岩土热导率的影响因素，开展岩土热导率预测模型的研究工作。然而与能源、化工、材料等领域传统多孔/颗粒介质如燃料电池、流化床和泡沫金属不同，岩土介质组分多样，结构随机，统计不确定性更强，特殊组构导致的传热复杂性使得完全反映真实状况的岩土热导率预测关联式模型建立十分困难，亟需深入研究。
作为典型的多相组分-多孔颗粒介质，可基于微细观力学领域均质化思想建立岩土介质热导率预测周期性单元结构模型[2]。该类研究可追溯到20世纪40、50年代[3]。1950年，Gemant[4]提出了采用热电类比方法分析土颗粒为球体单元结构的热导率，是该类研究的雏形。以该研究为基础，De[5]提出了类似的理想化单元结构模型，并引起De Vries和Makowski等的关注与在Nature的后续讨论与评论[3]。1979年，Zehner等建立了内部分别为球和圆柱的1/8圆柱单元结构模型，并由Hsu等[6]进行了修正。1983年，Gori[7]提出了平行热流线假设下的一维稳态非饱和冻土热导率预测模型，随后于2002年[8]对原模型进行改进使其适用于非饱和融土、模拟火壤等。Hsu等[9]在1995年提出了周期性分布多孔介质有效热导率预测的集总参数模型（lumped parameter model），考虑接触热阻对多种几何单元结构进行2D和3D理论分析。该方法假定研究对象单元结构内部温度场均匀且仅为一维热传导，将单元结构分为不同平行层，通过串并联方式计算得到总热阻。上述研究多聚焦岩土等多孔介质单元结构的特定几何特征，受其限制未涉及天然岩土介质孔隙率适用范围分析。
近年来，学者们进一步开展了岩土热导率预测单元结构模型的研究工作。Chen[10]在总结以往学者研究的基础上建立了内部颗粒为球的砂土热导率预测圆柱单元结构模型，但受其几何形状限制，该模型孔隙率适用范围仅为[0.33，1]。Gori等、Corasaniti等[12]提出了土热导率预测的准球形土颗粒立方体和球形土颗粒四棱柱单元结构模型，以0.4764为分界点覆盖[0.0349，1]孔隙率范围，但在高饱和度时，上述理论模型失效。受其启发，Chu等[13]针对Haigh模型在孔隙率方面的局限性进行了补充，可填补[0，0.33]这一低孔隙范围岩土热导率的预测需求。类似地，Jia等[14]等通过特定几何单元结构假设，以0.2146，0.4764为分界点将[0，1]孔隙率范围分三区间建立了岩土热导率预测方柱单元结构模型[15]。对比分析后发现该类模型需要特别关注颗粒接触、模型修正、孔隙水分布形式假设以及孔隙率/比的适用范围(对应假设结构几何特征)。已有大量该类问题的研究工作，但受制于岩土颗粒及单元结构几何形状的高度理想化假设，部分该类模型需进行空间修正，且同样缺乏对大部分天然岩土介质孔隙率范围（0~0.6，孔隙比0~1.5）的关注。
基于上述文献分析，笔者针对岩土多孔介质热导率预测单元结构模型研究的历史发展脉络进行了梳理分析，认为该类问题的关键是如何采用相关数学物理理论与方法建立岩土多孔介质特征单元结构热导率与相关参数(如固体基质（骨架）、孔隙内流体水或空气热导率，孔隙率（比），饱和度以及单元结构几何特征参数)之间的关系。因此，在前人已有研究的基础上采用热电类比-集总参数法建立了一种新的岩土热导率预测正三棱柱-准内切球单元结构模型。该模型可以克服球、圆柱单元结构需要空间修正的弊端，同时基本满足天然岩土的自然孔隙率全范围（0~0.6）。由于理论计算的复杂性，本文首先开展两相(干燥/饱和)状态分析，为后续拓展至三相非饱和状态奠定基础。
1. 理论模型
1.1 几何假设
宏观连续岩土体在微细观力学均质化思想的指导下可简化为两相或三相周期性三维几何单元结构。本模型考虑岩土干燥和饱和两相状态，在笛卡尔坐标系下进行几何建模与分析。在单元结构模型中，岩土固流两相被约束在单个正三棱柱单元结构中，固体颗粒以准球体形式与正三棱柱单元结构共享质心，正三棱柱棱高与准球体直径始终保持相等。定义临界状态如图 1（d）所示，此时岩土颗粒为球形，与正三棱柱单元结构五内表面均相切，两相状态下自由流体填充于空隙。通过改变正三棱柱上下面正三角形的边长来控制孔隙率大小（棱高始终保持不变）。当边长在指定范围内变动时，单元结构孔隙率Φ也随之在[0，0.597]范围内变动，该范围基本囊括了天然岩土材料孔隙率全范围。上述假设条件下，正三棱柱单元结构边长收缩调整过程中固相颗粒始终会超出单元结构三侧边界面，参考学者Gemant[4]和Gori等[11]的处理方法对单元结构局部进行切分，不考虑超出正三棱柱单元结构侧面的球冠，以此保证孔隙率的变化范围和增减形式与假设一致。同时，由于低孔隙率时被切球冠会产生交错进而导致不同组分体积计算与高孔隙率下不同，故在建立热导率计算模型时以0.144为界分两孔隙率区间计算，见图 1（a），（c）。此外，在具体的几何参数中，正三棱柱单元结构内的固体球颗粒半径根据实际岩土材料平均粒径尺寸确定，半径设为R1。根据几何假设，单元结构棱高相应为2R1，上下底面正三角形边长设为L，水与空气的热导率分别为λw，λa，统一为流体热导率，用λf表示，λs为固相颗粒热导率。引入无量纲几何特征因子α，表征单元结构底面正三角形边长与准球形颗粒半径的比值，即α=L/R1。α与L之间正相关，当α即L改变时，模型对应的孔隙率也随之发生改变。进一步引入r0=√3L/6，r1=√3L/3两个参数对后续计算过程进行分类简化。数学意义上，r0与r1分别代表正三角形内切圆和外接圆的半径。进一步引入无量纲热导率差异化因子ξ=1−λf/λs简化计算过程。当流体热导率越接近固体热导率时，ξ越接近0，表征两相组分热导率差异性越小。
![]()
图 1 本模型在高低孔隙率状态下的3D示意图Figure 1. 3D schematic diagram of model under high and low porosities1.2 物理假设
岩土复杂的组分和结构使其传热过程很难用严格的理论模型进行精确表征。为了能够兼顾模型结构的鲜明性和计算的合理性，对传热物理过程假设如下:
（1）模型只考虑干燥和饱和两相状态，忽略传热过程中流体迁移可能导致的重分布和结构变化。
（2）孔隙/颗粒细观尺度忽略对流传热，室温且常温度梯度下不考虑热辐射，即本模型在两相状态只考虑导热这一主要传热方式，且无化学反应和内热源。
（3）常温常压下，不考虑热导率的温变性，同时两相间的接触视为理想接触，不考虑接触热阻。
（4）基于热电类比-集总参数法的思想，认为热流方向平行Z轴，一维热传导下对单元结构内部穿过不同相态时的热流路径进行平行热流线简化假设。
1.3 有效热导率的计算
本模型在进行热导率计算时，采用热电类比-集总参数法[9]对单元结构整体热阻分段进行计算。如几何假设中所述，整体孔隙率范围内需要分高孔隙率(L> √3R1)和低孔隙率(L<√3R1)两种情况进行计算。
（1）高孔隙率(0.144<Φ<0.597)
高孔隙率下，几何特征因子α∈(√3,2√3)，对应孔隙率范围为(0.144,0.597)。如图 2（a）所示，此时传热路径有两种：①流体-固体-流体；②纯流体相。在两种热流路径分区的基础上，根据热阻分析法分为3个计算区域，其热阻分别命名为R−1，R−2，R−3，总热阻命名为Rt，如图 2（b）所示。
![]()
图 2 高孔隙率热阻分区及等效网络示意图Figure 2. Schematic diagram of equivalent thermal resistance partition and network under high porosity根据定义，单元结构孔隙率Φ可表示为
Φ=VvoidVtotal=Vtotal−VsolidVtotal=Vt−VsVt。 (1) 式中：Vsolid为固相体积，简写为Vs；Vvoid为孔隙体积，简写为Vv；Vtotal为单元体总体积，简写为Vt。
正三棱柱单元结构总体积Vt为
Vt=√32R1L2。 (2) 考虑固体球颗粒被正三棱柱三侧面剖切的球冠，固相体积Vs的计算式如下：
Vs=V球−3V球冠=−√372πL3+√32πR21L−23πR31。 (3) 将式（2），（3）代入式（1）中，可以得到孔隙率与正三棱柱单元结构上下面正三角形边长的关系式：
Φ=π36(LR1)3+(LR1)2−π(LR1)+4√39π(L/R1)2=π36α3+α2−πα+4√39πα2。 (4) 针对岩土材料或其他多孔介质，一般均默认其孔隙率为已知（可测/可算）参数。对于给定孔隙率为Φ的岩土材料，需要反向确定引入参数α用于后续计算。
欲求α，相当于求下面一元三次方程的根：
f(α)=π36α3+(1−Φ)α2−πα+4√39π=0。 (5) 进行求解，得到
α=−b′3a′+2√p3cos(13arccos3√3q2p√p)。 (6) 式中：a′=π36；b′=1−Φ；p=432(1−Φ)2+π2π2；q=−108π(1−Φ)−864(1−Φ)3−4√3π39π。
此时，在高孔隙率情况下，不同孔隙率都有唯一的α可以通过式（6）来确定，以此为基础进而分区计算高孔隙率下单元结构的等效热阻。
a）假设正三棱柱内有一同轴等高圆柱，其半径为r。则当0<r<r0时，作为第一热阻区域R−1进行计算。该区域热流穿过的横截面积为
S1=πr02。 (7) 根据该区域的等效热阻结构，取圆筒形热阻微元体，在热流方向上可视为固流两相热阻串联[10, 13-15]，其热阻可以表示为
dR−1=2√R21−r2/(λsds)+2(R1−√R21−r2)/(λfds)。 (8) 式中：微元体的热流截面面积ds=2πrdr。在r方向R−1可视为无数固流两相微元热阻并联[10, 13-15]：
1R−1=r0∫012(R1−√R21−r2)λf⋅2πrdr+2√R21−r2λs⋅2πrdr=r0∫0λsλfπrdrλs(R1−√R21−r2)+λf√R21−r2。 (9) 引入ξ=1−λf/λs简化并进行积分后得到：
R−1=−ξ2/{λfπRl[ln(1−ξ)+ξ−ln(1−ξ√1−112α2)−ξ√1−112α2]} (10) b）当r0<r<R1时，为计算区域二，对应热阻为R−2。该区域热流穿过的总横截面积为
S2=SR1−Sr0−3S球冠投影 =πR21−πr20−3[2arccosr0R1/(2π)⋅πR21−2×12r0√R21−r20]=[π−3arccosr0R1]R21−πr20+3r0√R21−r20。 (11) 取准圆筒形热阻微元体，其热阻可由下式求得：
dR−2=2(R1−√R21−r2)/(λfds)+2√R21−r2/(λsds)。 (12) 式中：ds为准圆筒形微元体的热流截面面积，
ds=2[π−3arccos(r0/r)]rdr。 (13) 与R−1计算类似，R−2亦可以通过微元体的并联组合得到整体热阻：
1R−2=∫R1r012(R1−√R21−r2)λf⋅2r dr(π−3arccosr0r)+2√R21−r2λs⋅2r dr(π−3arccosr0r)=∫R1r0λfλs(π−3arccosr0r)r drλs(R1−√R21−r2)+λf√R21−r2, (14) →R−2=1/λf∫R1r0(π−3arccosr0r)rdrR1−ξ√R21−r2。 (15) c）当R1<r<r1时，作为区域三进行计算，该区域包含纯流体相态。该区域对应的热流截面面积为
S3=S三角形−S1−S2=√3L2/4−πr20−[[π−3arccos(r0/R1)]R21−πr20+3r0√R21−r20]=√3L2/4−[π−3arccos(r0/R1)]R21−3r0√R21−r20。 (16) 根据热阻的定义可以得出R−3计算式为
R−3=2R1λfS3=2R1√3λfL2/4−[π−3arccos(r0/R1)]R21−3r0√R21−r20。 (17) 综上所述，高孔隙率下两相状态三区域热阻均已得出，正三棱柱单元体热流总横截面面积即边长为L正三角形面积为
S=√3L2/4。 (18) 正三棱柱单元结构的热阻可视为上述3部分热阻的并联，即
Rt=1/1∑ni=11R−i=1/1(1R−1+1R−2+1R−3)(1R−1+1R−2+1R−3)∑ni=11R−i=1/1(1R−1+1R−2+1R−3)(1R−1+1R−2+1R−3)。 (19) 根据热阻的定义可以得到高孔隙率下正三棱柱单元结构的有效热导率λe可以表示为
λe=8R1√3L2Rt。 (20) （2）低孔隙率(0<Φ<0.144)
当模型中几何特征因子α<√3时，固相球颗粒被三棱柱三侧面切除的球冠部分开始相互影响，相较于高孔隙率的情况，仅有流体-固体-流体一种热流路径。此时热阻分区仅为两个区域，仍以R−1，R−2来代表，Rt为代表单元结构整体等效热阻，如图 3所示。
![]()
图 3 低孔隙率热阻分区及等效网络示意图Figure 3. Schematic diagram of equivalent thermal resistance partition and network under low porosity与高孔隙率类似，后续计算需要确定Φ与α的关系。此时，单元结构内固体颗粒体积可由半径为R1球体体积减去被正三棱柱三个侧面所切除的球冠体积得到：
Vs=V球−3(V球冠−V类纺锤体)。 (21) 式中：V球=43πR31。球冠体积计算式为
V球冠=∫2π0dθ∫√R21−r200(√R21−r2−r0)rdr=π (13r30−R21r0+23R31)。 (22) 低孔隙率时，固相球颗粒被正三棱柱相邻两侧面剖切部分相互重叠影响，形成类纺锤体结构，这种情况下必须考虑交错区域的体积计算，如图 4所示。
柱坐标系下该纺锤体体积可由下式计算：
V类纺锤体=4∫√R21−r20dz∫β0dθ∫R1r(θ)rdr=43∫arcsin√R21−r20−12L2R10(R21−L2/12sin(π6−θ)2)32dθ。 (23) 式中：β=arcsin√R21−r20−12L2R1；r(θ)=√36L/ sin(π6−θ)。
整合式（1），（2），（21）~（23）和关系式α=L/R1，r0=√3L/6得到此情况下孔隙率Φ与无量纲几何特征因子α的关系：
Φ=Vt−[V球−3(V球冠−V类纺锤体)]Vt=Vt−[V球−3V球冠+3V类纺锤体]Vt={√32R1L2−[43πR31−3(13r30−R21r0+23R31)π+3⋅43∫arcsin(√R21−r20−12L)/(2R1)0(R21−L212sin(π6−θ)2)3/2dθ]/43∫arcsin(√R21−r20−12L)/(2R1)0(R21−L212sin(π6−θ)2)3/2dθ]√32R1L2}={136πα3+α2−πα+4√39π−8√33⋅∫arcsin(12√1−112α2−14α)0(1−α212sin(π6−θ)2)3/2dθ}/α2。 (24) 与高孔隙率状态下已知Φ. 通过理论求解一元三次方程获得α不同，低孔隙率下的式（24）很难解析求解。参考文献处理方法[14]，根据Φ与α间正相关特点，可采用二分法进行数值求解，这里不再赘述。
低孔隙率下的热阻分两部分计算：
（1）当0<r<r0时，与高孔隙率时一致，该区域热流穿过的横截面积可以仍用式（7）表示。该区域的热阻表示形式同样与高孔隙率时一致，即式（10）。
（2）当r0<r<r1时，该区域作为热阻计算的第二分区，计算方法与高孔隙率第二分区相同，仅在积分域上有所差别，其热阻可由以下积分求得：
R−2=1/[λf∫r1r0(π−3arccosr0r)rdrR1−ξ√R21−r2]。 (25) 类似地，结合式（18）~（20），低孔隙率下单元结构的有效热导率也能随之确定，组成(0,0.597)全范围。
2. 模型验证与对比分析
2.1 参数选择与计算流程
为了验证本文模型的合理性，以文献为参考设定固流相热导率，如表 1所示。基于本文模型的方程体系，通过MATLAB软件编程计算高低不同孔隙率时干燥/饱和固流两相状态典型多孔/颗粒岩土介质如砂土、砂岩的表观热导率。具体计算流程如图 5所示。
表 1 固流相热导率参考值Table 1. Thermal conductivity of solid-fluid pse2.2 模型对比分析
图 6给出了本模型孔隙率Φ随几何特征因子α的变化曲线，图 7对比显示了本模型与其它模型在两相状态下（干燥和饱和）、天然岩土孔隙率范围（0~0.6）内热导率预测结果的不同表现。
![]()
图 7 不同模型两相(干燥/饱和)状态下热导率预测对比Figure 7. Predictions of effective thermal conductivity of different models under dry or saturated conditions从图 6中可以看出孔隙率Φ与α正相关，随α增加而增大，且以α=1.732为分界点，高低孔隙区可以实现无缝衔接。孔隙率Φ与引入几何特征因子α的关系十分重要，影响表观热导率的计算。本文模型所提供的岩土孔隙率Φ与引入几何特征因子α的关系虽然复杂，但可通过编制相关应用程序实现快速求解。已有研究表明[17]，经典的岩土多孔-复合材料有效热导率计算混合理论模型中，Wiener并串联模型可以确定热导率预测结果的上下限。图 7显示结果表明，本文模型的预测值均严格位于Wiener上下边界内，说明了其预测结果整体范围的合理性。同时，由于岩土多孔介质固流相组分热导率的差异性（λs>λf），模型预测值随孔隙率的增加而减小，整体变化规律与其他模型一致，但在变化速率上相互间存在较为明显的差异。
除Wiener并串联模型外，对图 7所包含模型曲线解释说明如下。Chen[10]圆柱单元结构模型孔隙率适用范围为[0.33，1]，不能包含[0，0.6]这一天然岩土介质孔隙率主范围，因此，在[0，0.33]孔隙率范围内以Chu等[13]模型作为补充。Jia等[14-15]模型可将[0，0.6]孔隙率分为高中低3种情况，故分成3段进行绘制。Gori等[11-12]建立的立方体和四棱柱单元结构模型可组成连续的[0.0349，0.6]孔隙率范围，但由于存在一定的问题未参与对比分析。Chen[18]基于不同孔隙率砂土热导率探针测试数据集中于[0.3，0.5]孔隙率区间，极低与较高孔隙率时需对曲线进行延伸分析。
以图 8为例，结合图 7分析不同模型预测热导率随孔隙率的变化细节。在[0，0.6]孔隙率范围内，本文正三棱柱单元结构模型预测热导率随孔隙率增加呈凹形降低，dλ/dΦ<0且d2λ/dΦ2<0，尤其在低孔隙率阶段更为明显，整体趋向于串联模型下限。
与此相反的则是低孔隙率下的Jia等[14-15]方柱单元结构模型，预测热导率随孔隙率增加呈凸形降低，d2λ/dΦ2>0，低孔隙率时趋向于并联模型上限。但是，Jia等[14-15]模型在中高孔隙率时发生反转，热导率随孔隙率增加由凸形降低转变为凹形降低，即曲线整体呈S形，存在反曲点d2λ/dΦ2=0。Chen[10]和Chu等[13]圆柱单元结构模型则与Jia等[14-5]模型类似，呈准S形曲线变化。
图 7中还给出了本文后续用于模型验证的34组岩土热导率试验测试数据，包括低孔隙率砂岩、黏土和标准砂，可用于对比分析实际岩土介质热导率随孔隙率的变化。
可以发现低孔隙率砂岩热导率随孔隙率增加可认为呈凹形降低；黏土热导率试验测试值干燥时趋向于并联模型，饱和时趋向于串联模型下限；标准砂不论干燥和饱和热导率均随孔隙率增加线性降低。本文模型虽然能够在孔隙率范围上覆盖大部分天然岩土介质，但对低孔隙率岩石、水土作用更为复杂的黏土适用性相对较差。高度理想化岩土单元结构强假设是出现上述偏差的原因之一，固流组分热导率数量级差异则是另一原因。针对上述问题，众多学者已聚焦文献[5]开展了大量的评论[3]，此处不再赘述。
2.3 试验定量验证
为了进一步检验模型预测结果的准确性，本文结合已有文献的岩土热导率试验测试数据，对各理论模型和试验拟合的经验模型进行定量对比分析和验证, 符合模型对比和验证要求的相关数据列于表 2中。
表 2 热导率试验测试结果Table 2. Experimental data of thermal conductivity岩土试样 孔隙率Φ 饱和度Sr 热导率/
(W·(m·K)-1)砂岩[19] 0.02 0/1 2.8/3.2 0.03 0/1 3/3.6 0.04 0/1 2.5/2.8 0.06 0/1 2.3/3.3 0.12 0/1 1.7/3.1 0.15 0/1 2.1/3.3 0.16 0/1 1.7/3.0 标准砂[13, 18, 20] 0.354 0/1 0.555/2.968 0.396 0/1 0.402/2.72 0.434 0/1 0.333/2.49 0.472 0/1 0.237/2.25 0.509 0/1 0.199/2.134 0.547 0/1 0.141/1.937 黏土[21] 0.385 0/1 0.67/0.98 0.418 0/1 0.61/0.97 0.451 0/1 0.61/0.94 0.475 0/1 0.57/0.91 注：除黏土外，λs均采用Haigh文献中的7.69 W/(m·K)。 以上述试验数据为基准，对各理论模型和经验拟合模型不同孔隙率时干燥和饱和状态下的热导率进行计算，采用两种常见的性能指标：RMSE-均方根平均误差和NRMSE-归一化均方根平均误差开展误差评估。
各模型的误差评估结果如表 3所示，Φ∈(0，0.6)，Sr=0/1。干燥和饱和状态下，本模型与试验数据的均方根误差（正规化均方根误差）分别为0.889 W/(m·K)（31.1%）和1.004 W/(m·K)（37.3%），均优于根据试验拟合的Chen[18]模型和其它理论模型，也可以定量验证图 7显示结果。基于试验数据，图 9给出了包含Wiener串并联模型的各模型预测结果分布。从中可以发现，与试验值相比，本模型热导率预测值相对偏低，总体趋向串联模型。进一步结合图 7可以发现，低孔隙率时相对误差较大，而随着孔隙率的增加，本模型热导率预测值与试验值吻合度逐渐提高。当孔隙率介于0~0.476时，干燥状态下本模型预测精度与Jia等模型[14-15]接近，偏离程度要大于Chu等[13]模型；饱和状态下本模型预测精度要略强于Jia等[14-15]模型，偏离程度相较于Chu等[13]模型也未有明显差距。当孔隙率大于0.476，处于较高孔隙率时，本模型在干燥/饱和状态下的预测精度均优于其他理论模型，特别是在孔隙率接近0.5时，预测值几乎与Chen试验测试结果保持一致。而针对未修正时的Haigh[10]模型，在0.33~0.6孔隙率范围区间热导率预测值相对Chen[18]模型均偏低，因此Haigh尝试采用kbulk≈2.2kcell进行空间线性修正。考虑该修正的原因在于圆柱单元结构本身几何形状的固有缺陷。相比之下，本文正三棱柱模型在保证预测精度的同时克服了圆柱单元结构固有的空间修正缺陷，是其优势之一。
表 3 岩土热导率预测模型对比(RMSE/NRMSE)Table 3 Comparison of prediction models for thermal conductivity of geomaterials单位：W/(m·K) 3. 讨论：进化视角下组构主导的岩土热导率预测单元结构模型研究新思路
提及进化/演化，人们一直以来都坚信达尔文在19世纪就提出的“物竞天择”进化原则，用自然选择的概念对生物物种的构造和多样性进行了解释。但是，部分持反对观点的学者认为达尔文的进化论并没有能够从物理学的角度对这种选择的标准作出定义[22]。Bejan[23]基于热力学物理定律对能量和物质流动的表述提出了构形理论(constructual law)。陈林根[24]对Bejan提出的构形理论及研究进展进行了阐述，认为从进化论的观点出发组织结构是经过长时间演化而成，应该是某种最优或接近最优的结构，可精简表述为事物结构源自于性能达到最优。
基于上述思想开展类比分析，提出进化视角下组分和结构主导的岩土热导率预测关联式单元结构模型研究的新思路，主要体现在3方面。
（1）岩土介质是典型的固液气多相组分-多孔/颗粒材料，细观组分和结构与其宏观热力特性如热导率紧密相关。在以组分（固液气）为基础、结构（多孔/颗粒）是关键这一前提下开展的岩土介质热导率研究中，组分与结构二者在影响其热导率变化过程中的继承(相对稳定地)与选择(具有调控性)作用类似于生物进化过程中的DNA双螺旋结构中的基因组件遗传与配对组合变异（图 10）。
![]()
图 10 进化视角下组构主导的岩土热导率研究Figure 10. Composition-structure dominated ETC of geomaterials from an evolutionary perspective（2）在聚焦岩土细观孔隙/颗粒及单元结构方面，如图 10（a）所示从基本的(准)球、圆柱、立方体至四棱柱、三棱柱，再到遗传算法异形几何结构优化表征体现了趋向岩土相对真实结构的进化思想。这一由简至繁人们尝试逐步接近岩土真实结构的需求与生物进化过程中自然环境的选择类似，均提供了系统变化的驱动力。再结合基于均质化思想的不同单元结构周期性分布假设可以实现岩土介质从细观向宏观的跨尺度升级，表征宏观连续岩土介质、覆盖天然岩土介质孔隙率范围，分析热导率随孔隙率的不同变化（图 10（a））。
（3）本文模型及思想可扩展应用于更为复杂的岩土固液气三相非饱和状态，其物理基础为含湿多孔/颗粒介质中液态水分布特征。现代物理学认为[25]，多孔/颗粒介质中液态水的分布在[0，1]的饱和度全范围可以分为水合、钟摆、索道、毛细和悬浮等多种状态，如图 10（b）所示。不同含水率时孔隙水形态及展布特征的演化过程体现了对环境的适应性，可以进一步分析热导率随含水率/饱和度的变化。以土科学为例，部分学者已针对该问题开展了大量的研究工作[26-27]，通过土水特征曲线类比分析土-水-热导率关系，建立岩土介质持水与导热行为间的关联，从水气-土水势等物质运移和能量转换角度分析岩土热力学行为，同样体现了构形理论的适应性演化/进化思想。
需要说明的是，本文研究的单元结构模型仅限定在岩土孔隙/颗粒细观尺度。在微纳尺度，作为无机非金属固体的岩土材料中低温时主要通过晶格振动形成声子热传导，已经脱离了连续介质的假定范畴，不符合经典傅里叶热传导定律，不能通过分/原子尺度的相互作用计算得到宏观岩土介质的热导率，因而这种不符合尺度对称性规律的跨尺度热力参数计算与外推不成立[28]。而本文研究的细观至宏观工程应用尺度仍处在连续介质假定成立的条件下[29]，传热的尺度效应可能是由于尺度的减小使得传热介质的体积面积比减小, 改变了不同作用力或/和因素在传热中的相对重要性，可以通过假定单元结构进行量化分析。因此本文基于均质化思想的岩土多孔/颗粒介质热导率预测单元结构模型可以实现细观至宏观的跨尺度分析。
4. 结论
（1）本文建立了一个以正三棱柱为表征单元体，准球体为固相颗粒的满足大部分天然岩土孔隙率范围且无需考虑空间修正的岩土热导率预测单元结构模型。结合热电类比-集总参数法，对该细观单元结构模型热导率进行理论推导，最终得到干燥/饱和两相态岩土多孔/颗粒介质热导率预测的影响因素关联式。
（2）理论分析与文献试验验证结果表明：正三棱柱-准内切球单元结构模型预测岩土热导率随孔隙率整体呈凹形降低变化趋势，低孔隙率（小于0.2）时预测结果偏低且趋向串联模型下限，误差较大；高孔隙率(0.4~0.6)时理论预测结果与试验测试值吻合度较高；相对其他单元结构理论模型预测效果更好，尤其在干燥状态时均方根误差RMSE和归一化均方根误差NRMSE最小，分别为0.89W/(m·K)和31%。
（3）引入选择进化、构形优化思想，基于孔隙-颗粒和单元结构几何特征、孔隙水形态概念性类比提出了进化视角下固液气组分和多孔/颗粒结构主导的岩土热导率预测关联式单元结构模型研究的新思路。
-
![]()
图 1 精确缩尺系统和粗粒化系统的关联性
Figure 1. Relevance between exact scaling system and coarse-grained system
![]()
图 9 等径颗粒试验法向接触力分布
Figure 9. Distribution of normal contact force of equal diameter particle tests
![]()
图 10 二元颗粒试验法向接触力分布
Figure 10. Distribution of normal contact force of binary particle tests
表 1 主要物理量的精确缩尺准则
Table 1 Exact scaling criteria for major physical quantities
物理量 符号 量纲 缩放比尺 长度 L [L] h 时间 T [T] h 质量 m [M] h3 力 F [L][T]−2[M] h2 应力 σ [L]−1[T]−2[M] 1 应变 ε [1] 1 弹性模量 E [L]−1[T]−2[M] 1 泊松比 ν [1] 1 罚刚度 pc [L]−2[T]−2[M] h−1 摩擦系数 μ [1] 1 阻尼系数 βc [1] 1 
下载: 导出CSV
表 2 数值试样信息
Table 2 Information of numerical samples
类别 粒径/mm 颗粒数量 单元数 节点数 等径颗粒系统 15 15186 1214880 3113130 30 1898 151840 389090 45 562 44960 115210 60 237 18960 48585 二元颗粒系统 15~30 8543 683440 1751315 22.5~45 2532 202560 519060 30~60 1072 85760 219760
下载: 导出CSV
表 3 原始颗粒系统材料和接触参数
Table 3 Contact parameters of original particle system materials
参数名称 参数值 单位 弹性模量 40 GPa 泊松比 0.2 — 罚刚度 1.8×1011 N/m3 罚刚度比 1 — 摩擦系数 0.3 — 阻尼系数 0.2 — 阻尼系数比 1 —
下载: 导出CSV
表 4 各组数值试验设置
Table 4 Settings for each numerical test
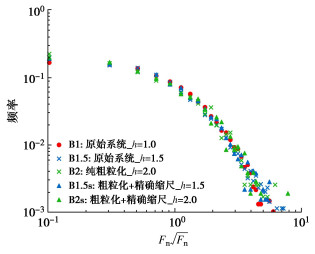
类别 编号 粒径/mm 缩放比尺h 是否引入精确缩尺准则 等径颗粒系统 E1 15 1.0 — E2 30 2.0 × E3 45 3.0 × E4 60 4.0 × E2s 30 2.0 √ E3s 45 3.0 √ E4s 60 4.0 √ 二元颗粒系统 B1 15~30 1.0 — B2 22.5~45 1.5 × B3 30~60 2.0 × B2s 22.5~45 1.5 √ B3s 30~60 2.0 √
下载: 导出CSV
表 5 峰值处平均法向接触力
Table 5 Mean normal contact forces at peak
类别 编号 峰值平均法向接触力/N 对原系统比值 等径颗粒系统 E1 80.30 1.00 E2 1172.19 4.18 E3 2703.42 9.64 E4 3831.52 13.67 E2s 1046.27 3.73 E3s 2070.92 7.39 E4s 3109.17 11.09 二元颗粒系统 B1 306.42 1.00 B2 788.65 2.57 B3 1323.10 4.32 B2s 658.55 2.15 B3s 1122.34 3.66
下载: 导出CSV
-
[1] 吴杨, 容浩俊, 王金莲, 等. 颗粒形状和中主应力对砂土力学特性耦合影响的真三轴试验研究[J]. 岩石力学与工程学报, 2023, 42(2): 497-507. WU Yang, RONG Haojun, WANG Jinlian, et al. A true triaxial experimental study on the coupled effect of particle shape and intermediate principal stress on the mechanical properties of sand[J]. Chinese Journal of Rock Mechanics and Engineering, 2023, 42(2): 497-507. (in Chinese)
[2] 康馨, 陈植欣, 雷航, 等. 基于3D打印研究颗粒形状对砂土宏观力学性质的影响[J]. 岩土工程学报, 2020, 42(9): 1765-1772. doi: 10.11779/CJGE202009022 KANG Xin, CHEN Zhixin, LEI Hang, et al. Effects of particle shape on mechanical performance of sand with 3D printed soil analog[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(9): 1765-1772. (in Chinese) doi: 10.11779/CJGE202009022
[3] GUO Y, CURTIS J S. Discrete element method simulations for complex granular flows[J]. Annual Review of Fluid Mechanics, 2015, 47: 21-46. . doi: 10.1146/annurev-fluid-010814-014644
[4] HUANG X, O'SULLIVAN C, HANLEY K J, et al. Discrete-element method analysis of the state parameter[J]. Géotechnique, 2014, 64(12): 954-965. doi: 10.1680/geot.14.P.013
[5] LU M, MCDOWELL G R. The importance of modelling ballast particle shape in the discrete element method[J]. Granular Matter, 2007, 9(1): 69-80.
[6] COETZEE C J. Calibration of the discrete element method and the effect of particle shape[J]. Powder Technology, 2016, 297: 50-70. doi: 10.1016/j.powtec.2016.04.003
[7] 徐琨, 周伟, 马刚, 等. 基于离散元法的颗粒破碎模拟研究进展[J]. 岩土工程学报, 2018, 40(5): 880-889. doi: 10.11779/CJGE201805013 XU Kun, ZHOU Wei, MA Gang, et al. Review of particle breakage simulation based on DEM[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(5): 880-889. (in Chinese) doi: 10.11779/CJGE201805013
[8] MCDOWELL G R, HARIRECHE O. Discrete element modelling of soil particle fracture[J]. Géotechnique, 2002, 52(2): 131-135. doi: 10.1680/geot.2002.52.2.131
[9] DE BONO J, MCDOWELL G. Particle breakage criteria in discrete-element modelling[J]. Géotechnique, 2016, 66(12): 1014-1027. doi: 10.1680/jgeot.15.P.280
[10] ZHOU W, WANG D, MA G, et al. Discrete element modeling of particle breakage considering different fragment replacement modes[J]. Powder Technology, 2020, 360: 312-323. doi: 10.1016/j.powtec.2019.10.002
[11] 肖宇轩, 马刚, 陆希, 等. 堆石颗粒在复杂约束模式的破碎特性[J]. 浙江大学学报(工学版), 2022, 56(8): 1514-1522, 1559. XIAO Yuxuan, MA Gang, LU Xi, et al. Breakage behaviour of rockfill particles in complicated constraint patterns[J]. Journal of Zhejiang University (Engineering Science), 2022, 56(8): 1514-1522, 1559. (in Chinese)
[12] 周剑, 马刚, 周伟, 等. 基于FDEM的岩石颗粒破碎后碎片形状的统计分析[J]. 浙江大学学报(工学版), 2021, 55(2): 348-357. ZHOU Jian, MA Gang, ZHOU Wei, et al. Statistical analysis of fragment shape of rock grain after crushing based on FDEM[J]. Journal of Zhejiang University (Engineering Science), 2021, 55(2): 348-357. (in Chinese)
[13] 邹宇雄, 马刚, 李易奥, 等. 抗转动对颗粒材料组构特性的影响研究[J]. 岩土力学, 2020, 41(8): 2829-2838. ZOU Yuxiong, MA Gang, LI Yiao, et al. Impact of rotation resistance on fabric of granular materials[J]. Rock and Soil Mechanics, 2020, 41(8): 2829-2838. (in Chinese)
[14] 邹宇雄, 周伟, 陈远, 等. 颗粒形状对岩土颗粒材料传力特性的影响机制[J]. 水力发电学报, 2020, 39(5): 17-26. ZOU Yuxiong, ZHOU Wei, CHEN Yuan, et al. Mechanism of particle shape affecting force transfer properties of granular geo-materials[J]. Journal of Hydroelectric Engineering, 2020, 39(5): 17-26. (in Chinese)
[15] MA G, ZHOU W, CHANG X L. Modeling the particle breakage of rockfill materials with the cohesive crack model[J]. Computers and Geotechnics, 2014, 61: 132-143. doi: 10.1016/j.compgeo.2014.05.006
[16] MA G, ZHOU W, CHANG X, et al. Formation of shear bands in crushable and irregularly shaped granular materials and the associated microstructural evolution[J]. Powder Technology, 2016, 301: 118-130. doi: 10.1016/j.powtec.2016.05.068
[17] MA G, ZHOU W, REGUEIRO R A, et al. Modeling the fragmentation of rock grains using computed tomography and combined FDEM[J]. Powder Technology, 2017, 308: 388-397. doi: 10.1016/j.powtec.2016.11.046
[18] LIU Q S, WANG W Q, MA H. Parallelized combined finite-discrete element (FDEM) procedure using multi-GPU with CUDA[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2020, 44(2): 208-238. doi: 10.1002/nag.3011
[19] LISJAK A, MAHABADI O K, HE L, et al. Acceleration of a 2D/3D finite-discrete element code for geomechanical simulations using General Purpose GPU computing[J]. Computers and Geotechnics, 2018, 100: 84-96. doi: 10.1016/j.compgeo.2018.04.011
[20] 程宏旸, WEINHART T. 关于采用粗粒化提高颗粒材料多尺度模拟守恒特性的研究[J]. 计算力学学报, 2022, 39(3): 373-380. CHENG Hongyang, WEINHART T. On the conservation properties of CG-enriched concurrent coupling methods for multi-scale modeling of granular materials[J]. Chinese Journal of Computational Mechanics, 2022, 39(3): 373-380. (in Chinese)
[21] 赵婷婷, 冯云田. 大规模颗粒系统的精确缩尺和粗粒化离散元方法[J]. 计算力学学报, 2022, 39(3): 365-372. ZHAO Tingting, FENG Yuntian. Exact scaling laws and coarse-grained discrete element modelling of large scale granular systems[J]. Chinese Journal of Computational Mechanics, 2022, 39(3): 365-372. (in Chinese)
[22] 季顺迎. 颗粒材料计算力学专辑序[J]. 计算力学学报, 2022, 39(3): 263-264. JI Shunying. Preface to computational mechanics of granular materials[J]. Chinese Journal of Computational Mechanics, 2022, 39(3): 263-264. (in Chinese)
[23] 谢亦朋, 张聪, 阳军生, 等. 基于局部粗粒化离散元的冰水堆积体隧道围岩破坏特征与加固措施研究[J]. 岩石力学与工程学报, 2021, 40(3): 576-589. XIE Yipeng, ZHANG Cong, YANG Junsheng, et al. Study on failure characteristics and reinforcement measures of surrounding rock of glacial deposit tunnels based on coarse-grained DEM[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(3): 576-589. (in Chinese)
[24] 易颖, 周伟, 马刚, 等. 基于精确缩尺的颗粒材料流变研究[J]. 岩土力学, 2016, 37(6): 1799-1808. YI Ying, ZHOU Wei, MA Gang, et al. Study of rheological behaviors of granular materials based on exact scaling laws[J]. Rock and Soil Mechanics, 2016, 37(6): 1799-1808. (in Chinese)
[25] FENG Y T, OWEN D R J. Discrete element modelling of large scale particle systems—Ⅰ: exact scaling laws[J]. Computational Particle Mechanics, 2014, 1(2): 159-168. doi: 10.1007/s40571-014-0010-y
[26] MA G, ZHOU W, CHANG X L, et al. Combined FEM/DEM modeling of triaxial compression tests for rockfills with polyhedral particles[J]. International Journal of Geomechanics, 2014, 14(4): 04014014. doi: 10.1061/(ASCE)GM.1943-5622.0000372
[27] AZÉMA E, RADJAI F, SAUSSINE G. Quasistatic rheology, force transmission and fabric properties of a packing of irregular polyhedral particles[J]. Mechanics of Materials, 2009, 41(6): 729-741. doi: 10.1016/j.mechmat.2009.01.021
计量
- 文章访问数: 407
- HTML全文浏览量: 75
- PDF下载量: 86
