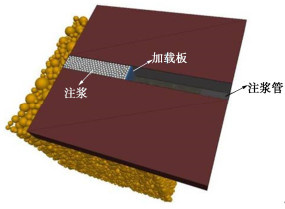
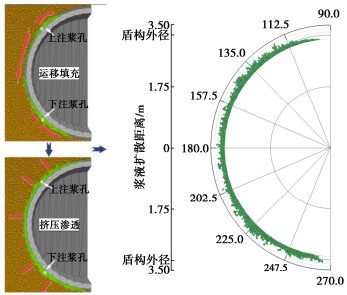
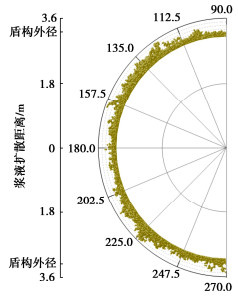
Synchronous grouting diffusion and parameter optimization of shield tunnels based on discrete element method
-
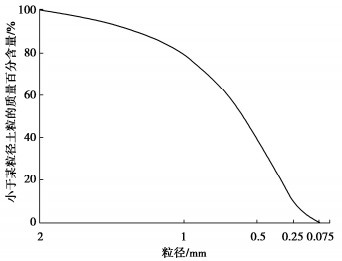
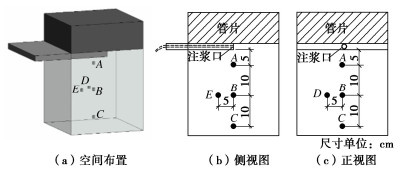
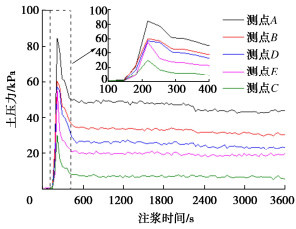
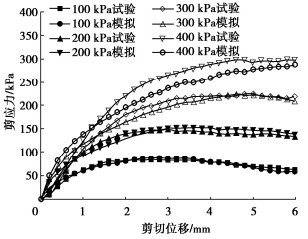
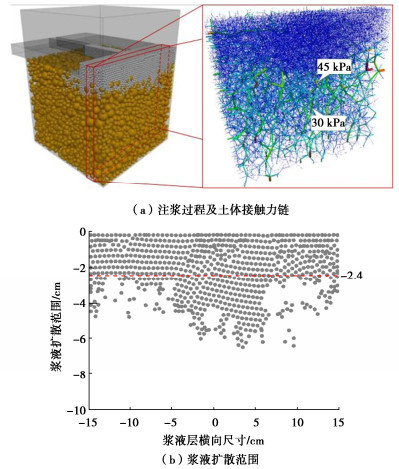
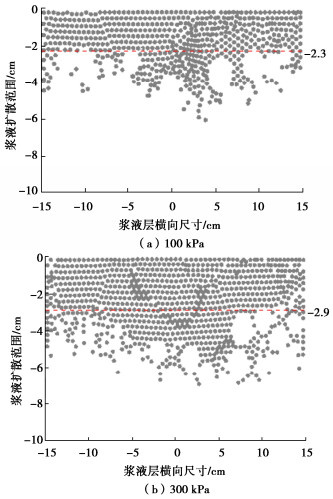
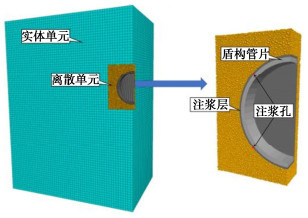
摘要: 为观察盾构施工中同步注浆扩散规律，并提出注浆参数调控手段，以滨海砂土地层为目标，设计并开展盾尾同步注浆模型试验，获得隧道外侧不同位置浆液扩散规律。在借助试验结果标定离散元模型中各颗粒间接触参数的基础上，建立盾尾同步注浆连续-离散元耦合模型，模拟浆液填充渗透过程，对照试验结果分析导致注浆层厚度差异的主要原因，进而通过调整注浆参数优化浆液填充效果。结果表明：离散元仿真模型中的颗粒运移特性能够有效展示浆液在盾尾间隙及周边土层中的填充、渗透现象；受流动性影响，浆液较易在注浆孔口聚集，而若注浆压力不足，将导致距离注浆孔较远的隧道上、下侧浆液层均匀性不良，通过调整不同部位注浆孔压力配比关系，可有效改善填充效果；注浆层受土层压力影响，隧道上方厚度相对下侧较薄，而侧面浆液在自身重力作用下向下沉积，呈上薄下厚分布。Abstract: In order to evaluate the quality of the synchronous grouting of shield construction and to propose the regulation means of grouting parameters, taking the coastal sandy soil stratum as the target, the model tests on shield synchronous grouting are designed and carried out to obtain the slurry diffusion laws at various locations at the outside of a tunnel. On the basis of calibrating the contact parameters between particles in the discrete element model with the help of the test results, a continuous-discrete element coupling model for the shield synchronous grouting is established to simulate the process of filling and penetration of the slurry, and to analyze the main reasons leading to the difference in the thickness of the slurry layer in comparison with the test results, and then to optimize the filling effects of the slurry by adjusting the grouting parameters. The results show that the particle migration characteristics of the discrete element simulation model can effectively display the filling and permeation phenomena of the slurry in the excavation gap and the surrounding soil layer. Affected by the mobility, the slurry is easy to gather in the grouting hole, and if the grouting pressure is insufficient, it will lead to poor homogeneity of the slurry layer at the upper and lower sides of the tunnel which are far away from the grouting hole. The filling effects can be effectively improved by adjusting the pressure difference between the grouting holes of the shield machine. Affected by the pressure of the soil layer, the thickness of the slurry layer at the upper side of the tunnel is relatively thinner compared to that at the lower side, and the slurry at the lateral side of the tunnel will deposit under the action of its own gravity, and shows a distribution of "thin on the upper part and thick on the lower part".
-
0. 引言
三峡工程运用后，进入长江中下游河道的水量略有减少，沙量急剧减少使得坝下游河流发生长距离、长时间的河床冲刷，导致崩岸年年发生[1]。据不完全统计，至2016年的60余年来，长江中下游累计崩岸长度达1600余公里。目前，长江中下游河道崩岸仍在发生，不仅影响防洪安全及河势稳定，还严重威胁沿江经济社会发展和群众生命财产安全。
目前学者按崩塌力学模式将崩岸主要分为浅层崩塌、平面滑动、圆弧滑动及悬臂崩塌（坍落）等[2]。崩岸模式与土体特性、地层特征、水流条件等有关[3-5]，并且崩岸是一个动态不连续的过程，作用机制较为复杂，其机理和变形特征尚未完全揭示。
学者通常采用模型试验、数值分析方法对河道岸坡的稳定性及崩岸过程进行分析。模型试验一般采用缩尺河工模型试验[6]，包括定床和动床模型，能较好的反映水流对岸坡的冲刷作用，但其对岸坡土体的模拟主要采用不同粒径的模型砂，在自重应力影响、土体特性、尺寸效应等方面存在不足，无法模拟岸坡土体的真实状态。数值模型包括一维尺度的BSTEM模型和CONCEPTS模型，以及在此基础上进行的改进和优化[7-9]。此外，有限元方法也用来对岸坡稳定性进行分析，能较好地得到水位变化条件下崩塌前岸坡的应力场变化规律。但这些数值方法无法进行开裂和崩塌等非连续大变形的分析计算，无法得到岸坡崩塌的变形过程。
本文以长江中游荆江河段南五洲长江村崩岸段作为代表，通过现场勘察获取地层与土体特性参数，采用简化岸坡模型开展离心模型试验研究，并与DDA非连续大变形数值分析结果进行对比，揭示水流冲刷条件下崩岸的变形特征。
1. 岸坡土体特性
南五洲长江村崩岸段位于公安河段长江右岸公安县杨家村镇长江村，起点为荆72断面处，崩岸长度约2350 m，如图 1所示。钻探断面位于民堤长支右36处的堤外滩地上，该处崩岸状态稳定。沿垂直河道方向共设3个钻孔ZK03、ZK04和ZK05，离河岸坡顶的距离分别为5，10，20 m。
三个钻孔的深度依次为35.30，35.00，32.00 m，均进入砂层中，钻孔取样揭示该处土层垂直方向从上到下依次为素填土、黏性土、粉砂和细砂，表现为典型的二元结构特征。表层素填土厚为1 m左右，黏土层与砂层的界线在19.40~22.00 m范围，黏土层厚18.4~21.00 m，以ZK03号钻孔为例，地层分布如图 2所示。
对3个钻孔中的黏性土从上到下进行分层取样开展室内物理力学试验，并对砂层进行原位标贯试验，得到地层土体分布特征与物理力学性质。其中黏性土室内试验结果列在表 1中，第一层表现为黄褐色，深度为1.0~4.2 m，塑性指数IP10为13.4~16.5；第二层为灰褐色，深度为4.0~14.0 m，IP10为13.0~13.7；第三层为灰褐色，深度为11.2~22.0 m，IP10为14.4~15.1。据湖北省地方标准《建筑地基基础技术规范》（DB42/242—2014），钻孔揭示的该地层黏性土塑性指数IP10在(10，17]范围内，均为粉质黏土。
表 1 土体物理力学特性试验结果Table 1. Test results of physical and mechanical properties of soil mass地层代号 土类名称 颜色 含水率
w湿密度ρ/
(kg·m-3)Gs 孔隙比
e饱和固结快剪 黏聚力
ccq/kPa内摩擦角
φcq/(°)②-1 粉质黏土 黄褐色 32.7%~33.5% 1.85~1.89 2.67~2.70 0.875~0.957 11.6~25.5
(18.7)21.1~24.1
(22.4)②-2 粉质黏土 灰褐色 29.8%~37.3% 1.83~1.92 2.66 0.798~0.996 9.7~11.8
(10.8)22.5~25.6
(23.8)②-3 粉质黏土 灰褐色 30.3%~39.6% 1.79~1.87 2.66~2.68 0.863~1.090 11.5~37.5
(17.8)21.6~24.7
(23.7)注：括号中的数字为平均值。 根据现场标准贯入试验结果，粉砂层密实度为稍密，细砂层密实度为中密到密实，如图 2所示。
因此，根据现场的地质勘察与土体特性研究，崩岸段的地层具有典型的二元结构特征，表现为上部为粉质黏土层，下部位粉细砂层。
2. 离心模型试验
2.1 模型装置
试验离心机为长江科学院CKY-200现代化多功能土工离心机，有效容量200g·t；最大加速度为200g，无级调速，调速精确到0.1g；吊篮净空尺寸1.2 m×1.0 m×1.5 m。使用的模型箱尺寸（长×宽×高）1.0 m×0.4 m×0.8 m，如图 3所示。
基于崩岸段断面实测地形，为研究坡顶崩退变形特征，采用如图 3所示的简化模型，下部为直立坡面，上部倾斜坡面。模型制作时预设掏空长度为20 cm，位于岸坡土体下部前段，对应斜坡面和坡顶前部。通过设置遇水软化解体的材料在加载过程中加水使其解体模拟掏空；后端采用刚性地基，不会发生掏空等变形。
2.2 试验过程
（1）模型制备
岸坡使用的土体为南五洲长江村崩岸段现场钻孔取样所得的②-2及②-3层粉质黏土。以5 cm为一层，计算每层所需土的质量，并用铅块捣实至设定刻度，每完成一层后作刨毛处理，以消除击实导致土体渗透性不均匀的问题。另外，在该阶段需要同时埋置示踪标记点等相关监测装置。
（2）监测指标
a）岸坡顶面沉降：采用3个激光位移计沿模型中线水平方向进行监测岸坡顶面关键位置处的沉降情况，激光位移计量程为30~80 mm，分辨率为8 μm。
b）岸坡内部沉降：利用模型土体内埋设的分层沉降标监测岸坡内部的沉降变形。
c）视频监控：设置两个监控摄像头，在试验全过程中实时监控模型断面和内部坡体变形的变化过程。
（3）加载过程：
调试完成后，逐步加载至15g，运行一段时间待岸坡变形稳定后，注水使支撑块软化解体，模拟淘刷过程，最后加载至20g，加速崩岸过程。试验中，在加载至15g过程中岸坡发生滑坡，第一级稳定荷载降至10g，待稳定后再加载至15g模拟淘刷，至20g加速崩塌，如图 4所示。
2.3 试验结果分析
根据整个试验的观察，试验过程中出现了两个阶段的岸坡破坏。第一阶段发生在离心加速度逐渐增大至14g左右时，此时模型箱内未注水，岸坡坡脚底部的支撑仍有效存在。根据离心模型试验缩尺比例，在14g离心加速度作用下，整个坡体放大比例后直立坡面高度达到4.2 m，在离心力作用下，坡面起初发生明显水平向外的变形（图 5（a）），之后在坡体顶部后方出现竖向裂缝，并不断扩大，坡顶竖向位移大小关系为LDS3 > LDS2 > LDS1（图 4），即越靠近坡顶角竖向位移越大。紧接着坡体发生滑坡，发生明显的错动变形（图 5（b）），靠近坡顶角的竖向位移突变，监测数据超出量程，滑坡体呈整体沿滑裂面下滑破坏。
第二阶段是在第一阶段滑坡完成、坡体继续运行一段时间后，离心加速度增加至15g并持续运行，加水使底部支撑块软化解体的基础上发生的。在模拟淘刷过程中，支撑块逐渐软化解体，上部土体逐渐向下变形，临空坡面处分层沉降标向下运动，坡体后方出现竖向裂缝（图 5（c）），随着底部支撑解体的逐渐完全，坡体上的竖向裂缝逐渐扩展，同时在坡底淘刷末端处也产生了竖向裂缝（图 5（d）），土体未表现出明显的悬空现象。之后进一步加载至20g离心加速度，裂缝逐渐扩展并变宽，上部土体发生明显的向下错动加向外转动变形（图 5（e）），土体表现为成块的突然崩落特征。由于模型箱中已崩塌土体逐渐占据了底部空间，使得坡面土体变形受限，无法发生进一步的崩塌，继续加载仅能使上部土体裂缝发展，最终破坏形态如图 5（f）所示，坡顶有明显的开裂，土体发生明显的“错动+转动”块状崩落。
在真实的河流冲刷条件下，从岸坡上崩塌下的土体会在高速水流作用下被冲走，已崩塌土体对岸坡进一步变形的阻碍作用以及对坡脚淘刷的防护作用不复存在，水流会进一步深入淘刷坡脚，导致岸坡持续崩塌，河岸不断后退。试验中表现为岸坡底部支撑进一步向内部失效，土体持续发生“错动+转动”变形，崩塌脱离岸坡。
3. 数值分析结果对比
针对具有完整1∶1坡比的岸坡，Xu等[10]、陈航等[11]采用DDA方法对由淘刷引起的崩岸全过程演化进行了数值模拟分析。采用逐步向内移除坡底刚性支撑来模拟淘刷过程，根据其分析结果，对于具有二元结构的完整岸坡，在底部砂层受水流作用逐步淘刷过程中，其受力和变形主要分为三个阶段。分别为坡面逐渐崩塌阶段、坡面转坡顶过渡阶段（图 6）以及坡顶崩退阶段[11]。其中DDA数值分析中反映的坡面转坡顶过渡阶段与试验第二阶段的变形特征变形特征基本一致。即在跨越坡顶角的土体崩塌过程中，坡顶处出现垂直顶部的破裂面，基底处出现近似直立的破裂面；随着土体的不断崩塌，坡体内部的受力与变形在逐渐调整与演化，拉裂缝不断发展延伸，土体沿裂缝发生塌落，最终在坡体上部形成了近似直立的坡面，原始坡面已全部崩塌。该近似直立的坡面与南五洲长江村崩岸水面上的表现形态一致。
![]()
图 6 崩岸坡面转坡顶过渡阶段DDA水平位移云图Figure 6. Horizontal displacements of DDA at the transition stage from slope surface to slope top4. 结论
对长江中游荆江河段南五洲长江村崩岸段进行勘察，得到岸坡土体特性，并开展离心模型试验，对具有二元结构的岸坡在淘刷作用下发生崩岸的变形规律进行研究，得到以下结论：
（1）钻孔揭示的地层结构从上到下依次为素填土、粉质黏土、粉砂和细砂，黏性土层主要为粉质黏土，具有典型的二元结构特征。
（2）离心模型试验模拟了坡脚淘刷的条件，重现了岸坡崩塌的过程，主要经历了坡体上部产生竖向裂缝并逐渐扩展、坡底淘刷末端处产生竖向裂缝、裂缝逐渐扩展并变宽、上部土体发生明显的向下错动加向外转动变形，表现为“错动+转动”的突然崩落特征。
-
![]()
图 8 不同注浆压力下浆液扩散范围
Figure 8. Ranges of slurry diffusion under different grouting pressures
表 1 浆液材料配比
Table 1 Ratios of slurry materials
单位: kg·m-3 水泥 粉煤灰 膨润土 砂 水 减水剂 187 313 37.5 770 375 4.25 
下载: 导出CSV
表 2 浆液基本性能
Table 2 Basic properties of slurry
流动度/
cm稠度/
cm泌水率/
%凝结时间/h 24 h无侧限抗压强度/kPa 18.8 8.4 0.5 8.5 58
下载: 导出CSV
表 3 注浆试验方案
Table 3 Schemes of grouting tests
工况 注浆压力/kPa 注浆位置 1 100 底部 2 200 底部 3 300 底部 4 200 顶部 5 200 侧部
下载: 导出CSV
表 4 土颗粒细观参数
Table 4 Microscopic parameters of soil particles
模型参数 取值 土体密度/(g·cm-3) 1.73 土体粒径范围/mm 1.25~5.00 土颗粒接触模量/MPa 20.00 土颗粒刚度比 1.00 土颗粒摩擦系数 0.55 土体模型孔隙率 0.40 土颗粒局部阻尼系数 0.70 土颗粒-墙体接触模量/MPa 25.00 墙体刚度比 1.00 土颗粒-墙体摩擦系数 0.20
下载: 导出CSV
表 5 分步放大法关键步骤土颗粒细观参数
Table 5 Microscopic parameters of soil particles in key steps of stepwise amplification method
模型参数 放大前 放大4倍 放大32倍 土体粒径范围/mm 0.63~2.50 2.50~10.00 20.00~80.00 土颗粒接触模量/MPa 20.00 10.00 10.00 土颗粒摩擦系数 0.55 0.25 0.15 土-墙接触模量/MPa 25.00 15.00 15.00 土颗粒-墙体摩擦系数 0.20 0.20 0.10
下载: 导出CSV
表 6 浆液颗粒细观参数
Table 6 Microscopic parameters of slurry particles
模型参数 取值 浆液颗粒与最大土体颗粒粒径比 0.1875 浆液密度/(g·cm-3) 3.70 浆液颗粒接触模量/MPa 1.00 浆液颗粒摩擦系数 0.00 浆液颗粒法向阻尼系数 0.20 浆液颗粒-土颗粒接触模量/MPa 10.00 浆液颗粒-土颗粒摩擦系数 0.00 浆液颗粒-土颗粒法向阻尼系数 0.20 浆液颗粒-墙体接触模量/MPa 1.00 浆液颗粒-墙体摩擦系数 0.00
下载: 导出CSV
表 7 不同注浆压力下计算结果
Table 7 Calculated results under different grouting pressures
注浆压力/kPa
上孔/下孔浆液注入颗粒 间隙颗粒 填充度/
%注入率/
%228/306 3038 1242 78.61 192.28 240/330 3648 1354 85.70 230.89 260/360 4256 1438 91.01 269.37 300/360 4864 1523 96.39 307.85 320/360 5168 1580 100.00 327.09 350/400 6080 1580 100.00 384.81
下载: 导出CSV
-
[1] 叶飞, 苟长飞, 刘燕鹏, 等. 盾构隧道壁后注浆浆液时变半球面扩散模型[J]. 同济大学学报(自然科学版), 2012, 40(12): 1789-1794. doi: 10.3969/j.issn.0253-374x.2012.12.008 YE Fei, GOU Changfei, LIU Yanpeng, et al. Half-spherical surface diffusion model of shield tunnel back-filled grouts[J]. Journal of Tongji University (Natural Science), 2012, 40(12): 1789-1794. (in Chinese) doi: 10.3969/j.issn.0253-374x.2012.12.008
[2] YE F, YANG T, MAO J H, et al. Half-spherical surface diffusion model of shield tunnel back-fill grouting based on infiltration effect[J]. Tunnelling and Underground Space Technology, 2019, 83: 274-281. doi: 10.1016/j.tust.2018.10.004
[3] 叶飞, 王斌, 韩鑫, 等. 盾构隧道壁后注浆试验与浆液扩散机理研究进展[J]. 中国公路学报, 2020, 33(12): 92-104. doi: 10.3969/j.issn.1001-7372.2020.12.007 YE Fei, WANG Bin, HAN Xin, et al. Review of shield tunnel backfill grouting tests and its diffusion mechanism[J]. China Journal of Highway and Transport, 2020, 33(12): 92-104. (in Chinese) doi: 10.3969/j.issn.1001-7372.2020.12.007
[4] 叶飞, 李思翰, 夏天晗, 等. 低渗地层盾构隧道壁后注浆压密-劈裂扩散模型研究[J]. 岩土工程学报, 2023, 45(10): 2014-2022. YE Fei, LI Sihan, XIA Tianhan, et al. Compaction-fracture diffusion model for backfill grouting of shield tunnels in low permeability strata[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(10): 2014-2022. (in Chinese)
[5] 李志明, 廖少明, 戴志仁. 盾构同步注浆填充机理及压力分布研究[J]. 岩土工程学报, 2010, 32(11): 1752-1757. LI Zhiming, LIAO Shaoming, DAI Zhiren. Theoretical study on synchronous grouting filling patterns and pressure distribution of EPB shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1752-1757. (in Chinese)
[6] 周佳媚, 刘欢, 张迁, 等. 考虑浆液稠度变化的盾构壁后注浆扩散模型[J]. 铁道科学与工程学报, 2018, 15(3): 710-717. doi: 10.3969/j.issn.1672-7029.2018.03.022 ZHOU Jiamei, LIU Huan, ZHANG Qian, et al. Backfilled grouting diffusion model of shield tunnel considering variation of slurry consistency[J]. Journal of Railway Science and Engineering, 2018, 15(3): 710-717. (in Chinese) doi: 10.3969/j.issn.1672-7029.2018.03.022
[7] 韩鑫, 叶飞, 应凯臣, 等. 考虑自重的盾构壁后注浆浆液驱替渗透扩散[J]. 华中科技大学学报(自然科学版), 2020, 48(4): 37-42. HAN Xin, YE Fei, YING Kaichen, et al. Displacement effect on penetration diffusion of backfill grouting of shield tunnel considering self-weight[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2020, 48(4): 37-42. (in Chinese)
[8] 白云, 戴志仁, 张莎莎, 等. 盾构隧道同步注浆浆液压力扩散模式研究[J]. 中国铁道科学, 2011, 32(4): 38-45. BAI Yun, DAI Zhiren, ZHANG Shasha, et al. Study on the grout pressure dissipation mode in simultaneous backfill grouting during shield tunneling[J]. China Railway Science, 2011, 32(4): 38-45. (in Chinese)
[9] 张聪, 梁经纬, 阳军生, 等. 考虑区间分布的幂律流体脉动渗透注浆扩散机制研究[J]. 岩土工程学报, 2018, 40(11): 2120-2128. doi: 10.11779/CJGE201811019 ZHANG Cong, LIANG Jingwei, YANG Junsheng, et al. Diffusion mechanism of pulsating seepage grouting slurry with power-law fluid considering interval distribution[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(11): 2120-2128. (in Chinese) doi: 10.11779/CJGE201811019
[10] 张莎莎, 戴志仁, 白云. 盾构隧道同步注浆浆液压力分布规律模型试验研究[J]. 中国铁道科学, 2015, 36(5): 43-53. doi: 10.3969/j.issn.1001-4632.2015.05.07 ZHANG Shasha, DAI Zhiren, BAI Yun. Model test research on distribution law of grout pressure for simultaneous backfill grouting during shield tunneling[J]. China Railway Science, 2015, 36(5): 43-53. (in Chinese) doi: 10.3969/j.issn.1001-4632.2015.05.07
[11] DING W Q, CHAO D, ZHU Y H, et al. The behavior of synchronous grouting in a quasi-rectangular shield tunnel based on a large visualized model test[J]. Tunnelling and Underground Space Technology, 2019, 83: 409-424. doi: 10.1016/j.tust.2018.10.006
[12] ZHAO T C, DING W Q, QIAO Y F, et al. A large-scale synchronous grouting test for a quasi-rectangular shield tunnel: observation, analysis and interpretation[J]. Tunnelling and Underground Space Technology, 2019, 91: 103018. doi: 10.1016/j.tust.2019.103018
[13] 张连震, 李志鹏, 刘人太, 等. 砂层劈裂-压密注浆模拟试验系统研发及试验[J]. 岩土工程学报, 2019, 41(4): 665-674. ZHANG Lianzhen, LI Zhipeng, LIU Rentai, et al. Simulation tests on fracture-compaction grouting process in sand layer[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(4): 665-674. (in Chinese)
[14] 张云, 殷宗泽, 徐永福. 盾构法隧道引起的地表变形分析[J]. 岩石力学与工程学报, 2002(3): 388-392. doi: 10.3321/j.issn:1000-6915.2002.03.019 ZHANG Yun, YING Zongze, XU Yongfu. Analysis on three-dimensional ground surface deformations due to shield tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2002(3): 388-392. (in Chinese) doi: 10.3321/j.issn:1000-6915.2002.03.019
[15] 李磊, 张孟喜, 吴惠明, 等. 近距离多线叠交盾构施工对既有隧道变形的影响研究[J]. 岩土工程学报, 2014, 36(6): 1036-1043. LI Lei, ZHANG Mengxi, WU Huiming, et al. Influence of short-distance multi-line overlapped shield tunnelling on deformation of existing tunnels[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(6): 1036-1043. (in Chinese)
[16] 李培楠, 英旭, 石来, 等. 基于CFD的盾构同步注浆填充扩散运动力学分析[J]. 地下空间与工程学报, 2021, 17(增刊1): 126-132. LI Peinan, YING Xu, SHI Lai, et al. Hydrodynamics analysis on fill diffusion in shield synchronous grouting based on CFD[J]. Chinese Journal of Underground Space and Engineering, 2021, 17(S1): 126-132. (in Chinese)
[17] KASPER T, MESCHKE G. On the influence of face pressure, grouting pressure and TBM design in soft ground tunnelling[J]. Tunnelling and Underground Space Technology, 2006, 21(2): 160-171. doi: 10.1016/j.tust.2005.06.006
[18] MICHAEL K, DIMITRIS L, IOANNIS V, et al. Development of a 3D finite element model for shield EPB tunnelling[J]. Tunnelling and Underground Space Technology, 2017, 65: 22-34. doi: 10.1016/j.tust.2017.02.001
[19] 王胤, 陶奕辰, 程旷, 等. 任意解流流固耦合数值方法及在砂土渗流分析中应用[J]. 岩土工程学报, 2021, 43(11): 2084-2093. doi: 10.11779/CJGE202111015 WANG Yin, TAO Yichen, CHENG Kuang, et al. Arbitrary resolved-unresolved CFD-DEM coupling method and its application to seepage flow analysis in sandy soil[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(11): 2084-2093. (in Chinese) doi: 10.11779/CJGE202111015
[20] 土工试验方法标准: GB/T 50123—2019[S]. 北京: 中国计划出版社, 2019. Standard for Geotechnical Testing Method: GB/T 50123—2019[S]. Beijing: China Planning Press, 2019. (in Chinese)
[21] 梁精华. 盾构隧道壁后注浆材料配比优化及浆体变形特性研究[D]. 南京: 河海大学, 2006. LIANG Jinghua. Study on the Proportion of Backfill-Grouting Materials and Grout Deformation Properties of Shield Tunnel[D]. Nanjing: Hohai University, 2006. (in Chinese)
[22] CAVARRETTA I, COOP M, O'SULLIVAN C. The influence of particle characteristics on the behaviour of coarse grained soils[J]. Géotechnique, 2010, 60(6): 413-423. doi: 10.1680/geot.2010.60.6.413
[23] DI RENZO A, DI MAIO F P. Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes[J]. Chemical Engineering Science, 2004, 59(3): 525-541. doi: 10.1016/j.ces.2003.09.037
[24] ZHANG Z X, HU X Y, SCOTT K D. A discrete numerical approach for modeling face stability in slurry shield tunnelling in soft soils[J]. Computers and Geotechnics, 2011, 38(1): 94-104. doi: 10.1016/j.compgeo.2010.10.011
[25] 周健, 池永. 砂土力学性质的细观模拟[J]. 岩土力学, 2003, 24(6): 901-906. doi: 10.3969/j.issn.1000-7598.2003.06.006 ZHOU Jian, CHI Yong. Mesomechanical simulation of sand mechanical properties[J]. Rock and Soil Mechanics, 2003, 24(6): 901-906. (in Chinese) doi: 10.3969/j.issn.1000-7598.2003.06.006
[26] HUANG X, HANLEY K J, O'SULLIVAN C, et al. Effect of sample size on the response of DEM samples with a realistic grading[J]. Particuology, 2014, 15: 107-115. doi: 10.1016/j.partic.2013.07.006
[27] KODICHERLA S K. Exploring the Mechanical Behaviour of Granular Materials Considering Particle Shape Characteristics: A Discrete Element Investigation[D]. Liverpool: University of Liverpool, 2021.
[28] WANG J, GUTIERREZ M. Discrete element simulations of direct shear specimen scale effects[J]. Géotechnique, 2010, 60(5): 395-409. doi: 10.1680/geot.2010.60.5.395
[29] PENG C, LIU W R, WANG Z. Parameter checking method of large scale particle model[J]. Geotechnical and Geological Engineering, 2021, 39(2): 1533-1540. doi: 10.1007/s10706-020-01574-1
-
期刊类型引用(1)
1. 陈娟，姜命强，赵源. 基于多目标优化的动水注浆参数设计. 水利规划与设计. 2025(02): 76-79+102 . 
百度学术
其他类型引用(1)
-
其他相关附件
计量
- 文章访问数: 446
- HTML全文浏览量: 49
- PDF下载量: 104
- 被引次数: 2
