基于贝叶斯理论和条件协同模拟的海上风电场土体参数空间变异性表征

徐加宝; 张泽超; 张璐璐; 曹子君; 王宇; 张一凡; 张德; 陈杨明

doi:10.11779/CJGE20221585

基于贝叶斯理论和条件协同模拟的海上风电场土体参数空间变异性表征 English Version

徐加宝^{1, 2,},
张泽超³,
张璐璐^{1, 4, 5, ,},
曹子君⁶,
王宇²,
张一凡¹,
张德¹,
陈杨明¹

1.
上海交通大学土木工程系海洋工程国家重点实验室, 上海 200240
2.
香港城市大学建筑学及土木工程学系, 香港 999077
3.
中国长江三峡集团有限公司科学技术研究院, 北京 100038
4.
高新船舶与深海开发装备协同创新中心, 上海 200240
5.
上海市公共建筑和基础设施数字化运维重点实验室, 上海 200240
6.
西南交通大学智慧城市与交通学院高速铁路线路工程教育部重点实验室, 四川成都 611756

基金项目:

中国长江三峡集团有限公司科研资助项目 WWKY-2020-0741

国家自然科学基金项目 52025094

国家自然科学基金项目 51979158

上海市教育委员会科研创新计划项目 2021-01-07-00-02-E00089

详细信息

作者简介:
徐加宝(1993—)，男，博士，主要从事岩土工程可靠度方面的研究工作。E-mail: jiabaoxu2-c@my.cityu.edu.hk

通讯作者:
张璐璐, E-mail: lulu_zhang@sjtu.edu.cn

中图分类号: TU43
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
出版历程
- 收稿日期: 2022-12-28
- 网络出版日期: 2024-03-24
- 刊出日期: 2024-07-31

Spatial variability characterization of soil properties in offshore wind farms based on Bayesian theory and conditional co-simulation method

XU Jiabao^{1, 2,},
ZHANG Zechao³,
ZHANG Lulu^{1, 4, 5, ,},
CAO Zijun⁶,
WANG Yu²,
ZHANG Yifan¹,
ZHANG De¹,
CHEN Yangming¹

1.
State Key Laboratory of Ocean Engineering, Department of Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China
2.
Department of Architecture and Civil Engineering, City University of Hong Kong, Hong Kong 999077, China
3.
Institute of Science and Technology, China Three Gorges Corporation, Beijing 100038, China
4.
Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration (CISSE), Shanghai 200240, China
5.
Shanghai Key Laboratory for Digital Maintenance of Buildings and Infrastructure, Shanghai 200240, China
6.
MOE Key Laboratory of High-speed Railway Engineering, Institute of Smart City and Intelligent Transportation, Southwest Jiaotong University, Chengdu 611756, China

摘要

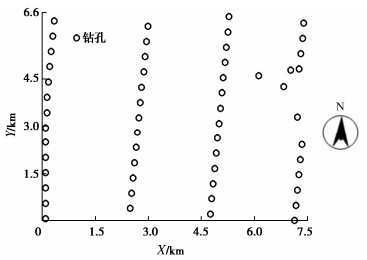
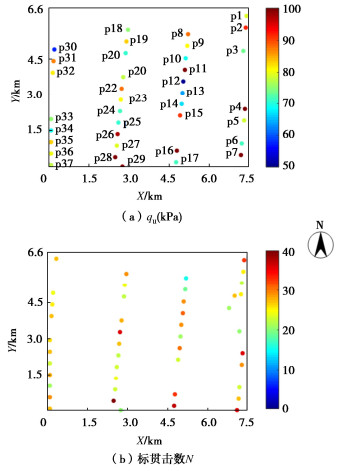
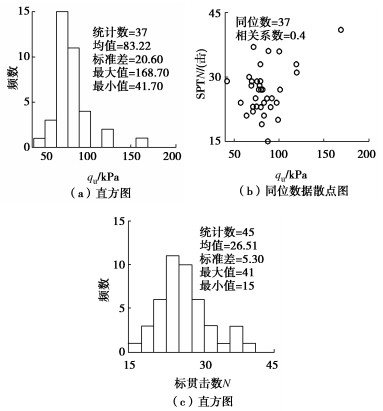
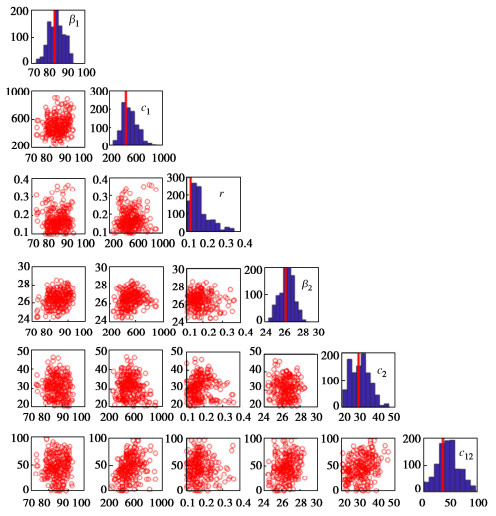
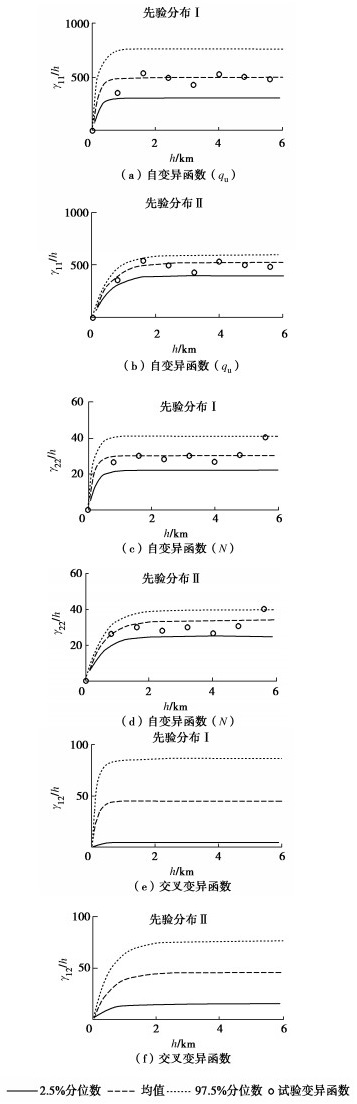
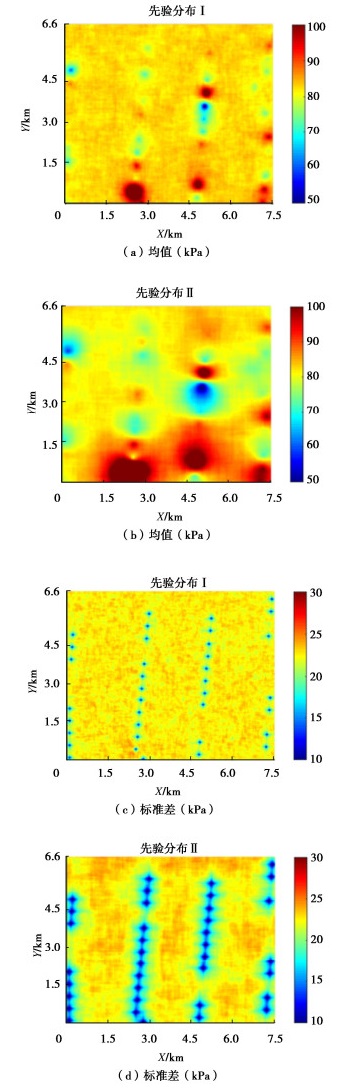
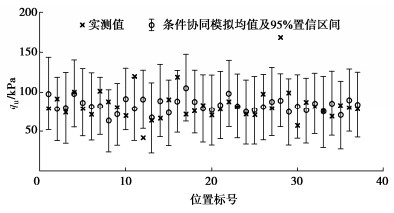
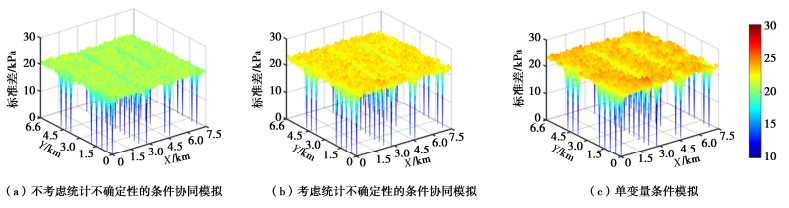
摘要: 海上风电场土体参数的空间变异性表征对海上风电工程具有重要意义，多源土体参数融合可降低表征结果的不确定性。然而，现有方法无法利用非同位多源土体参数数据，且不考虑统计不确定性对空间变异性表征的影响。为此，提出了基于贝叶斯理论的条件协同模拟方法，该方法根据非同位多源土体参数数据，利用贝叶斯理论估计交叉变异函数，再利用条件协同模拟方法生成大量土体参数空间分布的模拟样本，表征参数空间变异性，表征过程中合理地考虑模型参数的统计不确定性。以某海上风电场为工程背景，利用提出的方法融合无侧限抗压强度(q_u)和标准贯入试验(SPT)击数N值，表征q_u的空间变异性。结果表明：提出的方法可以根据有限非同位的q_u和N值数据，表征q_u的空间变异性，合理地反映了有限数据条件下统计不确定性的影响。此外，利用强信息先验分布或者融合标准贯入数据，可以降低变异函数模型参数统计不确定性和条件协同模拟结果的不确定性。
- 海上风电场 /
- 空间变异性 /
- 条件协同模拟 /
- 贝叶斯理论 /
- 多源数据融合
Abstract: The spatial variability characterization of soil properties in offshore wind farms is essential for offshore engineering. The multi-source data fusion can reduce the uncertainty of characterization. However, the existing methods cannot simulate geotechnical properties based on the non-co-located multi-source data, and do not consider the effects of statistical uncertainty. To overcome these challenges, a conditional co-simulation method based on the Bayesian theory is proposed. The Bayesian theory is first used to estimate the cross-variogram model based on the non-co-located multi-source data. Then, the conditional co-simulation is used to generate realizations of spatially varied soil properties, which can characterize the spatial variability with consideration of statistical uncertainty. The proposed method is applied to an offshore wind farm to establish the spatial variability model for the unconfined compression strength (q_u) by integrating data on q_u and standard penetration test (SPT) N value. The results show that the proposed method can characterize the spatial variability of q_u from the non-co-located data on the values of q_u and N, and statistical uncertainty is properly taken into account. In addition, the uncertainties of the variogram models and the conditional co-simulation results can be reduced when the prior distribution with more information and/or SPT data is used.
- offshore wind farm /
- spatial variability /
- conditional co-simulation /
- Bayesian theory /
- multi-source data fusion

HTML全文

图 1 基于贝叶斯理论的条件协同模拟流程图

Figure 1. Flow chart of conditional co-simulation based on Bayesian theory

下载: 全尺寸图片幻灯片

图 2 海上风电场钻孔平面布置图

Figure 2. Layout of boreholes in offshore wind farm

下载: 全尺寸图片幻灯片

图 3 q_u和SPT数据的钻孔位置平面图

Figure 3. Layout of boreholes with q_u and SPT data

下载: 全尺寸图片幻灯片

图 4 实测数据直方图及同位数据散点图

Figure 4. Histogram of measurements and scatter plot between co-located measurements

下载: 全尺寸图片幻灯片

图 5 后验参数直方图及散点图

Figure 5. Marginal distributions and scatter plots of posterior samples

下载: 全尺寸图片幻灯片

图 6 基于先验分布Ⅰ和先验分布Ⅱ估计的变异函数模型对比

Figure 6. Comparison between estimated variogram models based on prior distribution Ⅰ and Ⅱ

下载: 全尺寸图片幻灯片

图 7 基于先验分布Ⅰ和先验分布Ⅱ的条件协同模拟结果对比

Figure 7. Comparison between conditional co-simulation results based on prior distribution Ⅰ and Ⅱ

下载: 全尺寸图片幻灯片

图 8 基于先验分布Ⅰ的条件协同模拟与验证数据对比

Figure 8. Comparison between validation data and conditional co-simulation results based on prior distribution Ⅰ

下载: 全尺寸图片幻灯片

图 9 不考虑统计不确定性的条件协同模拟、考虑统计不确定性的条件协同模拟和单变量条件模拟的标准差对比

Figure 9. Comparison of standard deviations among conditional co-simulation without considering statistical uncertainty, conditional co-simulation considering statistical uncertainty, and univariate conditional simulation

下载: 全尺寸图片幻灯片

图 10 融合SPT数据对自变异函数模型估计的影响

Figure 10. Effects of SPT data on estimation of variogram models

下载: 全尺寸图片幻灯片

表 1 常用的变异函数与协方差函数模型

Table 1 Commonly used variogram and covariance models

类型	变异函数	协方差函数
指数模型	$\left\{ \begin{array}{l} {c_1}\left[ {1 - \exp \left( { - \frac{h}{r}} \right)} \right]{\text{ (}}h > 0) \hfill \\ 0{\text{ (}}h = 0) \hfill \\ \end{array} \right.$	$\left\{ {\begin{array}{*{20}{l}} {{c_1}\exp \left( { - \frac{h}{r}} \right){\text{ (}}h > 0)} \\ {{c_1}{\text{ (}}h = 0)} \end{array}} \right.$
高斯模型	$\left\{ {\begin{array}{*{20}{l}} {{c_1}\left[ {1 - \exp \left( { - \frac{{{h^2}}}{{{r^2}}}} \right)} \right]{\text{ (}}h > 0)} \\ {0{\text{ (}}h = 0)} \end{array}} \right.$	$\left\{ {\begin{array}{*{20}{l}} {{c_1}\exp \left( { - \frac{{{h^2}}}{{{r^2}}}} \right){\text{ (}}h > 0)} \\ {{c_1}{\text{ (}}h = 0)} \end{array}} \right.$
球状模型	$\left\{ \begin{array}{l} 0{\text{ (}}h = 0) \hfill \\ {c_1}\left( {\frac{{3h}}{{2r}} - \frac{{{h^3}}}{{2{r^3}}}} \right){\text{ (}}0 < h \leqslant r) \hfill \\ {c_1}{\text{ (}}h > r) \hfill \\ \end{array} \right.$	$\left\{ \begin{array}{l} {c_1}{\text{ (}}h = 0) \hfill \\ {c_1}\left( {1 - \frac{{3h}}{{2r}} + \frac{{{h^3}}}{{2{r^3}}}} \right){\text{ (}}0 < h \leqslant r) \hfill \\ 0{\text{ }}(h > r) \hfill \\ \end{array} \right.$

下载: 导出CSV

表 2 先验分布Ⅰ

Table 2 Prior distribution Ⅰ of parameters

参数	β₁/kPa	c₁/kPa	r/km	β₂/击	c₂/击	c₁₂
下限	0	0	0.1	0	0	0
上限	200	1000	2	50	100	200

下载: 导出CSV

表 3 先验分布Ⅱ

Table 3 Prior distribution Ⅱ of parameters

参数	β₁/kPa	c₁/kPa	r/km	β₂/击	c₂/击	c₁₂
下限	0	100	0.5	0	0	10
上限	200	600	2	50	40	100

下载: 导出CSV

参考文献(27)

[1]	任灏, 刘博, 刘晓建, 等. 阳江沙扒海上风电三桶吸力桩基础局部冲刷试验研究[J]. 人民珠江, 2022, 43(5): 107-113. https://www.cnki.com.cn/Article/CJFDTOTAL-RMZJ202205016.htm REN Hao, LIU Bo, LIU Xiaojian, et al. Study on local scour of suction bucket foundations at offshore wind farms in shapa of Yangjiang[J]. Pearl River, 2022, 43(5): 107-113. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-RMZJ202205016.htm
[2]	刘润, 闫澍旺. 渤海湾地基土随机场特性及可靠度分析[J]. 岩土工程学报, 2004, 26(4): 464-467. http://cge.nhri.cn/cn/article/id/11445 LIU Run, YAN Shuwang. Random field model and reliability analysis of foundation soil in Bohai Gulf[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(4): 464-467. (in Chinese) http://cge.nhri.cn/cn/article/id/11445
[3]	张强林, 吴衍剑, 张祥龙. 海上风电超大直径单桩基础水平位移计算影响因素研究[J]. 水电与新能源, 2021, 35(12): 54-56, 63. https://www.cnki.com.cn/Article/CJFDTOTAL-HBFD202112014.htm ZHANG Qianglin, WU Yanjian, ZHANG Xianglong. On the influencing factors of horizontal displacement calculation of super-large diameter mono-pile foundation for offshore wind turbine[J]. Hydropower and Nwe Energy, 2021, 35(12): 54-56, 63. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HBFD202112014.htm
[4]	沈晓雷, 陈洪飞, 王欣怡. 海上风电高桩承台基础承载特性数值模拟研究[J]. 水力发电, 2021, 47(12): 72-75. https://www.cnki.com.cn/Article/CJFDTOTAL-SLFD202112016.htm SHEN Xiaolei, CHEN Hongfei, WANG Xinyi. Numerical simulation on the bearing characteristics of the high-pile cap foundation for offshore wind power[J]. Water Power, 2021, 47(12): 72-75. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLFD202112016.htm
[5]	VANMARCKE E. Random Fields, Analysis and Synthesis[M]. Cambridge: MIT Press, 1983.
[6]	JOURNEL A G. Geostatistics for conditional simulation of ore bodies[J]. Economic Geology, 1974, 69(5): 673-687. doi: 10.2113/gsecongeo.69.5.673
[7]	CHEN Q S, WANG C F, JUANG C H. Probabilistic and spatial assessment of liquefaction-induced settlements through multiscale random field models[J]. Engineering Geology, 2016, 211: 135-149. doi: 10.1016/j.enggeo.2016.07.002
[8]	LI X Y, ZHANG L M, LI J H. Using conditioned random field to characterize the variability of geologic profiles[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2016, 142(4): 04015096. doi: 10.1061/(ASCE)GT.1943-5606.0001428
[9]	朱彬. 基于可靠度理论的海床稳定性分析及评价方法[D]. 大连: 连理工大学, 2021. ZHU Bin. Analysis and Evaluation Method of Seabed Stability Based on Reliability Theory[D]. Dalian: Dalian University of Technology, 2021. (in Chinese)
[10]	LUO N, ARWADE S R, DEGROOT D J. Probabilistic analysis of offshore geotechnical site investigation in a homogeneous stiff clay deposit[J]. Journal of Physics Conference Series, 2020, 1452: 012037. doi: 10.1088/1742-6596/1452/1/012037
[11]	林军, 蔡国军, 邹海峰, 等. 基于随机场理论的江苏海相黏土空间变异性评价研究[J]. 岩土工程学报, 2015, 37(7): 1278-1287. doi: 10.11779/CJGE201507014 LIN Jun, CAI Guojun, ZOU Haifeng, et al. Assessment of spatial variability of Jiangsu marine clay based on random field theory[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(7): 1278-1287. (in Chinese) doi: 10.11779/CJGE201507014
[12]	蒋水华, 魏博文, 张文举, 等. 基于多源试验数据空间变异土体参数概率反演及边坡可靠度更新[J]. 岩土力学, 2018, 39(4): 1491-1499. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201804042.htm JIANG Shuihua, WEI Bowen, ZHANG Wenju, et al. Probabilistic back analysis of spatially varying soil properties and reliability updating of slopes with multiple sources of test data[J]. Rock and Soil Mechanics, 2018, 39(4): 1491-1499. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201804042.htm
[13]	MIAO C, CAO Z J, XIAO T, et al. BayLUP: A Bayesian framework for conditional random field simulation of the liquefaction-induced settlement considering statistical uncertainty and model error[J/OL]. Gondwana Research, 2022. https://doi.org/10.1016/j.gr.2022.10.020.
[14]	夏侯云山, 张抒, 唐辉明, 等. 考虑参数空间变异结构的结构化交叉约束随机场模拟方法研究[J]. 岩土力学, 2019, 40(12): 4935-4945, 4962. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201912044.htm XIAHOU Yunshan, ZHANG Shu, TANG Huiming, et al. Study of structural cross-constraint random field simulation method considering spatial variation structure of parameters[J]. Rock and Soil Mechanics, 2019, 40(12): 4935-4945, 4962. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201912044.htm
[15]	REMY N, BOUCHER A, WU J. Applied Geostatistics with SGeMS: A User's Guide[M]. New York: Cambridge University Press, 2009.
[16]	XU J B, ZHANG L L, WANG Y, et al. Probabilistic estimation of cross-variogram based on Bayesian inference[J]. Engineering Geology, 2020, 277: 105813. doi: 10.1016/j.enggeo.2020.105813
[17]	杜文凤, 彭苏萍. 利用地质统计学预测煤层厚度[J]. 岩石力学与工程学报, 2010, 29(增刊1): 2762-2767. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2010S1028.htm DU Wenfeng, PENG Suping. Coalseam thickness prediction with geostatistics[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S1): 2762-2767. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2010S1028.htm
[18]	张仁铎. 空间变异理论及应用[M]. 北京: 科学出版社, 2005. ZHANG Renduo. Spatial Variation Theory and Its Application[M]. Beijing: Science Press, 2005. (in Chinese)
[19]	WEBSTER R, OLIVER M A. Geostatistics for Environmental Scientists[M]. 2nd ed. Chichester: Wiley, 2007.
[20]	张蕾, 李典庆, 唐小松, 等. 基于贝叶斯理论的抗剪强度参数最优Copula函数识别[J]. 岩土力学, 2016, 37(增刊2): 578-588. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2016S2073.htm ZHANG Lei, LI Dianqing, TANG Xiaosong, et al. Bayesian Copula selection for shear strength parameters of soils and rocks[J]. Rock and Soil Mechanics, 2016, 37(S2): 578-588. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2016S2073.htm
[21]	蒋水华, 冯泽文, 刘贤, 等. 基于自适应贝叶斯更新方法的岩土参数概率分布推断[J]. 岩土力学, 2020, 41(1): 325-335. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202001038.htm JIANG Shuihua, FENG Zewen, LIU Xian, et al. Inference of probability distributions of geotechnical parameters using adaptive Bayesian updating approach[J]. Rock and Soil Mechanics, 2020, 41(1): 325-335. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202001038.htm
[22]	JOURNEL A G. Geostatistics: models and tools for the earth sciences[J]. Mathematical Geology, 1986, 18(1): 119-140. doi: 10.1007/BF00897658
[23]	田密, 李典庆, 曹子君, 等. 基于贝叶斯理论的土性参数空间变异性量化方法[J]. 岩土力学, 2017, 38(11): 3355-3362. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201711036.htm TIAN Mi, LI Dianqing, CAO Zijun, et al. Quantification of spatial variability of soil parameters using Bayesian approaches[J]. Rock and Soil Mechanics, 2017, 38(11): 3355-3362. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201711036.htm
[24]	CAO Z J, WANG Y, LI D Q. Quantification of prior knowledge in geotechnical site characterization[J]. Engineering Geology, 2016, 203, 107-116. doi: 10.1016/j.enggeo.2015.08.018
[25]	VRUGT J A, TER BRAAK C J F, CLARK M P, et al. Treatment of input uncertainty in hydrologic modeling: doing hydrology backward with Markov chain Monte Carlo simulation[J]. Water Resources Research, 2008, 44(12): W00B09.
[26]	左自波, 张璐璐, 程演, 等. 基于MCMC法的非饱和土渗流参数随机反分析[J]. 岩土力学, 2013, 34(8): 2393-2400. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201308057.htm ZUO Zibo, ZHANG Lulu, CHENG Yan, et al. Probabilistic back analysis of unsaturated soil seepage parameters based on Markov chain Monte Carlo method[J]. Rock and Soil Mechanics, 2013, 34(8): 2393-2400. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201308057.htm
[27]	余志雄, 周创兵, 李俊平, 等. 基于v-SVR算法的边坡稳定性预测[J]. 岩石力学与工程学报, 2005, 24(14): 2468-2475. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200514012.htm YU Zhixiong, ZHOU Chuangbing, LI Junping, et al. Predicting slope stability based on v-SVR algorithm[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(14): 2468-2475. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200514012.htm