基于全连接神经网络的地铁车站响应分析与地震强度指标优选

钟紫蓝; 倪博; 史跃波; 张成明; 申家旭; 杜修力

doi:10.11779/CJGE20221448

基于全连接神经网络的地铁车站响应分析与地震强度指标优选 English Version

北京工业大学城市与工程安全减灾教育部重点实验室, 北京 100124

基金项目:

国家自然科学基金面上项目 51978020

详细信息

作者简介:
钟紫蓝(1986—)，男，博士，副研究员，主要从事地下结构抗震研究。E-mail: zilanzhong@bjut.edu.cn

通讯作者:
申家旭, E-mail: shenjx@bjut.edu.cn

中图分类号: TU443
计量
- 文章访问数: 362
- HTML全文浏览量: 60
- PDF下载量: 95
出版历程
- 收稿日期: 2022-11-22
- 网络出版日期: 2024-03-14
- 刊出日期: 2024-02-29

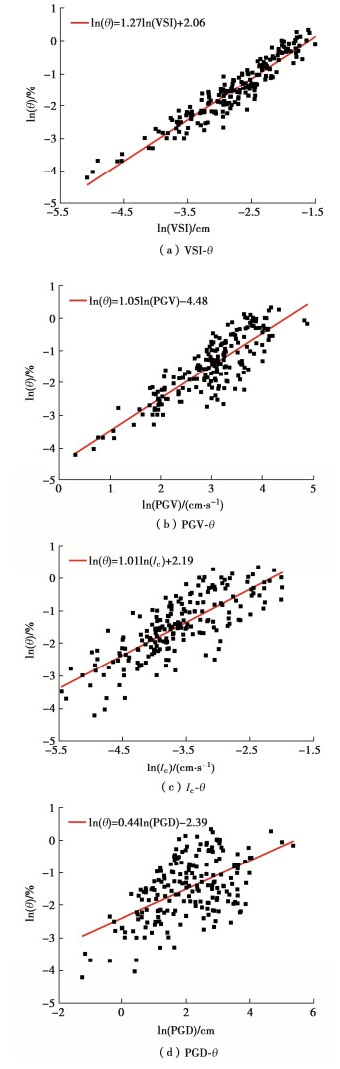
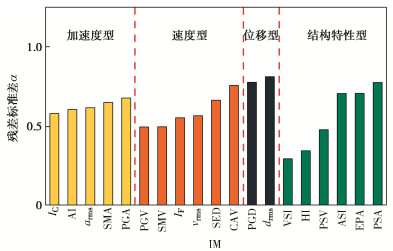
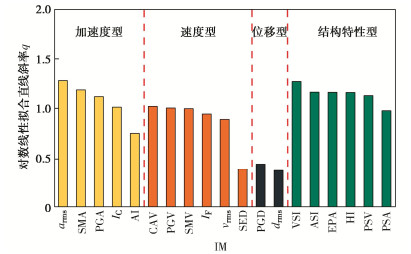
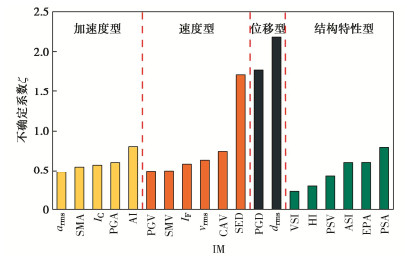
Response analysis of subway station and optimization of seismic intensity measures based on fully connected neural network

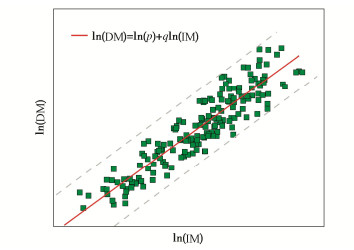
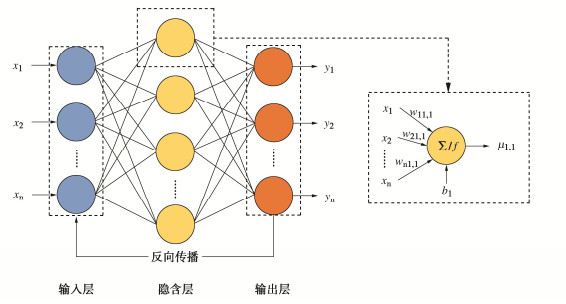
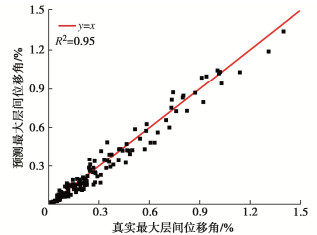
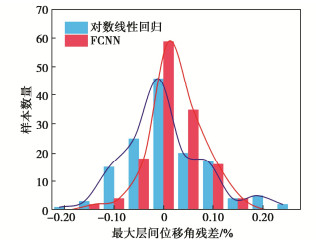
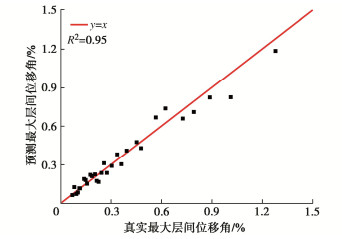
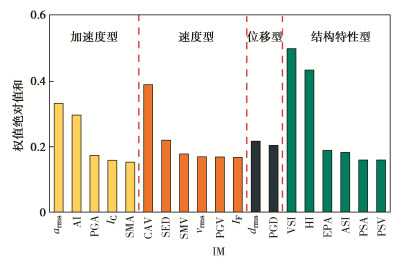
Key Laboratory of Urban Security and Disaster Engineering of Ministry of Education, Beijing University of Technology, Beijing 100124, China

摘要

摘要: 为了降低随机地震响应分析的计算成本，将人工神经网络方法用于构建概率地震需求模型（PSDM），以预测地铁车站结构的地震响应，并对适用于地铁车站结构响应预测的地震强度指标（IM）进行了优选。首先选取了200条实测地震动，计算IM，并对典型的三层三跨地铁车站结构进行有限元建模，将IM与最大层间位移角作为输入与输出训练全连接神经网络模型（FCNN），得到了最大层间位移角的预测模型。最后基于训练后FCNN输入层到隐含层中的权重矩阵与传统方法对IM进行优选，得出了对最大层间位移角影响最大的IM。研究结果表明：训练后FCNN能以0.95的精度预测地铁车站最大层间位移角，且计算耗时仅为数值模拟的1/5；针对矩形地下结构最大层间位移角，速度型和速度反应谱型指标的影响明显高于其他类型指标，其中速度谱强度（VSI）对最大层间位移角的影响最大。
- 全连接神经网络 /
- 概率地震需求模型 /
- 地铁车站结构 /
- 地震强度指标
Abstract: In order to reduce the calculation cost of random seismic response analysis, the artificial neural network method is used to build a probabilistic seismic demand model (PSDM) to predict the seismic response of subway station structures, and the seismic intensity measure (IM) suitable for the prediction of subway station structural response is optimized. First, 200 measured ground motions are selected, IM is calculated, and the typical three-story and three-span subway station structure is modeled by the finite element method. Then, the IM and the maximum layer drift are used as the input and output to train the fully connected neural network (FCNN), and the prediction model for the maximum layer drift is obtained. Finally, the IM is optimized based on the weight matrix from the FCNN input layer to the hidden layer after training and the traditional methods, and the IM that has the greatest impact on the maximum layer drift is obtained. The results show that the FCNN after training can predict the maximum layer drift of subway station with an accuracy of 0.95, and the calculation efficiency is 18000 times higher than that of numerical simulation. For the maximum layer drift, the impact of velocity type and velocity response spectrum type indices is significantly higher than other types of indices, among which the velocity spectrum intensity (VSI) has the largest impact on the maximum layer drift.
- FCNN /
- probabilistic seismic demand model /
- subway station structure /
- seismic intensity measure

HTML全文

0. 引言

桩−筏复合地基因对不均匀沉降问题具有较好的控制效果,在高速公路、高速铁路和地铁路基的建设中已获得应用^[1]。

目前,在刚性桩复合地基方面国内外学者取得了一定的研究成果。在理论分析方面,相关研究人员分别基于荷载传递方法、传递函数法与单元体相结合的方法、最小势能原理与弹簧组模型、桩-土-筏非线性共同作用模型,分析了路堤荷载下桩筏复合地基中桩、土、垫层三者之间的彼此影响；研究了桩-土荷载分担比与桩之间的距离、路堤土的剪切模量、路堤的高度以及桩土相对刚度之间的关系,垫层对应力调节和沉降的影响；提出了求解地基固结沉降的简化分析方法、桩和筏板的沉降计算方法^[2-7]。在数值模拟方面,相关学者分析了路堤荷载下孔隙水压力、竖向变形及侧向水平变形的变化规律；计算了桩间距对降低路堤沉降和不均匀沉降的影响^[8-12]。在现场试验方面,相关学者研究了群桩效应系数与桩数、桩帽、桩长、褥垫层、荷载的关系；分析了筏板应力、应变、桩顶应力及土压力与时间的关系,路堤-桩-地基的相互作用,地基土孔隙水压力、沉降、分层沉降及荷载传递的规律^[13-15]。

已有的关于刚性桩复合地基的研究大多集中在静力范围内。在交通荷载作用下,关于桩-筏复合地基的研究仍较少,尤其是将X形桩替换其中的圆形桩方面的研究更少^[16]。为此,笔者所在团队在动力荷载作用下进行了一些X形桩承式路堤模型试验。基于X形桩-网路堤模型试验,揭示了沥青加铺层对路面顶部位移的影响、X形桩周土体的非对称运动以及加垫层后的集中系数^[17-18]；交通荷载作用下的土拱高度小于静载作用下的土拱高度^[19]。此外,研究人员比较了X形桩-筏复合地基在风干砂土和饱和砂土地基中的动力响应^[21]。结果表明,地基振动速度的大小和变化与地基的饱和程度密切相关,列车速度是影响X形桩筏复合地基动力响应的一个重要因素。然而,在交通荷载作用下,不同路堤高度下X形桩-筏复合地基的动力响应变化规律尚不清楚。为此,本文基于模型试验方法,着重分析不同路堤高度下振动速度、动土压力和桩身动应力随交通荷载的变化规律。

1. 大比例模型试验概况

1.1 模型试验布置及模型相似比

为研究不同路堤高度下X形桩-筏复合地基的动力响应,本文选取4种路堤高度（h₁～h₄）下路堤横截面方向上中间的两排桩进行研究,如图1所示。开展模型加载试验时,首先将不同的路堤高度换算成对应的恒载x（kN）预先施加于筏板上,然后再在筏板上施加循环的车辆荷载,试验加载示意图见图2。图中模型槽的长、宽和高分别为5,4和7 m。本试验的几何相似常数为1∶5,各物理量的相似比见表1。

图 1 不同路堤高度下X形桩-筏复合地基

Figure 1. XCC pile−raft composite foundation under different embankment heights

下载: 全尺寸图片幻灯片

图 2 试验加载示意图

Figure 2. Schematic diagram of test loading

下载: 全尺寸图片幻灯片

表 1 模型相似比

Table 1. Similarity ratios for model

参数	相似比	参数	相似比
长度/m	1/5	体积/m³	1/125
密度/(kg·m^-3)	1	弹性模量/MPa	1
加速度/(m·s^-2)	1	力/kN	1/5
应力/kPa	5	速度/(m·s^-1)	$1 / \sqrt{5}$
时间/s	$1 / \sqrt{5}$	频率/kPa	$\sqrt{5}$

下载: 导出CSV

| 显示表格

1.2 X形桩-筏复合地基系统的制备

本模型试验的X形桩-筏复合地基从下至上依次由地基土、X形桩、碎石垫层和筏板组成。其中地基土为中砂,表2为其物理参数。在模型槽四周墙壁上预先布置“两布三膜”,以减小反射波对试验结果的影响^[16]。在填筑砂土的过程中,用夯机将每层相同重量相同厚度（300 mm）的砂土均匀压实到250 mm厚,后经试验测得每层填土的相对密实度为0.66<D_r<0.8,属于中密状态。用填筑砂土相类似的方法,在桩顶处均匀填筑100 mm厚级配良好的碎石（C_u=6,C_c=2.89）,然后压实到60 mm。

表 2 砂土基本物理指标

Table 2. Physical indices of sand

天然密度/(g·cm^-3)	天然含水率/%	G_s	不均匀系数C_u	曲率系数C_c
1.478	4.08	2.67	2.42	0.93

下载: 导出CSV

| 显示表格

X形桩的截面形状受3个参数2a（开弧间距）、θ（开弧角度）和2R（外包圆直径）控制,见图3。本试验中3个参数依次为39 mm、90°和152 mm,桩长为3960 mm,4根X形桩分别命名为A、B、C和D桩,其布置方式见图3。

图 3 X形桩及布置示意图

Figure 3. Arrangement of XCC piles

下载: 全尺寸图片幻灯片

1.3 试验仪器布置及加载与数据采集系统

试验仪器布置如图4所示,在4根桩的正中心每间隔1 m布置一个速度计,在筏板面层中心点附近对称布置2个速度计。在速度计附近对应埋设5个具有温度补偿功能的动土压力盒,同时为了保证其测量精度,经过计算动土压力盒的量程分别选用0.1～0.3 MPa,其准确度误差≤0.3°%F·S。

图 4 试验仪器布置示意图

Figure 4. Layout of instruments for model tests

下载: 全尺寸图片幻灯片

静动力试验加载控制系统由静动力作动器、控制器、荷载输入控制机、液压系统等组成。控制器可模拟不同的交通荷载,数据采集分析系统可进行连续不间断的数据采集。

2. 荷载形式及试验工况设计

本模型试验通过简化,采用正弦波荷载模拟列车的一个轮轴荷载^[16],其荷载形式为

$Q (t) = x + A sin ω (t - T / 4)$ 。

(1)

式中 Q(t)为施加在筏板表面中心的荷载（kN）；x为路堤高度对应的等效恒载（kN）；A为振幅（kN）；ω=2πf为角速度（rad/s）,其中f为频率（Hz）；t为时间（s）；T为荷载循环周期（s）。

图5为式（1）对应的轮轴荷载,表3为试验加载工况。

图 5 施加的正弦波荷载

Figure 5. Dine wave loads

下载: 全尺寸图片幻灯片

表 3 试验加载工况

Table 3. Load cases of tests

荷载Q(t)/kN	恒载x/kN	振幅A/kN	频率f/Hz	循环次数/次
Q(t)	20	5	10	25000
Q(t)	25	5	10	25000
Q(t)	30	5	10	25000
Q(t)	35	5	10	25000

下载: 导出CSV

| 显示表格

3. 试验结果与分析

3.1 速度分析

（1）速度响应时程曲线

以恒载20 kN、振幅5 kN的循环荷载为例,筏板顶部、地基深度0,1,2,3,4 m处的速度响应时程曲线见图6。

图 6 速度响应时程曲线

Figure 6. Time-history curves of velocity response

下载: 全尺寸图片幻灯片

在筏板处,速度响应的波峰和波谷与所施加的正弦波荷载相同步,呈现正弦波形。在1 m处,当荷载处于峰值时,速度响应曲线出现了一小一大的双峰值。随着地基深度的增加,速度响应的两个峰值大小逐渐趋近于相等。在4 m处,这两个峰值大小基本相等,呈明显的M形。由上述分析可知,在筏板处速度响应的大小和振动形式主要受循环荷载的影响,随着振动向地基深层转播的过程中,速度响应受深度、密实度等其它因素的影响越来越重,其大小逐渐衰减、形状逐渐趋于复杂。

（2）速度响应与深度的关系

在振幅为5 kN,恒载分别为20,25,30,35 kN的循环荷载作用下,X形桩筏复合地基的速度响应如图7所示。

图 7 速度响应与深度的关系

Figure 7. Vibration velocities recorded at different layers

下载: 全尺寸图片幻灯片

由图7可知,恒载越大（即路堤高度越大）,筏板的速度响应越小,筏板振动越弱。反之,路堤高度越小,筏板的速度响应越大,筏板振动越强。在深度0 m以下,对于不同的路堤高度,速度响应随深度的增加均近似呈线性减小。需要注意的是,从筏板经碎石垫层到地基表层（深度0 m处）的0.36 m范围内,速度响应衰减尤为显著,基本衰减为筏板的34%～40%,文献[16]也得到了相似的结果。因筏板刚度大,对振动速度衰减的影响可忽略不计,由此可得出0.06 m厚的碎石垫层是振动速度骤减的主要原因,碎石垫层具有良好的阻尼效果。在实际工程中,高铁、地铁列车大部分穿过城区,为最大限度降低列车运行引起的振动对轨道沿线周围建筑物的影响,国内外学者及工程师提出了许多减振措施。基于上述模型试验结果可知,碎石垫层具有良好的减振效果,在考虑减振措施时可供工程师参考使用。

同时注意到,当不同大小的振动速度从筏板传递到在地基深度3 m处时,各速度响应基本相同,在3～4 m范围内,速度响应的大小及变化规律也基本相同,这表明轮轴荷载引起速度响应的差异主要集中在从筏板到地基深度3 m处的范围内,而3 m以下的速度响应大小及变化规律基本相同。

（3）速度响应与恒载的关系

筏板顶部速度响应 $v^{'}$ （mm/s）与恒载x（kN）之间的关系曲线如图8所示, $v^{'}$ 与x可用回归方程（2）进行描述：

$v^{'} = a + b x + c x^{2}$ ,

(2)

图 8 筏板速度响应与恒载的关系曲线

Figure 8. Relationship between velocity response of raft and dead load

下载: 全尺寸图片幻灯片

本例中参数a=12.648,b=-0.519,c=0.007,相关系数R²=0.999。

从图8可知,在循环荷载的振幅为5 kN,恒载分别为20,25,30,35 kN的情况下,随着恒载（即路堤高度）的增加,轮轴荷载引起的筏板振动情况逐渐减弱,恒载与筏板的速度响应之间的关系曲线呈一元二次函数形式。

3.2 动土压力分析

循环荷载加载一周时轴向土压力波峰与波谷的差值为动土压力 $σ_{sd}$ 。图9为不同正弦波循环荷载作用下地基表层的动土压力时程曲线。由图9可知,动土压力随荷载的加、卸载过程也呈现同样的增加、减小变化过程,且循环周期与所施加的荷载周期保持一致,时程曲线的峰值与一个轮轴荷载相对应。

图 9 动土压力时程曲线

Figure 9. Time-history curves of dynamic soil pressure

下载: 全尺寸图片幻灯片

当循环荷载振动到25000次时,选取最后20个循环周期内动土压力响应的平均值作为此时的动土压力值,通过对此循环次数的动土压力进行回归分析,地基表面的动土压力 $σ_{sd}$ （kPa）与恒载x（kN）之间的关系曲线如图10所示, $σ_{sd}$ - x曲线可用下面的回归方程（3）进行描述：

$σ_{sd} = a + b x$ ,

(3)

图 10 地基表层动土压力与恒载的关系曲线

Figure 10. Relationship between dynamic soil pressure of foundation surface and dead load

下载: 全尺寸图片幻灯片

本例中a=7.629,b=-0.085,相关系数R²=0.954。由图10可知,恒载越小（即路堤高度越小）,地基表层的动土压力越大；反之,路堤高度越大,动土压力越小。地基表层的动土压力与路堤高度两者之间近似呈线性关系。

3.3 桩身动应力

将试验测得的桩顶应变转换成桩顶动应力 $σ_{pd}$ 归分析见图11, $σ_{pd}$ -x之间的关系曲线可用回归方程（4）进行描述：

$σ_{pd} = a + b x$ 。

(4)

图 11 桩顶动应力与恒载关系曲线

Figure 11. Dynamic stress of pile top versus dead load

下载: 全尺寸图片幻灯片

本例中a=284.978,b=-3.660,相关系数R²=0.991。由图11可知,随着恒载（即路堤高度）的增加,桩顶动应力呈线性逐渐减小。这表明,路堤高度越小,轮轴荷载传递到桩顶的动应力越大,桩身的振动越强烈；反之,路堤高度越大,轮轴荷载传递到桩顶的动应力越小,桩身的振动越弱。因此在实际工程中,如果要达到降低桩身振动的目的,可以考虑通过增加路堤高度的方法来实现。

4. 结论

本文通过开展循环荷载作用下X形桩−筏复合地基模型试验,分析不同恒载（即路堤高度）的动力响应,可以得出以下结论：

（1）在不同路堤高度下,轮轴荷载引起的速度响应的差异主要集中在从筏板到地基深度3 m处的范围内,而3 m以下的速度响应大小及变化规律基本相同。由于碎石垫层的存在,速度响应从筏板顶部到地基深度0 m的0.36 m范围内速度响应锐减了34%～40%。

（2）随着路堤高度（恒载）的增加,轮轴荷载引起的筏板振动情况呈一元二次函数形式逐渐减弱。

（3）路堤高度（恒载）越大,轮轴荷载传递到地基表层的动土压力和桩顶的动应力就越小,随着恒载的增加,动土压力与桩顶动应力均呈线性减小。

图 1 传统PSDM

Figure 1. Traditional PSDM

下载: 全尺寸图片幻灯片

图 2 全连接神经网络结构

Figure 2. Structure of FCNN

下载: 全尺寸图片幻灯片

图 3 动剪切模量比和动阻尼比曲线

Figure 3. G/G_max-γ and λ-γ cureves of soil layers

下载: 全尺寸图片幻灯片

图 4 地铁车站结构横断面示意图

Figure 4. Schematic diagnam of cross-section of subway station structure

下载: 全尺寸图片幻灯片

图 5 钢筋和混凝土的本构模型

Figure 5. Constitutive models for concrete and reinforcement

下载: 全尺寸图片幻灯片

图 6 土-结构相互作用有限元模型

Figure 6. Finite element model for soil-structure model

下载: 全尺寸图片幻灯片

图 7 地震动加速度反应谱曲线

Figure 7. Spectral curves of seismic acceleration response

下载: 全尺寸图片幻灯片

图 8 损失函数变化趋势

Figure 8. Tendency of loss function

下载: 全尺寸图片幻灯片

图 9 FCNN对于训练集预测结果

Figure 9. Predicted results of FCNN for training set

下载: 全尺寸图片幻灯片

图 10 基于FCNN和对数线性回归结果的残差分布

Figure 10. Residual distribution based on FCNN and log-linear regression results

下载: 全尺寸图片幻灯片

图 11 FCNN模型的测试结果

Figure 11. Predicted results of FCNN model for testing set

下载: 全尺寸图片幻灯片

图 12 基于FCNN权值绝对值和的IM排序

Figure 12. Ranking of IM based on FCNN

下载: 全尺寸图片幻灯片

图 13 IM指标与θ对数线性回归图

Figure 13. IM and θ Log linear regression

下载: 全尺寸图片幻灯片

图 14 基于最大层间位移角的各IM指标α值

Figure 14. Values of α based on maximum layer drift

下载: 全尺寸图片幻灯片

图 15 基于最大层间位移角的各IM指标q值

Figure 15. Values of q based on maximum layer drift

下载: 全尺寸图片幻灯片

图 16 基于最大层间位移角的各IM指标ζ值

Figure 16. Values of ζ based on maximum layer drift

下载: 全尺寸图片幻灯片

表 1 采用的地震强度指标

Table 1 Selected intensity measures

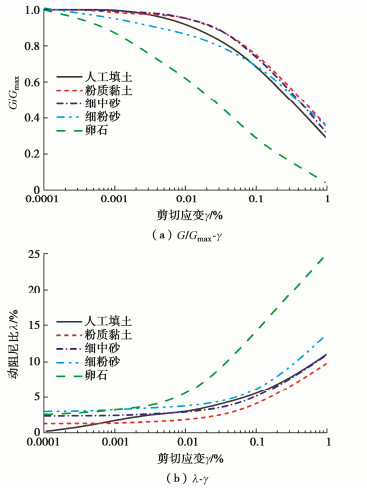
类型	编号	名称	定义
加速度型	1	峰值加速度(PGA)	PGA = max(\|a(t)\|)
	2	Arias强度(AI)	${\text{AI}} = \frac{{\rm{\mathsf{π}}}}{{{\text{2g}}}}\int_0^{{t_{\text{f}}}} a {(t)^2}{\text{d}}t$
	3	持续最大加速度(SMA)	加速度时程中第三个最大值
	4	均方根加速度(a_rms)	${a_{{\text{rms}}}} = \sqrt {\int_{{t_{\text{5}}}}^{{t_{{\text{95}}}}} {a{{{\text{(}}t{\text{)}}}^{\text{2}}}} {\text{d}}t/{t_{\text{d}}}}$
	5	特征强度(I_C)	I_C = a_rms^1.5t_d^0.5
速度型	6	累计绝对速度(CAV)	${\text{CAV}} = \int_0^{{t_{\text{f}}}} {\left\| {a(t)} \right\|{\text{d}}t}$
	7	峰值速度(PGV)	PGV = max(\|v(t)\|)
	8	均方根速度(v_rms)	${v_{{\text{rms}}}} = \sqrt {\int_{{t_5}}^{{t_{95}}} {v{{(t)}^2}{\text{d}}t/{t_{\text{d}}}} }$
	9	能量密度指标(SED)	${\text{SED}} = \int_0^{{t_{\text{f}}}} {v{{(t)}^2}{\text{d}}t}$
	10	复合指标(I_F)	I_F = PGV × t_d^0.25
	11	持续最大速度(SMV)	速度时程中第三个最大值
位移型	12	峰值位移(PGD)	PGD = max(\|d(t)\|)
位移型	13	均方根位移(d_rms)	${d_{{\text{rms}}}} = \sqrt {\int_{{t_5}}^{{t_{95}}} {d{{(t)}^2}{\text{d}}t/{t_{\text{d}}}} }$
与反应谱单值相关	14	伪加速度谱峰值(PSA)	PSA=max(PS_a)
与反应谱单值相关	15	伪速度谱峰值(PSV)	PSV=max(PS_V)
与反应谱时间段积分相关	16	加速度谱强度(ASI)	${\text{ASI}} = \int_{0.1}^{0.5} {P{S_{\text{a}}}{\text{d}}T}$
	17	速度谱强度(VSI)	${\text{VSI}} = \int_{0.1}^{2.5} {{S_{\text{v}}}{\text{d}}T}$
	18	Housner强度(HI)	${\text{HI}} = \int_{0.1}^{2.5} {P{S_{\text{v}}}{\text{d}}T}$
	19	有效峰值加速度(EPA)	${\text{EPA}} = {\text{mean(}}\int_{{\text{0}}{\text{.1}}}^{{\text{0}}{\text{.5}}} {{S_{\text{a}}}{\text{d}}T/2.5} )$

下载: 导出CSV

表 2 Ⅱ类场地土层物理参数

Table 2 Physical parameters of Type Ⅱ site soil

土层	土类	土层厚度/m	密度/(kg·m^-3)	剪切波速/(m·s^-1)	剪切模量/MPa
1	人工填土	5.0	1750	180	57
2	粉质黏土	10.0	1900	250	118.8
3	细中砂	10.0	2000	300	180
4	细粉砂	15.0	2000	320	205
5	卵石	20.0	2280	500	525

下载: 导出CSV

表 3 计算效率对比

Table 3 Comparison of efficiency

耗时项目	数值模拟	FCNN
数据处理	—	10 min
模型训练^*	—	2 h
响应计算	20 min×30=10 h	2 s
合计	10 h	2.2 h
^*注：FCNN训练耗时包括搭建至调至最优模型耗时。

下载: 导出CSV

参考文献(36)

[1]	CORNELL C A, JALAYER F, HAMBURGER R O, et al. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J]. Journal of Structural Engineering, 2002, 128(4): 526-533 doi: 10.1061/(ASCE)0733-9445(2002)128:4(526)
[2]	钟紫蓝, 申轶尧, 郝亚茹, 等. 基于IDA方法的两层三跨地铁地下结构地震易损性分析[J]. 岩土工程学报, 2020, 42(5): 916-924. doi: 10.11779/CJGE202005014 ZHONG Zilan, SHEN Yiyao, HAO Yaru, et al. Seismic fragility analysis of two-story and three-span metro station structures based on IDA method[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(5): 916-924. (in Chinese) doi: 10.11779/CJGE202005014
[3]	ARGYROUDIS S A, PITILAKIS K D. Seismic fragility curves of shallow tunnels in alluvial deposits[J]. Soil Dynamics and Earthquake Engineering, 2012, 35: 1-12. doi: 10.1016/j.soildyn.2011.11.004
[4]	LIU T, CHEN Z Y, YUAN Y, et al. Fragility analysis of a subway station structure by incremental dynamic analysis[J]. Advances in Structural Engineering, 2016, 20(7): 1111-1124.
[5]	RAMAMOORTHY S K, GARDONI P, BRACCI J M. Probabilistic demand models and fragility curves for reinforced concrete frames[J]. Journal of Structural Engineering, 2006, 132(10): 1563-1572. doi: 10.1061/(ASCE)0733-9445(2006)132:10(1563)
[6]	SIMON J, BRACCI J M, GARDONI P. Seismic response and fragility of deteriorated reinforced concrete bridges[J]. Journal of Structural Engineering, 2010, 136(10): 1273-1281. doi: 10.1061/(ASCE)ST.1943-541X.0000220
[7]	HE Z M, XU H, GARDONI P, et al. Seismic demand and capacity models, and fragility estimate for underground structures spatially varying soil properties[J]. Tunnelling and Underground Space Technology incorporating Trenchless Technology Research, 2022(119): 104231.
[8]	XU H, GARDONI P. Probabilistic capacity and seismic demand models and fragility estimates for reinforced concrete buildings based on three-dimensional analyses[J]. Engineering Structures, 2016(112): 200-214.
[9]	ZHANG W, SHOKRABADI M, BOZORGNIA Y, et al. A methodology for fragility analysis of buried water pipes considering coupled horizontal and vertical ground motions[J]. Computers and Geotechnics, 2020, 126(4): 103709.
[10]	ZHENG K F, CHEN L B, ZHUANG W L, et al. Bridge vulnerability analysis based on probabilistic seismic demand models[J]. Engineering Mechanics, 2013, 30(5): 165-171.
[11]	于晓辉, 吕大刚, 王光远. 关于概率地震需求模型的讨论[J]. 工程力学, 2013, 30(8): 172-179. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201308027.htm YU Xizohui, LÜ Dagang, WANG Guangyuan. Discussions on probabilistic seismic demand models[J]. Engineering Mechanics, 2013, 30(8): 172-179. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201308027.htm
[12]	YANG C T, XIE L L, LI A Q, et al. Ground motion intensity measures for seismically isolated RC tall buildings[J]. Soil Dynamics and Earthquake Engineering, 2019, 125: 105727. doi: 10.1016/j.soildyn.2019.105727
[13]	PADGETT J E, NIELSON B G, DESROCHES R. Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios[J]. Earthquake Engineering and Structural Dynamics, 2008, 37(5): 711-725. doi: 10.1002/eqe.782
[14]	ZHANG C M, ZHAO M, ZHONG Z L, DU X L. Seismic intensity measures and fragility analysis for subway stations subjected to near-fault ground motions with velocity pulses[J]. Journal of Earthquake Engineering, 2022, 26(16): 8724-8750. doi: 10.1080/13632469.2021.1994056
[15]	DING Y J, CHEN J, SHEN J X. Prediction of spectral accelerations of aftershock ground motion with deep learning method[J]. Soil Dynamics and Earthquake Engineering, 2021, 150(25): 106951.
[16]	DING Y J, CHEN J, SHEN J X. Conditional generative adversarial network model for simulating intensity measures of aftershocks[J]. Soil Dynamics and Earthquake Engineering, 2020, 139(17): 106281.
[17]	HUANG P F, CHEN Z Y. Deep learning for nonlinear seismic responses prediction of subway station[J]. Engineering Structures, 2021, 244(13): 112735.
[18]	XU Z K, CHEN J, SHEN J X, XIANG M J. Recursive long short-term memory network for predicting nonlinear structural seismic response[J]. Engineering Structures, 2022, 250(26): 113406.
[19]	TORKY AHMED A, SUSUMU O. Deep learning techniques for predicting nonlinear multi-component seismic responses of structural buildings[J]. Computers and Structures, 2021, 252(15): 106570.
[20]	HUANG P F, CHEN Z Y. Fragility analysis for subway station using artificial neural network[J]. Journal of Earthquake Engineering, 2021(3): 1-21.
[21]	RIDDELL R. On ground motion intensity indices[J]. Earthquake Spectra, 2007, 23(1): 147-173. doi: 10.1193/1.2424748
[22]	PENZIEN J. Seismically induced racking of tunnel linings[J]. Earthquake Engineering and Structural Dynamics, 2000, 29(5): 683-691. doi: 10.1002/(SICI)1096-9845(200005)29:5<683::AID-EQE932>3.0.CO;2-1
[23]	CHEN Z Y, LIU Z Q. Stochastic seismic lateral deformation of a multi-story subway station structure based on the probability density evolution method[J]. Tunnelling and Underground Space Technology, 2019, 103114.
[24]	城市轨道交通结构抗震设计规范[S]. 北京: 中国建筑工业出版社, 2014. Code for Seismic Design of Urban Rail Transit Structures[S]. Beijing: China Architecture & Building Press, 2014. (in Chinese)
[25]	陈国兴, 刘雪珠, 朱定华, 等. 江苏长江以南地区新近沉积土动剪切试验研究[J]. 地下空间与工程学报, 2007, 3(4): 745-750. https://www.cnki.com.cn/Article/CJFDTOTAL-BASE200704034.htm CHEN Guoxing, LIU Xuezhu, ZHU Dinghua, et al. A study on dynamic shear of recently deposited soils for southern Jiangsu Province along Yangtze River[J]. Chinese Journal of Underground Space and Engineering, 2007, 3(4): 745-750. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BASE200704034.htm
[26]	杜修力, 许紫刚, 许成顺, 等. 基于等效线性化的土-地下结构整体动力时程分析方法研究[J]. 岩土工程学报, 2018, 40(12): 2155-2163. doi: 10.11779/CJGE201812001 DU Xiuli, XU Zigang, XU Chengshun, et al. Time-history analysis method for soil-underground structure system based on equivalent linear method[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(12): 2155-2163. (in Chinese) doi: 10.11779/CJGE201812001
[27]	曲哲, 叶列平. 基于有效累积滞回耗能的钢筋混凝土构件承载力退化模型[J]. 工程力学, 2011, 28(6): 45-51. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201106009.htm QU Zhe, YE Lieping. Strength deterioration model based on effective hysteretic energy dissipation for rc members under cyclic loading[J]. Engineering Mechanics, 2011, 28(6): 45-51. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201106009.htm
[28]	TSINIDIS G, PITILAKIS K, TRIKALIOTIA D. Numerical simulation of round robin numerical test on tunnels using a simplified kinematic hardening model[J]. Acta Geotechnica, 2013, 9(4): 641-659.
[29]	YAROTSKY D. Error bounds for approximations with deep ReLU networks[J]. Neural Networks, 2017, 94: 103-114. doi: 10.1016/j.neunet.2017.07.002
[30]	KINGMA D P, BA J L. Adam: a method for stochastic optimization[J]. Computer Research Repository, 2014(1412): 74-89.
[31]	HE K M, ZHANG X Y, REN S Q, SUN J. Delving deep into rectifiers: surpassing human-level performance on imagenet classification[C]//2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile: Institute of Electrical and Electronics Engineers, 2015.
[32]	ZAREMBA W, SUTSKEVER I, VINYALS O. Recurrent neural network regularization[J]. Computer Research Repository, 2014(1409): 68-76.
[33]	ABADI M, BARHAM P, CHEN J M, et al. TensorFlow: a system for large-scale machine learning[J]. Computer Research Repository, 2016(1605): 1-18.
[34]	SREEJAYA K P, BASU J, RAGHUKANTH S, SRINAGESH D. Prediction of ground motion intensity measures using an artificial neural network[J]. Pure and Applied Geophysics, 2021, 178: 2025-2058. doi: 10.1007/s00024-021-02752-9
[35]	张成明, 钟紫蓝, 甄立斌, 等. 适用于圆形隧道损伤评价的地震动强度指标研究[J]. 工程力学, 2021, 38(1): 100-108. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX202101011.htm ZHANG Chengming, ZHONG Zilan, ZHEN Libin, et al. Seismic intensity measures for the damage evaluation of circular tunnels[J]. Engineering Mechanics, 2021, 38(1): 100-108. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX202101011.htm
[36]	LUCO N, CORNELL C A. Structure-specific scalar intensity measures for near-source and ordinary earthquake ground motions[J]. Earthquake Spectra, 2007, 23(2): 357-392. doi: 10.1193/1.2723158

施引文献(2)

期刊类型引用(0)

其他类型引用(2)

资源附件(1)

其他相关附件
- PDF格式
  12-202402-G22-1448审稿意见与作者答复点击下载(1141KB)

图(16) / 表(3)

计量

文章访问数: 362
HTML全文浏览量: 60
PDF下载量: 95
被引次数: 2

0. 引言
1. 大比例模型试验概况
1.1 模型试验布置及模型相似比
1.2 X形桩-筏复合地基系统的制备
1.3 试验仪器布置及加载与数据采集系统
2. 荷载形式及试验工况设计
3. 试验结果与分析
3.1 速度分析
3.2 动土压力分析
3.3 桩身动应力
4. 结论

基于全连接神经网络的地铁车站响应分析与地震强度指标优选 English Version

作者简介: 钟紫蓝(1986—)，男，博士，副研究员，主要从事地下结构抗震研究。E-mail: zilanzhong@bjut.edu.cn

通讯作者: 申家旭, E-mail: shenjx@bjut.edu.cn

计量

出版历程

Response analysis of subway station and optimization of seismic intensity measures based on fully connected neural network

0. 引言

1. 大比例模型试验概况

1.1 模型试验布置及模型相似比

1.2 X形桩-筏复合地基系统的制备

1.3 试验仪器布置及加载与数据采集系统

2. 荷载形式及试验工况设计

3. 试验结果与分析

3.1 速度分析

3.2 动土压力分析

3.3 桩身动应力

4. 结论

期刊类型引用(0)

其他类型引用(2)

其他相关附件

PDF格式

计量

出版历程

目录

0. 引言

1. 大比例模型试验概况

1.1 模型试验布置及模型相似比

1.2 X形桩-筏复合地基系统的制备

1.3 试验仪器布置及加载与数据采集系统

2. 荷载形式及试验工况设计

3. 试验结果与分析

3.1 速度分析

3.2 动土压力分析

3.3 桩身动应力

4. 结论

作者简介:
钟紫蓝(1986—)，男，博士，副研究员，主要从事地下结构抗震研究。E-mail: zilanzhong@bjut.edu.cn

通讯作者:
申家旭, E-mail: shenjx@bjut.edu.cn