Coupled model for one-dimensional nonlinear consolidation and contaminant transport in a compacted clay liner considering mechanical-chemical loading
-
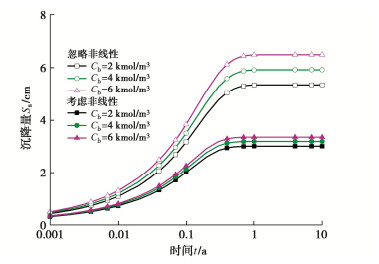
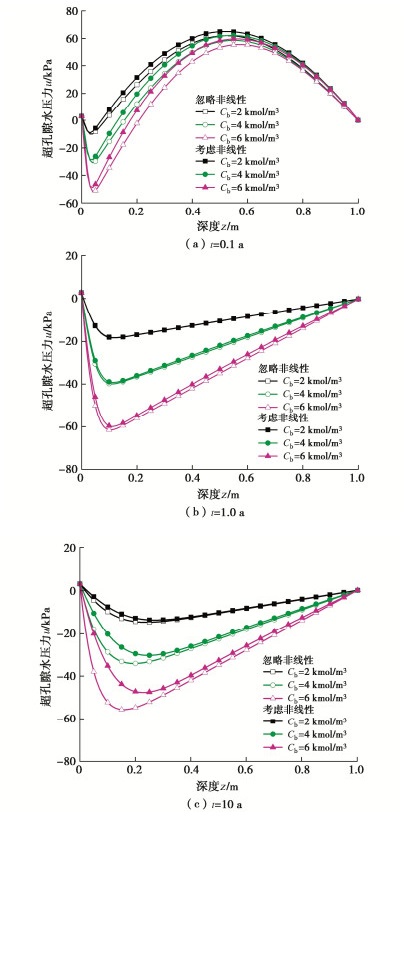
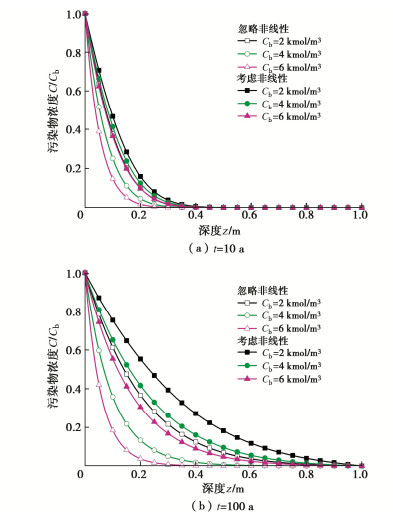
摘要: 针对力学-化学荷载下压实黏土垫层中一维固结与污染物运移耦合过程，考虑了土体压缩性和渗透性的非线性变化，建立了相应的耦合模型，并利用有限差分法对该模型进行了求解。通过与有限元软件COMSOL Multiphysics计算结果和已有解析解计算结果展开对比分析，对所建耦合模型正确性进行了验证。基于所建模型，比较研究了两种假定情况下力学荷载pu和渗滤液中污染物浓度Cb对耦合过程的影响。结果表明：当忽略非线性压缩和渗透特性时，力学荷载pu的增大会使污染物运移速率降低；但当考虑非线性压缩和渗透特性时，pu的增大会使污染物运移速率增大，这主要是由于污染物运移过程会受对流和扩散作用的综合影响。污染物浓度Cb的增大会使沉降量增大，超孔隙水压力值减小，也会使得污染物运移速率降低；相比于忽略非线性的情况，考虑非线性情况下Cb对沉降量、超孔隙水压力和污染物运移速率的影响会减弱。Abstract: For the coupled process of one-dimensional consolidation and contaminant transport in a compacted clay liner under mechanical-chemical loading, the corresponding coupled model is established by considering the nonlinear changes of compressibility and permeability of soils, and the finite difference method is adopted for solving the model. The correctness of the proposed coupled model is validated by comparing its results with the calculation ones of the finite element software COMSOL Multiphysics and the existing analytical solution. Based on the proposed model, the effects of mechanical loading pu and contaminant concentration Cb in leachate on the coupled process under two assumptions are compared and investigated. The results show that when the nonlinear compressibility and permeability characteristics are neglected, the increase of pu reduces the transport rate of contaminants. However, when the nonlinear compressibility and permeability characteristics are considered, the increase of pu leads to the increase of transport rate, which is mainly due to the comprehensive effects of advection and diffusion on the transport process. The increase of Cb increases the settlement, reduces the excess pore water pressure and decreases the transport rate of contaminants. Compared with the case of ignoring nonlinearity, the effects of Cb on the settlement, excess pore water pressure and transport rate of contaminants are reduced when the nonlinearity is considered.
-
-
![]()
图 2 本文所建耦合模型与COMSOL Multiphysics的对比情况
Figure 2. Comparison between proposed coupled model and COMSOL Multiphysics
![]()
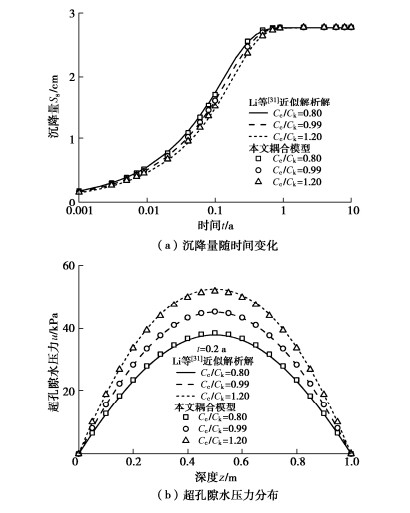
图 3 本文所建耦合模型与Li等[31]近似解析解的对比情况
Figure 3. Comparison between proposed coupled model and Li et al' s approximate analytical solutions
![]()
图 5 不同力学荷载pu下污染物浓度的分布
Figure 5. Distribution of contaminant concentration under different pu
![]()
图 6 不同渗滤液中污染物浓度Cb下沉降量的变化
Figure 6. Variation of settlement with time under different Cb
![]()
图 7 不同渗滤液中污染物浓度Cb下超孔隙水压力的分布
Figure 7. Distribution of excess pore water pressure under different Cb
![]()
图 8 不同渗滤液中污染物浓度Cb下污染物浓度的分布
Figure 8. Distribution of contaminant concentration under different Cb
表 1 耦合模型的计算参数
Table 1 Parameters for proposed coupled model
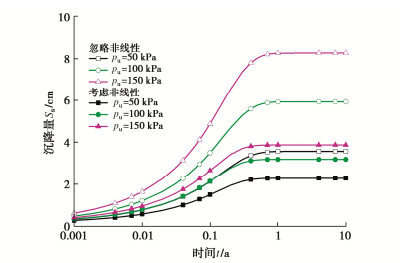
参数 取值 厚度L/m 1.0 初始孔隙率n0 0.5 液相密度ρf/(kg·m-3) 1000 固相密度ρs/(kg·m-3) 2600 渗透指数Ck 0.198 压缩指数Cc 0.13 初始有效应力σ′0/kPa 60 渗透系数kv0/(m·s-1) 1.0×10-10 力学荷载pu/kPa 100 渗滤液水头hb/m 0.3 比值ζ 0.005 化学渗透效率系数ω 0.005 温度T/K 293.15 污染物浓度Cb/(kmol·m-3) 4 线性吸附系数Kd/(m3·kg-1) 0.8142×10-3 经验系数β 1.82 自由扩散系数D0/(m2·s-1) 5.0×10-10 注：表中参数的取值源于参考文献[3, 16~19, 24, 30]。 
下载: 导出CSV
表 2 t=10 a时不同力学荷载pu下的沉降量
Table 2 Settlements under different pu when t=10 a
力学荷载
pu/kPa忽略非线性/
cm考虑非线性/
cm沉降差/
cm50 3.57 2.28 1.29 100 5.92 3.19 2.73 150 8.27 3.88 4.39
下载: 导出CSV
-
[1] 谢海建, 詹良通, 陈云敏, 等. 我国四类衬垫系统防污性能的比较分析[J]. 土木工程学报, 2011, 44(7): 133-141. doi: 10.15951/j.tmgcxb.2011.07.004 XIE Haijian, ZHAN Liangtong, CHEN Yunmin, et al. Comparison of the performance of four types of liner systems in China[J]. China Civil Engineering Journal, 2011, 44(7): 133-141. (in Chinese) doi: 10.15951/j.tmgcxb.2011.07.004
[2] 李涛, 刘利, 丁洲祥. 大变形黏土防渗层中的污染物迁移和转化规律研究[J]. 岩土力学, 2012, 33(3): 687-694. doi: 10.3969/j.issn.1000-7598.2012.03.007 LI Tao, LIU Li, DING Zhouxiang. Study of transport and transformation of contaminant through a clay layer with large deformation[J]. Rock and Soil Mechanics, 2012, 33(3): 687-694. (in Chinese) doi: 10.3969/j.issn.1000-7598.2012.03.007
[3] 张志红, 师玉敏, 朱敏. 黏土垫层水力-力学-化学耦合模型研究[J]. 岩土工程学报, 2016, 38(7): 1283-1290. doi: 10.11779/CJGE201607016 ZHANG Zhihong, SHI Yumin, ZHU Min. Coupled hydro-mechanical-chemical model for clay liner[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(7): 1283-1290. (in Chinese) doi: 10.11779/CJGE201607016
[4] 邱金伟, 权全, 刘军, 等. 考虑非等温环境下污染物在黏土中的运移解析模型[J]. 岩土力学, 2022, 43(2): 423-431, 442. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202202014.htm QIU Jinwei, QUAN Quan, LIU Jun, et al. Analytical solutions of contaminant transport in clay liner system under non-isothermal condition[J]. Rock and Soil Mechanics, 2022, 43(2): 423-431, 442. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202202014.htm
[5] 谢海建, 严华祥, 张春华, 等. 考虑固结、扩散和降解耦合作用下污染物在黏土中的运移解析模型[J]. 水利学报, 2015, 46(增刊1): 124-128. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB2015S1023.htm XIE Haijian, YAN Huaxiang, ZHANG Chunhua, et al. Analytical models for contaminant transport in clayey soils considering coupled effect of consolidation, diffusion and degradation[J]. Journal of Hydraulic Engineering, 2015, 46(S1): 124-128. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB2015S1023.htm
[6] SMITH D W. One-dimensional contaminant transport through a deforming porous medium: theory and a solution for a quasi-steady-state problem[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2000, 24: 693-722. doi: 10.1002/1096-9853(200007)24:8<693::AID-NAG91>3.0.CO;2-E
[7] PETERS G P, SMITH D W. Solute transport through a deforming porous medium[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2002, 26(7): 683-717. doi: 10.1002/nag.219
[8] ALSHAWABKEH A N, RAHBAR N. Parametric study of one-dimensional solute transport in deformable porous media[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(8): 1001-1010. doi: 10.1061/(ASCE)1090-0241(2006)132:8(1001)
[9] LEWIS T W, PIVONKA P, FITYUS S G, et al. Parametric sensitivity analysis of coupled mechanical consolidation and contaminant transport through clay barriers[J]. Computers and Geotechnics, 2009, 36(1/2): 31-40.
[10] LEWIS T W, PIVONKA P, SMITH D W. Theoretical investigation of the effects of consolidation on contaminant transport through clay barriers[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2009, 33(1): 95-116. doi: 10.1002/nag.708
[11] PU H F, FOX P J, SHACKELFORD C D. Assessment of consolidation-induced contaminant transport for compacted clay liner systems[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2016, 142(3): 04015091. doi: 10.1061/(ASCE)GT.1943-5606.0001426
[12] 李江山, 江文豪, 葛尚奇, 等. 非等温分布条件下压实黏土衬垫中固结与污染物运移耦合模型研究[J]. 岩土工程学报, 2022, 44(11): 2071-2080. doi: 10.11779/CJGE202211013 LI Jiangshan, JIANG Wenhao, GE Shangqi, et al. Coupling model for consolidation and contaminant transport in compacted clay liners under non-isothermal condition[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(11): 2071-2080. (in Chinese) doi: 10.11779/CJGE202211013
[13] FRITZ S J. Ideality of clay membranes in osmotic processes: a review[J]. Clays and Clay Minerals, 1986, 34(2): 214-223. doi: 10.1346/CCMN.1986.0340212
[14] KACZMAREK M, HUECKEL T. Chemo-mechanical consolidation of clays: analytical solutions for a linearized one-dimensional problem[J]. Transport in Porous Media, 1998, 32(1): 49-74. doi: 10.1023/A:1006530405361
[15] KACZMAREK M. Chemically induced deformation of a porous layer coupled with advective-dispersive transport. Analytical solutions[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25(8): 757-770. doi: 10.1002/nag.150
[16] PETERS G P, SMITH D W. The influence of advective transport on coupled chemical and mechanical consolidation of clays[J]. Mechanics of Materials, 2004, 36(5/6): 467-486.
[17] 张志红, 师玉敏. 双荷载共同作用下土体变形影响机理及计算方法[J]. 东南大学学报(自然科学版), 2016, 46(增刊1): 148-152. https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX2016S1026.htm ZHANG Zhihong, SHI Yumin. Influence mechanism and calculation method for soil deformation under double load[J]. Journal of Southeast University (Natural Science Edition), 2016, 46(S1): 148-152. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX2016S1026.htm
[18] ZHANG Z H, MASUM S A, THOMAS H R, et al. Modeling fully coupled hydraulic-mechanical-chemical processes in a natural clay liner under mechanical and chemico-osmotic consolidation[J]. Environmental Science and Pollution Research, 2018, 25(36): 36173-36183.
[19] ZHANG Z H, MASUM S A, TIAN G L, et al. Modelling non-isothermal volume change and solute transport behaviours of a semi-permeable clay soil under the combined influence of mechanical loading, chemical-osmosis, and thermo-osmosis[J]. Engineering Geology, 2021, 293: 106271.
[20] 田改垒, 张志红. 考虑热效应的污染物在土中扩散、渗透和固结耦合模型[J]. 岩土工程学报, 2022, 44(2): 278-287. doi: 10.11779/CJGE202202009 TIAN Gailei, ZHANG Zhihong. Coupled model for contaminant diffusion, osmosis and consolidation in soil considering thermal effects[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(2): 278-287. (in Chinese) doi: 10.11779/CJGE202202009
[21] CHEN Y M, ZHAN T L T, WEI H Y, et al. Aging and compressibility of municipal solid wastes[J]. Waste Management, 2009, 29(1): 86-95.
[22] FENG S J, GAO K W, CHEN Y X, et al. Geotechnical properties of municipal solid waste at Laogang Landfill, China[J]. Waste Management, 2017, 63: 354-365.
[23] YU Y, ROWE R K. Modelling deformation and strains induced by waste settlement in a centrifuge test[J]. Canadian Geotechnical Journal, 2018, 55(8): 1116-1129.
[24] PU H F, QIU J W, ZHANG R J, et al. Assessment of consolidation-induced VOC transport for a GML/GCL/CCL composite liner system[J]. Geotextiles and Geomembranes, 2018, 46(4): 455-469.
[25] LI J S, JIANG W H, GE S Q, et al. General analytical solutions for one-dimensional nonlinear consolidation of saturated clay under non-isothermal distribution condition[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2022, 46(10): 1811-1830.
[26] 庄迎春, 刘世明, 谢康和. 萧山软粘土一维固结系数非线性研究[J]. 岩石力学与工程学报, 2005, 24(24): 4565-4569. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200524026.htm ZHUANG Yingchun, LIU Shiming, XIE Kanghe. Study on nonlinearity of one-dimensional consolidation coefficient of Xiaoshan clay[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(24): 4565-4569. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200524026.htm
[27] ABBASI N, RAHIMI H, JAVADI A A, et al. Finite difference approach for consolidation with variable compressibility and permeability[J]. Computers and Geotechnics, 2007, 34(1): 41-52.
[28] 齐添. 软土一维非线性固结理论与试验对比研究[D]. 杭州: 浙江大学, 2008. QI Tian. Theoretical and Experimental Studies on One-Dimensional Nonlinear Consolidation of Soft Soil[D]. Hangzhou: Zhejiang University, 2008. (in Chinese)
[29] 刘建国, 王洪涛, 聂永丰. 多孔介质中溶质有效扩散系数预测的分形模型[J]. 水科学进展, 2004, 15(4): 458-462. https://www.cnki.com.cn/Article/CJFDTOTAL-SKXJ200404010.htm LIU Jianguo, WANG Hongtao, NIE Yongfeng. Fractal model for predicting effective diffusion coefficient of solute in porous media[J]. Advances in Water Science, 2004, 15(4): 458-462. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SKXJ200404010.htm
[30] LEE J, FOX P J, LENHART J J. Investigation of consolidation-induced solute transport: I effect of consolidation on transport parameters[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(9): 1228-1238.
[31] LI C X, HUANG J S, WU L Z, et al. Approximate analytical solutions for one-dimensional consolidation of a clay layer with variable compressibility and permeability under a ramp loading[J]. International Journal of Geomechanics, 2018, 18(11): 06018032.
-
其他相关附件
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
