区域土特征函数：概念与原理

袁晓铭; 卢坤玉; 汪云龙; 袁近远; 陈龙伟

doi:10.11779/CJGE20220828

区域土特征函数：概念与原理 English Version

1.
中国地震局工程力学研究所, 中国地震局地震工程与工程振动重点实验室, 黑龙江哈尔滨 150800
2.
黑龙江科技大学, 黑龙江哈尔滨 150027

基金项目:

中国地震局工程力学研究所基本科研业务费专项项目 2021EEEV0208

黑龙江省自然科学基金重点项目 ZD2019E009

详细信息

作者简介:
袁晓铭(1963—)，男，博士，研究员，主要从事岩土地震工程研究。Email: yxmiem@163.com

中图分类号: TU45
计量
- 文章访问数: 582
- HTML全文浏览量: 83
- PDF下载量: 231
出版历程
- 收稿日期: 2022-07-03
- 网络出版日期: 2023-03-05
- 刊出日期: 2023-11-30

Characteristic functions of regional soils: concepts and principles

1.
Institute of Engineering Mechanics, China Earthquake Administration; Key Laboratory of Earthquake Engineering and Engineering Vibration, China Earthquake Administration, Harbin 150080, China
2.
Heilongjiang University of Science and Technology, Harbin 150027, China

摘要

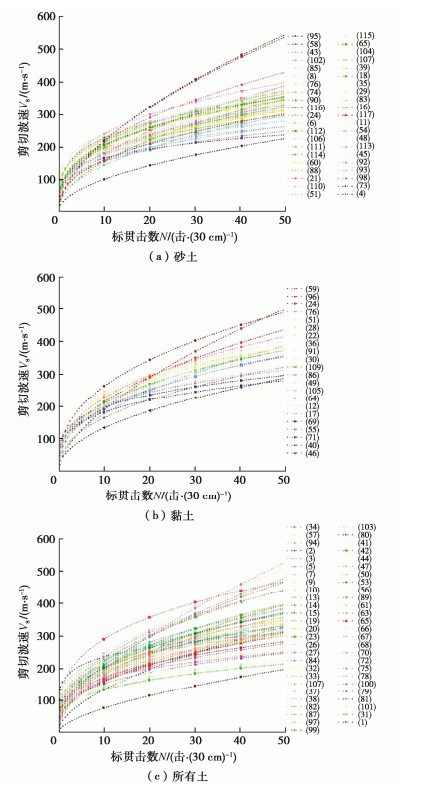
摘要: 作为区域土特征理论研究的起点，以土力学和土动力学经典理论和实际资料为基础，提出了相应的概念、原理、准则和实证。从土的经典本构模型出发，提出了双控制参数的概念，以此作为区域土特征理论的基础。提出了区域土特征函数的概念，阐明了其定义、内涵和外延，提出了包括控制性、普适性、完备性、原位性、一致性、可操作性和存在性等属性要求在内的区域土特征函数构建准则。针对常见的砂土和黏土，提出了采用 $N{\text{ - }}{v_{\text{s}}}$ 特征函数表征其区域土力学和工程特性的思想，给出了构建方法，阐明了其原理，通过17个国家77个地区实际 $N{\text{ - }}{v_{\text{s}}}$ 函数关系的分布特征，论证了砂土和黏土 $N{\text{ - }}{v_{\text{s}}}$ 特征函数的存在性。
- 土的区域性特征 /
- 双控制参数 /
- 区域土特征函数 /
- N-v_s特征函数
Abstract: As the starting point of the theoretical study on the regional soil characteristics, based on the classical theories of soil mechanics and soil dynamics and the actual data, the related concept, principle, criterion and demonstration are put forward. Based on the classical constitutive model for soils, the concept of dual-control parameter is proposed, which is a basis for the theoretical study on the regional soil characteristics. The concept of regional soil characteristic function is put forward, its definition, connotation and extension are clarified, and the construction criteria including control, universality, completeness, in situ, consistency, operability and existence are put forward. For the conventional sand and clay, the idea of using $N{\text{ - }}{v_{\text{s}}}$ characteristic function to characterize its regional soil characteristics is proposed, the construction method is given, and its principle is clarified. The existence of $N{\text{ - }}{v_{\text{s}}}$ characteristic function of sand and clay is proved by analyzing the distribution characteristics of N-v_s function relations in 77 regions of 17 countries of the world.
- regional soil feature /
- dual-control parameter /
- regional soil characteristic function /
- N-v_s characteristic function

HTML全文

0. 引言

足尺试验是了解盾构隧道结构力学行为的有效方法。许多学者开展了足尺管片接头试验来研究纵缝接头的变形特征和力学特性^[1-3]。隧道管片纵缝接头在持续加载作用下的力学性能是以往研究的重点，而很少研究在应用修复措施治理隧道大变形时纵向接缝的变形和力学特性、可恢复性以及恢复效率^[4]。

本文通过开展盾构隧道拱顶双缝接头和拱腰单缝接头的原型足尺试验，旨在探究两类接头在隧道上方堆载作用下的变形发展规律，分析盾构隧道管片在恢复过程中各性态特征的演化规律，评价不同既有变形条件下隧道管片不同部位接头变形的恢复效果。

1. 接头试件设计

本文针对上海地铁隧道运用的管片衬砌环中的纵缝接头进行一系列室内结构原型试验，隧道衬砌环和纵缝接头构造形式如图 1所示。试验试件包括两类接头，分别为位于隧道管片环拱顶位置受正弯矩作用的纵缝接头(即封顶块和邻接块连接处接头，以下称为拱顶接头)和位于隧道管片环拱腰位置受负弯矩作用的纵缝接头(即邻接块和标准块连接处接头，以下称为拱腰接头)，如图 2所示。弯矩以衬砌环内侧受拉为正，轴力以受压为正。

图 1 上海地铁盾构隧道管片衬砌结构

Figure 1. Structure of segment linings of shield tunnel in Shanghai Metro

下载: 全尺寸图片幻灯片

图 2 试验现场照片：(a)拱顶接头试件；(b)拱腰接头试件；(c)位移传感器布置；(d)隧道衬砌环横截面图

Figure 2. Photos of test set-up: (a) Specimen of longitudinal joint at tunnel crown, (b) Specimen of longitudinal joint at tunnel waist, (c) Arrangement of displacement sensors, (d) Cross-sectional view of tunnel lining ring

下载: 全尺寸图片幻灯片

值得注意的是，隧道拱腰和拱脚纵缝是径向平直面，而拱顶纵缝是与径向斜交的平直面，拱顶纵缝接头是楔形结构，见图 1(a)。然而，以往研究中采用的是简化的如拱腰一样的直缝结构，不能准确描述拱顶处实际的斜接缝构造的力学行为。本文采用隧道拱顶双接头形式进行试验研究。

2. 管片接头内力计算

采用考虑接头非线性刚度的盾构隧道衬砌分析模型^[5]计算接头内力(弯矩、轴力和剪力)。如所示，隧道埋深15 m，周围土体为典型的上海软土，饱和重度( $\gamma$ )为18 kN/m³，静止侧压力系数(K₀)为0.65，地层抗力系数(K_S)为6000 kN/m³。该模型首先通过对隧道结构施加竖向压力来模拟地面超载对隧道变形的影响。然后，通过移除竖向压力来模拟卸载。最后，通过对隧道结构施加侧向压力模拟注浆对隧道变形的恢复作用。根据接头内力计算结果可以确定足尺试验中对应不同工况的加载路径。

图 3 接头内力计算模型

Figure 3. Computational model for internal force of joints

下载: 全尺寸图片幻灯片

试验中，通过水平和垂直液压千斤顶向试件施加水平载荷和垂直载荷，以模拟接头内力(即弯矩、轴力和剪力)，见图 2中(a)和(b)。图 4和图 5分别为试验中拱顶接头和拱腰接头的受力分析图。根据力矩平衡方程，拱顶接头试件和拱腰接头试件的外部载荷和内力之间的关系可由式(1)和式(2)分别推导得到。

$\left\{ \begin{array}{l} M = G \cdot {L_2} + P \cdot ({L_2} - {L_1}) - N' \cdot h \hfill \\ N = N' \cdot \cos \theta + \frac{1}{2}G \cdot \sin \theta \hfill \\ Q = N' \cdot \sin \theta + \frac{1}{2}G \cdot \cos \theta \hfill \\ \end{array} \right. \text{，}$

(1)

$\left\{\begin{array}{l} M=P \cdot L_2-G \cdot\left(L_1-L_2-L_3\right)-N^{\prime} \cdot h \\ N=N^{\prime} \end{array}\right.。$

(2)

图 4 拱顶接头试件受力分析

Figure 4. Stress analysis of longitudinal joints at tunnel crown

下载: 全尺寸图片幻灯片

图 5 拱腰接头试件受力分析

Figure 5. Stress analysis of longitudinal joints at tunnel waist

下载: 全尺寸图片幻灯片

式中G为管片重力；M，N，Q分别为接头处弯矩、轴力和剪力； $N'$ 和P分别为由水平液压千斤顶和竖向液压千斤顶施加的水平向荷载和垂向载荷，通过POP-M工控PC电液伺服多通道控制器实现试验进程的自动控制。

3. 试验加载方案

针对拱顶接头和拱腰接头共开展了6组试验，工况Ⅰ~Ⅲ和工况IV~VI分别研究拱顶接头和拱腰接头超载变形后通过卸载和注浆的变形恢复过程，具体试验过程见表 1。试验在同济大学岩土及地下工程教育部重点实验室进行，采用TJ-GPJ2000盾构管片接头试验加载系统。试验过程中接缝张开量由线性位移传感器(LVDT)测得，如图 2中(c)所示。

表 1 试验工况

Table 1. Test design

工况编号	接头类型	试验内容	加载过程	试验控制变量	变量值	正常荷载水平
工况Ⅰ	拱顶接头	变形恢复过程	加载至正常荷载水平→施加超载→卸载至正常荷载水平→注浆过程模拟	超载程度/接头内力；弯矩M，轴力S，剪力Q	M=178 kN/m， N=593 kN， Q=88 kN	拱顶接头： M=118 kN/m， N=590 kN， Q=87 kN 拱腰接头： M=98 kN/m， N=816 kN
工况Ⅱ					M=278 kN/m， N=927 kN， Q=134 kN
工况Ⅲ					M=378 kN/m， N=1260 kN， Q=181 kN
工况Ⅳ	拱腰接对				M=155 kN/m， N=968 kN
工况Ⅴ					M=171 kN/m， N=1068 kN，
工况Ⅵ					M=188 kN/m， N=1175 kN

下载: 导出CSV

| 显示表格

4. 试验结果与分析

4.1 拱顶接头

图 6对比显示了受正弯矩作用的隧道拱顶接头在工况Ⅰ~Ⅲ中接缝张开增量的变化。在超载过程中，接头张开量随着荷载的增加而增大。当3工况试件达到最大荷载时，接头变形也达到峰值。在卸载过程中，试验结果表明卸载能在一定程度上恢复接头变形，但不能完全恢复。接头变形卸载恢复百分比，即卸载减少的接缝张开增量与卸载前接缝张开增量的比值，分别为68%，56%，43%。这表明超载越小即变形程度越小，接头变形的可恢复性越好。

图 6 工况Ⅰ~Ⅲ中拱顶接头在超载、卸载和土体注浆过程中的荷载–变形关系曲线

Figure 6. Load-deformation curves of longitudinal joints at tunnel crown during overloading, unloading and soil grouting conditions for test cases Ⅰ~Ⅲ

下载: 全尺寸图片幻灯片

针对土体注浆对拱顶接头变形恢复的试验模拟，试验结果表明，其荷载–变形曲线的斜率比卸载过程小得多。减小相同的弯矩，土体注浆可使接头变形得到更有效的恢复，这是因为土体注浆引起的拱顶弯矩减小和轴力增大导致偏心距减小。为了在卸载后将接头变形完全恢复到正常载荷状态下的水平，工况Ⅰ~Ⅲ需要通过模拟土体注浆分别减小弯矩值为20，25，40 kN·m，如图 6所示。

4.2 拱腰接头

图 7对比显示了受负弯矩作用的隧道拱腰接头在工况Ⅳ~Ⅵ中接缝张开增量的变化。在超载阶段，相同载荷水平下，3工况的接缝张开增量几乎相同。荷载–变形曲线斜率的减小表明拱腰接头试件的抗弯刚度随着超载水平的增加而降低。在此基础上，研究了卸载和注浆作用下的变形恢复效果。接头变形卸载恢复百分比分别为65%，42%，36%。显然，与拱顶接头呈现的特性一样，变形程度越小卸载恢复效果百分比越大。

图 7 工况Ⅳ~Ⅵ中拱腰接头在超载、卸载和土体注浆过程中的荷载–变形关系曲线

Figure 7. Load-deformation curves of longitudinal joints at tunnel waist during overloading, unloading and soil grouting conditions for test cases Ⅳ~Ⅵ

下载: 全尺寸图片幻灯片

在试验模拟土体注浆阶段，荷载–变形曲线的斜率明显小于卸载阶段。在隧道两侧注浆产生的侧向挤压力的作用下，接头偏心距减小。因此，通过减少相同的弯矩，土体注浆比卸载获得更有效的恢复。此外，为了将变形恢复到正常荷载状态的水平，即将接缝张开增量减小到零，试验结果显示工况Ⅳ~Ⅵ分别需要减少弯矩为16，42，48 kN·m。

从两类接头的试验结果可知：超载作用下接头张开变形呈现出非线性发展规律，总体上，两类接头的抗弯刚度随着接头已有张开变形的增大而降低；超载引起的变形可以通过卸载得到部分恢复，既有变形越小，恢复效果越好，但不能完全恢复到超载之前状态；注浆作用下，拱顶接头的变形恢复效果较拱腰接头更为显著，这是由于注浆产生的横向挤压作用在减小拱顶接头弯矩的同时亦增大了其轴力，即有效降低了拱顶接头处的偏心距。

5. 结论

本文介绍了上海地铁隧道管片衬砌纵缝接头的一系列室内足尺试验结果，初步探究了卸载和土体注浆对超载引起接头变形的可恢复性，得出以下结论：

(1) 在地面超载作用下，衬砌环发生较大的横向变形，拱顶接头向隧道管片内侧张开，拱腰接头向隧道管片外侧张开，导致渗漏水等隧道病害发生的概率增大。

(2) 超载引起的变形能够通过卸载恢复部分变形，既有变形越小，恢复效率越高。当减少相同的弯矩时，土体注浆比卸载能实现更有效的恢复。

(3) 由于隧道衬砌环中的所有纵缝接头钢螺栓均靠近管片内侧，拱腰接头抗弯能力较拱顶接头差，转动刚度较小，变形较大，变形恢复效果较差。此外，注浆作用下，拱顶接头的变形恢复效果较拱腰接头更为显著，其原因是注浆有效降低了拱顶接头处的偏心距。因此，建议加强拱腰接头处结构设计，增强其抗弯强度，从而提升隧道衬砌的整体安全性能。

图 1 土的典型弹塑性本构模型

Figure 1. Typical elastoplastic constitutive model for soils

下载: 全尺寸图片幻灯片

图 2 土的典型等价非线性黏-弹性本构模型

Figure 2. Typical equivalent nonlinear viscoelastic constitutive model for soils

下载: 全尺寸图片幻灯片

图 3 场地中的两个土单元

Figure 3. Two soil elements in sites

下载: 全尺寸图片幻灯片

图 4 双参数控制下两个土单元弹塑性本构性质的异同

Figure 4. Differences and similarities of elastoplastic constitutive relations for two soil elements under dual-parameter control

下载: 全尺寸图片幻灯片

图 5 双参数控制下两个土单元等价非线性黏-弹性本构性质的异同

Figure 5. Differences and similarities of the equivalent nonlinear viscoelastic constitutive relations for two soil elements under dual parameter control

下载: 全尺寸图片幻灯片

图 6 两个地区双控制参数的集合

Figure 6. A set of dual parameter control in two regions

下载: 全尺寸图片幻灯片

图 7 一个地区内N-v_s特征函数的样本

Figure 7. Samples of N-v_s characteristic function in a region

下载: 全尺寸图片幻灯片

图 8 世界不同地区既有的N-V_s关系曲线

Figure 8. Existing N-V_s relationship curves of soils in different regions of the world

下载: 全尺寸图片幻灯片

图 9 世界不同地区既有N-v_s函数关系中两个系数的分布特征

Figure 9. Distribution characteristics of two coefficients for existing N-v_s function relationship of soils in different regions of the world

下载: 全尺寸图片幻灯片

表 1 世界不同地区既有N-v_s关系曲线的基本信息

Table 1 Basic information of existing N-v_s relationship curves of soils in different regions of the world

序号	研究者	国家（地区）	土壤类型	公式	序号	研究者	国家（地区）	土壤类型	公式
1	Kanai(1966年)	日本（^*）	所有土	${v_{\text{s}}} = 18.9{N^{0.6}}$	60	刘斌等(2013年)	中国（毛乌素沙漠）	砂土	${v_{\text{s}}} = 118.277{N^{0.267}}$
2	Ohba和Toriumi (1970年)	日本（大阪）	所有土	${v_{\text{s}}} = 84{N^{0.31}}$	61	Sun等(2013年)	韩国（^*）	所有土	${v_{\text{s}}} = 65.64{N^{0.407}}$
3	Imai和Yoshimura (1970年)	日本（^*）	所有土	${v_{\text{s}}} = 76{N^{0.33}}$	62	Sun等(2013年)	韩国（^*）	砂土	${v_{\text{s}}} = 75.76{N^{0.371}}$
4	Shibata (1970年)	日本（^*）	砂土	${v_{\text{s}}} = 32{N^{0.5}}$	63	Chatterjee和Choudhury (2013年)	印度（加尔各答）	所有土	${v_{\text{s}}} = 78.21{N^{0.37669}}$
5	Fujiwara (1972年)	日本（^*）	所有土	${v_{\text{s}}} = 92.1{N^{0.337}}$	64	Chatterjee和Choudhury (2013年)	印度（加尔各答）	黏土	${v_{\text{s}}} = 77.11{N^{0.39256}}$
6	Ohta等(1972年)	日本（^*）	砂土	${v_{\text{s}}} = 87{N^{0.36}}$	65	Olapour和Emam (2013年)	伊朗（阿瓦兹）	所有土	${v_{\text{s}}} = 276.8{N^{0.173}}$
7	Ohsaki和Iwasak (1973年)	日本（^*）	所有土	${v_{\text{s}}} = 81.4{N^{0.39}}$	66	Sil和Sitharam (2013年)	印度（阿加尔塔拉）	所有土	${v_{\text{s}}} = 116.4{N^{0.272}}$
8	Ohsaki和Iwasak (1973年)	日本（^*）	砂土	${v_{\text{s}}} = 59.4{N^{0.47}}$	67	陆万海等(2014年)	中国（澳门）	所有土	${v_{\text{s}}} = 139.4{N^{0.216}}$
9	Imai等(1975年)	日本（^*）	所有土	${v_{\text{s}}} = 89.9{N^{0.341}}$	68	Naik等(2014年)	印度（坎普尔）	所有土	${v_{\text{s}}} = 78.46{N^{0.39}}$
10	Imai (1977年)	日本（^*）	所有土	${v_{\text{s}}} = 91{N^{0.337}}$	69	Naik等(2014年)	印度（坎普尔）	黏土	${v_{\text{s}}} = 81.18{N^{0.377}}$
11			砂土	${v_{\text{s}}} = 80.6{N^{0.331}}$	70	Fauzi等(2014年)	印度尼西亚（雅加达）	所有土	${v_{\text{s}}} = 105.03{N^{0.286}}$
12			黏土	${v_{\text{s}}} = 102{N^{0.292}}$	71	Fabbrocino等(2015年)	意大利（莫利塞）	黏土	${v_{\text{s}}} = 110.5{N^{0.252}}$
13	Ohta和Goto (1978年)	日本（^*）	所有土	${v_{\text{s}}} = 85.35{N^{0.348}}$	72	Fatehnia等(2015年)	美国（北佛罗里达州）	所有土	${v_{\text{s}}} = 77.1{N^{0.355}}$
14	Seed等(1983年)	美国（加利福尼亚）	所有土	${v_{\text{s}}} = 56{N^{0.5}}$	73	王梦龙(2016年)	中国（巴楚）	砂土	${v_{\text{s}}} = 98.787{N^{0.22483}}$
15	Imai和Tonouchi (1982年)	日本（^*）	所有土	${v_{\text{s}}} = 96.9{N^{0.314}}$	74	Khan等(2016年)	阿联酋（沙迦）	砂土	${v_{\text{s}}} = 94.655{N^{0.3512}}$
16			砂土	${v_{\text{s}}} = 87.8{N^{0.314}}$	75	Kirar等(2016年)	印度（洛克）	所有土	${v_{\text{s}}} = 99.5{N^{0.345}}$
17			黏土	${v_{\text{s}}} = 107{N^{0.274}}$	76			砂土	${v_{\text{s}}} = 100.3{N^{0.338}}$
18	Sykora和Stokoe (1983年)	美国（加利福尼亚）	砂土	${v_{\text{s}}} = 100.5{N^{0.29}}$	77			黏土	${v_{\text{s}}} = 94.4{N^{0.379}}$
19	Lin等(1984年)	中国（台北盆地）	所有土	${v_{\text{s}}} = 65.58{N^{0.502}}$	78	Anbazhagan等(2016年)	印度（班加罗尔）	所有土	${v_{\text{s}}} = 65.67{N^{0.39}}$
20	Yokota等(1991年)	日本（^*）	所有土	${v_{\text{s}}} = 121{N^{0.27}}$	79		印度（钦奈）	所有土	${v_{\text{s}}} = 75.916{N^{0.3019}}$
21	Lee (1990年)	中国（台湾）	砂土	${v_{\text{s}}} = 57.4{N^{0.49}}$	80		印度（哥印拜陀）	所有土	${v_{\text{s}}} = 159.1{N^{0.17}}$
22	Lee (1990年)	中国（台湾）	黏土	${v_{\text{s}}} = 114{N^{0.31}}$	81		印度（维扎格）	所有土	${v_{\text{s}}} = 36.68{N^{0.56}}$
23	Kalteziotis等(1992年)	希腊（^*）	所有土	${v_{\text{s}}} = 76.2{N^{0.423}}$	82	Gautam (2016年)	尼泊尔（加德满都谷地）	所有土	${v_{\text{s}}} = 115.8{N^{0.251}}$
24			砂土	${v_{\text{s}}} = 49.1{N^{0.502}}$	83	Gautam (2016年)	尼泊尔（加德满都谷地）	砂土	${v_{\text{s}}} = 78.7{N^{0.352}}$
25			黏土	${v_{\text{s}}} = 76.55{N^{0.445}}$	84	Jhinkwan和Jain (2016年)	印度（中央邦）	所有土	${v_{\text{s}}} = 80.446{N^{0.3814}}$
26	Athanasopoulos (1994年)	希腊（^*）	所有土	${v_{\text{s}}} = 107.6{N^{0.36}}$	85			砂土	${v_{\text{s}}} = 84.229{N^{0.3875}}$
27	Iyisan (1996年)	土耳其（埃尔津詹）	所有土	${v_{\text{s}}} = 51.5{N^{0.516}}$	86			黏土	${v_{\text{s}}} = 57.077{N^{0.49}}$
28	Pitilakis等(1999年)	希腊（米格顿盆地）	黏土	${v_{\text{s}}} = 132{N^{0.271}}$	87	Pérez-Santisteban等(2016年)	西班牙（马德里）	所有土	${v_{\text{s}}} = 62.6{N^{0.52}}$
29	郑灿堂等(1999年)	中国（山东）	砂土	${v_{\text{s}}} = 80{N^{0.35}}$	88	Pérez-Santisteban等(2016年)	西班牙（马德里）	砂土	${v_{\text{s}}} = 98.69{N^{0.321}}$
30	郑灿堂等(1999年)	中国（山东）	黏土	${v_{\text{s}}} = 80{N^{0.4}}$	89	Rahman等(2018年)	孟加拉国（达卡）	所有土	${v_{\text{s}}} = 97.3062{N^{0.3393}}$
31	Kiku (2001年)	土耳其（阿达帕扎里）	所有土	${v_{\text{s}}} = 68.3{N^{0.292}}$	90			砂土	${v_{\text{s}}} = 82.01{N^{0.3829}}$
32	蔡宗文(2003年)	中国（福建）	所有土	${v_{\text{s}}} = 100.7459{N^{0.32}}$	91			黏土	${v_{\text{s}}} = 100.58{N^{0.341}}$
33	Sun等(2005年)	韩国（首尔）	所有土	${v_{\text{s}}} = 65.55{N^{0.4}}$	92	孙东风等(2018年)	中国（如东）	砂土	${v_{\text{s}}} = 100.2{N^{0.247}}$
34	Koukis等(2005年)	希腊（帕特雷）	所有土	${v_{\text{s}}} = 145{N^{0.3}}$	93	刘福兴等(2018年)	中国（黄河三角洲）	砂土	${v_{\text{s}}} = 79.68{N^{0.305}}$
35	李存志等(2006年)	中国（昆明盆地）	砂土	${v_{\text{s}}} = 103.54{N^{0.28}}$	94	Kumar等(2018年)	印度（古瓦哈提）	所有土	${v_{\text{s}}} = 46.56{N^{0.62}}$
36	李存志等(2006年)	中国（昆明盆地）	黏土	${v_{\text{s}}} = 101.49{N^{0.34}}$	95			砂土	${v_{\text{s}}} = 58.66{N^{0.57}}$
37	Sun等(2006年)	韩国（洪城）	所有土	${v_{\text{s}}} = 122.33{N^{0.185}}$	96			黏土	${v_{\text{s}}} = 47.84{N^{0.6}}$
38	Hasancebi和Ulusay (2007年)	土耳其（耶尼谢希尔）	所有土	${v_{\text{s}}} = 90{N^{0.308}}$	97	Win等(2019年)	缅甸（曼德勒）	所有土	${v_{\text{s}}} = 100.49{N^{0.2801}}$
39			砂土	${v_{\text{s}}} = 90.82{N^{0.319}}$	98	Lu和Hwang (2019年)	中国（台湾）	砂土	${v_{\text{s}}} = 80.1{N^{0.29}}$
40			黏土	${v_{\text{s}}} = 97.89{N^{0.269}}$	99	Rao和Choudhury (2020年)	印度（哈里亚纳邦）	所有土	${v_{\text{s}}} = 84{N^{0.38}}$
41	Anbazhagan和Sitharam (2008年)	印度（班加罗尔）	所有土	${v_{\text{s}}} = 78{N^{0.4}}$	100	Rahimi等(2020年)	美国（梅尔文-普莱斯）	所有土	${v_{\text{s}}} = 94.5{N^{0.248}}$
42	Hanumantharao和Ramana (2008年)	印度（新德里）	所有土	${v_{\text{s}}} = 82.6{N^{0.43}}$	101	Rahimi等(2020年)	新西兰（克赖斯特彻奇）	所有土	${v_{\text{s}}} = 75.79{N^{0.278}}$
43	Hanumantharao和Ramana (2008年)	印度（新德里）	砂土	${v_{\text{s}}} = 79{N^{0.434}}$	102	袁晓铭等(2020年)	中国（哈尔滨）	砂土	${v_{\text{s}}} = 116.55{N^{0.3149}}$
44	Dikmen (2009年)	土耳其（埃斯基谢希尔）	所有土	${v_{\text{s}}} = 58{N^{0.39}}$	103	Ashikuzzaman等(2021年)	孟加拉国（拉杰沙希）	所有土	${v_{\text{s}}} = 72.202{N^{0.3779}}$
45			砂土	${v_{\text{s}}} = 73{N^{0.33}}$	104			砂土	${v_{\text{s}}} = 74.446{N^{0.3977}}$
46			黏土	${v_{\text{s}}} = 44{N^{0.48}}$	105			黏土	${v_{\text{s}}} = 85.558{N^{0.362}}$
47	Maheswari等(2010年)	印度（钦奈）	所有土	${v_{\text{s}}} = 95.64{N^{0.301}}$	106	Alhuay-León和Trejo-Noreña(2021年)	秘鲁（奥尔莫斯）	砂土	${v_{\text{s}}} = 142.59{N^{0.222}}$
48			砂土	${v_{\text{s}}} = 100.53{N^{0.265}}$	107	Hossain等(2021年)	孟加拉国（迪纳杰布尔）	所有土	${v_{\text{s}}} = 76.285{N^{0.3748}}$
49			黏土	${v_{\text{s}}} = 89.31{N^{0.358}}$	108			砂土	${v_{\text{s}}} = 75.772{N^{0.3768}}$
50	Tsiambaos和Sabatakakis(2011年)	希腊（^*）	所有土	${v_{\text{s}}} = 105.7{N^{0.327}}$	109			黏土	${v_{\text{s}}} = 91.573{N^{0.3591}}$
51			砂土	${v_{\text{s}}} = 79.7{N^{0.365}}$	110	王梦龙(2016年)	中国（北京）	砂土	${v_{\text{s}}} = 85.9{N^{0.349}}$
52			黏土	${v_{\text{s}}} = 112.2{N^{0.324}}$	111		中国（秦皇岛）	砂土	${v_{\text{s}}} = 114.82{N^{0.287}}$
53	Thaker和Rao(2011年)	印度（苏拉特）	所有土	${v_{\text{s}}} = 59.72{N^{0.42}}$	112		中国（烟台）	砂土	${v_{\text{s}}} = 120.8{N^{0.275}}$
54			砂土	${v_{\text{s}}} = 51.21{N^{0.45}}$	113		中国（唐山）	砂土	${v_{\text{s}}} = 92.1{N^{0.284}}$
55			黏土	${v_{\text{s}}} = 62.41{N^{0.42}}$	114		中国（南京）	砂土	${v_{\text{s}}} = 99{N^{0.32}}$
56	Mhaske和Choudhury (2011年)	印度（孟买）	所有土	${v_{\text{s}}} = 72{N^{0.4}}$	115		中国（下辽河平原）	砂土	${v_{\text{s}}} = 69.1{N^{0.4}}$
57	Anbazhagan等(2013年)	印度（勒克瑙）	所有土	${v_{\text{s}}} = 68.96{N^{0.51}}$	116		中国（武汉）	砂土	${v_{\text{s}}} = 91{N^{0.35}}$
58			砂土	${v_{\text{s}}} = 60.17{N^{0.56}}$	117	卢坤玉	中国（邢台）	砂土	${v_{\text{s}}} = 64.01{N^{0.3971}}$
59			黏土	${v_{\text{s}}} = 106.63{N^{0.39}}$
注^*：多为早期研究工作，笔者提及数据来源于一个地区，但没有给出具体名称。

下载: 导出CSV

参考文献(15)

[1]	周镜. 岩土工程中的几个问题[J]. 岩土工程学报, 1999, 21(1): 2-8. http://www.cgejournal.com/cn/article/id/10244 ZHOU Jing. Some cases in geotechnical engineering[J]. Chinese Journal of Geotechnical Engineering, 1999, 21(1): 2-8. (in Chinese) http://www.cgejournal.com/cn/article/id/10244
[2]	龚晓南. 21世纪岩土工程发展展望[J]. 岩土工程学报, 2000, 22(2): 238-242. http://www.cgejournal.com/cn/article/id/10487 GONG Xiaonan. Prospects for the development of geotechnical engineering in the 21th century[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(2): 238-242. (in Chinese) http://www.cgejournal.com/cn/article/id/10487
[3]	李兆焱, 袁晓铭, 曹振中, 等. 标贯法对巴楚地震液化场地适用性及误判原因分析[J]. 世界地震工程, 2010, 26(增刊1): 282-286. https://www.cnki.com.cn/Article/CJFDTOTAL-SJDC2010S1057.htm LI Zhaoyan, YUAN Xiaoming, CAO Zhenzhong, et al. SPT method's feasibility for liquefaction decision of sites and analysis of its misjudge in Bachu earthquake[J]. World Earthquake Engineering, 2010, 26(S1): 282-286. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SJDC2010S1057.htm
[4]	王梦龙. 国家标准液化判别方法区域化修正初探[D]. 哈尔滨: 中国地震局工程力学研究所, 2016. WANG Menglong. Preliminary Study on Regional Method of National Standard of Liquefaction Discrimination Formula[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2016. (in Chinese)
[5]	KANAI K. Conference on Cone Penetrometer[R]. Ankara: The Ministry of Public Works and Settlement, 1966.
[6]	NAIK S P, PATRA N R, MALIK J N. Spatial distribution of shear wave velocity for late quaternary alluvial soil of Kanpur city, northern India[J]. Geotechnical and Geological Engineering, 2014, 32(1): 131-149. doi: 10.1007/s10706-013-9698-3
[7]	陆万海, 李熙烨, 吴玉棠. 澳门土壤剪切波速的相关性分析[J]. 华南地震, 2014, 34(3): 6-11. https://www.cnki.com.cn/Article/CJFDTOTAL-HNDI201403002.htm LU Wanhai, LI Xiye, WU Yutang. Correlations analysis of shear wave velocity of Macau soils[J]. South China Journal of Seismology, 2014, 34(3): 6-11. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HNDI201403002.htm
[8]	袁晓铭, 卢坤玉, 林颖, 等. 哈尔滨地区砂土层N-V关系特征曲线及对比研究[J]. 地震工程与工程振动, 2020, 40(6): 1-15. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC202006001.htm YUAN Xiaoming, LU Kunyu, LIN Ying, et al. The N-V relationship curve of sand layers in Harbin region and its comparison with those in other regions of China[J]. Earthquake Engineering and Engineering Dynamics, 2020, 40(6): 1-15. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC202006001.htm
[9]	XIAO S H, ZHANG J, YE J M, et al. Establishing region-specific N-V_s relationships through hierarchical Bayesian modeling[J]. Engineering Geology, 2021, 287: 106105. doi: 10.1016/j.enggeo.2021.106105
[10]	HASANCEBI N, ULUSAY R. Empirical correlations between shear wave velocity and penetration resistance for ground shaking assessments[J]. Bulletin of Engineering Geology and the Environment, 2007, 66(2): 203-213.
[11]	KUMAR A, HARINARAYAN N H, VERMA V, et al. Seismic site classification and empirical correlation between standard penetration test N value and shear wave velocity for guwahati based on thorough subsoil investigation data[J]. Pure and Applied Geophysics, 2018, 175(8): 2721-2738.
[12]	李广信. 高等土力学[M]. 北京: 清华大学出版社, 2004. LI Guangxin. Advanced Soil Mechanics[M]. Beijing: Tsinghua University Press, 2004. (in Chinese)
[13]	张克绪, 谢君斐. 土动力学[M]. 北京: 地震出版社, 1989. ZHANG Kexu, XIE Junfei. Soil Dynamics[M]. Beijing: Seismological Press, 1989. (in Chinese)
[14]	THOKCHOM S, RASTOGI B K, DOGRA N N, et al. Empirical correlation of SPT blow counts versus shear wave velocity for different types of soils in Dholera, Western India[J]. Natural Hazards, 2017, 86(3): 1291-1306.
[15]	RAHIMI S, WOOD C M, WOTHERSPOON L M. Influence of soil aging on SPT-V_s correlation and seismic site classification[J]. Engineering Geology, 2020, 272: 105653.