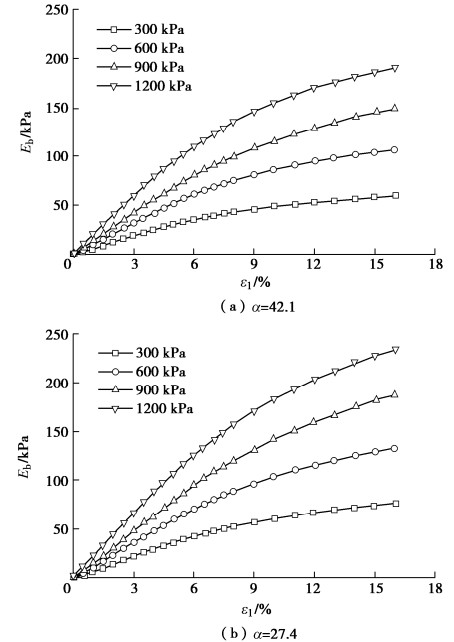
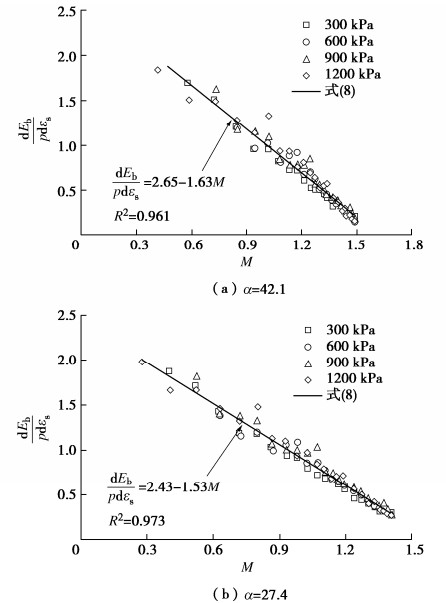
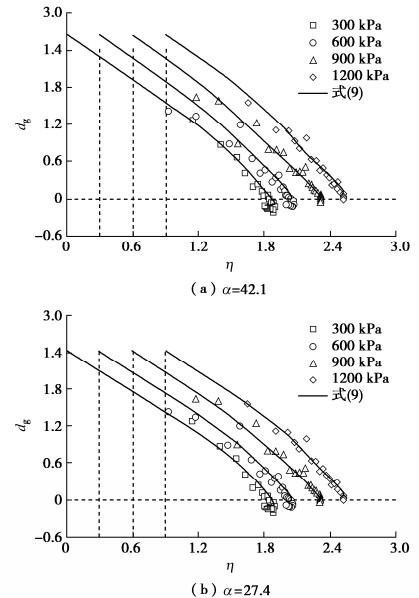
Dilatancy equation for coarse-grained soils incorporating particle breakage energy
-
摘要: 粗粒料颗粒破碎和应力变形的内在联系可以用颗粒破碎耗能反映。研究了三轴试验过程中粗粒料的颗粒破碎变化规律，根据此规律对Ueng等提出的考虑颗粒破碎的能量平衡方程中的摩擦系数M进行了修正，以此解决依据该能量平衡方程计算出的颗粒破碎耗能违反热力学定律的问题。在此基础上，发展了一个形式简单且适用于粗粒料的剪胀方程。主要结论如下：①提出的颗粒破碎指标与围压及轴向应变之间的数学关系可以较好地描述三轴试验过程中粗粒料的颗粒破碎变化规律；②通过对能量平衡方程中的摩擦系数进行修正实现了颗粒破碎耗能的合理计算，满足了热力学定律；③试验结果表明，剪胀耗能在总的输入功里占比甚微，在能量平衡方程中可以忽略剪胀耗能；④dEb/pdεs与M之间存在一个明显的线性关系，将其代入忽略剪胀耗能的能量平衡方程得到了最终的剪胀方程。研究表明，该剪胀方程可以较好地模拟粗粒料的剪胀行为，而且其数学形式简单，可以推出其塑性势函数，为后续考虑颗粒破碎的分数阶本构模型的研究提供了条件。Abstract: The internal relationship between particle breakage and stress deformation of coarse-grained soils can be reflected by the particle breakage energy. The change law of particle breakage of coarse-grained soils during triaxial tests is studied. According to this law, the fraction coefficient M in the energy balance equation proposed by Ueng and Chen is modified to solve the problem that the particle breakage energy calculated by the energy balance equation violates the thermodynamic law. On this basis, a simple dilatancy equation for coarse-grained soils is developed. The main conclusions are as follows: (1) The proposed mathematical relationship among particle breakage index, confining pressure and axial strain can describe the change law of particle breakage well. (2) The reasonable calculation of particle breakage energy is realized by modifying the fraction coefficient in the energy balance equation, which satisfies the thermodynamic law. (3) The test results show that the ratio of the dilatancy energy to the total input work is very small, so it can be ignored in the energy balance equation. (4) There is an obvious linear relationship between dEb/dεs and M, and a dilatancy equation can be developed by substituting this linear relationship into the energy balance equation, and this dilatancy equation can well simulate the dilatancy behaviors of coarse-grained soils, and its mathematical form is simple enough, so that its plastic potential function can be derived, which provides conditions for the subsequent studies on the fraction-order constitutive model considering particle breakage.
-
0. 引言
施工或构造挤压易诱发岩石变形甚至破裂,变形速率作为描述岩石变形的重要力学参数,能反映岩石变形与破坏的时效过程,对岩石工程施工安全、灾害预测预警等意义重大,关于岩石应变速率的研究备受重视。张传庆等[1]基于变形速率建立了深埋软岩隧洞围岩稳定性评估方法；Li等[2]指出隧道“三锚”支护时机应根据围岩变形速率作严格要求；曹海静等[3]、张民庆等[4]利用变形速率分析进行隧道三台阶施工围岩变形预留量确定和分级预警。王学滨[5]探究了煤岩弹性段和软化段应变速率对岩石破坏的敏感性；Rosea等[6]用岩体位移分析Fukuzono速度倒数与时间图线,王延平等[7]进一步建立了滑坡预测模型。《公路隧道施工技术规范》[8]和《铁路隧道设计规范》[9]等技术规程中均以变形速率作为隧道围岩稳定性判定的重要依据。此外,Yamamoto[10]提出基于应变速率的DAR地应力测量法,谢强等[11]、王海军等[12]、Hsieh等[13]、葛伟凤等[14]还从声发射、黏聚力、侧向应变、Kaiser效应等不同角度,对DAR测量法进行完善。可见,掌握荷载作用下应变速率的演化规律,对理解岩石变形行为,分析岩石工程稳定性,制定合理的支护方案,以及地应力精准测量等方面具有重要作用。
目前关于岩石应变速率的研究大多针对单调加载作用条件。然而大量工程实践表明,岩石工程在施工和服役过程中,疲劳荷载和应力周期性重分布现象普遍存在,如矿山巷道、高边坡、隧道岩体的分布开挖、库岸边坡岩体受水位周期性大幅升降作用,岩基受通车、地震动态周期荷载等。不少学者已开展了疲劳荷载作用下岩石力学性质的研究工作,如葛修润等[15]、Shahnazari等[16]、Liu等[17-18]通过室内试验和数值模拟方法,分别对岩石在疲劳荷载作用下的变形特性、残余体积应变、动弹性模量等力学行为进行了深入研究。但是,上述研究的重点主要是讨论岩石在疲劳荷载下的强度、残余变形和弹性常数等问题,而对于应变速率,特别是岩石疲劳累积损伤过程的应变速率响应规律研究鲜有报道。
鉴于此,本文进行了不同围压和不同应力比条件下的大理岩等幅循环加卸载三轴压缩试验,研究不同条件下大理岩疲劳累积损伤过程中,弹性模量、损伤因子、轴向应变速率和体变速率等参量的响应规律,并尝试进行循环过程中应变速率和损伤因子的相关性讨论。其规律性认识有助于进一步了解疲劳荷载作用下岩石变形和损伤演化的相关性,为建立基于变形速率的岩石工程安全预警体系和科学支护方法提供参考。
1. 试验条件及方法
1.1 试验条件
试验在华侨大学与长春市科意试验仪器有限公司联合研制的TFD–2000/D型电液伺服三轴压缩试验机上完成,见图1。设备最大围压为200 MPa,最大轴压为2000 kN,应力传感器测量精度0.01 kN。岩样变形采用轴向引伸计（最大量程为10 mm）和环向链式引伸计（最大量程为3 mm）,测量分辨率为0.0001 mm。控制系统采用德国DOLI公司的EDC全数字伺服控制器,可实现轴向力控制、轴向变形控制、轴向位移控制、环向变形控制和环向应力控制等多种控制方式。
![]()
图 1 三轴试验机、引伸计和大理岩试样Figure 1. Triaxial test apparatus, strain meter and marble specimens1.2 试样准备
岩样取自广西贺州市某采石厂白色粗晶粒大理岩,质地均匀,无杂质,少裂隙,完整性和均匀性较好,见图1。按国际岩石力学学会（ISRM）试验规程建议方法,将试样加工50 mm×100 mm（直径×长度）的标准型圆柱试样,并对试样两端面进行磨平,端面平整度在0.02 mm以内,直径误差控制在0.3 mm范围内。试验前,各岩样均经过纵波波速测试,并去除波速异常试样,进一步保证试样一致性。图2为不同围压的单调压缩条件下,大理岩的轴向、环向全应力–应变关系曲线,为后续疲劳试验中确定各围压下疲劳荷载幅值提供依据。为了和疲劳试验中循环加卸载的控制方式一致,单调加载控制方式也设为应力控制。由图2可知,岩样峰值应力随围压的增大而增大,且延性逐渐增强。
![]()
图 2 不同围压下单调压缩加载应力–应变曲线Figure 2. Stress-strain curves under different confining pressures of monotonic compression loading1.3 疲劳试验方案
疲劳试验通过等幅循环加卸载方式实现,试验中控制围压和循环幅值两个因素,设置4×4的正交试验,见表1。围压设为0 (单轴条件),2,5,10 MPa,每组围压下的疲劳荷载幅值设置4组应力比,分别为0.90,0.85,0.80,0.75倍峰值应力。由表1可知,各围压的疲劳荷载目标值均大于各自扩容点应力,故4种应力比均超过了岩石的弹性极限。加卸载过程均为应力控制,控制速度为1 MPa/s,直到试样破坏为止,加载方式见示意图3。若500次循环加卸载后试样仍不破坏,则停止循环,改为单调加载方式直至试样破坏。
表 1 不同围压下疲劳荷载的预设目标值Table 1. Fatigue loading under different confining pressures(Mpa) 围压 峰值应力 应力比 扩容点应力 0.90 0.85 0.80 0.75 0 50.00 45.00 42.50 40.00 37.50 34.0 2 60.00 54.00 51.00 48.00 45.00 43.4 5 72.00 64.80 61.25 57.60 54.00 52.3 10 93.00 83.70 79.05 74.60 69.75 65.0 2. 应力–应变关系及弹性参数分析
2.1 应力–应变关系
表2为不同应力比和不同围压下,大理岩受疲劳荷载作用破坏时所需的循环次数。由表2可知：相同应力比疲劳荷载条件下,随着围压的增大,岩样越来越难以破坏。说明围压对环向变形的约束对疲劳劣化有明显的抑制作用,使大理岩抗疲劳承载能力增强。图4为单轴疲劳荷载下大理岩应力–应变关系曲线（有围压下的岩石变形差异性与图4类似,篇幅所限不再列出）,其中体积应变（以下简称为体变）由
εv =ε1 +2ε2 计算得到（εv 为体变,ε1 为轴向应变,ε2 为环向应变）。由图4可见：①在单轴压缩条件下,随着应力比的增大,大理岩破坏时所需的循环荷载次数降低；②随着循环次数增加残余应变不断发展,滞回圈也随之沿应变坐标轴向右移动,且应力比越高移动越显著；③第一次加卸载产生明显的残余应变,滞回圈面积较大。自第二次加载开始,随着循环次数增加滞回圈相互重叠、缓慢右移,临近破坏时滞回圈加速右移且面积明显增大。上述现象可解释为相同围压下,应力比越大疲劳应力超越弹性极限程度也就越大,使单次循环加卸载过程中的塑性变形更大,导致相同循环次数后岩样累计残余变形也就越大。发生破坏岩样的前期循环以弹性变形为主,塑性变形较小,故滞回圈缓慢右移,而当残余变形累积到一定程度后,循环加卸载过程中塑性变形增加,故滞回圈增大且加速右移。表 2 岩样破坏情况及循环次数Table 2. Failure situation of rock samples and number of cycles at failure应力比 围压 0 MPa 2 MPa 5 MPa 10 MPa 0.90 10 16 33 未破坏 0.85 19 22 未破坏 未破坏 0.80 50 未破坏 未破坏 未破坏 0.75 未破坏 未破坏 未破坏 未破坏 ![]()
图 4 不同应力比下大理岩疲劳试验应力–应变曲线Figure 4. Stress-strain relationship of marble fatigue tests under different stress ratios需强调的是,第一次加载时,由于受到超过历史最大应力水平的作用（即岩石具有的“记忆性”）,岩样产生较大的残余变形和滞回圈面积[19]。从第二次循环加载开始,岩石受到的疲劳荷载应力水平与第一次加卸载相等,其力学行为与第一次的超过应力历史加卸载有较大区别。第二次加载开始才是真正意义上的等幅疲劳累积损伤过程,因此在分析弹性模量、损伤因子和应变速率的演化规律时,将第二次加载作为疲劳损伤的初始状态进行分析。
2.2 弹性模量变化规律
图5为不同围压下弹性模量E（E=
Δσ/Δε ,Δσ ,Δε 取该围压下单调压缩峰值50%偏应力附近5 MPa左右的应力差值和对应的应变差值）与循环次数的关系曲线。由图5可见：①自第二次循环荷载开始,随着循环次数的增加,发生疲劳破坏岩样的弹性模量逐渐下降,且围压越大下降越平缓。未发生疲劳破坏的岩样在0.90,0.85应力比下,弹性模量先小幅下降后缓慢上升,最后逐渐趋于稳定；在0.80,0.75应力比下,弹性模量小幅升高后趋于稳定。②在循环次数相同,应力比也相同时,随着围压的提高弹性模量有不同程度的提高；在相同围压和循环次数下,随着应力比的降低,弹性模量也有不同程度的提高。![]()
图 5 弹性模量与循环次数关系对比Figure 5. Comparison between elastic modulus and cycle number of elastic segments以上现象解释如下：①随循环次数增加,发生疲劳破坏岩样因受多次的较高应力作用,内部裂隙不断扩展、交汇、贯通,抗变形能力不断下降,导致弹性模量下降越来越快。由于围压对岩样的裂隙开展有抑制作用,围压越大弹性模量下降越缓慢。未发生疲劳破坏的岩样在0.80,0.75应力比下,距离弹性极限对应的应力比较近,几乎不会产生塑性变形和累积损伤效应。根据文献[20,21]对疲劳变形和蠕变（也被称为“应力疲劳”）中应变硬化现象的解释：较低应力的疲劳荷载导致裂隙面相互作用和晶象学优势面出现,晶粒边界处产生的位错堆积阻碍位错运动的后续发展,岩石内微裂隙压密闭合更为充分,颗粒排列更加密实,裂隙总数相对减少,产生裂隙面“黏溶”的自愈合现象,因此弹性模量随循环次数增加会缓慢上升。当硬化至一定程度,岩石进入近似弹性状态的变形阶段,弹性模量趋于稳定。文献[20]还指出,疲劳应变硬化阶段也可能存在着稍许软化现象。在0.90,0.85应力比条件下的前几次循环加卸载过程中,较高应力的疲劳荷载产生的岩石内部损伤使弹模下降,即软化现象占主导。之后硬化作用越来越明显,故弹性模量随循环次数增加开始缓慢上升并最终稳定。②围压升高可使岩石晶粒间更加紧凑,裂隙发展段的应力门槛值提高,抗变形能力增大,从而出现围压越高岩样弹性模量越高的现象。
3. 应变速率演化特征
3.1 疲劳作用对应变速率的影响
为分析疲劳荷载作用过程中应变速率的演化特征,图6（a）,（b）分别为应力比为0.90的单轴（低周）疲劳作用下,第2,4,6,8,10次加载和第2,4,6,8次卸载过程中岩石偏应力、轴向应变速率与轴向应变的关系曲线,其中轴向应变速率通过对时间求差分的方式获得,由
ε′=(εt1−εt2)/(t1−t2) 计算得到。εt1,εt2分别表示相邻时刻的应变。由于不同围压和应力比条件下破坏岩样的曲线形态大致相同,未破坏岩样曲线形态接近弹性状态,考虑篇幅不再列出。![]()
图 6 偏应力、应变速率与应变关系Figure 6. Relationship among the deviatoric stress, axial strain rate and axial strain由图6可见：①随循环次数增加,残余应变（即当次卸载终了和下一次加载初始时刻应变值）不断增大。②每次加载时岩样的轴向变形曲线形态类似,均经历曲线下凹的裂隙压密阶段、斜直线的弹性变形阶段以及曲线上凸的塑性变形阶段。轴向应变速率随应变发展均呈现先减小后趋稳,最后逐渐增大的“U”型演化规律,且不同循环次数下稳定段对应的应变速率值基本保持一致。③末次加载前,岩样轴向应变速率始终保持在相对较低的水平上,加载初始和终了时刻的轴向应变速率与其对应的残余应变均呈线性正相关关系。末次加载至接近目标荷载时,轴向应变速率明显突增,岩样随即破坏。④每次加载进入速率稳定段时刻的偏应力与其对应的轴向应变呈线性正相关关系,加载超出速率稳定段时刻偏应力与其对应的轴向应变呈线性负相关关系,应变速率曲线稳定段长度随加卸载次数增加明显缩短。⑤每次卸载时岩样大致经历了近似线性的回弹和非线性回弹两个阶段。轴向应变速率呈现先小幅度上升后趋稳,最后增大的倒“S”型演化规律,且卸载初始与终了时刻的轴向应变速率绝对值与其对应的残余应变也呈线性正相关关系。卸载进入速率稳定段时刻的偏应力较接近,跃出速率稳定段时刻的偏应力与其对应的轴向应变呈线性正相关关系。
以上现象解释如下：①因塑性变形不可逆,随加载次数增加积累越来越大,故残余应变也越来越大。②加载开始时岩样内部原有裂隙随应力增加逐渐闭合,岩样抵抗变形的能力逐渐提高,轴向应变速率逐渐减小,待岩样达到最致密状态时进入弹性变形阶段,应变速率保持稳定。偏应力进一步增加后,原生裂隙张开,新生裂隙开始增多,岩样发生塑性变形,故应变速率显著增大。稳定段应变速率基本一致说明不同循环加载次数下,岩样的最致密状态较接近,抵抗变形的能力亦较接近,临近破坏时应变速率迅速增大则反映了岩石接近失稳的变形状态（图7为不同围压、不同应力比下稳定段应变速率图,显示了围压越大速率越低的规律,可与图5中围压越大弹性模量越高的现象相互印证）。③试验结果显示加载初始和终了时刻的轴向应变速率与残余应变均呈线性正相关关系,张世殊等[22]采用残余变形表征岩石损伤,从这个角度不难推断,加载初始和终了时刻的轴向应变速率也可反映疲劳作用下岩样的累积损伤进程（应变速率与弹模表征的损伤因子间的相关性在下一节讨论）。④随加卸载次数增加,岩样内部裂隙的长度、宽度、密度均不断增大,维持岩样稳定的内部结构单元体不断被破坏,损伤不断累积。加载至弹性段后随着轴向应力增加,稳定的单元体不断减少,岩样结构稳定性下降,裂隙越来越难以维持闭合状态,应变速率在经历短暂稳定阶段后很快又因裂隙的重新扩展贯通而快速上升,故应变速率稳定段随加载次数增加而缩短。⑤与加载一样,每次卸载初始和终了时刻的轴向应变速率也可反映疲劳作用下的累积损伤进程。
![]()
图 7 不同围压、不同应力比下的稳定段速率Figure 7. Stable segment rates under different confining pressures and stress ratios图8（a）,（b）分别为应力比=0.90的单轴疲劳作用下,第2,4,6,8,10次加载和第2,4,6,8次卸载过程中岩石偏应力、体变速率与体变（以下简称体变）的关系曲线。由图8可见：①随循环次数增加,残余体变（即当次卸载终了和下一次加载初始时刻的体变值）的绝对值不断增大。②每次加载时岩样的体变曲线形态类似,均经历先体缩（体变增量为正值）至扩容点,之后体胀（体变增量为负值）的体变过程。体缩阶段的体变速率先快速减小,再进入平缓段,之后加速下降,至扩容点时体变速率降至0,进入体胀阶段后体变速率绝对值快速增大,整体上体变速率随体变发展呈反“L”型演化趋势。③末次加载前,岩样体变速率均保持在相对较低的水平,加载初始和终了阶段的体变速率绝对值都与其对应的残余体变绝对值呈线性正相关关系。末次加载至接近目标荷载时,体变应变速率绝对值明显突增。④随循环次数增加,每次加载到扩容点时对应的偏应力逐渐减小,且偏应力与其对应的体变绝对值呈线性负相关关系。⑤卸载阶段岩样体积始终处于膨胀过程,体变速率绝对值整体呈先减小再稳定最后加速增长的“U”型演化趋势,且稳定段对应的体变速率值基本保持不变。卸载初始与终了时刻的体变速率绝对值与其对应的残余体变绝对值呈线性正相关关系,且终了时刻体变速率绝对值较大。此外,卸载进入体变速率稳定段时刻对应的偏应力较接近,跃出体变速率稳定段时刻的偏应力与其对应的体变绝对值呈线性正相关关系。
![]()
图 8 偏应力、体变速率与体变关系Figure 8. Relationship among deviatoric stress, volumetric strain and volume strain rate以上现象解释如下：①与残余应变一样,因塑性变形积累,残余体变随循环次数增加而增大。②岩石变形全过程可依次分为裂隙压密、弹性变形、裂隙稳定扩展和非稳定扩展4阶段,体缩段包含前3个阶段。在体缩段初期的裂隙压密阶段,岩石内部越来越密实,抵抗变形能力增强,体变速率快速减小,进入弹性变形阶段体变速率变化趋于平缓,进入裂隙稳定扩展阶段后体变速率又快速下降,达到扩容点时体变增量为0,故体变速率为0。超越扩容点后岩石进入裂隙非稳定扩展段,裂隙快速交汇贯通,体变速率加速增加。③与应变速率类似,加载初始和终了时刻的体变速率绝对值与残余体变绝对值呈线性正相关关系,表明此刻的体变速率也可反映疲劳作用过程中岩样的累积损伤进程。④随循环次数增加,损伤也随之积累增加,闭合裂隙也易被更低的偏应力再次激活,岩样承载能力不断下降,使扩容点越来越早出现。⑤与加载一样,每次卸载初始和终了时刻的体变速率也可反映疲劳作用过程中岩样的累积损伤进程。
3.2 初始应变速率与损伤因子关系
损伤因子可直接表征岩石的损伤程度,为研究不同围压、不同应力比疲劳作用下岩石的损伤累积进程、应变速率演化及其相互关系,作出不同围压和不同应力比下,自第二次加卸载开始的岩样损伤因子与循环次数的关系图,见图9。其中损伤因子由常规的弹性模量法算出（
D=1−E/E0 ,E0 为第二次加载时的弹性模量）。如图9所示：①发生疲劳破坏岩样的损伤因子随循环次数增加不断增大,循环至后期损伤因子爆发式增大,直观体现了疲劳荷载下岩石的累计损伤进程；②未发生疲劳破坏岩样的损伤因子先小幅波动后逐渐趋于稳定；③无论破坏或未破坏,应力比越低或围压越大,相同循环次数时岩样的损伤因子越小,较大围压和较低应力比下损伤因子最终稳定至负值,这可能是因为较大的围压使疲劳荷载对岩石产生了小幅硬化作用[20]。同样的,自第二次加卸载开始绘制加载时刻初始轴向应变速率（以下简称为初始速率）与循环次数的关系曲线,见图10。由图10可知：①发生疲劳破坏岩样的初始速率随循环次数增加不断增大,循环至后期初始速率爆发式增大；②未发生疲劳破坏岩样的初始速率先小幅波动后逐渐趋于稳定；③无论破坏或未破坏,应力比越低或围压越大,相同循环次数时岩样的初始速率越小。需强调的是,图10与图9对比可见,两类关系曲线的演化规律几乎是一致的,进一步验证了图6的分析结论,即加载初始应变速率可反映岩石的损伤程度,也就是当次循环的初始轴向应变速率可表征其之前循环过程中的损伤累积情况。
![]()
图 10 初始轴向应变速率变化Figure 10. Variation of axial strain rate at beginning of loading phase为进一步分析初始速率与损伤因子的定量关系,参照损伤因子计算形式对初始速率进行归一化处理,
D′=1−V1/V （V1 取第二次加载时的初始速率,V 为之后循环加载的初始速率,D′ 为归一化初始速率）,对疲劳破坏岩样绘制D′ 与损伤因子的线性拟合关系图,见图11,拟合相关度见表3。由图11和表3可见,不同围压和应力比下,破坏岩样的线性拟合相关度均在0.991以上,说明可以利用初始速率表征损伤因子,D=K(1−V1/V) （K为受围压与循环应力比影响的拟合系数,K值随围压的增大而减小,随应力比降低而减小）。![]()
图 11 归一化初始速率与损伤因子相关性（疲劳破坏岩样）Figure 11. Relationship between normalized initial rate and damage factor of damaged rock samples表 3 疲劳破坏岩样归一化初始速率与损伤因子相关性Table 3. Correlation fitting between normalized initial rate and damage factor of damaged rock samples应力状态 围压/MPa K值 相关度 拟合函数 0.90倍峰值 0 0.74676 0.99959 D=KD′ 2 0.59077 0.99732 5 0.49197 0.99700 0.85倍峰值 0 0.38372 0.99154 2 0.32274 0.99732 0.80倍峰值 0 0.27233 0.99492 图12为10 MPa围压的不同应力比下岩石归一化速率与损伤因子关系图。由图12可见：①未破坏岩样在前期循环加卸载阶段归一化速率与损伤因子基本符合线性关系,而在后期循环加卸载时出现回缩和聚拢现象。这是由于未破坏岩样在疲劳累积损伤作用至一定程度后不再继续劣化,而开始出现不同幅度的硬化现象,损伤因子和归一化速率不增反降,致使整个曲线呈“弯钩”型。②应力比为0.90,0.85时,曲线位于损伤因子与归一化速率为正值的第一象限。而当应力比为0.80,0.75时,由于应力比较低,累积损伤非常微弱,此时硬化作用起主导,循环加卸载的硬化作用使损伤因子出现负值情况,变形速率也随之降低,故关系曲线位于速率为正,损伤因子为负的第四象限。总体上呈现随应力比降低,曲线沿顺时针方向分布,且应力比越低弯曲回缩现象越明显的变化趋势。
![]()
图 12 归一化初始速率与损伤因子相关性（未破坏岩样）Figure 12. Relationship between damage factor and normalized initial rate of undamaged rock samples4. 结论
（1）相同围压下,随应力比升高,岩样疲劳破坏需经历的循环加卸载次数减少；相同应力比下,随围压增大,岩样越来越难以破坏。发生疲劳破坏岩样的弹性模量随循环次数增加迅速减小。
（2）发生疲劳破坏的岩样在每次加载时轴向应变速率随轴向应变发展呈“U”型演化规律,体变速率随体变发展呈反“L”型演化趋势,且加载初始和终了时刻的轴向应变速率与其对应的残余应变均呈线性正相关关系,体变速率绝对值与其对应的残余体变绝对值呈线性正相关关系。
（3）发生疲劳破坏的岩样在每次卸载时轴向应变速率随轴向应变发展呈倒“S”型演化规律,体变速率随体变发展呈“U”型演化趋势,且卸载初始与终了时刻的轴向应变速率与其对应的残余应变呈线性正相关关系,体变速率与其对应的残余体变绝对值呈线性正相关关系。
（4）当次循环加载的初始轴向应变速率可表征其之前循环过程中的损伤累积程度。发生疲劳破坏岩样的归一化初始速率后与损伤因子有良好的线性关系,系数K随围压增大或应力比值减小而减小。未发生疲劳破坏岩样的归一化速率和损伤因子关系曲线产生“弯钩”型回缩现象。
-
![]()
图 7 粗粒料C剪胀比的试验值与预测值
Figure 7. Test data and prediction of dilatancy ratio of coarse-grained soil C
![]()
图 8 粗粒料D剪胀比的试验值与预测值
Figure 8. Test data and prediction of dilatancy ratio of coarse-grained soil D
![]()
图 15 粗粒料C剪胀比的实测值与预测值
Figure 15. Measured and predictive data of dilatancy ratio of coarse-grained soil C
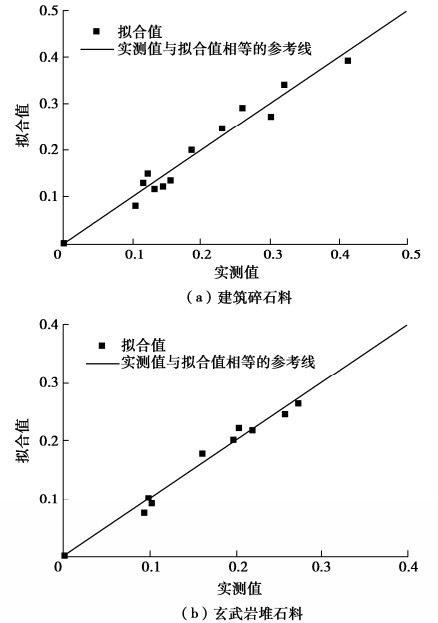
表 1 颗粒破碎试验数据
Table 1 Particle breakage data
粗粒料 围压/kPa 轴向应变/% 破碎指标BE/% 建筑碎
石料[14]200 4.58 10.60 200 9.72 14.40 200 12.90 15.60 500 3.88 11.60 500 7.96 18.70 500 14.40 23.10 1000 3.17 12.20 1000 9.40 26.00 1000 15.80 32.00 1500 2.05 13.20 1500 6.31 30.20 1500 17.20 41.40 玄武岩
堆石料[15]1000 2.16 9.40 1000 7.84 16.10 1000 15.10 21.90 1500 2.41 10.20 1500 8.24 19.70 1500 15.60 25.70 2000 2.47 9.90 2000 8.61 20.30 2000 15.10 27.20 
下载: 导出CSV
表 2 式（1）的拟合结果
Table 2 Fitting results of Eq. (1)
粗粒料 β α ω 决定系数R2 建筑碎石料 0.417 19.5 5.42 0.962 玄武岩堆石料 0.260 21.4 5.18 0.980
下载: 导出CSV
-
[1] 郭庆国. 粗粒土的工程特性及应用[M]. 郑州: 黄河水利出版社, 1998. GUO Qing-guo. Engineering characteristic and pplication of coarse-grained soil[M]. Zhengzhou: Yellow River Conservancy Press, 1998. (in Chinese)
[2] 姚仰平, 刘林, 罗汀. 砂土的UH模型[J]. 岩土工程学报, 2016, 38(12): 2147–2153. doi: 10.11779/CJGE201612002 YAO Yang-ping, LIU Lin, LUO Ting. UH model for sands[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(12): 2147–2153. (in Chinese) doi: 10.11779/CJGE201612002
[3] YAO Y P, LIU L, LUO T, et al. Unified hardening (UH) model for clays and sands[J]. Computers and Geotechnics, 2019, 110: 326–343. doi: 10.1016/j.compgeo.2019.02.024
[4] YAO Y P, YAMAMOTO H, WANG N D. Constitutive model considering sand crushing[J]. Soils and Foundations, 2008, 48(4): 603–608. doi: 10.3208/sandf.48.603
[5] 郭万里, 蔡正银, 武颖利, 等. 粗粒土的颗粒破碎耗能及剪胀方程研究[J]. 岩土力学, 2019, 40(12): 4703–4710. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201912018.htm GUO Wan-li, CAI Zheng-yin, WU Ying-li, et al. Study on the particle breakage energy and dilatancy of coarse-grained soils[J]. Rock and Soil Mechanics, 2019, 40(12): 4703–4710. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201912018.htm
[6] UENG T S, CHEN T J. Energy aspects of particle breakage in drained shear of sands[J]. Géotechnique, 2000, 50(1): 65–72. doi: 10.1680/geot.2000.50.1.65
[7] GUO W L, ZHU J G. Particle breakage energy and stress dilatancy in drained shear of rockfills[J]. Géotechnique Letters, 2017, 7(4): 304–308. doi: 10.1680/jgele.17.00099
[8] 米占宽, 李国英, 陈生水. 基于破碎能耗的粗颗粒料本构模型[J]. 岩土工程学报, 2012, 34(10): 1801–1811. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract14871.shtml MI Zhan-kuan, LI Guo-ying, CHEN Sheng-shui. Constitutive model for coarse granular materials based on breakage energy[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(10): 1801–1811. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract14871.shtml
[9] 王占军, 陈生水, 傅中志. 堆石料的剪胀特性与广义塑性本构模型[J]. 岩土力学, 2015, 36(7): 1931–1938. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201507019.htm WANG Zhan-jun, CHEN Sheng-shui, FU Zhong-zhi. Dilatancy behaviors and generalized plasticity constitutive model of rockfill materials[J]. Rock and Soil Mechanics, 2015, 36(7): 1931–1938. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201507019.htm
[10] 姚仰平, 黄冠, 王乃东, 等. 堆石料的应力–应变特性及其三维破碎本构模型[J]. 工业建筑, 2011, 41(9): 12–17, 104. https://www.cnki.com.cn/Article/CJFDTOTAL-GYJZ201109004.htm YAO Yang-ping, HUANG Guan, WANG Nai-dong, et al. Stress-strain characteristic and three-dimensional constitutive model of rockfill considering crushing[J]. Industrial Construction, 2011, 41(9): 12–17, 104. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GYJZ201109004.htm
[11] 贾宇峰, 迟世春, 林皋. 考虑颗粒破碎影响的粗粒土本构模型[J]. 岩土力学, 2009, 30(11): 3261–3266, 3272. doi: 10.3969/j.issn.1000-7598.2009.11.007 JIA Yu-feng, CHI Shi-chun, LIN Gao. Constitutive model for coarse granular aggregates incorporating particle breakage[J]. Rock and Soil Mechanics, 2009, 30(11): 3261–3266, 3272. (in Chinese) doi: 10.3969/j.issn.1000-7598.2009.11.007
[12] 陈生水, 傅中志, 韩华强, 等. 一个考虑颗粒破碎的堆石料弹塑性本构模型[J]. 岩土工程学报, 2011, 33(10): 1489–1495. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract14194.shtml CHEN Sheng-shui, FU Zhong-zhi, HAN Hua-qiang, et al. An elastoplastic model for rockfill materials considering particle breakage[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(10): 1489–1495. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract14194.shtml
[13] 张丙印, 贾延安, 张宗亮. 堆石体修正Rowe剪胀方程与南水模型[J]. 岩土工程学报, 2007, 29(10): 1443–1448. doi: 10.3321/j.issn:1000-4548.2007.10.002 ZHANG Bing-yin, JIA Ya-nan, ZHANG Zong-liang. Modified Rowe's dilatancy law of rockfill and Shen Zhujiang's double yield surfaces elastoplastic model[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(10): 1443–1448. (in Chinese) doi: 10.3321/j.issn:1000-4548.2007.10.002
[14] 郭万里, 朱俊高, 彭文明. 粗粒土的剪胀方程及广义塑性本构模型研究[J]. 岩土工程学报, 2018, 40(6): 1103–1110. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17386.shtml GUO Wan-li, ZHU Jun-gao, PENG Wen-ming. Dilatancy equation and generalized plastic constitutive model for coarse-grained soils[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(6): 1103–1110. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17386.shtml
[15] 孙逸飞, 高玉峰, 鞠雯. 分数阶塑性力学及其砂土本构模型[J]. 岩土工程学报, 2018, 40(8): 1535–1541. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17490.shtml SUN Yi-fei, GAO Yu-feng, JU Wen. Fractional plasticity and its application in constitutive model for sands[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(8): 1535–1541. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17490.shtml
[16] ROWE P W. The stress-dilatancy relation for static equilibrium of an assembly of particles in contact[J]. Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences, 1962, 269(1339): 500–527.
[17] 郭万里. 粗粒土颗粒破碎演化规律及本构模型研究[D]. 南京: 河海大学, 2018. GUO Wan-li. Particle Breakage Evolution Model of Coarse-Grained Soil and Constitutive Model[D]. Nanjing: Hohai Universiyt, 2018. (in Chinese)
[18] 王峰, 张建清. 考虑颗粒强度尺寸效应的原型堆石料破碎特性研究[J]. 岩土力学, 2020, 41(1): 87–94. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202001011.htm WANG Feng, ZHANG Jian-qing. Study of breakage behaviour of original rockfill materials considering size effect on particle strength[J]. Rock and Soil Mechanics, 2020, 41(1): 87–94. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202001011.htm
[19] 吴二鲁, 朱俊高, 黄维, 等. 三轴剪切过程中粗粒料颗粒破碎变化规律研究[J]. 岩土工程学报, 2020, 42(12): 2330–2335. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18383.shtml WU Er-lu, ZHU Jun-gao, HUANG Wei, et al. Evolution law of particle breakage of coarse-grained soil during triaxial shearing[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(12): 2330–2335. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18383.shtml
[20] PRÉVOST J, HØEG K. Soil mechanics and plasticity analysis of strain softening[J]. Géotechnique, 1975, 25: 279–297. doi: 10.1680/geot.1975.25.2.279
[21] 秦红玉, 刘汉龙, 高玉峰, 等. 粗粒料强度和变形的大型三轴试验研究[J]. 岩土力学, 2004, 25(10): 1575–1580. doi: 10.3969/j.issn.1000-7598.2004.10.013 QIN Hong-yu, LIU Han-long, GAO Yu-feng, et al. Research on strength and deformation behavior of coarse aggregates based on large-scale triaxial tests[J]. Rock and Soil Mechanics, 2004, 25(10): 1575–1580. (in Chinese) doi: 10.3969/j.issn.1000-7598.2004.10.013
[22] 贾宇峰, 迟世春, 杨峻, 等. 粗粒土的破碎耗能计算及影响因素[J]. 岩土力学, 2009, 30(7): 1960–1966. doi: 10.3969/j.issn.1000-7598.2009.07.015 JIA Yu-feng, CHI Shi-chun, YANG Jun, et al. Measurement of breakage energy of coarse granular aggregates[J]. Rock and Soil Mechanics, 2009, 30(7): 1960–1966. (in Chinese) doi: 10.3969/j.issn.1000-7598.2009.07.015
[23] WANG L, ZHU J G, ZHANG Z L, et al. Effects of dry density on shear behavior and particle breakage for slate rockfill material[J]. Bulletin of Engineering Geology and the Environment, 2021, 80(2): 1181–1192. doi: 10.1007/s10064-020-01971-z
-
期刊类型引用(3)
1. 李珍玉，单世杰，林坤，朱航. 微生物促进矿物相变及其改良膨胀土胀缩特性试验研究. 岩石力学与工程学报. 2025(01): 209-220 . 
百度学术
2. 廖嵩隆. 基于荷载作用的膨胀土工程特性试验研究. 黄河水利职业技术学院学报. 2024(01): 36-39 . 百度学术
3. 白玉霞，常顺，肖衡林，李丽华，何俊，邱季，周文卓，邓永锋. 膨胀土生态治理研究进展. 岩土工程学报. 2024(S2): 60-66+176 . 本站查看
其他类型引用(5)
计量
- 文章访问数: 241
- HTML全文浏览量: 33
- PDF下载量: 110
- 被引次数: 8
