Method for calculating seismic active earth pressures on cantilever retaining walls
-
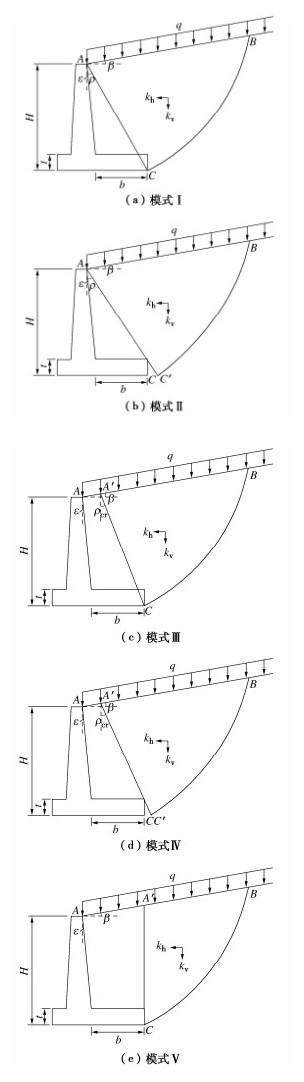
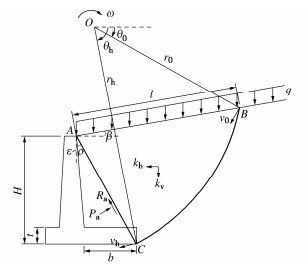
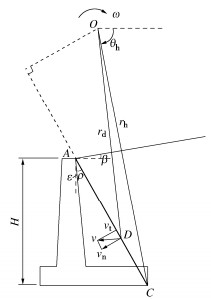
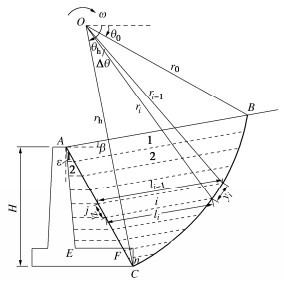
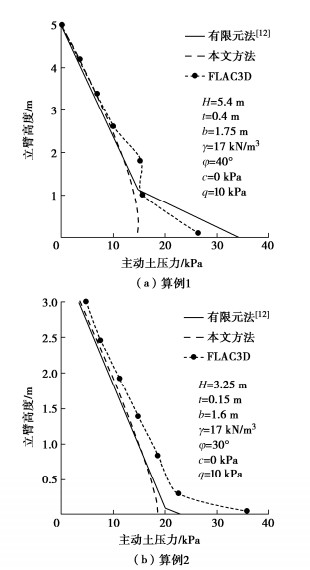
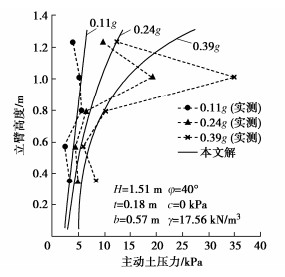
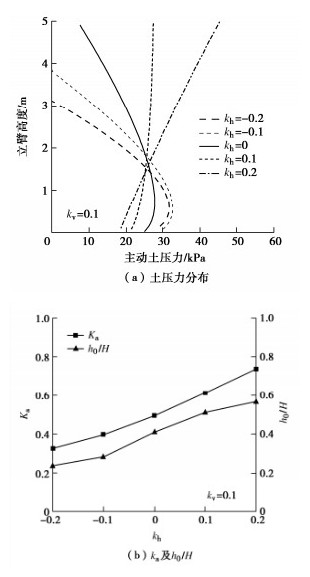
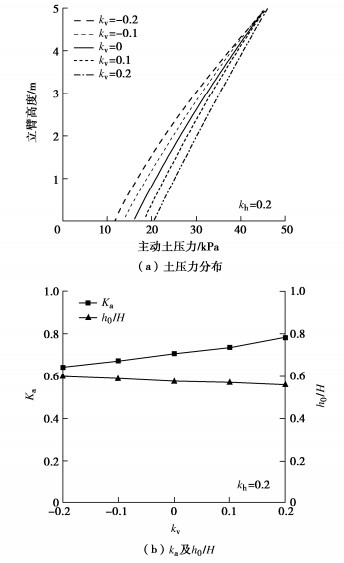
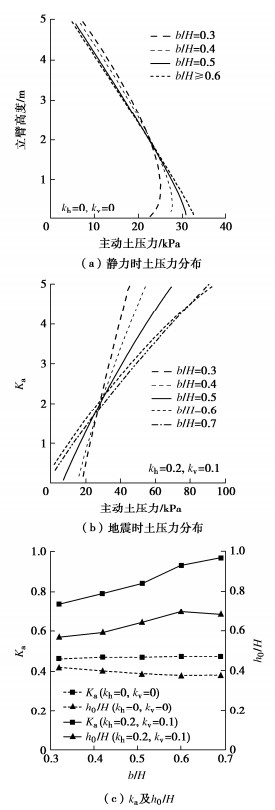
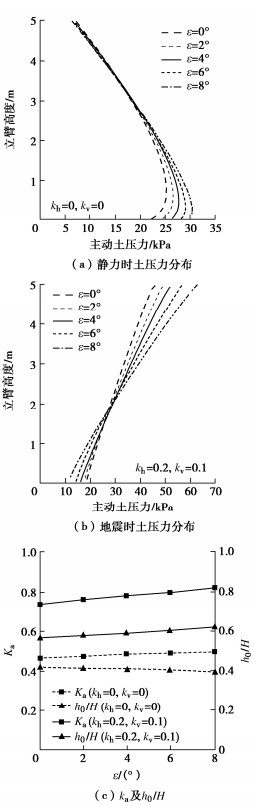
摘要: 为确定悬臂式挡土墙立臂的地震主动土压力,针对墙后填土的5种可能失稳破坏模式,基于对数螺旋式滑裂面形态,采用极限分析上限定理与拟静力法推导了作用于假想坦墙背上的地震土压力合力;在此基础上,对坦墙背后滑楔体、立臂与坦墙背之间的土体分别采用斜条分与水平条分法,并通过土压力合力的上限解对坦墙背上的土压应力进行修正,进而求得立臂上的土压力分布。实例分析表明,立臂静土压力沿深度分布呈顶点位于下部的抛物线模式;地震土压力分布一般呈非线性递减模式,计算值与试验值有良好的一致性;两种工况下合力作用点分别位于立臂下半段与上半段。参数分析显示,水平地震影响系数、踵板宽度和立臂倾角的增加均使立臂中上部地震主动土压力显著增大;地震条件下增长踵板宽度会导致立臂受力增加。在强震条件下,本法得到的立臂土压力比铁路规范法的结果高出约9%~14%,立臂底端弯矩更显著高于规范法结果,规范法进行强震条件下悬臂墙的抗震设计可能偏于不安全。Abstract: In order to determine the seismic active earth pressures on the stem of a cantilever wall, the resultant of the earth pressures on the assumed plane wall back is firstly derived using the upper-bound limit analysis and the pseudo-static method for five types of potential failure modes based on the log-spiral slip surface. The oblique and horizontal slice methods are secondly adopted respectively for the slide wedge mass and the local soils between the stem and the plane wall back to determine the earth pressure distribution on the stem, in which the earth pressure on the plane wall back are calibrated by the upper bound solution for the resultant of earth pressures. Some examples show that the proposed distribution of the earth pressures on the stem with depth takes on a parabolic profile with the peak point on the lower segment of the stem under the static condition, whereas it presents a nonlinear decreasing mode fairly identical with the test results under the seismic condition. The application point of the resultant is located on the lower and upper segments of the stem under the static and seismic conditions, respectively. The parameter study shows that the increase of horizontal seismic coefficient, heel plate width and stem back inclination induces a significant increase of the seismic active earth pressures on the middle and upper segments of the stem. Under the seismic condition, broadening the width of heel plate can cause the increase of the stresses on the stem. In particular, the proposed earth pressures on the stem are 9%~14% higher than those by China's code for design of retaining structures of railway earth works under strong earthquakes, and the proposed bending moments at the stem bottom are noticeably greater than those by the above code, which naturally means the Norm is not safely suitable for the aseismic design under strong earthquakes.
-
0. 引言
近年来,中国已建成多座高坝大库,库区水位变动带的滑坡现象也大量出现,造成了严重的人员伤亡和财产损失,库区边坡安全面临重大挑战。
抗滑桩-锚杆组合结构是一种比传统抗滑桩受力更加合理的加固结构,近年来已经在工程中得到广泛应用,但其加固机理以及安全性评价研究仍落后于工程实践,并缺乏完善的设计规范[1]。刘英朴等[2]提出了锚杆抗滑桩内力计算的初参数法,Dong等[3]基于多种破坏模式,建立了同时考虑锚杆预应力和桩体影响的复合材料结构稳定性分析模型;Wang等[4]研究了锚杆抗滑桩的内力分布与组合加固机理,Huang等[5]研究了锚杆抗滑桩在地震响应下的破坏模式;郑颖人等[6]通过极限平衡法计算了水位下降时边坡的安全系数;Liu等[7-8]进行了水位变动条件下普通抗滑桩的离心模型试验。现有研究大多关注于滑坡过程中桩的响应情况,缺乏对桩土耦合规律的认识,特别是很少涉及水位变动条件下锚杆-桩-土的相互作用机制。
本文采用离心模型试验方法,再现了水位下降时锚杆抗滑桩组合结构加固黏性土坡的变形和破坏过程。测量了土坡的位移变化,分析了土坡的破坏形式,探讨了锚杆抗滑桩结构的加固机理。
1. 试验设备与条件
1.1 设备
离心模型试验采用清华大学土工离心机进行。该离心机的有效半径为2 m,最大加载能力为50g·t,最大离心加速度为250g。试验使用的铝合金模型箱尺寸为60 cm×20 cm×50 cm(长×宽×高),模型箱一侧装有有机厚玻璃,并在该侧固定摄像头,对试验过程中水位变化和边坡变形情况进行拍摄。模型箱连接有输水管道和排水管道,可以在离心过程中远程控制水位升降[9]。
1.2 非接触位移测量系统
本试验采用基于光信号的高质量图像采集与位移测量系统记录离心场中边坡与结构的位移[10]。基于图像系列,通过像素灰度相关系数分析捕捉标定点,可以测量模型任意点任意时刻的位移[10]。相较于传感器测量方法,非接触位移测量系统可以避免仪器布设对试验模型的干扰,同时可以得到模型侧面任意点的位移场。
需要指出,本文测量结果均以模型尺寸表示。位移在水平方向以指向坡外为正、在竖直方向以向下为正。
1.3 试验模型
试验分别针对锚杆抗滑桩加固土坡和未加固的素土坡进行。图 1,2分别给出了加固土坡的模型照片和结构示意图。两种土坡除了锚杆抗滑桩加固结构外,其他条件均相同。土坡采用黏性土制备,土的干密度为1.6 g/cm3,初始含水率为18%。饱和黏性土的内摩擦角为30°,黏聚强度为27 kPa。坡高23 cm,坡度0.8∶1,坡顶宽18 cm。制样时按干密度控制分6层击实,其中底层为厚7.5 cm的水平垫层,用以防止边坡底面与模型箱直接接触产生的摩擦力干扰试验。加固土坡底层击实后摆放抗滑桩,第二层击实后插入锚杆末端,之后逐层击实。在土坡紧贴有机玻璃侧嵌入随机分布的白色泡沫片(图 1),以形成具有随机性分布的较大像素灰度差的测量区域,便于进行基于相关分析的位移测量。完成土坡制样后在模型箱侧壁均匀涂抹凡士林以减小摩擦,进而减小边界效应对试验的影响。
本试验采用方形钢管作为模型桩,桩高200 mm,截面正方形边长15 mm。材料弹性模量为70 GPa,泊松比为0.3。加固土坡中共排布4根桩,间隔为67 mm。特别地,为了真实反映模型剖面的情况,与模型箱两侧壁接触部分采用半截面桩。锚杆采用外径3 mm、长320 mm、表面刻有螺纹的铝制细杆。锚杆铰接于距桩顶23 mm处。
1.4 试验过程
将模型箱放入离心机后,以10g为梯度逐级增加离心加速度,待每一级土坡沉降稳定后再增加下一级加速度,直至达到50g。土坡在50g离心场沉降稳定后,以50 mm为梯度从0 mm开始增加水位,待每一级水位稳定(即充分渗流)后再增加下一级水位直至水位达到200 mm。此时等待15分钟确保水充分渗流进入边坡。之后打开排水口,水位从200 mm降至0 mm。降水过程进行全程录像。
2. 破坏特性
图 3给出了素土坡与加固土坡滑裂面及其发展过程,可以发现锚杆抗滑桩结构改变了滑裂面连续性。加固土坡的滑裂面在桩左侧从坡顶延续至桩脚;在桩右侧从桩中下部延续至坡脚。
图 4为加固土坡沿滑裂面两侧连线垂直于滑裂面切线的一组点对的切向相对位移ds和法向相对位移dn随水位的变化(点对的位置见图 3)。可以观察到,该点对的切向相对位移在某一水位之后快速增加,该水位可认为是土坡在这一位置的破坏水位。其他点对的相对位移也有相同的规律,破坏水位在图 3中点对旁的括号中标出。可以发现,素土坡的破坏过程为沿滑裂面从上至下破坏,加固土坡在桩两侧分别沿各自的滑裂面从上至下破坏。同时,加固土坡破坏水位低于素土坡,说明锚杆抗滑桩加固后边坡能够抵抗更大幅度的水位下降,边坡安全系数提高。
3. 机理分析
3.1 破坏机理
图 5给出素土坡和加固土坡的最大剪应变水平分布。两土坡最大剪应变都在滑裂面处达到极大值。并且可以发现,加固土坡在破坏前(如水位为80 mm时)滑裂面附近已经出现较大应变,说明土坡出现了变形局部化,并导致了局部破坏;而另一方面,在破坏后(如水位为60 mm时)最大剪应变继续增加,说明局部破坏进一步增强了其附近的变形局部化程度,破坏过程与变形局部化呈现相互耦合的特点。
3.2 加固机理
对比图 5(a),(b)可以发现,加固土坡最大剪应变的最值明显小于素土坡。同时注意到素土坡的高剪应变集中分布在一个区间内,而加固土坡的高剪应变区较为均匀。这说明锚杆抗滑桩通过减小土坡的变形局部化程度、均匀化土坡变形以增强边坡稳定性。另一方面,考虑两土坡剪应变分布随水位的变化可以发现:在素土坡中,破坏前剪应变较小,破坏时剪应变快速增大并在破坏后继续增大;而在加固土坡中,破坏前后剪应变变化幅度不大。这一现象说明素土坡破坏呈现突变性,而加固土坡在破坏前已经具有变形局部化现象,体现了渐进破坏的特点。
图 6给出了素土坡与加固土坡在桩内侧附近的水平位移的竖向分布。可以发现,素土坡的位移在下部几乎为0,在滑裂面处发生陡增,在上部基本不变。同时,由于抗滑桩是刚性结构,在转动过程中位移随高程线性分布,所以加固土坡桩内侧土体的水平位移也随高程近似线性分布,且相比素土坡显著减小。该现象说明抗滑桩改变了土体的位移大小与分布,通过限制桩侧土体滑动起到加固作用。
图 7给出了水位h=40 mm时两土坡水平位移水平分布的对比图。可以看出,素土坡与加固土坡的水平位移在坡较深处都基本为0,在某一点后开始从零增加(由图 7中虚线标出),该位置反映出坡体破坏的最深影响位置。对比两图可以发现,在较高高程处素土坡的最深影响位置显著深于加固土坡,而在较低高程处最深影响位置整体后移,且加固土坡的最深影响位置深于素土坡。这一现象说明锚杆抗滑桩结构改变了坡体的位移分布。坡体上部经加固后受破坏影响小,而坡体下部由于锚杆结构将力传至土体深层而加深了坡体破坏的最深影响位置,反映出锚杆抗滑桩使整个坡体位移分布更加均匀。
综合来看,锚杆抗滑桩结构降低了边坡的破坏水位,推迟了破坏过程,限制了桩侧土体滑动,进而减小了滑动体位移,使整个边坡抗滑力增加,安全系数提高。
4. 结论
本文进行了水位下降条件下素土坡与锚杆抗滑桩组合结构加固边坡的离心模型试验,测量了水位下降过程中边坡和加固结构的位移,分析了土坡的变形破坏特性和组合结构加固机理,得到了以下4点结论。
(1)锚杆抗滑桩加固结构减小了滑动体的位移,推迟了土坡的破坏过程,提高了土坡的稳定性。
(2)锚杆抗滑桩改变了滑裂面的位置和连续性,增强了坡体破坏的渐进性。
(3)水位下降条件下锚杆抗滑桩加固土坡的局部破坏与变形局部化的过程表现出显著的耦合特性。
(4)锚杆抗滑桩使得土坡变形均匀化,限制了桩侧土体的滑动,提高了土坡的安全系数。
-
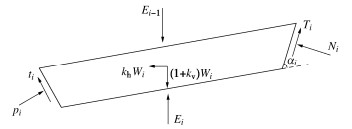
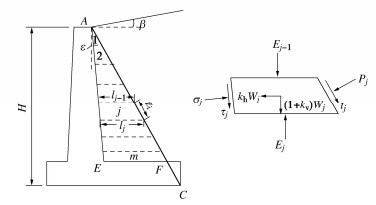
图 2 模式Ⅰ相应的旋转破坏机构
Figure 2. Rotational failure mechanism of Mode Ⅰ in Fig. 1
-
[1] 铁路路基支挡结构设计规范: TB 10025—2019[S]. 北京: 中国铁道出版社, 2019. Code for Design of Retaining Structures of Railway Earthworks: TB 10025—2019[S]. Beijing: China Railway Publishing House, 2019. (in Chinese)
[2] 李海光. 新型支挡结构设计与工程实例[M]. 2版. 北京: 人民交通出版社, 2011. LI Haiguang. Design and Engineering Example of New Retaining Structure[M]. 2nd ed. Beijing: China Communications Press, 2011. (in Chinese)
[3] BARGHOUTHI A F. Active earth pressure on walls with base projection[J]. Journal of Geotechnical Engineering, 1990, 116(10): 1570-1575. doi: 10.1061/(ASCE)0733-9410(1990)116:10(1570)
[4] GRECO V R. Analytical active earth thrust on cantilever walls with short heel[J]. Canadian Geotechnical Journal, 2008, 45(12): 1649-1658. doi: 10.1139/T08-078
[5] GRECO V R. Seismic active thrust on cantilever walls with short heel[J]. Soil Dynamics and Earthquake Engineering, 2009, 29(2): 249-252. doi: 10.1016/j.soildyn.2008.03.003
[6] KARKANAKI A R, GANJIAN N, ASKARI F. Stability analysis and design of cantilever retaining walls with regard to possible failure mechanisms: an upper bound limit analysis approach[J]. Geotechnical and Geological Engineering, 2017, 35(3): 1079-1092. doi: 10.1007/s10706-017-0164-5
[7] ALPER KAMILOĞLU H, SADOĞLU E. Experimental and theoretical investigation of short- and long-heel cases of cantilever retaining walls in active state[J]. International Journal of Geomechanics, 2019, 19(5): 1-17.
[8] CHEN F Q, ZHANG Y B, LIN Y J, et al. Active earth pressure against inverted T-type retaining walls under translation mode[J]. International Journal of Geomechanics, 2021, 21(6): 04021077. doi: 10.1061/(ASCE)GM.1943-5622.0002013
[9] EVANGELISTA A, SCOTTO D S A, SIMONELLI A L. Evaluation of pseudostatic active earth pressure coefficient of cantilever retaining walls[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(11): 1119-1128. doi: 10.1016/j.soildyn.2010.06.018
[10] SCOTTO DI SANTOLO A, EVANGELISTA A. Dynamic active earth pressure on cantilever retaining walls[J]. Computers and Geotechnics, 2011, 38(8): 1041-1051. doi: 10.1016/j.compgeo.2011.07.015
[11] 李志浩, 肖世国. 地震条件下悬臂式挡墙主动土压力的极限分析方法[J]. 中国地质灾害与防治学报, 2020, 31(5): 79-87. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDH202005012.htm LI Zhihao, XIAO Shiguo. Limit analysis method of active earth pressure on cantilever retaining wall subjected to earthquake[J]. The Chinese Journal of Geological Hazard and Control, 2020, 31(5): 79-87. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDH202005012.htm
[12] 戴自航, 林智勇, 郑也平, 等. L型挡土墙主动土压力计算的基底摩擦系数折减有限元法[J]. 岩土工程学报, 2009, 31(4): 508-514. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract13209.shtml DAI Zihang, LIN Zhiyong, ZHENG Yeping, et al. Finite element method for computations of active earth pressures acting on L-shaped retaining walls with reduced friction coefficients of base bottoms[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(4): 508-514. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract13209.shtml
[13] CHUGHASHOK K, LABUZJOSEPH F. Numerical simulation of an instrumented cantilever retaining wall[J]. Canadian Geotechnical Journal, 2011, 48(9): 1303-1313. doi: 10.1139/t11-037
[14] 高洪梅, 卜春尧, 王志华, 等. 回填EPS混合土的防滑悬臂式挡墙地震稳定性分析[J]. 岩土工程学报, 2017, 39(12): 2278-2286. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17241.shtml GAO Hongmei, BU Chunyao, WANG Zhihua, et al. Seismic stability of anti-sliding cantilever retaining wall with EPS composite soil[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(12): 2278-2286. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17241.shtml
[15] JO S B, HA J G, LEE J S, et al. Evaluation of the seismic earth pressure for inverted T-shape stiff retaining wall in cohesionless soils via dynamic centrifuge[J]. Soil Dynamics and Earthquake Engineering, 2017, 92: 345-357. doi: 10.1016/j.soildyn.2016.10.009
[16] 肖世国. 似土质边(滑)坡抗滑桩后滑坡推力分布模式的近似理论解析[J]. 岩土工程学报, 2010, 32(1): 120-123. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract11907.shtml XIAO Shiguo. Approximate theoretical solution of distribution modes of landslide thrust on anti-sliding piles in soil-like slopes or landslides[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(1): 120-123. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract11907.shtml
[17] GERAILI MIKOLA R, CANDIA G, SITAR N. Seismic earth pressures on retaining structures and basement walls in cohesionless soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2016, 142(10): 1–9.
[18] CANADIAN GEOTECHNICAL SOCIETY. Canadian Foundation Engineering Manual[M]. Richmond: BiTech Publisher Ltd., 2006.
[19] XIAO S G, YAN Y P, XIA P. General solution for active earth pressure on rigid walls under strip surcharge on retained soils using variational method[J]. International Journal of Civil Engineering, 2021, 19: 881–896. doi: 10.1007/s40999-020-00579-4
[20] 陈建功, 胡日成, 许明. 考虑合力作用点位置的主动土压力计算[J]. 工程力学, 2016, 33(11): 132-139. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201611015.htm CHEN Jiangong, HU Richeng, XU Ming. Active earth pressure calculation considering force point location[J]. Engineering Mechanics, 2016, 33(11): 132-139. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201611015.htm
[21] CHEN W F. Limit analysis and soil plasticity[M]. Amsterdam; New York: Elsevier Scientific Pub. Co. 1975.
[22] LIN Y L, LENG W M, YANG G L, et al. Seismic active earth pressure of cohesive-frictional soil on retaining wall based on a slice analysis method[J]. Soil Dynamics and Earthquake Engineering, 2015, 70: 133-147.
[23] 李傲赢. 加筋悬臂式复合支挡结构振动台模型试验研究[D]. 成都: 西南交通大学, 2019. LI Aoying. Study of Shaking Table Test for Reinforced Cantilever Composite Retaining Structure[D]. Chengdu: Southwest Jiaotong University, 2019. (in Chinese)
[24] BENTLER J G, LABUZ J F. Performance of a cantilever retaining wall[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(8): 1062-1070.
[25] 朱宏伟, 姚令侃, 赖军. 基于性能的重力式挡墙地震易损性分析[J]. 岩土工程学报, 2020, 42(1): 150-157. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18106.shtml ZHU Hongwei, YAO Lingkan, LAI Jun. Seismic vulnerability assessment of gravity retaining walls based on performance[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(1): 150-157. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18106.shtml
-
其他相关附件




 下载:
下载: