0.   引言

高孔隙率砂岩是油气藏、地下水、CO₂地质封存等的重要储层,对其在不同应力条件下变形破坏模式的研究具有重要意义。研究表明,在三轴压缩试验中,高孔隙率砂岩（孔隙率超过13%）在低围压下呈剪切破坏模式,随着围压升高逐步向压缩破坏模式转变,此过程伴随着变形带与最大主应力方向夹角的逐步增大^[1-4]。研究者针对这一现象,开展了许多理论及数值模拟研究,解释围压与变形带角度之间的关系^[5-7]。同时,基于微观力学的离散元（DEM）模型,可以在刻画变形带角度随围压变化的同时,对不同类型变形带产生的微观机理进行直观的分析^[8-9]。

钻孔是油气藏开采、地下空间利用等工程活动中的常用手段,对其稳定性的研究是岩土工程和石油工程领域的一个经典课题^[10-11]。传统上,有限元方法（FEM）被广泛用于钻孔稳定性的分析^[12-13]；近年来,出于对微观破坏机理的关注,DEM也常被用于不同钻孔破坏类型的数值分析^[14-16]。特别值得一提的是,为研究钻孔的破坏机理,Haimson等对花岗岩、灰岩与砂岩等开展了一系列的钻孔模型试验,对不同类型岩石中由膨胀、剪切、压缩等机理控制的钻孔破坏进行了系统的试验研究^[17-19]。

需要指出,即使是在试验条件受到良好控制的单元试验（如三轴压缩试验）中,试样中也可能出现由材料性质的不均匀或应力的不均匀分布等导致的复杂破坏模式^[20]。Dresen等^[21]在对高孔隙率砂岩的钻孔试验中,通过某试样的显微照片也观察到了破坏机理随应力条件演化的现象。考虑到高孔隙率砂岩的储层属性,在对其饱和试样进行加载的过程中,孔隙液体压力的变化也可能通过影响有效围压而导致破坏模式的演化^[22]。然而,现有研究多重视对复杂破坏模式的宏观分类,强调边界条件、应力状态、材料性质等因素对试样整体破坏模式的影响；对同一试样中破坏模式随加载过程而演化的现象尚缺乏足够的研究。

事实上,针对高孔隙率砂岩在双轴压缩试验、钻孔稳定性问题、水岩耦合问题等不同边值问题中,不同类型变形带的产生、发展及其微观机理,笔者已经通过采用一种基于有限元与离散元分层耦合（FEM×DEM）的多尺度模拟方法进行了系统性的研究^[22-25]。以此为基础,本文着眼同一种高孔隙率砂岩材料,对其在不同边值问题中变形带演化特征的共性与不同进行针对性的对比分析,讨论边值问题中复杂破坏模式的可能成因。本文将首先简要介绍基于FEM×DEM的高孔隙率砂岩多尺度模拟方法；继而通过双轴压缩试验呈现高孔隙率砂岩中具备显著几何特征的两种典型破坏模式；随后通过钻孔稳定性问题与水岩耦合问题的典型算例,展现两种典型破坏模式间随加载过程发生的相互演化；最后通过对不同边值问题中材料应力路径的对比分析,探讨模式演化中的控制因素。

1.   高孔隙率砂岩多尺度模拟方法

1.1   FEM×DEM多尺度模拟方法

有限元与离散元分层耦合（FEM×DEM）的多尺度模拟方法,通过有限元方法求解宏观尺度的边值问题；在有限元网格的每个高斯积分点上附着一个由离散颗粒组成的代表性单元体（RVE）,以该高斯点的变形梯度作为边界条件,通过离散元计算,获取材料的应力信息并反馈给有限元,以此取代传统有限元方法中的唯象本构模型。同时,将基于RVE中颗粒接触的均化应力视作有效应力,利用著名的$u$-p公式与有效应力原理,本方法亦可以扩展至水岩耦合问题。有关该方法的详细公式及算法可以参考文献[23, 26～28],在此不做赘述。

岩土工程中常见的砂土、砂岩等均为颗粒材料,人们广泛采用基于微观力学的离散元模型研究其宏观力学特征的微观机理^[29-31]。然而,采用离散元方法如实的模拟颗粒材料,需要极大的颗粒数量,即意味着需要极大的计算资源；同时离散元方法在大尺度试样的制备和边界条件的施加等方面也面临着一定的问题。FEM×DEM多尺度模拟方法在微观尺度上采用基于微观力学的离散元模型,尊重颗粒材料的离散属性；在宏观尺度上采用有限元模型,便于初始状态的准备与边界条件的施加,可以方便地应用于岩土工程边值问题,提供跨尺度的分析视角；采用包含几百个颗粒（二维情况）的RVE,即可较好的表征材料的力学属性,通过并行计算同时求解多个RVE,极大的提高了计算效率。

1.2   高孔隙率颗粒砂岩的RVE

在FEM×DEM多尺度模拟方法中,通过离散元计算直接建立颗粒材料的本构关系,此过程中RVE作为真实材料的数值“替身”,接受微观加载、输出应力信息。因此,构建恰当的RVE在多尺度模拟中至关重要。同时,考虑到离散元模型可以反映颗粒材料对应力历史与应力路径等的敏感性,RVE在构建完成后,即可作为真实材料的数值“替身”,应用于各种类型的边值问题中,分析该种材料在不同岩土工程问题中的力学表现。

本文以高孔隙率颗粒砂岩为研究对象,采用移除特定颗粒的方法形成高孔隙率结构,并在移除颗粒前在颗粒间施加胶结,以保持结构的稳定。为保持模型的简洁性,在颗粒间采用线性接触模型,即粒间法向与切向接触刚度分别为$k_{\text{n}}=E_{\text{c}}\times \frac{2r_1{r}_2}{r_1+r_2}$与$k_{\text{t}}={\nu }_{\text{c}}{k}_{\text{n}}$,其中,r₁,r₂为2个颗粒的半径,$E_{\text{c}}$,${\nu }_{\text{c}}$为接触参数；粒间胶结采用点胶结模型,通过最大拉力$F_{\text{n}}^{\max }=$ $c\min {(r_1,r_2)}^2$与最大切向力$F_{\text{t}}^{\max }=c\min (r_1,r_2)+$ $F_{\text{n}}\tan (\varphi )$控制胶结的破坏,其中,c为胶结强度参数,$\varphi$为内摩擦角；在任一阈值达到后,胶结即发生破坏,之后的颗粒间接触由库伦摩擦力控制,即$F_{\text{t}}^{}$≤ $F_{\text{n}}\tan (\varphi )$。高孔隙率RVE的详细制备流程与接触模型等可以参考文献[22～24]。

图1绘制了本研究所采用的高孔隙率RVE,其中红蓝短线表示颗粒间的法向接触力,红色表示压力而蓝色表示拉力,其粗细与力的大小成正比,类似的RVE结构在文献[22, 24, 32]中均有采用。该RVE中颗粒半径在0.2～0.3 mm线性分布,孔隙率为0.326。通过模型参数校准,采用E_c=950 GPa,${\nu }_{\text{c}}$=1.0,c=6.8 GPa,$\varphi$=35°,其单轴压缩强度为24.9 MPa,杨氏模型为11.0 GPa,符合发育压缩带的典型高孔隙率砂岩的力学特征^{[19, 33]}。该高孔隙率RVE将被用于双轴压缩试验、钻孔稳定性分析及水岩耦合问题的多尺度模拟,探究同一种材料在不同边值问题中破坏模式的演化规律。

图  1  高孔隙率砂岩RVE的微观结构^[22]

Figure  1.  Microstructure of RVEs for high-porosity sandstones

下载: 全尺寸图片 幻灯片

2.   双轴压缩试验中破坏模式的演化

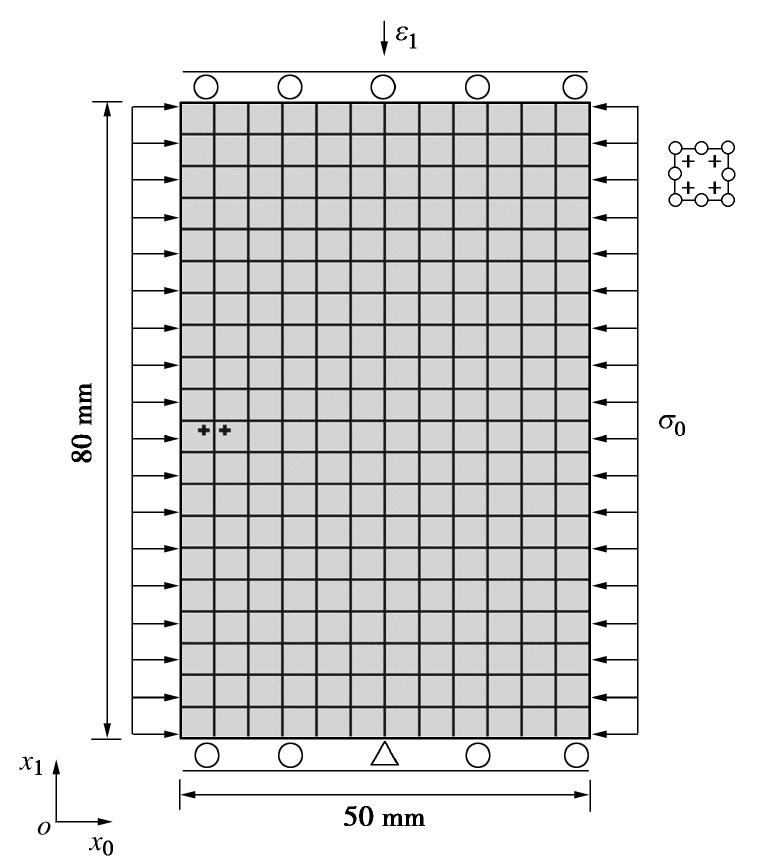
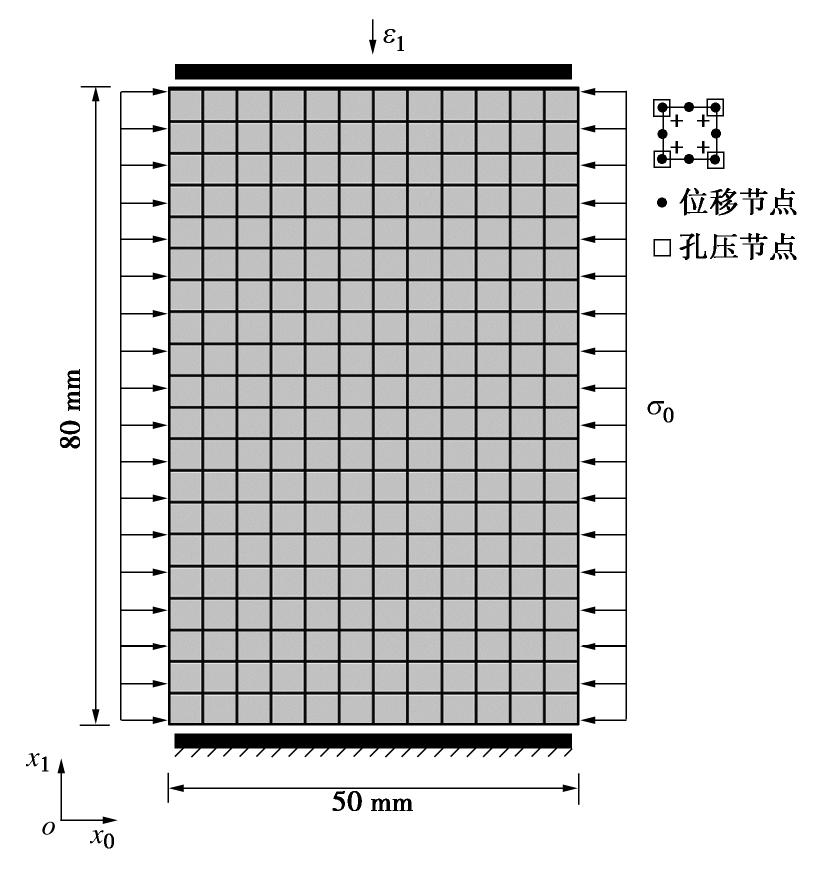
双轴压缩试验是岩土工程中的经典试验条件,本研究首先采用双轴压缩试验,呈现高孔隙率砂岩中具备显著几何特征的两种典型破坏模式。本节的模拟中只包含颗粒系统,等效于水岩耦合问题中的排水条件。有限元网格及边界条件采用与文献[22, 32]中类似的方案（如图2所示）,试样尺寸为50 mm×80 mm,划分为12×20个8节点矩形单元,每个单元具有4个高斯积分点；试样上下边界为光滑边界条件,底边中点固定；在双轴压缩试验过程中,顶部边界以恒定速率向下移动,左右边界上围压保持不变。图2中两个黑色十字标示了预置的具有较低胶结强度（0.8倍正常值,即c=5.44 GPa）的软弱点,以诱发变形带的产生。

图  2  双轴压缩试验的有限元网格及边界条件

Figure  2.  Mesh discretization and boundary conditions for biaxial compression tests

下载: 全尺寸图片 幻灯片

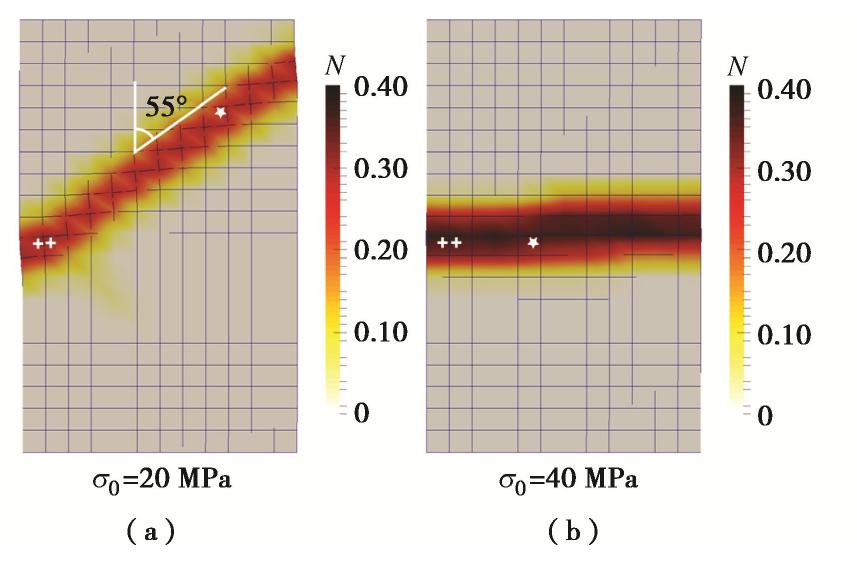
高孔隙率砂岩破坏模式随围压增加从剪切带向压缩带演化的现象已经为人们所熟知。Tembe 等^[2]研究了Diemelstadt砂岩随着围压增加,破坏模式从膨胀剪切带逐步演化为压缩剪切带、高角度剪切带及压缩带的过程。Wu等^[32]通过多尺度模拟研究了从膨胀带到剪切带及压缩带的全谱系变形带。本文以20 MPa与40 MPa两个围压为例,展示变形带与最大主应力${\sigma }_1$方向夹角随围压增大而增大的现象。图3画出了两个算例在2%轴向应变时的归一化胶结破坏数N。可以看出,围压为20 MPa时,变形带与${\sigma }_1$呈55°夹角,该变形带按Wu等^[32]基于微观变形特征的分类应属于剪切强化的压缩带,而按照Tembe等^[2]基于变形带角度的分类则应属于高角度剪切带。围压为40 MPa时,变形带呈水平状,与${\sigma }_1$夹角为90°,在两种分类体系中均属于纯压缩带。

图  3  双轴压缩试验中砂岩破坏模式随围压的演化

Figure  3.  Evolution of failure mode with confining pressure in biaxial compression tests

下载: 全尺寸图片 幻灯片

本文讨论的围压范围较小,变形带类型跨度不大,为便于对变形带演化现象进行直观的描述,采用基于变形带角度的定性分类方式,将与${\sigma }_1$方向夹角接近90°的变形带称为压缩带,角度显著小于90°的统称为含剪切变形带。随着围压增加,在双轴压缩试验中破坏模式从含剪切变形带向压缩带演化。下文将通过对比图3中不同变形带内典型RVE（白星）的应力路径,对破坏模式产生差异的原因进行分析。

3.   钻孔稳定性问题中破坏模式的演化

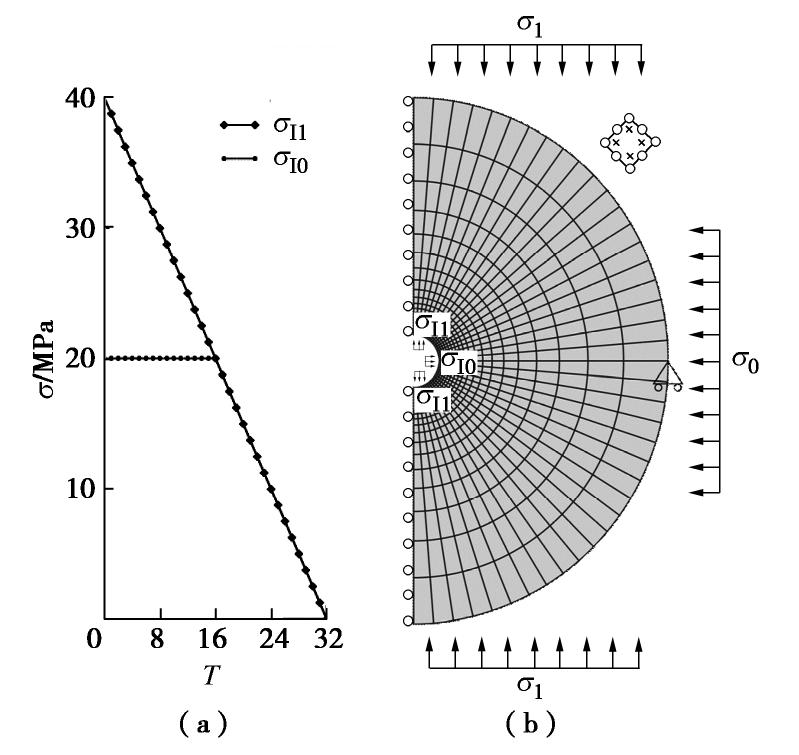
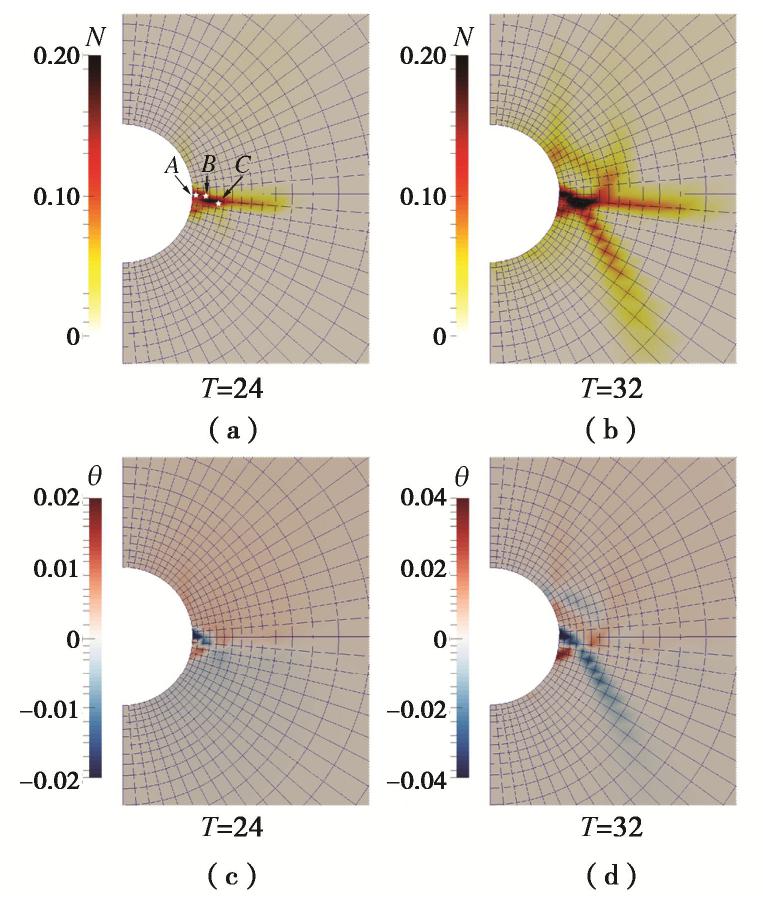
高孔隙率砂岩是油气藏、地下水等的重要储层,相关工程开展过程中涉及钻孔问题,分析钻孔的稳定性至关重要。Haimson^[17]对高孔隙率砂岩中的钻孔崩落问题进行了分析,指出剪切带与压缩带是其中两种重要的破坏模式。Wu等^[24]对高孔隙率砂岩中钻孔周围发育的剪切带与压缩带进行了多尺度分析,提出了剪切带破坏模式、压缩带破坏模式和两者兼具的混合破坏模式。在此,将通过一个钻孔周围变形带演化的算例,展现钻孔周围破坏模式的复杂性。为加快计算速度,依据问题的对称性,选取半空间进行分析,有限元网格划分及边界条件的施加如图4（b）所示。以内边界上的支撑应力（${\sigma }_{\text{I0}}$,${\sigma }_{\text{I1}}$）代替钻孔内的原岩,并通过逐步降低支撑力来模拟钻孔的过程。初始状态${\sigma }_1={\sigma }_{\text{I1}}=40$ MPa,${\sigma }_0={\sigma }_{\text{I0}}=20$ MPa；支撑力的降低采用一种简单的应力路径,如图4（a）所示,同时${\sigma }_0$,${\sigma }_1$保持不变。鉴于岩土材料力学行为对应力路径的敏感性,卸荷路径将影响钻孔周围的破坏模式,系统性的分析参见文献[24]。需要指出,本研究中进行的分析的均为准静态分析,不涉及动态过程,此处的T为加载步数而非实际时间。

图  4  钻孔问题的有限元网格及边界条件

Figure  4.  Finite mesh and boundary conditions for borehole stability problem

下载: 全尺寸图片 幻灯片

随着支撑力的降低,钻孔周围出现由钻孔壁向远端发展的破坏区。钻孔壁附近（图5中点A处）首先形成剪切破坏区；随着支撑力的进一步降低,在剪切破坏区的尖端发展出了压缩带破坏模式。图5（a）展示了T = 24时的破坏模式,靠近钻孔壁的“V”形破坏区为剪切破坏区,而远离钻孔壁的破坏区与${\sigma }_1$接近垂直,为压缩破坏区。图5（c）所示的颗粒平均转动角$\theta$可以支撑这一观点,“V”形破坏区的两臂呈现出方向相反的颗粒转动,符合共轭剪切带的特征；而由“V”形尖端延伸出的破坏区中无明显的颗粒转动,符合压缩带的特征。内壁支撑力减为0的最终状态如图5（b）,（d）所示,各变形带进一步发展,呈现出两条清晰的共轭剪切带和一条压缩带。破坏模式从剪切破坏向压缩破坏演化的内在机理将在下文通过图5（a）中A,B,C点的应力路径进行详细分析。

图  5  钻孔稳定性问题中高孔隙率砂岩破坏模式的演化

Figure  5.  Evolution of failure mode around a borehole in high-porosity sandstones

下载: 全尺寸图片 幻灯片

4.   水岩耦合问题中破坏模式的演化

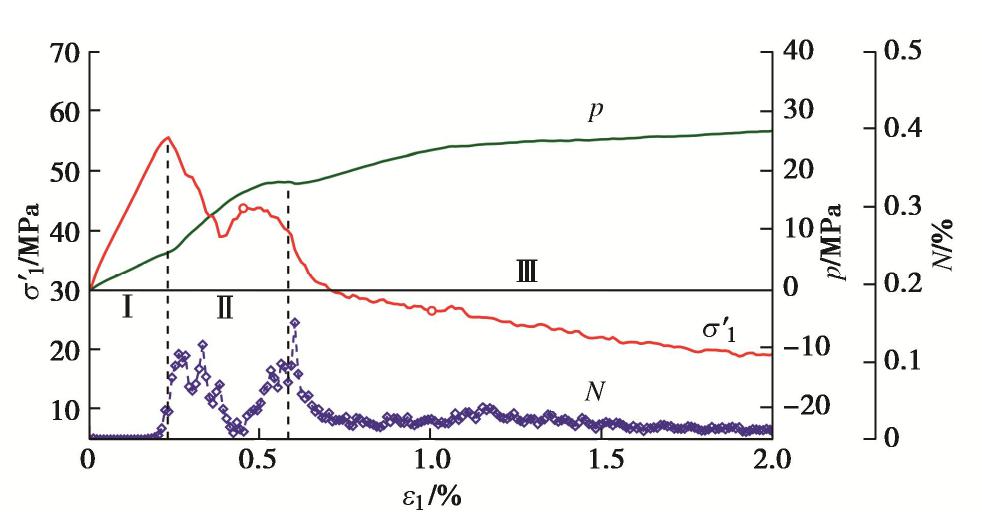
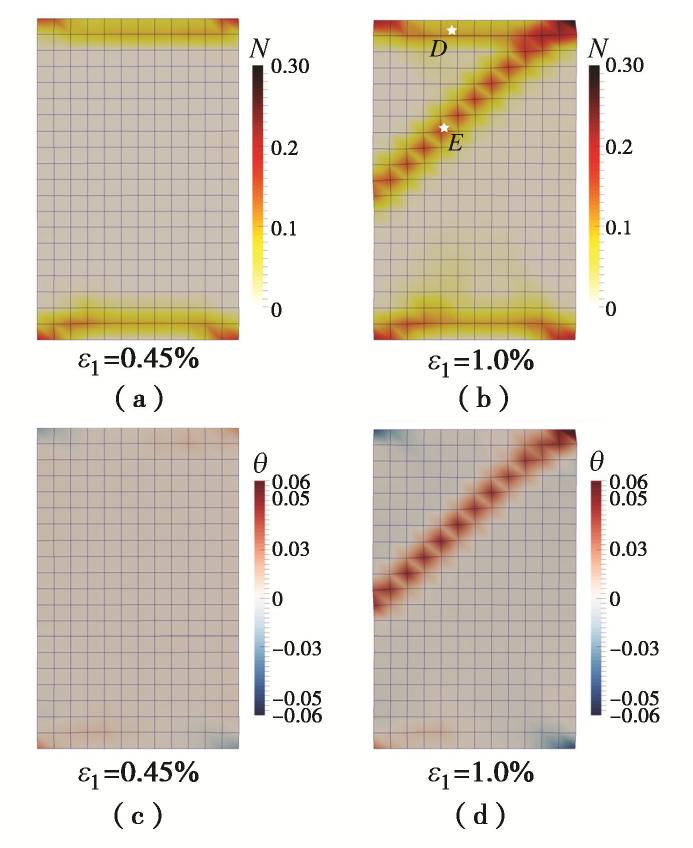
作为重要的储层岩石,高孔隙率砂岩中岩石与流体的耦合过程对破坏模式的影响值得注意。本文中的水岩耦合问题采用与双轴压缩问题相同的试样及网格（图6）,网格中的每个单元含有8个位移节点与4个孔压节点。试样的上下边界为粗糙边界,限制水平位移,类似于试验中润滑不畅的加载板。试样四周均为不排水边界条件,但试样内为局部排水条件。图7,8分别呈现了总围压30 MPa情况下,试样的宏观力学响应及破坏模式的演化。从图7可以看出,在不排水双轴压缩试验中,一个显著的特征是孔压p随轴向应变的增加逐渐升高并趋于稳定,从而引起有效围压（${{\sigma }^{\prime }}_0={\sigma }_0-p$）的降低,影响破坏模式的发展。基于宏观响应特征及局部变量的分布图,可以将试样的变形破坏过程粗略地分为3个阶段：①Ⅰ弹性阶段；②Ⅱ压缩带阶段；③Ⅲ含剪切变形带阶段。Ⅱ,Ⅲ阶段试样的典型破坏模式如图8所示：阶段Ⅱ以压缩带为主导,在试样顶底两端均出现了与${\sigma }_1$方向垂直的压缩带；随着孔压的进一步积累,阶段Ⅲ演化为受含剪切变形带控制的破坏模式。下文将通过对典型RVE（图8中D,E点）有效应力路径的分析,揭示破坏模式演化的机理。

图  6  水岩耦合问题的有限元网格及边界条件

Figure  6.  Finite mesh and boundary conditions for hydro-mechanical problem

下载: 全尺寸图片 幻灯片

图  7  水岩耦合问题中有效轴向应力${{\sigma }^{\prime }}_1$、孔压p、归一化胶结破坏数N随轴向应变${\epsilon }_1$的演化

Figure  7.  Evolution of effective axial stress ${{\sigma }^{\prime }}_1$, pore pressurep, normalized debonding numberN with axial strain ${\epsilon }_1$ in hydro-mechanical problem of high-porosity sandstones

下载: 全尺寸图片 幻灯片

图  8  水岩耦合问题中高孔隙率砂岩破坏模式的演化

Figure  8.  Evolution of failure mode in hydro-mechanical problem of high-porosity sandstones

下载: 全尺寸图片 幻灯片

5.   平均应力在模式演化中的控制作用

前述三节展示了高孔隙率砂岩在双轴压缩试验、钻孔问题与水岩耦合问题中破坏模式的演化。在双轴压缩试验中,随着围压的增加破坏模式从含剪切变形带演化为压缩带；在钻孔问题中,随着钻孔内壁支撑力的降低,试样首先表现出剪切破坏的特征,进而演化为压缩破坏模式；在水岩耦合问题中,则首先表现出压缩带的破坏模式,随着轴向加载逐渐演化为含剪切变形带。人们对三轴压缩试验中破坏模式的研究较为充分,通过将不同围压下试样发生破坏时的应力状态绘制在由（有效）平均应力P和偏应力Q组成的应力平面上,发现破坏模式随围压增加由剪切主导向压缩主导的演化过程中伴随着P的增加^[2-3]。同时,通过对变形带内RVE在P-Q平面上应力路径的分析,可以有效的解释不同破坏模式的产生^{[22, 24]}。本节将通过对不同边值问题中变形带内RVE应力路径的对比分析,探究不同边值问题中应力路径的特点及其对破坏模式的影响。

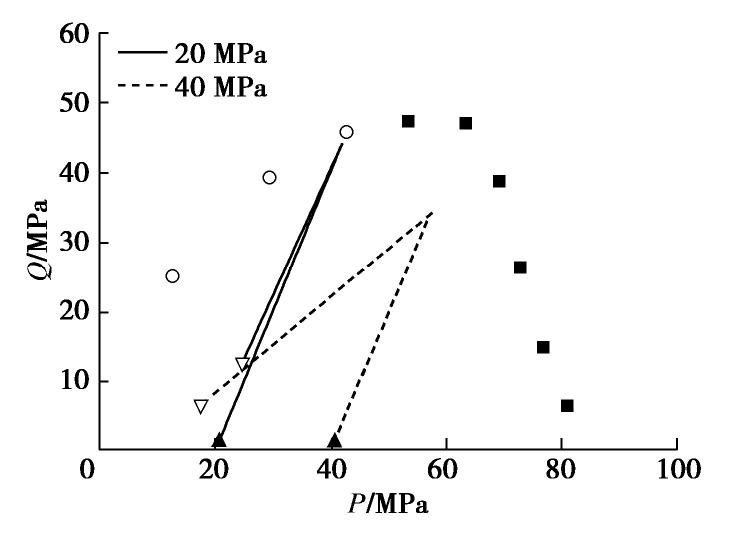
图9绘制了围压为20,40 MPa的两个（排水）双轴压缩试验中变形带内典型RVE（位置见图3）在P-Q空间中的应力路径（截取至破坏发生后,其中实心三角为起点,空心三角为终点）。如图所示,双轴压缩试样在初始状态时,Q接近于0,随着轴向加载增加,P,Q成比例增加至发生破坏,随后P,Q开始降低。通过DEM程序对初始状态RVE开展双轴压缩试验所得的屈服应力如图中红色圆圈和方块所示,其中圆圈表示在多尺度双轴压缩试验中发育含剪切破坏,方块表示发育压缩破坏。基于有限的多尺度试验,发现破坏模式的转变发生在围压20～30 MPa。观察RVE的屈服应力可以发现,屈服状态的Q随围压增加呈先增加后降低的趋势；而P则呈现出单调增加的趋势,即随围压增加,破坏模式由含剪切破坏向压缩破坏的转变可以通过P值的增加来解释。

图  9  双轴压缩试验中代表性RVE的应力路径

Figure  9.  Stress paths for typical RVEs in biaxial compression tests

下载: 全尺寸图片 幻灯片

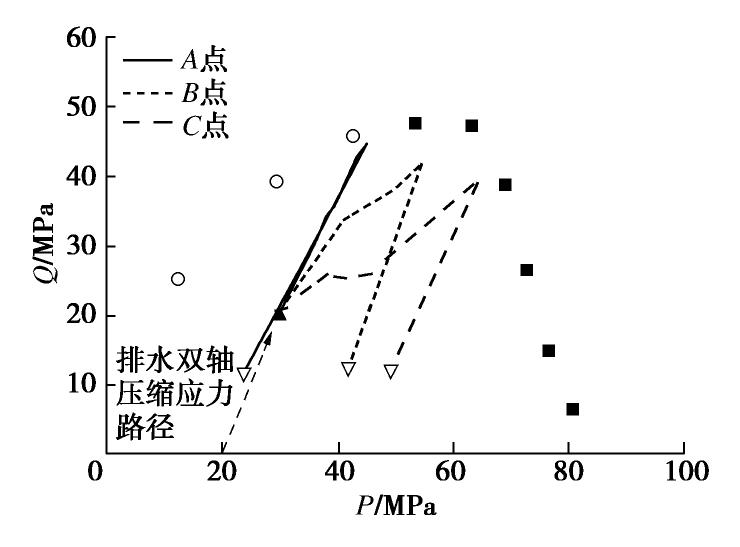
图10绘制了钻孔问题中3个典型RVE（位置见图5）的应力路径。其中A点的应力路径与（排水）双轴压缩试验的应力路径类似,P,Q成比例增加至发生破坏；B,C点的应力路径则随位置远离孔壁而逐渐向右偏移,其主要原因是钻孔导致的应力集中与破坏区尖端应力集中的共同作用。Wu等^[24]对钻孔周围的应力集中进行了计算,指出破坏发生前Q应力集中随与孔壁距离增加的衰减较P更快；通过对压缩带尖端应力集中的分析,指出破坏发生后P的应力集中区域呈哑铃状而Q的应力集中区域呈蝴蝶状。此例中共轭剪切带引起的应力集中与压缩带类似,即应力集中会导致在共轭剪切带尖端形成更大的P,引起应力路径向右偏移,致使C点发生破坏前的P已经超过60 MPa,控制了破坏模式从剪切破坏向压缩破坏的演化。

图  10  钻孔问题中代表性RVE的应力路径

Figure  10.  Stress paths for typical RVEs in borehole stability problem

下载: 全尺寸图片 幻灯片

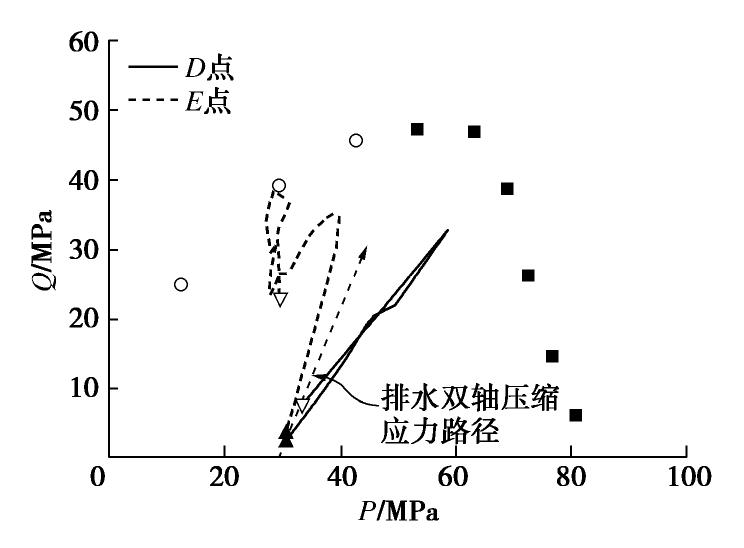
图11绘制了水岩耦合问题中压缩带与含剪切变形带内典型RVE（位置见图8）的应力路径。值得注意的是,在不排水双轴压缩试验中,孔隙水压力随着轴向加载逐渐升高,导致有效围压逐渐降低,在阶段I结束时,孔压已接近10 MPa,即有效围压接近20 MPa。按照图9中对排水试样的分析,破坏模式应为含剪切变形带,但在该饱和不排水算例中却首先表现出了压缩带破坏模式。根据典型RVE应力路径分析可知,在靠近粗糙边界处,横向约束引起的P的升高超过了孔隙水压力引起的P的降低,二者的综合作用导致了D点的破坏前应力路径相较排水双轴压缩应力路径向右偏移,即表现出更大的P,控制了粗糙边界处压缩带的形成。而在远离边界处的E点,则主要受孔隙水压力影响,相较排水双轴压缩应力路径向左偏移,即表现出较小的P,阻碍了压缩带的进一步发展,控制了破坏模式从压缩带向含剪切变形带的演化。

图  11  水岩耦合问题中代表性RVE的应力路径

Figure  11.  Stress paths for typical RVEs in hydro-mechanical problem

下载: 全尺寸图片 幻灯片

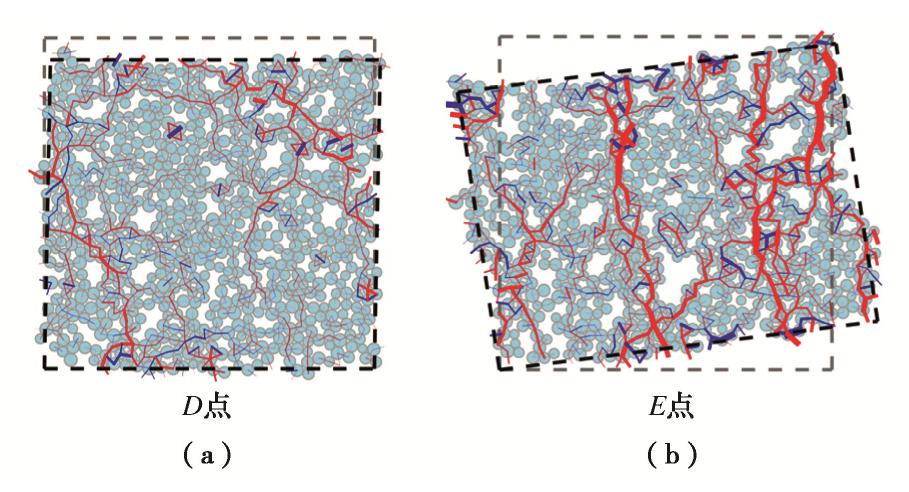
为直观的展示压缩带与含剪切变形带在微观变形特征上的差异,图12绘制了水岩耦合问题中D,E点在最终状态ε₁=2.0%时的RVE结构。可以看出D点与E点的RVE结构存在显著不同：D点以纵向压缩为主,符合压缩带的变形特征；E点则表现出了一定程度的旋转与剪切,主要由变形带内的剪切变形所导致。

图  12  水岩耦合问题中代表性RVE的最终状态

Figure  12.  Final states of typical RVEs in hydro-mechanical problem

下载: 全尺寸图片 幻灯片

6.   结论

本文采用FEM×DEM多尺度研究方法,对高孔隙率砂岩在（排水）双轴压缩问题、钻孔稳定性问题、水岩耦合问题等岩土工程代表性边值问题进行研究,重点对同一材料在不同边值问题中破坏模式的演化进行了对比分析,指出在不同边值问题中,RVE的应力路径可能受多方面因素影响,相较典型的双轴压缩应力路径产生偏移,控制了破坏模式的演化。

（1）高孔隙率砂岩在不同加载条件下可以产生包括压缩带、含剪切变形带等在内的不同破坏模式,两者呈现出截然不同的几何特征,压缩带与最大主应力呈近90°夹角,而含剪切变形带与最大主应力的夹角则显著小于90°。

（2）在岩土工程边值问题中,受应力集中、边界条件约束、孔隙水压力变化等因素的影响,材料所经历的应力路径可能较典型轴向（双轴、三轴）压缩试验的应力路径产生向右或向左偏移的现象,即产生（有效）平均应力的增加或降低。

（3）有效平均应力增加可以导致破坏模式从含剪切变形带演化为压缩带,有效平均应力降低也可以导致破坏模式从压缩带演化为含剪切变形带。破坏模式随加载条件的演化是边值问题中复杂破坏模式形成的可能原因。