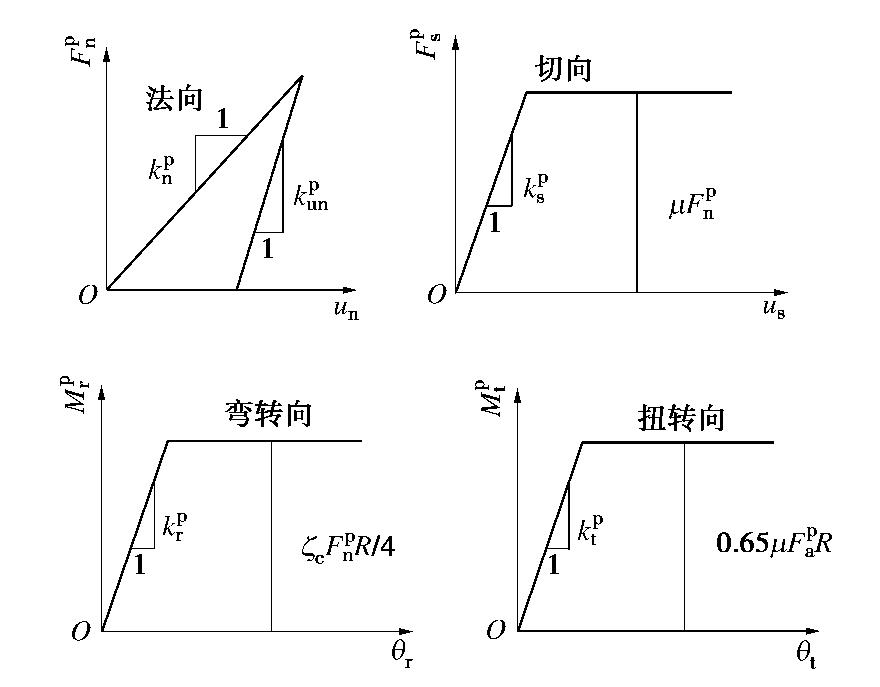
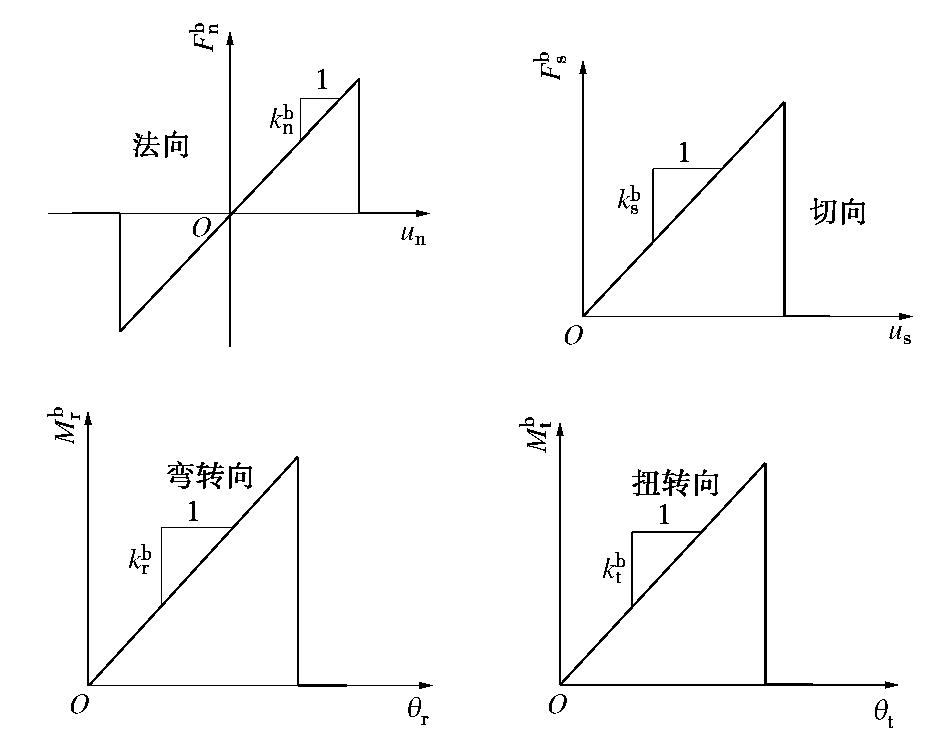
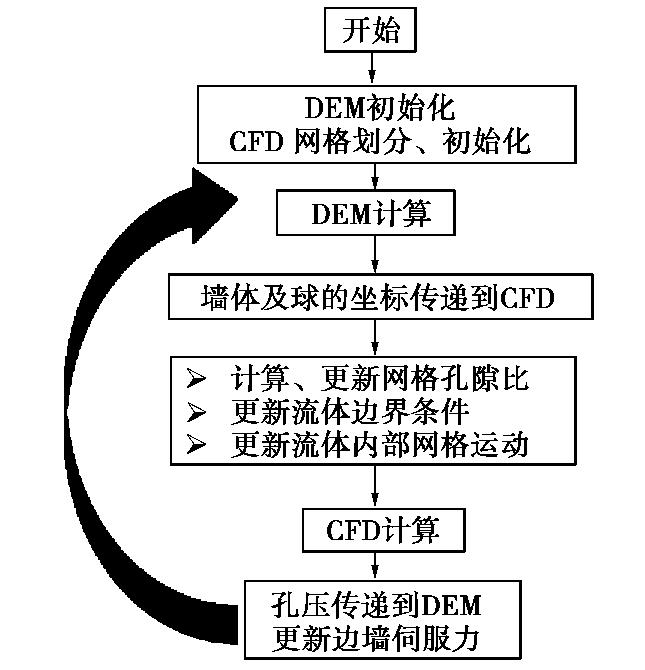
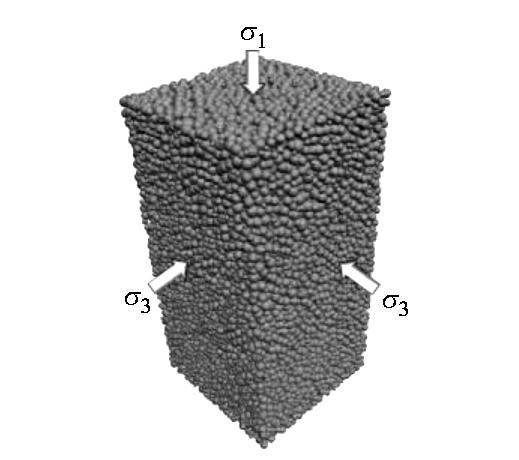
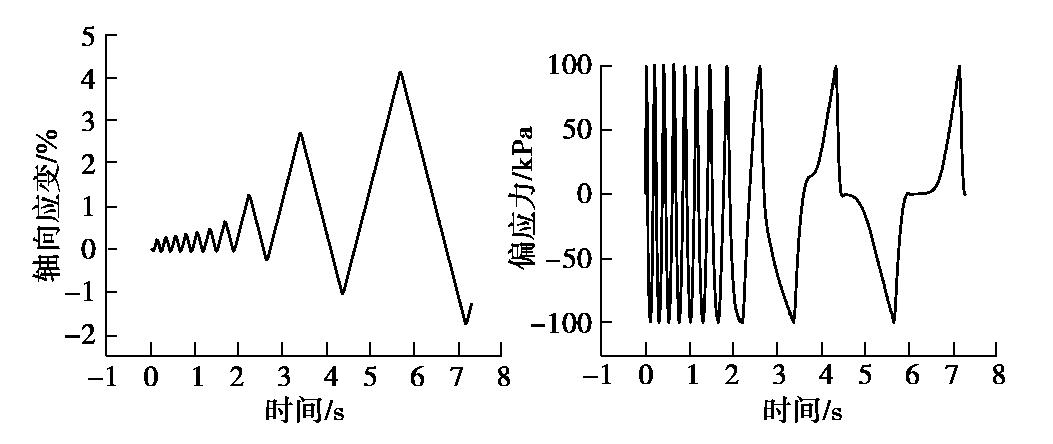
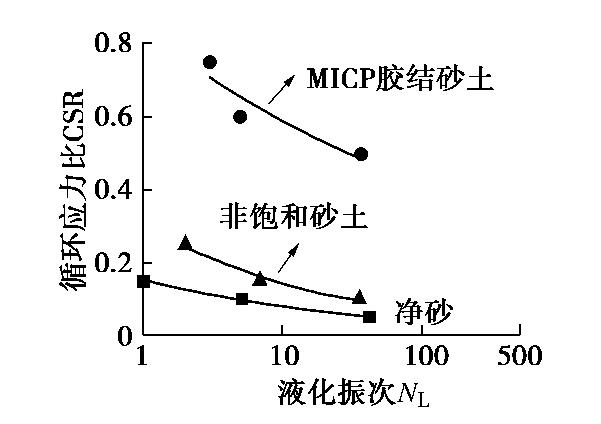
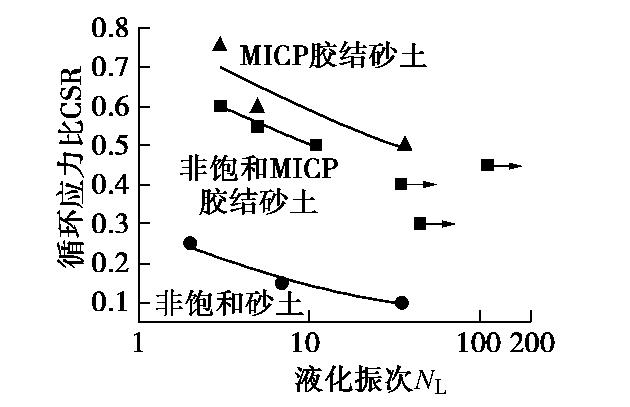
CFD-DEM simulation of microbially treated sands under undrained consolidated cyclic triaxial tests
-
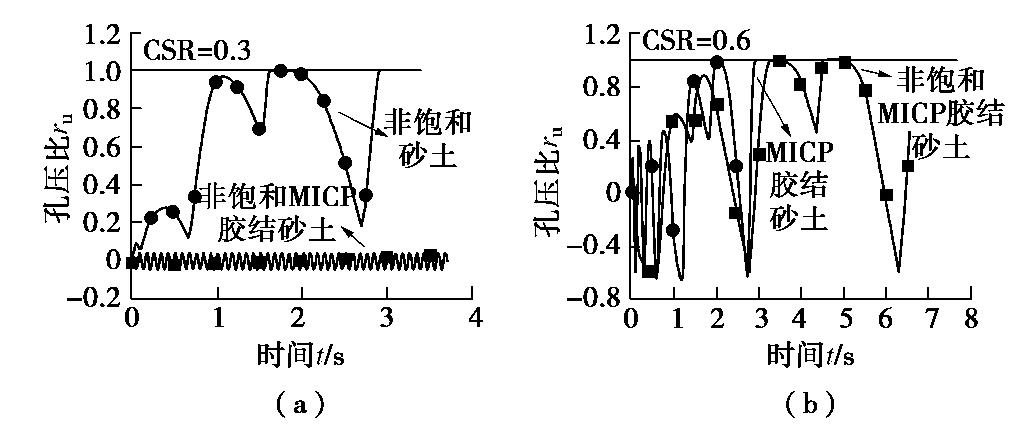
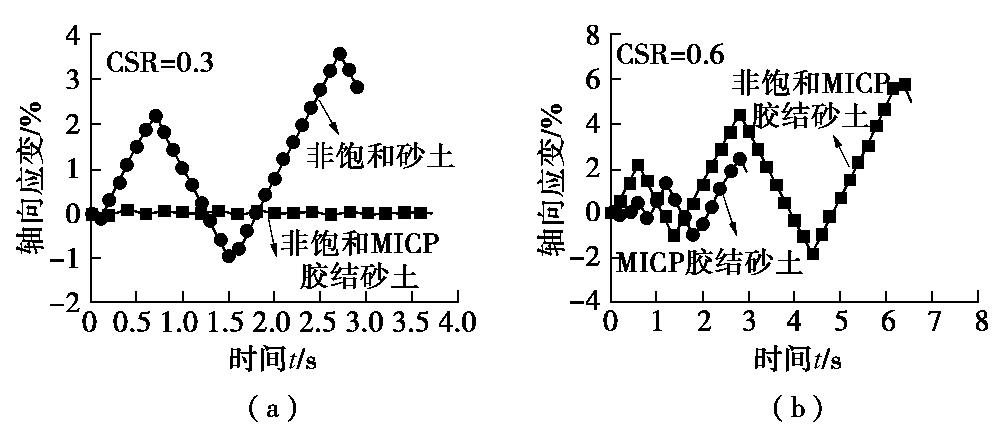
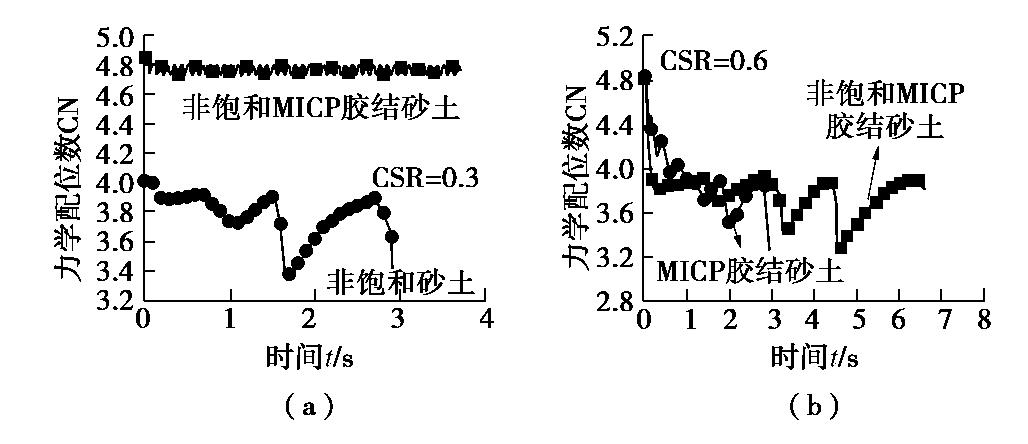
摘要: 微生物诱导碳酸钙沉积是一种新型的地基处理技术,处理后的土体可以看成一种结构性土。首先,在已有三维含颗粒抗转动和抗扭转模型及三维胶结破坏准则的基础上,通过考虑颗粒碰撞接触过程中颗粒本身的塑性变形及率相关性的接触黏滞阻尼,建立考虑循环荷载作用下的三维胶结模型;然后,参考已有研究,建立了反硝化反应在加固砂土中的时效性关系。并引入CFD-DEM耦合程序,用以模拟分析不同胶结含量以及不同气泡含量下,微生物处理砂土在固结不排水循环剪切试验中的力学特性;最后,从宏微观角度分析生物胶结与生物气泡对砂土抗液化性能的影响及其作用机理。研究表明,胶结和气泡共同存在对抗液化能力的提升并没有起到“1+1=2”的效果;胶结的存在提高了非饱和砂土的抗液化能力,明显抑制孔压比和轴向应变的发展,力学配位数得到了提升;而气泡的存在却降低了胶结砂土的抗液化能力,使得胶结砂土达到初始液化的振次减少,轴向应变向受拉方向大幅增长,力学配位数下降明显。
-
关键词:
- 微生物诱导碳酸钙沉积 /
- CFD-DEM耦合 /
- 不排水循环三轴剪切 /
- 地基液化 /
- 离散单元法
Abstract: The microbially induced calcite precipitation is a promising technology to improve ground, and the treated soil can be regarded as the structural one. In this study, firstly, based on the three-dimensional (3D) contact model for granulates incorporating rolling and twisting resistances and 3D bonds failure criteria, and considering both the slight plastic deformation of particles during collisions and the rate-dependency, a cyclic bonded contact model is established. A time-dependent relationship is then proposed to describe the denitrification reaction in reinforced sand. Next, the mechanical responses of microbially treated sands at different cementation and bubble contents are investigated by the coupled CFD-DEM in undrained-consolidated cyclic triaxial tests. The effects of biological bond and biological bubbles on the liquefaction resistance of sands are analyzed in link with the mechanism from macroscopic and microscopic scales. The results show that the coexistence of cementation and bubble does not increase the liquefaction resistance as expected in the form of "1+1=2". The presence of cementation enhances the liquefaction resistance of unsaturated sands evidenced by the decrease of excess pore water pressure ratio and axial strain, and the increase of coordination number. However, the presence of bubbles reduces the liquefaction resistance of cemented sands, where the number of cycles to the initial liquefaction decreases, the axial strain increases significantly in the tensile direction, and the coordination number decreases significantly. -
0. 引言
液化泛指土体在现场发生类似于液体性态的现象及其后果[1]。美国土木工程师协会岩土工程分会土动力学委员会对液化的定义是:“任何物质转化为液体的行为或过程”[2]。Seed等[3]从不排水循环剪切试验中试样的应力状态出发,提出了“初始液化”的概念:首次瞬态零有效应力状态或孔压比ru首次到达100%,其中,ru为超静孔隙水压力ue与初始有效平均主应力p′0之比。已有研究证实[1, 4],循环荷载下土体虽未达到初始液化状态,但由于孔压上升引起的土结构损伤和软化,具有液化流动的性态。因此,饱和砂土液化可视为孔压上升而引起的强度快速降低过程中与土性、应力状态密切相关的一种流动破坏。
为了澄清可液化的力学特性,一些研究者采用黏度或表观黏度η描述和量化液化土的流体特性。Towhata等[5]利用振动台和动三轴试验研究了液化后砂土的流动特性,液化后砂土具有典型的剪切稀化非牛顿流体性质。陈育民等[6]开展振动台拖球试验,结果表明:剪切稀化非牛顿流体模型能够再现液化土的应力-应变率关系。王志华等[7-8]将饱和砂土的液化行为定义为“超静孔压触变性”,提出了一种统一的触变流体模型。该模型构建了连接循环剪切前的土结构与液化触发及维持状态的渐进循环反应的有效桥梁,并建立了基于触变流体理论的可液化土的孔压增长及本构模型。Chen等[9]通过饱和砂土的振动台模型试验和液化后细砂的单调轴向压缩试验,研究了表观黏度η的演化过程与液化的触发条件,提出了剪应变率˙γ的概念及其算法,发现η与˙γ服从幂律函数关系,饱和砂土可视为幂律剪切稀化非牛顿流体。Lirer等[10]和Mele[11]认为η可作为液化触发标准的一个物理参数,依据Chen等[9]提出的研究思路,试验证实了η与˙γ之间的关系是表征非牛顿流体的幂律函数。η与ru具有强相关性,且随ru的增大而减小,当饱和砂土接近液化时ru → 1.0和η趋近一个很小的稳定值[9-11]。土单元中循环应力主轴方向角ασ会随地震波入射角度的变化而改变[12]。循环加载方向角对无粘性土的液化特性具有显著影响[13-14],已有研究大多是在简单应力条件下开展[5-11],模拟地震、波浪等复杂荷载作用下饱和砂土的液化流体特性未见报道。
珊瑚砂作为一种海洋生物成因的特殊岩土介质,主要分布于地震动水平较高的南北纬30°间的区域,其赋存条件特殊,具有棱角度高、强度低、易破碎、形状不规则等特征[13-14],导致其循环加载下的不排水反应特性与陆源石英砂存在显著差异[15-17]。珊瑚砂液化是珊瑚岛礁地震地质灾害的主要原因[14-17],许多学者试验研究了不同地区饱和珊瑚砂的液化机理与特性[15, 18-24],但所有这些试验均基于固体连续介质力学理论来描述珊瑚砂的不排水反应与液化特性。本文将可液化珊瑚砂视为流体,开展了不同循环加载频率、应力主轴90°跳转和连续旋转的均等固结不排水循环剪切试验,首次探究不同循环加载方式下饱和珊瑚砂的液化流动特性。
1. 试验方案
1.1 试验仪器
试验在英国GDS公司研制的空心圆柱扭剪仪(HCA)上完成。该仪器可对空心圆柱试样独立施加四向循环荷载(轴力W、扭矩MT、外围压po、内围压pi),空心圆柱试样受力与单元应力状态如图 1所示。通过HCA仪对土样同时施加自定义W,MT,po和pi波形来实现控制中主应力系数b为定值的复杂循环应力路径下的不排水循环剪切(UCS)试验,HCA仪的技术指标见参考文献[14]。
1.2 试验材料及试样制备
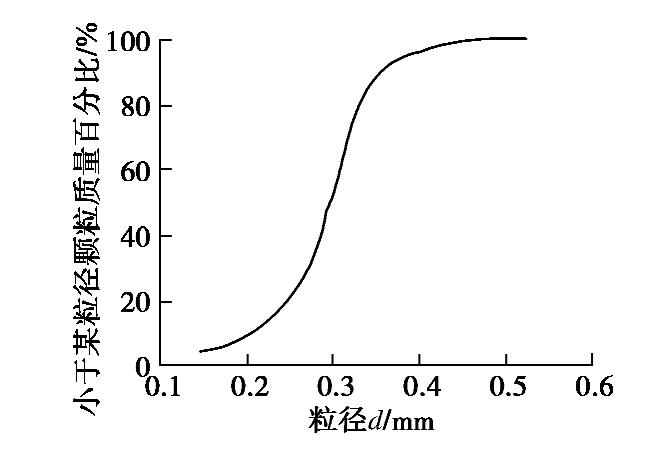
试验所用的珊瑚砂取自南沙群岛某岛礁,经测定,该珊瑚砂含有55.5%的文石,41.5%的高镁方解石和3.0%的方解石,其中CaCO3含量约为90.28%[14]。测得试验珊瑚砂的颗粒相对质量密度Gs为2.80;最大与最小孔隙比分别为emax = 1.72,emin = 0.99[25]。珊瑚砂的颗粒分布曲线如图 2所示,计算得到平均粒径d50 = 0.31,不均匀系数Cu = 4.67,曲率系数Cc = 0.86。
试验采用高H = 200 mm、外径do = 100 mm和内径di = 60 mm空心圆柱试样。采用干装法制样,控制初始相对密度Dr为45%。将烘干的珊瑚砂按级配对每层所需的颗粒称量后均匀混合,均分5层倒入制样模具中,各层之间进行刮毛处理,以保证试样的均匀性。为使试样达到饱和,先通入15 min的CO2以置换土体中的空气;再从试样底部通入无气水,直至无气泡排出;最后分级反压饱和,直至测得B ≥ 0.97。试样饱和后,进行p′0 = 100 kPa的均等固结,依据规范规定[25],关闭排水通道后5 min内孔隙水压力不再上升,即可认为固结完成,计算得到的固结后相对密度Drc列于表 2。
1.3 试验方案
对固结后试样施加频率f为0.1 Hz的正弦波循环偏应力进行UCS试验,循环应力路径如图 3所示。对循环应力主轴90°跳转试验,以ασ表示循环加载偏离垂直轴的初始方向,分别取ασ = 0°,22.5°,45°,67.5°,90°。对循环应力主轴连续旋转试验,以ασmax表示循环加载偏离垂直轴的最大方向,分别取ασmax = 22.5°,45°,67.5°,90°。对ασ = 22.5°和ασmax = 45°的UCS试验,开展了f = 1,0.5,0.05 Hz的对比试验。表 1给出了试验工况的详细信息。循环应力比CSR定义如下:
表 1 不排水循环剪切试验方案Table 1. Schemes of undrained cyclic shear testsNo. 循环应力路径 ασ/(°) Drc /% f/Hz CSR η0/(kPa⋅s) ηfluid/(kPa⋅s) ˙γL/s - 1 ˉκth/(s−1⋅kPa−1) 01 循环应力主轴90°跳转 0↔90 49.83 0.1 0.25 — — — — 02 50.42 0.1 0.30 26012 157 0.191 0.0041 03 50.22 0.1 0.35 14906 125 0.278 0.0043 04 22.5↔-67.5 50.32 0.1 0.25 6447 78 0.320 0.0070 05 49.73 0.1 0.30 5197 82 0.365 0.0075 06 49.91 1 0.35 3948 102 0.343 0.0076 07 49.59 0.5 0.35 4601 103 0.340 0.0082 08 50.10 0.1 0.35 3848 79 0.440 0.0078 09 49.52 0.05 0.35 4218 69 0.507 0.0083 10 45↔-45 49.84 0.1 0.25 4260 28 0.885 0.0128 11 49.62 0.1 0.30 3427 27 1.096 0.0132 12 50.08 0.1 0.35 2433 25 1.383 0.0136 13 67.5↔-22.5 50.17 0.1 0.25 6435 80 0.310 0.0072 14 50.19 0.1 0.30 5579 78 0.383 0.0074 15 50.07 0.1 0.35 4586 68 0.516 0.0075 16 90↔0 49.98 0.1 0.25 — — — — 17 49.82 0.1 0.30 23210 136 0.220 0.0042 18 50.00 0.1 0.35 19048 178 0.196 0.0043 19 循环应力主轴连续旋转 22.5↔-22.5 50.14 0.1 0.30 12123 951 0.032 0.0045 20 49.63 0.1 0.35 8324 905 0.039 0.0044 21 49.88 0.1 0.40 2906 912 0.044 0.0043 22 45↔45 49.94 0.1 0.20 5031 46 0.435 0.0116 23 49.62 0.1 0.25 4310 51 0.488 0.0120 24 49.32 1 0.30 3054 50 0.601 0.0128 25 49.10 0.5 0.30 2866 66 0.455 0.0116 26 49.72 0.1 0.30 3150 57 0.525 0.0124 27 49.26 0.05 0.30 2930 97 0.309 0.0114 28 67.5↔-67.5 49.82 0.1 0.20 8004 41 0.493 0.0118 29 49.59 0.1 0.25 7016 47 0.529 0.0128 30 51.61 0.1 0.30 5031 38 0.783 0.0132 31 90↔-90 50.14 0.1 0.20 — — — — 32 49.64 0.1 0.25 8946 131 0.191 0.0098 33 49.87 0.1 0.30 7861 117 0.255 0.0101 注:Drc为固结后相对密度;η0为初始表观黏度;ηfluid为流动表观黏度;˙γL为ru = 1.0时对应的最大偏应变率;ˉκth为相变平均流动系数;未液化试验工况未给出相应数据。 CSR=qa/p′0, (1) 式中,qa为循环偏应力幅值(kPa)。
2. 可液化珊瑚砂的流体特性
2.1 不排水循环反应
图 4,5分别为循环应力主轴90°跳转和连续旋转下代表性试样的不排水循环反应。由实测的循环应力路径可知,GDS空心圆柱扭剪仪可以精准实现设定循环应力路径的加载。对于均等固结UCS试验,不同循环加载路径下超静孔隙水压力ue均可达到初始有效平均主应力p′0 (p′0=100 kPa)。由图 4(c)和(d)可知,对于循环应力主轴90°跳转的UCS试验,ασ = 22.5°和67.5°的应力路径的相位差为90°。由图 5(c)和(d)可知,对于循环应力主轴连续旋转的UCS试验,瞬态的循环主应力方向角α为周期变化的正弦曲线。循环应力主轴转动下饱和珊瑚砂各应变分量随N的发展差异显著[14],可在以(εz−εθ)/2和γzθ轴表示的偏应变平面中的循环应变路径描述循环加载过程中各应变分量的演化过程[24]。ασ = 22.5°和67.5°时试样的循环应变路径都向(εz−εθ)/2轴的正方向移动,但两者在γzθ轴的移动方向则反向(图 4(e)),这与其扭剪应力方向有关。ασmax = 45°和90°时试样的循环应变路径分别向(εz−εθ)/2轴的正、负方向移动,且均绕γzθ=0轴线对称振荡(图 5(e))。由于均等固结条件下中主应变ε2(ε2=εr)无明显发展,本文采用偏应变γq表征试样的整体变形发展特征[23]:
γq=(ε1−ε3)/2=√(εz−εθ)2/4+γ2zθ。 (2) 式中:ε1,ε3分别为大、小主应变;εz为轴向应变;εθ为环向应变;γzθ为扭剪应变。
不同循环应力路径下γq随循环次数N的发展都呈现出先慢后快的趋势(图 4(f)和5(f))。Chen等[9]以剪应变率˙γ定量表示应变发展的速率:
˙γi=12(γi+1−γiti+1−ti+γi−γi−1ti−ti−1), (3) 式中,˙γi+1,˙γi,˙γi−1分别为剪应变γ在ti+1,ti,ti-1时刻的值(s-1)。本文以˙γq量化试样的整体变形速率。
由图 4(g)和5(g)可知,对不同循环加载路径的UCS试验,˙γq随N的增长速率差异很大。循环荷载作用下ue不断累积,应力-应变率滞回曲线呈现出不同的阶段性特征,从类似“椭圆形”向着类似“哑铃形”渐变(图 4(h),4(i),5(h),5(i))。
2.2 表观黏度与孔压比的相关性
定量表征可液化土流体特性的表观黏度η可定义为[9]
η=τ/˙γ, (4) 式中,τ为剪应力(kPa)。本文分别采用偏应力q和偏应变率˙γq代替式(4)的剪应力τ和剪应变率˙γ。
图 6给出了不同循环加载路径下试样的η随N的变化。可以发现:循环加载路径、循环应力水平对η-N衰减曲线的演化过程具有显著影响。η随N的演化过程表征了饱和砂土从固态、过渡态到液态的过程。循环加载初始阶段,超静孔压水平很低,饱和砂土呈固态特征,η衰减很小;随着N的增大,ue逐渐增大,饱和砂土的强度和刚度逐渐呈现出较明显的降低,砂土也从固态渐进到过渡态,η呈渐进衰退特征;随着N的继续增大,饱和砂土的ue急剧上升而临近液化,其强度和刚度几近完全损失,在对数坐标下η呈“断崖式”下降为很小值。同时,CSR越大,η-N曲线衰减越快。对循环应力主轴90°跳转的UCS试验,ασ = 45°时η-N曲线衰减最快;ασ = 0°或90°且CSR = 0.25时η-N曲线几乎无衰减(未液化),在对数坐标下η-N曲线近似为直线。对循环应力主轴连续旋转的UCS试验,CSR相同时,η的衰减随ασmax的增大呈现出先增后减的现象;ασmax = 90°和CSR = 0.20时η-N曲线几乎无衰减,饱和珊瑚砂的性态不会发生从固态到液态的演化过程,也即不会发生液化现象,对于不同的循环加载路径,存在门槛值,当CSR小于门槛值时,饱和珊瑚砂在循环荷载下不会液化,且此门槛值与循环加载应力路径密切相关。
依据以结构概念为基础的流体触变性理论[8, 26],流体内部结构可视为网状分布,循环剪切作用下网状结构的破坏和重构会引起表观黏度的变化。据此本文将可液化珊瑚砂视为“孔压触变性流体”,将其描述为:一种处于初始平衡状态的“假想流体”,即ru = 0时的η为初始表观黏度η0;随着循环剪切作用的不断施加,其内部结构逐渐发生破坏,最终达到极限平衡状态,即ru = 1.0时的η为流动表观黏度ηfluid。图 7展示了典型循环应力路径下η、ru与N的关系。可以发现,η的衰减与ru的累积有很好的对应关系,当ru → 1.0时饱和珊瑚砂液化触发,η趋近很小的稳定值ηfluid。饱和砂土的均等固结UCS试验表明[8]:剪应变率˙γ与1-ru服从双曲线关系。对于复杂循环加载条件的均等固结UCS试验,本文以最大偏应变率˙γqmax取代˙γmax,˙γqmax与1-ru也满足式的双曲线关系(图 8):
˙γqmax=1A+B(1−ru), (5) 式中,A=ηfluid/qa,B=(η0−ηfluid)/qa。通过试验数据计算的η0和ηfluid值,见表 1。
图 9给出了不同循环加载方式下规准化表观黏度η/η0与ru的关系。对应力主轴90°跳转的UCS试验,发现循环应力路径ασ和90°-ασ的η/η0-ru关系是一致的;对给定的循环应力路径,f,CSR对η/η0-ru关系的影响均不敏感。不同循环加载方式下η/η0-ru关系可用统一的形式表示:
ηη0=a⋅{12[1−cos(π ⋅(1−ru))]}c+d, (6) 式中,a,c,d为最佳拟合参数。
2.3 平均流动系数与孔压比的相关性
为了表征循环荷载下饱和砂土的固-液相变特征,引入平均流动系数ˉκ作为量化指数[7, 27]:
ˉκ=(˙γmax−˙γmin)⋅(˙γmax−˙γmin)A, (7) A=∬dˉτd˙γ。 (8) 式中:A为一周循环荷载作用下τ -˙γ曲线围成的面积(kPa·s-1);ˉτ为一周循环荷载作用的平均剪应力(kPa);˙γmax,˙γmin分别为一周循环加载中˙γ的最大、最小值(s-1)。本文分别采用q-˙γq曲线代替τ-˙γ曲线。
从ˉκ的定义可知,ˉκ越大,则该周循环荷载下单位平均偏应力引起的最大偏应变率越大,饱和珊瑚砂的流动性越强。图 10为不同循环加载路径下饱和珊瑚砂的ˉκ-ru关系。可以看出,随着ru的增大,ˉκ-ru关系的演化经历了3个阶段:初始阶段ru累积较慢,ˉκ几近无增长且其值很小,饱和珊瑚砂不具有流动性,呈固态特征;而在ru > 0.90阶段,随着ru的增大,ˉκ急剧增大,饱和珊瑚砂呈现出强流动性,呈液态特征;而在ru = 0.6~0.9的中间阶段,随着ru的增大,ˉκ的增速逐渐加快,饱和珊瑚砂的流动性逐渐增大,处于固态向液态转化的过渡阶段。这一特征与文献[7,27]中饱和石英砂和砂-砾混合料的ˉκ-ru关系的基本特征是类似的。从图 10也可以看出,对给定的循环应力路径,f,CSR对ˉκ-ru关系的影响均不敏感。不同循环加载方式下饱和珊瑚砂的ˉκ-ru关系可用统一的指数函数形式表示:
ˉκ=mexp(nrpu), (9) 式中,m,n,p为最佳拟合参数。
2.4 饱和珊瑚砂的固-液相变特征
图 11给出了不同循环加载方式下饱和珊瑚砂的表观黏度梯度∆η/η、平均流动系数梯度Δˉκ/ˉκ与超静孔压比ru的关系,其中,∆η/η = |ηi–ηi+1|/ηi,Δˉκ/ˉκ= |ˉκi−ˉκi + 1|/ˉκi。以表观黏度梯度及平均流动系数梯度分别表征饱和砂土在循环荷载作用下表观黏度衰减(η-N)及流动曲线(ˉκ-N)的变化情况。对所有试验工况,∆η/η和Δˉκ/ˉκ均随ru的增大呈现先增后减的特征,其反转点位于ru≈0.9处,饱和珊瑚砂试样自循环加载开始至完全液化的演化过程中,历经超静孔隙水压力逐步累积,珊瑚砂颗粒间的接触逐步减弱,直至液化触发时珊瑚砂颗粒间接触完全脱离,导致珊瑚砂宏观结构发生破坏。表观黏度梯度和平均流动系数梯度从逐步增大和突变急降,意味着饱和珊瑚砂颗粒间的接触发生了从量变到质变的过程,经历了从固态到固-液过渡态、再到液态的转变。定义突变时的ru为饱和珊瑚砂由固-液过渡状态向液态转变的相变孔压比ruth,则ruth ≈ 0.9。已有的研究表明:饱和南京砂的ruth ≈ 0.8[7];砂-砾混合料的ruth ≈ 0.95[23]。这表明:ruth的取值与试验材料相关。定义与ruth对应的ˉκ为相变平均流动系数ˉκth。表 1列出本次试验所有工况的ˉκth值。
图 12展示了不同循环加载路径下饱和珊瑚砂的ˉκth值。ˉκth的差异主要与循环加载过程中试样的最大剪切作用面与其薄弱面的关系及薄弱面上的剪应力大小有关[28]。对应力主轴90°跳转的UCS试验,ασ = 45°时试样受扭剪应力作用,最易液化[14],故其液化流动性最强,ˉκth值最大;ασ = 0°和90°时,引起试样的超静孔压累积和应变增长的荷载主要为轴向循环荷载,其液化抗力基本相同,最不易液化[14],故其液化流动性最差,ˉκth值最小。对应力主轴连续旋转的UCS试验,ˉκth随ασmax呈现出先增后减的趋势,ασmax = 45°~67.5°时最大,ασmax = 22.5°时试样所受荷载主要为轴向压缩,最不易液化[14],故液化流动性最差。
图 13给出了本文所有试验的规准化平均流动系数ˉκ/ˉκth与ru的关系。可以发现,ˉκ/ˉκth-ru的数据点落在一条较窄的范围内,ˉκ/ˉκth随ru增长的最佳拟合关系服从指数函数关系:
ˉκˉκth=0.0785exp(3.64r3.95u)。 (10) 3. 结论
本文通过不同循环加载频率、应力主轴90°跳转和连续旋转的均等固结不排水循环剪切(UCS)试验,探究了不同循环加载方式下饱和珊瑚砂的液化流动特性,得到以下3点结论。
(1) 循环应力比CSR、循环加载路径对饱和珊瑚砂的表观黏度η随循环次数N的发展影响显著,以初始表观黏度η0规准的表观黏度比η/η0与超静孔压比ru的关系对CSR和频率f不敏感。
(2) 对应力主轴90°跳转的UCS试验,循环加载方向角ασ = 45°时饱和珊瑚砂的平均流动系数ˉκ随N增长的速率最快,ασ = 22.5°和67.5°时次之,ασ = 0°和90°时最慢。对应力主轴连续旋转的UCS试验,ˉκ随N增长的速率随最大加载方向角ασmax的增加呈现先增后减的趋势。
(3) 不同循环加载方式下表观黏度梯度和平均流动系数梯度均随ru的增大呈现出先增大后减小的特征,其反转点的ru ≈ 0.9,可视为饱和珊瑚砂由固-液过渡状态向液态转变的相变孔压比ruth,相应的ˉκ为相变平均流动系数ˉκth,CSR与f对ˉκth的影响不敏感,循环加载路径对ˉκth的影响显著。所有试验的ˉκ/ˉκth-ru数据点处于窄带内,且ˉκ/ˉκth随ru增长的最佳拟合曲线服从指数函数关系。
-
表 1 胶结颗粒模型微观参数
Table 1 Microscopic parameters of model for bond grains
组成 参数名称 数值 颗粒部分 颗粒模量Ep/Pa 3×108 颗粒法向与切向刚度比 ξ 1.5 颗粒摩擦系数 μ 0.5 颗粒抗转动系数 β 0.2 颗粒局部破损系数 ξc 2.1 颗粒法向接触加卸载刚度比 en 0.95 胶结部分 胶结半径比例系数 η (0.5)* 胶结模量Eb/Pa 2×108 胶结泊松比 νb 0.2 胶结抗拉强度 σt /Pa1.6×106 胶结抗压强度 σc /Pa8×107 黏滞阻尼 法向临界阻尼比 βn 0.6 切向临界阻尼比 βs 0.6 注: 胶结半径比例系数η 在标定过程中取0.5,在此后的模拟中为控制胶结含量的研究变量。表 2 数值模拟试样微生物处理过程时效性
Table 2 Time-dependent characteristics of microbial processing of numerical simulation samples
反应时间/d 微生物处理生成胶结 微生物处理生成气泡 胶结体积/mm3 胶结半径比例系数η 气泡体积/mm3 饱和度Sr/% 孔隙流体压缩系数C 0 0 0 0 100 4.5×10-7 2 0.718 0.231 2.46 98.3 3.87×10-5 表 3 微生物处理砂土循环三轴数值模拟工况与结果列表
Table 3 Simulation program and main results of cyclic triaxial compression tests on different microbial treatment time on sand
试样编号 模拟工况 模拟结果 土体种类 微生物处理时间/d 胶结半径比例系数η 孔隙流体压缩系数C 循环应力比CSR 破坏振次NL 破坏模式 L0 净砂 0 0 0.15 1 I.L. MU2-1 非饱和MICP胶结砂土 2 0.273 3.87×10-5 0.30 45+ — MU2-6 非饱和MICP胶结砂土 2 0.273 3.87×10-5 0.60 3 I.L. MP2-2 MICP胶结砂土 2 0.273 0.60 5 I.L. US2-4 非饱和砂土 2 3.87×10-5 0.30 2 I.L. -
[1] 沈珠江. 理论土力学[M]. 北京: 中国水利水电出版社, 2000. SHEN Zhu-jiang. Theoretical Soil Mechanics[M]. Beijing: China Water and Power Press, 2000. (in Chinese)
[2] GAO Y F, HANG L, HE J, et al. Mechanical behaviour of biocemented sands at various treatment levels and relative densities[J]. Acta Geotechnica, 2019, 14(3): 697-707. doi: 10.1007/s11440-018-0729-3
[3] WANG Y, SOGA K, DEJONG J T, et al. A microfluidic chip and its use in characterising the particle-scale behaviour of microbial-induced calcium carbonate precipitation (MICP)[J]. Géotechnique, 2019, 69(12): 1-9.
[4] INAGAKI Y, TSUKAMOTO M, MORI H, et al. A centrifugal model test of microbial carbonate precipitation as liquefaction countermeasure[J]. Japanese Geotechnical Journal, 2011, 6(2): 157-167. doi: 10.3208/jgs.6.157
[5] HAN Z G, CHENG X H, MA Q. An experimental study on dynamic response for MICP strengthening liquefiable sands[J]. Earthquake Engineering and Engineering Vibration, 2016, 15(4): 673-679. doi: 10.1007/s11803-016-0357-6
[6] 刘汉龙, 肖鹏, 肖扬, 等. MICP胶结钙质砂动力特性试验研究[J]. 岩土工程学报, 2018, 40(1): 38-45. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201801003.htm LIU Han-long, XIAO Peng, XIAO Yang, et al. Dynamic behaviors of MICP-treated calcareous sand in cyclic tests[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(1): 38-45. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201801003.htm
[7] REBATA-LANDA V, SANTAMARINA J C. Mechanical effects of biogenic nitrogen gas bubbles in soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(2): 128-137. doi: 10.1061/(ASCE)GT.1943-5606.0000571
[8] HE J. Mitigation of liquefaction of sand using microbial methods[D]. Singapore: Nanyang Technological University, 2013.
[9] CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 1979, 29(1): 47-65. doi: 10.1680/geot.1979.29.1.47
[10] KHOUBANI A, EVANS T M, MONTOYA B M. Particulate simulations of triaxial tests on bio-cemented sand using a new cementation model[C]//Proceedings of GeoChicago: Sustainability, Energy, and the Geoenvironment. Chicago, 2016: 1-10.
[11] FENG K, MONTOYA B M, EVANS T M. Discrete element method simulations of bio-cemented sands[J]. Computers and Geotechnics, 2017, 85: 139-150. doi: 10.1016/j.compgeo.2016.12.028
[12] ANDERSON J D, WENDT J. Computational Fluid Dynamics[M]. New York: McGraw-Hill, 1995.
[13] CHANG C Y, SCHMIDT J, DÖRENKÄMPER M, et al. A consistent steady state CFD simulation method for stratified atmospheric boundary layer flows[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 172: 55-67. doi: 10.1016/j.jweia.2017.10.003
[14] PAREKH J, RZEHAK R. Euler-Euler multiphase CFD-simulation with full Reynolds stress model and anisotropic bubble-induced turbulence[J]. International Journal of Multiphase Flow, 2018, 99: 231-245. doi: 10.1016/j.ijmultiphaseflow.2017.10.012
[15] EL SHAMY U, ZEGHAL M. A micro-mechanical investigation of the dynamic response and liquefaction of saturated granular soils[J]. Soil Dynamics and Earthquake Engineering, 2007, 27(8): 712-729. doi: 10.1016/j.soildyn.2006.12.010
[16] 蒋明镜, 张望城. 一种考虑流体状态方程的土体CFD-DEM耦合数值方法[J]. 岩土工程学报, 2014, 36(5): 793-801. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201405002.htm JIANG Ming-jing, ZHANG Wang-cheng. Coupled CFD-DEM method for soils incorporating equation of state for liquid[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(5): 793-801. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201405002.htm
[17] 蒋明镜. 现代土力学研究的新视野—宏微观土力学[J]. 岩土工程学报, 2019, 41(2): 195-254. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902002.htm JIANG Ming-jing. New paradigm for modern soil mechanics: Geomechanics from micro to macro[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(2): 195-254. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902002.htm
[18] JIANG M J, SHEN Z F, WANG J F. A novel three- dimensional contact model for granulates incorporating rolling and twisting resistances[J]. Computers and Geotechnics, 2015, 65: 147-163. doi: 10.1016/j.compgeo.2014.12.011
[19] 金树楼. 结构性砂土三维微观接触力学试验及离散元数值模拟[D]. 上海: 同济大学, 2016. JIN Shu-lou. Three Dimensional Experimental and Numerical Study on Micro- and Macro-mechanical Behaviors of Structural Sands[D]. Shanghai: Tongji University, 2016. (in Chinese)
[20] THORNTON C, CUMMINS S J, CLEARY P W. An investigation of the comparative behavior of alternative contact force models during inelastic collisions[J]. Powder Technology, 2013, 233(3): 30-46.
[21] SHEN Z F, JIANG M J, THORNTON C. DEM simulation of bonded granular material: Part I contact model and application to cemented sand[J]. Computers & Geotechnics 2016, 75: 192-209.
[22] 谭亚飞鸥. 考虑循环荷载的三维微观胶结模型及微生物处理砂土循环三轴CFD-DEM耦合模拟[D]. 上海: 上海理工大学, 2018. TAN Ya-fei-ou. A Novel Three-dimensional Bonded Contact Model Incorporating the Effect of Cyclic Loads and CFD-DEM Simulation of Microbially Treated Sands Under Undrained Consolidated Cyclic Triaxial Tests[D]. Shanghai: University of Shanghai for Science and Technology, 2018. (in Chinese)
[23] ZHANG A, JIANG M J. Numerical simulation of undrained triaxial tests for granular soil using a coupled CFD-DEM method with moving mesh[J]. Acta Geotechnica, 2019. (to be submitted)
[24] ZHAO T. Investigation of Landslide-induced Debris Flows by the DEM and CFD[D]. Oxford: University of Oxford, 2014.
[25] VAN PAASSEN L A, DAZA C M, STAAL M, et al. Potential soil reinforcement by biological denitrification[J]. Ecological Engineering, 2010, 36(2): 168-175.
[26] AL QABANY A, SOGA K, SANTAMARINA C, et al. Factors affecting efficiency of microbially induced calcite precipitation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(8): 992-1001.
[27] SCHUURMAN I E. The compressibility of an air/water mixture and a theoretical relation between the air and water pressures[J]. Géotechnique, 1966, 16(4): 269-281.
[28] 刘侃, 朱小军, 张帆舸, 等. 含气泡土的孔隙流体压缩系数计算分析[J]. 岩土工程学报, 2017, 39(增刊2): 120-123. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2017S2031.htm LIU Kan, ZHU Xiao-jun, ZHANG Fan-ge, et al. Calculation of coefficient of compressibility for air-water mixture in gassy soils[J]. Chinese Journal of Geotechnical Engineering,2017, 39(S2): 120-123. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2017S2031.htm
[29] DORSEY N E. Properties of Ordinary Water-Substance[M]. New York: Reinhold Publishing Corporation, 1940.
[30] FENG K, MONTOYA B M. Influence of confinement and cementation level on the behavior of microbial-induced calcite precipitated sands under monotonic drained loading[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2016, 142(1): 04015057.
[31] JIANG M J, KONRAD J M, LEROUEIL S. An efficient technique for generating homogeneous specimens for DEM studies[J]. Computers and Geotechnics, 2003, 30(5): 579-597.
[32] KUHN M R, RENKEN H E, MIXSELL A D, et al. Investigation of cyclic liquefaction with discrete element simulations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140(12): 04014075.
-
期刊类型引用(4)
1. 秦悠,杜歆宇,马维嘉,吴琪,陈国兴. 不同初始剪应力下饱和珊瑚砂的液化特性. 哈尔滨工程大学学报. 2025(02): 197-204+209 .  百度学术
百度学术
2. 魏怡童,杨洋. 基于剪切波速的地震液化概率性评估方法综述. 世界地震工程. 2025(02): 160-172 .  百度学术
百度学术
3. Chen Guoxing,Qin You,Ma Weijia,Liang Ke,Wu Qi,C.Hsein Juang. Liquefaction susceptibility and deformation characteristics of saturated coral sandy soils subjected to cyclic loadings——a critical review. Earthquake Engineering and Engineering Vibration. 2024(01): 261-296 .  必应学术
必应学术
4. 周正龙,华凌霄,徐令宇,赵凯,吴琪,陈国兴. 初始剪应力作用下饱和粉土液化流动特性试验研究. 岩土力学. 2024(11): 3295-3303 .  百度学术
百度学术
其他类型引用(2)




 下载:
下载: